Dynamics of Functionally Graded Laminated (FGL) Media—Theoretical Tolerance Modelling
Abstract
1. Introduction
2. Modelling Preliminaries
3. Modelling Technique
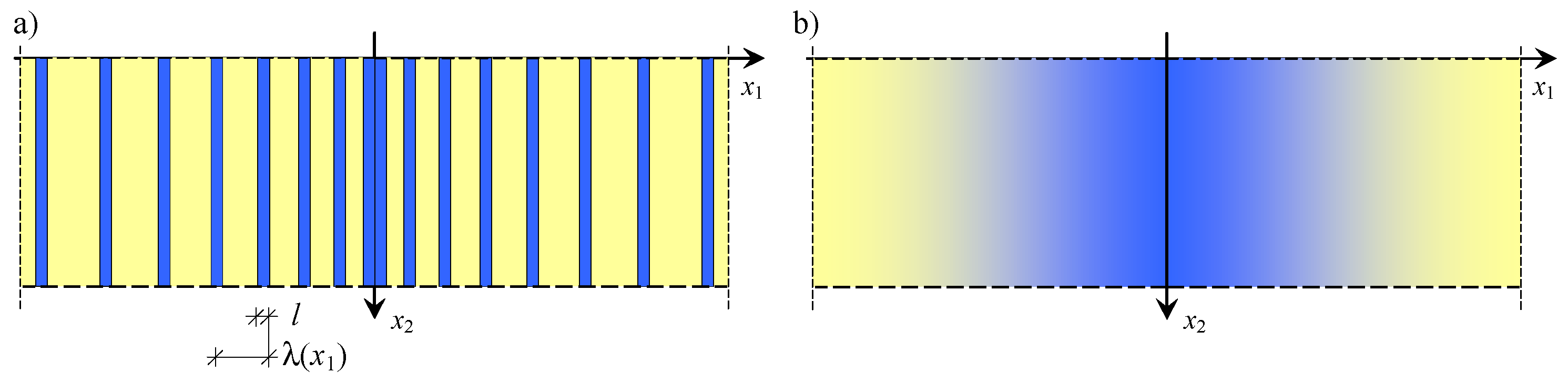
3.1. Basic Concepts
3.2. Modelling Assumptions
3.3. Modelling Procedure
4. Model Equations
4.1. Tolerance Model Equations
4.2. Asymptotic Model Equations
5. An Example: Vibrations of a Special Laminated Layer
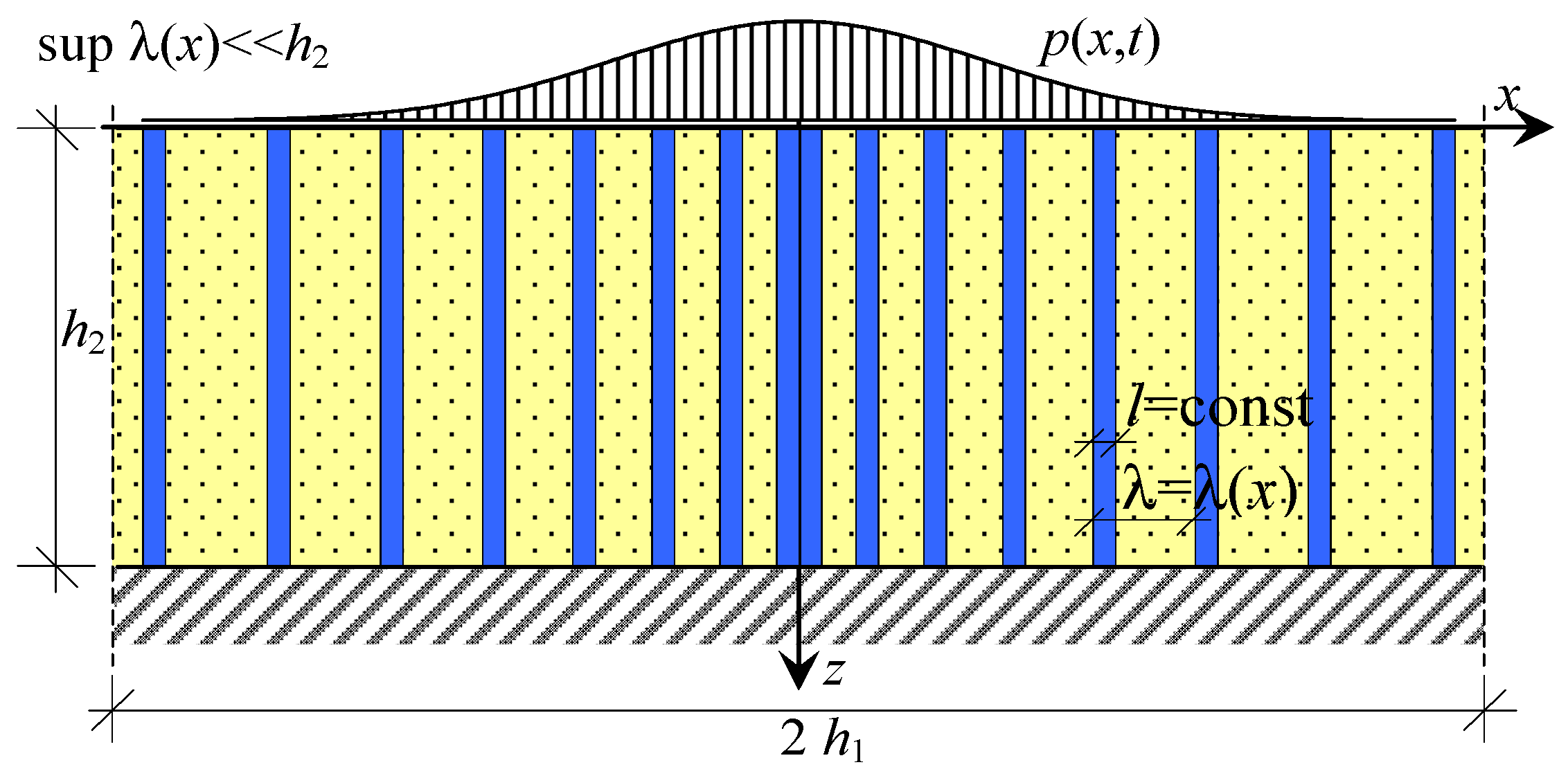
5.1. Preliminaries
5.2. Vibrations Equations
- The tolerance model
- The asymptotic model
5.3. Solutions of Special Problem of Vibrations
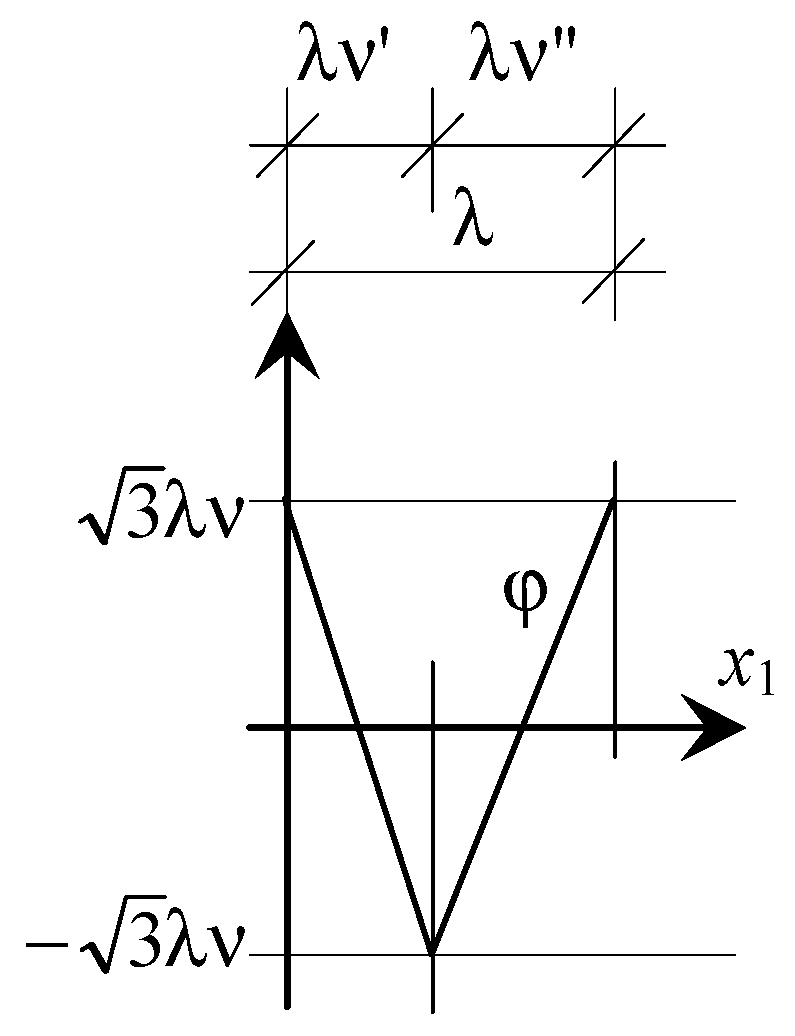
5.3.1. Introductory Assumptions and Denotations
5.3.2. Equations of Vibrations
- the macro-vibrations equation
- the micro-vibrations equation
- the non-dimensional macro-vibrations equation
- the non-dimensional micro-vibrations equation
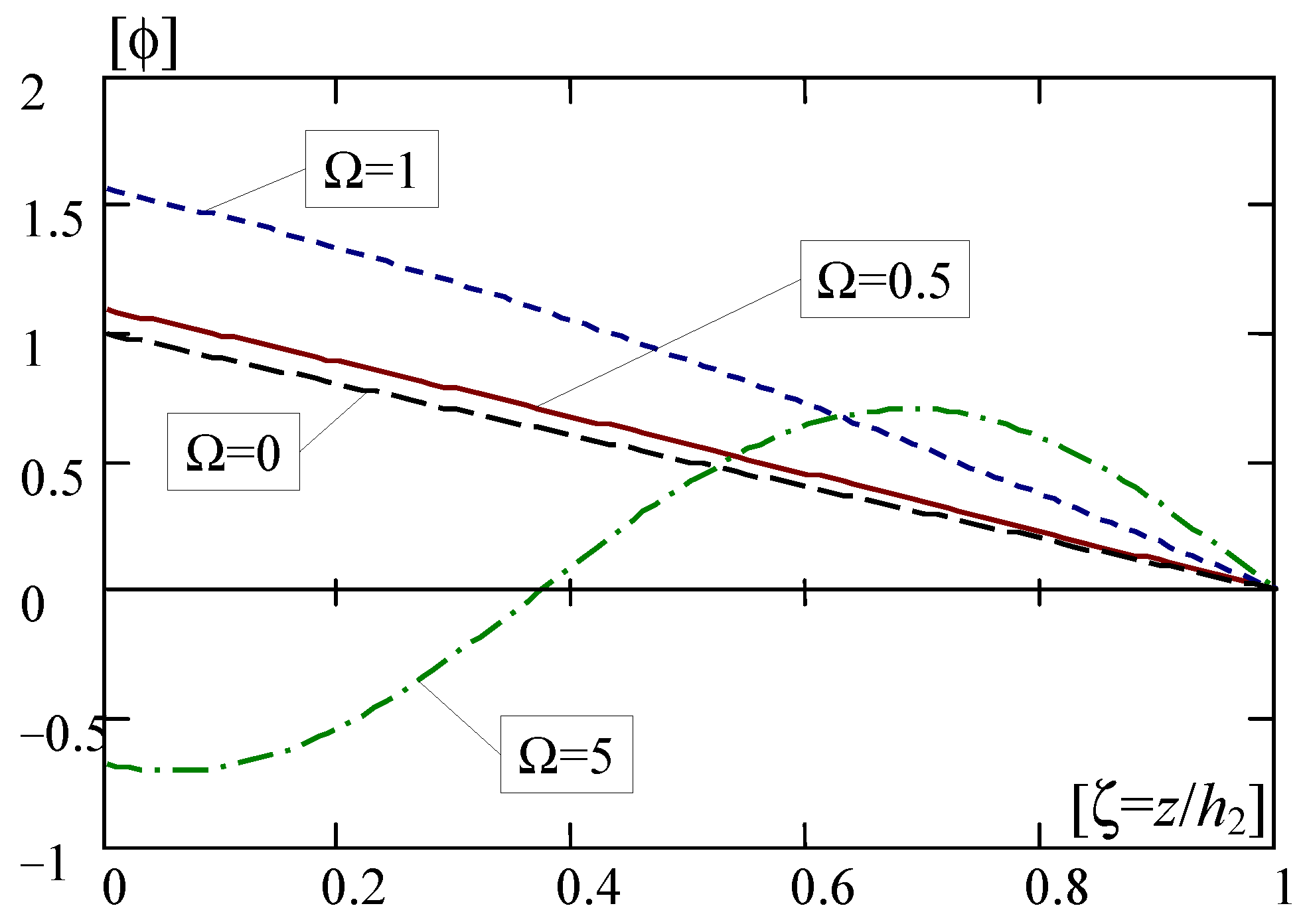
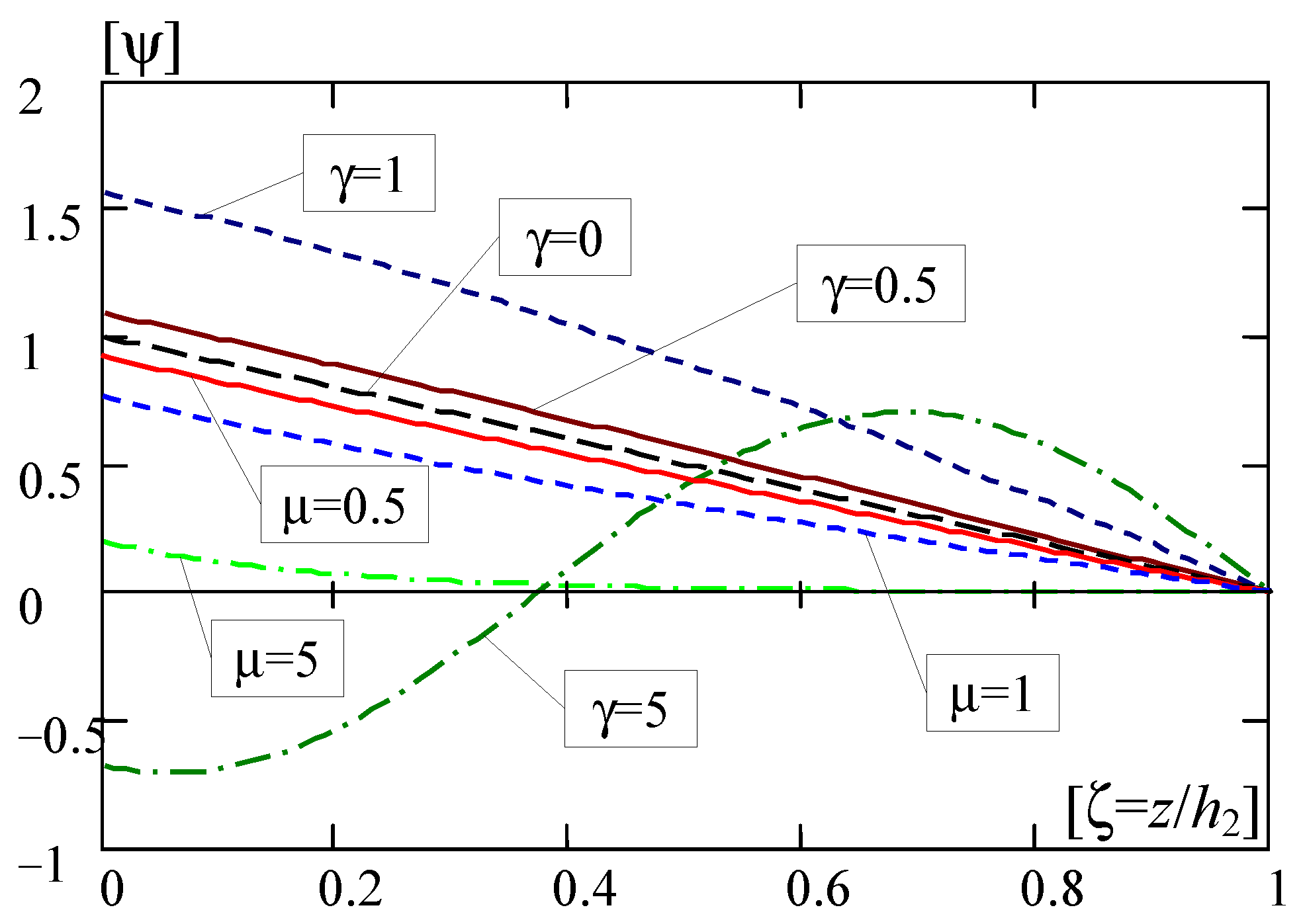
5.3.3. Non-Dimensional Solutions of Vibrations
6. Remarks
- It has been shown that only the tolerance model makes it possible to investigate the effect of the micro-oscillations of the boundary loading, and also the effect of macro-oscillations.
- The asymptotic model allows for the analysis of only the effects of the macro-oscillations of the loading.
- Introduced various additional assumptions and restrictions make it possible to obtain the analytical formulas of solutions.
- It can be observed that the solutions of macro-vibrations can decay linearly, decay and oscillate, or they not exist.
- Solutions of micro-vibrations can decay exponentially, decay linearly, decay and oscillate, or they not exist.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Suresh, S.; Mortensen, A. Fundamentals of Functionally Graded Materials; The University Press: Cambridge, UK, 1998. [Google Scholar]
- Woźniak, C.; Michalak, B.; Jędrysiak, J. (Eds.) Thermomechanics of Microheterogeneous Solids and Structures: Tolerance Averaging Approach; Lodz University of Technology: Lodz, Poland, 2008. [Google Scholar]
- Reiter, T.; Dvorak, G.J.; Tvergaard, V. Micromechanical models for graded composite materials. J. Mech. Phys. Solids 1997, 45, 1281–1302. [Google Scholar] [CrossRef]
- Bensoussan, A.; Lions, J.-L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North-Holland: Amsterdam, Holland, 1978. [Google Scholar]
- Matysiak, S.J.; Nagórko, W. Microlocal parameters in the modelling of microperiodic plates. Ing. Arch. 1989, 59, 434–444. [Google Scholar] [CrossRef]
- Hajianmaleki, M.; Qatu, M.S. Vibrations of straight and curved composite beams: A review. Compos. Struct. 2013, 100, 218–232. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Fidalgo, D.S.; Ferreira, A.J.M.; Reddy, J.N. A study of a microstructure-dependent composite laminated Timoshenko beam using a modified couple stress theory and a meshless method. Compos. Struct. 2013, 96, 532–537. [Google Scholar] [CrossRef]
- Batra, R.C.; Xiao, J. Finite deformations of curved laminated St. Venant–Kirchhoff beam using layer-wise third order shear and normal deformable beam theory (TSNDT). Compos. Struct. 2013, 97, 147–164. [Google Scholar] [CrossRef]
- Magnucka-Blandzi, E. Non-linear analysis of dynamic stability of metal foam circular plate. J. Theor. Appl. Mech. 2010, 48, 207–217. [Google Scholar]
- Grygorowicz, M.; Magnucki, K.; Malinowski, M. Elastic buckling of a sandwich beam with variable mechanical properties of the core. Thin-Walled Struct. 2015, 87, 127–132. [Google Scholar] [CrossRef]
- Wittenbeck, L.; Grygorowicz, M.; Paczos, P. Numerical analysis of sandwich beam with corrugated core under three-point bending. AIP Conf. Proc. 2015, 1648, 800007-1–800007-3. [Google Scholar]
- Grygorowicz, M.; Lewiński, J. Bending of I-beam with the transvers shear effect included—FEM calculated. AIP Conf. Proc. 2016, 1738, 480041. [Google Scholar]
- Grygorowicz, M.; Magnucka-Blandzi, E. Mathematical modeling for dynamic stability of sandwich beam with variable mechanical properties of core. Appl. Math. Mech. 2016, 37, 361–374. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Fraska, A. Torsion of elliptical composite beams with auxetic phase. Phys. Status Solidi Basic Res. 2016, 253, 1359–1368. [Google Scholar] [CrossRef]
- Jopek, H.; Strek, T. Torsion of a two-phased composite bar with helical distribution of constituents. Phys. Status Solidi 2017, 254, 1700050. [Google Scholar] [CrossRef]
- Matuszewska, A.; Strek, T. Vibration properties of auxetic beam. Vib. Phys. Syst. 2018, 29, 2018031. [Google Scholar]
- Arruda, M.R.T.; Castro, L.M.S.; Ferreira, A.J.M.; Garrido, M.; Gonilha, J.; Correia, J.R. Analysis of composite layered beams using Carrera unified formulation with Legendre approximation. Compos. Part B-Eng. 2018, 137, 39–50. [Google Scholar] [CrossRef]
- Pawlus, D. Stability of Three-Layered Annular Plate with Composite Facings. Appl. Compos. Mat. 2017, 24, 141–158. [Google Scholar] [CrossRef]
- Marczak, J. Vibrations of sandwich plates—Comparison of chosen modelling approaches. Vib. Phys. Syst. 2018, 29, 2018036. [Google Scholar]
- Michalski, J.; Strek, T. Response of a Sandwich Plate with Auxetic Anti-tetrachiral Core to Puncture. In Lecture Notes in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–14. [Google Scholar]
- Aboudi, J.; Pindera, M.-J.; Arnold, S.M. Thermo-inelastic response of functionally graded composites. Int. J. Solid Struct. 1995, 32, 1675–1710. [Google Scholar] [CrossRef]
- Aboudi, J.; Pindera, M.-J.; Arnold, S.M. A coupled higher-order theory for functionally graded composites with partial homogenization. Compos. Eng. 1995, 5, 771–792. [Google Scholar] [CrossRef]
- Aboudi, J.; Pindera, M.-J.; Arnold, S.M. Higher-order theory for functionally graded materials. Compos. Part B 1999, 30, 777–832. [Google Scholar] [CrossRef]
- Pindera, M.-J.; Dunn, P. Evaluation of the higher-order theory for functionally graded materials via the finite-element method. Compos. Part B 1997, 28B, 109–119. [Google Scholar] [CrossRef]
- Goldberg, R.K.; Hopkins, D.A. Thermal analysis of a functionally graded material subject to a thermal gradient using the boundary element method. Compos. Eng. 1995, 5, 793–806. [Google Scholar] [CrossRef]
- Martínez-Pañeda, M. On the finite element implementation of functionally graded materials. Materials 2019, 12, 287. [Google Scholar] [CrossRef]
- Bui, T.Q.; Khosravifard, A.; Zhang, C.; Hematiyan, M.R.; Golu, M.V. Dynamic analysis of sandwich beams with functionally graded core using a truly meshfree radial point interpolation method. Eng. Struct. 2013, 47, 90–104. [Google Scholar] [CrossRef]
- Murin, J.; Aminbaghai, M.; Hrabovsky, J.; Kutiš, V.; Kugler, S. Modal analysis of the FGM beams with effect of the shear correction function. Compos. Part B 2013, 45, 1575–1582. [Google Scholar] [CrossRef]
- Carpentieri, G.; Tornabene, F.; Ascione, A.; Fraternali, F. An accurate one-dimensional theory for the dynamics of laminated composite curved beams. J. Sound Vib. 2015, 336, 96–105. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Martins, P.A.L.S.; Ferreira, A.J.M.; Jorge, R.M.N. Differential evolution for free vibration optimization of functionally graded nano beams. Compos. Struct. 2016, 156, 29–34. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.; Qiu, X.; Zhang, G. Bending and Wave Propagation Analysis of Magneto-Electro-Elastic Functionally Graded Porous Microbeams. Crystals 2022, 12, 732. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Wei, D.; Zhang, G. Bending and wave propagation analysis of axially functionally graded beams based on a reformulated strain gradient elasticity theory. Appl. Math. Mech. 2023, 44, 1803–1820. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Schnack, E. The stability of functionally graded cylindrical shells under linearly increasing dynamic torsional loading. Eng. Struct. 2004, 26, 1321–1331. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Batra, R.C.; Roque, C.M.C.; Qian, L.F.; Jorge, R.M.N. Natural frequencies of functionally graded plates by a meshless method. Compos. Struct. 2006, 75, 593–600. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Ferreira, A.J.M.; Jorge, R.M.N. A radial basis function approach for the free vibration analysis of functionally graded plates using a refined theory. J. Sound Vib. 2007, 300, 1048–1070. [Google Scholar] [CrossRef]
- Tornabene, F.; Liverani, A.; Caligiana, G. FGM and laminated doubly curved shells and panels of revolution with a free-form meridian: A 2-D GDQ solution for free vibrations. Int. J. Mech. Sci. 2011, 53, 443–470. [Google Scholar] [CrossRef]
- Akbarzadeha, A.H.; Abbasib, M.; Eslami, M.R. Coupled thermoelasticity of functionally graded plates based on the third-order shear deformation theory. Thin-Walled Struct. 2012, 53, 141–155. [Google Scholar] [CrossRef]
- Oktem, A.S.; Mantari, J.L.; Guedes Soares, C. Static response of functionally graded plates and doubly-curved shells based on a higher order shear deformation theory. Eur. J. Mech.-A/Sol. 2012, 36, 163–172. [Google Scholar] [CrossRef]
- Kugler, S.; Fotiu, P.A.; Murin, J. The numerical analysis of FGM shells with enhanced finite elements. Eng. Struct. 2013, 49, 920–935. [Google Scholar] [CrossRef]
- Jha, D.K.; Kant, T.; Singh, R.K. Free vibration response of functionally graded thick plates with shear and normal deformations effects. Compos. Struct. 2013, 96, 799–823. [Google Scholar] [CrossRef]
- Sheikholeslami, S.A.; Saidi, A.R. Vibration analysis of functionally graded rectangular plates resting on elastic foundation using higher-order shear and normal deformable plate theory. Compos. Struct. 2013, 106, 350–361. [Google Scholar] [CrossRef]
- Derras, M.; Kaci, A.; Draiche, K.; Tounsi, A. Non-linear analysis of functionally graded plates in cylindrical bending based on a new refined shear deformation theory. J. Theor. Appl. Mech. 2013, 51, 339–348. [Google Scholar]
- Huangfu, Y.-G.; Chen, F.-Q. Single-pulse chaotic dynamics of functionally graded materials plate. Acta Mech. Sinica 2013, 29, 593–601. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E. Static analysis of functionally graded doubly-curved shells and panels of revolution. Meccanica 2013, 48, 901–930. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Batra, R.C. Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos. Struct. 2015, 119, 67–89. [Google Scholar] [CrossRef]
- Tornebene, F.; Fantuzzi, N.; Bacciocchi, M. On the mechanics of laminated doubly-curved shells subjected to point and line loads. Int. J. Eng. Sci. 2016, 109, 115–164. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Viola, E.; Ferreira, A.J.M. A strong formulation finite element method (SFEM) based on RBF and GDQ techniques for the static and dynamic analyses of laminated plates of arbitrary shape. Meccanica 2014, 49, 2503–2542. [Google Scholar] [CrossRef]
- Kołakowski, Z.; Mania, R.J. Dynamic response of thin FG plates with a static unsymmetrical stable postbuckling path. Thin-Walled Struct. 2015, 86, 10–17. [Google Scholar] [CrossRef]
- Teter, A.; Mania, R.J.; Kołakowski, Z. Non-linear multi-mode buckling of non-symmetric FML/FGM thin-walled columns with open cross-sections under compression. Compos. Struct. 2017, 167, 38–49. [Google Scholar] [CrossRef]
- Kołakowski, Z.; Mania, R.J. Influence of the coupling matrix B on the interactive buckling of FML-FGM columns with closed cross-sections under axial compression. Compos. Struct. 2017, 173, 70–77. [Google Scholar] [CrossRef]
- Mania, R.J.; Madeo, A.; Zucco, G.; Kubiak, T. Imperfection sensitivity of post-buckling of FML channel section column. Thin-Walled Struct. 2017, 114, 32–38. [Google Scholar] [CrossRef]
- Ashoori, A.R.; Sadough Vanini, S.A. Thermal buckling of annular microstructure-dependent functionally graded material plates resting on an elastic medium. Compos. Part B Eng. 2016, 87, 245–255. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F. Strong Formulation Isogeometric Analysis (SFIGA) for laminated composite arbitrarily shaped plates. Compos. Part B Eng. 2016, 96, 173–203. [Google Scholar] [CrossRef]
- Liu, B.; Ferreira, A.J.M.; Xing, Y.F.; Neves, A.M.A. Analysis of composite plates using a layerwise theory and a differential quadrature finite element method. Compos. Struct. 2016, 156, 393–398. [Google Scholar] [CrossRef]
- Sadowski, T.; Burlayenko, V.N. Three-dimensional free vibration analysis of thermally loaded FGM sandwich plates. Materials 2019, 12, 2377. [Google Scholar] [CrossRef]
- Cao, Z.; Liang, X.; Deng, Y.; Zha, X.; Zhu, R.; Leng, J. Novel semi-analytical solutions for the transient behaviors of functionally graded material plates in the thermal environment. Materials 2019, 12, 4084. [Google Scholar] [CrossRef] [PubMed]
- Jafari, M.; Chaleshtari, M.H.B.; Abdolalian, H.; Craciun, E.-M.; Feo, L. Determination of forces and moments per unit length in symmetric exponential FG plates with a quasi-triangular hole. Symmetry 2020, 12, 834. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R. Natural frequency responses of hybrid polymer/carbon fiber/FG-GNP nanocomposites paraboloidal and hyperboloidal shells based on multiscale approaches. Aerosp. Sci. Tech. 2021, 119, 107111. [Google Scholar] [CrossRef]
- Sobhani, E.; Moradi-Dastjerdi, R.; Behdinan, K.; Masoodi, A.R.; Ahmadi-Pari, A.R. Multifunctional trace of various reinforcements on vibrations of three-phase nanocomposite combined hemispherical-cylindrical shells. Compos. Struct. 2022, 279, 114798. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures; Dover Publications Inc.: Dover, UK, 1953. [Google Scholar]
- Xiang, H.-J.; Shi, Z.-F. Analysis of flexural vibration band gaps in periodic beams using differential quadrature method. Comp. Struct. 2009, 87, 1559–1566. [Google Scholar] [CrossRef]
- Wu, Z.-J.; Li, F.-M.; Wang, Y.-Z. Vibration band gap properties of periodic Mindlin plate structure using the spectral element method. Meccanica 2014, 49, 725–737. [Google Scholar] [CrossRef]
- Robinson, C.W.; Leppelmeier, G.W. Experimental verification of dispersion relations for layered composites. J. Appl. Mech. 1974, 41, 89–91. [Google Scholar] [CrossRef]
- Woźniak, C.; Wierzbicki, E. Averaging Techniques in Thermomechanics of Composite Solids. Tolerance Averaging versus Homogenization; Częstochowa University of Technology: Częstochowa, Poland, 2000. [Google Scholar]
- Woźniak, C. (Ed.) Mathematical Modelling and Analysis in Continuum Mechanics of Microstructured Media; Silesian University of Technology: Gliwice, Poland, 2010. [Google Scholar]
- Dell’Isola, F.; Rosa, L.; Woźniak, C. A micro-structural continuum modelling compacting fluid-saturated grounds. Acta Mech. 1998, 127, 165–182. [Google Scholar] [CrossRef]
- Jędrysiak, J. Dynamics of thin periodic plates resting on a periodically inhomogeneous Winkler foundation. Arch. Appl. Mech. 1999, 69, 345–356. [Google Scholar] [CrossRef]
- Wierzbicki, E.; Woźniak, C. On the dynamics of combined plane periodic structures. Arch. Appl. Mech. 2000, 70, 387–398. [Google Scholar] [CrossRef]
- Michalak, B. The meso-shape functions for the meso-structural models of wavy-plates. ZAMM 2001, 81, 639–641. [Google Scholar] [CrossRef]
- Nagórko, W.; Woźniak, C. Nonasymptotic modelling of thin plates reinforced by a system of stiffeners. Electr. J. Polish Agric. Univ.-Civil Eng. 2002, 5, 8. [Google Scholar]
- Baron, E. On dynamic behaviour of medium-thickness plates with uniperiodic structure. Arch. Appl. Mech. 2003, 73, 505–516. [Google Scholar] [CrossRef]
- Jędrysiak, J. The length-scale effect in the buckling of thin periodic plates resting on a periodic Winkler foundation. Meccanica 2003, 38, 435–451. [Google Scholar] [CrossRef]
- Mazur-Śniady, K.; Woźniak, C.; Wierzbicki, E. On the modelling of dynamic problems for plates with a periodic structure. Arch. Appl. Mech. 2004, 74, 179–190. [Google Scholar] [CrossRef]
- Tomczyk, B. A non-asymptotic model for the stability analysis of thin biperiodic cylindrical shells. Thin-Walled Struct. 2007, 45, 941–944. [Google Scholar] [CrossRef]
- Tomczyk, B. Dynamic stability of micro-periodic cylindrical shells. Mech. Mech. Eng. 2010, 14, 137–150. [Google Scholar]
- Tomczyk, B.; Gołąbczak, M. Tolerance and asymptotic modelling of dynamic thermoelasticity problems for thin micro-periodic cylindrical shells. Meccanica 2020, 55, 2391–2411. [Google Scholar] [CrossRef]
- Tomczyk, B.; Bagdasaryan, V.; Gołąbczak, M.; Litawska, A. Stability of thin micro-periodic cylindrical shells; extended tolerance modeling. Compos. Struct. 2020, 253, 112743. [Google Scholar] [CrossRef]
- Tomczyk, B.; Bagdasaryan, V.; Gołąbczak, M.; Litawska, A. On the modelling of stability problems for thin cylindrical shells with two-directional micro-periodic structure. Compos. Struct. 2021, 275, 114495. [Google Scholar] [CrossRef]
- Tomczyk, B.; Gołąbczak, M.; Litawska, A.; Gołąbczak, A. Mathematical modelling of thermoelasticity problems for thin biperiodic cylindrical shells. Cont. Mech. Thermodyn. 2022, 34, 367–385. [Google Scholar] [CrossRef]
- Domagalski, Ł.; Jędrysiak, J. On the elastostatics of thin periodic plates with large deflections. Meccanica 2012, 47, 1659–1671. [Google Scholar] [CrossRef]
- Domagalski, Ł.; Jędrysiak, J. Nonlinear vibrations of periodic beams. J. Theor. Appl. Mech. 2016, 54, 1095–1108. [Google Scholar] [CrossRef]
- Domagalski, Ł.; Świątek, M.; Jędrysiak, J. An analytical-numerical approach to vibration analysis of periodic Timoshenko beams. Compos. Struct. 2019, 211, 490–501. [Google Scholar] [CrossRef]
- Domagalski, Ł. Comparison of the natural vibration frequencies of timoshenko and bernoulli periodic beams. Materials 2021, 14, 7628. [Google Scholar] [CrossRef]
- Marczak, J.; Jędrysiak, J. Some remarks on modelling of vibrations of periodic sandwich structures with inert core. Compos. Struct. 2018, 202, 752–758. [Google Scholar] [CrossRef]
- Jędrysiak, J. Modelling of Vibrations and Stability for Periodic Slender Visco-Elastic Beams on a Foundation with Damping. Revisiting. Materials 2020, 13, 3939. [Google Scholar] [CrossRef]
- Marczak, J.; Michalak, B.; Wirowski, A. A multi-scale analysis of stress distribution in thin composite plates with dense system of ribs in two directions. Adv. Enging. Soft. 2021, 153, 102960. [Google Scholar] [CrossRef]
- Pazera, E. Heat Transfer in Periodically Laminated Structures-Third Type Boundary Conditions. Int. J. Comput. Methods 2021, 18, 2041011. [Google Scholar] [CrossRef]
- Ostrowski, P.; Jędrysiak, J. Dependence of temperature fluctuations on randomized material properties in two-component periodic laminate. Compos. Struct. 2021, 2571, 113171. [Google Scholar] [CrossRef]
- Jędrysiak, J.; Wierzbicki, E.; Woźniak, C. The elastic response for microlayered functionally graded media. PAMM 2006, 6, 385–386. [Google Scholar] [CrossRef]
- Rychlewska, J.; Woźniak, C.; Woźniak, M. Modelling of Functionally Graded Laminates Revisited. Electr. J. Polish Agric. Univ. 2006, 9, 6. Available online: www.ejpau.media.pl (accessed on 11 October 2023).
- Szymczyk, J.; Woźniak, C. Continuum modelling of laminates with a slowly graded microstructure. Arch. Mech. 2006, 58, 445–458. [Google Scholar]
- Michalak, B.; Wirowski, A. Dynamic modelling of thin plate made of certain functionally graded materials. Meccanica 2012, 47, 1487–1498. [Google Scholar] [CrossRef][Green Version]
- Wirowski, A. On some problems of choice of the shape function in the tolerance averaging technique in modeling free vibrations of the composite plate resting on elastic foundation. In Shell Structures: Theory and Applications, Proceedings of the 10th SSTA 2013 Conference, Gdańsk, Poland, 16–18 October 2013; CRC Press: Boca Raton, FL, USA, 2014; Volume 3, pp. 465–468. [Google Scholar]
- Perliński, W.; Gajdzicki, M.; Michalak, B. Modelling of annular plates stability with functionally graded structure interacting with elastic heterogeneous subsoil. J. Theor. Appl. Mech. 2014, 52, 485–498. [Google Scholar]
- Wirowski, A.; Michalak, B.; Gajdzicki, M. Dynamic modelling of annular plates of functionally graded structure resting on elastic heterogeneous foundation with two modules. J. Mech. 2015, 31, 493–504. [Google Scholar] [CrossRef]
- Kaźmierczak, M.; Jędrysiak, J. A new combined asymptotic-tolerance model of vibrations of thin transversally graded plates. Eng. Struct. 2013, 46, 322–331. [Google Scholar] [CrossRef]
- Michalak, B. 2D tolerance and asymptotic models in elastodynamics of a thin-walled structure with dense system of ribs. Arch. Civil Mech. Eng. 2015, 15, 449–455. [Google Scholar] [CrossRef]
- Rabenda, M.; Michalak, B. Natural vibrations of prestressed thin functionally graded plates with dense system of ribs in two directions. Compos. Struct. 2015, 133, 1016–1023. [Google Scholar] [CrossRef]
- Ostrowski, P.; Michalak, B. The combined asymptotic-tolerance model of heat conduction in a skeletal micro-heterogeneous hollow cylinder. Compos. Struct. 2015, 134, 343–352. [Google Scholar] [CrossRef]
- Ostrowski, P.; Michalak, B. A contribution to the modelling of heat conduction for cylindrical composite conductors with non-uniform distribution of constituents. Int. J. Heat Mass Transfer 2016, 92, 435–448. [Google Scholar] [CrossRef]
- Jędrysiak, J. Tolerance modelling of free vibrations of medium thickness functionally graded plates. Compos. Struct. 2018, 202, 1253–1262. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. Tolerance and asymptotic modelling of dynamic problems for thin microstructured transversally graded shells. Compos. Struct. 2017, 162, 365–373. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. Combined asymptotic-tolerance modelling of dynamic problems for functionally graded shells. Compos. Struct. 2018, 183, 176–184. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. A new asymptotic-tolerance model of dynamic and stability problems for longitudinally graded cylindrical shells. Compos. Struct. 2018, 202, 473–481. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jędrysiak, J. Dynamics of Functionally Graded Laminated (FGL) Media—Theoretical Tolerance Modelling. Materials 2023, 16, 7162. https://doi.org/10.3390/ma16227162
Jędrysiak J. Dynamics of Functionally Graded Laminated (FGL) Media—Theoretical Tolerance Modelling. Materials. 2023; 16(22):7162. https://doi.org/10.3390/ma16227162
Chicago/Turabian StyleJędrysiak, Jarosław. 2023. "Dynamics of Functionally Graded Laminated (FGL) Media—Theoretical Tolerance Modelling" Materials 16, no. 22: 7162. https://doi.org/10.3390/ma16227162
APA StyleJędrysiak, J. (2023). Dynamics of Functionally Graded Laminated (FGL) Media—Theoretical Tolerance Modelling. Materials, 16(22), 7162. https://doi.org/10.3390/ma16227162




