The Influence Mechanism of Interfacial Characteristics between CSH and Montmorillonite on the Strength Properties of Cement-Stabilized Montmorillonite Soil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Materials
2.2. Experimental Methods
2.2.1. Molecular Simulation Method
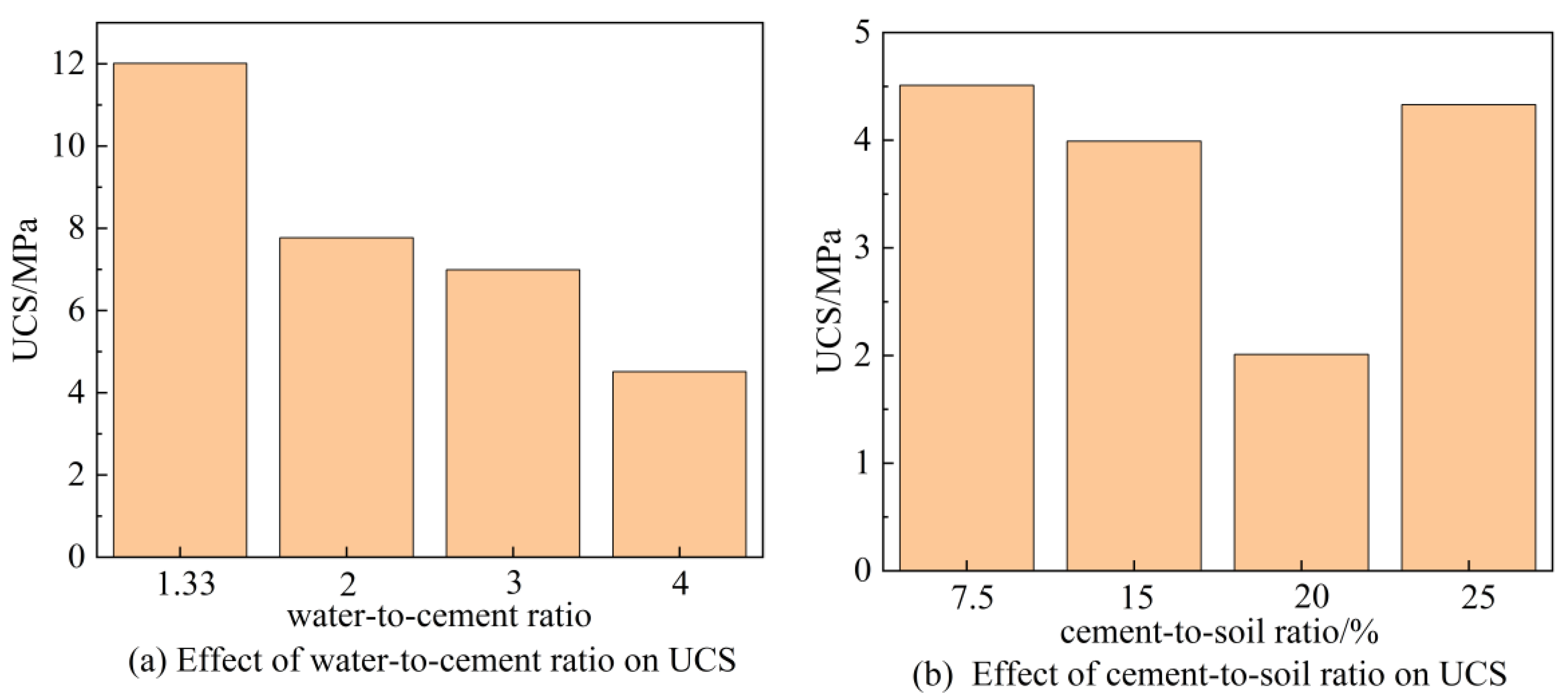
2.2.2. UCS Testing and Sample Preparation
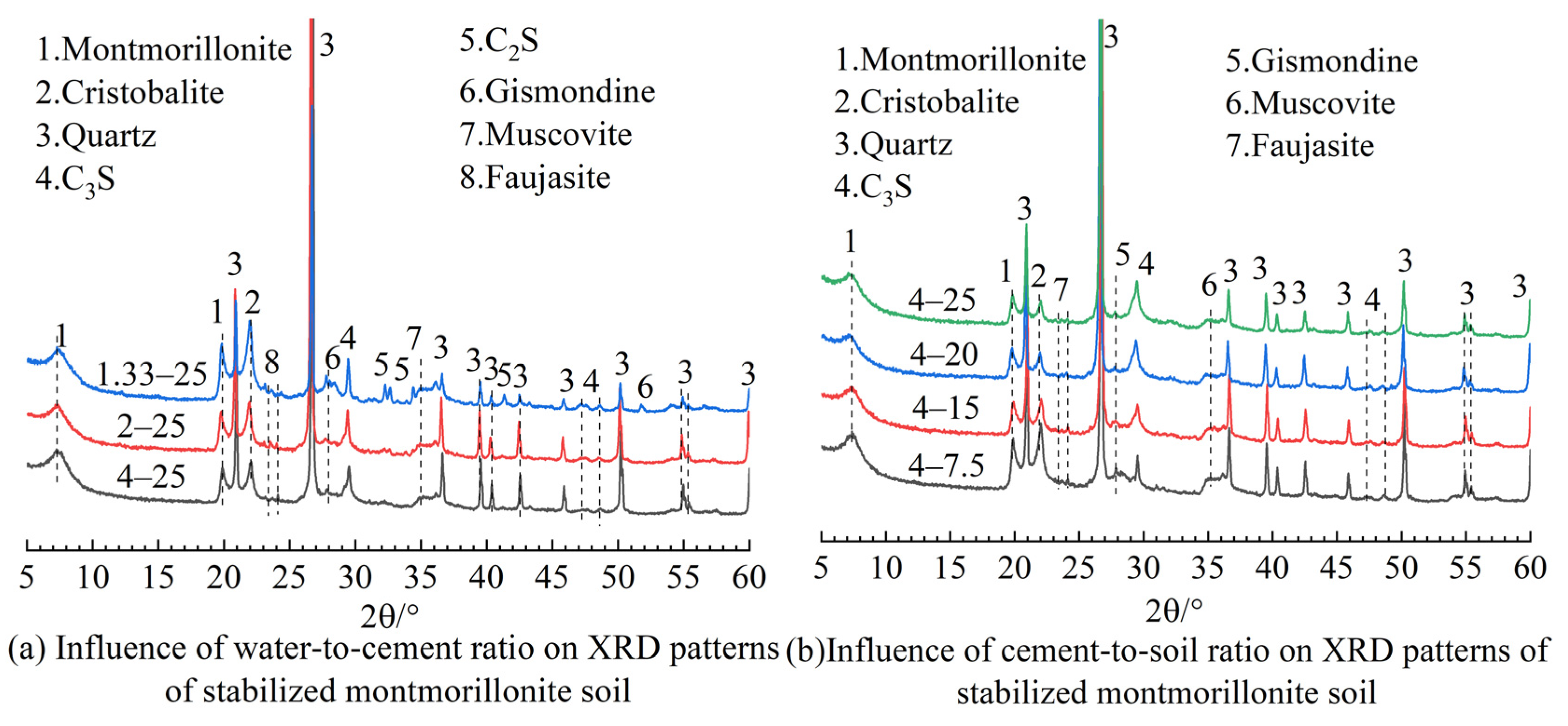
2.2.3. XRD
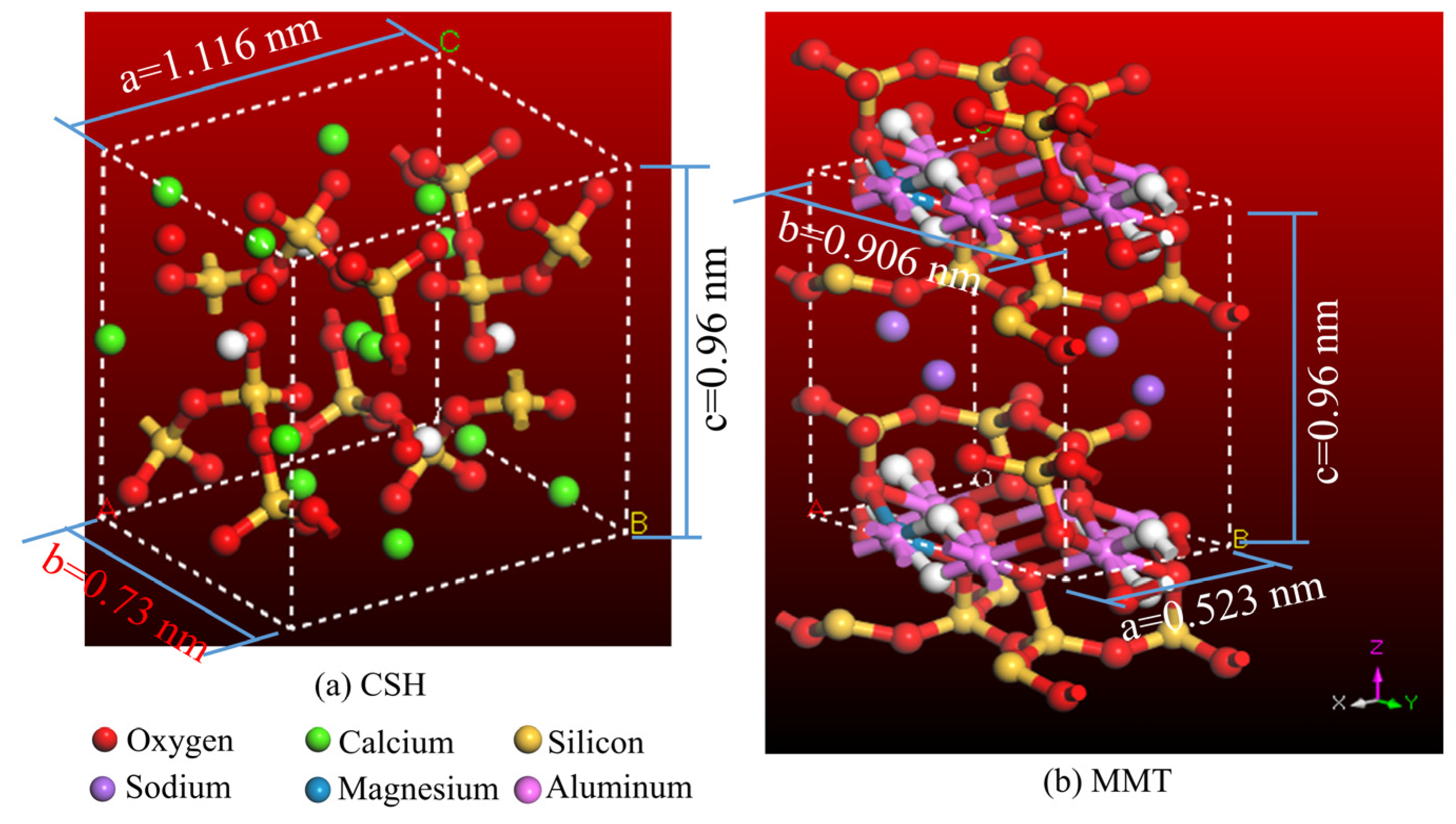
2.3. Establishment and Rational Validation of MD Models
2.3.1. Construction and Verification of Typical CSH and MMT MD Models
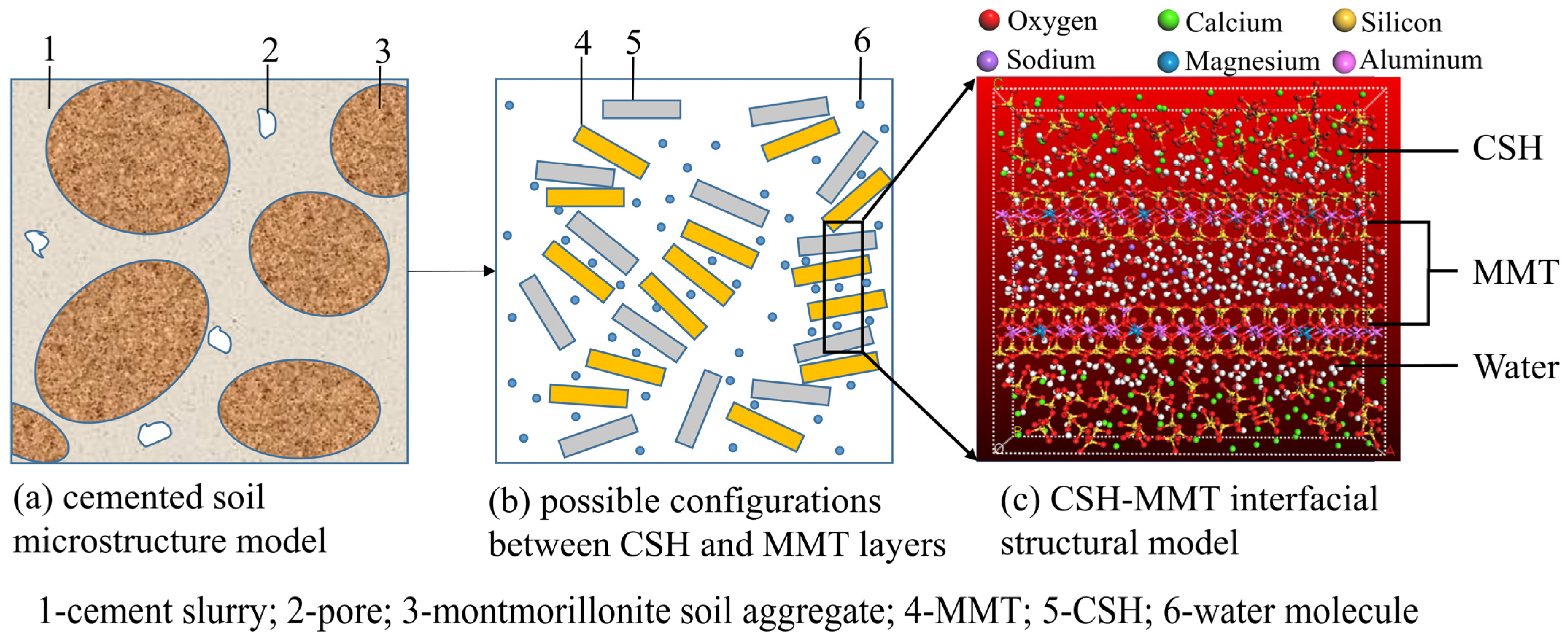
2.3.2. Construction of the CSH-MMT Interfacial Model
3. Results
3.1. CSH-MMT Interfacial Energy
3.1.1. MD Calculation of the Interface between CSH and MMT
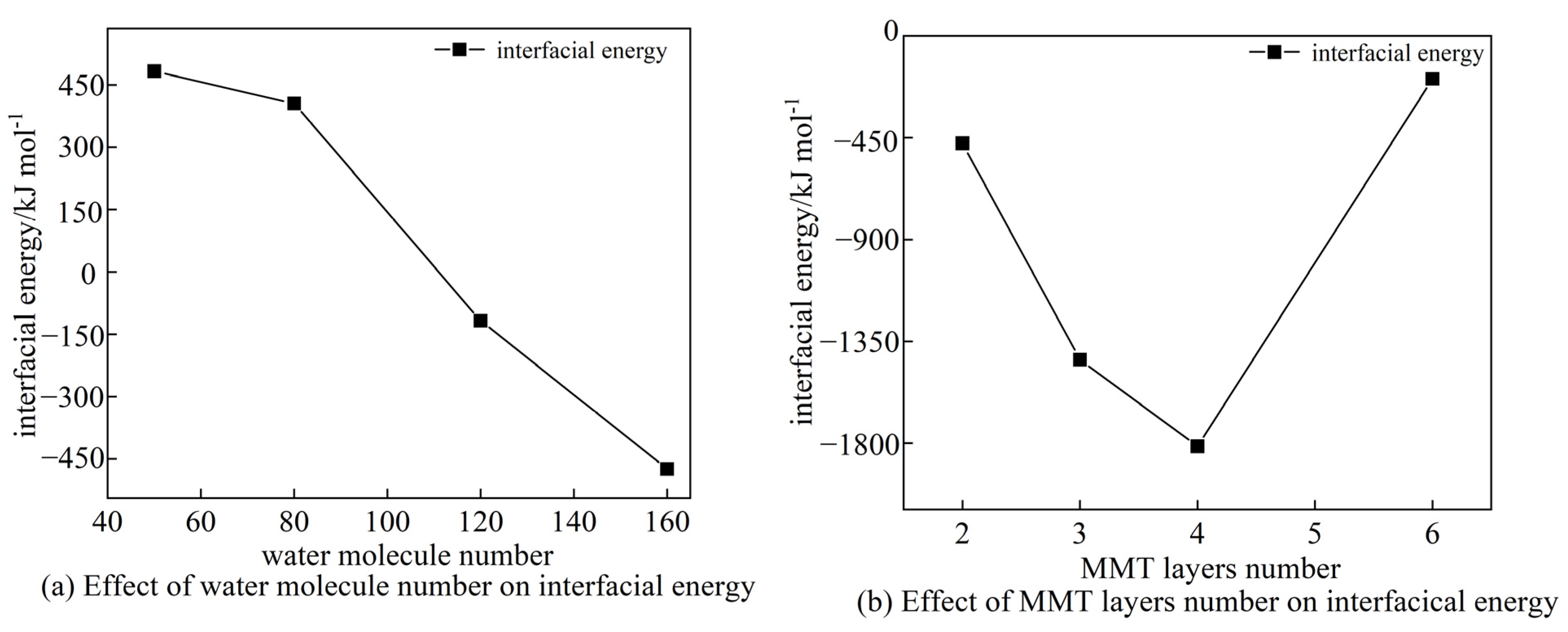
3.1.2. CSH-MMT Interfacial Energy
3.2. UCS and Its Correlation with CSH-MMT Interfacial Energy
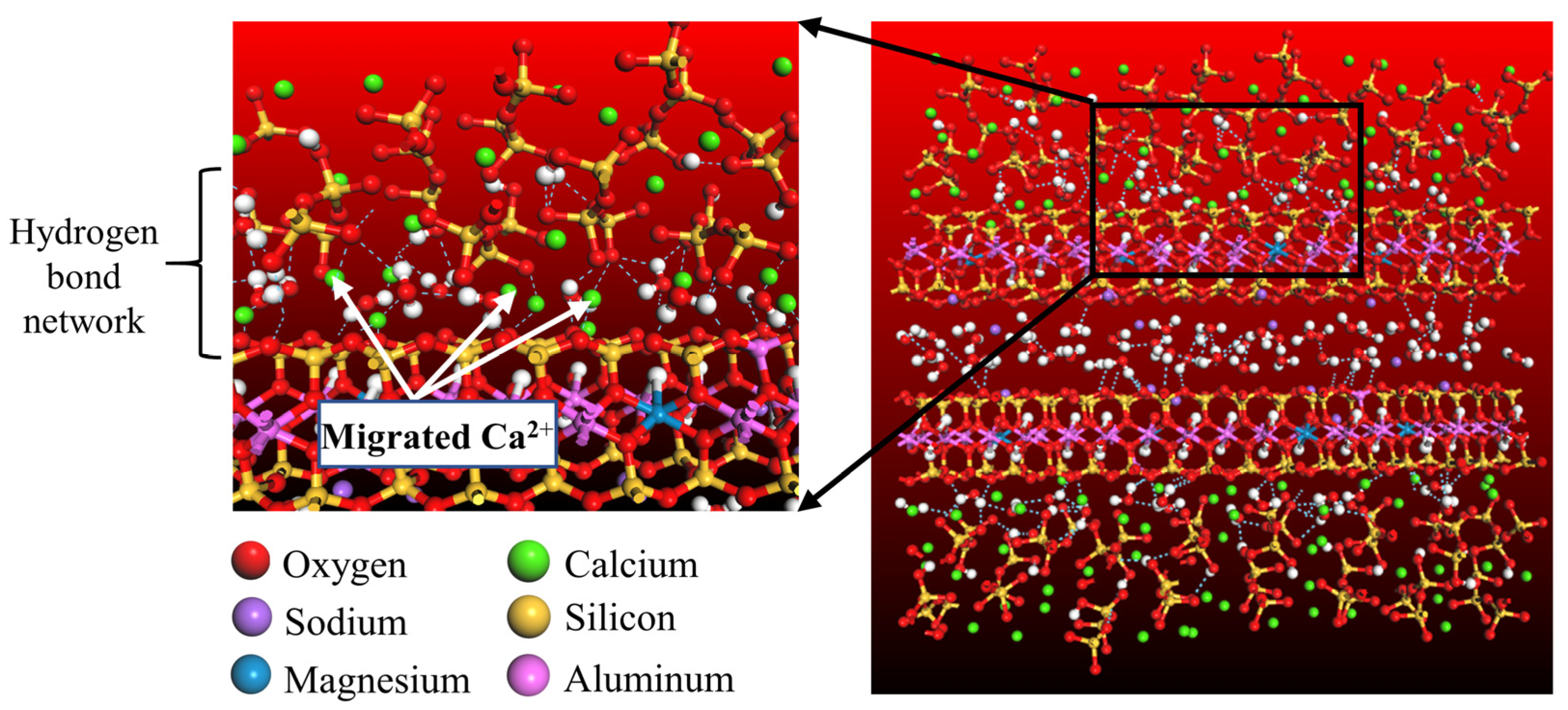
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anbleyth-Evans, J. Aggregate Dredging Impacts in South East England: Improving Ecological Health by Integrating Fisher Ecological Knowledge with Scientific Research. Mar. Pollut. Bull. 2018, 135, 129–138. [Google Scholar] [CrossRef] [PubMed]
- Beukema, J.J. Well-Founded and Supposed Negative Effects of Cockle Dredging on Tidal-Flat Sediment and Fauna: A Review of Contributions of Ecological Research. J. Sea Res. 2023, 194, 102408. [Google Scholar] [CrossRef]
- Chen, X.; Kang, B.; Li, M.; Du, Z.; Zhang, L.; Li, H. Identification of Priority Areas for Territorial Ecological Conservation and Restoration Based on Ecological Networks: A Case Study of Tianjin City, China. Ecol. Indic. 2023, 146, 109809. [Google Scholar] [CrossRef]
- Wang, B.; Li, G.; Han, J.; Zheng, Y.; Liu, H.; Song, W. Study on the Properties of Artificial Flood-Prevention Stone Made by Yellow River Silt. Constr. Build. Mater. 2017, 144, 484–492. [Google Scholar] [CrossRef]
- Sukmak, G.; Sukmak, P.; Horpibulsuk, S.; Arulrajah, A.; Horpibulsuk, J. Generalized Strength Prediction Equation for Cement Stabilized Clayey Soils. Appl. Clay Sci. 2023, 231, 106761. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, A.; Deng, Y.; Cui, Y.; Yu, Z.; Yu, C. Strength Performance of Cement/Slag-Based Stabilized Soft Clays. Constr. Build. Mater. 2019, 211, 909–918. [Google Scholar] [CrossRef]
- Sasanian, S.; Newson, T.A. Basic Parameters Governing the Behaviour of Cement-Treated Clays. Soils Found. 2014, 54, 209–224. [Google Scholar] [CrossRef]
- Tremblay, H.; Duchesne, J.; Locat, J.; Leroueil, S. Influence of the Nature of Organic Compounds on Fine Soil Stabilization with Cement. Can. Geotech. J. 2002, 39, 535–546. [Google Scholar] [CrossRef]
- Elert, K.; Azañón, J.M.; Nieto, F. Smectite Formation upon Lime Stabilization of Expansive Marls. Appl. Clay Sci. 2018, 158, 29–36. [Google Scholar] [CrossRef]
- Sharma, L.K.; Sirdesai, N.N.; Sharma, K.M.; Singh, T.N. Experimental Study to Examine the Independent Roles of Lime and Cement on the Stabilization of a Mountain Soil: A Comparative Study. Appl. Clay Sci. 2018, 152, 183–195. [Google Scholar] [CrossRef]
- Cadars, S.; Guégan, R.; Garaga, M.N.; Bourrat, X.; Le Forestier, L.; Fayon, F.; Huynh, T.V.; Allier, T.; Nour, Z.; Massiot, D. New Insights into the Molecular Structures, Compositions, and Cation Distributions in Synthetic and Natural Montmorillonite Clays. Chem. Mater. 2012, 24, 4376–4389. [Google Scholar] [CrossRef]
- Huang, H.; Fu, Y.; Li, F.; Wang, Z.; Zhang, S.; Wang, X.; Wang, Z.; Li, H.; Gao, F. Orderly Self-Assembly of New Ionic Copolymers for Efficiently Protecting Copper in Aggressive Sulfuric Acid Solution. Chem. Eng. J. 2020, 384, 123293. [Google Scholar] [CrossRef]
- Li, Y.; Narayanan Nair, A.K.; Kadoura, A.; Yang, Y.; Sun, S. Molecular Simulation Study of Montmorillonite in Contact with Water. Ind. Eng. Chem. Res. 2019, 58, 1396–1403. [Google Scholar] [CrossRef]
- Liu, T.; Chen, Y.-Q. A Molecular Dynamics Study of the Swelling Patterns of Na/Cs-Montmorillonites and the Hydration of Interlayer Cations. Chin. Phys. B 2013, 22, 027103. [Google Scholar] [CrossRef]
- Peng, J.; Yi, H.; Song, S.; Zhan, W.; Zhao, Y. Driving Force for the Swelling of Montmorillonite as Affected by Surface Charge and Exchangeable Cations: A Molecular Dynamic Study. Results Phys. 2019, 12, 113–117. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, S.; Du, X.; Chen, M.; Jin, Y. Molecular Dynamics Simulation of Strength Weakening Mechanism of Deep Shale. J. Pet. Sci. Eng. 2019, 181, 106123. [Google Scholar] [CrossRef]
- Zheng, C.; Shan, C.; Liu, J.; Zhang, T.; Yang, X.; Lv, D. Microscopic Adhesion Properties of Asphalt–Mineral Aggregate Interface in Cold Area Based on Molecular Simulation Technology. Constr. Build. Mater. 2021, 268, 121151. [Google Scholar] [CrossRef]
- Poulsen, S.L.; Kocaba, V.; Le Saoût, G.; Jakobsen, H.J.; Scrivener, K.L.; Skibsted, J. Improved Quantification of Alite and Belite in Anhydrous Portland Cements by 29Si MAS NMR: Effects of Paramagnetic Ions. Solid State Nucl. Magn. Reson. 2009, 36, 32–44. [Google Scholar] [CrossRef]
- Rahromostaqim, M.; Sahimi, M. Molecular Dynamics Simulation of Hydration and Swelling of Mixed-Layer Clays. J. Phys. Chem. C 2018, 122, 14631–14639. [Google Scholar] [CrossRef]
- Cygan, R.T.; Liang, J.-J.; Kalinichev, A.G. Molecular Models of Hydroxide, Oxyhydroxide, and Clay Phases and the Development of a General Force Field. J. Phys. Chem. B 2004, 108, 1255–1266. [Google Scholar] [CrossRef]
- Gallé, C. Effect of Drying on Cement-Based Materials Pore Structure as Identified by Mercury Intrusion Porosimetry. Cem. Concr. Res. 2001, 31, 1467–1477. [Google Scholar] [CrossRef]
- Pellenq, R.J.-M.; Lequeux, N.; van Damme, H. Engineering the Bonding Scheme in C–S–H: The Iono-Covalent Framework. Cem. Concr. Res. 2008, 38, 159–174. [Google Scholar] [CrossRef]
- Soyer-Uzun, S.; Chae, S.R.; Benmore, C.J.; Wenk, H.-R.; Monteiro, P.J.M. Compositional Evolution of Calcium Silicate Hydrate (C-S-H) Structures by Total X-Ray Scattering. J. Am. Ceram. Soc. 2012, 95, 793–798. [Google Scholar] [CrossRef]
- Skipper, N.T. Monte Carlo Simulation of Interlayer Molecular Structure in Swelling Clay Minerals. 2. Monolayer Hydrates. Clays Clay Miner. 1995, 43, 294–303. [Google Scholar] [CrossRef]
- Du, J.; Zhou, A.; Lin, X.; Bu, Y.; Kodikara, J. Revealing Expansion Mechanism of Cement-Stabilized Expansive Soil with Different Interlayer Cations through Molecular Dynamics Simulations. J. Phys. Chem. C 2020, 124, 14672–14684. [Google Scholar] [CrossRef]
- Carrier, B.; Vandamme, M.; Pellenq, R.J.-M.; Van Damme, H. Elastic Properties of Swelling Clay Particles at Finite Temperature upon Hydration. J. Phys. Chem. C 2014, 118, 8933–8943. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Cates, M.E. Effective Elastic Properties of Solid Clays. Geophysics 2001, 66, 428–440. [Google Scholar] [CrossRef]
- Myers, R.J.; Bernal, S.A.; Provis, J.L. A Thermodynamic Model for C-(N-)A-S-H Gel: CNASH_ss. Derivation and Validation. Cem. Concr. Res. 2014, 66, 27–47. [Google Scholar] [CrossRef]
- Bohinc, K.; Spada, S.; Maset, S. Impact of Added Salt on the Characteristics of Electric Double Layer Composed of Charged Nanoparticles. J. Mol. Liq. 2023, 385, 122117. [Google Scholar] [CrossRef]
- Yang, S.; Yang, G. Modeling the Adsorption of Metal Ions at Clay Minerals/Water Interfaces. In Encyclopedia of Solid-Liquid Interfaces; Elsevier: Amsterdam, The Netherlands, 2024; pp. 547–563. ISBN 978-0-323-85670-6. [Google Scholar]
- García-Lodeiro, I.; Cherfa, N.; Zibouche, F.; Fernández-Jimenez, A.; Palomo, A. The Role of Aluminium in Alkali-Activated Bentonites. Mater. Struct. 2015, 48, 585–597. [Google Scholar] [CrossRef]
- Marsh, A.; Heath, A.; Patureau, P.; Evernden, M.; Walker, P. Phase Formation Behaviour in Alkali Activation of Clay Mixtures. Appl. Clay Sci. 2019, 175, 10–21. [Google Scholar] [CrossRef]


| Density/g cm−3 | Specific Surface Area/m2 kg−1 | Water Requirement of Normal Consistency/% | Initial Setting Time/min | Final Setting Time/min |
|---|---|---|---|---|
| 3.03 | 397 | 27.5 | 195 | 305 |
| Water-to-Cement Ratio | 1.33 | 2 | 3 | 4 | Grey Relational Degree |
|---|---|---|---|---|---|
| ξ0 | 1 | 0.85 | 0.33 | 1 | 0.80 |
| Cement-to-Soil Ratio/% | 7.5 | 15 | 20 | 25 | Grey Relational Degree |
|---|---|---|---|---|---|
| ξ0 | 0.61 | 0.33 | 1 | 0.79 | 0.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, J.; Xu, F.; Wei, H.; Wang, Q.; Peng, H.; Zhou, J.; Li, H. The Influence Mechanism of Interfacial Characteristics between CSH and Montmorillonite on the Strength Properties of Cement-Stabilized Montmorillonite Soil. Materials 2023, 16, 7141. https://doi.org/10.3390/ma16227141
Ge J, Xu F, Wei H, Wang Q, Peng H, Zhou J, Li H. The Influence Mechanism of Interfacial Characteristics between CSH and Montmorillonite on the Strength Properties of Cement-Stabilized Montmorillonite Soil. Materials. 2023; 16(22):7141. https://doi.org/10.3390/ma16227141
Chicago/Turabian StyleGe, Jinyu, Fei Xu, Hua Wei, Qiang Wang, Hu Peng, Juan Zhou, and Huaisen Li. 2023. "The Influence Mechanism of Interfacial Characteristics between CSH and Montmorillonite on the Strength Properties of Cement-Stabilized Montmorillonite Soil" Materials 16, no. 22: 7141. https://doi.org/10.3390/ma16227141
APA StyleGe, J., Xu, F., Wei, H., Wang, Q., Peng, H., Zhou, J., & Li, H. (2023). The Influence Mechanism of Interfacial Characteristics between CSH and Montmorillonite on the Strength Properties of Cement-Stabilized Montmorillonite Soil. Materials, 16(22), 7141. https://doi.org/10.3390/ma16227141






