A Systematic Study on the Processing Strategy in Femtosecond Laser Scribing via a Two-Temperature Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
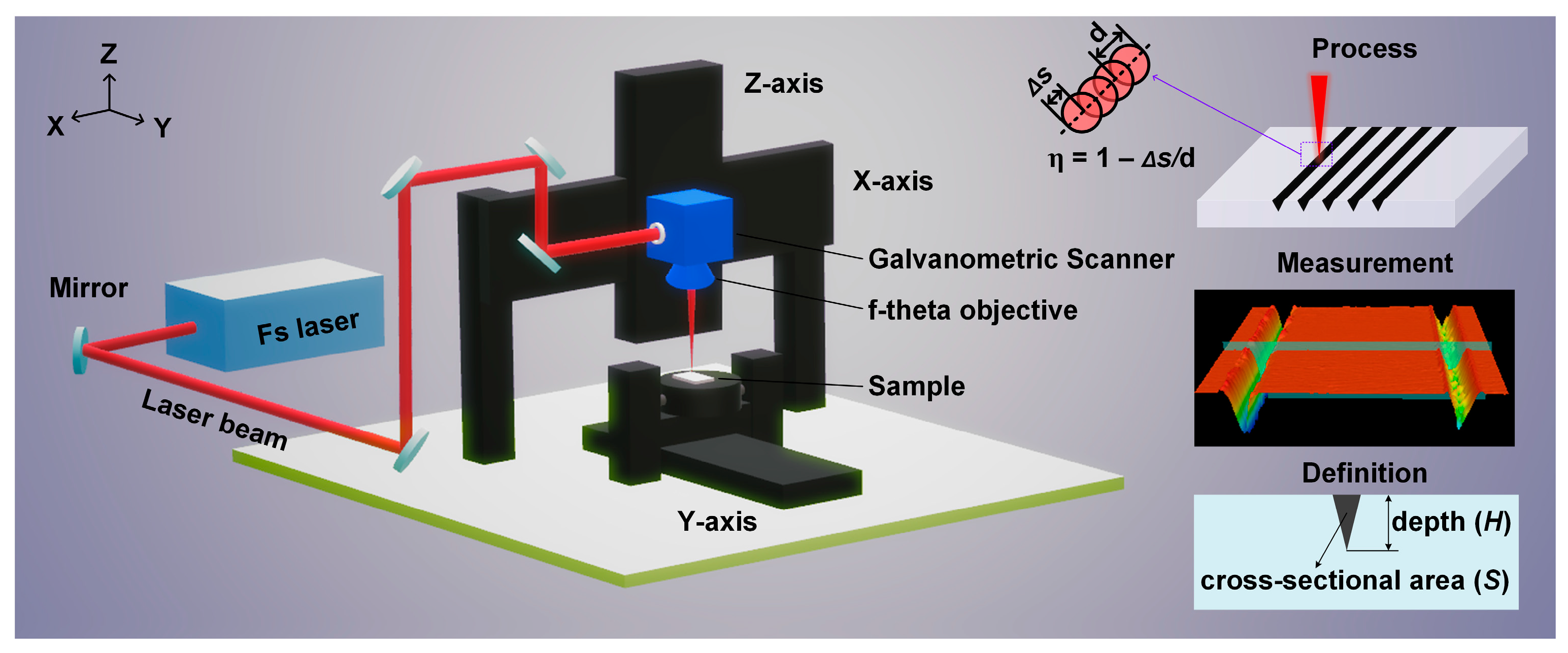
2.2. Laser Machining System
2.3. Experimental Arrangement
2.4. Characterization Analysis
3. Results and Discussion
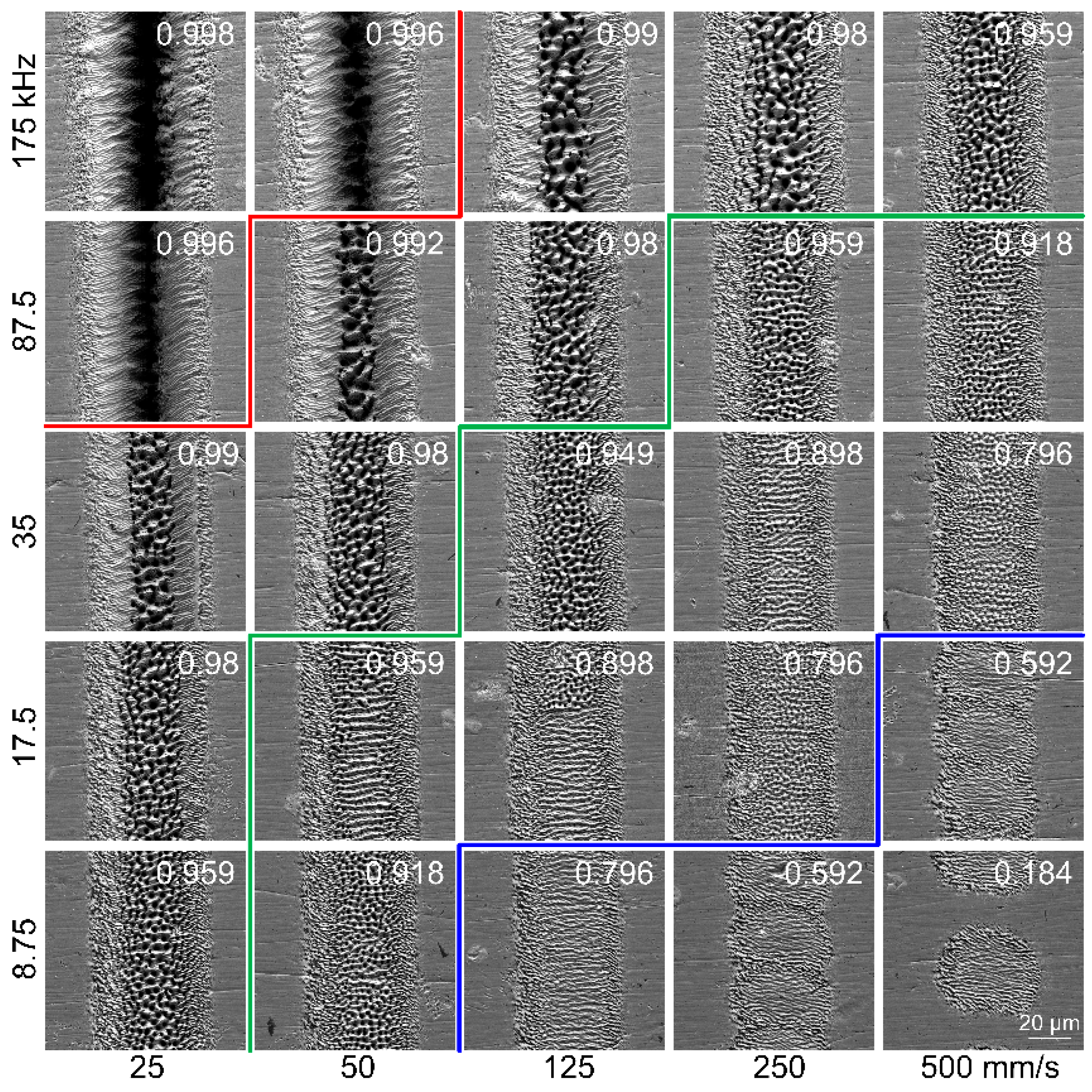
3.1. Morphology of Grooves Scribed by the Femtosecond Laser
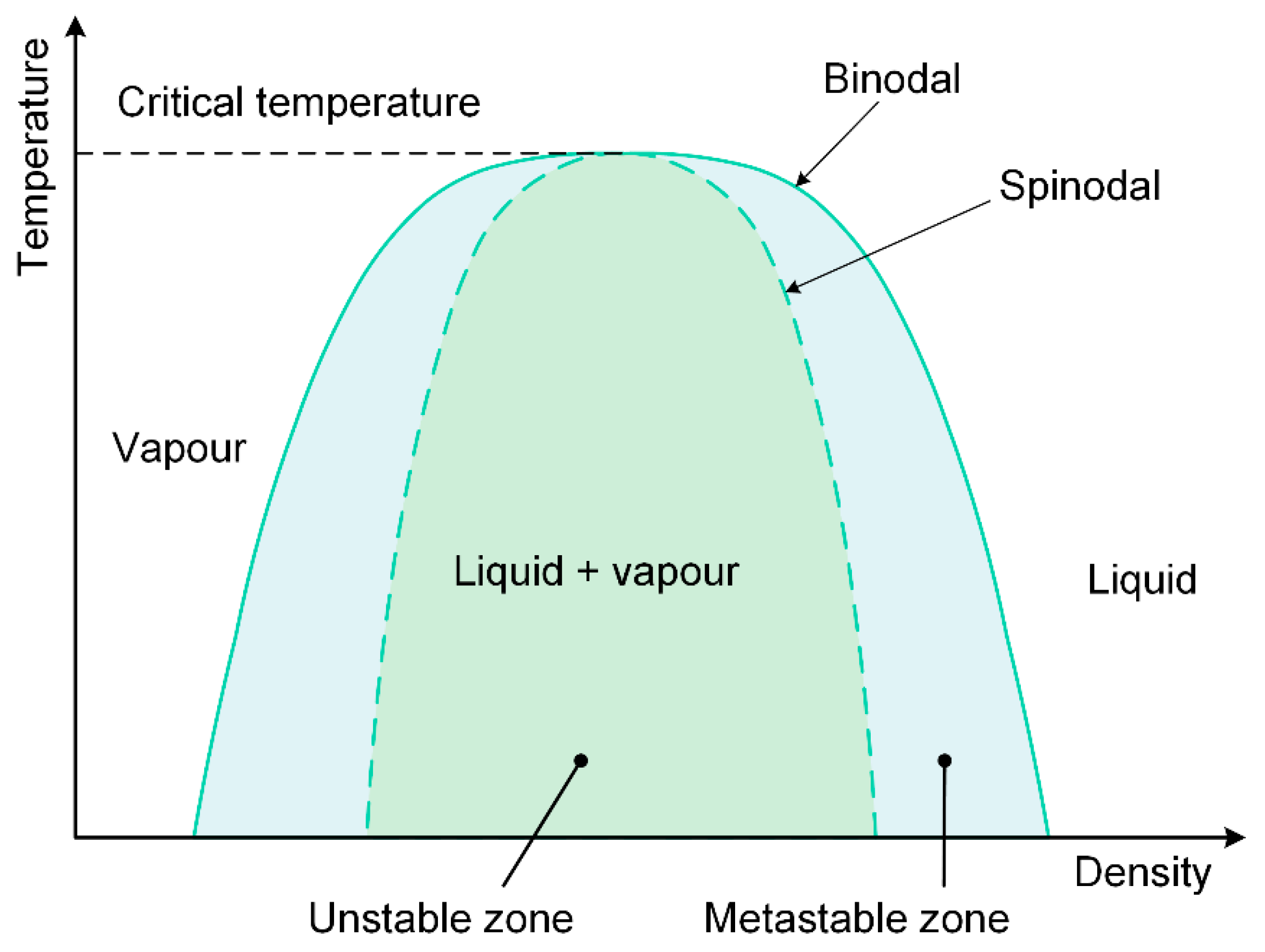
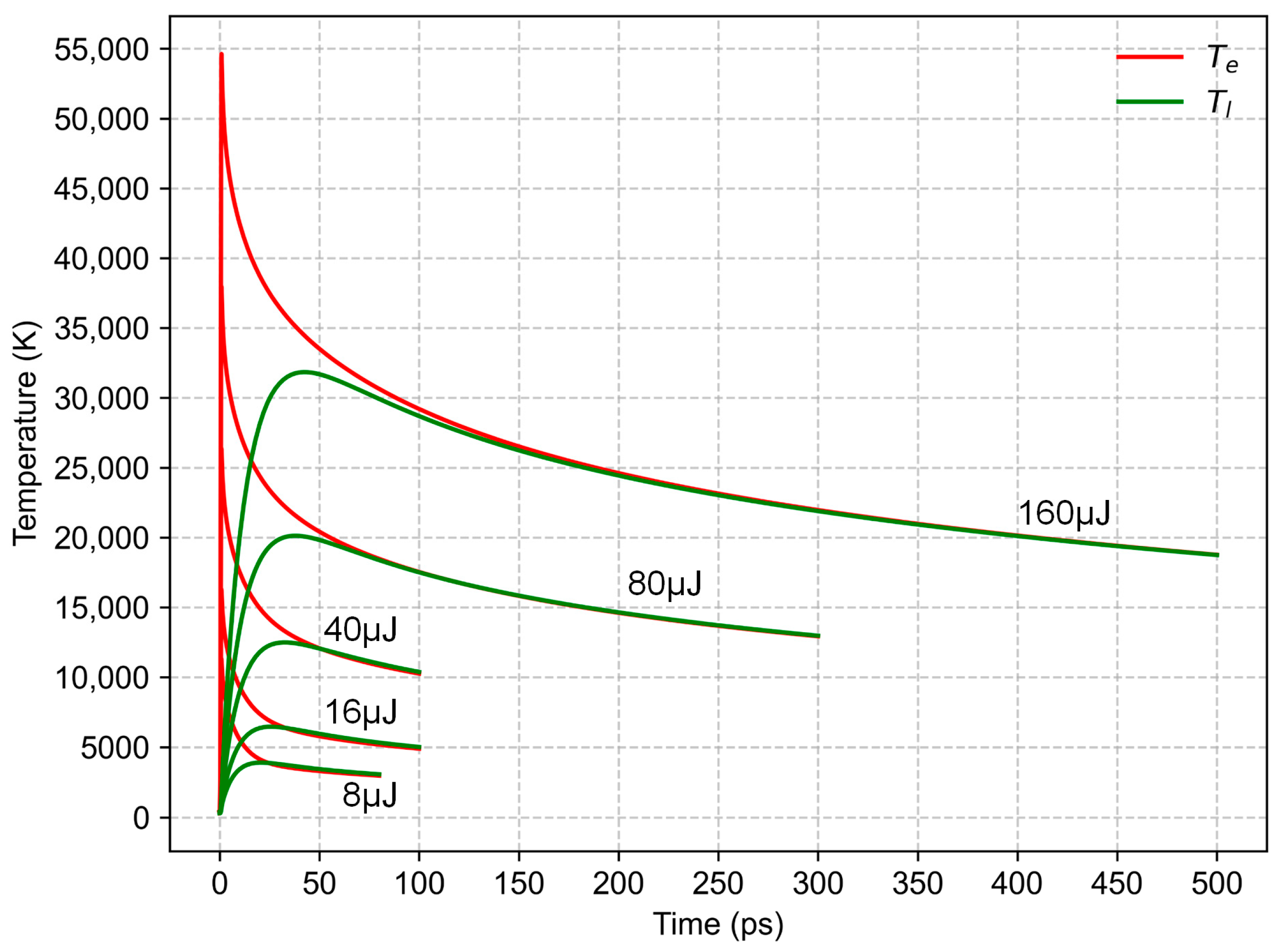
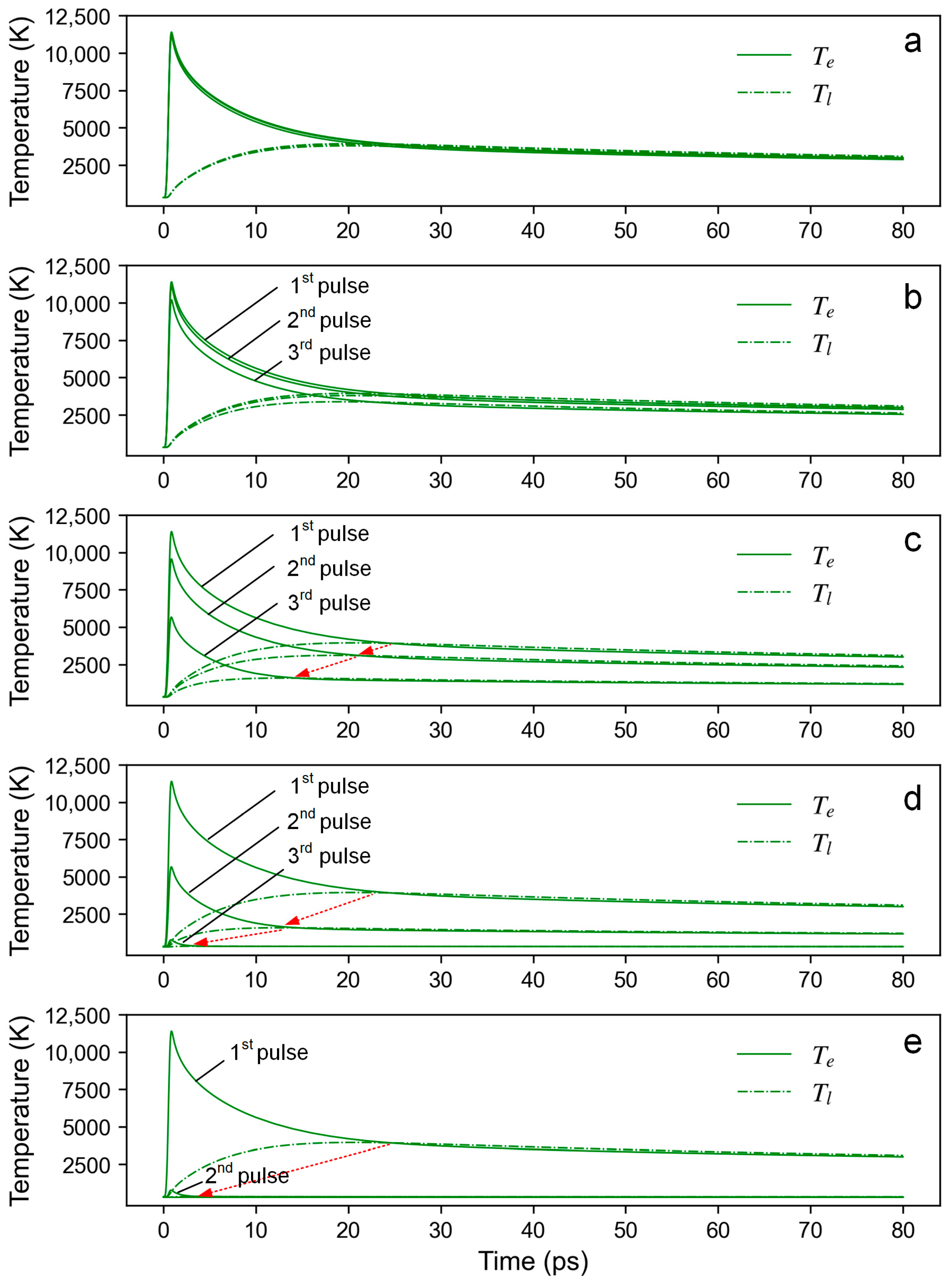
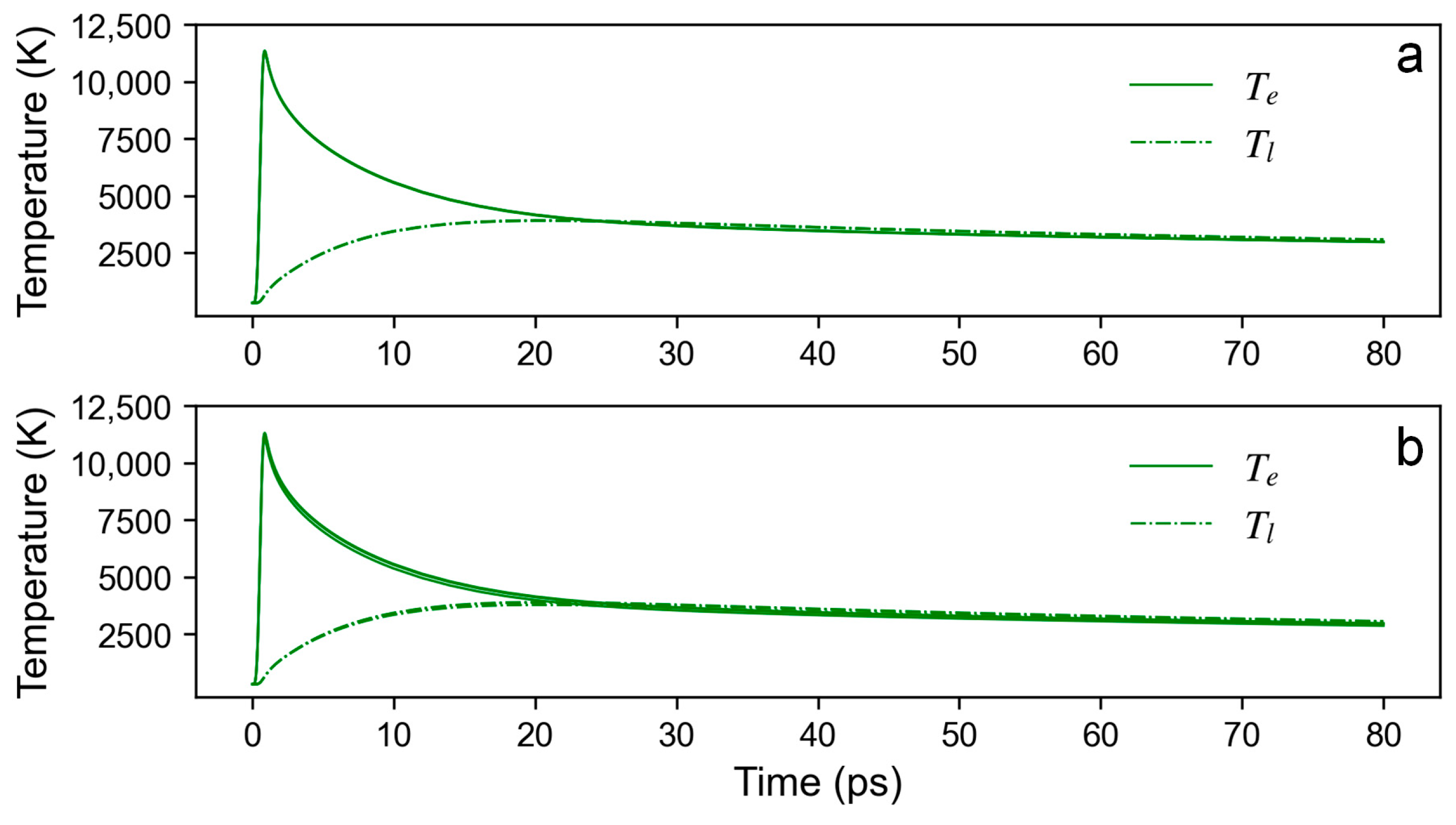
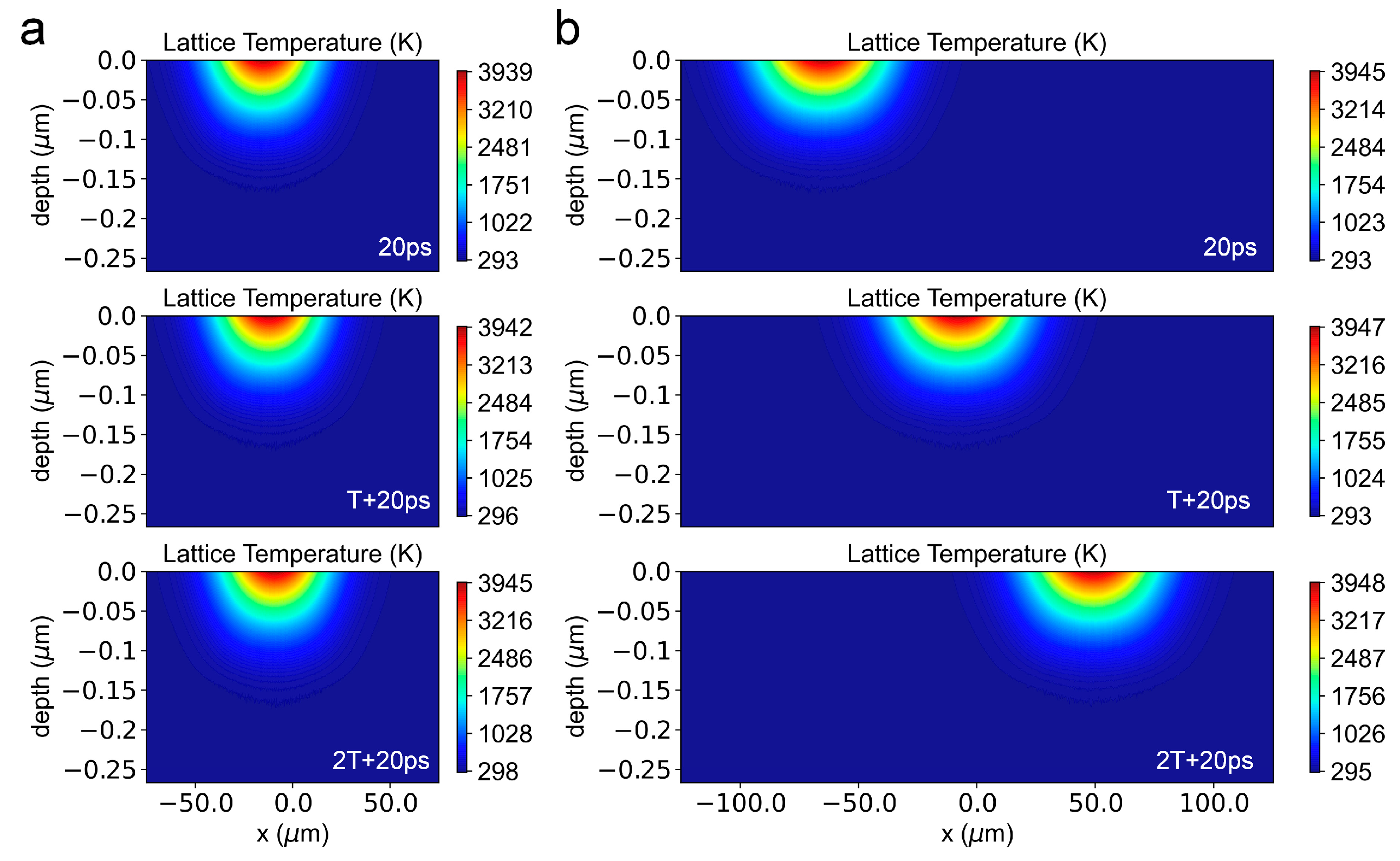
3.2. Temperature Evolution Revealed by the Theoretical Analysis
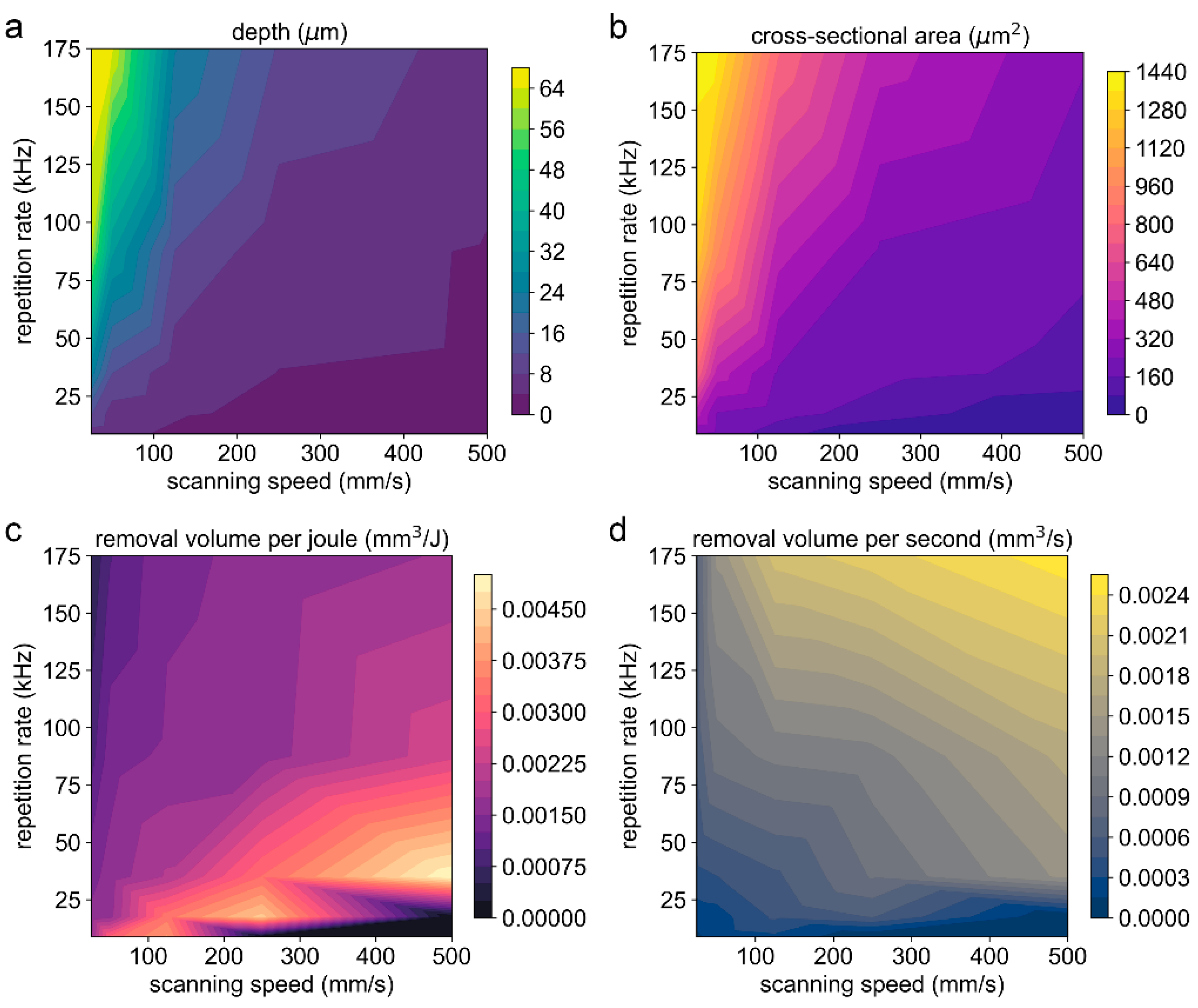
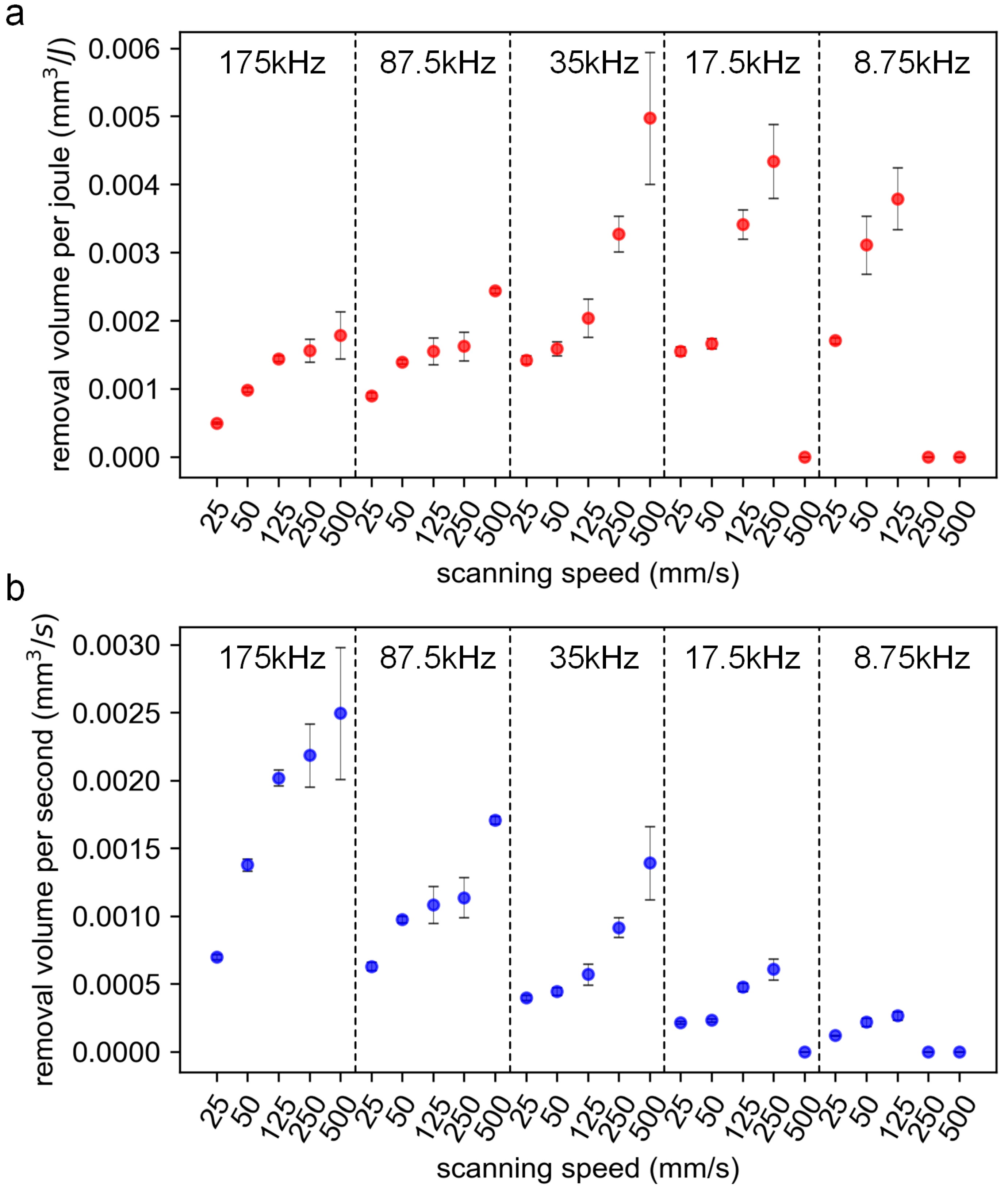
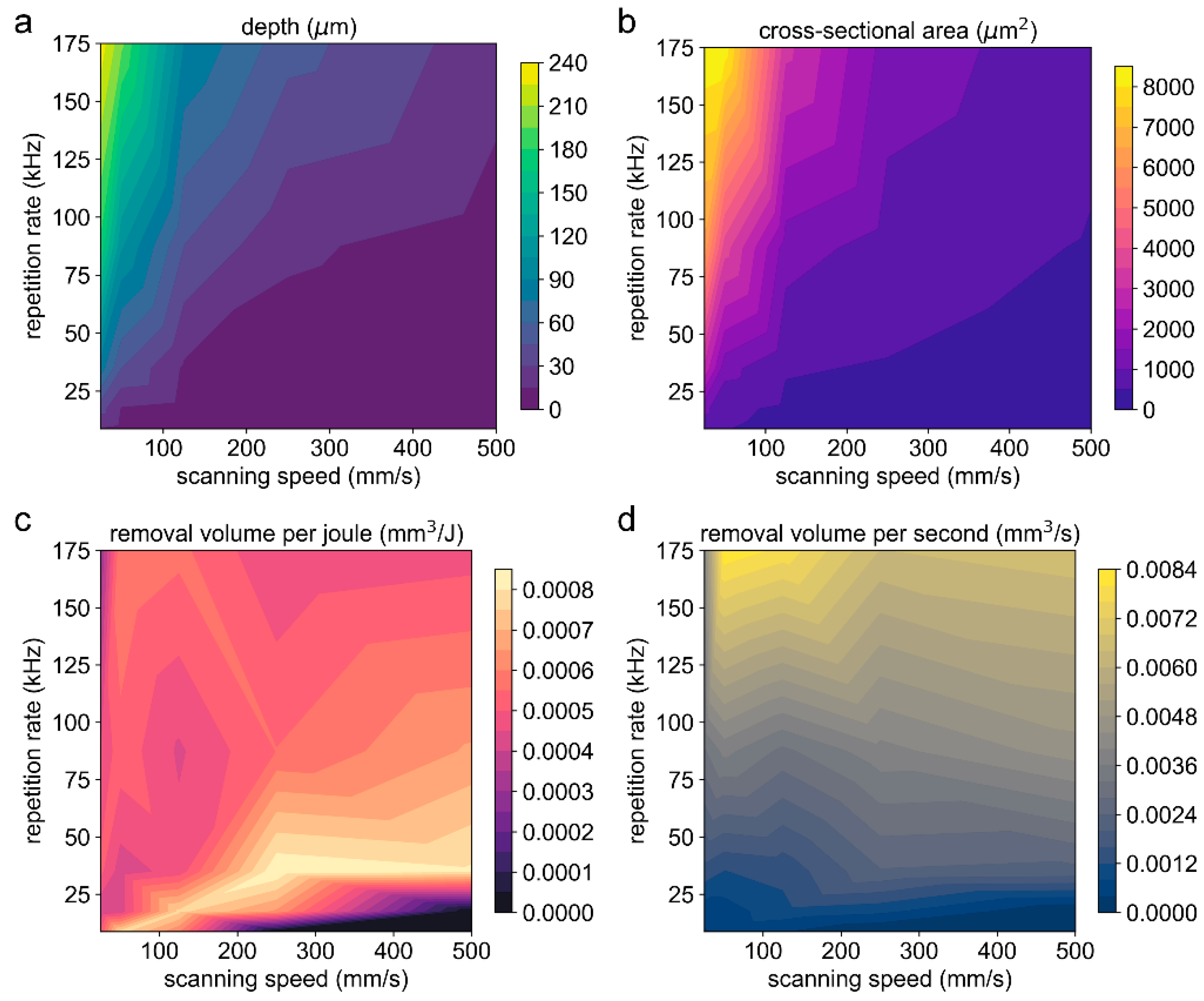
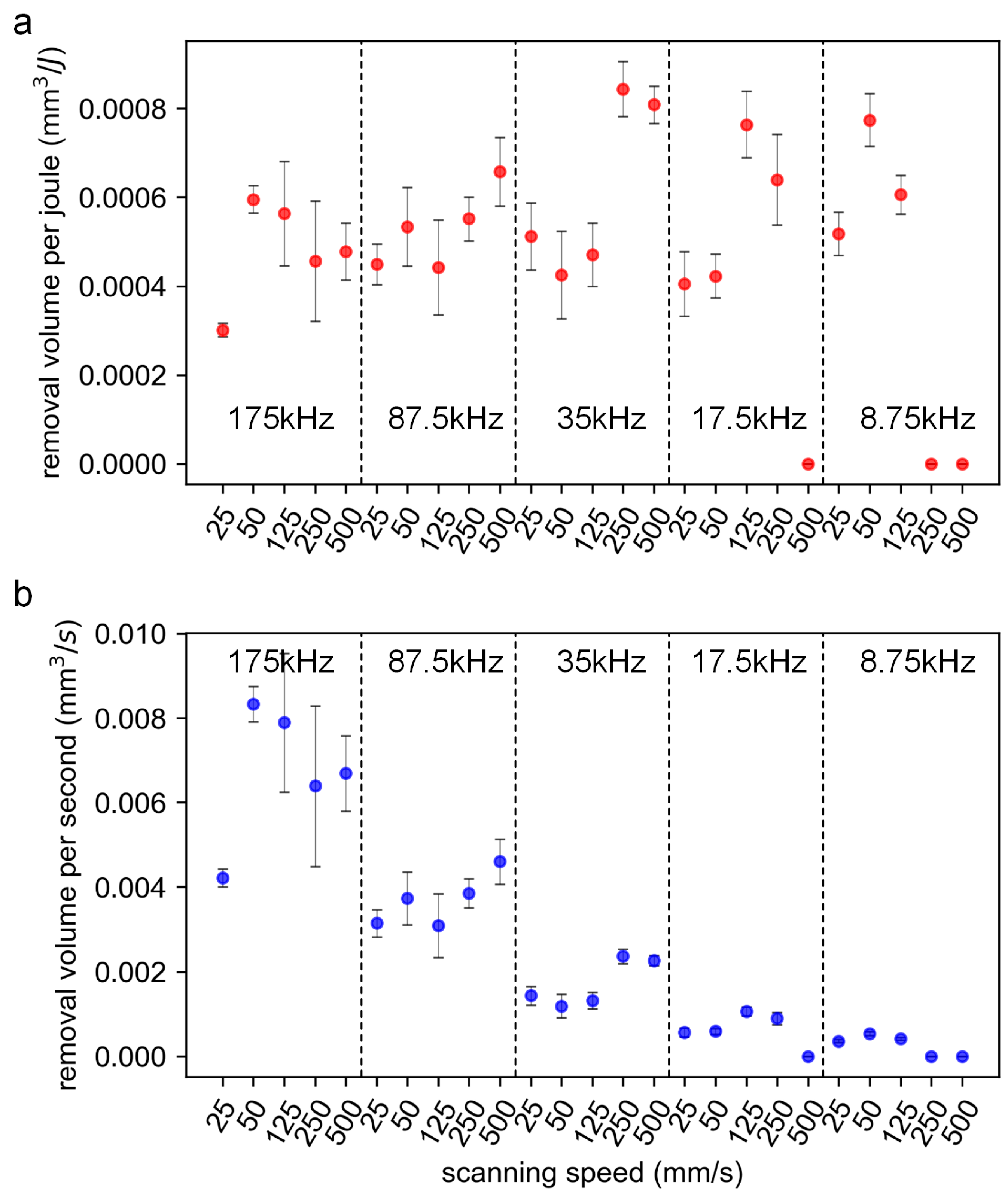
3.3. Ablation Characteristics Influenced by Multiple Process Parameters
4. Conclusions
- (1)
- Pulse energy determines the peak thermal equilibrium temperature between the electron and lattice. When the equilibrium temperature far exceeds the critical temperature, obvious thermal ablation occurs in the groove, and the processing quality deteriorates. In this experiment, a pulse energy smaller than 40 μJ is preferred to improve the surface quality.
- (2)
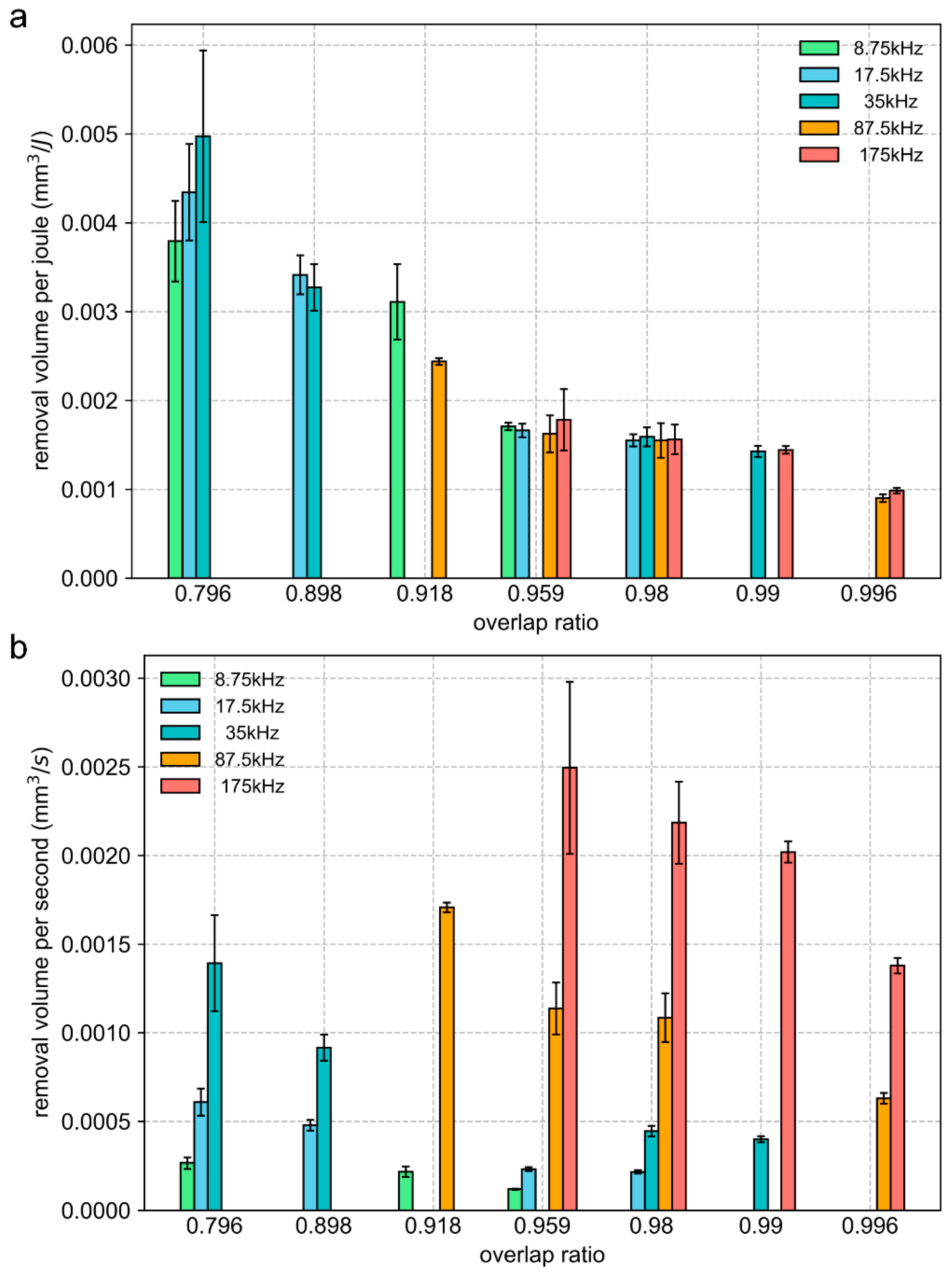
- As indicated by the simulation model, the temperature evolution at the initial position influenced by subsequent pulses is strongly associated with the overlap ratio. The thermal effect of subsequent pulses is significantly weakened when the overlap ratio is 0.796 and is negligible when the overlap ratio is 0.184.
- (3)
- At the same laser fluence, the groove morphology has a stable correspondence with the overlap ratio, which is controllable by selecting the overlap ratio.
- (4)
- For energy utilization efficiency, due to its insensitivity to changes in the repetition rate at the same overlap ratio, the number of experimental samples can be reduced, and the cost of the test can be decreased in determining the optimal overlap ratio. For ablation efficiency, at the same overlap ratio with the same laser fluence, the ablation efficiency increases with the increase in the repetition rate.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Axente, E.; Mihailescu, I.N.; Hermann, J.; Itina, T.E. Probing electron-phonon coupling in metals via observations of ablation plumes produced by two delayed short laser pulses. Appl. Phys. Lett. 2011, 99, 081502. [Google Scholar] [CrossRef]
- Liu, N.; Sun, Y.; Wang, H.; Liang, C. Femtosecond laser-induced nanostructures on Fe-30Mn surfaces for biomedical applications. Opt. Laser Technol. 2021, 139, 106986. [Google Scholar] [CrossRef]
- Ye, X.; Long, J.; Lin, Z.; Zhang, H.; Zhu, H.; Zhong, M. Direct laser fabrication of large-area and patterned graphene at room temperature. Carbon 2014, 68, 784–790. [Google Scholar] [CrossRef]
- Lv, J.; Bai, J.; Zhou, K.; Mei, X.; Wang, K.; Li, M.; Cheng, G. Transmission performance of 90 degrees -bend optical waveguides fabricated in fused silica by femtosecond laser inscription. Opt. Lett. 2017, 42, 3470–3473. [Google Scholar] [CrossRef]
- Bae, J.E.; Calmano, T.; Kränkel, C.; Rotermund, F. Controllable Dynamic Single- and Dual-Channel Graphene Q-Switching in a Beam-Splitter-Type Channel Waveguide Laser. Laser Photonics Rev. 2022, 16, 2100501. [Google Scholar] [CrossRef]
- Bae, J.E.; Mateos, X.; Aguiló, M.; Díaz, F.; Ajates, J.G.; Romero, C.; Vázquez de Aldana, J.R.; Rotermund, F. Multi-gigahertz mode-locked femtosecond Yb:KLuW waveguide lasers. Photonics Res. 2022, 10, 2584–2589. [Google Scholar] [CrossRef]
- Liu, C.; Li, C.; Gao, L.; Shen, R. Micro-hole drilling of 2.5D C/SiC composite with picosecond laser: Numerical modeling and experimental validation on hole shape evolution. J. Manuf. Process 2022, 81, 852–864. [Google Scholar] [CrossRef]
- Xia, K.; Ren, N.; Lin, Q.; Yang, H. Femtosecond laser drilling in superalloy with water-based magnetic assistance. Opt. Commun. 2023, 527, 128902. [Google Scholar] [CrossRef]
- Sun, X.M.; Dong, X.; Wang, K.D.; Wang, R.J.; Fan, Z.J.; Duan, W.Q. Experimental investigation on thermal effects in picosecond laser drilling of thermal barrier coated In718. Opt. Laser Technol. 2019, 113, 150–158. [Google Scholar] [CrossRef]
- Eaton, S.M.; Zhang, H.; Herman, P.R. Heat accumulation effects in femtosecond laser-written waveguides with variable repetition rate. Opt. Express 2005, 13, 4708–4716. [Google Scholar] [CrossRef]
- Wang, F.; Duan, W.; Wang, K.; Dong, X.; Gao, M.; Zhai, Z.; Mei, X.; Lv, J.; Wang, W.; Zhu, C. Graphitized hierarchically porous carbon nanosheets derived from bakelite induced by high-repetition picosecond laser. Appl. Surf. Sci. 2018, 450, 155–163. [Google Scholar] [CrossRef]
- Di Niso, F.; Gaudiuso, C.; Sibillano, T.; Mezzapesa, F.P.; Ancona, A.; Lugarà, P.M. Role of heat accumulation on the incubation effect in multi-shot laser ablation of stainless steel at high repetition rates. Opt. Express 2014, 22, 12200–12210. [Google Scholar] [CrossRef] [PubMed]
- Finger, J.; Bornschlegel, B.; Reininghaus, M.; Dohrn, A.; Nießen, M.; Gillner, A.; Poprawe, R. Heat input and accumulation for ultrashort pulse processing with high average power. Adv. Opt. Technol. 2018, 7, 145–155. [Google Scholar] [CrossRef]
- Weber, R.; Graf, T.; Berger, P.; Onuseit, V.; Wiedenmann, M.; Freitag, C.; Feuer, A. Heat accumulation during pulsed laser materials processing. Opt. Express 2014, 22, 11312–11324. [Google Scholar] [CrossRef] [PubMed]
- Bauer, F.; Michalowski, A.; Kiedrowski, T.; Nolte, S. Heat accumulation in ultra-short pulsed scanning laser ablation of metals. Opt. Express 2015, 23, 1035–1043. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, W.; Jin, C.; Jiang, R.; Xiong, Y.; Zhang, X.; Mao, Z. Investigation on efficiency and quality for ultrashort pulsed laser ablation of nickel-based single crystal alloy DD6. Int. J. Adv. Manuf. Technol. 2021, 114, 883–897. [Google Scholar] [CrossRef]
- Neuenschwander, B.; Bucher, G.F.; Nussbaum, C.; Joss, B.; Muralt, M.; Hunziker, U.W.; Schuetz, P. Processing of metals and dielectric materials with ps-laserpulses: Results, strategies, limitations and needs. In Laser Applications in Microelectronic and Optoelectronic Manufacturing XV, San Francisco, California, United States, 2010; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; Volume 7584. [Google Scholar]
- Neuenschwander, B.; Jaeggi, B.; Schmid, M.; Rouffiange, V.; Martin, P.-E. Optimization of the volume ablation rate for metals at different laser pulse-durations from ps to fs. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XVII, San Francisco, California, United States, 2012; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; p. 824307. [Google Scholar]
- Raciukaitis, G.; Brikas, M.; Gecys, P.; Voisiat, B.; Gedvilas, M. Use of High Repetition Rate and High Power Lasers in Microfabrication: How to Keep the Efficiency High? J. Laser Micro Nanoeng. 2009, 4, 186–191. [Google Scholar] [CrossRef]
- Shimahara, K.; Tani, S.; Sakurai, H.; Kobayashi, Y. A deep learning-based predictive simulator for the optimization of ultrashort pulse laser drilling. Commun. Eng. 2023, 2, 1. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.; Zhang, Y.; Wang, C.; Zhang, S.; Yang, Z.; Xu, W. Optimization of low-power femtosecond laser trepan drilling by machine learning and a high-throughput multi-objective genetic algorithm. Opt. Laser Technol. 2022, 148, 107688. [Google Scholar] [CrossRef]
- Tani, S.; Kobayashi, Y. Ultrafast laser ablation simulator using deep neural networks. Sci. Rep. 2022, 12, 5837. [Google Scholar] [CrossRef]
- Anisimov, S.; Kapeliovich, B.; Perelman, T. Electron emission from metal surfaces exposed to ultrashort laser pulses. Zh Eksp Teor Fiz 1974, 66, 375–377. [Google Scholar]
- Zhou, Y.; Wu, D.; Luo, G.; Hu, Y.; Qin, Y. Efficient modeling of metal ablation irradiated by femtosecond laser via simplified two-temperature model coupling molecular dynamics. J. Manuf. Process 2022, 77, 783–793. [Google Scholar] [CrossRef]
- Zhan, N.; Guo, B.; Jiang, L.; Zhang, T.; Chen, M.; Lin, G. Multiphysics modeling of femtosecond laser–copper interaction: From electron dynamics to plasma eruption. Phys. Fluids 2023, 35, 012003. [Google Scholar] [CrossRef]
- Bonse, J.; Wrobel, J.M.; Krüger, J.; Kautek, W. Ultrashort-pulse laser ablation of indium phosphide in air. Appl. Phys. A 2001, 72, 89–94. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Z.; Shimada, K.; Mizutani, M.; Kuriyagawa, T. Electric field analysis coupled with the two-temperature model to elucidate the generation process of laser-induced periodic surface structure. J. Mater. Process. Technol. 2022, 305, 117601. [Google Scholar] [CrossRef]
- Mannion, P.T.; Magee, J.; Coyne, E.; O’Connor, G.M.; Glynn, T.J. The effect of damage accumulation behaviour on ablation thresholds and damage morphology in ultrafast laser micro-machining of common metals in air. Appl. Surf. Sci. 2004, 233, 275–287. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, G.; Wang, W.; Mei, X.; Wang, K.; Cui, J.; Wang, J. Porous microstructures induced by picosecond laser scanning irradiation on stainless steel surface. Opt. Lasers Eng. 2016, 78, 55–63. [Google Scholar] [CrossRef]
- Spellauge, M.; Donate-Buendia, C.; Barcikowski, S.; Gokce, B.; Huber, H.P. Comparison of ultrashort pulse ablation of gold in air and water by time-resolved experiments. Light Sci. Appl. 2022, 11, 68. [Google Scholar] [CrossRef]
- Lorazo, P.; Lewis, L.J.; Meunier, M. Short-pulse laser ablation of solids: From phase explosion to fragmentation. Phys. Rev. Lett. 2003, 91, 225502. [Google Scholar] [CrossRef]
- Perez, D.; Lewis, L.J. Molecular-dynamics study of ablation of solids under femtosecond laser pulses. Phys. Rev. B 2003, 67, 184102. [Google Scholar] [CrossRef]
- Lewis, L.J.; Perez, D. Theory and Simulation of Laser Ablation—From Basic Mechanisms to Applications. In Laser Precision Microfabrication; Sugioka, K., Meunier, M., Piqué, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 35–61. [Google Scholar]
- Bizi-Bandoki, P.; Benayoun, S.; Valette, S.; Beaugiraud, B.; Audouard, E. Modifications of roughness and wettability properties of metals induced by femtosecond laser treatment. Appl. Surf. Sci. 2011, 257, 5213–5218. [Google Scholar] [CrossRef]
- Schille, J.; Schneider, L.; Loeschner, U.; Ebert, R.; Scully, P.; Goddard, N.; Steiger, B.; Exner, H. Micro processing of metals using a high repetition rate femtosecond laser: From laser process parameter study to machining examples. In Proceedings of the 30th International Congress on Applications of Lasers & Electro-Optics, Orlando, FL, USA, 23–27 October 2011; pp. 773–782. [Google Scholar]
- Qiu, Z.; Jiang, L.; Hu, J.; Liu, H.; Liu, W.; Li, Z.; Wang, S.; Chen, Z.; Niu, X. High-quality micropore drilling by using orthogonally polarized femtosecond double-pulse bursts. Appl. Surf. Sci. 2023, 613, 156033. [Google Scholar] [CrossRef]
- Wellershoff, S.-S.; Hohlfeld, J.; Güdde, J.; Matthias, E. The role of electron–phonon coupling in femtosecond laser damage of metals. Appl. Phys. A 1999, 69, S99–S107. [Google Scholar]
- Roth, J.; Sonntag, S.; Karlin, J.; Trichet Paredes, C.; Sartison, M.; Krauss, A.; Trebin, H.R. Molecular Dynamics Simulations Studies of Laser Ablation in Metals. In Proceedings of the International Symposium on High Power Laser Ablation 2012, Santa Fe, NM, USA, 30 April–3 May 2012; pp. 504–523. [Google Scholar]
- Yang, Z.; Ji, P.; Zhang, Z.; Ju, Y.; Wang, Z.; Zhang, Q.; Wang, C.; Xu, W. Fundamental 3D simulation of the femtosecond laser ablation for cooling hole drilling on Ni and Fe based aero-engine components. Opt. Commun. 2020, 475, 126237. [Google Scholar] [CrossRef]
- Wang, R.; Duan, W.; Wang, K.; Dong, X.; Fan, Z.; Mei, X.; Wang, W.; Zhang, S. Computational and experimental study on hole evolution and delamination in laser drilling of thermal barrier coated nickel superalloy. Opt. Lasers Eng. 2018, 107, 161–175. [Google Scholar] [CrossRef]
- Ivanov, D.S.; Zhigilei, L.V. Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films. Phys. Rev. B 2003, 68, 064114. [Google Scholar] [CrossRef]
- Cheng, C.; Xu, X. Mechanisms of decomposition of metal during femtosecond laser ablation. Phys. Rev. B Condens. 2005, 72, 165415. [Google Scholar] [CrossRef]
- Glover, T.E. Hydrodynamics of particle formation following femtosecond laser ablation. J. Opt. Soc. Am. B 2003, 20, 125–131. [Google Scholar] [CrossRef]




| Elements | C | Al | Ti | Cr | Co | Ni | Mo | Ta | W |
|---|---|---|---|---|---|---|---|---|---|
| wt.% | 6.58 | 2.92 | 4.75 | 12.09 | 8.82 | Bal. | 1.37 | 2.56 | 4.30 |
| Parameters | Symbol | Value | Units |
|---|---|---|---|
| Pulse energy | Ep | 8, 16, 40, 80, 160 | μJ |
| Repetition rate | f | 8.75, 17.5, 35, 87.5, 175 | kHz |
| Scanning speed | v | 25, 50, 125, 250, 500 | mm/s |
| Focus diameter | d | 70 | μm |
| Number of scans | N | 50 | |
| Overlap ratio | f) |
| Physical Parameter | Symbol | Value | Reference |
|---|---|---|---|
| The reflectance of the target material | R | 0.65 | [39] |
| Thermal conductivity of electron at T = 273 K | ke,0 | 91 J m−1 K−1 s−1 | [37] |
| Electronic heat capacity parameter | γ | 1065 J m−3 K−2 | [38] |
| Thermal conductivity of lattice | kl | 3.496 + 0.026733 Tl − 1.11803 × 10−5 Tl2 + 3.60684 × 10−9 Tl3 + 8.23555 × 10−14 Tl 4 | [40] |
| Heat capacity of lattice | Cl | 106 J m−3 K−1 | [37] |
| Electron–phonon coupling strength | g | 1017 W m−3 K−1 | [41] |
| The optical absorption depth | Lp | 13.5 nm | [39] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Wang, Y.; Yang, Y.; Zhang, S.; Liu, Y.; Yao, J.; Zhang, W. A Systematic Study on the Processing Strategy in Femtosecond Laser Scribing via a Two-Temperature Model. Materials 2023, 16, 6895. https://doi.org/10.3390/ma16216895
Wang R, Wang Y, Yang Y, Zhang S, Liu Y, Yao J, Zhang W. A Systematic Study on the Processing Strategy in Femtosecond Laser Scribing via a Two-Temperature Model. Materials. 2023; 16(21):6895. https://doi.org/10.3390/ma16216895
Chicago/Turabian StyleWang, Rujia, Yufeng Wang, Yong Yang, Shuowen Zhang, Yunfeng Liu, Jianhua Yao, and Wenwu Zhang. 2023. "A Systematic Study on the Processing Strategy in Femtosecond Laser Scribing via a Two-Temperature Model" Materials 16, no. 21: 6895. https://doi.org/10.3390/ma16216895
APA StyleWang, R., Wang, Y., Yang, Y., Zhang, S., Liu, Y., Yao, J., & Zhang, W. (2023). A Systematic Study on the Processing Strategy in Femtosecond Laser Scribing via a Two-Temperature Model. Materials, 16(21), 6895. https://doi.org/10.3390/ma16216895






