Ellipsometric Study on the Uniformity of Al:ZnO Thin Films Deposited Using DC Sputtering at Room Temperature over Large Areas
Abstract
:1. Introduction
2. Materials and Methods
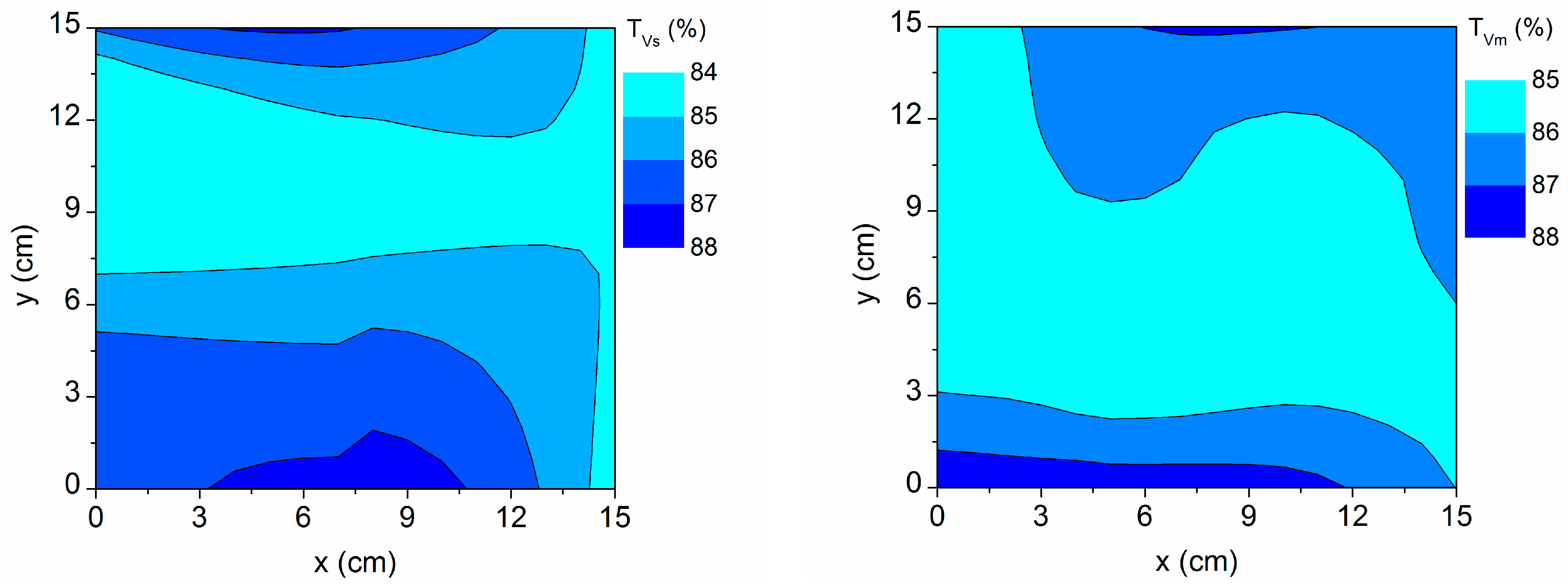
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benhaliliba, M. ZnO a multifunctional material: Physical properties, spectroscopic ellipsometry and surface examination. Optik 2021, 241, 167197. [Google Scholar] [CrossRef]
- Papadimitriou, D.N. Engineering of optical and electrical properties of electrodeposited highly doped Al:ZnO and In:ZnO for cost-effective photovoltaic device technology. Micromachines 2022, 13, 1966. [Google Scholar] [CrossRef] [PubMed]
- Kim, I.; Yun, J.; Badloe, T.; Park, H.; Seo, T.; Yang, Y.; Kim, J.; Chung, Y.; Rho, J. Structural color switching with a doped indium-gallium-zinc-oxide semiconductor. Photonics Res. 2020, 8, 1409. [Google Scholar] [CrossRef]
- Jin, W.; Park, K.; Cho, J.Y.; Bae, S.H.; Siyar, M.; Jang, H.; Park, C. Thermochromic properties of ZnO/VO2/ZnO films on soda lime silicate glass deposited by RF magnetron sputtering. Ceram. Int. 2023, 49, 10437–10444. [Google Scholar] [CrossRef]
- Niemelä, J.P.; Macco, B.; Barraud, L.; Descoeudres, A.; Badel, N.; Despeisse, M.; Christmann, G.; Nicolay, S.; Ballif, C.; Kessels, W.M.M.; et al. Rear-emitter silicon heterojunction solar cells with atomic layer deposited ZnO:Al serving as an alternative transparent conducting oxide to In2O3:Sn. Sol. Energy Mater. Sol. Cells 2019, 200, 109953. [Google Scholar] [CrossRef]
- Sarma, B.; Barman, D.; Sarma, B.K. AZO (Al:ZnO) thin films with high figure of merit as stable indium free transparent conducting oxide. Appl. Surf. Sci. 2019, 479, 786–795. [Google Scholar] [CrossRef]
- Haacke, G. New figure of merit for transparent conductors. J. Appl. Phys. 1976, 47, 4086–4089. [Google Scholar] [CrossRef]
- Sharmin, A.; Tabassum, S.; Bashar, M.S.; Mahmood, Z.H. Depositions and characterization of sol–gel processed Al-doped ZnO (AZO) as transparent conducting oxide (TCO) for solar cell application. J. Theor. Appl. Phys. 2019, 13, 123–132. [Google Scholar] [CrossRef]
- Kumar, A.; Ahmad, M.I. Role of defects in the electronic properties of Al doped ZnO films deposited by spray pyrolysis. J. Mater. Sci. 2022, 57, 7877–7895. [Google Scholar] [CrossRef]
- Cui, J.; Sun, S.; Lan, M.; Liu, S.; Piao, Y.; Li, G.; Wang, Q. Effect of low-dimensional carbon composite on the thermoelectric properties of vacuum evaporated ZnO:Al films. Thin Solid Film. 2023, 766, 139641. [Google Scholar] [CrossRef]
- Badgujar, A.C.; Yadav, B.S.; Jha, G.K.; Dhage, S.R. Room temperature sputtered aluminum-doped ZnO thin film transparent electrode for application in solar cells and for low-band-gap optoelectronic devices. ACS Omega 2022, 7, 14203–14210. [Google Scholar] [CrossRef] [PubMed]
- Guillén, C.; Herrero, J. Structure, optical and electrical properties of Al:ZnO thin films deposited by DC sputtering at room temperature on glass and plastic substrates. Phys. Status Solidi 2009, 206, 1531–1536. [Google Scholar] [CrossRef]
- Guillén, C.; Herrero, J. Optical, electrical and structural characteristics of Al:ZnO thin films with various thicknesses deposited by DC sputtering at room temperature and annealed in air or vacuum. Vacuum 2010, 84, 924–929. [Google Scholar] [CrossRef]
- Guillén, C.; Herrero, J. Structural and plasmonic characteristics of sputtered SnO2:Sb and ZnO:Al thin films as a function of their thickness. J. Mater. Sci. 2016, 51, 7276–7285. [Google Scholar] [CrossRef]
- Bohórquez, C.; Bakkali, H.; Delgado, J.J.; Blanco, E.; Herrera, M.; Domínguez, M. Spectroscopic ellipsometry study on tuning the electrical and optical properties of Zr-doped ZnO thin films grown by atomic layer deposition. ACS Appl. Electron. Mater. 2022, 4, 925–935. [Google Scholar] [CrossRef] [PubMed]
- Gâlcă, A.C.; Secu, M.; Vlad, A.; Pedarnig, J.D. Optical properties of zinc oxide thin films doped with aluminum and lithium. Thin Solid Film. 2010, 518, 4603–4606. [Google Scholar] [CrossRef]
- Makai, L.; Lehto, T.; Fodor, B.; King, P. Breakthrough instruments and products: Investigation of atomic layer deposited Al:ZnO layer by spectroscopic ellipsometry from the deep-UV to the mid-IR in one instrument. Rev. Sci. Instrum. 2021, 92, 119501. [Google Scholar] [CrossRef]
- Sago, Y.; Fujiwara, H. Mapping characterization of SnO2:F transparent conductive oxide layers by ellipsometry technique. Jpn. J. Appl. Phys. 2012, 51, 10NB01. [Google Scholar] [CrossRef]
- Hisashi Yoshikawa, H.Y.; Sadao Adachi, S.A. Optical Constants of ZnO. Jpn. J. Appl. Phys. 1997, 36, 6237. [Google Scholar] [CrossRef]
- Jenkins, T.E. Multiple-angle-of-incidence ellipsometry. J. Phys. D Appl. Phys. 1999, 32, R45–R56. [Google Scholar] [CrossRef]
- Sun, L.; Grant, J.T.; Jones, J.G.; Murphy, N.R. Tailoring electrical and optical properties of Al-doped ZnO thin films grown at room temperature by reactive magnetron co-sputtering: From band gap to near infrared. Opt. Mater. 2018, 84, 146–157. [Google Scholar] [CrossRef]
- Kim, J.S.; Jeong, J.-H.; Park, J.K.; Baik, Y.J.; Kim, I.H.; Seong, T.-Y.; Kim, W.M. Optical analysis of doped ZnO thin films using nonparabolic conduction-band parameters. J. Appl. Phys. 2012, 111, 123507. [Google Scholar] [CrossRef]
- Kim, W.M.; Kim, I.H.; Ko, J.H.; Cheong, B.; Lee, T.S.; Lee, K.S.; Kim, D.; Seong, T.-Y. Density-of-state effective mass and non-parabolicity parameter of impurity doped ZnO thin films. J. Phys. D Appl. Phys. 2008, 41, 195409. [Google Scholar] [CrossRef]
- Minami, T.; Sato, H.; Nanto, H.; Takata, S. Group III impurity doped zinc oxide thin films prepared by RF magnetron sputtering. Jpn. J. Appl. Phys. 1985, 24, L781. [Google Scholar] [CrossRef]
- Detor, A.J.; Hodge, A.M.; Chason, E.; Wang, Y.; Xu, H.; Conyers, M.; Nikroo, A.; Hamza, A. Stress and microstructure evolution in thick sputtered films. Acta Mater. 2009, 57, 2055–2065. [Google Scholar] [CrossRef]
- Sarma, B.K.; Rajkumar, P. Al-doped ZnO transparent conducting oxide with appealing electro-optical properties—Realization of indium free transparent conductors from sputtering targets with varying dopant concentrations. Mater. Today Commun. 2020, 23, 100870. [Google Scholar] [CrossRef]
- Brehme, S.; Fenske, F.; Fuhs, W.; Nebauer, E.; Poschenrieder, M.; Selle, B.; Sieber, I. Free-carrier plasma resonance effects and electron transport in reactively sputtered degenerate ZnO:Al films. Thin Solid Film. 1999, 342, 167–173. [Google Scholar] [CrossRef]
- Akagawa, M.; Fujiwara, H. Optical characterization of textured SnO2:F layers using spectroscopic ellipsometry. J. Appl. Phys. 2012, 112, 83507. [Google Scholar] [CrossRef]
- Guillén, C.; Trigo, J.F. Optical absorption enhancement in ultrathin chalcopyrite solar cells with Ag reflective back contact. Opt. Mater. 2022, 133, 113041. [Google Scholar] [CrossRef]
- Aouaj, M.A.; Diaz, R.; Belayachi, A.; Rueda, F.; Abd-Lefdil, M. Comparative study of ITO and FTO thin films grown by spray pyrolysis. Mater. Res. Bull. 2009, 44, 1458–1461. [Google Scholar] [CrossRef]
- Anandhi, R.; Ravichandran, K.; Mohan, R. Conductivity enhancement of ZnO:F thin films by the deposition of SnO2:F over layers for optoelectronic applications. Mater. Sci. Eng. B Solid-State Mater. Adv. Technol. 2013, 178, 65–70. [Google Scholar] [CrossRef]
- Koo, B.R.; Ahn, H.J. Structural, electrical, and optical properties of Sb-doped SnO2 transparent conductive oxides fabricated using an electrospray technique. Ceram. Int. 2014, 40, 4375–4381. [Google Scholar] [CrossRef]


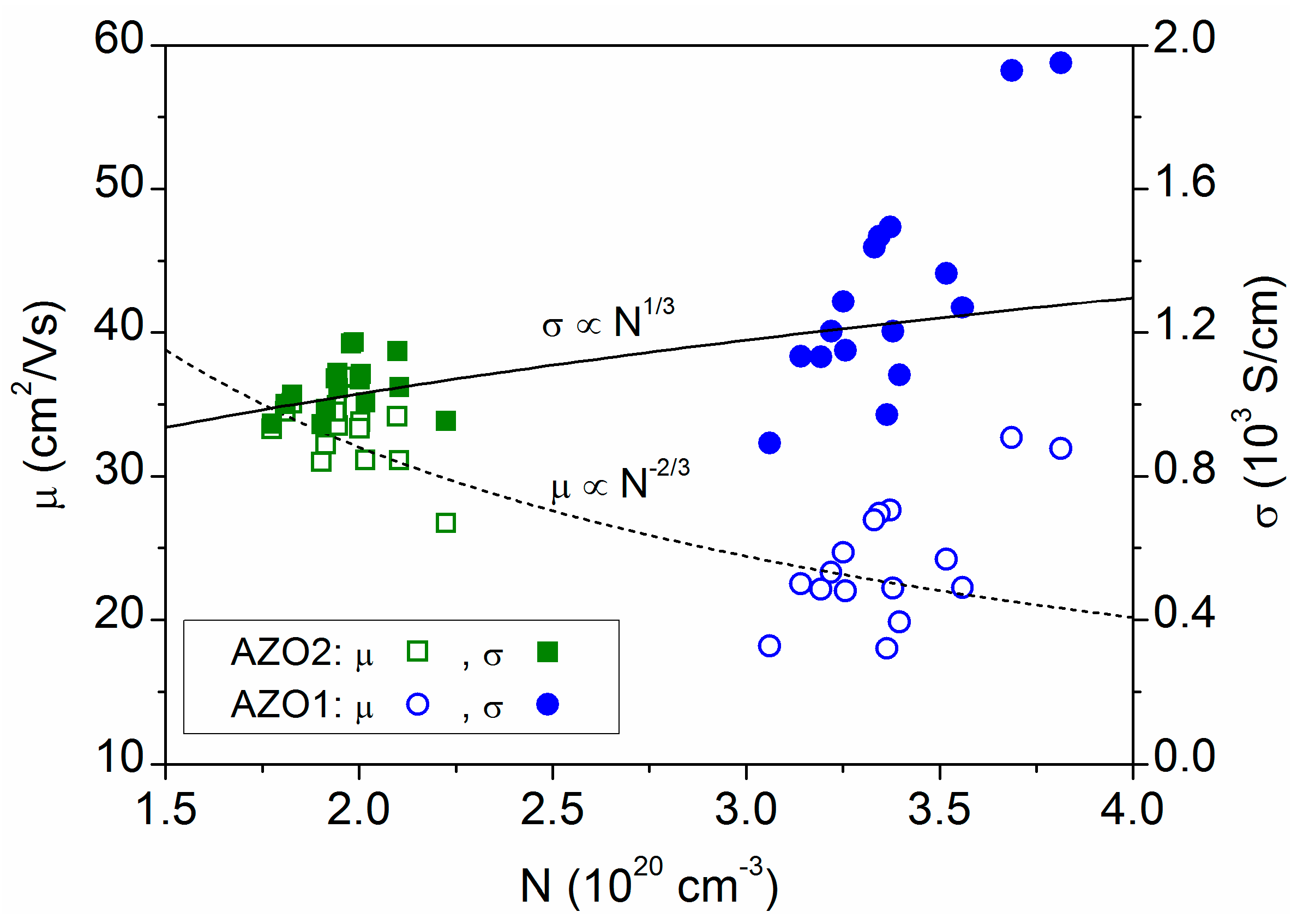
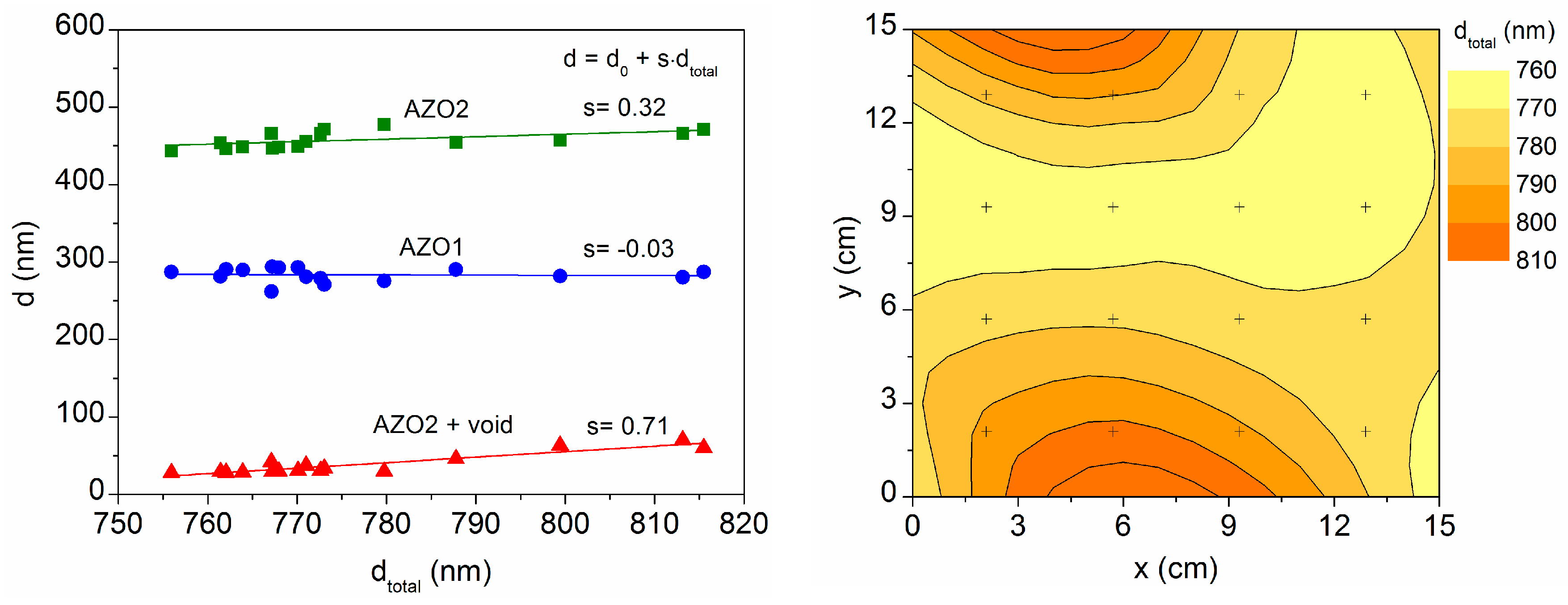

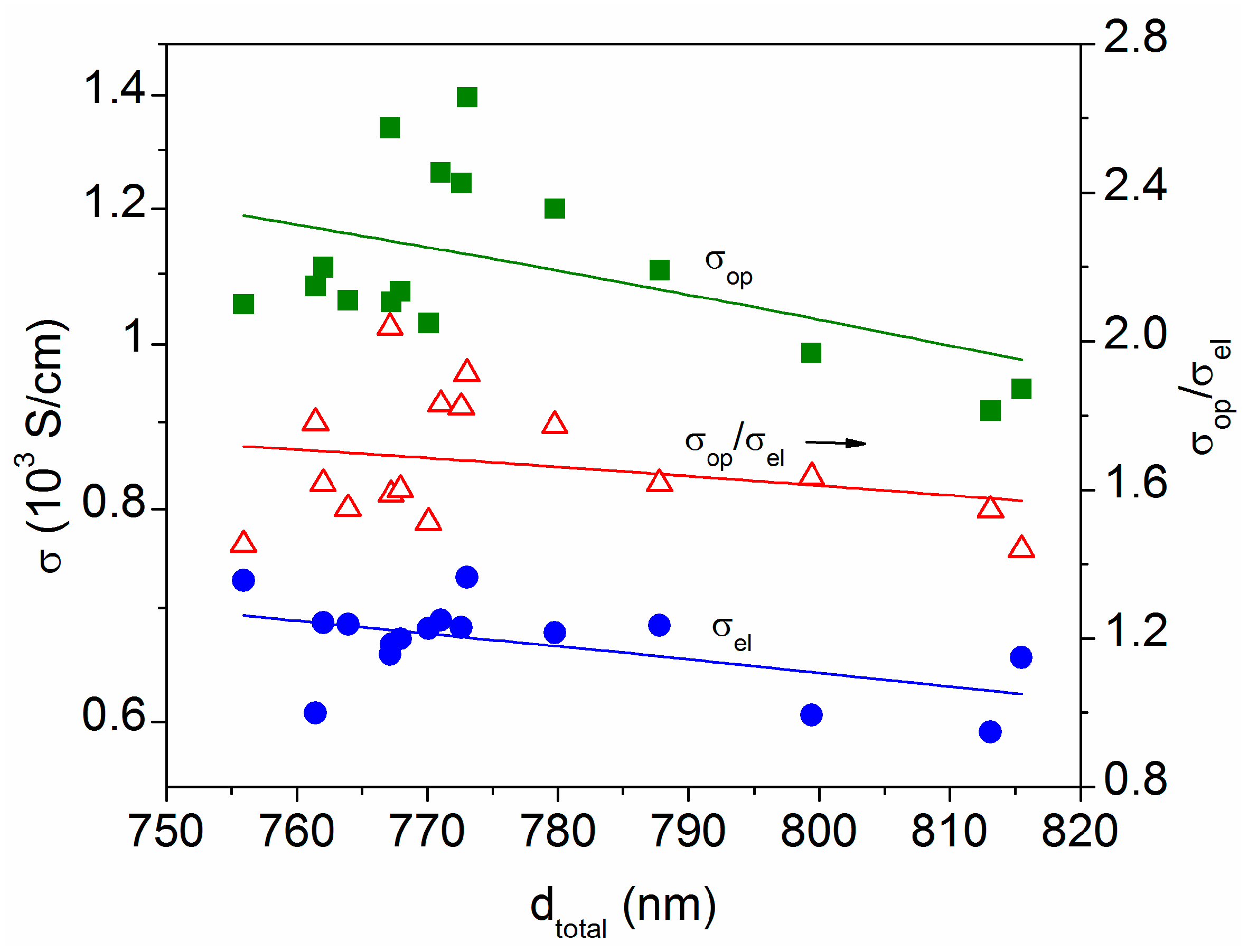
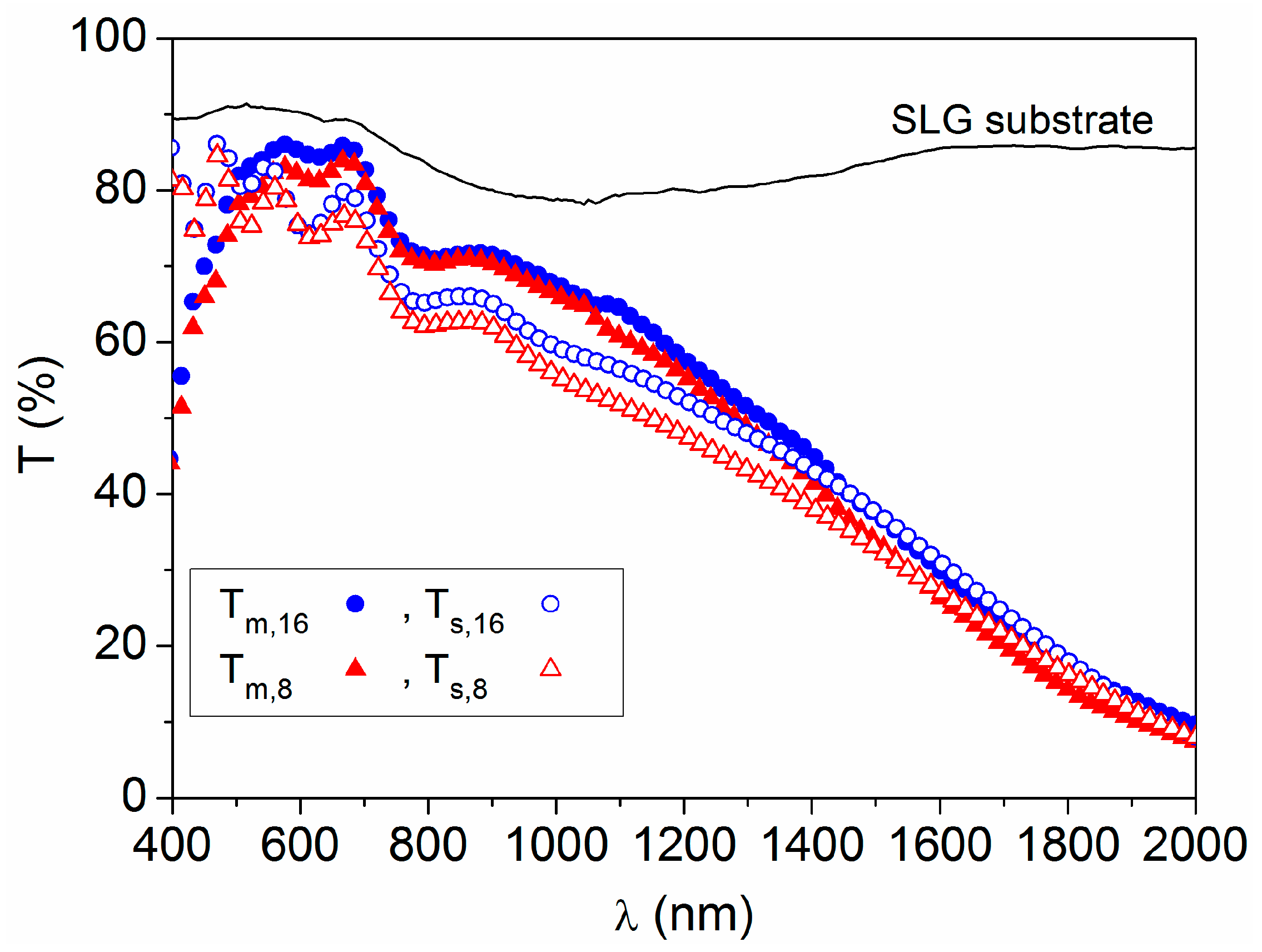

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillén, C.; Trigo, J.F. Ellipsometric Study on the Uniformity of Al:ZnO Thin Films Deposited Using DC Sputtering at Room Temperature over Large Areas. Materials 2023, 16, 6644. https://doi.org/10.3390/ma16206644
Guillén C, Trigo JF. Ellipsometric Study on the Uniformity of Al:ZnO Thin Films Deposited Using DC Sputtering at Room Temperature over Large Areas. Materials. 2023; 16(20):6644. https://doi.org/10.3390/ma16206644
Chicago/Turabian StyleGuillén, Cecilia, and Juan Francisco Trigo. 2023. "Ellipsometric Study on the Uniformity of Al:ZnO Thin Films Deposited Using DC Sputtering at Room Temperature over Large Areas" Materials 16, no. 20: 6644. https://doi.org/10.3390/ma16206644
APA StyleGuillén, C., & Trigo, J. F. (2023). Ellipsometric Study on the Uniformity of Al:ZnO Thin Films Deposited Using DC Sputtering at Room Temperature over Large Areas. Materials, 16(20), 6644. https://doi.org/10.3390/ma16206644







