Experimental and Numerical Study of Concrete Fracture Behavior with Multiple Cracks Based on the Meso-Model
Abstract
:1. Introduction
2. Three-Point Bending (TPB) Experiments of a Double-Crack Concrete Beam
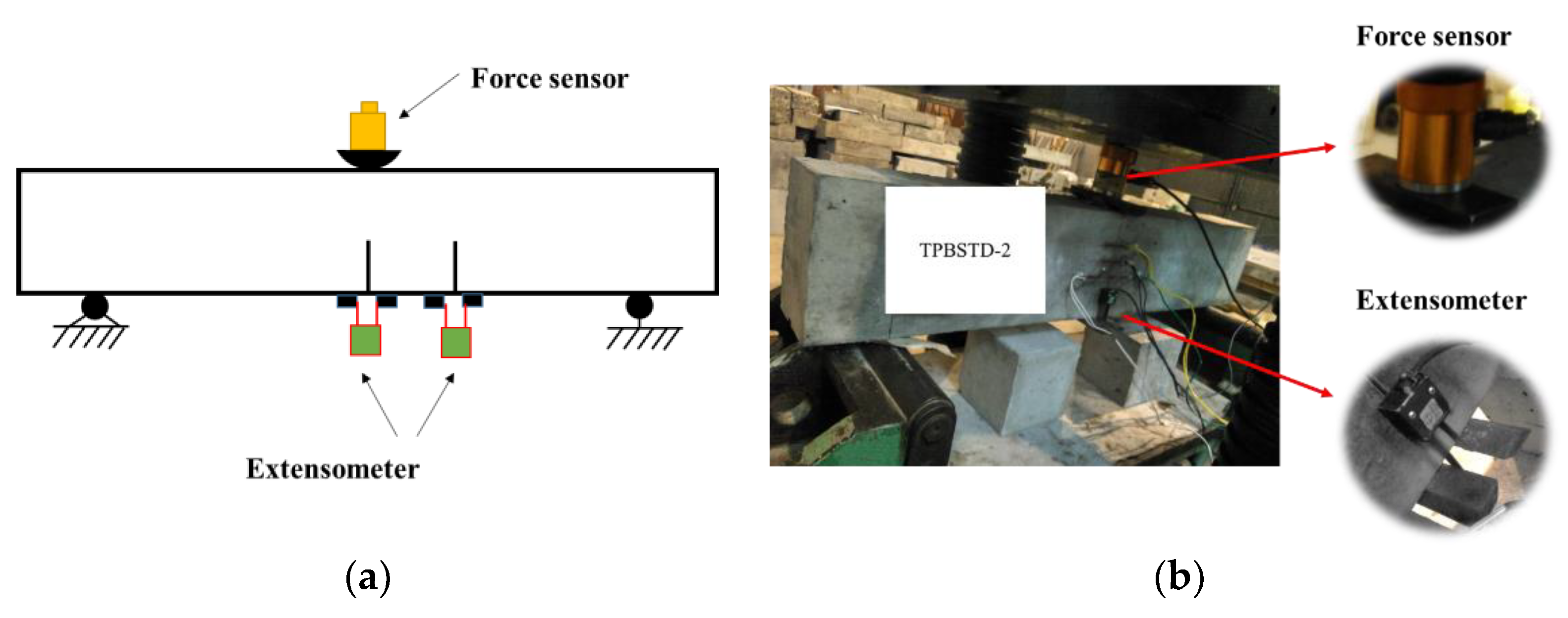
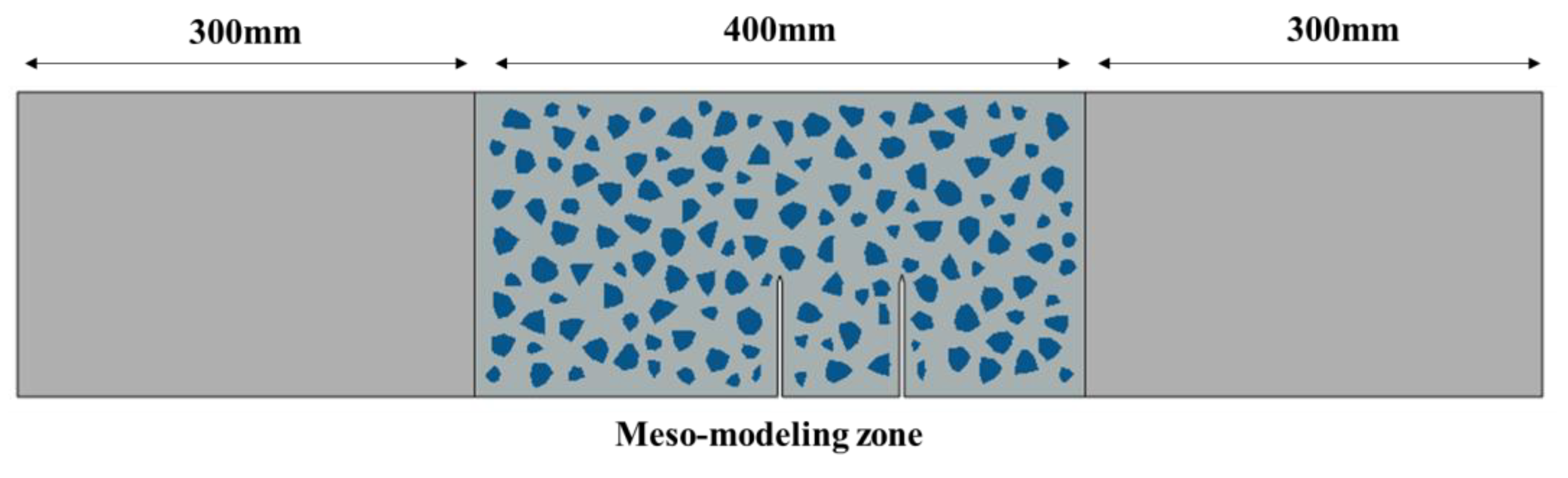
2.1. Geometry and Loading Scheme
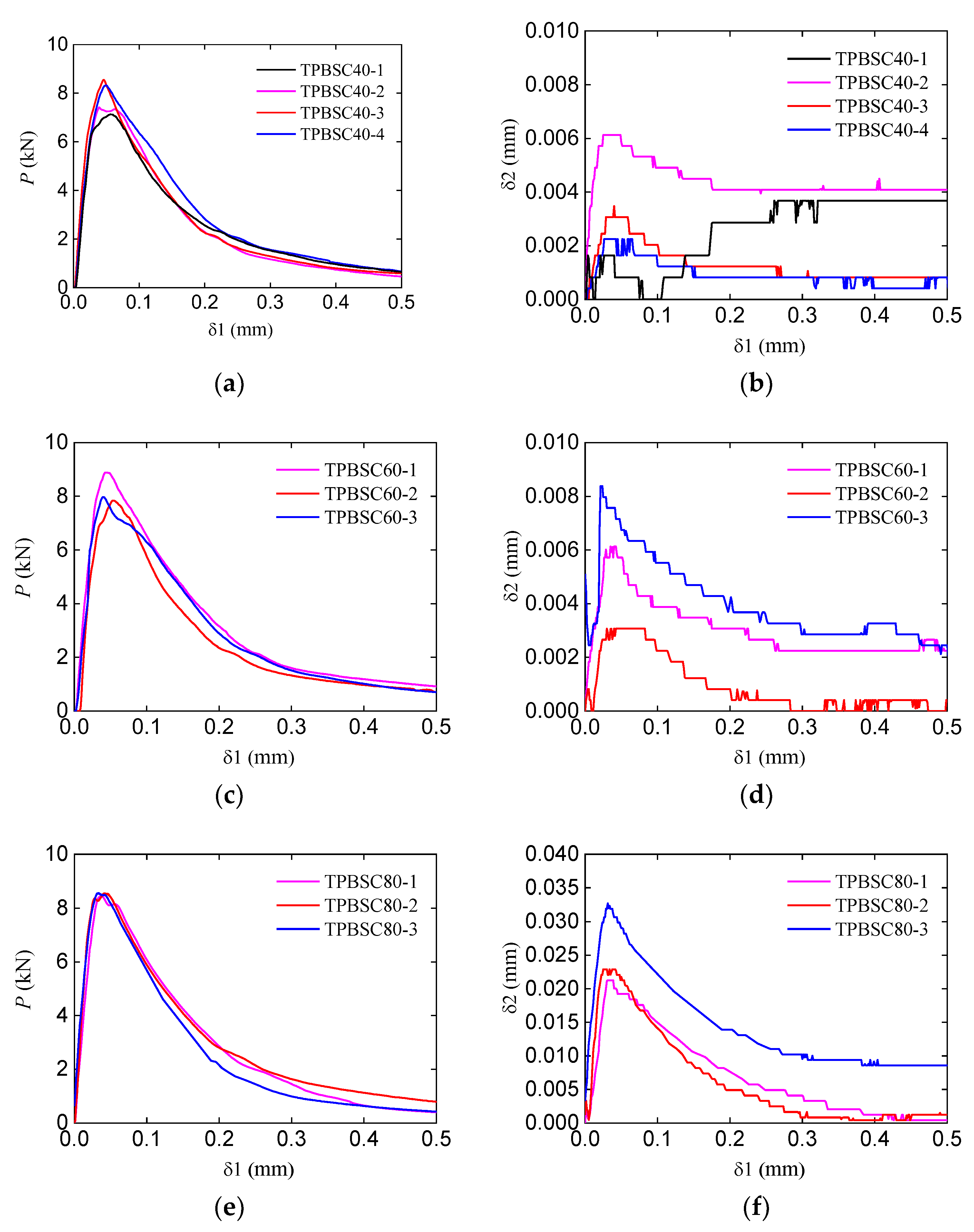
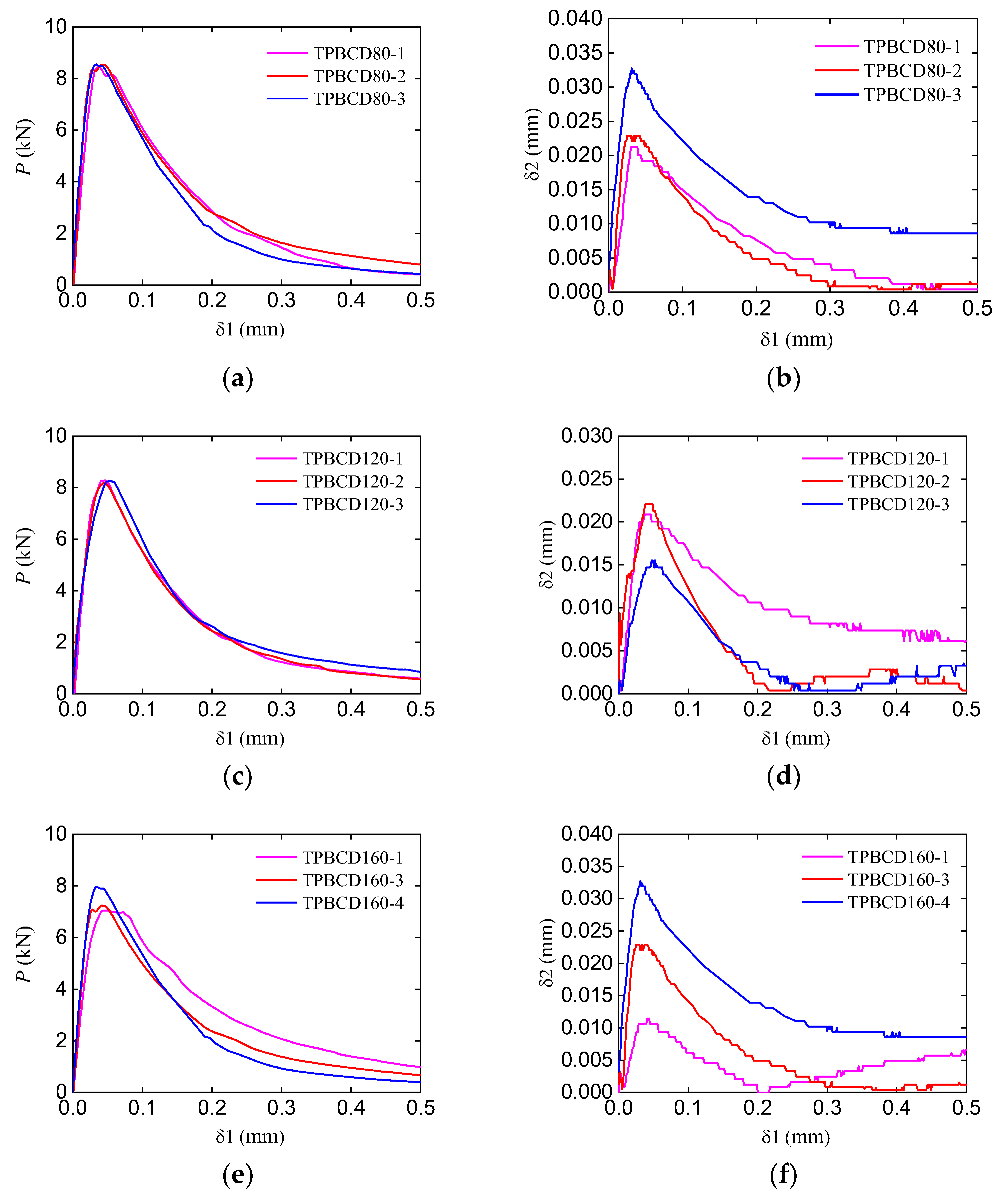
2.2. Experimental Results
3. Establishment of a Numerical Model Based on the Cohesive Zone Model
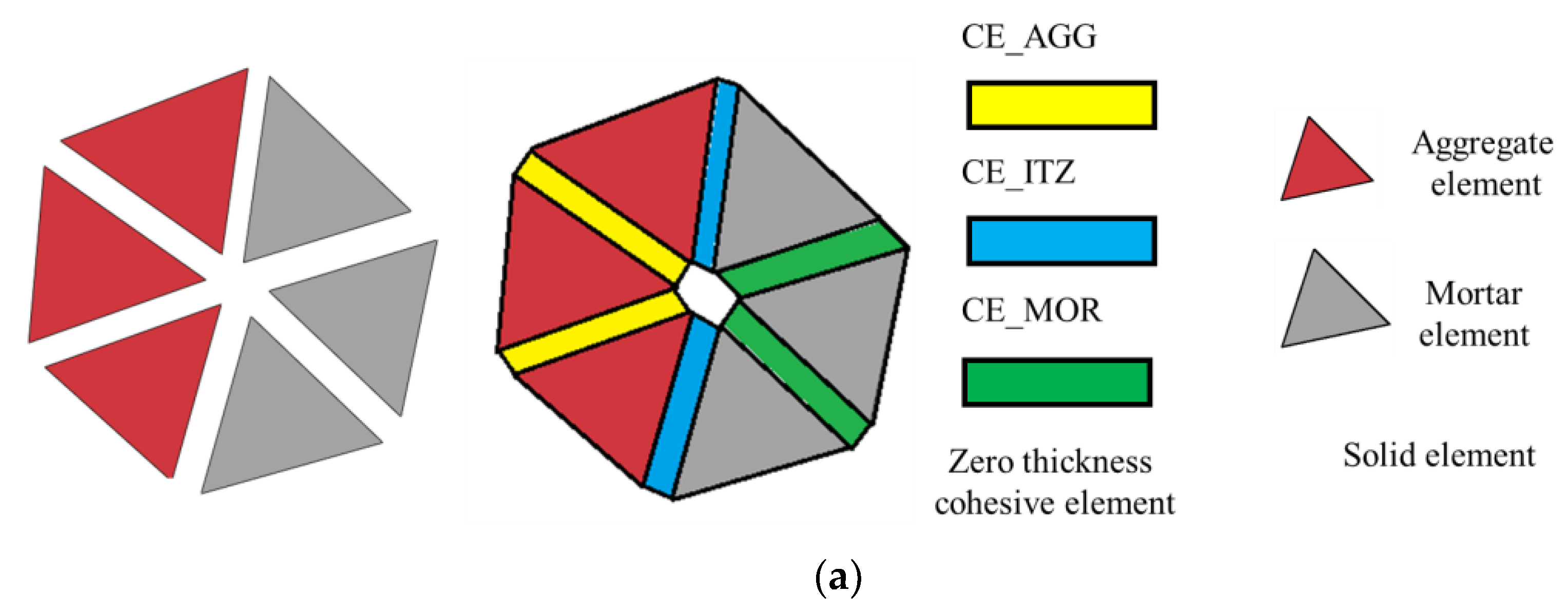
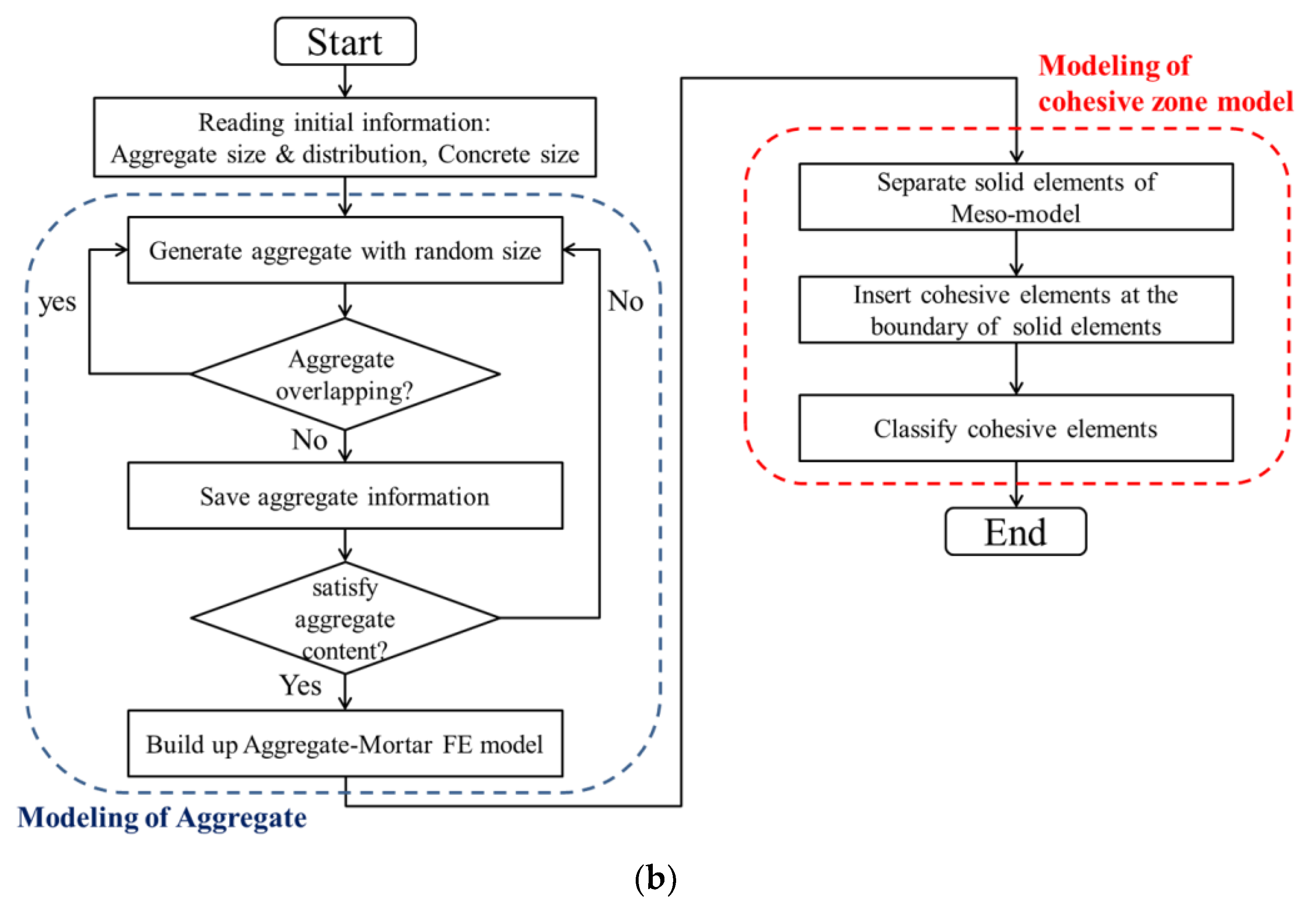
3.1. Meso-Modeling Method
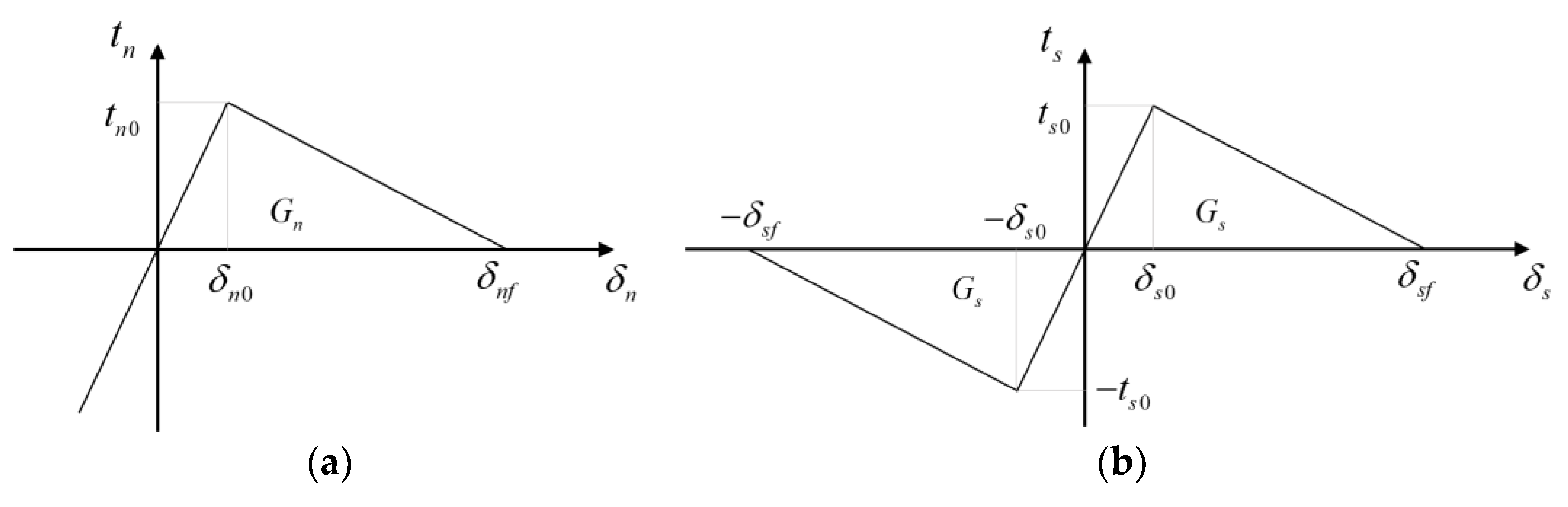
3.2. Constitutive Model of Concrete Potential Fracture Surfaces
- (1)
- Single-mode damage relation
- (2)
- Mixed-mode damage relation
- (3)
- Friction effect
- (4)
- Stresses in the mixed model
- (5)
- Internal energy calculation
4. Numerical Analysis and Discussion of the TPB Experiments
4.1. Input Data of the Finite Element Model
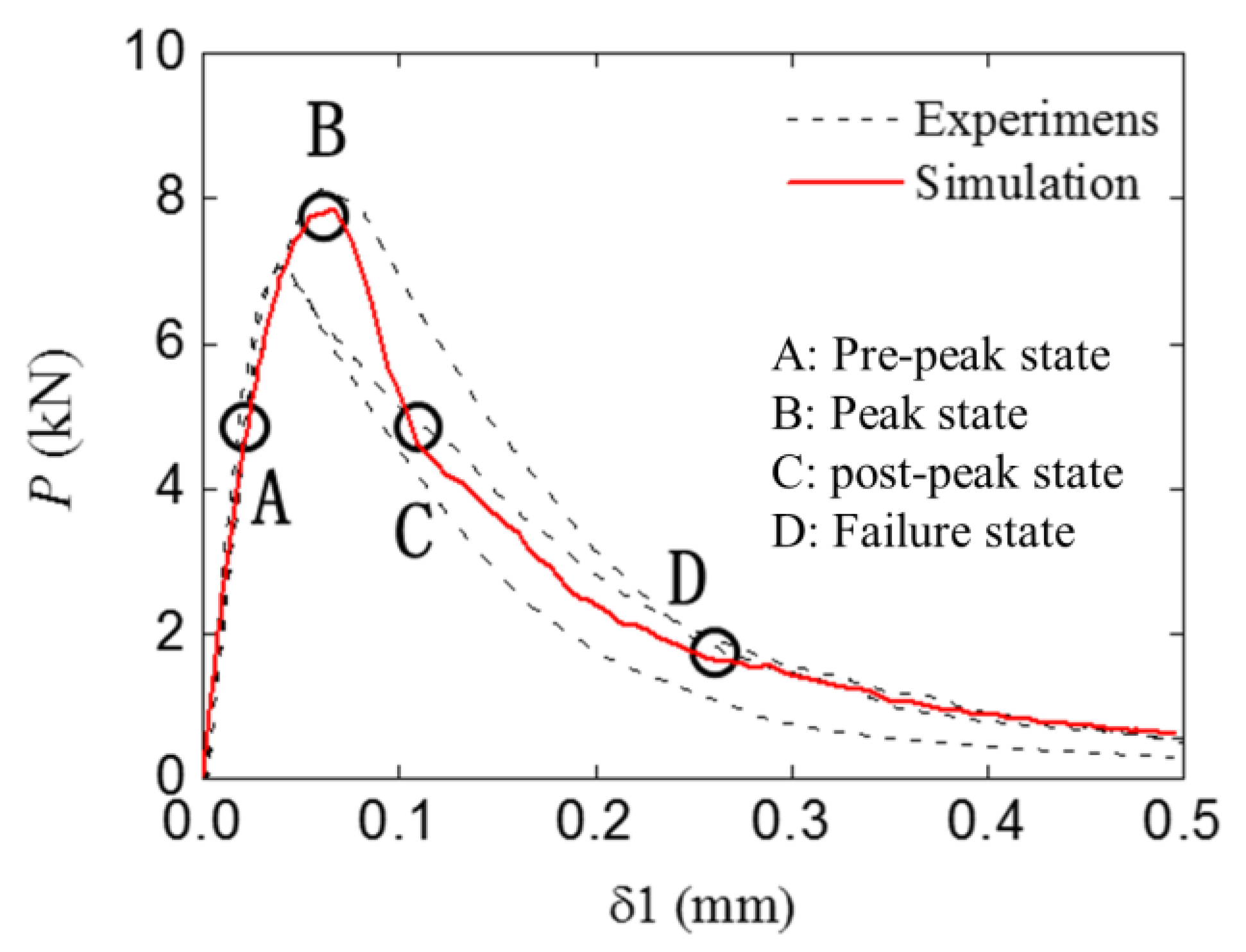
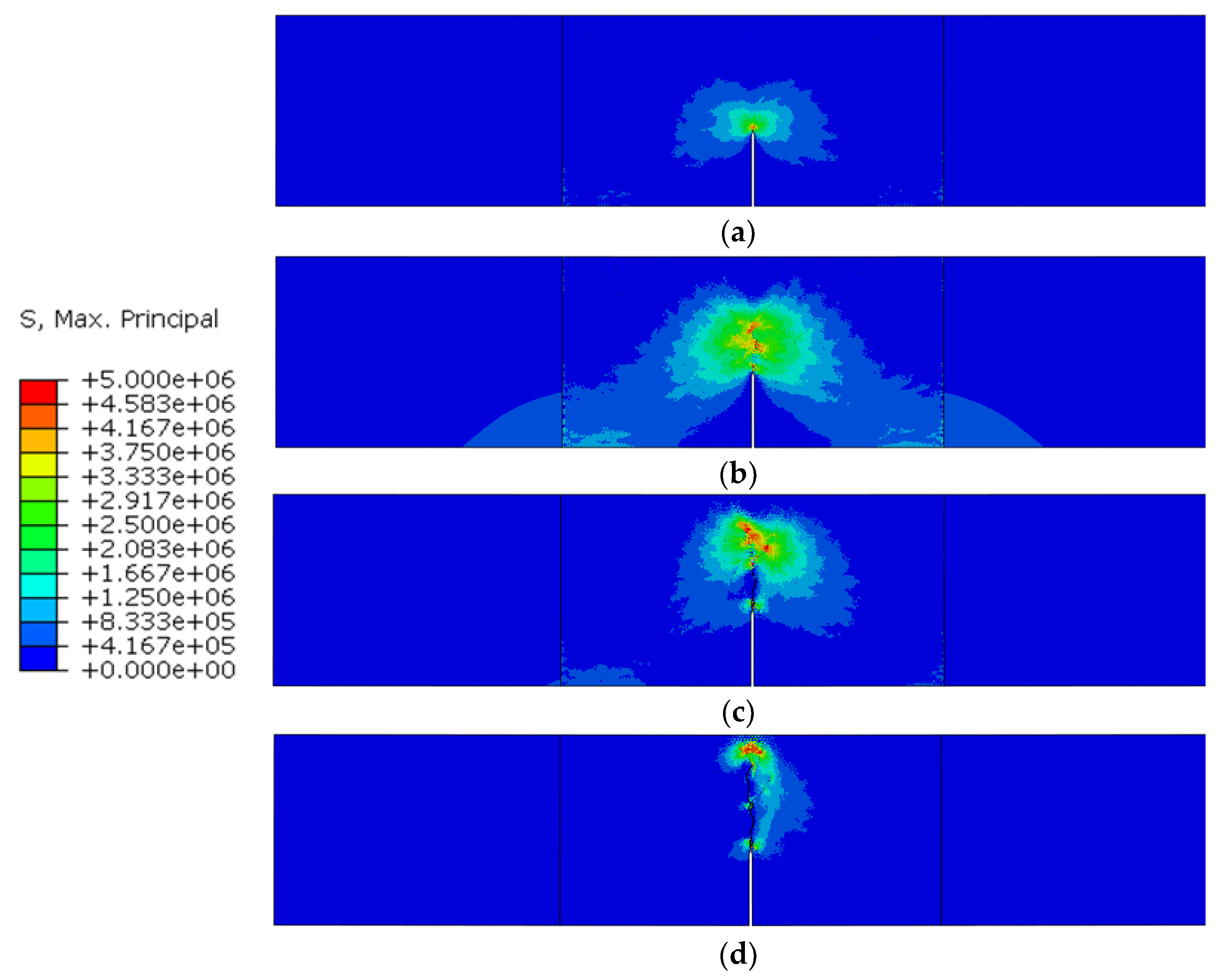
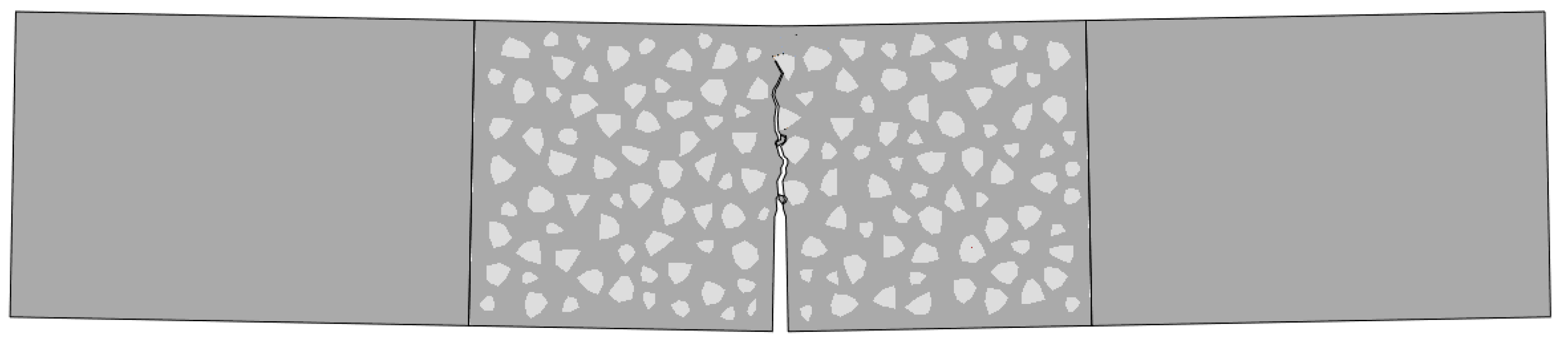
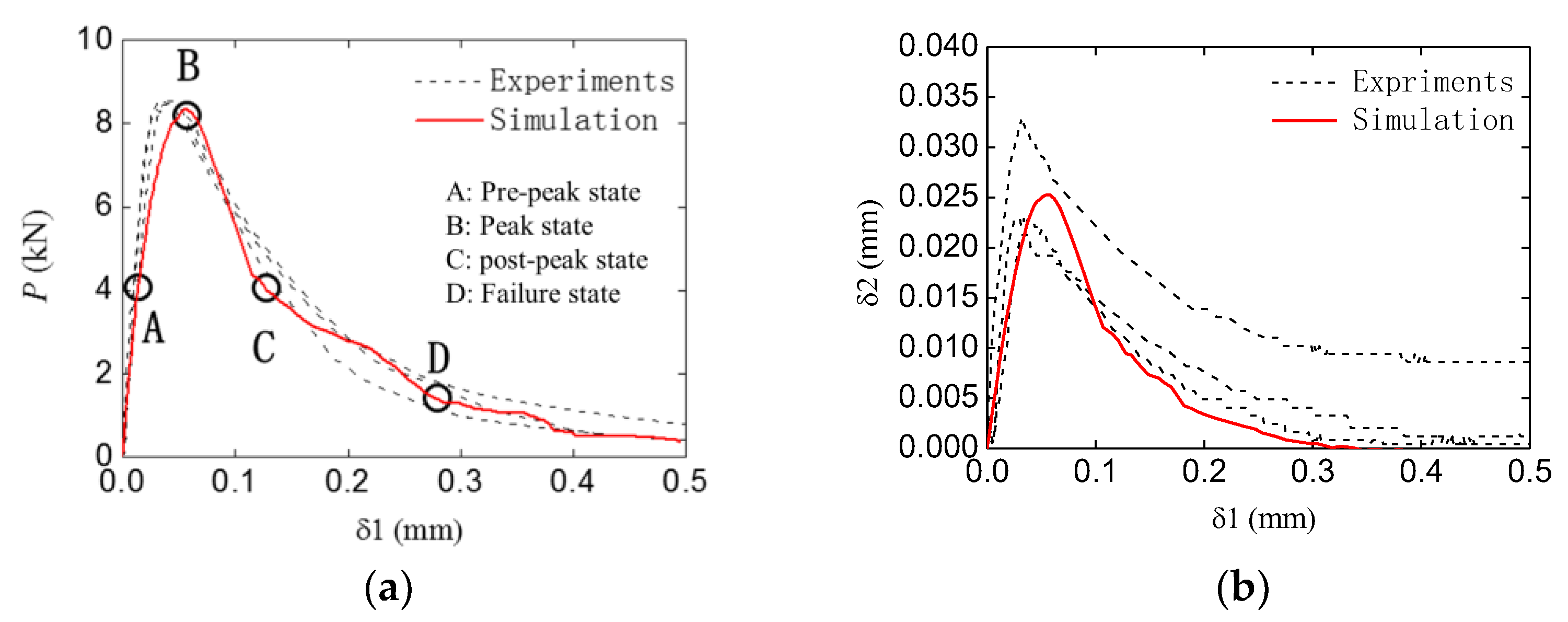
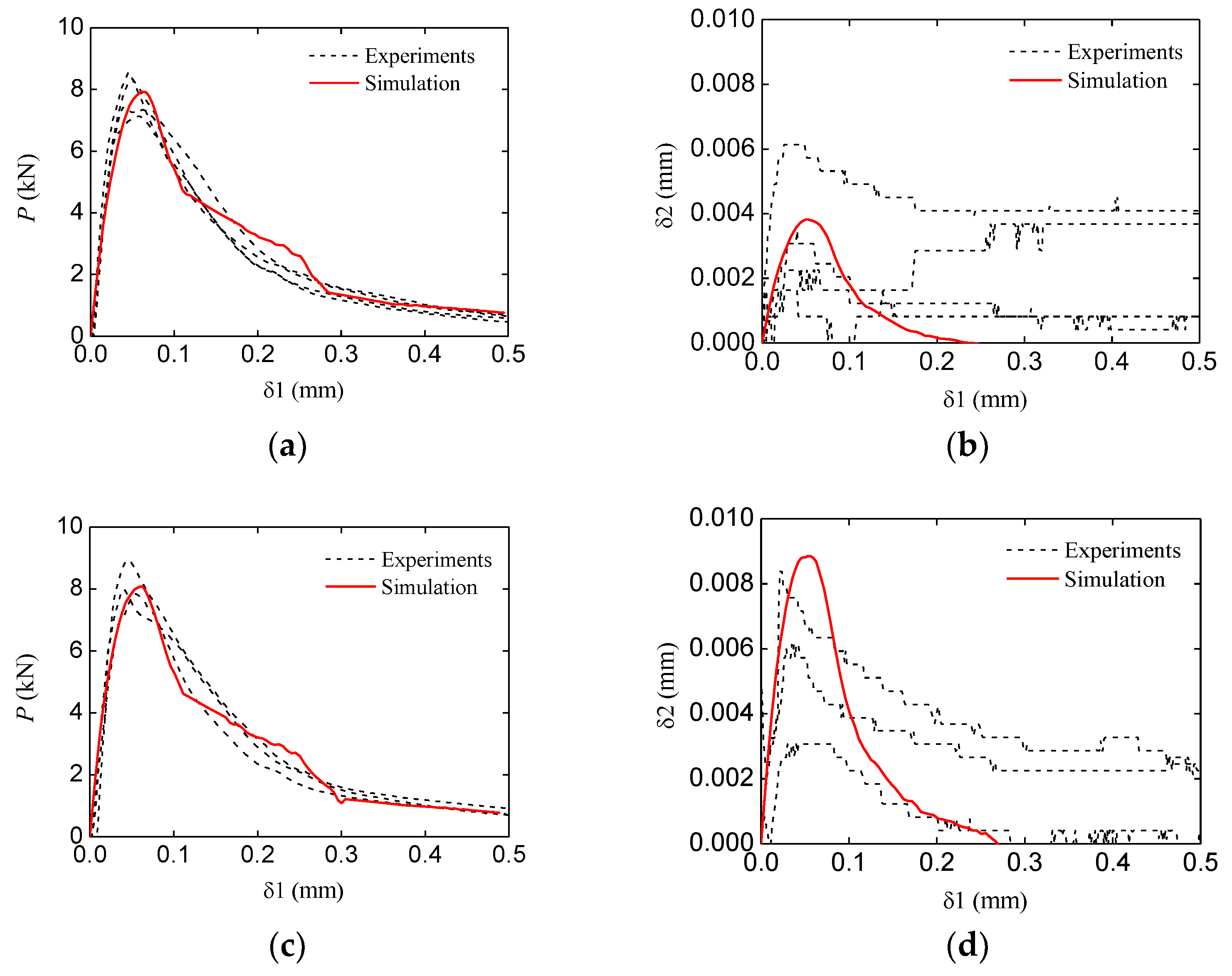
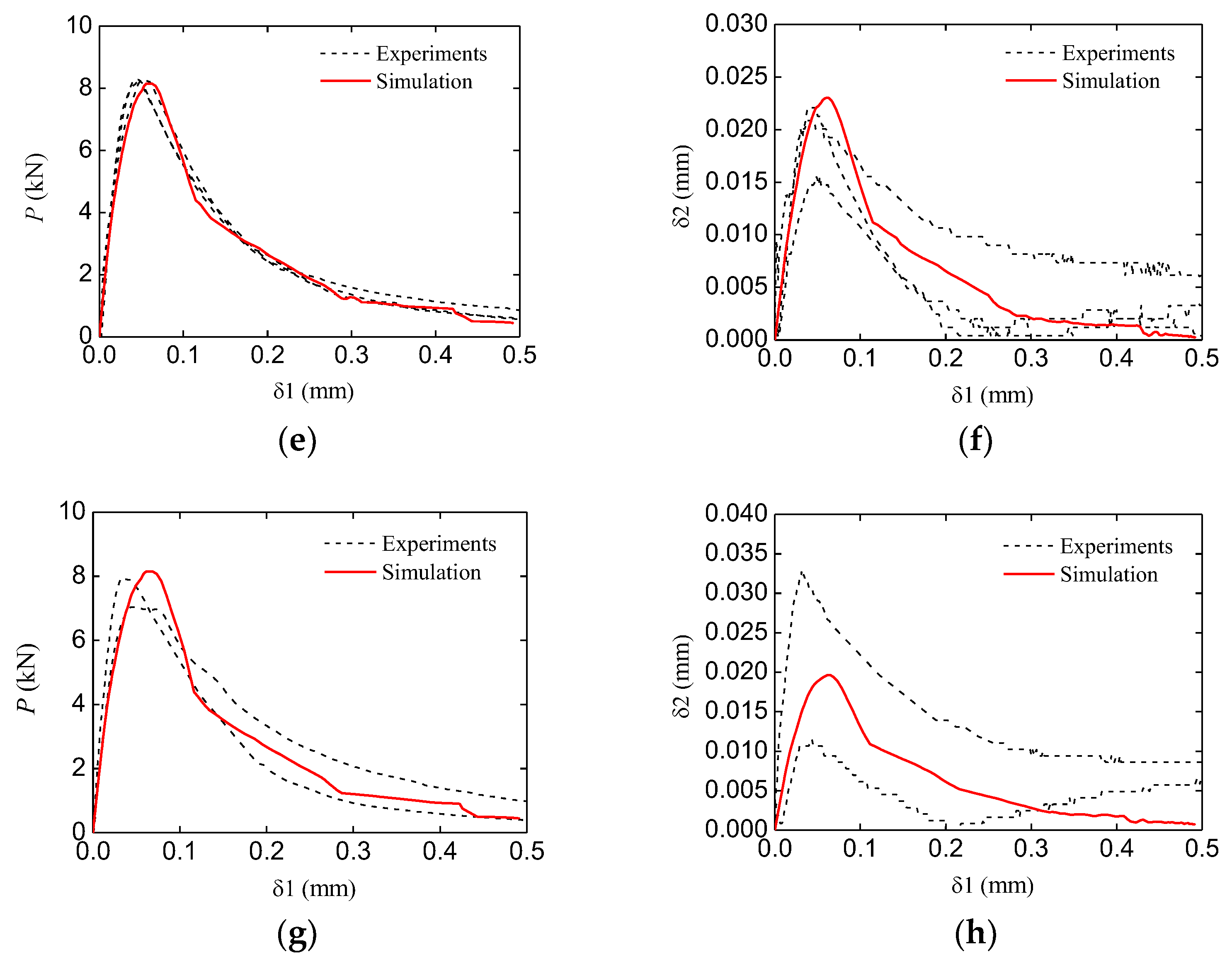
4.2. Fracture Behavior of the Standard and Double-Crack Beams
4.3. Bearing Capacity Analysis
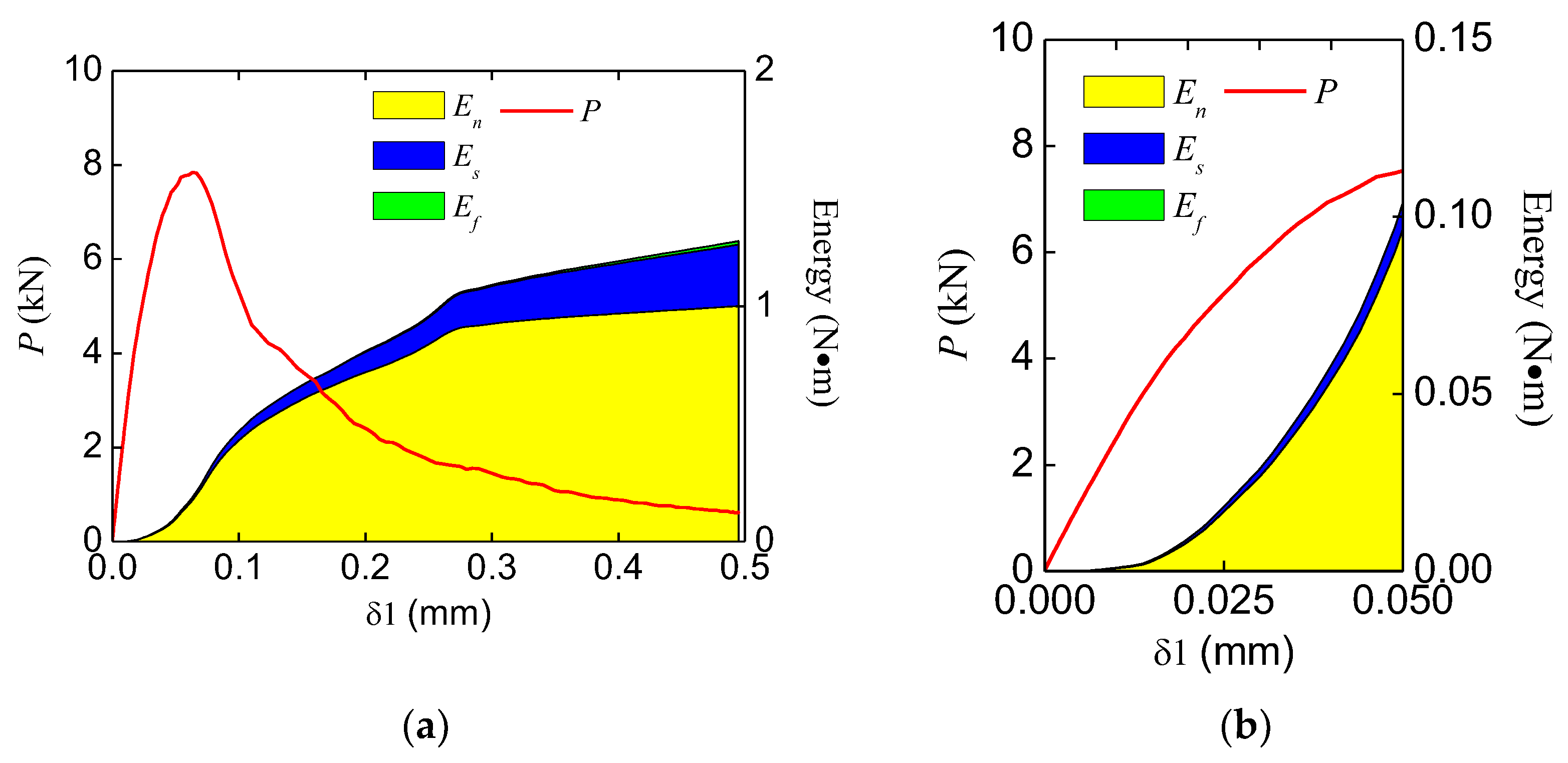
4.4. Energy Analysis
5. Conclusions
- In the mode Ⅰ fracture (or composite fracture dominated by mode Ⅰ fracture) condition, multiple cracks in a small zone will slightly increase the bearing capacity of the concrete. With an increase in the other crack’s lengths or with a decrease in the distance between cracks, the bearing capacity increases.
- In terms of energy consumption, the proportion of shear stress work (mode II) is highly relevant to the bearing capacity of multiple-parallel-crack concrete. Multiple parallel cracks change the proportion of mode Ⅱ fractures and finally cause an increase in the concrete bearing capacity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Damage factor in the mode-Ⅰ, mode-Ⅱ, and mixed-mode conditions | |
| Tensile strength of the interface | |
| Relative tensile strength of the interface | |
| f | Friction coefficient |
| Fracture energy in the mode-Ⅰ condition | |
| Fracture energy in the mode-Ⅱ condition | |
| Energy release rate in the normal direction | |
| Energy release rate in the tangential direction | |
| Interface stiffness in the normal direction | |
| Friction stresses in the tangential direction | |
| Maximum friction stress | |
| Normal stress | |
| Shear stress | |
| Shear strength | |
| Relative shear strength | |
| Displacement in the normal direction | |
| Normal displacement at the onset of interfacial softening in the mode-Ⅰ condition | |
| Relative normal displacement at the onset of interfacial softening in the mixed-mode condition | |
| Normal displacement at the onset of interfacial failure in the mode-Ⅰ condition | |
| Relative normal displacement at the onset of interfacial failure in the mixed-mode condition | |
| Total displacement in the tangential direction | |
| Tangential displacement at the onset of interfacial softening in the mode-Ⅱ/Ⅲ condition | |
| Relative tangential displacement at the onset of interfacial softening in the mixed-mode condition | |
| Tangential displacement at the onset of interfacial failure in the mode-Ⅱ/Ⅲ condition | |
| Relative tangential displacement at the onset of interfacial failure in the mixed-mode condition | |
| Tangential sliding displacement that has been generated during the loading process | |
| Total relative displacement | |
| Total relative displacement at the onset of interfacial softening in the mixed-mode condition | |
| Total relative displacement at the onset of interfacial failure in the mixed-mode condition | |
| TPB | Three-point bending |
| CMOD | Crack mouth opening displacement |
| CZM | Cohesive zone model |
References
- Sun, B.; Xiao, R.; Ruan, W.; Wang, P. Corrosion-induced cracking fragility of RC bridge with improved concrete carbonation and steel reinforcement corrosion models. Eng. Struct. 2020, 208, 110313. [Google Scholar] [CrossRef]
- Chen, S.; Duffield, C.; Miramini, S.; Raja, B.N.K.; Zhang, L. Life-cycle modelling of concrete cracking and reinforcement corrosion in concrete bridges: A case study. Eng. Struct. 2021, 237, 112143. [Google Scholar] [CrossRef]
- Rosso, M.M.; Asso, R.; Aloisio, A.; Di Benedetto, M.; Cucuzza, R.; Greco, R. Corrosion effects on the capacity and ductility of concrete half-joint bridges. Constr. Build. Mater. 2022, 360, 129555. [Google Scholar] [CrossRef]
- Pelle, A.; Briseghella, B.; Bergami, A.V.; Fiorentino, G.; Giaccu, G.F.; Lavorato, D.; Quaranta, G.; Rasulo, A.; Nuti, C. Time-dependent cyclic behavior of reinforced concrete bridge columns under chlorides-induced corrosion and rebars buckling. Struct. Concr. 2022, 23, 81–103. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Planas, J. Fracture and Size Effect in Concrete and Other Quasibrittle Materials; Routledge: Oxfordshire, UK, 2019. [Google Scholar]
- Hoover, C.G.; Bažant, Z.P.; Vorel, J.; Wendner, R.; Hubler, M.H. Comprehensive concrete fracture tests: Description and results. Eng. Fract. Mech. 2013, 114, 92–103. [Google Scholar] [CrossRef]
- Hoover, C.G.; Bažant, Z.P. Comprehensive concrete fracture tests: Size effects of types 1 & 2, crack length effect and postpeak. Eng. Fract. Mech. 2013, 110, 281–289. [Google Scholar]
- Ožbolt, J.; Sharma, A.; Reinhardt, H. Dynamic fracture of concrete–compact tension specimen. Int. J. Solids Struct. 2011, 48, 1534–1543. [Google Scholar] [CrossRef]
- Chen, C.; Fan, X.; Chen, X. Experimental investigation of concrete fracture behavior with different loading rates based on acoustic emission. Constr. Build. Mater. 2020, 237, 117472. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, K.; Wang, X.; Zhou, W. Strength, fracture and fatigue of pervious concrete. Constr. Build. Mater. 2013, 42, 97–104. [Google Scholar] [CrossRef]
- Zhou, C.; Zhu, Z.; Wang, Z.; Qiu, H. Deterioration of concrete fracture toughness and elastic modulus under simulated acid-sulfate environment. Constr. Build. Mater. 2018, 176, 490–499. [Google Scholar] [CrossRef]
- Sarker, P.K.; Haque, R.; Ramgolam, K.V. Fracture behaviour of heat cured fly ash based geopolymer concrete. Mater. Des. 2013, 44, 580–586. [Google Scholar] [CrossRef]
- Hu, S.; Xu, A.; Hu, X.; Yin, Y. Study on fracture characteristics of reinforced concrete wedge splitting tests. Comput. Concr. Int. J. 2016, 18, 337–354. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Wu, Z.; Yu, H.; Fang, Q. Fracture properties of steel fiber reinforced concrete: Size effect study via mesoscale modelling approach. Eng. Fract. Mech. 2022, 260, 108193. [Google Scholar] [CrossRef]
- Kazemian, F.; Rooholamini, H.; Hassani, A. Mechanical and fracture properties of concrete containing treated and untreated recycled concrete aggregates. Constr. Build. Mater. 2019, 209, 690–700. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, X.; Gao, H.; Zhu, H. Heterogeneous fracture simulation of three-point bending plain-concrete beam with double notches. Acta Mech. Solida Sin. 2016, 29, 232–244. [Google Scholar] [CrossRef]
- Pedersen, R.R.; Simone, A.; Sluys, L.J. Mesoscopic modeling and simulation of the dynamic tensile behavior of concrete. Cem. Concr. Res. 2013, 50, 74–87. [Google Scholar] [CrossRef]
- Shen, L.; Ren, Q.; Xia, N.; Sun, L.; Xia, X. Mesoscopic numerical simulation of effective thermal conductivity of tensile cracked concrete. Constr. Build. Mater. 2015, 95, 467–475. [Google Scholar] [CrossRef]
- Liu, J.; Yu, W.; Du, X.; Zhang, S.; Li, D. Meso-scale modelling of the size effect on dynamic compressive failure of concrete under different strain rates. Int. J. Impact Eng. 2019, 125, 1–12. [Google Scholar]
- Karavelić, E.; Nikolić, M.; Ibrahimbegovic, A.; Kurtović, A. Concrete meso-scale model with full set of 3D failure modes with random distribution of aggregate and cement phase. Part I: Formulation and numerical implementation. Comput. Methods Appl. Mech. Eng. 2019, 344, 1051–1072. [Google Scholar] [CrossRef]
- Sun, B.; Huang, X.; Zheng, Y.; Guo, L. Multi-scale lattice method for mesoscopic crack growth simulation of concrete structures. Theor. Appl. Fract. Mech. 2020, 106, 102475. [Google Scholar] [CrossRef]
- Grassl, P. 3D lattice meso-scale modelling of the effect of lateral compression on tensile fracture processes in concrete. Int. J. Solids Struct. 2022, 262, 112086. [Google Scholar] [CrossRef]
- Roth, S.; Léger, P.; Soulaïmani, A. A combined XFEM–damage mechanics approach for concrete crack propagation. Comput. Methods Appl. Mech. Eng. 2015, 283, 923–955. [Google Scholar] [CrossRef]
- Chen, H.; Xu, B.; Wang, J.; Nie, X.; Mo, Y. XFEM-based multiscale simulation on monotonic and hysteretic behavior of reinforced-concrete columns. Appl. Sci. 2020, 10, 7899. [Google Scholar] [CrossRef]
- Xia, X.; Chen, F.; Gu, X.; Fang, N.; Zhang, Q. Interfacial debonding constitutive model and XFEM simulation for mesoscale concrete. Comput. Struct. 2021, 242, 106373. [Google Scholar] [CrossRef]
- Murali, K.; Deb, A. Effect of meso-structure on strength and size effect in concrete under tension. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 181–207. [Google Scholar] [CrossRef]
- Ma, G.; Xie, Y.; Long, G.; Tang, Z.; Zhou, X.; Zeng, X.; Li, J. Mesoscale investigation on concrete creep behaviors based on discrete element method. Constr. Build. Mater. 2022, 342, 127957. [Google Scholar] [CrossRef]
- Luo, J.; Wang, Y.; Asamoto, S.; Nagai, K. Mesoscopic simulation of crack propagation and bond behavior in ASR damaged concrete with internal/external restraint by 3D RBSM. Cem. Concr. Compos. 2022, 129, 104488. [Google Scholar] [CrossRef]
- López, C.M.; Carol, I.; Aguado, A. Meso-structural study of concrete fracture using interface elements. II: Compression, biaxial and Brazilian test. Mater. Struct. 2008, 41, 601–620. [Google Scholar] [CrossRef]
- López, C.M.; Carol, I.; Aguado, A. Meso-structural study of concrete fracture using interface elements. I: Numerical model and tensile behavior. Mater. Struct. 2008, 41, 583–599. [Google Scholar] [CrossRef]
- Wang, X.F.; Yang, Z.J.; Yates, J.R.; Jivkov, A.P.; Zhang, C. Monte Carlo simulations of mesoscale fracture modelling of concrete with random aggregates and pores. Constr. Build. Mater. 2015, 75, 35–45. [Google Scholar] [CrossRef]
- Huang, Y.; Hu, S. A cohesive model for concrete mesostructure considering friction effect between cracks. Comput. Concr. Int. J. 2019, 24, 51–61. [Google Scholar]
- Huang, Y.; Zhang, W.; Liu, X. Assessment of Diagonal Macrocrack-Induced Debonding Mechanisms in FRP-Strengthened RC Beams. J. Compos. Constr. 2022, 26, 4022056. [Google Scholar] [CrossRef]
- De Maio, U.; Greco, F.; Leonetti, L.; Blasi, P.N.; Pranno, A. An investigation about debonding mechanisms in FRP-strengthened RC structural elements by using a cohesive/volumetric modeling technique. Theor. Appl. Fract. Mech. 2022, 117, 103199. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, X. Determination of fracture parameters for crack propagation in concrete using an energy approach. Eng. Fract. Mech. 2008, 75, 4292–4308. [Google Scholar] [CrossRef]
- Simulia. Abaqus Analysis User’s Guide, Version 6.14; Dassault Systemes Providence: Johnston, RI, USA, 2014. [Google Scholar]
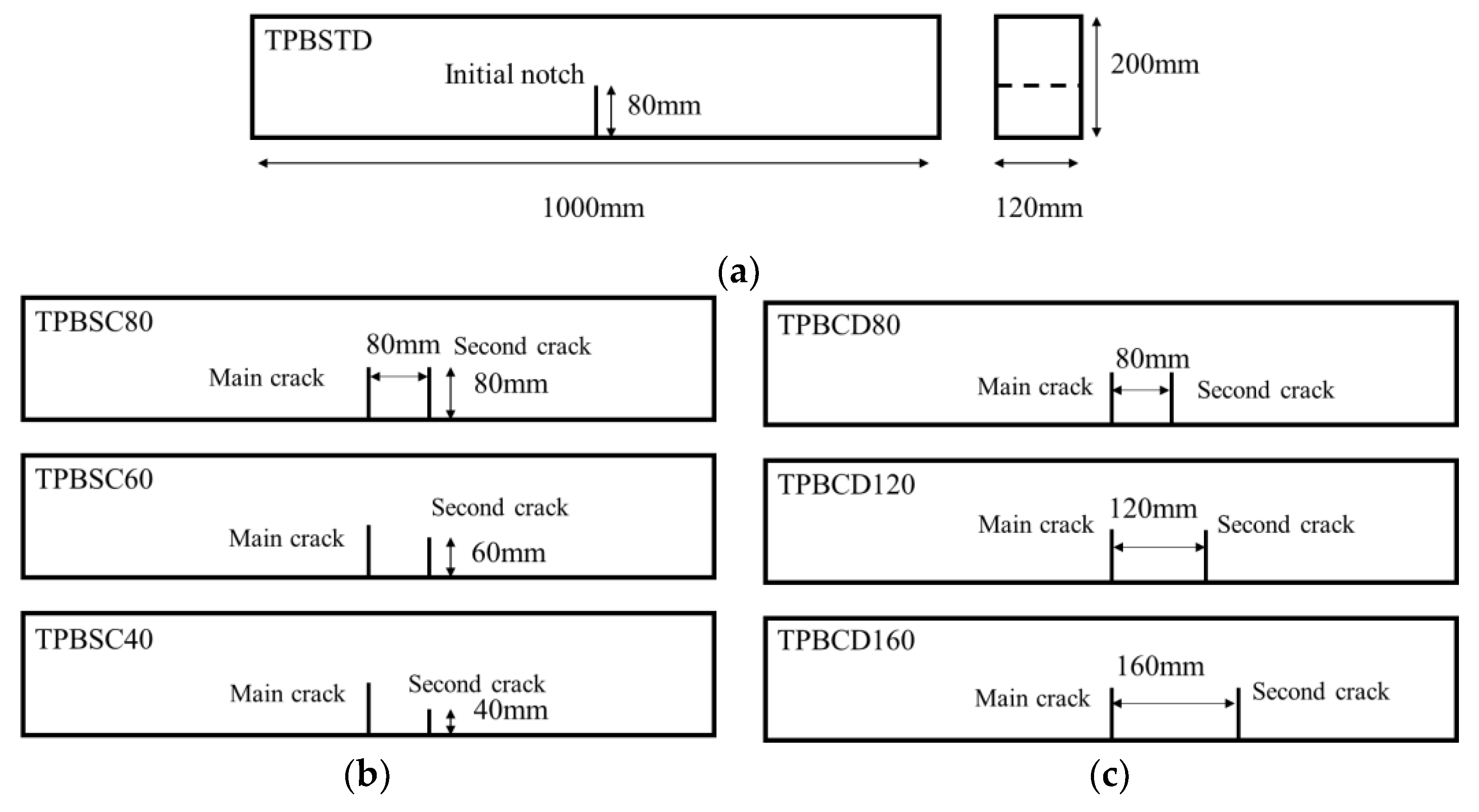







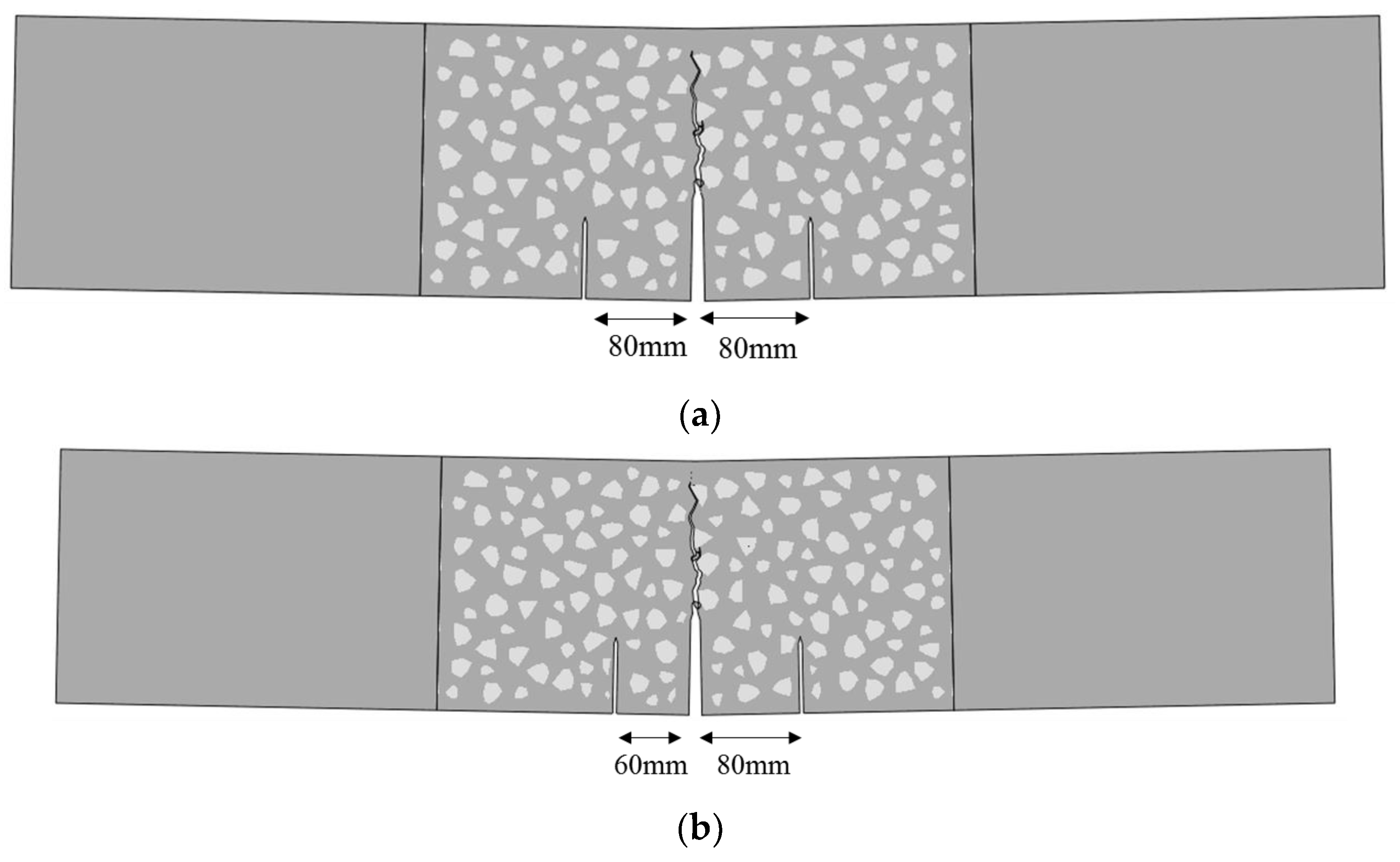
| Specimens | Main Crack Length a0/mm | Second Crack Length a1/mm | Cracks Distance d/mm |
|---|---|---|---|
| TPBSTD-1~4 | 80 | — | |
| TPBSC40-1~4 | 80 | 40 | 80 |
| TPBSC60-1~4 | 80 | 60 | 80 |
| TPBSC80-1~4 (TPBCD80-1~4) | 80 | 80 | 80 |
| TPBCD120-1~4 | 80 | 80 | 120 |
| TPBCD160-1~4 | 80 | 80 | 160 |
| Specimens | Peak Load (kN) | Corresponding CMOD (mm) | Corresponding CMOD (mm) |
|---|---|---|---|
| TPBSTD-1 | 7.02 | 0.0388 | — |
| TPBSTD-2 | 7.04 | 0.0387 | — |
| TPBSTD-4 | 8.07 | 0.0613 | — |
| Average | 7.38 | 0.0462 | |
| TPBSC40-1 | 7.37 | 0.0387 | 0.0016 |
| TPBSC40-2 | 8.48 | 0.0463 | 0.0061 |
| TPBSC40-3 | 8.26 | 0.0500 | 0.0031 |
| TPBSC40-4 | 7.07 | 0.0375 | 0.0017 |
| Average | 7.80 | 0.0431 | 0.0031 |
| TPBSC60-1 | 8.82 | 0.0463 | 0.0057 |
| TPBSC60-2 | 7.78 | 0.0525 | 0.0031 |
| TPBSC60-3 | 7.91 | 0.0400 | 0.0076 |
| Average | 8.17 | 0.0463 | 0.0055 |
| TPBSC80-1 | 8.39 | 0.0363 | 0.0213 |
| TPBSC80-2 | 8.48 | 0.0450 | 0.0221 |
| TPBSC80-3 | 8.49 | 0.0337 | 0.0324 |
| Average | 8.45 | 0.0383 | 0.0253 |
| TPBCD120-1 | 8.21 | 0.0413 | 0.0208 |
| TPBCD120-2 | 8.03 | 0.0450 | 0.0221 |
| TPBCD120-3 | 8.20 | 0.0537 | 0.0147 |
| Average | 8.15 | 0.0467 | 0.0192 |
| TPBCD160-2 | 7.09 | 0.0450 | 0.0106 |
| TPBCD160-4 | 7.83 | 0.0350 | 0.0319 |
| Average | 7.46 | 0.0400 | 0.0213 |
| Element Type | (GPa/m) | (MPa) | (MPa) | (N/m) | (N/m) | |
|---|---|---|---|---|---|---|
| CE_MOR | 106 | 4.2 | 14.7 | 70 | 700 | 0.35 |
| CE_ITZ | 106 | 2.1 | 7.35 | 35 | 350 | 0.35 |
| CE_AGG | 106 | - | - | - | - | - |
| Experiment Group | Peak Force (kN) | (N∙m) | (N∙m) | Total Energy Increment (N∙m) | Proportion (%) | Proportion (%) |
|---|---|---|---|---|---|---|
| Standard TPBSTD | 7.84 | 0.156 | 0.012 | 0.167 | 93.0 | 7.0 |
| TPBSC40 | 7.92 | 0.163 | 0.013 | 0.176 | 92.9 | 7.1 |
| TPBSC60 | 8.08 | 0.144 | 0.013 | 0.157 | 91.7 | 8.3 |
| TPBSC80 (TPBCD80) | 8.34 | 0.151 | 0.014 | 0.165 | 91.5 | 8.5 |
| TPBSC120 | 8.15 | 0.145 | 0.013 | 0.158 | 92.0 | 8.0 |
| TPBSC160 | 7.98 | 0.141 | 0.012 | 0.153 | 92.5 | 7.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhang, W.; Huang, Y. Experimental and Numerical Study of Concrete Fracture Behavior with Multiple Cracks Based on the Meso-Model. Materials 2023, 16, 6311. https://doi.org/10.3390/ma16186311
Wang Z, Zhang W, Huang Y. Experimental and Numerical Study of Concrete Fracture Behavior with Multiple Cracks Based on the Meso-Model. Materials. 2023; 16(18):6311. https://doi.org/10.3390/ma16186311
Chicago/Turabian StyleWang, Zhanliang, Wei Zhang, and Yiqun Huang. 2023. "Experimental and Numerical Study of Concrete Fracture Behavior with Multiple Cracks Based on the Meso-Model" Materials 16, no. 18: 6311. https://doi.org/10.3390/ma16186311
APA StyleWang, Z., Zhang, W., & Huang, Y. (2023). Experimental and Numerical Study of Concrete Fracture Behavior with Multiple Cracks Based on the Meso-Model. Materials, 16(18), 6311. https://doi.org/10.3390/ma16186311







