A Mini Review on Fluid Topology Optimization
Abstract
1. Introduction
2. Explicit Methods
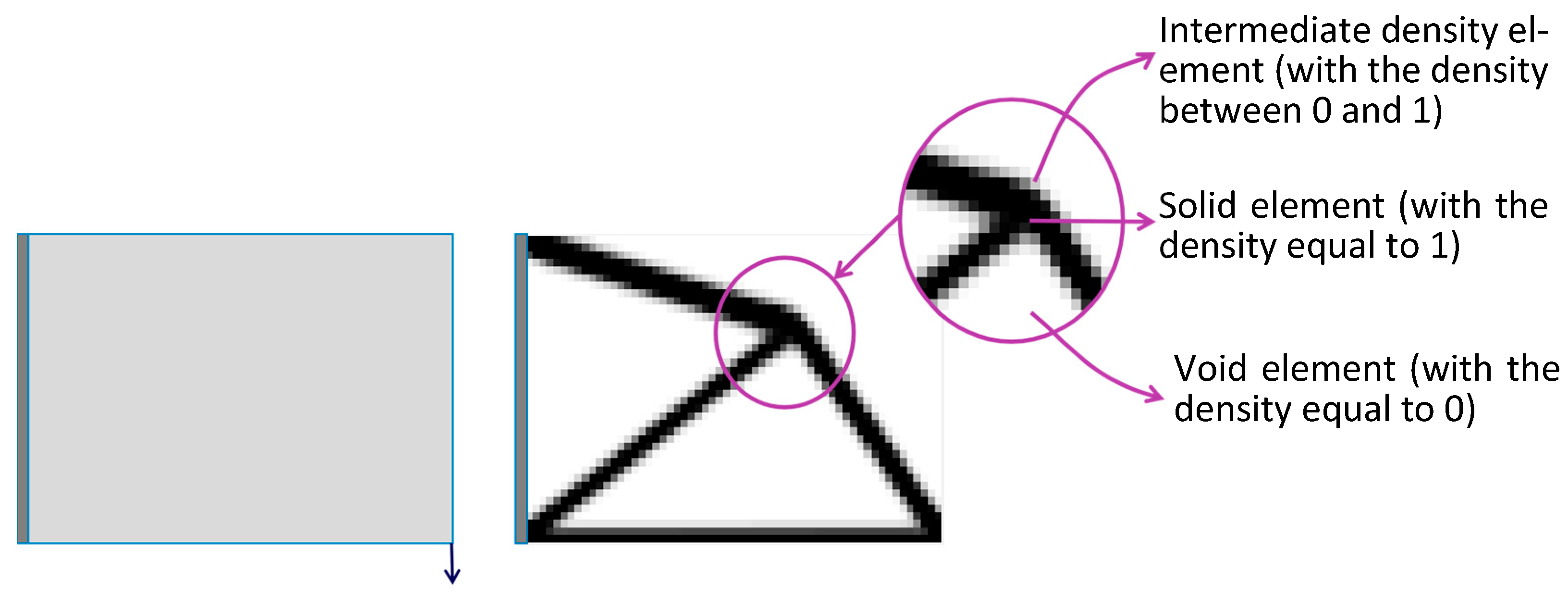
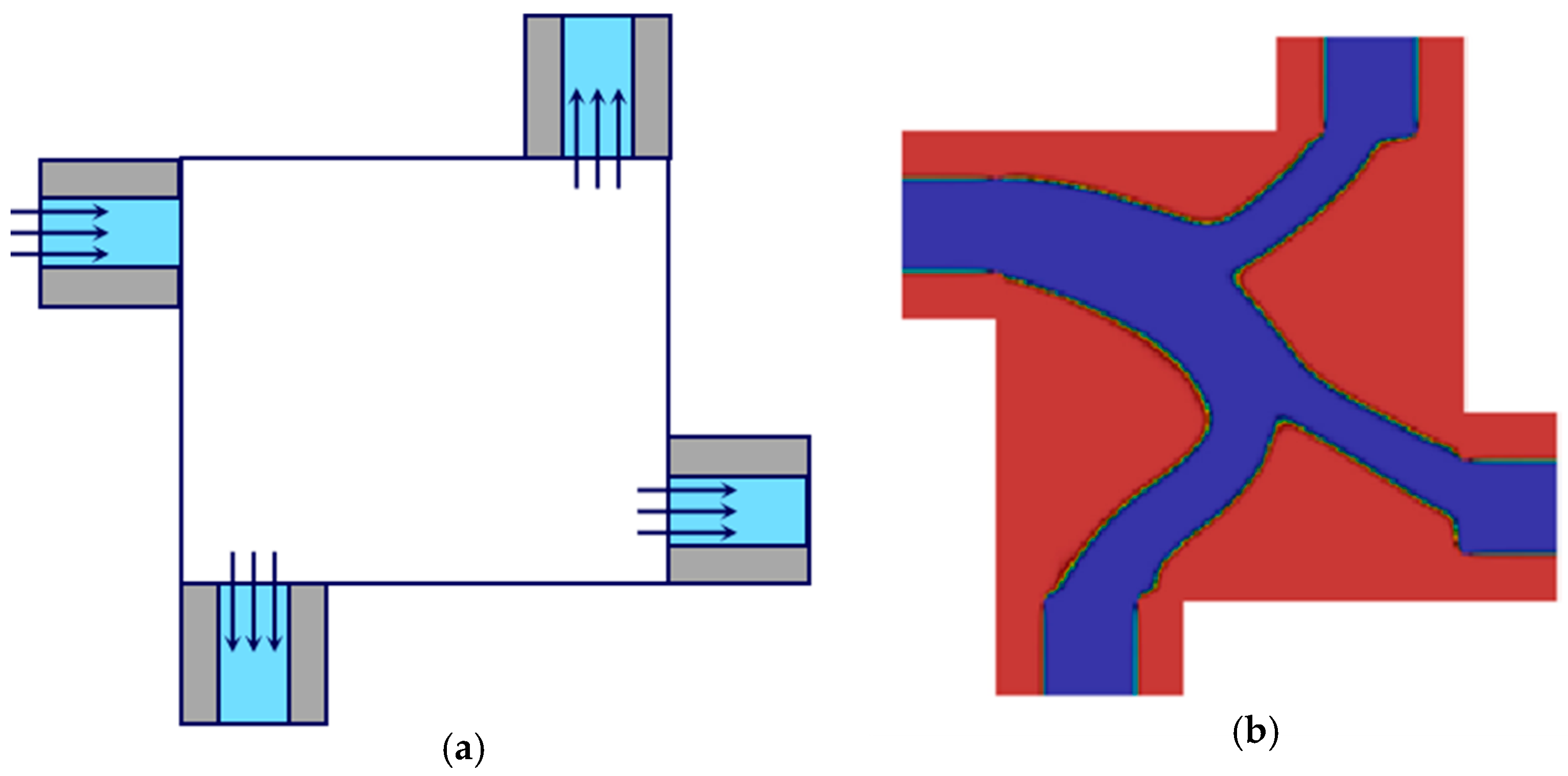
2.1. Density-Based Method
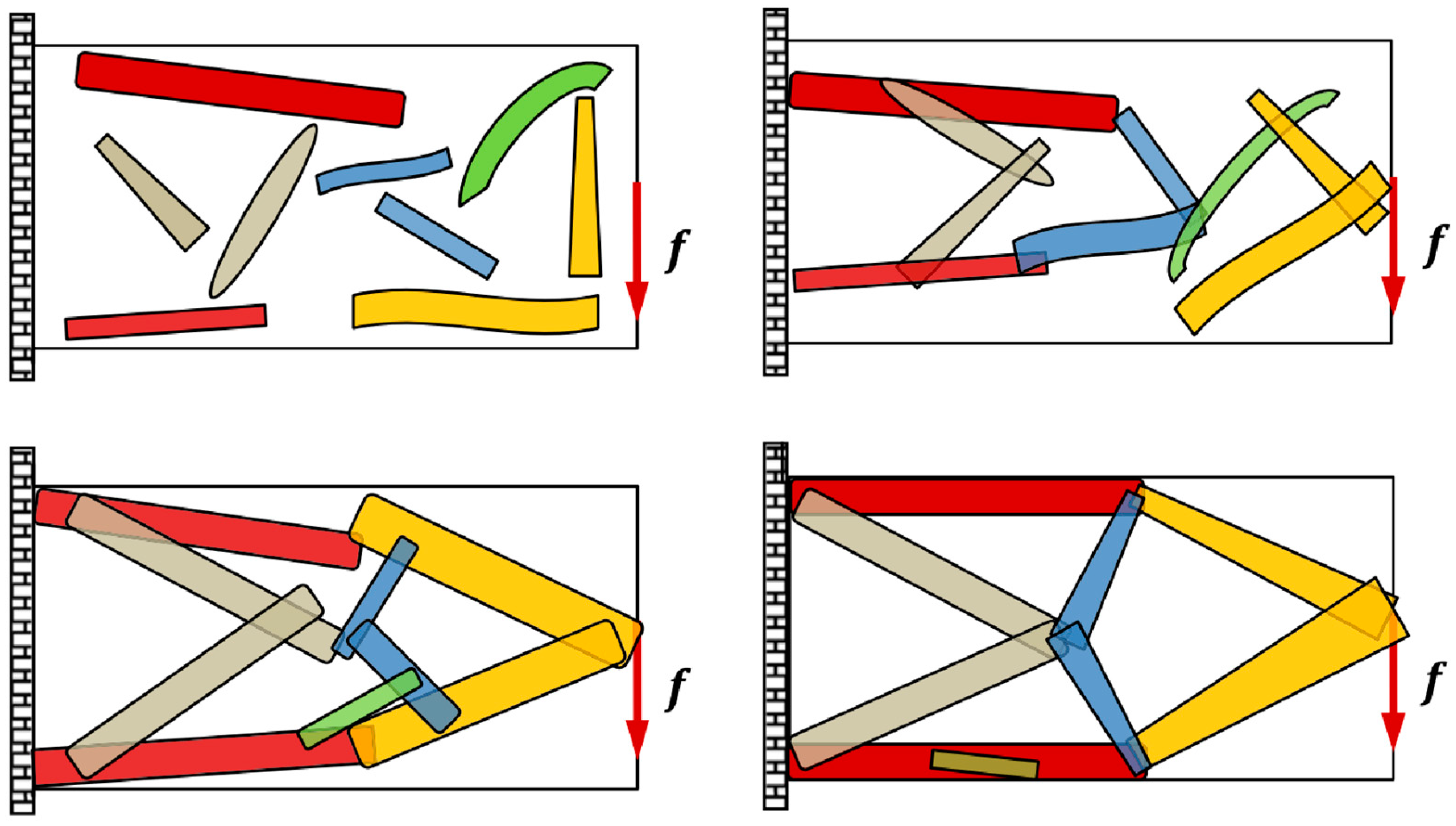
2.2. Moving Morphable Components/Voids Method
3. Implicit Methods
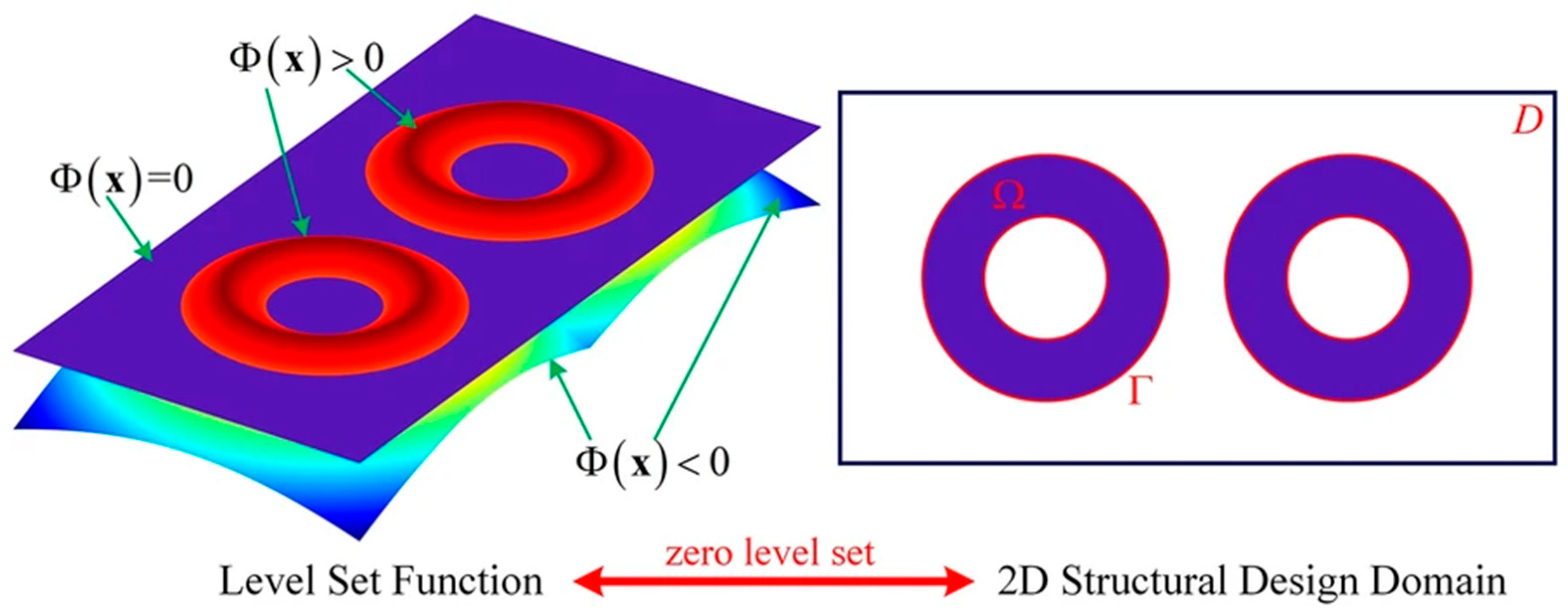
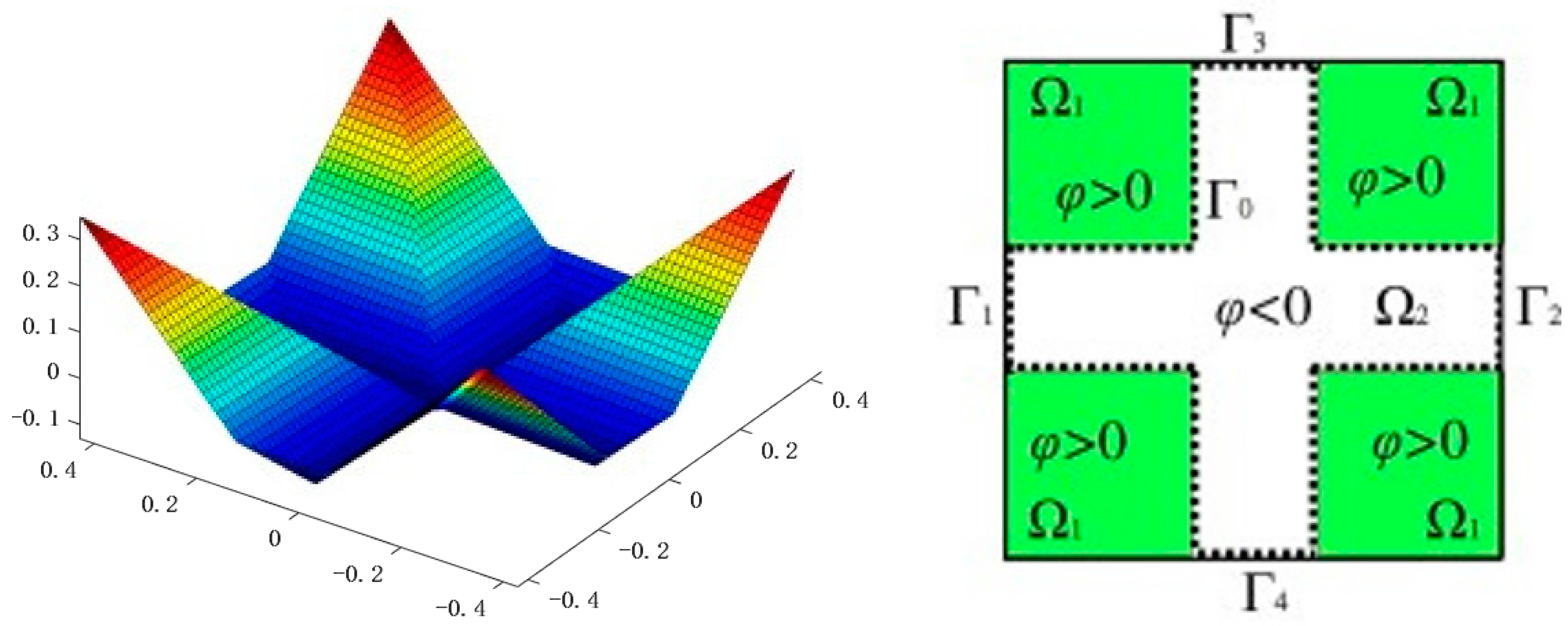
3.1. The Level Set Method
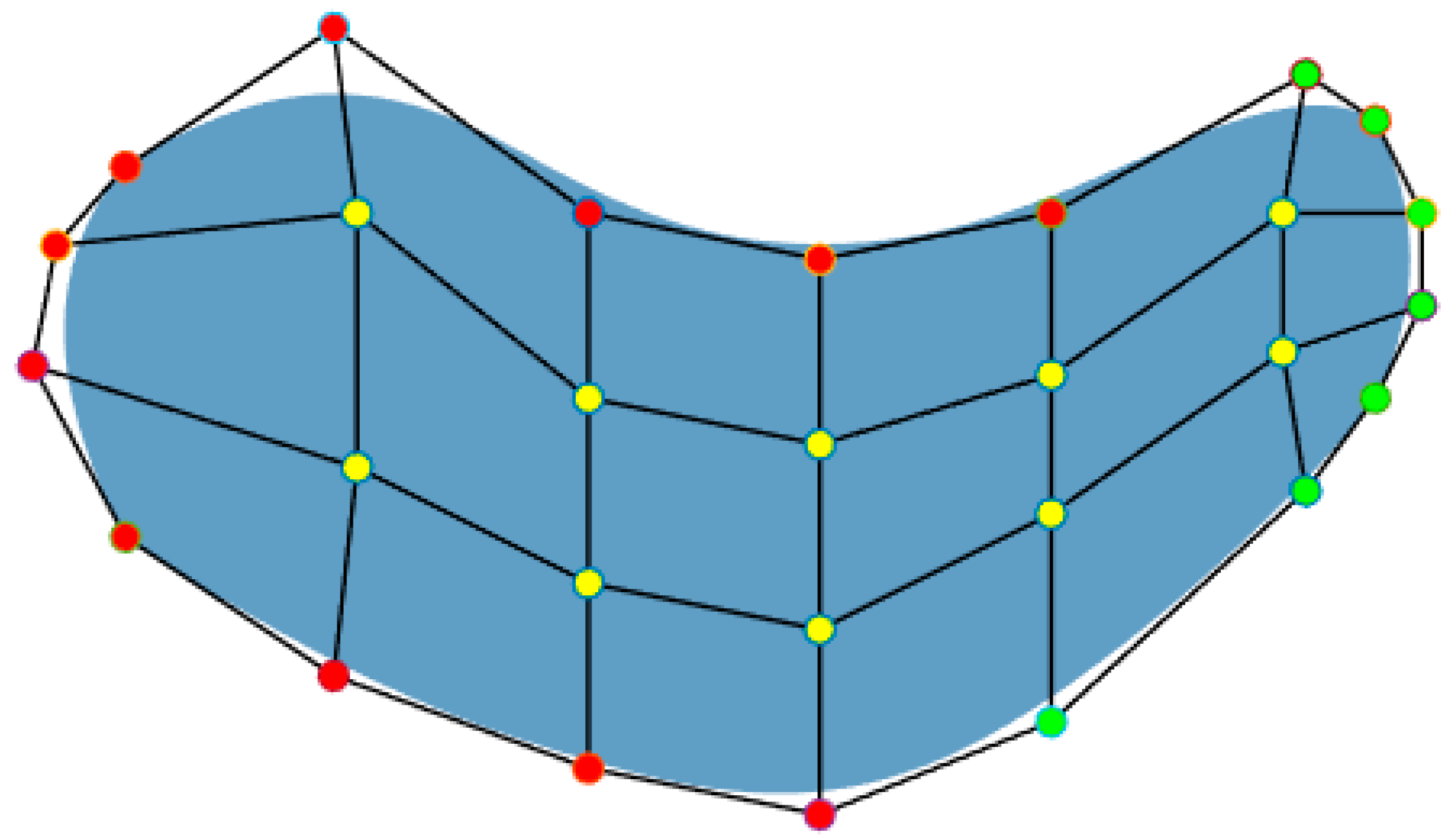
3.2. NURBS Method
3.3. Machine Learning Method
4. Comparisons and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin, Germany, 2003. [Google Scholar]
- Remouchamps, A.; Bruyneel, M.; Fleury, C.; Grihon, S. Application of a bi-level scheme including topology optimization to the design of an aircraft pylon. Struct. Multidiscip. Optim. 2011, 44, 739–750. [Google Scholar] [CrossRef]
- Zhu, J.-H.; Zhang, W.-H.; Xia, L. Topology optimization in aircraft and aerospace structures design. Arch. Comput. Methods Eng. 2016, 23, 595–622. [Google Scholar] [CrossRef]
- Munk, D.J.; Auld, D.J.; Steven, G.P.; Vio, G.A. On the benefits of applying topology optimization to structural design of aircraft components. Struct. Multidiscip. Optim. 2019, 60, 1245–1266. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, Y.; Zhang, P.; Liu, Z.; Wu, Y. Experimental investigation of passive micromixers conceptual design using the layout optimization method. J. Mech. Eng. 2013, 23, 075002. [Google Scholar] [CrossRef]
- Chen, X.; Li, T. A novel design for passive misscromixers based on topology optimization method. Biomed. Microdevices 2016, 18, 57. [Google Scholar] [CrossRef]
- Dehghani, T.; Moghanlou, F.S.; Vajdi, M.; Asl, M.S.; Shokouhimehr, M.; Mohammadi, M. Mixing enhancement through a micromixer using topology optimization. Chem. Eng. Res. Des. 2020, 161, 187–196. [Google Scholar] [CrossRef]
- Yoon, G.H. Topological design of heat dissipating structure with forced convective heat transfer. J. Mech. Sci. Technol. 2010, 24, 1225–1233. [Google Scholar] [CrossRef]
- Subramaniam, V.; Dbouk, T.; Harion, J.-L. Topology optimization of conjugate heat transfer systems: A competition between heat transfer enhancement and pressure drop reduction. Int. J. Heat Fluid Flow 2019, 75, 165–184. [Google Scholar] [CrossRef]
- Lin, Y.; Zhu, W.; Li, J.; Ke, Y. A stabilized parametric level-set XFEM topology optimization method for thermal-fluid problem. Int. J. Numer. Methods Eng. 2022, 123, 924–952. [Google Scholar] [CrossRef]
- Borrvall, T.; Petersson, J. Topology optimization of fluids in Stokes flow. Int. J. Numer. Methods Fluids 2003, 41, 77–107. [Google Scholar] [CrossRef]
- Gersborg-Hansen, A.; Sigmund, O.; Haber, R.B. Topology optimization of channel flow problems. Struct. Multidiscip. Optim. 2005, 30, 181–192. [Google Scholar] [CrossRef]
- Guest, J.K.; Prévost, J.H. Topology optimization of creeping fluid flows using a Darcy–Stokes finite element. Int. J. Numer. Methods Eng. 2006, 66, 461–484. [Google Scholar] [CrossRef]
- Olesen, L.H.; Okkels, F.; Bruus, H. A high-level programming-language implementation of topology optimization applied to steady-state Navier–Stokes flow. Int. J. Numer. Methods Eng. 2006, 65, 975–1001. [Google Scholar] [CrossRef]
- Pingen, G.; Evgrafov, A.; Maute, K. Topology optimization of flow domains using the lattice Boltzmann method. Struct. Multidiscip. Optim. 2007, 34, 507–524. [Google Scholar] [CrossRef]
- Othmer, C. A continuous adjoint formulation for the computation of topological and surface sensitivities of ducted flows. Int. J. Numer. Methods Fluids 2008, 58, 861–877. [Google Scholar] [CrossRef]
- Pereira, A.; Talischi, C.; Paulino, G.H.; Menezes, I.F.M.; Carvalho, M.S. Fluid flow topology optimization in polytop: Stability and computational implementation. Struct. Multidiscip. Optim. 2016, 54, 1345–1364. [Google Scholar] [CrossRef]
- Talischi, C.; Paulino, G.H.; Pereira, A.; Menezes, I.F. PolyMesher: A general-purpose mesh generator for polygonal elements written in Matlab. Struct. Multidiscip. Optim. 2012, 45, 309–328. [Google Scholar] [CrossRef]
- Talischi, C.; Paulino, G.H.; Pereira, A.; Menezes, I.F. PolyTop: A Matlab implementation of a general topology optimization framework using unstructured polygonal finite element meshes. Struct. Multidiscip. Optim. 2012, 45, 329–357. [Google Scholar] [CrossRef]
- Kreissl, S.; Pingen, G.; Maute, K. Topology optimization for unsteady flow. Int. J. Numer. Methods Eng. 2011, 87, 1229–1253. [Google Scholar] [CrossRef]
- Nørgaard, S.; Sigmund, O.; Lazarov, B. Topology optimization of unsteady flow problems using the lattice Boltzmann method. J. Comput. Phys. 2016, 307, 291–307. [Google Scholar] [CrossRef]
- Nobis, H.; Schlatter, P.; Wadbro, E.; Berggren, M.; Henningson, D.S. Topology optimization of unsteady flows using the spectral element method. Comput. Fluids 2022, 239, 105387. [Google Scholar] [CrossRef]
- Yoon, G.H. Topology optimization for turbulent flow with Spalart–Allmaras model. Comput. Methods Appl. Mech. Eng. 2016, 303, 288–311. [Google Scholar] [CrossRef]
- Dilgen, C.B.; Dilgen, S.B.; Fuhrman, D.R.; Sigmund, O.; Lazarov, B.S. Topology optimization of turbulent flows. Comput. Methods Appl. Mech. Eng. 2018, 331, 363–393. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Y. Aerodynamic Design Based on Topology Optimization of Turbulent Flow. arXiv 2022, arXiv:2207.11711. [Google Scholar]
- Pingen, G.; Maute, K. Optimal design for non-Newtonian flows using a topology optimization approach. Comput. Math. Appl. 2010, 59, 2340–2350. [Google Scholar] [CrossRef]
- Suárez, M.A.; Romero, J.S.; Pereira, A.; Menezes, I.F. On the virtual element method for topology optimization of non-Newtonian fluid-flow problems. Eng. Comput. 2022, 38, 5445–5466. [Google Scholar] [CrossRef]
- Lin, S.; Zhao, L.; Guest, J.K.; Weihs, T.P.; Liu, Z. Topology optimization of fixed-geometry fluid diodes. J. Mech. Des. 2015, 137, 081402. [Google Scholar] [CrossRef]
- Lim, D.K.; Song, M.S.; Chae, H.; Kim, E.S. Topology optimization on vortex-type passive fluidic diode for advanced nuclear reactors. Nucl. Eng. Technol. 2019, 51, 1279–1288. [Google Scholar] [CrossRef]
- Sá, L.; Romero, J.; Horikawa, O.; Silva, E.C.N. Topology optimization applied to the development of small scale pump. Struct. Multidiscip. Optim. 2018, 57, 2045–2059. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, T.; Simon, T.W.; Cui, T. Simulation and experiments on a valveless micropump with fluidic diodes based on topology optimization. J. Mech. Syst. 2021, 31, 292–297. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Zhong, W. Doing topology optimization explicitly and geometrically—A new moving morphable components based framework. J. Appl. Mech. 2014, 81, 081009. [Google Scholar] [CrossRef]
- Zhang, W.; Yuan, J.; Zhang, J.; Guo, X. A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model. Struct. Multidiscip. Optim. 2016, 53, 1243–1260. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Yuan, J.; Song, J.; Guo, X. A new three-dimensional topology optimization method based on moving morphable components (mmcs). Comput. Mech. 2017, 59, 647–665. [Google Scholar] [CrossRef]
- Zhang, W.; Song, J.; Zhou, J.; Du, Z.; Zhu, Y.; Sun, Z.; Guo, X. Topology optimization with multiple materials via moving morphable component (MMC) method. Int. J. Numer. Methods Eng. 2018, 113, 1653–1675. [Google Scholar] [CrossRef]
- Xue, R.; Liu, C.; Zhang, W.; Zhu, Y.; Tang, S.; Du, Z.; Guo, X. Explicit structural topology optimization under finite deformation via moving morphable void (MMV) approach. Comput. Methods Appl. Mech. Eng. 2019, 344, 798–818. [Google Scholar] [CrossRef]
- Yu, M.; Ruan, S.; Wang, X.; Li, Z.; Shen, C. Topology optimization of thermal-fluid problem using the MMC-based approach. Struct. Multidiscip. Optim. 2019, 60, 151–165. [Google Scholar] [CrossRef]
- Yu, M.; Wang, X.; Gu, J.; Ruan, S.; Li, Z.; Qian, S.; Zhang, J.; Shen, C. A synergic topology optimization approach on distribution of cooling channels and diverse-intensity heat sources for liquid-cooled heat sink. Struct. Multidiscip. Optim. 2022, 65, 48. [Google Scholar] [CrossRef]
- Liang, X.; Li, A.; Rollett, A.D.; Zhang, Y.J. An isogeometric analysis-based topology optimization framework for 2D cross-flow heat exchangers with manufacturability constraints. Eng. Comput. 2022, 38, 4829–4852. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Van Dijk, N.P.; Maute, K.; Langelaar, M.; Van Keulen, F. Level-set methods for structural topology optimization: A review. Struct. Multidiscip. Optim. 2013, 48, 437–472. [Google Scholar] [CrossRef]
- Gao, J.; Xiao, M.; Zhang, Y.; Gao, L. A Comprehensive Review of Isogeometric Topology Optimization: Methods, Applications and Prospects. Chin. J. Mech. Eng. 2020, 33, 1–14. [Google Scholar] [CrossRef]
- Duan, X.; Ma, Y.; Zhang, R. Optimal shape control of fluid flow using variational level set method. Phys. Lett. A 2008, 372, 1374–1379. [Google Scholar] [CrossRef]
- Duan, X.-B.; Ma, Y.-C.; Zhang, R. Shape-topology optimization for Navier–Stokes problem using variational level set method. J. Comput. Appl. Math. 2008, 222, 487–499. [Google Scholar] [CrossRef]
- Duan, X.-B.; Ma, Y.-C.; Zhang, R. Shape-topology optimization of stokes flow via variational level set method. Appl. Math. Comput. 2008, 202, 200–209. [Google Scholar] [CrossRef]
- Zhou, S.; Li, Q. A variational level set method for the topology optimization of steady-state Navier–Stokes flow. J. Comput. Phys. 2008, 227, 10178–10195. [Google Scholar] [CrossRef]
- Challis, V.J.; Guest, J.K. Level set topology optimization of fluids in Stokes flow. Int. J. Numer. Methods Eng. 2009, 79, 1284–1308. [Google Scholar] [CrossRef]
- Pingen, G.; Waidmann, M.; Evgrafov, A.; Maute, K. A parametric level-set approach for topology optimization of flow domains. Struct. Multidiscip. Optim. 2010, 41, 117–131. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Z.; Wu, J.; Wu, Y. Topology optimization of steady Navier–Stokes flow with body force. Comput. Methods Appl. Mech. Eng. 2013, 255, 306–321. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, P.; Liu, Y.; Wu, Y.; Liu, Z. Optimization of unsteady incompressible Navier–Stokes flows using variational level set method. Int. J. Numer. Methods Fluids 2013, 71, 1475–1493. [Google Scholar] [CrossRef]
- Kreissl, S.; Pingen, G.; Maute, K. An explicit level set approach for generalized shape optimization of fluids with the lattice Boltzmann method. Int. J. Numer. Methods Fluids 2011, 65, 496–519. [Google Scholar] [CrossRef]
- Kreissl, S.; Maute, K. Levelset based fluid topology optimization using the extended finite element method. Struct. Multidiscip. Optim. 2012, 46, 311–326. [Google Scholar] [CrossRef]
- Jenkins, N.; Maute, K. Level set topology optimization of stationary fluid-structure interaction problems. Struct. Multidiscip. Optim. 2015, 52, 179–195. [Google Scholar] [CrossRef]
- Duan, X.; Qin, X.; Li, F. Topology optimization of Stokes flow using an implicit coupled level set method. Appl. Math. Model. 2016, 40, 5431–5441. [Google Scholar] [CrossRef]
- Duan, X.; Li, F.; Qin, X. Topology optimization of incompressible Navier–Stokes problem by level set based adaptive mesh method. Comput. Math. Appl. 2016, 72, 1131–1141. [Google Scholar] [CrossRef]
- Duan, X.-B.; Li, F.-F.; Qin, X.-Q. Adaptive mesh method for topology optimization of fluid flow. Appl. Math. Lett. 2015, 44, 40–44. [Google Scholar] [CrossRef]
- Sasaki, Y.; Sato, Y.; Yamada, T.; Izui, K.; Nishiwaki, S. Topology optimization for fluid flows using the MPS method incorporating the level set method. Comput. Fluids 2019, 188, 86–101. [Google Scholar] [CrossRef]
- Nguyen, T.; Isakari, H.; Takahashi, T.; Yaji, K.; Yoshino, M.; Matsumoto, T. Level-set based topology optimization of transient flow using lattice Boltzmann method considering an oscillating flow condition. Comput. Math. Appl. 2020, 80, 82–108. [Google Scholar] [CrossRef]
- Duan, X.; Dang, Y.; Lu, J. A variational level set method for topology optimization problems in Navier-Stokes flow. IEEE Access 2020, 8, 48697–48706. [Google Scholar] [CrossRef]
- Li, G.; Wang, H.; Zhang, M.; Tupin, S.; Qiao, A.; Liu, Y.; Ohta, M.; Anzai, H. Prediction of 3D Cardiovascular hemodynamics before and after coronary artery bypass surgery via deep learning. Commun. Biol. 2021, 4, 99. [Google Scholar] [CrossRef]
- Stanley, N.; Ciero, A.; Timms, W.; Hewlin, R.L. A 3-D Printed Optically Clear Rigid Diseased Carotid Bifurcation Arterial Mock Vessel Model for Particle Image Velocimetry Analysis in Pulsatile Flow. ASME Open J. Eng. 2023, 2, 021010. [Google Scholar] [CrossRef]
- Kumar, N.; Kumar, S.; Shenoy, B.G. Advances in the application of computational fluid dynamics in cardiovascular flow. Cogent Eng. 2023, 10, 2178367. [Google Scholar] [CrossRef]
- Hewlin, R.L., Jr.; Tindall, J.M. Computational Assessment of Magnetic Nanoparticle Targeting Efficiency in a Simplified Circle of Willis Arterial Model. Int. J. Mol. Sci. 2023, 24, 2545. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, X. Topology optimization study of arterial bypass configurations using the level set method. Struct. Multidiscip. Optim. 2015, 51, 773–798. [Google Scholar] [CrossRef]
- Kumar, A.V.; Parthasarathy, A. Topology optimization using B-spline finite elements. Struct. Multidiscip. Optim. 2011, 44, 471–481. [Google Scholar] [CrossRef]
- Gao, J.; Gao, L.; Luo, Z.; Li, P. Isogeometric topology optimization for continuum structures using density distribution function. Int. J. Numer. Methods Eng. 2019, 119, 991–1017. [Google Scholar] [CrossRef]
- Gao, J.; Wang, L.; Luo, Z.; Gao, L. Igatop: An implementation of topology optimization for structures using IGA in MATLAB. Struct. Multidiscip. Optim. 2021, 64, 1669–1700. [Google Scholar] [CrossRef]
- Wang, Y.; Benson, D.J. Isogeometric analysis for parameterized LSM-based structural topology optimization. Comput. Mech. 2016, 57, 19–35. [Google Scholar] [CrossRef]
- Wang, C.; Xie, Y.M.; Lin, X.; Zhou, S. A reaction diffusion-based B-spline level set (RDBLS) method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2022, 398, 115252. [Google Scholar] [CrossRef]
- Hou, W.; Gai, Y.; Zhu, X.; Wang, X.; Zhao, C.; Xu, L.; Jiang, K.; Hu, P. Explicit isogeometric topology optimization using moving morphable components. Comput. Methods Appl. Mech. Eng. 2017, 326, 694–712. [Google Scholar] [CrossRef]
- Xie, X.; Wang, S.; Xu, M.; Jiang, N.; Wang, Y. A hierarchical spline based isogeometric topology optimization using moving morphable components. Comput. Methods Appl. Mech. Eng. 2020, 360, 112696. [Google Scholar] [CrossRef]
- Seo, Y.-D.; Kim, H.-J.; Youn, S.-K. Isogeometric topology optimization using trimmed spline surfaces. Comput. Methods Appl. Mech. Eng. 2010, 199, 3270–3296. [Google Scholar] [CrossRef]
- Park, B.-U.; Seo, Y.-D.; Sigmund, O.; Youn, S.-K. Shape optimization of the stokes flow problem based on isogeometric analysis. Struct. Multidiscip. Optim. 2013, 48, 965–977. [Google Scholar] [CrossRef]
- Nørtoft, P.; Gravesen, J. Isogeometric shape optimization in fluid mechanics. Struct. Multidiscip. Optim. 2013, 48, 909–925. [Google Scholar] [CrossRef][Green Version]
- Xu, G.; Mourrain, B.; Duvigneau, R.; Galligo, A. Parameterization of computational domain in isogeometric analysis: Methods and comparison. Comput. Methods Appl. Mech. Eng. 2011, 200, 2021–2031. [Google Scholar] [CrossRef]
- Chen, L.; Wang, K.; Li, B.; Mao, Y. Shape optimization of fluid cooling channel based on Darcy reduced-order isogeometric analysis. J. Comput. Appl. Math. 2022, 411, 114262. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Banga, S.; Gehani, H.; Bhilare, S.; Patel, S.; Kara, L. 3D topology optimization using convolutional neural networks. arXiv 2018, arXiv:180807440. [Google Scholar]
- Sosnovik, I.; Oseledets, I. Neural networks for topology optimization. Russ. J. Numer. Anal. Math. Model. 2019, 34, 215–223. [Google Scholar] [CrossRef]
- Kallioras, N.A.; Lagaros, N.D. MLGen: Generative Design Framework Based on Machine Learning and Topology Optimization. Appl. Sci. 2021, 11, 12044. [Google Scholar] [CrossRef]
- Gaymann, A.; Montomoli, F. Deep neural network and Monte Carlo tree search applied to fluid-structure topology optimization. Sci. Rep. 2019, 9, 15916. [Google Scholar] [CrossRef] [PubMed]
- Ban, N.; Yamazaki, W. Black-Box Function Aerodynamic Topology Optimization Algorithm via Machine Learning Technologies. AIAA J. 2021, 59, 5174–5185. [Google Scholar] [CrossRef]
- Hammond, J.; Pietropaoli, M.; Montomoli, F. Topology optimisation of turbulent flow using data-driven modelling. Struct. Multidiscip. Optim. 2022, 65, 49. [Google Scholar] [CrossRef]
- Furrokh, F.; Zhang, N. A stochastic topology optimization algorithm for improved fluid dynamics systems. AI EDAM 2022, 36, e35. [Google Scholar] [CrossRef]
- Deng, C.; Wang, Y.; Qin, C.; Fu, Y.; Lu, W. Self-directed online machine learning for topology optimization. Nat. Commun. 2022, 13, 388. [Google Scholar] [CrossRef]
- Kubo, S.; Yaji, K.; Yamada, T.; Izui, K.; Nishiwaki, S. A level set-based topology optimization method for optimal manifold designs with flow uniformity in plate-type microchannel reactors. Struct. Multidiscip. Optim. 2017, 55, 1311–1327. [Google Scholar] [CrossRef]
- Asmussen, J.; Alexandersen, J.; Sigmund, O.; Andreasen, C.S. A “poor man’s” approach to topology optimization of natural convection problems. Struct. Multidiscip. Optim. 2019, 59, 1105–1124. [Google Scholar] [CrossRef]
- Alonso, D.H.; de Sá, L.F.N.; Saenz, J.S.R.; Silva, E.C.N. Topology optimization based on a two-dimensional swirl flow model of Tesla-type pump devices. Comput. Math. Appl. 2019, 77, 2499–2533. [Google Scholar] [CrossRef]
- Zhao, X.; Zhou, M.; Sigmund, O.; Andreasen, C.S. A “poor man’s approach” to topology optimization of cooling channels based on a Darcy flow model. Int. J. Heat Mass Transf. 2018, 116, 1108–1123. [Google Scholar] [CrossRef]
- Aage, N.; Andreassen, E.; Lazarov, B.S. Topology optimization using petsc: An easy-to-use, fully parallel, open source topology optimization framework. Struct. Multidiscip. Optim. 2015, 51, 565–572. [Google Scholar] [CrossRef]
- Alexandersen, J.; Sigmund, O.; Aage, N. Large scale three-dimensional topology optimisation of heat sinks cooled by natural convection. Int. J. Heat Mass Transf. 2016, 100, 876–891. [Google Scholar] [CrossRef]


| Article | Year | Objective Function (Extremization) | Solver | Method | Fluid Type |
|---|---|---|---|---|---|
| Duan et al. [45] | 2008 | Dissipated power | FEM | Level set | Steady Navier–Stokes |
| Zhou & Li [47] | 2008 | Dissipated power | FEM | Level set | Steady Navier–Stokes |
| Challis & Guest [48] | 2009 | Dissipated power | FEM | Level set | Stokes |
| Pingen et al. [49] | 2010 | Pressure drop | LBM | Level set | Steady Navier–Stokes |
| Jenkins and Maute [54] | 2015 | Strain energy augmented by a perimeter penalty | XFEM | Level set | Steady Navier–Stokes |
| Zhang and Liu [65] | 2015 | The integral of the squared shear rate | FEM | Level set | non-Newtonian |
| Pereira et al. [18] | 2016 | Local velocity/Dissipated power | Polygonal element method | Density | Stokes |
| Duan et al. [55] | 2016 | Dissipated power | FEM | Coupled Level set | Stokes |
| Yoon [24] | 2016 | Dissipated power | FEM | Density | The Reynolds- Averaged Navier–Stokes |
| Dilgen et al. [25] | 2017 | Dissipated power | FVM | Density | The Reynolds- Averaged Navier–Stokes |
| Sasaki et al. [58] | 2019 | Pressure drop | FEM | Level set | Steady Navier–Stokes |
| Nguyen et al. [59] | 2020 | Dissipated kinetic energy | LBM | Level set | Unsteady Navier–Stokes |
| Nobis et al. [23] | 2022 | Dissipated power | Spectral element method | Density | Steady/Unsteady Navier–Stokes |
| Suárez et al. [28] | 2022 | Dissipated power | Virtual element method | Density | non-Newtonian |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, C.; Zhang, X.; Li, J.; Shen, J.; Zhou, S. A Mini Review on Fluid Topology Optimization. Materials 2023, 16, 6073. https://doi.org/10.3390/ma16186073
Li H, Wang C, Zhang X, Li J, Shen J, Zhou S. A Mini Review on Fluid Topology Optimization. Materials. 2023; 16(18):6073. https://doi.org/10.3390/ma16186073
Chicago/Turabian StyleLi, He, Cong Wang, Xuyu Zhang, Jie Li, Jianhu Shen, and Shiwei Zhou. 2023. "A Mini Review on Fluid Topology Optimization" Materials 16, no. 18: 6073. https://doi.org/10.3390/ma16186073
APA StyleLi, H., Wang, C., Zhang, X., Li, J., Shen, J., & Zhou, S. (2023). A Mini Review on Fluid Topology Optimization. Materials, 16(18), 6073. https://doi.org/10.3390/ma16186073








