Numerical Study on the Seismic Performance of Cold-Formed Steel Shear Walls with Steel Sheathing and Gypsum Board
Abstract
:1. Introduction
2. Simulation of Monotonic Test
2.1. Finite Element Modeling
2.1.1. Materials and Elements
2.1.2. Connections Modeling
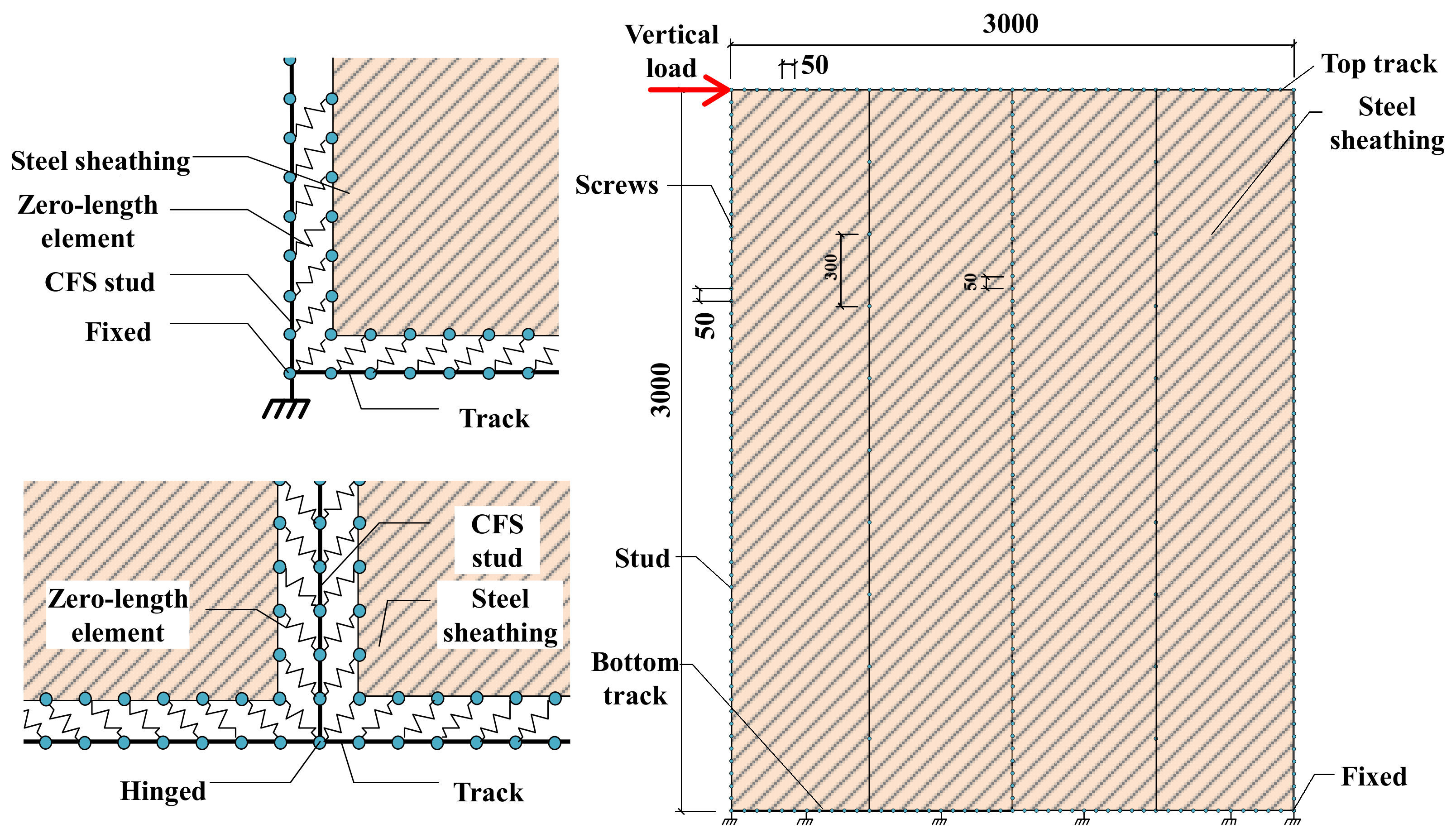
2.1.3. Boundary Conditions
2.2. Numerical Results
2.2.1. Failure Modes
2.2.2. Load-Displacement Relationships
3. Simulation of Cyclic Test
3.1. Finite Element Modeling
3.1.1. Model Simplification
3.1.2. Element Types
3.1.3. Material Properties
3.1.4. Screw Connections
3.1.5. Boundary Conditions
3.2. Numerical Results
4. Seismic Performance Mid-Rise Buildings
4.1. Design of Mid-Rise Buildings
4.2. Modeling of the Mid-Rise Buildings
4.3. Modal Analysis
4.4. Elastic Analysis
4.5. Elastoplastic Analysis
5. Conclusions
- The CFS shear wall with steel sheathing and gypsum board exhibits two primary failure modes, namely, boundary stud buckling failure and steel sheet failure. The FE method employed in this study can effectively simulate the shear performance of the proposed shear wall under monotonic loading and predict the failure modes of specimens.
- The modeling method used in this study, including model simplification and screw connection modeling using Pinching4 material, could effectively simulate the hysteresis behavior of the proposed shear wall under cyclic loading.
- Through verification of natural vibration periods, the equivalent spring model demonstrates good capability for simulating the seismic performance of the proposed shear wall system.
- Through a comparison of the maximum roof displacement and maximum story drift ratio between models subjected to frequent and rare earthquakes, it can be concluded that the proposed shear wall significantly enhances the structural stiffness and improves the seismic performance of the structure under seismic action.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schafer, B.W. Cold-formed steel structures around the world: A review of recent advances in applications, analysis and design. Steel Constr. 2011, 4, 141–149. [Google Scholar] [CrossRef]
- Yu, C.; Chen, Y.J. Detailing recommendations for 1.83 m wide cold-formed steel shear walls with steel sheathing. J. Constr. Steel Res. 2011, 67, 93–101. [Google Scholar] [CrossRef]
- Balh, N.; DaBreo, J.; Ong-Tone, C.; El-Saloussy, K.; Yu, C.; Rogers, C.A. Design of steel sheathed cold-formed steel framed shear walls. Thin-Walled Struct. 2014, 75, 76–86. [Google Scholar] [CrossRef]
- Shamim, I.; Rogers, C.A. Steel sheathed/CFS framed shear walls under dynamic loading: Numerical modelling and calibration. Thin-Walled Struct. 2013, 71, 57–71. [Google Scholar] [CrossRef]
- Fiorino, L.; Terracciano, M.T.; Landolfo, R. Experimental investigation of seismic behaviour of low dissipative CFS strap-braced stud walls. J. Constr. Steel Res. 2016, 127, 92–107. [Google Scholar] [CrossRef]
- Zeynalian, M.; Ronagh, H.R. A numerical study on seismic performance of strap-braced cold-formed steel shear walls. Thin-Walled Struct. 2012, 60, 229–238. [Google Scholar] [CrossRef]
- Xu, Z.F.; Chen, Z.F.; Osman, B.H.; Yang, S.H. Seismic performance of high-strength lightweight foamed concrete-filled cold-formed steel shear walls. J. Constr. Steel Res. 2018, 143, 148–161. [Google Scholar] [CrossRef]
- Dao, T.N.; van de Lindt, J.W. Seismic Performance of an Innovative Light-Frame Cold-Formed Steel Frame for Midrise Construction. J. Struct. Eng. 2013, 139, 837–848. [Google Scholar] [CrossRef]
- Derveni, F.; Gerasimidis, S.; Schafer, B.W.; Peterman, K.D. High-Fidelity Finite Element Modeling of Wood-Sheathed Cold-Formed Steel Shear Walls. J. Struct. Eng. 2021, 147, 04020316. [Google Scholar] [CrossRef]
- Yu, C. Shear resistance of cold-formed steel framed shear walls with 0.686 mm, 0.762 mm, and 0.838 mm steel sheet sheathing. Eng. Struct. 2010, 32, 1522–1529. [Google Scholar] [CrossRef]
- Mohebbi, S.; Mirghaderi, R.; Farahbod, F.; Sabbagh, A.B. Experimental work on single and double-sided steel sheathed cold-formed steel shear walls for seismic actions. Thin-Walled Struct. 2015, 91, 50–62. [Google Scholar] [CrossRef]
- Feng, R.Q.; Zhu, B.C.; Xu, P.H.; Qiu, Y. Seismic performance of cold-formed steel framed shear walls with steel sheathing and gypsum board. Thin-Walled Struct. 2019, 143, 106238. [Google Scholar] [CrossRef]
- Ye, J.H.; Feng, R.Q.; Chen, W. Seismic Technical Manual of Cold-Formed Steel Structures in Villages and Towns; Southeast University Press: Nanjing, China, 2013. (In Chinese) [Google Scholar]
- Abaqus, Version 6.14; Dassault Systemes Simulia Corporation: Waltham, MA, USA, 2014.
- Niari, S.E.; Rafezy, B.; Abedi, K. Seismic behavior of steel sheathed cold-formed steel shear wall: Experimental investigation and numerical modeling. Thin-Walled Struct. 2015, 96, 337–347. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. OpenSees command language manual. PEER Cent. 2006, 264, 137–158. [Google Scholar]
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- Wang, X. Experimental and Simplified Calculation Method Research on the Lateral Performance of Mid-Rise Cold-Formed Steel Shear Walls Simulation of Shear and Compressive Performance of Cold-Formed Steel Wall. Ph.D. Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- FEMA 356; Prestandard and Commentary for the Seismic Rehabilitation of Buildings. American Society of Civil Engineers: Reston, VA, USA, 2000.
- JGJ 227-2011; Technical Specification for Low-Rise Cold-Formed Thin-Walled Steel Buildings. China Architecture & Building Press: Beijing, China, 2012.
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.



















| Name | Dimensions | Sheathing | Stud Thickness | Steel Sheet Thickness | |
|---|---|---|---|---|---|
| Side 1 | Side 2 | ||||
| M1 | 3.0 m × 2.4 m | steel sheet + gypsum | steel sheet + gypsum | 0.9 mm | 0.8 mm |
| M2 | 3.0 m × 2.4 m | steel sheet + gypsum | gypsum | 2.5 mm | 0.9 mm |
| Name | Yield Point | Peak Point | Ps (kN/m) | |||
|---|---|---|---|---|---|---|
| Py (kN) | Δy (mm) | Pmax (kN) | Δmax (mm) | |||
| M1 | Test results | 101.9 | 28.1 | 106.6 | 38.9 | 44.4 |
| FE results | 102.8 | 19.6 | 121.6 | 40.7 | 50.7 | |
| FE/test | 1.01 | 0.70 | 1.14 | 1.05 | 1.14 | |
| M2 | Test results | 53.5 | 26.2 | 58.4 | 29.1 | 24.3 |
| FE results | 44.6 | 20.7 | 52.8 | 31.7 | 22.0 | |
| FE/test | 0.83 | 0.79 | 0.90 | 1.09 | 0.91 | |
| Name | Dimensions | Sheathing | Stud Thickness | Steel Sheet Thickness | |
|---|---|---|---|---|---|
| Side 1 | Side 2 | ||||
| C1 | 3.0 m × 2.4 m | steel sheet + gypsum | gypsum | 2.5 mm | 0.9 mm |
| C2 | 3.0 m × 2.4 m | steel sheet + gypsum | gypsum | 2.5 mm | 0.8 mm |
| C3 | 3.0 m × 2.4 m | steel sheet + gypsum | gypsum | 2.5 mm | 0.8 mm |
| C4 | 3.0 m × 3.6 m | steel sheet + gypsum | gypsum | 2.5 mm | 0.8 mm |
| Name | Force (kN) | Displacement (mm) | Unloading and Reloading Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pf1 | Pf2 | Pf3 | Pf4 | Pd1 | Pd2 | Pd3 | Pd4 | RDisP | RForceP | UForceP | |
| C2.5S0.8 | 2.576 | 3.296 | 3.856 | 1.578 | 2.40 | 3.60 | 4.80 | 12.00 | 0.6 | 0.2 | 0 |
| C2.5S0.9 | 2.898 | 3.708 | 4.338 | 1.775 | 2.40 | 3.60 | 4.80 | 12.00 | 0.6 | 0.2 | 0 |
| Name | gKi | gDi | gFi | |||||
|---|---|---|---|---|---|---|---|---|
| gK1,2 | gK3,4 | gKLim | gD1,2 | gD3,4 | gDLim | gF1,2,3,4 | gFLim | |
| C2.5S0.8 | 0.5 | 0.2 | 0.3 | 0.08 | 1.5 | 0.25. | 0.0 | 0.0 |
| C2.5S0.9 | 0.5 | 0.2 | 0.3 | 0.08 | 1.5 | 0.25. | 0.0 | 0.0 |
| Name | Yield Point | Peak Point | Ps (kN/m) | |||
|---|---|---|---|---|---|---|
| Py (kN) | Δy (mm) | Pmax (kN) | Δmax (mm) | |||
| C1 | Test results | 101.9 | 38.9 | 113.4 | 44.9 | 47.7 |
| FE results | 107.3 | 31.3 | 118.9 | 38.4 | 49.5 | |
| FE/test | 1.05 | 0.80 | 1.05 | 0.86 | 1.04 | |
| C2 | Test results | 100.6 | 40.5 | 105.8 | 43.2 | 44.4 |
| FE results | 102.1 | 31.5 | 112.8 | 38.4 | 47.0 | |
| FE/test | 1.01 | 0.78 | 1.07 | 0.89 | 1.06 | |
| C3 | Test results | 47.9 | 49.5 | 53.9 | 66.7 | 47.3 |
| FE results | 48.2 | 33.1 | 53.6 | 47.1 | 44.7 | |
| FE/test | 1.01 | 0.67 | 0.99 | 0.71 | 0.95 | |
| C4 | Test results | 165.8 | 22.3 | 178.1 | 33.8 | 47.9 |
| FE results | 171.7 | 20.9 | 190.2 | 25.6 | 52.8 | |
| FE/test | 1.04 | 0.94 | 1.07 | 0.76 | 1.10 | |
| No | Wall-B1 | Wall-B2 | Wall-B3 | Wall-L1 | Wall-L2 | The Proportion of Wall-GS (%) | ||
|---|---|---|---|---|---|---|---|---|
| Z Direction | X Direction | All | ||||||
| M-1 | Wall-GC | Wall-GC | Wall-GC | Wall-GC | Wall-GC | 0 | 0 | 0 |
| M-2 | Wall-GS | Wall-GC | Wall-GC | Wall-GC | Wall-GC | 20 | 0 | 9.1 |
| M-3 | Wall-GC | Wall-GS | Wall-GC | Wall-GC | Wall-GC | 40 | 0 | 18.2 |
| M-4 | Wall-GS | Wall-GC | Wall-GS | Wall-GC | Wall-GC | 60 | 0 | 27.3 |
| M-5 | Wall-GC | Wall-GS | Wall-GS | Wall-GC | Wall-GC | 80 | 0 | 36.4 |
| M-6 | Wall-GS | Wall-GS | Wall-GS | Wall-GC | Wall-GC | 100 | 0 | 45.5 |
| Name | Dimensions | Shear Capacity | Pinching4 Material Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pmax | Δmax | Pf1 | Pf2 | Pf3 | Pf4 | Pd1 | Pd2 | Pd3 | Pd4 | ||
| Wall-GC | 3.0 m × 3.6 m | 90.7 | 35.3 | 23.4 | 56.7 | 78.1 | 54.7 | 3.2 | 13.9 | 21.8 | 44.2 |
| Wall-GS | 3.0 m × 3.6 m | 178.1 | 33.8 | 41.4 | 89.7 | 115.9 | 67.3 | 2.9 | 13.6 | 25.9 | 47.4 |
| Name | Wall-GS Proportion (%) | Simulated Natural Periods | Specified Natural Periods | ||||
|---|---|---|---|---|---|---|---|
| X-Axis | Y-Axis | All | T1 | T2 | T3 | ||
| M-1 | 0 | 0 | 0 | 0.473 | 0.432 | 0.157 | ASCE/FEMA Code [19] T = 0.05 H3/4 = 0.437 Chinese Code [20] T = 0.02 H~0.03 H = 0.36~0.54 |
| M-2 | 20 | 0 | 9.1 | 0.443 | 0.430 | 0.149 | |
| M-3 | 40 | 0 | 18.2 | 0.428 | 0.417 | 0.143 | |
| M-4 | 60 | 0 | 27.3 | 0.426 | 0.395 | 0.142 | |
| M-5 | 80 | 0 | 36.4 | 0.424 | 0.376 | 0.141 | |
| M-6 | 100 | 0 | 45.5 | 0.421 | 0.359 | 0.140 | |
| Name | Wall-GS Proportion (%) | Peak Ground Acceleration | ||||
|---|---|---|---|---|---|---|
| X-Axis | Y-Axis | All | 0.035 g | 0.07 g | 0.14 g | |
| M-1 | 0 | 0 | 0 | 4.85 | 9.79 | 21.18 |
| M-2 | 20 | 0 | 9.1 | 4.61 | 9.23 | 19.83 |
| M-3 | 40 | 0 | 18.2 | 4.38 | 8.75 | 18.69 |
| M-4 | 60 | 0 | 27.3 | 3.17 | 8.20 | 17.22 |
| M-5 | 80 | 0 | 36.4 | 2.99 | 6.21 | 15.29 |
| M-6 | 100 | 0 | 45.5 | 2.75 | 5.71 | 13.74 |
| Name | Wall-GS (%) | PGA: 0.22 g | PGA: 0.40 g | PGA: 0.62 g | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | El Centro | TAFT | Artificial | El Centro | TAFT | Artificial | El Centro | TAFT | Artificial | |
| M-1 | 0 | 0 | 33.14 | 25.17 | 28.54 | 59.98 | 49.82 | 56.67 | 91.86 | 80.08 | 97.97 |
| M-2 | 20 | 0 | 31.32 | 23.04 | 26.80 | 57.10 | 46.58 | 53.76 | 88.63 | 79.83 | 91.33 |
| M-3 | 40 | 0 | 29.04 | 21.79 | 25.85 | 55.25 | 41.83 | 51.12 | 85.69 | 77.34 | 86.66 |
| M-4 | 60 | 0 | 25.38 | 21.47 | 23.24 | 51.20 | 39.78 | 48.64 | 80.51 | 71.83 | 81.07 |
| M-5 | 80 | 0 | 21.03 | 19.91 | 20.41 | 45.54 | 38.71 | 46.16 | 73.41 | 65.56 | 78.16 |
| M-6 | 100 | 0 | 18.71 | 20.03 | 19.05 | 38.97 | 34.90 | 44.54 | 67.73 | 62.05 | 74.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Feng, R.; Zhong, Y. Numerical Study on the Seismic Performance of Cold-Formed Steel Shear Walls with Steel Sheathing and Gypsum Board. Materials 2023, 16, 5685. https://doi.org/10.3390/ma16165685
Liu S, Feng R, Zhong Y. Numerical Study on the Seismic Performance of Cold-Formed Steel Shear Walls with Steel Sheathing and Gypsum Board. Materials. 2023; 16(16):5685. https://doi.org/10.3390/ma16165685
Chicago/Turabian StyleLiu, Shen, Ruoqiang Feng, and Yuting Zhong. 2023. "Numerical Study on the Seismic Performance of Cold-Formed Steel Shear Walls with Steel Sheathing and Gypsum Board" Materials 16, no. 16: 5685. https://doi.org/10.3390/ma16165685
APA StyleLiu, S., Feng, R., & Zhong, Y. (2023). Numerical Study on the Seismic Performance of Cold-Formed Steel Shear Walls with Steel Sheathing and Gypsum Board. Materials, 16(16), 5685. https://doi.org/10.3390/ma16165685





