Broadband Waterborne Multiphase Pentamode Metastructure with Simultaneous Wavefront Manipulation and Energy Absorption Capabilities
Abstract
1. Introduction
2. Materials and Methods
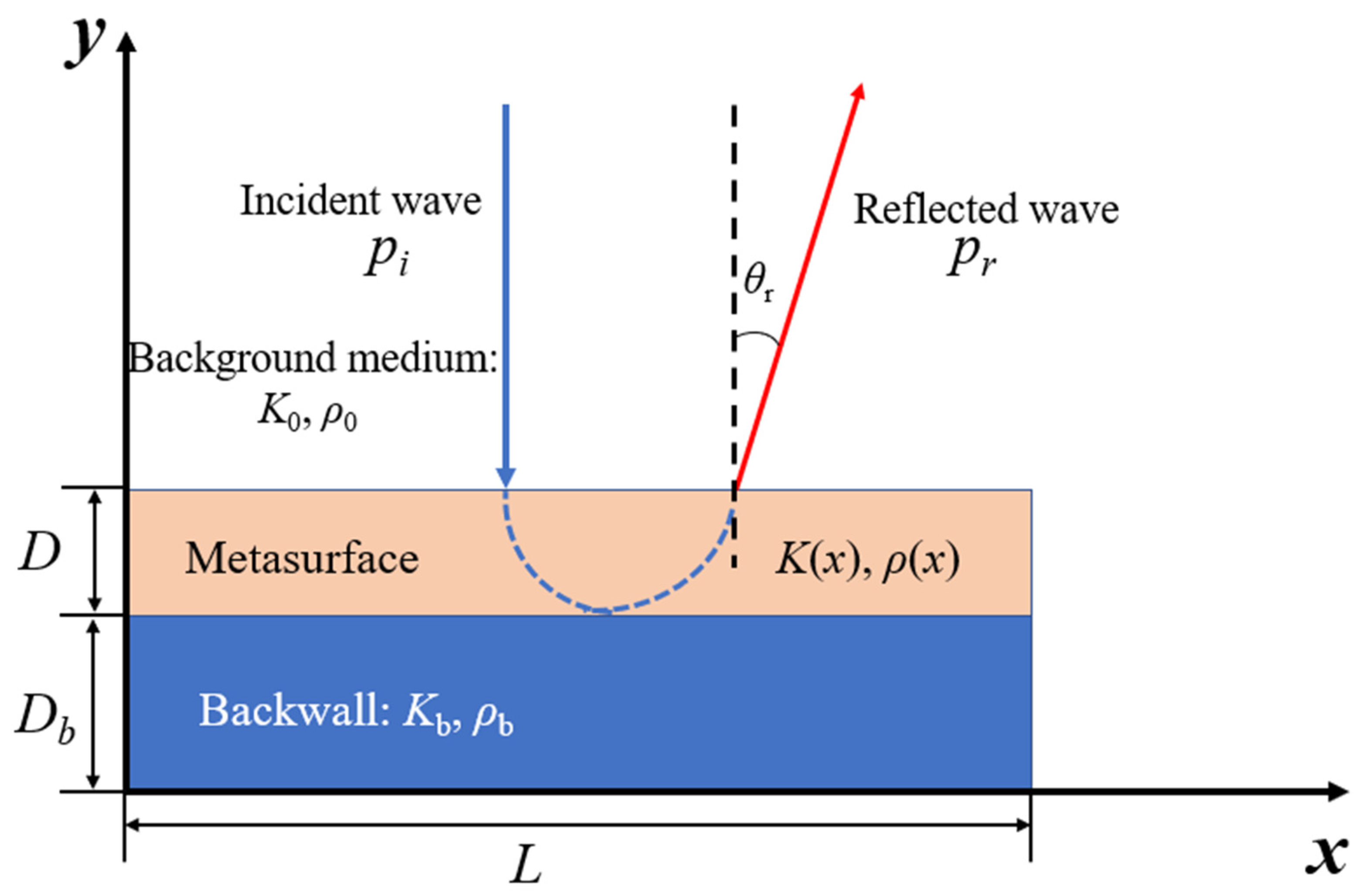
2.1. Generalized Snell Law (GSL)
2.2. Configurations of Unit Cells
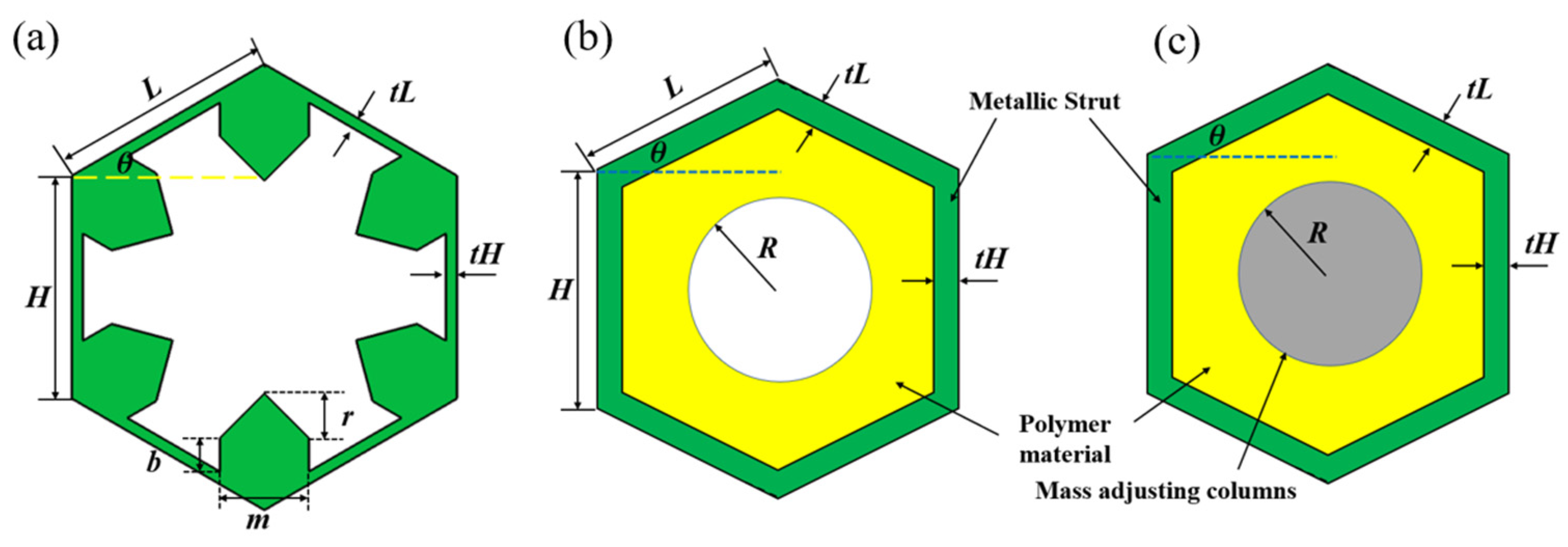
2.3. Method for Equivalent Physical Properties Calculation
3. Results and Discussions
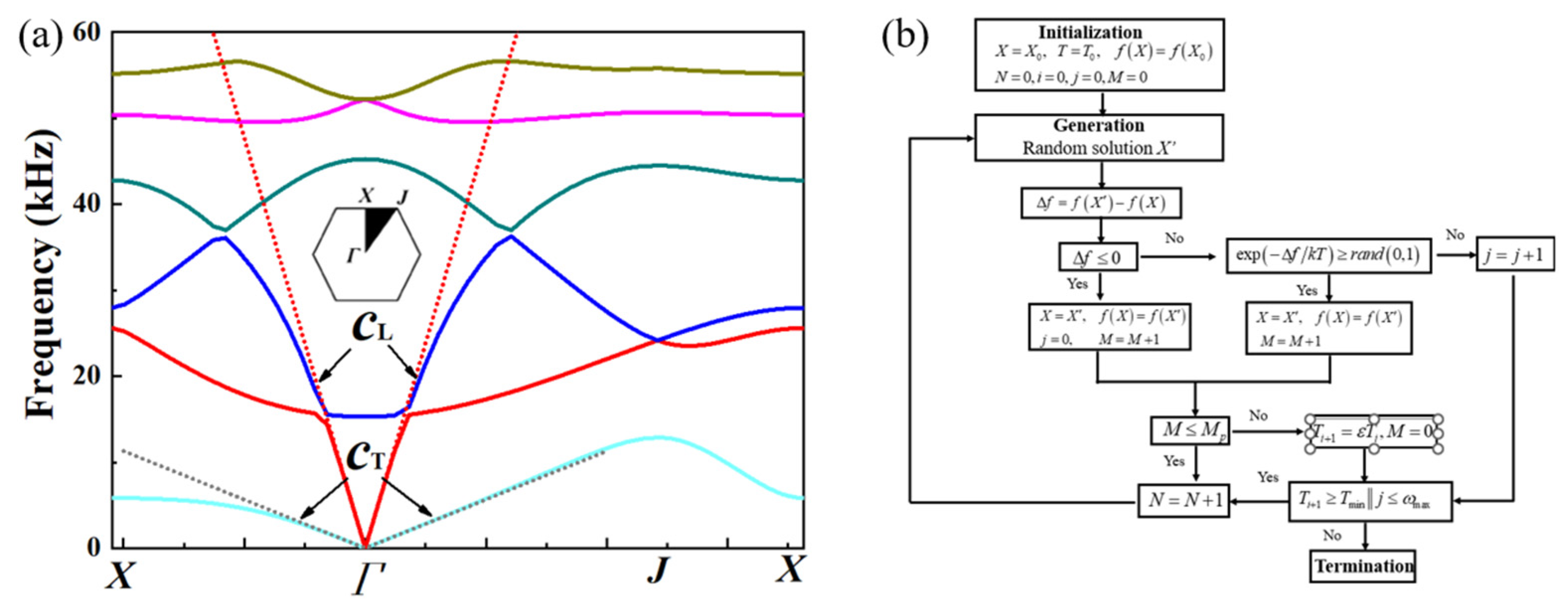
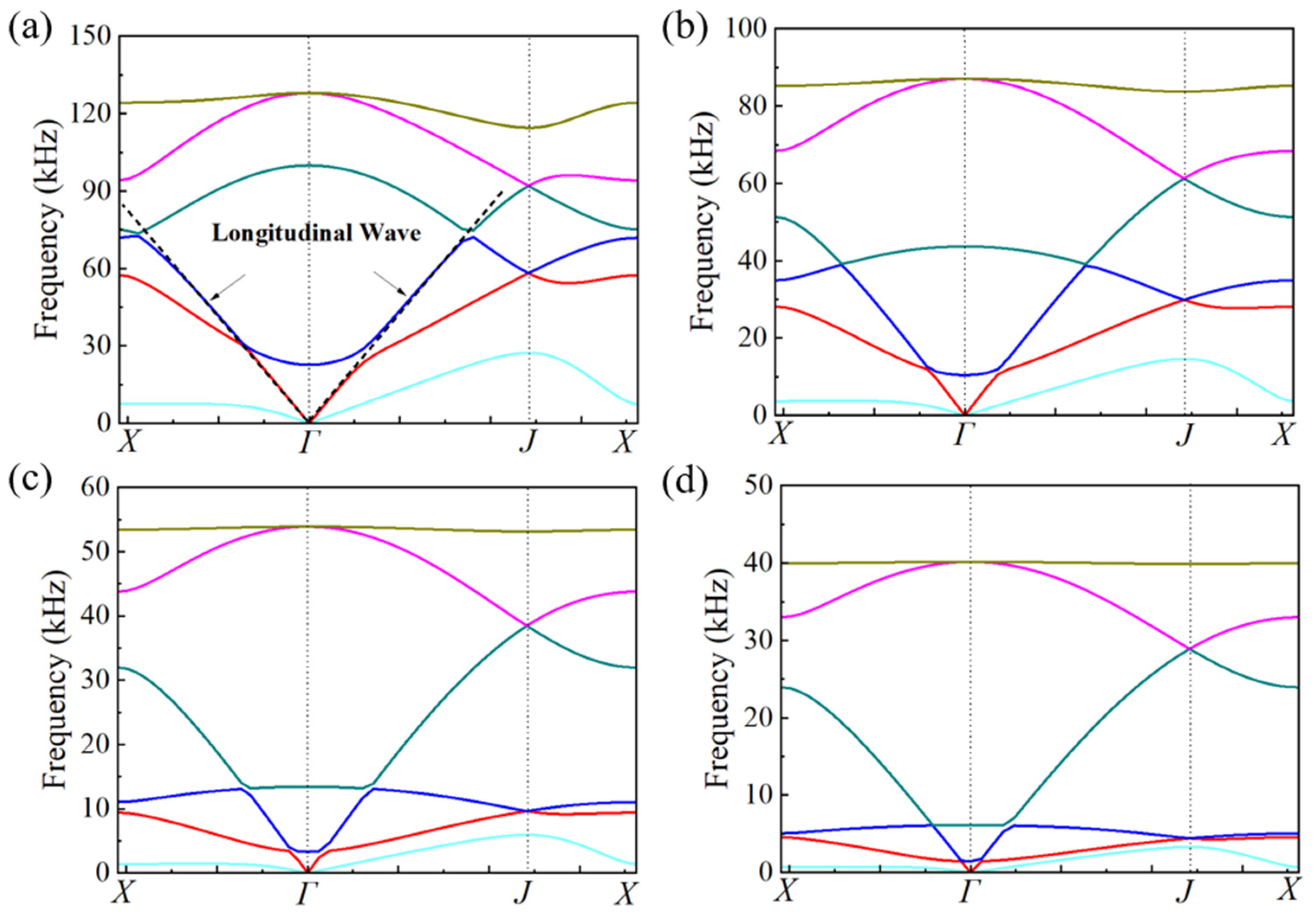
3.1. Influences of Damping Coefficient on Acoustic Properties of Ideal Metastructure
3.2. Microstructure Design of Single-Phase and Multiphase Metastructure
3.3. Formatting of Mathematical Components
3.4. Advantages for Withstanding External Pressure
4. Conclusions
- (1)
- A multiphase pentamode configuration composed of hexagonal latticed microstructures, polymer materials and mass-balancing lead columns was proposed to realize the desired physical properties. Compared with the single-phase pentamode unit cell which was mostly designed with metallic materials and the damping coefficient was relatively small, significant damping is introduced in the configuration design. Additionally, more degrees of freedom were introduced, which facilitated the designing of the metastructure.
- (2)
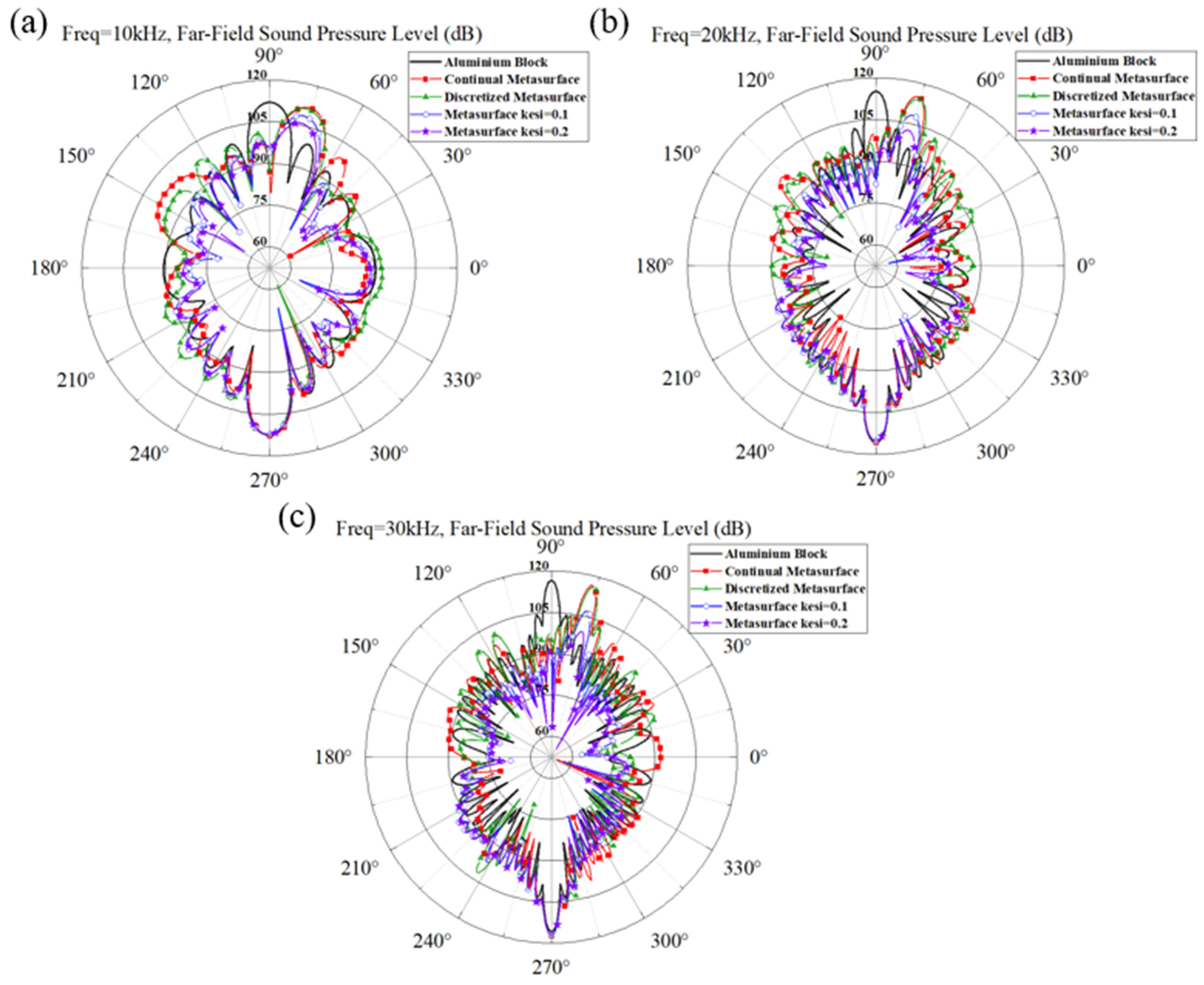
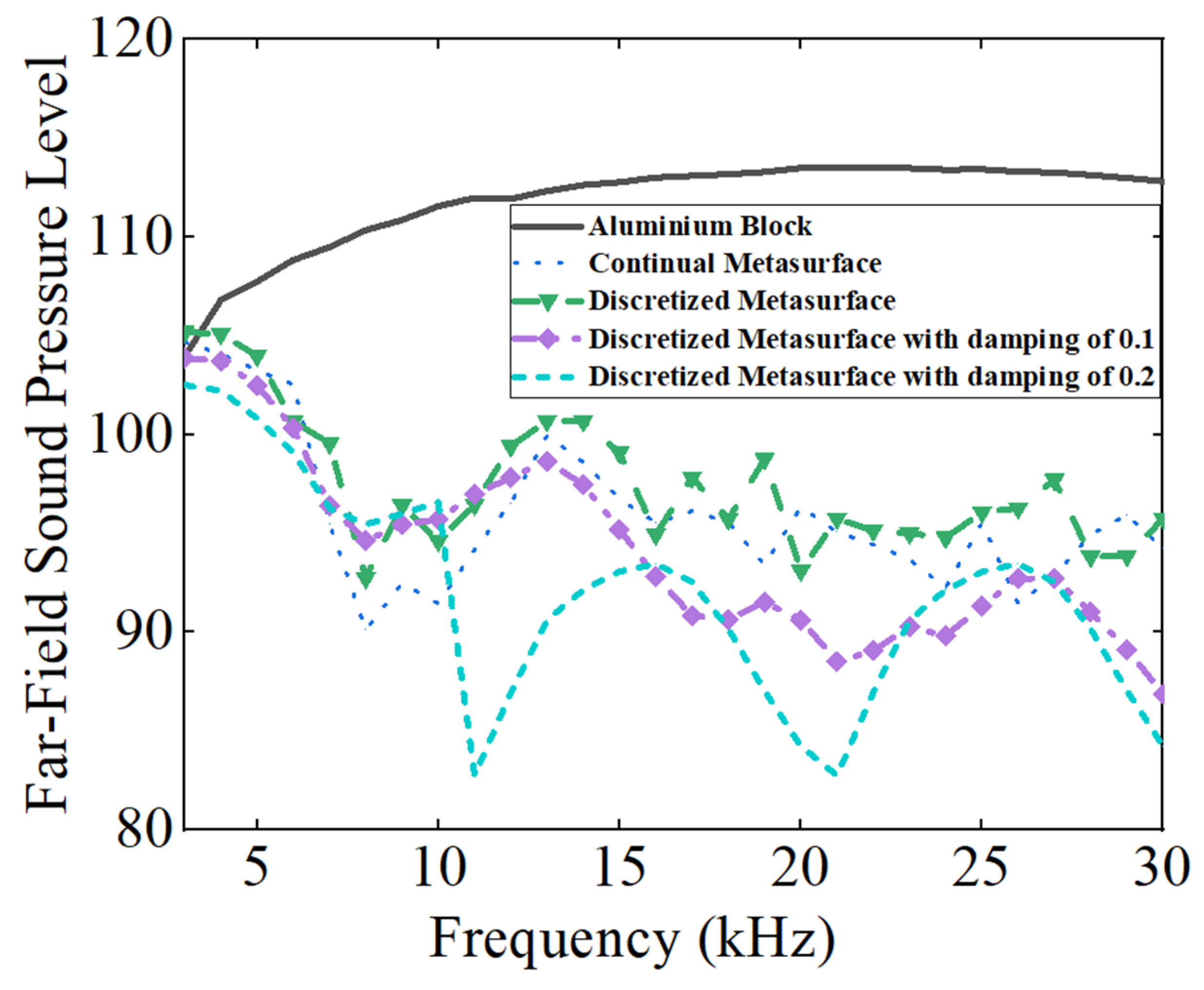
- An abnormal directional reflection metastructure with a length of 693.2 mm and width of 80 mm was proposed and numerically verified. Both the simulation results of the scattering acoustic pressure field map and the Far-Field Sound Pressure Level (FFSPL) in the frequency range of 3 kHz~30 kHz revealed that the metastructure could reflect the scattering acoustic wave by an azimuth angle of 15°, which was in agreement with the original design. It was also shown that the introducing of material damping will not alter the direction of the scattering acoustic wave, but it could abate the scattering acoustic pressure amplitude obviously.
- (3)
- Both multiphase and single-phase metastructures were designed for the same theoretical metastructure. It is revealed that both metastructures demonstrated the abilities of changing the propagation direction of scattering acoustic wave, but the amplitude of the scattering wave could not be abated for the single-phase metastructure due to the lack of damping properties of the single-phase unit cell. Utilizing the damping properties of the polymer materials inside the multiphase unit cells, the multiphase metastructure could abate the amplitude of the scattering acoustic pressure on the basis of reflecting the scattering wave. Quantitative calculations reveal that the average Far-Field Sound Pressure Level for single-phase metastructure decreased by 13.19 dB compared to the aluminum block within the frequency range of 3 kHz~30 kHz, while that of the multiphase metastructure decreased by 4.82 dB compared to the single-phase metastructure.
- (4)
- The pressure resistance capabilities of both metastructures were studied and compared. It was illustrated that the linearized mean stress for the multiphase metastructure is only about 1/3 of that of the single-phase metastructure under the same hydrostatic pressure, which suggested that the metastructure designed with a multiphase configuration could withstand three times the hydrostatic pressure than the one designed with a single-phase unit cell.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fu, Y.; Kabir, I.I.; Yeoh, G.H.; Peng, Z. A review on polymer-based materials for underwater sound absorption. Polym. Test. 2021, 96, 107115. [Google Scholar] [CrossRef]
- Wang, Y.; Miao, X.; Jiang, H.; Chen, M.; Meng, D. Review on underwater sound absorption materials and mechanisms. Adv. Mech. 2017, 47, 92. [Google Scholar]
- Bai, H.; Zhan, Z.; Liu, J.; Ren, Z. From Local Structure to Overall Performance: An Overview on the Design of an Acoustic Coating. Materials 2019, 12, 2509. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Zhao, H.; Lv, L.; Yuan, B.; Wang, G.; Wen, X. Effects of locally resonant modes on underwater sound absorption in viscoelastic materials. J. Acoust. Soc. Am. 2011, 130, 1201. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, H.; Zheng, J.; Pan, J. Underwater sound scattering and absorption by a coated infinite plate with attached periodically located inhomogeneities. J. Acoust. Soc. Am. 2015, 138, 2707. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, W.; Chen, M.; Yang, T.; Wang, K.; Huang, X.; Jiang, H.; Wang, Y. Three-dimensional fractal structure with double negative and density-near-zero properties on a subwavelength scale. Mater. Des. 2020, 188, 108470. [Google Scholar] [CrossRef]
- Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. Sound absorption by rubber coatings with periodic voids and hard inclusions. Appl. Acoust. 2019, 143, 200. [Google Scholar] [CrossRef]
- Lin, H.-C.; Lu, S.-C.; Huang, H.-H. Evaluation of a Hybrid Underwater Sound-Absorbing Metastructure by Using the Transfer Matrix Method. Materials 2023, 16, 1718. [Google Scholar] [CrossRef]
- Gu, Y.; Zhong, H.; Bao, B.; Wang, Q.; Wu, J. Experimental investigation of underwater locally multi-resonant metamaterials under high hydrostatic pressure for low frequency sound absorption. Appl. Acoust. 2021, 172, 107605. [Google Scholar] [CrossRef]
- Chen, M.; Meng, D.; Zhang, H.; Jiang, H.; Wang, Y. Resonance-coupling effect on broad band gap formation in locally resonant sonic metamaterials. Wave. Motion. 2016, 63, 111. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, X.; Tao, W.; Wang, S.; Flowers, G.T.; Hu, Q.; Gaidai, O. Meta-Structure Hull Design with Periodic Layered Phononic Crystals Theory for Wide-Band Low-Frequency Sound Insolation. Materials 2023, 16, 4429. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhang, Z.; Huang, Q.; Li, S. A sandwich anechoic coating embedded with a micro-perforated panel in high-viscosity condition for underwater sound absorption. Compos. Struct. 2020, 235, 111761. [Google Scholar] [CrossRef]
- Gao, N.; Lu, K. An underwater metamaterial for broadband acoustic absorption at low frequency. Appl. Acoust. 2020, 169, 107500. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, X.; Mei, Z.; Li, H.; Wu, D. Investigation of the Underwater Absorption and Reflection Characteristics by Using a Double-Layer Composite Metamaterial. Materials 2023, 16, 49. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Huang, Y.; Zhang, X.; Li, L.; Chen, M.; Fang, D. Broadband underwater sound absorbing structure with gradient cavity shaped polyurethane composite array supported by carbon fiber honeycomb. J. Sound Vib. 2020, 479, 115375. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; Li, T.; Huang, Q. A novel semi-analytical approach for predicting the sound absorptions of a new underwater composite coating with transversely arranged SWCNTs. Compos. Struct. 2021, 274, 114335. [Google Scholar] [CrossRef]
- Fan, J.; Song, B.; Zhang, L.; Wang, X.; Zhang, Z.; Wei, S.; Xiang, X.; Zhu, X.; Shi, Y. Structural design and additive manufacturing of multifunctional metamaterials with low-frequency sound absorption and load-bearing performances. Int. J. Mech. Sci. 2023, 238, 107848. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar photonics with metasurfaces. Science 2013, 339, 6125. [Google Scholar] [CrossRef]
- Zhou, H.; Fu, W.; Li, X.; Wang, Y.; Wang, Y. Loosely coupled reflective impedance metasurfaces: Precise manipulation of waterborne sound by topology optimization. Mech. Sys. Sig. Pro. 2022, 177, 109228. [Google Scholar] [CrossRef]
- Cai, M.; Liu, X.; Hu, G.; Zhou, P. Customization of two-dimensional extremal materials. Mater. Des. 2022, 217, 110657. [Google Scholar] [CrossRef]
- Li, Z.; Luo, Z.; Zhang, L.; Wang, C. Topological design of pentamode lattice metamaterials using a ground structure method. Mater. Des. 2021, 202, 109523. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, X.; Zhou, J. Acoustic porous metasurface for excellent sound absorption based on wave manipulation. J. Sound Vib. 2018, 434, 273–283. [Google Scholar] [CrossRef]
- Duan, H.; Yang, F.; Shen, X.; Yin, Q.; Wang, E.; Zhang, X.; Yang, X.; Shen, C.; Peng, W. Acoustic Metamaterials for Low-Frequency Noise Reduction Based on Parallel Connection of Multiple Spiral Chambers. Materials 2022, 15, 3882. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Wang, S.; Wu, Q.; Xu, X.; Huang, X.; Huang, G.; Liu, Y.; Fan, Z. An inverse design paradigm of multi-functional elastic metasurface via data-driven machine learning. Mater. Des. 2023, 226, 111560. [Google Scholar] [CrossRef]
- Wu, X.; Wen, Z.; Jin, Y.; Rabczuk, T.; Zhuang, X.; Djafari, B. Broadband Rayleigh wave attenuation by gradient metamaterials. Int. J. Mech. Sci. 2021, 205, 106592. [Google Scholar] [CrossRef]
- Jiang, S.; Guo, D.; Zhang, L.; Li, K.; Song, B.; Huang, Y. Electropolishing-enhanced, high-precision 3D printing of metallic pentamode metamaterials. Mater. Des. 2022, 223, 111211. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, F.; Negahban, M.; Zheng, L. Resonator-based reflective metasurface for low-frequency underwater acoustic waves. J. Appl. Phys. 2020, 128, 055305. [Google Scholar] [CrossRef]
- Wu, B.; Chen, B.; Ma, S.; Zhang, D.; Zu, H.-R. An Ultra-Broadband and Highly-Efficient Metamaterial Absorber with Stand-Up Gradient Impedance Graphene Films. Materials 2023, 16, 1617. [Google Scholar] [CrossRef]
- Wu, X.; Xia, X.; Tian, J.; Liu, Z.; Wen, W. Broadband reflective metasurface for focusing underwater ultrasonic waves with linearly tunable focal length. Appl. Phys. Lett. 2016, 108, 163502. [Google Scholar] [CrossRef]
- Chen, J.; Rao, J.; Lisevych, D.; Fan, Z. Broadband ultrasonic focusing in water with an ultra-compact metasurface lens. Appl. Phys. Lett. 2019, 114, 104101. [Google Scholar] [CrossRef]
- Yu, G.; Qiu, Y.; Li, Y.; Wang, X.; Wang, N. Underwater acoustic stealth by a broadband 2-bit coding metasurface. Phys. Rev. A 2021, 15, 064064. [Google Scholar] [CrossRef]
- Fang, Y.; Zhang, X.; Zhou, J.; Guo, J.; Huang, X. Acoustic metaporous layer with composite structures for perfect and quasi-omnidirectional sound absorption. Compos. Struct. 2019, 223, 110948. [Google Scholar] [CrossRef]
- Yuan, T.; Song, X.; Xu, J.; Pan, B.; Sui, D.; Xiao, H.; Zhou, J. Tunable acoustic composite metasurface based porous material for broadband sound absorption. Compos. Struct. 2022, 298, 116014. [Google Scholar] [CrossRef]
- Miltion, G.W.; Cherkaev, A.V. Which elasticity tensor are realizable. J. Eng. Mater. Tech. 1995, 117, 483–493. [Google Scholar] [CrossRef]
- Gokhale, N.H.; Cipolla, J.L.; Norris, A.N. Special transformations for pentamode acoustic cloaking. J. Acoust. Soc. Am. 2012, 132, 2932–2941. [Google Scholar] [CrossRef]
- Zhang, L.; Song, B.; Zhao, A.; Liu, R.; Yang, L.; Shi, Y. Study on mechanical properties of honeycomb pentamode structures fabricated by laser additive manufacturing: Numerical simulation and experimental verification. Compos. Struct. 2019, 226, 111199. [Google Scholar] [CrossRef]
- Amendola, A.; Smith, C.J.; Goodall, R.; Auricchio, F.; Feo, L.; Benzoni, G.; Fraternali, F. Experimental response of additively manufactured metallic pentamode materials confined between stiffening plates. Compos. Struct. 2016, 142, 254–262. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, M.; Liu, X.; Bi, Y.; Sun, Z.; Xiang, P.; Yang, J.; Hu, G. Broadband solid cloak for underwater acoustics. Phys. Rev. B 2017, 95, 180104. [Google Scholar] [CrossRef]
- Cai, X.; Wang, L.; Zhao, Z.; Zhao, A.; Zhang, X.; Wu, T.; Chen, H. The mechanical and acoustic properties of two-dimensional pentamode metamaterials with different structural parameters. Appl. Phys. Lett. 2016, 109, 131904. [Google Scholar] [CrossRef]
- Zhao, A.; Zhao, Z.; Zhang, X.; Cai, X.; Wang, L.; Wu, T.; Chen, H. Design and experimental verification of a water-like pentamode material. Appl. Phys. Lett. 2017, 110, 011907. [Google Scholar] [CrossRef]
- Su, X.; Norris, A.N.; Cushing, C.W. Broadband focusing of underwater sound using a transparent pentamode lens. J. Acoust. Soc. Am. 2017, 141, 4408–4417. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Hu, G. Broadband and high-transmission metasurface for converting underwater cylindrical waves to plane waves. Phys. Rev. Appl. 2019, 12, 044046. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, X.; Jia, H.; Bi, Y.; Yang, J. Quasi-isotropic underwater acoustic carpet cloak based on latticed pentamode metafluid. Appl. Phys. Lett. 2019, 114, 094101. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, H.; Zhao, Z.; Zhao, A.; Cai, X.; Wang, L. Experimental demonstration of a broadband waterborne acoustic metasurface for shifting reflected waves. J. Appl. Phys. 2020, 127, 174902. [Google Scholar] [CrossRef]
- Dong, H.; Zhao, S.; Miao, X.; Shen, C.; Zhang, X.; Zhao, Z.; Zhang, C.; Wang, Y.; Cheng, L. Customized broadband pentamode metamaterials by topology optimization. J. Mech. Phys. Solids 2021, 152, 104407. [Google Scholar] [CrossRef]
- Dong, H.; Zhao, S.; Oudich, M.; Shen, C.; Zhang, C.; Cheng, L.; Wang, Y.; Fang, D. Reflective metasurfaces with multiple elastic mode conversions for broadband underwater sound absorption. Phys. Rev. Appl. 2022, 17, 044013. [Google Scholar] [CrossRef]
- Ren, Z.; Dong, H.; He, X.; Chen, M.; Fang, D. Underwater gradient metalens for broadband subwavelength focusing. Int. J. Mech. Sci. 2022, 229, 107521. [Google Scholar] [CrossRef]
- Zhao, A.; Zhang, X.; Yu, W.; Zhao, Z.; Cai, X.; Chen, H. Design and simulation of broadband multiphase pentamode metamaterials. Appl. Phys. Lett. 2021, 118, 224103. [Google Scholar] [CrossRef]
- Zhao, A.; Jia, H.; Zhang, M.; Wang, Z.; Zhou, P.; Liu, C.; Zhao, Z.; Zhang, X.; Wu, T.; Chen, H.; et al. Design and experimental verification of a broadband multiphase pentamode material. Phys. Rev. Appl. 2022, 18, 034001. [Google Scholar] [CrossRef]
- Zhao, A.; Liu, C.; Zou, H.; Jia, H.; Zhang, M.; Wu, T.; Chen, H.; Zhang, X.; Wang, Z. Massive and fast fabrication of pentamode devices through a multiphase honeycomb-corrugation configuration. Mater. Des. 2023, 228, 111816. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.; Vecchi, M. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Goo, S.; Kook, J. Design of a local resonator using topology optimization to tailor bandgaps in plate structures. Mater. Des. 2020, 191, 108627. [Google Scholar] [CrossRef]

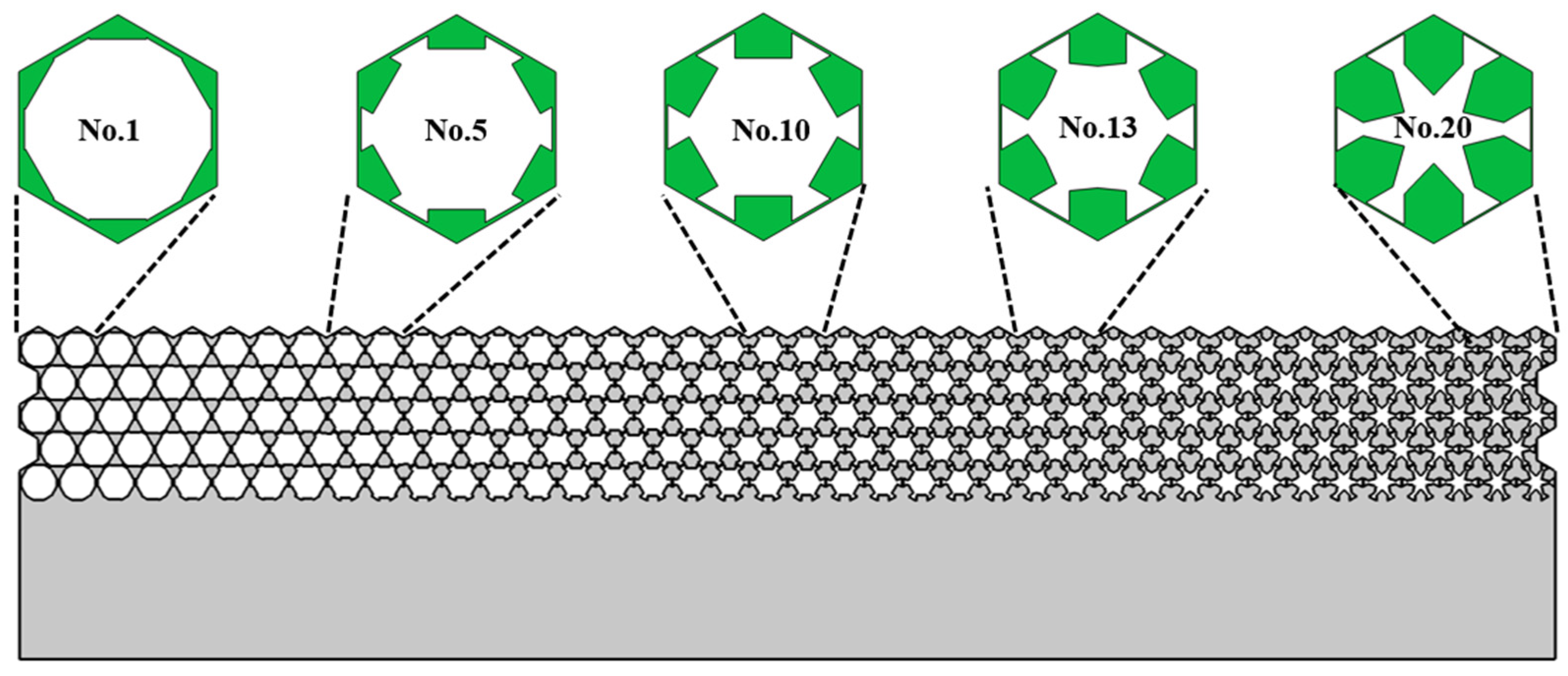
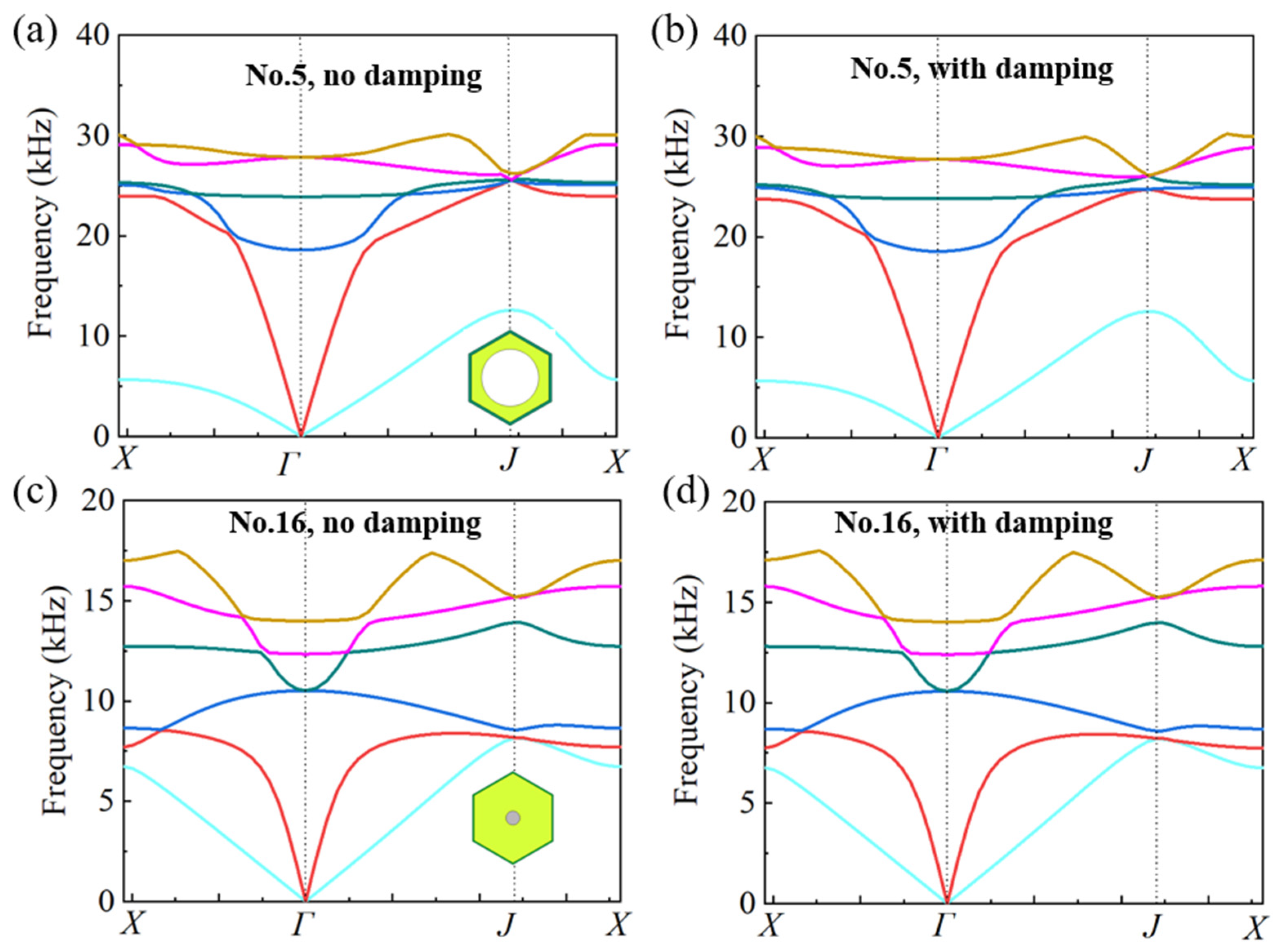
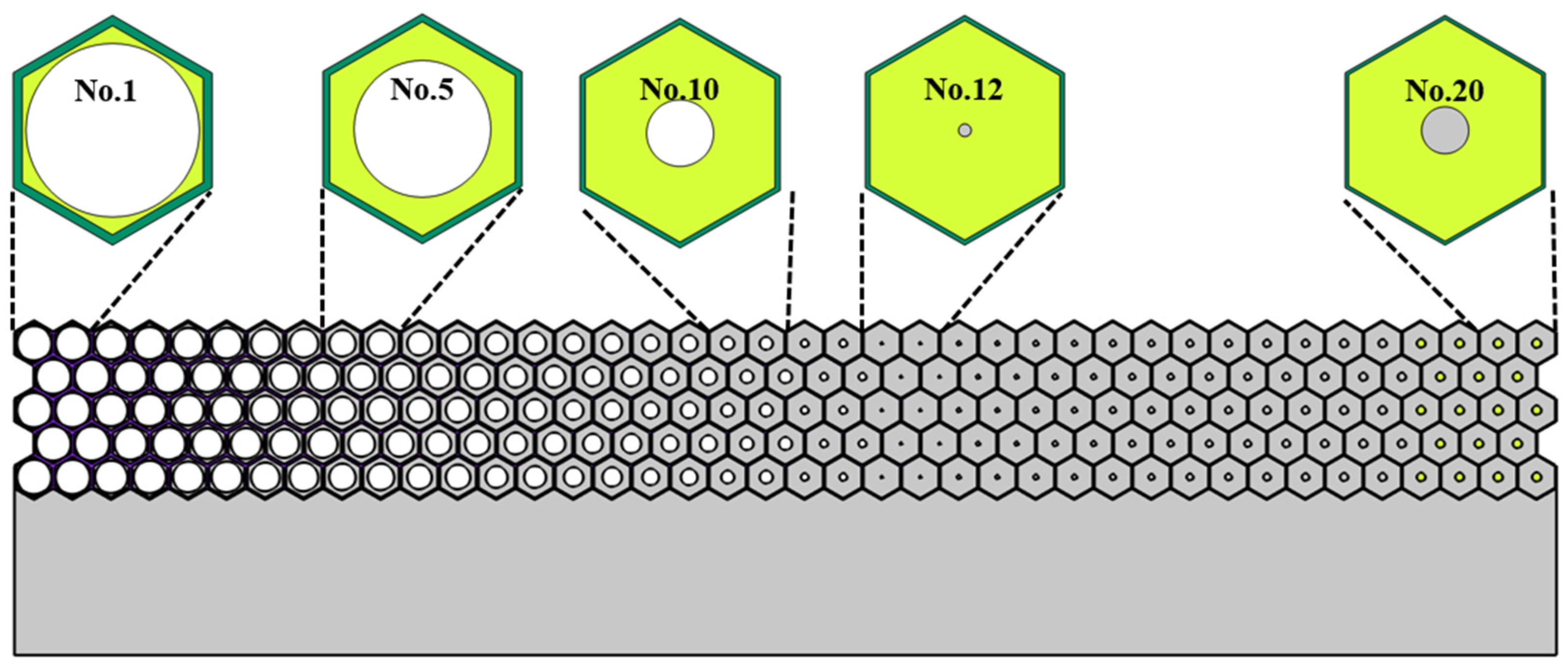

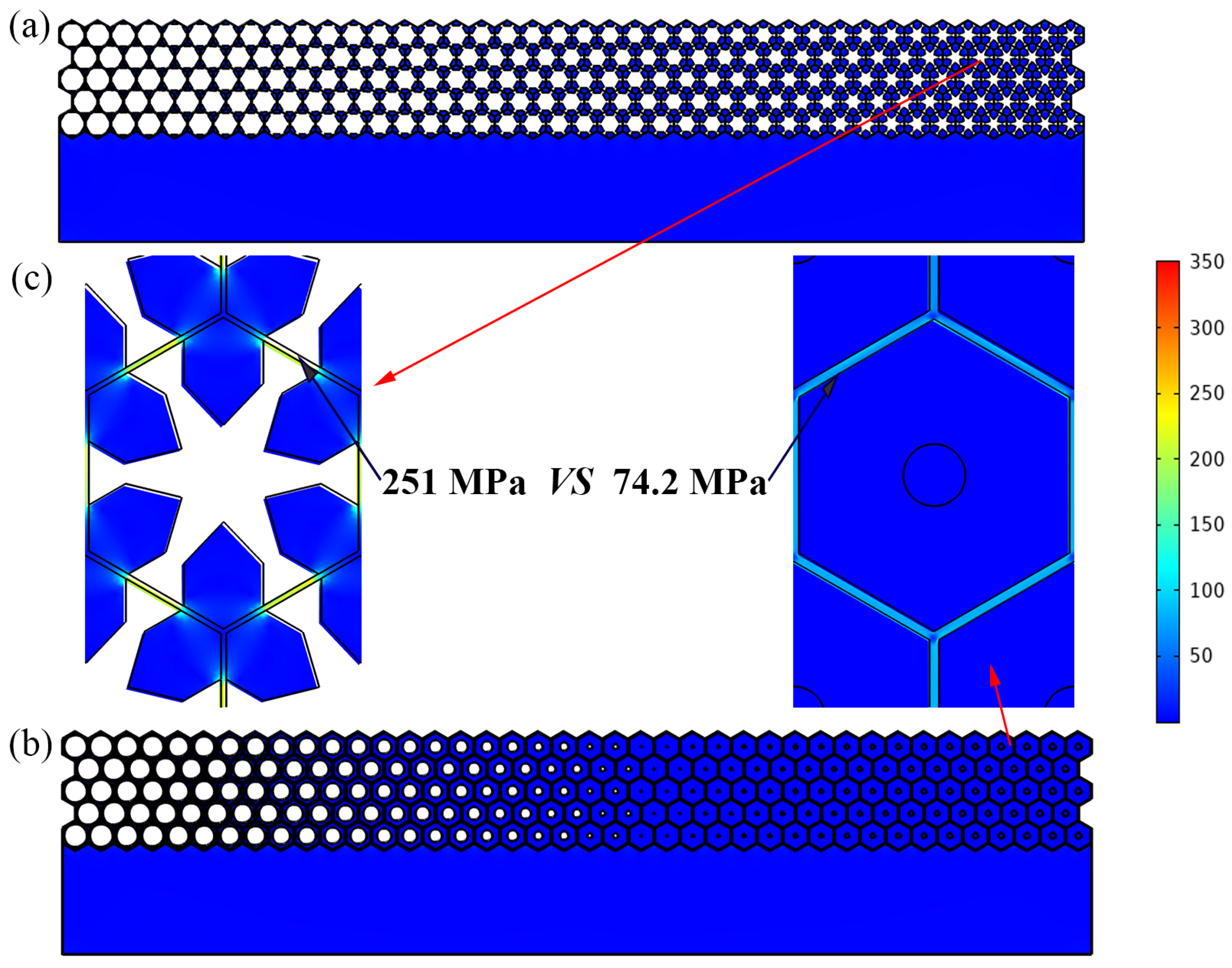
| Cell No. | Equivalent Properties | Single-Phase | Multiphase | ||||||
|---|---|---|---|---|---|---|---|---|---|
| X Coordinate (m) | Density (ρ0) | Modulus (κ0) | t (mm) | b (mm) | m (mm) | r (mm) | t’ (mm) | R (mm) | |
| 1 | −0.3291 | 0.5677 | 1.7616 | 1.000 | 2.5 | 0.13 | 0 | 1.55 | 7.75 |
| 2 | −0.2944 | 0.6237 | 1.6033 | 0.900 | 2.5 | 0.40 | 0 | 1.45 | 7.30 |
| 3 | −0.2598 | 0.6797 | 1.4711 | 0.820 | 2.5 | 0.66 | 0 | 1.35 | 6.90 |
| 4 | −0.2252 | 0.7358 | 1.3591 | 0.760 | 2.5 | 0.89 | 0 | 1.25 | 6.45 |
| 5 | −0.1905 | 0.7918 | 1.2629 | 0.680 | 2.5 | 1.15 | 0 | 1.17 | 5.95 |
| 6 | −0.1559 | 0.8478 | 1.1795 | 0.630 | 2.5 | 1.38 | 0 | 1.10 | 5.50 |
| 7 | −0.1212 | 0.9039 | 1.1063 | 0.545 | 2.5 | 1.64 | 0 | 1.03 | 4.90 |
| 8 | −0.0866 | 0.9599 | 1.0418 | 0.530 | 2.5 | 1.84 | 0 | 0.98 | 4.35 |
| 9 | −0.0520 | 1.0159 | 0.9843 | 0.515 | 2.5 | 2.03 | 0 | 0.93 | 3.70 |
| 10 | −0.0173 | 1.0720 | 0.9329 | 0.490 | 2.5 | 2.23 | 0 | 0.88 | 2.90 |
| 11 | 0.0173 | 1.1280 | 0.8865 | 0.465 | 2.5 | 2.44 | 0 | 0.82 | 1.70 |
| 12 | 0.0520 | 1.1841 | 0.8446 | 0.445 | 2.5 | 2.64 | 0 | 0.77 | 0.55 |
| 13 | 0.0866 | 1.2401 | 0.8064 | 0.425 | 2.5 | 2.70 | 0.27 | 0.74 | 0.90 |
| 14 | 0.1212 | 1.2961 | 0.7715 | 0.405 | 2.5 | 2.70 | 0.67 | 0.71 | 1.13 |
| 15 | 0.1559 | 1.3522 | 0.7396 | 0.380 | 2.5 | 2.70 | 1.08 | 0.68 | 1.33 |
| 16 | 0.1905 | 1.4082 | 0.7101 | 0.360 | 2.5 | 2.70 | 1.48 | 0.66 | 1.50 |
| 17 | 0.2252 | 1.4642 | 0.6830 | 0.350 | 2.5 | 2.70 | 1.85 | 0.64 | 1.65 |
| 18 | 0.2598 | 1.5203 | 0.6578 | 0.340 | 2.5 | 2.70 | 2.23 | 0.62 | 1.80 |
| 19 | 0.2944 | 1.5763 | 0.6344 | 0.330 | 2.5 | 2.70 | 2.62 | 0.60 | 1.92 |
| 20 | 0.3291 | 1.6323 | 0.6126 | 0.300 | 2.58 | 2.70 | 2.68 | 0.58 | 2.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, Y.; Zou, H.; Zhao, A. Broadband Waterborne Multiphase Pentamode Metastructure with Simultaneous Wavefront Manipulation and Energy Absorption Capabilities. Materials 2023, 16, 5051. https://doi.org/10.3390/ma16145051
An Y, Zou H, Zhao A. Broadband Waterborne Multiphase Pentamode Metastructure with Simultaneous Wavefront Manipulation and Energy Absorption Capabilities. Materials. 2023; 16(14):5051. https://doi.org/10.3390/ma16145051
Chicago/Turabian StyleAn, Yi, Han Zou, and Aiguo Zhao. 2023. "Broadband Waterborne Multiphase Pentamode Metastructure with Simultaneous Wavefront Manipulation and Energy Absorption Capabilities" Materials 16, no. 14: 5051. https://doi.org/10.3390/ma16145051
APA StyleAn, Y., Zou, H., & Zhao, A. (2023). Broadband Waterborne Multiphase Pentamode Metastructure with Simultaneous Wavefront Manipulation and Energy Absorption Capabilities. Materials, 16(14), 5051. https://doi.org/10.3390/ma16145051






