Interplay between Diffusion and Bond Cleavage Reaction for Determining Release in Polymer–Drug Conjugates
Abstract
1. Introduction
2. Numerical Methods
3. Results and Discussion
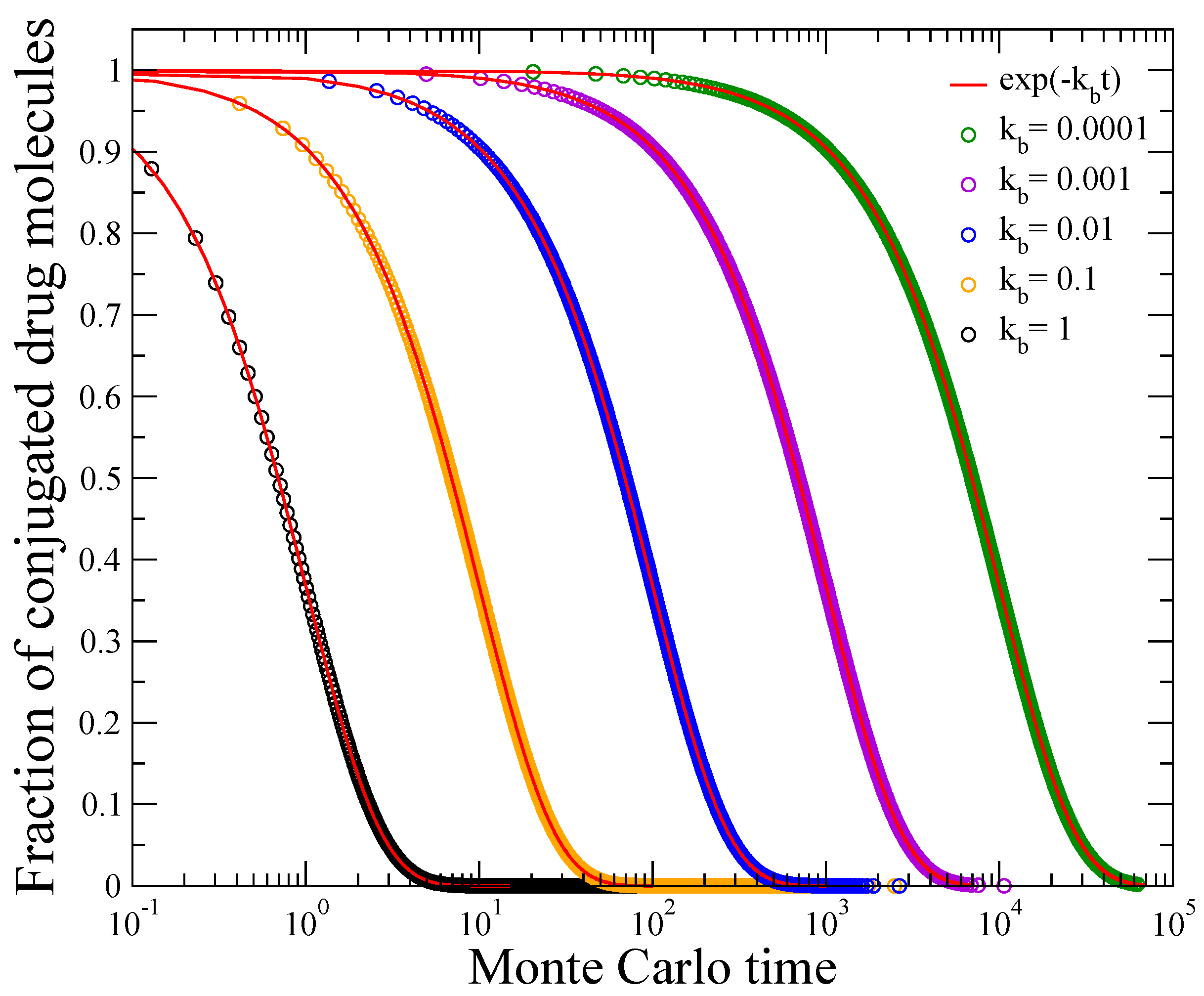
3.1. Cleavage Reaction: First-Order Kinetics
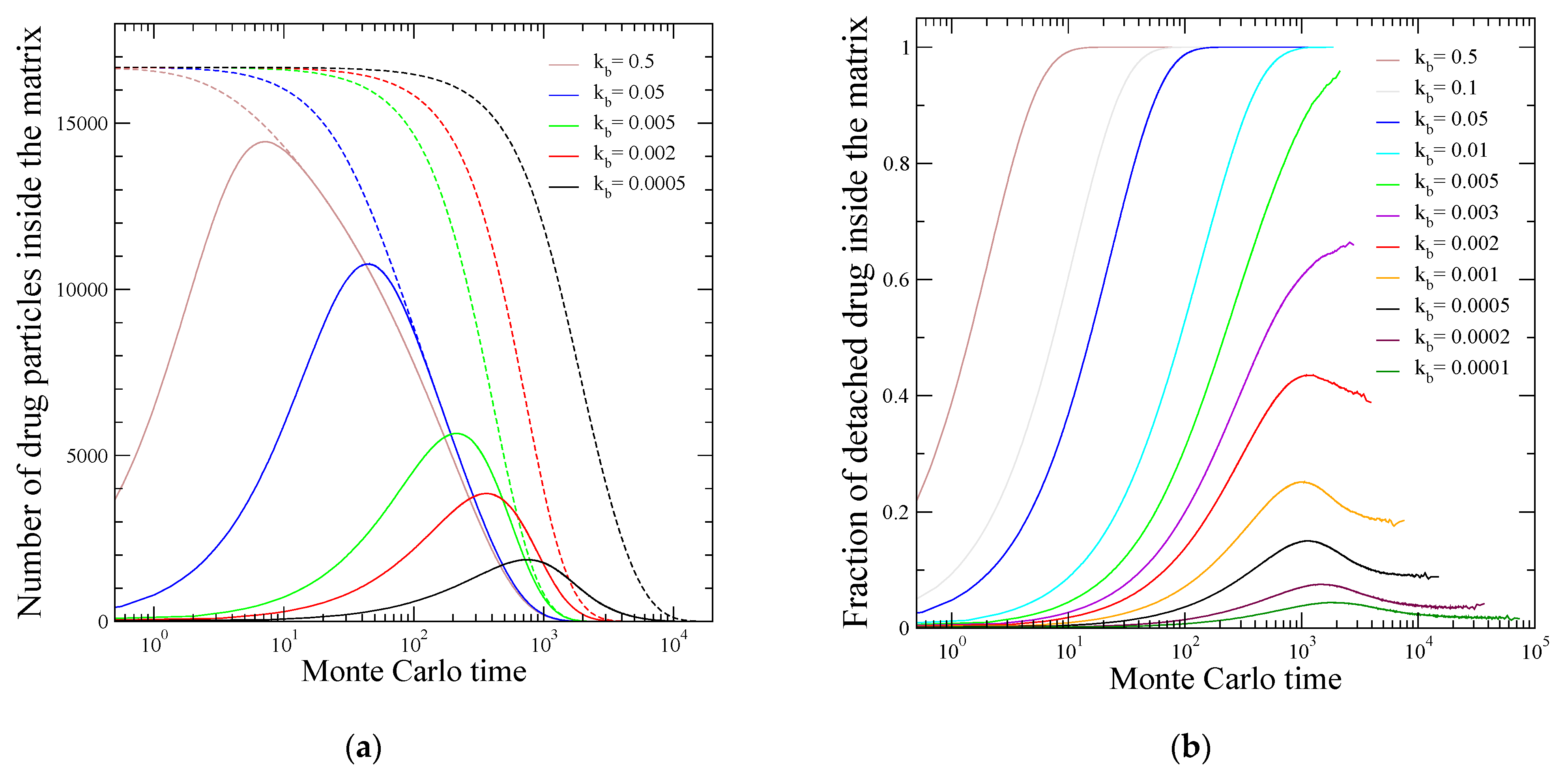
3.2. Fraction of the Freely Diffusing Molecules within the Polymer Matrix
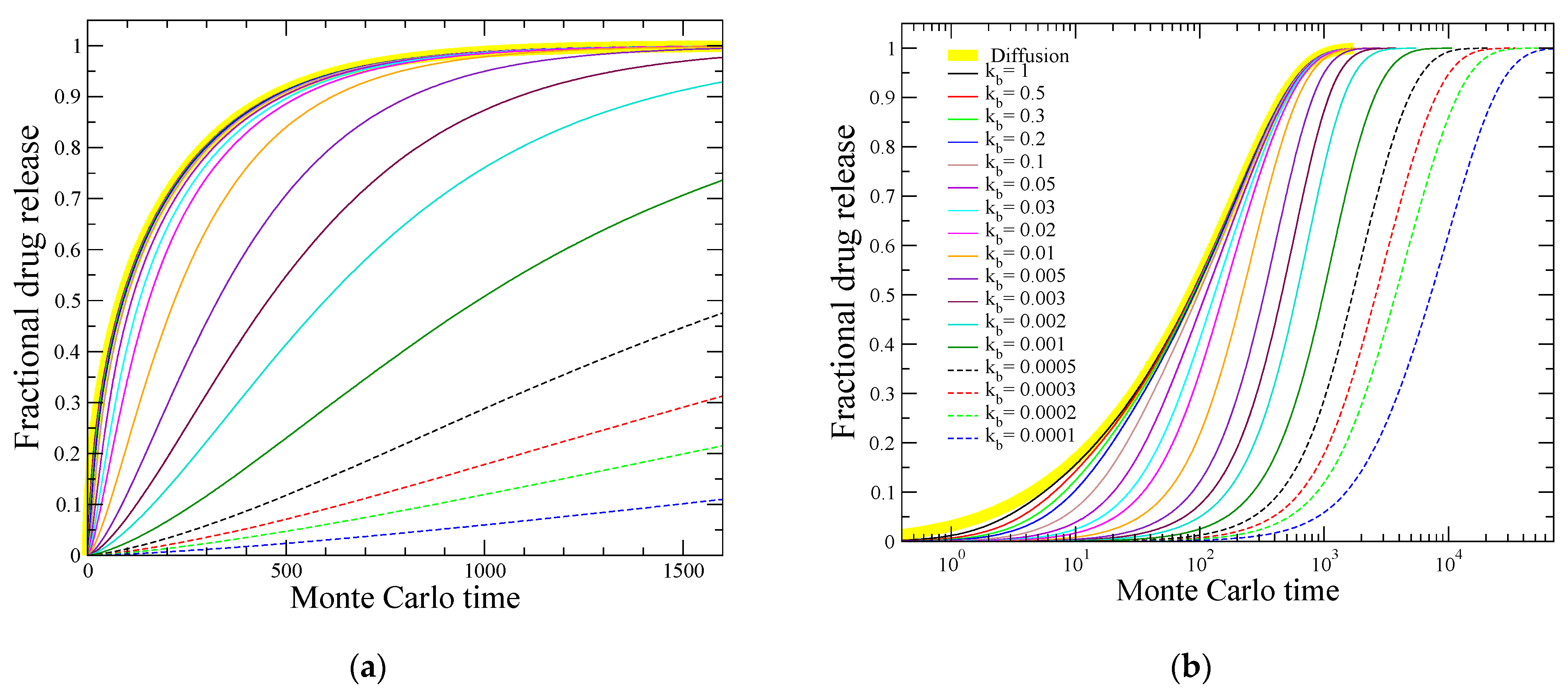
3.3. Drug Release Profiles
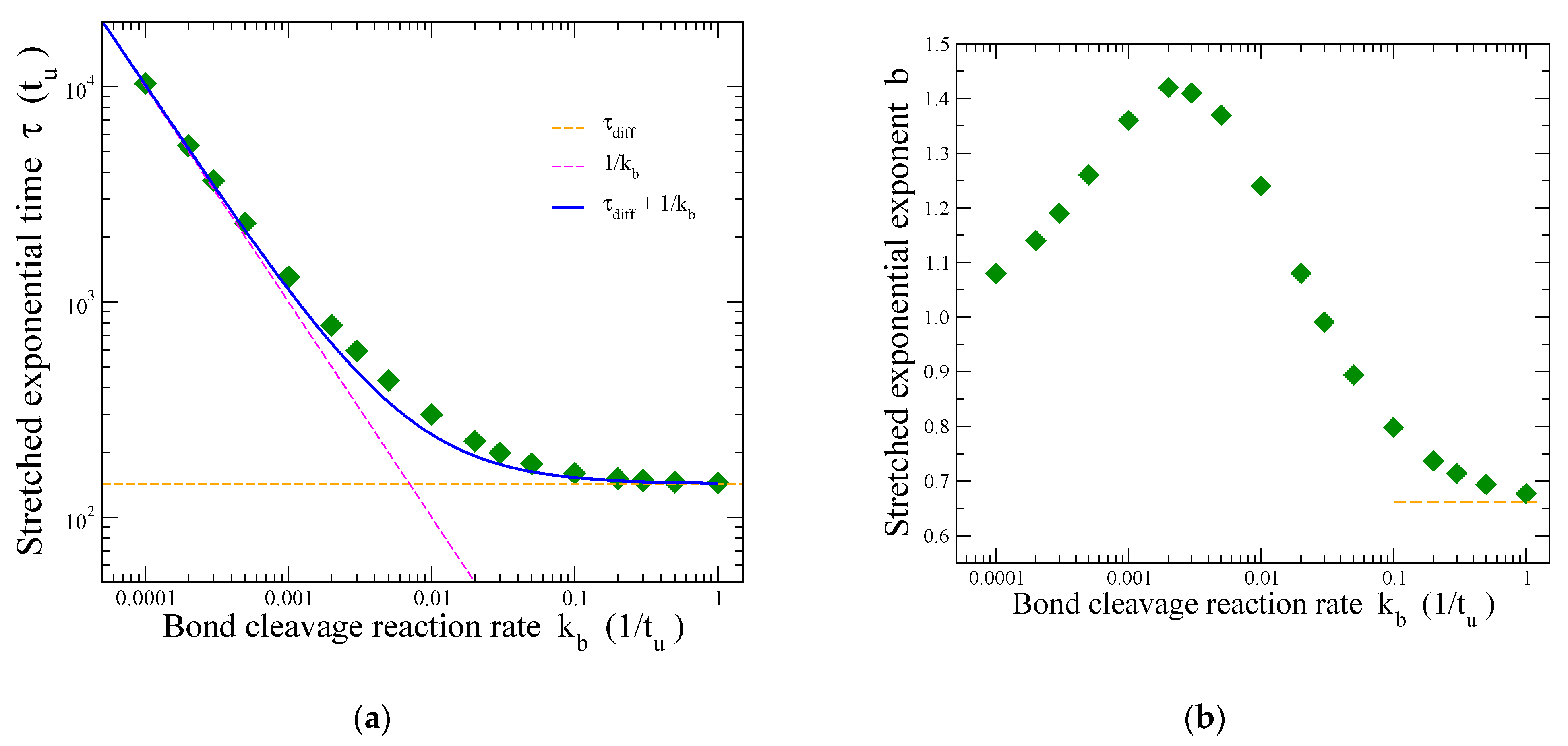
3.4. Characteristic Release Time Scales
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Abune, L.; Wang, Y. Affinity Hydrogels for Protein Delivery. Trends Pharm. Sci. 2021, 42, 300–312. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Feng, Q.; Fang, Z.; Gu, L.; Bian, L. Structurally Dynamic Hydrogels for Biomedical Applications: Pursuing a Fine Balance between Macroscopic Stability and Microscopic Dynamics. Chem. Rev. 2021, 121, 11149–11193. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Reaume, M.; Hennenfent, M.; Lee, B.P.; Rajachar, R. Biomimetic hydrogels with spatial- and temporal-controlled chemical cues for tissue engineering. Biomater. Sci. 2020, 8, 3248–3269. [Google Scholar] [CrossRef] [PubMed]
- Chao, Y.; Chen, Q.; Liu, Z. Smart Injectable Hydrogels for Cancer Immunotherapy. Adv. Funct. Mater. 2020, 30, 1902785. [Google Scholar] [CrossRef]
- Picheth, G.F.; Pirich, C.L.; Sierakowski, M.R.; Woehl, M.A.; Sakakibara, C.N.; De Souza, C.F.; Martin, A.A.; Da Silva, R.; De Freitas, R.A. Bacterial cellulose in biomedical applications: A review. Int. J. Biol. Macromol. 2017, 104, 97–106. [Google Scholar] [CrossRef]
- Vulic, K.; Shoichet, M.S. Affinity-Based Drug Delivery Systems for Tissue Repair and Regeneration. Biomacromolecules 2014, 15, 3867–3880. [Google Scholar] [CrossRef]
- Baroli, B. Hydrogels for Tissue Engineering and Delivery of Tissue-Inducing Substances. J. Pharm. Sci. 2007, 96, 2197–2223. [Google Scholar] [CrossRef]
- Kost, J.; Langer, R. Responsive polymeric delivery systems. Adv. Drug Deliv. Rev. 2001, 46, 125–148. [Google Scholar] [CrossRef]
- Lin, C.-C.; Metters, A.T. Hydrogels in controlled release formulations: Network design and mathematical modeling. Adv. Drug Deliv. Rev. 2006, 58, 1379–1408. [Google Scholar] [CrossRef]
- Javia, A.; Vanza, J.; Bardoliwala, D.; Ghosh, S.; Misra, L.A.; Patel, M.; Thakkar, H. Polymer-drug conjugates: Design principles, emerging synthetic strategies and clinical overview. Int. J. Pharm. 2022, 623, 121863. [Google Scholar] [CrossRef]
- Seidi, F.; Jenjob, R.; Crespy, D. Designing Smart Polymer Conjugates for Controlled Release of Payloads. Chem. Rev. 2018, 118, 3965–4036. [Google Scholar] [CrossRef]
- Pang, X.; Jiang, Y.; Xiao, Q.; Leung, A.W.; Hua, H.; Xu, C. pH-responsive polymer-drug conjugates: Design and progress. J. Control. Release 2016, 222, 116–129. [Google Scholar] [CrossRef]
- Khandare, J.; Minko, T. Polymer–drug conjugates: Progress in polymeric prodrugs. Prog. Polym. Sci. 2006, 31, 359–397. [Google Scholar] [CrossRef]
- Elvira, C.; Gallardo, A.; San Roman, J.; Cifuentes, A. Covalent Polymer-Drug Conjugates. Molecules 2005, 10, 114–125. [Google Scholar] [CrossRef]
- Greenwald, R.B.; Choe, Y.H.; McGuire, J.; Conover, C.D. Effective drug delivery by PEGylated drug conjugates. Adv. Drug Deliv. Rev. 2003, 55, 217–250. [Google Scholar] [CrossRef]
- Psarrou, M.; Kothri, M.G.; Vamvakaki, M. Photo- and Acid-Degradable Polyacylhydrazone–Doxorubicin Conjugates. Polymers 2021, 13, 2461. [Google Scholar] [CrossRef]
- Chen, W.-H.; Luo, G.-F.; Lei, Q.; Jia, H.-Z.; Hong, S.; Wang, Q.-R.; Zhuo, R.-X.; Zhang, X.-Z. MMP-2 responsive polymeric micelles for cancer-targeted intracellular drug delivery. Chem. Commun. 2015, 51, 465–468. [Google Scholar] [CrossRef]
- Xiong, L.; Luo, Q.; Wang, Y.; Li, X.; Shen, Z.; Zhu, W. An Injectable Drug-Loaded Hydrogel Based on a Supramolecular Polymeric Prodrug. Chem. Commun. 2015, 51, 14644–14647. [Google Scholar] [CrossRef]
- Su, Y.; Hu, Y.; Du, Y.; Huang, X.; He, J.; You, J.; Yuan, H.; Hu, F. Redox-Responsive Polymer-Drug Conjugates Based on Doxorubicin and Chitosan Oligosaccharide-g-stearic Acid for Cancer Therapy. Mol. Pharm. 2015, 12, 1193–1202. [Google Scholar] [CrossRef]
- Sun, C.-Y.; Dou, S.; Du, J.-Z.; Yang, X.-Z.; Li, Y.-P.; Wang, J. Doxorubicin Conjugate of Poly (Ethylene Glycol)-Block-Polyphosphoester for Cancer Therapy. Adv. Healthc. Mater. 2014, 3, 261–272. [Google Scholar] [CrossRef]
- Chen, W.; Shah, L.A.; Yuan, L.; Siddiq, M.; Hu, J.; Yang, D. Polymer-paclitaxel conjugates based on disulfide linkers for controlled drug release. RSC Adv. 2015, 5, 7559–7566. [Google Scholar] [CrossRef]
- Lv, S.; Tang, Z.; Zhang, D.; Song, W.; Li, M.; Lin, J.; Liu, H.; Chen, X. Well-defined polymer-drug conjugate engineered with redox and pH-sensitive release mechanism for efficient delivery of paclitaxel. J. Control. Release 2014, 194, 220–227. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, W.; Hu, J.; Du, M.; Yang, D. Polymerizable disulfide paclitaxel prodrug for controlled drug delivery. Mater. Sci. Eng. C 2014, 44, 386–390. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, C.-K.; Law, W.-C.; Mok, J.; Zou, J.; Prasad, P.N.; Cheng, C. Well-Defined Degradable Brush Polymer-Drug Conjugates for Sustained Delivery of Paclitaxel. Mol. Pharm. 2013, 10, 867–874. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Zhang, H.; He, W.; Zhao, D.; Song, A.; Luan, Y. Disulfide-Linked Amphiphilic Polymer-Docetaxel Conjugates Assembled Redox-Sensitive Micelles for Efficient Antitumor Drug Delivery. Biomacromolecules 2016, 17, 1621–1632. [Google Scholar] [CrossRef]
- Dubashynskaya, N.V.; Bokatyi, A.N.; Golovkin, A.S.; Kudryavtsev, I.V.; Serebryakova, M.K.; Trulioff, A.S.; Dubrovskii, Y.A.; Skorik, Y.A. Synthesis and Characterization of Novel Succinyl Chitosan-Dexamethasone Conjugates for Potential Intravitreal Dexamethasone Delivery. Int. J. Mol. Sci. 2021, 22, 10960. [Google Scholar] [CrossRef]
- Ehrbar, M.; Metters, A.; Zammaretti, P.; Hubbell, J.A.; Zisch, A.H. Endothelial cell proliferation and progenitor maturation by fibrin-bound VEGF variants with differential susceptibilities to local cellular activity. J. Control. Release 2005, 101, 93–109. [Google Scholar] [CrossRef]
- Seliktar, D.; Zisch, A.H.; Lutolf, M.P.; Wrana, J.L.; Hubbell, J.A. MMP-2 sensitive, VEGF-bearing bioactive hydrogels for promotion of vascular healing. J. Biomed. Mater. Res. A 2004, 68, 704–716. [Google Scholar] [CrossRef]
- Zhao, X.; Harris, J.M. Novel Degradable Poly(ethylene glycol) Hydrogels for Controlled Release of Protein. J. Pharm. Sci. 1998, 87, 1450–1458. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.S.; Kulkarni, M.G.; Mashelkar, R.A. Release kinetics of pendant substituted bioactive molecules from swellable hydrogels: Role of chemical reaction and diffusive transport. J. Membr. Sci. 1990, 51, 83–104. [Google Scholar] [CrossRef]
- Arifin, D.Y.; Lee, L.Y.; Wang, C.-H. Mathematical modeling and simulation of drug release from microspheres: Implications to drug delivery systems. Adv. Drug Deliv. Rev. 2006, 58, 1274–1325. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug delivery. Int. J. Pharm. 2008, 364, 328–343. [Google Scholar] [CrossRef]
- Lao, L.L.; Peppas, N.A.; Boey, F.Y.C.; Venkatraman, S.S. Modeling of drug release from bulk-degrading polymers. Int. J. Pharm. 2011, 418, 28–41. [Google Scholar] [CrossRef] [PubMed]
- Versypt, A.N.F.; Pack, D.W.; Braatz, R.D. Mathematical modeling of drug delivery from autocatalytically degradable PLGA microspheres—A review. J. Control. Release 2013, 165, 29–37. [Google Scholar] [CrossRef]
- Peppas, N.A.; Narasimhan, B. Mathematical models in drug delivery: How modeling has shaped the way we design new drug delivery systems. J. Control. Release 2014, 190, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Casalini, T.; Perale, G. From Microscale to Macroscale: Nine Orders of Magnitude for a Comprehensive Modeling of Hydrogels for Controlled Drug Delivery. Gels 2019, 5, 28. [Google Scholar] [CrossRef] [PubMed]
- Quesada-Pérez, M.; Pérez-Mas, L.; Carrizo-Tejero, D.; Maroto-Centeno, J.-A.; Ramos-Tejada, M.d.M.; Martín-Molina, A. Coarse-Grained Simulations of Release of Drugs Housed in Flexible Nanogels: New Insights into Kinetic Parameters. Polymers 2022, 14, 4760. [Google Scholar] [CrossRef]
- Pitt, C.G.; Schindler, A. The kinetics of drug cleavage and release from matrices containing covalent polymer-drug conjugates. J. Control. Release 1995, 33, 391–395. [Google Scholar] [CrossRef]
- DuBose, J.W.; Cutshall, C.; Metters, A.T. Controlled release of tethered molecules via engineered hydrogel degradation: Model development and validation. J. Biomed. Mater. Res. A 2005, 74, 104–116. [Google Scholar] [CrossRef]
- Siepmann, J.; Faisant, N.; Benoit, J.-P. A New Mathematical Model Quantifying Drug Release from Bioerodible Microparticles Using Monte Carlo Simulations. Pharm. Res. 2002, 19, 1885–1893. [Google Scholar] [CrossRef]
- Kosmidis, K.; Argyrakis, P.; Macheras, P. A Reappraisal of Drug Release Laws Using Monte Carlo Simulations: The Prevalence of the Weibull Function. Pharm. Res. 2003, 20, 988–995. [Google Scholar] [CrossRef] [PubMed]
- Vlugt-Wensink, K.D.; Vlugt, T.J.; Jiskoot, W.; Crommelin, D.J.; Verrijk, R.; Hennink, W.E. Modeling the release of proteins from degrading crosslinked dextran microspheres using kinetic Monte Carlo simulations. J. Control. Release 2006, 111, 117–127. [Google Scholar] [CrossRef] [PubMed]
- Villalobos, R.; Cordero, S.; Vidales, A.M.; Domínguez, A. In silico study on the effects of matrix structure in controlled drug release. Phys. A Stat. Mech. Its Appl. 2006, 367, 305–318. [Google Scholar] [CrossRef]
- Bertrand, N.; LeClair, G.; Hildgen, P. Modeling drug release from bioerodible microspheres using a cellular automaton. Int. J. Pharm. 2007, 343, 196–207. [Google Scholar] [CrossRef]
- Wang, X.-P.; Chen, T.-N.; Yang, Z.-X. Modeling and simulation of drug delivery from a new type of biodegradable polymer micro-device. Sens. Actuators A Phys. 2007, 133, 363–367. [Google Scholar] [CrossRef]
- Kosmidis, K.; Macheras, P. Monte Carlo simulations for the study of drug release from matrices with high and low diffusivity areas. Int. J. Pharm. 2007, 343, 166–172. [Google Scholar] [CrossRef]
- Kosmidis, K.; Macheras, P. Monte Carlo simulations of drug release from matrices with periodic layers of high and low diffusivity. Int. J. Pharm. 2008, 354, 111–116. [Google Scholar] [CrossRef]
- Martínez, L.; Villalobos, R.; Sánchez, M.; Cruz, J.; Ganem, A.; Melgoza, L.M. Monte Carlo simulations for the study of drug release from cylindrical matrix systems with an inert nucleus. Int. J. Pharm. 2009, 369, 38–46. [Google Scholar] [CrossRef]
- Hadjitheodorou, A.; Kalosakas, G. Quantifying diffusion-controlled drug release from spherical devices using Monte Carlo simulations. Mater. Sci. Eng. C 2013, 33, 763–768. [Google Scholar] [CrossRef]
- Hadjitheodorou, A.; Kalosakas, G. Analytical and numerical study of diffusion-controlled drug release from composite spherical matrices. Mater. Sci. Eng. C 2014, 42, 681–690. [Google Scholar] [CrossRef]
- Dan, N. Drug release through liposome pores. Colloids Surf. B Biointerfaces 2015, 126, 80–86. [Google Scholar] [CrossRef]
- Kalosakas, G.; Martini, D. Drug release from slabs and the effects of surface roughness. Int. J. Pharm. 2015, 496, 291–298. [Google Scholar] [CrossRef]
- Christidi, E.V.; Kalosakas, G. Dynamics of the fraction of drug particles near the release boundary; Justifying a stretched exponential kinetics in Fickian drug release. Eur. Phys. J. Spec. Top. 2016, 225, 1245–1254. [Google Scholar] [CrossRef]
- Ignacio, M.; Chubynsky, M.V.; Slater, G.W. Interpreting the Weibull fitting parameters for diffusion-controlled release data. Phys. A Stat. Mech. Its Appl. 2017, 486, 486–496. [Google Scholar] [CrossRef]
- Singh, K.; Satapathi, S.; Jha, P.K. Ant-Wall model to study drug release from excipient matrix. Phys. A 2019, 519, 98–108. [Google Scholar] [CrossRef]
- Hoffmann, F.; Machatschek, R.; Lendlein, A. Understanding the impact of crystal lamellae organization on small molecule diffusion using a Monte Carlo approach. MRS Adv. 2020, 5, 2737–2749. [Google Scholar] [CrossRef]
- Gomes-Filho, M.S.; Oliveira, F.A.; Barbosa, M.A.A. Modeling the diffusion-erosion crossover dynamics in drug release. Phys. Rev. E 2022, 105, 044110. [Google Scholar] [CrossRef] [PubMed]
- Kalosakas, G.; Panagopoulou, E. Lag Time in Diffusion-Controlled Release Formulations Containing a Drug-Free Outer Layer. Processes 2022, 10, 2592. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Jonnalagadda, S. Levonorgestrel loaded biodegradable microparticles for injectable contraception: Preparation, characterization and modelling of drug release. Int. J. Pharm. 2022, 624, 121994. [Google Scholar] [CrossRef]
- Reid, R.; Sgobba, M.; Raveh, B.; Rastelli, G.; Sali, A.; Santi, D.V. Analytical and Simulation-Based Models for Drug Release and Gel-Degradation in a Tetra-PEG Hydrogel Drug-Delivery System. Macromolecules 2015, 48, 7359–7369. [Google Scholar] [CrossRef]
- Mezhuev, Y.O.; Varankin, A.V.; Luss, A.L.; Dyatlov, V.A.; Tsatsakis, A.M.; Shtilman, M.I.; Korshak, Y.V. Immobilization of dopamine on the copolymer of N-vinyl-2-pyrrolidone and allyl glycidyl ether and synthesis of new hydrogels. Polym. Int. 2020, 69, 1275–1282. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalosakas, G. Interplay between Diffusion and Bond Cleavage Reaction for Determining Release in Polymer–Drug Conjugates. Materials 2023, 16, 4595. https://doi.org/10.3390/ma16134595
Kalosakas G. Interplay between Diffusion and Bond Cleavage Reaction for Determining Release in Polymer–Drug Conjugates. Materials. 2023; 16(13):4595. https://doi.org/10.3390/ma16134595
Chicago/Turabian StyleKalosakas, George. 2023. "Interplay between Diffusion and Bond Cleavage Reaction for Determining Release in Polymer–Drug Conjugates" Materials 16, no. 13: 4595. https://doi.org/10.3390/ma16134595
APA StyleKalosakas, G. (2023). Interplay between Diffusion and Bond Cleavage Reaction for Determining Release in Polymer–Drug Conjugates. Materials, 16(13), 4595. https://doi.org/10.3390/ma16134595





