Fractal Characterization of the Mass Loss of Bronze by Erosion–Corrosion in Seawater
Abstract
1. Introduction
2. Materials and Methods
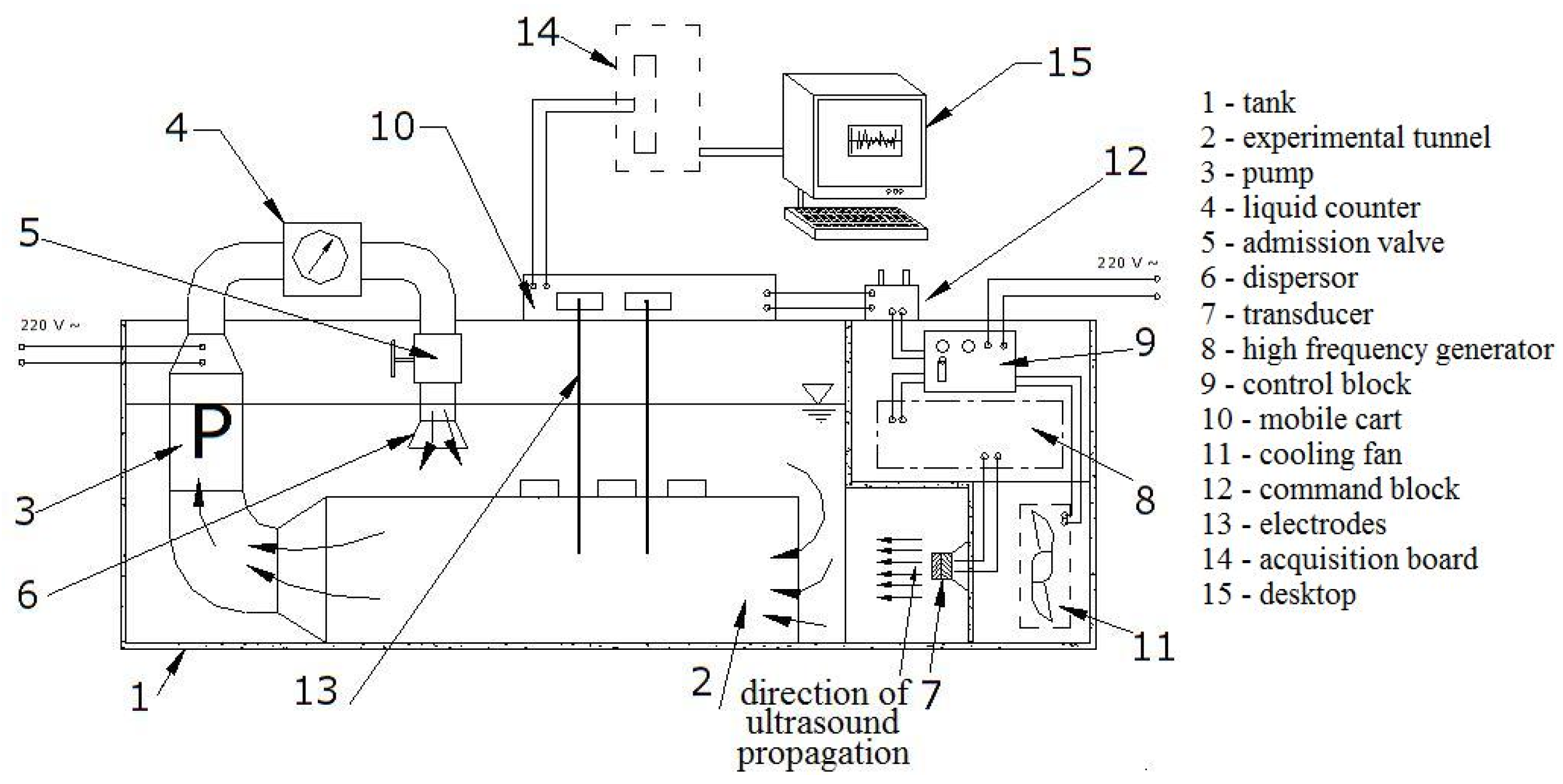
2.1. Experimental Setup and Materials
2.2. Methodology
3. Results and Discussion
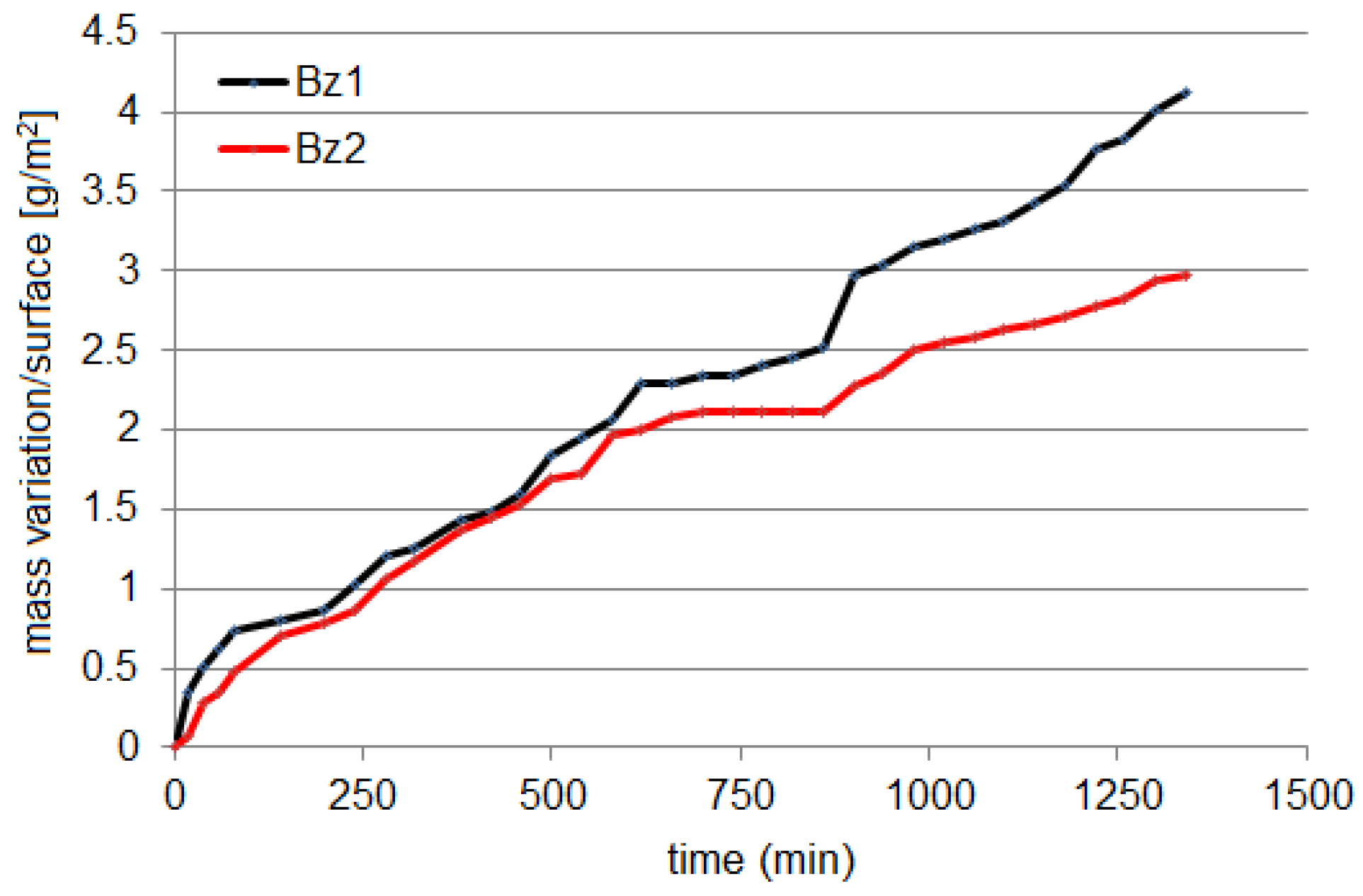
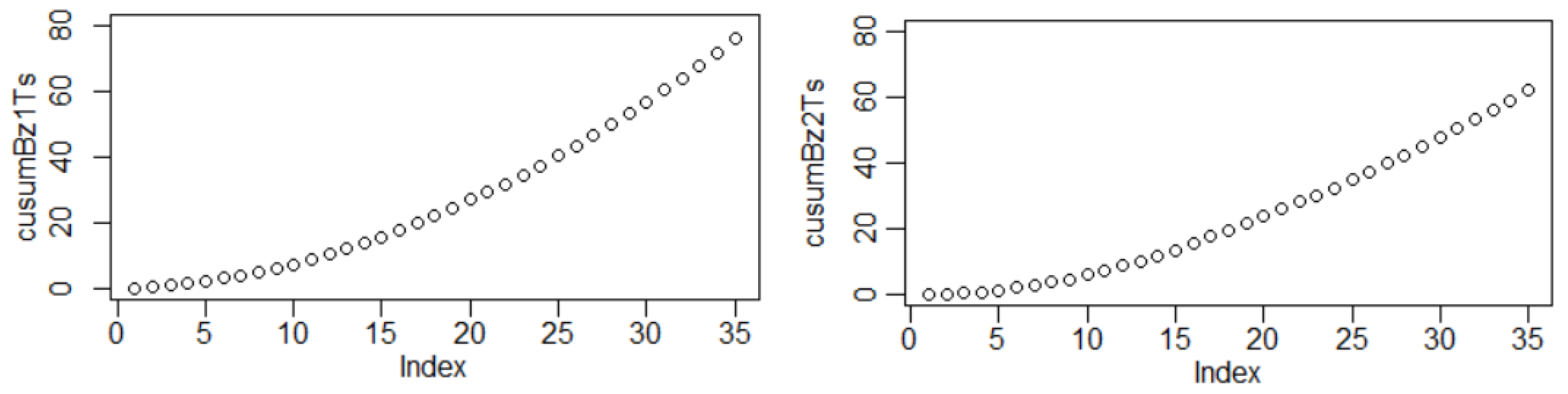
3.1. Models of the Data Series
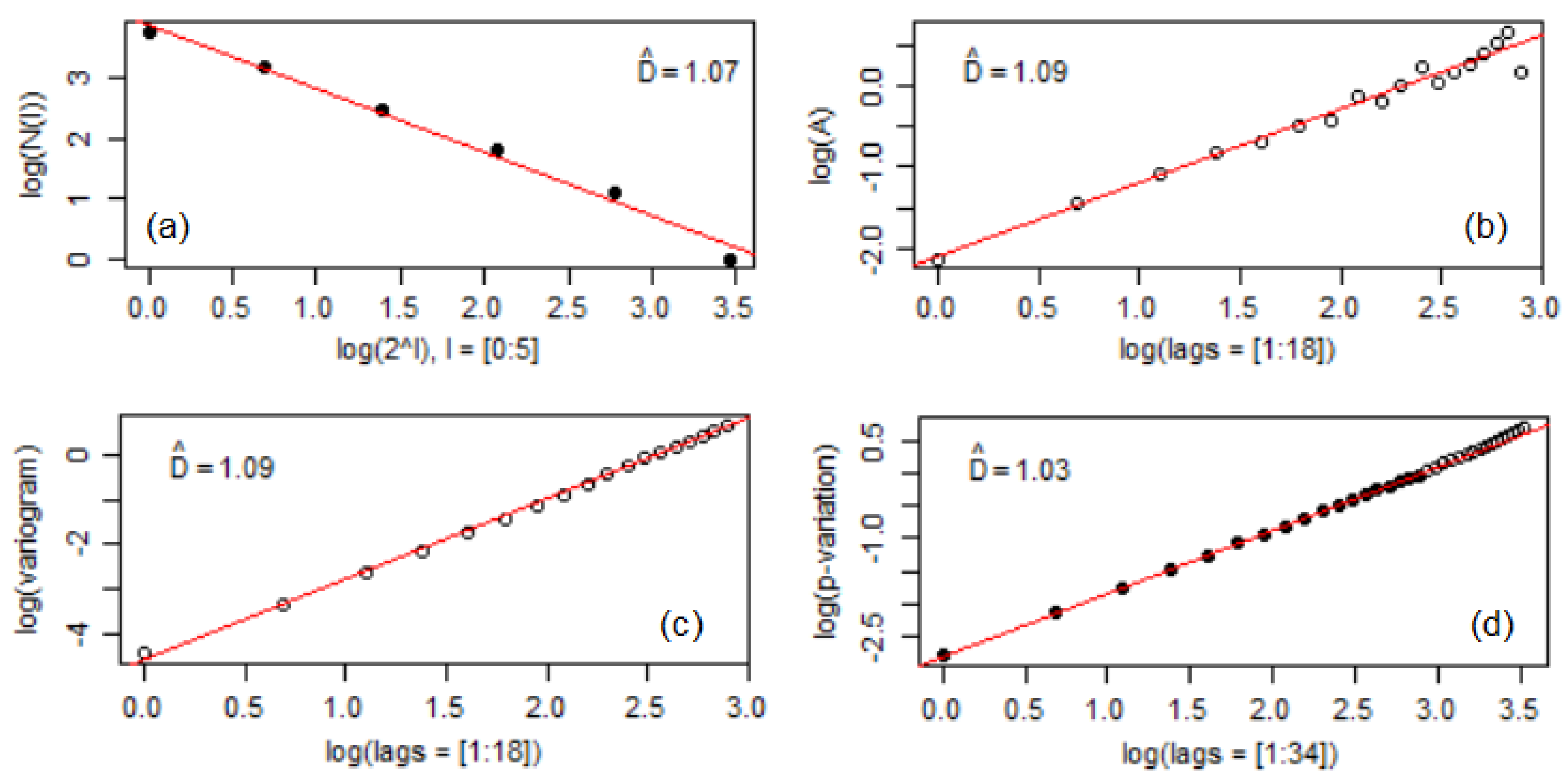
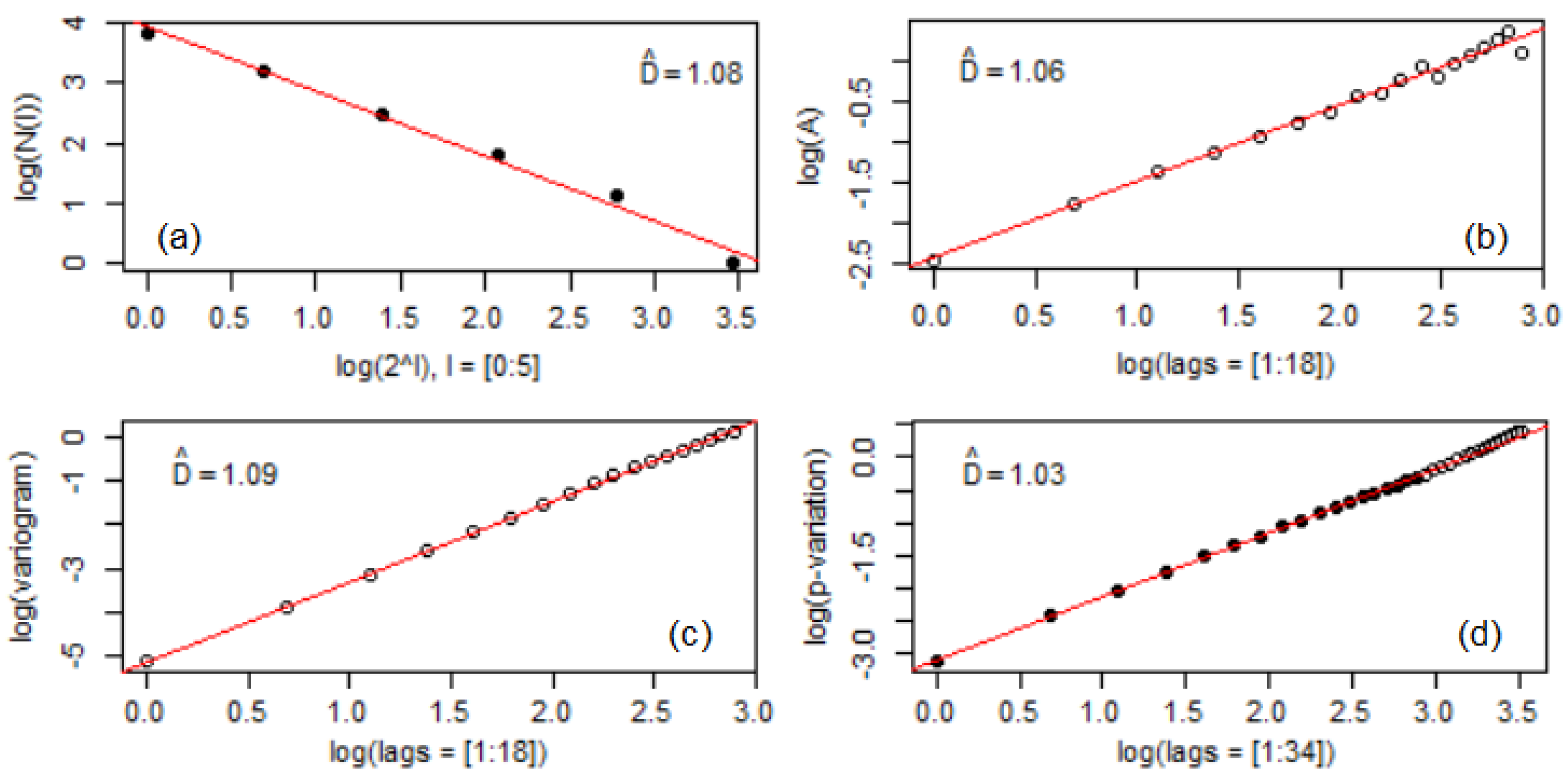
3.2. Fractal Analysis of the Sample Surface after Corrosion
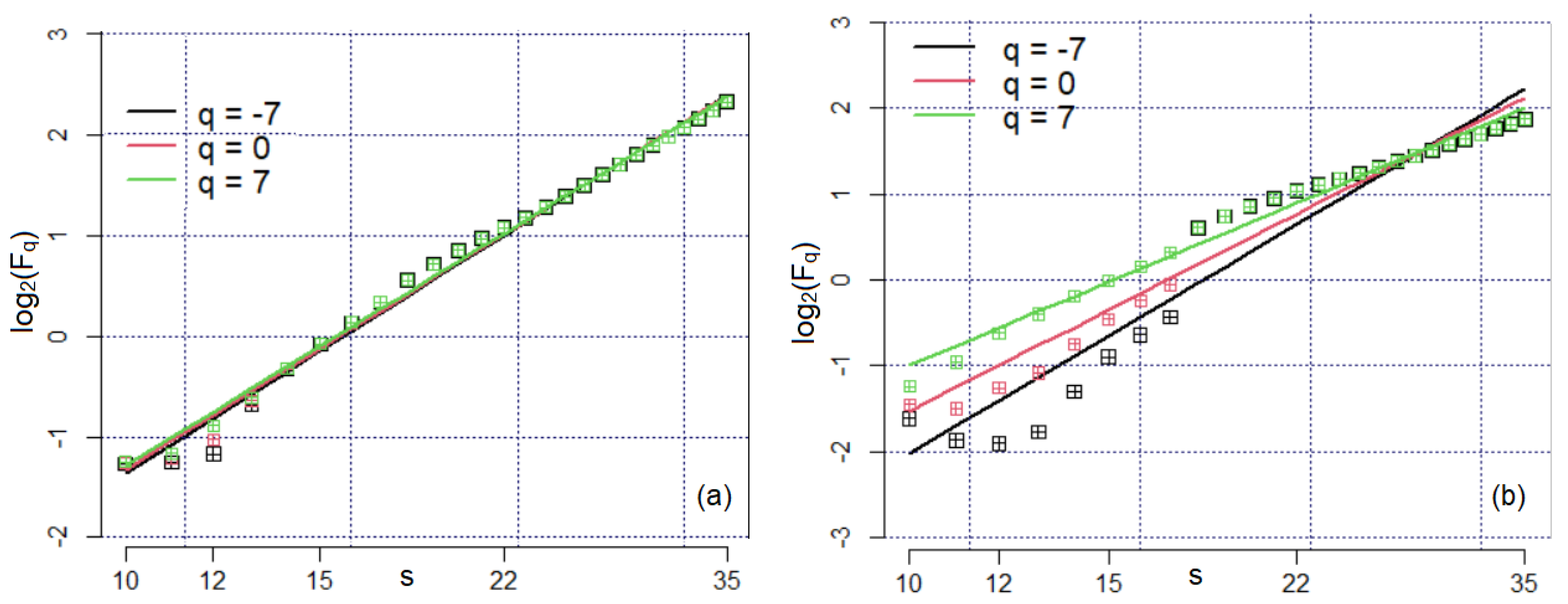
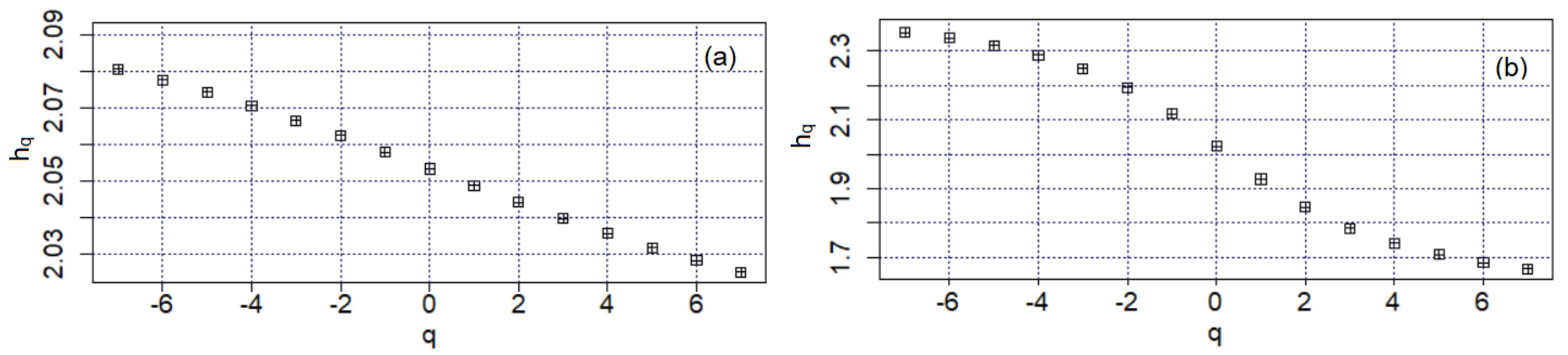
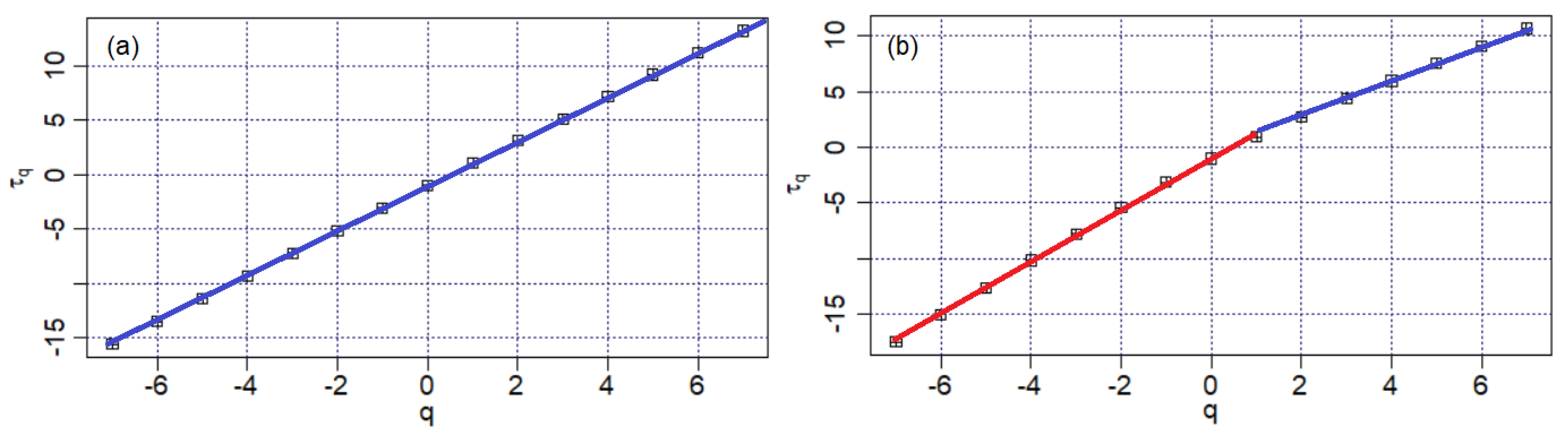
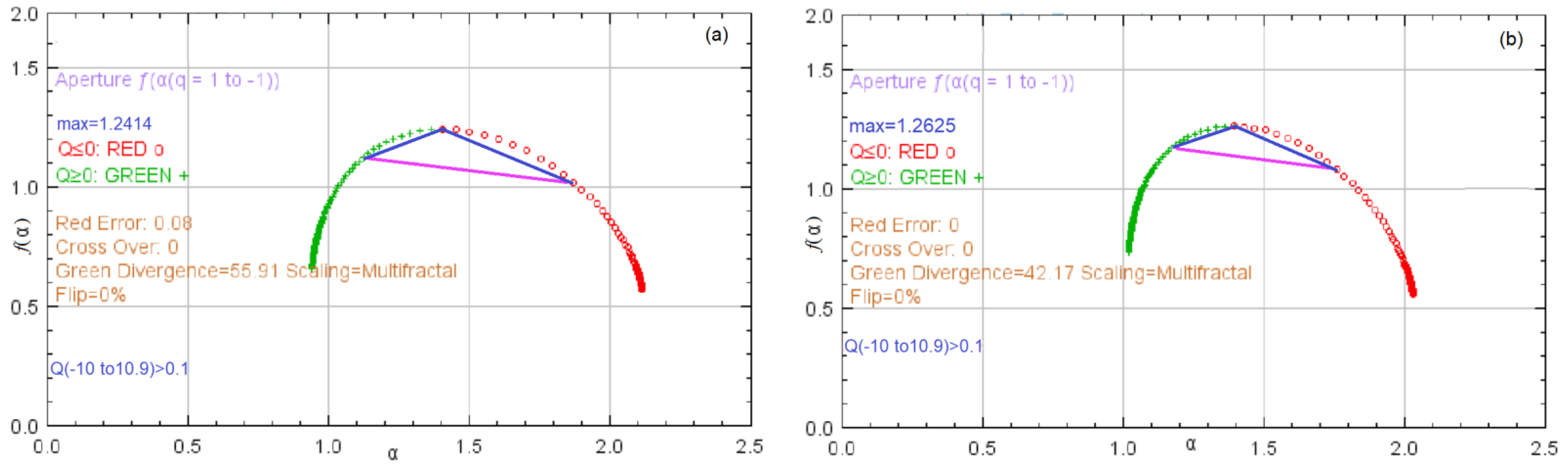
3.3. Multifractal Analysis of the Sample Surface after Corrosion
- The fractal dimensions of all series do not significantly differ.
- The lowest capacity dimension corresponds to the brass series − = 1.22.
- The Bz1 and Bz2 series have a multifractal character that is not evident for the brass series, for which the f-alpha shape indicates multifractality, whereas that of Dq indicates a monofractal character of this series.
4. Conclusions
- Experiments have been conducted using an installation designed by us for the study of ultrasound influence on materials in different liquids.
- The bronzes used in the study were analyzed only in some of our research from the viewpoint of their behavior in the cavitation field, but no study has been carried out to describe the mass loss using fractal techniques.
- The models of mass loss of some materials in general, and in a cavitation field especially, together with fractal dimensions can distinguish between different materials’ behavior.
- Investigation of the materials’ mass loss using the multifractal technique leads to determining the pattern process and the changes that appear when the process advances.
- It was proved that the multifractal character of the mass loss of the brass sample cannot be sustained, whereas the bronzes’ series have no such issue.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wharton, J.A.; Barik, R.C.; Kear, G.; Wood, R.J.K.; Stokes, K.R.; Walsh, F.C. The corrosion of nickel-aluminium bronze in seawater. Corros. Sci. 2005, 47, 3336–3367. [Google Scholar] [CrossRef]
- Basumatary, J.; Wood, R.J.K. Synergistic effects of cavitation erosion and corrosion for nickel aluminium bronze with oxide film in 3.5% NaCl solution. Wear 2017, 376–377, 1286–1297. [Google Scholar] [CrossRef]
- Basumatary, J.; Nie, M.; Wood, J.K. The synergistic effects of cavitation erosion-corrosion in ship propeller materials. J. Bio- Tribo-Corros. 2015, 1, 12. [Google Scholar] [CrossRef]
- Schüssler, A.; Exner, H.E. The corrosion of nickel-aluminium bronzes in seawater—I. Protective layer formation and the passivation mechanism. Corros. Sci. 1993, 3, 1793–1802. [Google Scholar] [CrossRef]
- Wharton, J.A.; Stokes, K.R. The influence of nickel–aluminium bronze microstructure and crevice solution on the initiation of crevice corrosion. Electrochim. Acta 2008, 53, 2463–2473. [Google Scholar] [CrossRef]
- Kwok, C.; Cheng, F.; Man, H. Synergistic effect of cavitation erosion and corrosion of various engineering alloys in 3.5% NaCl solution. Mater. Sci. Eng. A 2000, 290, 145–154. [Google Scholar] [CrossRef]
- Peng, S.; Xu, J.; Li, Z.; Jiang, S.; Xie, Z.-H.; Munroe, P. Electrochemical noise analysis of cavitation erosion corrosion resistance of NbC nanocrystalline coating in a 3.5 wt.% NaCl solution. Surf. Coat. Technol. 2021, 415, 127133. [Google Scholar] [CrossRef]
- Dumitriu, C.S.; Bărbulescu, A. Studies on the Copper Based Alloys Used in Naval Constructions-Modeling the Mass Loss in Different Media; Sitech: Craiova, Romania, 2007. (In Romanian) [Google Scholar]
- Bakhshandeh, H.R.; Allahkaram, S.R.; Zabihi, A.H. An investigation on cavitation-corrosion behavior of Ni/β-SiC nanocomposite coatings under ultrasonic field. Ultrason. Sonochem. 2019, 56, 229–239. [Google Scholar] [CrossRef]
- Hamidah, I.; Solehudin, A.; Hamdani, A.; Hasanah, L.; Khairurrijal, K.; Kurniawan, T.; Mamat, R.; Maryanti, R.; Nandiyanto, A.B.D.; Belkheir, H. Corrosion of copper alloys in KOH, NaOH, NaCl, and HCl electrolyte solutions and its impact to the mechanical properties. Alexandria Eng. J. 2021, 60, 2235–2243. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals, Form, Chance and Dimension; W. H. Freeman & Co., Ltd.: San Francisco, CA, USA, 1977. [Google Scholar]
- Chen, G.; Cheng, Q. Fractal density modeling of crustal heterogeneity from the KTB deep hole. J. Geophys. Res. Solid Earth 2017, 122, 1919–1933. [Google Scholar] [CrossRef]
- Burlando, P.; Menduni, G.; Rosso, R. (Eds.) Fractals, scaling and nonlinear variability in hydrology. J. Hydrol. 1996, 187, 1–264. [Google Scholar]
- Bărbulescu, A.; Șerban, C. Statistical and multifractal analysis of rainfall of Romania. Int. J. Ecol. Econ. Stat. 2012, 25, 1–11. [Google Scholar]
- Bărbulescu, A.; Șerban, C.; Maftei, C. Statistical analysis and evaluation of Hurst coefficient for annual and monthly precipitation time series. WSEAS Trans. Math 2010, 9, 791–800. [Google Scholar]
- Maftei, C.; Bărbulescu, A.; Carsteanu, A.A. Long-range dependence in the time series of Taiţa River discharges. Hydrol. Sci. J. 2016, 61, 1740–1747. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Deguenon, J. About the variations of precipitation and temperature evolution in the Romanian Black Sea Littoral. Rom. Rep. Phys. 2015, 67, 625–637. [Google Scholar]
- Bărbulescu, A.; Dumitriu, C.S. Assessing the Fractal Characteristics of Signals in Ultrasound Cavitation. In Proceedings of the 25th International Conference on System Theory, Control and Computing (ICSTCC), Iasi, Romania, 20–23 October 2021. [Google Scholar] [CrossRef]
- Sun, W.; Xu, G.; Gong, P.; Liang, S. Fractal analysis of remotely sensed images: A review of methods and applications. Int. J. Remote Sens. 2006, 27, 4963–4990. [Google Scholar] [CrossRef]
- Gupta, V.; Suryanarayanan, S.; Redd, N.P. Fractal analysis of surface EMG signals from the biceps. Int. J. Med. Inform. 1997, 45, 185–192. [Google Scholar] [CrossRef]
- Akhrif, A.; Romanis, M.; Domschke, K.; Schmitt-Boehrer, A.; Neufang, S. Fractal analysis of BOLD time series in a network associated with waiting impulsivity. Front. Physiol. 2018, 9, 1378. [Google Scholar] [CrossRef]
- Parkinson, I.H.; Fazzalari, N.L. Methodological principles for fractal analysis of trabecular bone. J. Microscopy 2000, 198 Pt 2, 138–142. [Google Scholar] [CrossRef]
- Updike, S.X.; Nowzari, H. Fractal analysis of dental radiographs to detect periodontitis-induced trabecular changes. J. Periodont. Res. 2008, 43, 658–664. [Google Scholar] [CrossRef]
- Tanabe, N.; Sato, S.; Suki, B.; Hirai, T. Fractal Analysis of Lung Structure in Chronic Obstructive Pulmonary Disease. Front. Physiol. 2020, 11, 603197. [Google Scholar] [CrossRef]
- Nichita, M.-V.; Paun, M.-A.; Paun, V.-A.; Paun, V.-P. Pulmonary X-Ray Images. A Fractal Analysis. AIP Conf. Proc. 2020, 2218, 050003. [Google Scholar] [CrossRef]
- Kato, C.N.; Barra, S.G.; Tavares, N.P.; Amaral, T.M.; Brasileiro, C.B.; Mesquita, R.A.; Abreu, L.G. Use of fractal analysis in dental images: A systematic review. Dentomaxillofac. Radiol. 2020, 49, 20180457. [Google Scholar] [CrossRef]
- Borodich, F.M. Fractals and fractal scaling in fracture mechanics. Int. J. Fract. 1999, 95, 239–259. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, D.-M. Estimation of fracture toughness, driving force, and fracture energy for fractal cracks using the method of imaginary smooth crack. Eng. Fract. Mech. 2010, 77, 621–630. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Passoja, D.E.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Ji, H.; Jiang, H.; Zhao, R.; Tian, Y.; Jin, X.; Jin, N.; Tong, J. Fractal Characteristics of Corrosion-Induced Cracks in Reinforced Concrete. Materials 2020, 13, 3715. [Google Scholar] [CrossRef]
- Shi, D.W.; Jiang, J.; Lung, C.W. Correlation between the scale-dependent fractal dimension of fracture surfaces and the fracture toughness. Phys. Rev. B Condens. Matter. 1996, 54, R17355–R17358. [Google Scholar] [CrossRef]
- Dlouhý, I.; Strnadel, B. The effect of crack propagation mechanism on the fractal dimension of fracture surfaces in steel. Eng. Fracture Mech. 2008, 75, 726–738. [Google Scholar] [CrossRef]
- Songbo, R.; Song, G.; Chao, K.; Shenghui, Z.; Ying, G.; Gang, L.; Tao, Y.; Liqiong, Y. Fractal characteristic of corroded steel surface and application to the fracture analyses. Constr. Build. Mater. 2022, 340, 127759. [Google Scholar] [CrossRef]
- Li, W.; Wu, M.; Shi, T.; Yang, P.; Pan, Z.; Liu, W.; Liu, J.; Yang, X. Experimental Investigation of the Relationship between Surface Crack of Concrete Cover and Corrosion Degree of Steel Bar Using Fractal Theory. Fractal Fract. 2022, 6, 325. [Google Scholar] [CrossRef]
- López, J.L.; Veleva, L. 2D-DFA as a tool for non-destructive characterisation of copper surface exposed to substitute ocean water. Phys. A: Stat. Mech. Appl. 2022, 586, 126490. [Google Scholar] [CrossRef]
- García-Ochoa, E.; Corvo, F. Copper patina corrosion evaluation by means of fractal geometry using electrochemical noise (EN) and image analysis. Electrochem. Commun. 2010, 12, 826–830. [Google Scholar] [CrossRef]
- Sarmiento, E.; Gonzalez-Rodriquez, J.G.; Urichurtu, J. Fractal Analysis of the Corrosion Inhibition of Carbon Steel in a Bromide Solution by Molybdates. ECS Trans. 2008, 15, 221. [Google Scholar] [CrossRef]
- Xu, Y.; Qian, C.; Pan, L.; Wang, B.; Lou, C. Comparing Monofractal and Multifractal Analysis of Corrosion Damage Evolution in Reinforcing Bars. PLoS ONE 2012, 7, e29956. [Google Scholar] [CrossRef] [PubMed]
- Davies, S.; Hall, P. Fractal analysis of surface roughness by using spatial data. J. Royal Stat. Soc. Ser. B 1999, 61, 3–37. [Google Scholar] [CrossRef]
- Kim, J.J.; Hwang, W.S. Evaluation of a fractal analysis technique for corrosion studies. Met. Mater. Int. 2012, 18, 783–789. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Dumitriu, C.Ș. Fractal Characterization of Brass Corrosion in Cavitation Field in Seawater. Sustainability 2023, 15, 3816. [Google Scholar] [CrossRef]
- Dumitriu, C.S. On the corrosion of two types of bronzes under cavitation. Ann. Dunarea Jos Univ. Galati Fasc. IX Metall. Mat. Sci. 2021, 4, 12–16. [Google Scholar] [CrossRef]
- Dumitriu, C.S.; Bărbulescu, A. Artificial intelligence models for the mass loss of copper-based alloys under the cavitation. Materials 2022, 15, 6695. [Google Scholar] [CrossRef]
- Gao, J.; Cao, Y.; Tung, W.-W.; Hu, J. Multiscale Analysis of Complex Time Series: Integration of Chaos and Random Fractal Theory, and Beyond; Wiley Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications, 3rd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2014. [Google Scholar]
- Hall, P.; Wood, A. On the performance of box-counting estimators of fractal dimension. Biometrika 1993, 80, 246–252. [Google Scholar] [CrossRef]
- Genton, M.G. Highly robust variogram estimation. Math. Geol. 1998, 30, 213–221. [Google Scholar] [CrossRef]
- Gneiting, T.; Ševčıková, H.; Percival, D.B. Estimators of Fractal Dimension: Assessing the Roughness of Time Series and Spatial Data. Available online: https://stat.uw.edu/sites/default/files/files/reports/2010/tr577.pdf (accessed on 10 April 2023).
- Rosenberg, E. Fractal Dimensions of Networks; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S.; Kantelhardt, J.W.; Penzel, T.; Peter, J.H.; Voigt, K. Correlated and Uncorrelated Regions in Heart-Rate Fluctuations during Sleep. Phys. Rev. Lett. 2000, 85, 3736. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef]
- Movahed, M.S.; Jafari, G.R.; Ghasemi, F.; Rahvar, S.; Rahimi Tabar, M.R. Multifractal detrended fluctuation analysis of sunspot time series. J. Stat. Mech. 2006, 2006, P02003. [Google Scholar] [CrossRef]
- Bacry, E.; Delour, J.; Muzy, J.F. Multifractal random walk. Phys. Rev. E 2001, 64, 026103. [Google Scholar] [CrossRef]
- Feder, J. Fractals; Plenum: New York, NY, USA, 1988. [Google Scholar]
- Frish, U.; Parisi, G. On the Singularity Structure of Fully Developed Turbulence. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics; Ghil, M., Benzi, R., Parisi, G., Eds.; North-Holland: New York, NY, USA, 1985; pp. 84–88. [Google Scholar]
- Zhang, X.; Zhang, G.; Qiu, L.; Zhang, B.; Sun, Y.; Gui, Z.; Zhang, Q. A Modified Multifractal Detrended Fluctuation Analysis (MFDFA) Approach for Multifractal Analysis of Precipitation in Dongting Lake Basin, China. Water 2019, 11, 891. [Google Scholar] [CrossRef]
- Halsey, T.; Jensen, M.; Kadanoff, L.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Hentschel, H.G.E.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Phys. D 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Bausk, E.A.; Volchuk, V.M.; Uzlov, O.V. Multifractal analysis of the S235J2 steel structure with corrosion wear. AIP Conf. Proc. 2022, 2656, 020030. [Google Scholar] [CrossRef]
- Ramírez-Platas, M.; Morales-Cabrera, M.A.; Rivera, V.M.; Morales-Zarate, E.; Hernandez-Martinez, E. Fractal and multifractal analysis of electrochemical noise to corrosion evaluation in A36 steel and AISI 304 stainless steel exposed to MEA-CO2 aqueous solutions. Chaos Solitons Fractals 2021, 145, 110802. [Google Scholar] [CrossRef]
- Sanchez-Ortiz, W.; Andrade-Gómez, C.; Hernandez-Martinez, E.; Puebla, H. Multifractal Hurst analysis for identification of corrosion type in AISI 304 stainless steel. Int. J. Electrochem. Sci. 2015, 10, 1054–1064. [Google Scholar]
| Aperture Length Q (1 to 0) | Aperture Slope Q(1 to 0) | Aperture Length Q (0 to −1) | Aperture Slope Q(0 to −1) | Aperture Length Q(1 to −1) | Aperture Slope Q(1 to −1) | |
|---|---|---|---|---|---|---|
| Bz1 | 0.3061 | 0.4135 | 0.5135 | −0.4764 | 0.7536 | −0.1392 |
| Bz2 | 0.2400 | 0.4134 | 0.4065 | −0.4870 | 0.5936 | −0.1469 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bărbulescu, A. Fractal Characterization of the Mass Loss of Bronze by Erosion–Corrosion in Seawater. Materials 2023, 16, 3877. https://doi.org/10.3390/ma16103877
Bărbulescu A. Fractal Characterization of the Mass Loss of Bronze by Erosion–Corrosion in Seawater. Materials. 2023; 16(10):3877. https://doi.org/10.3390/ma16103877
Chicago/Turabian StyleBărbulescu, Alina. 2023. "Fractal Characterization of the Mass Loss of Bronze by Erosion–Corrosion in Seawater" Materials 16, no. 10: 3877. https://doi.org/10.3390/ma16103877
APA StyleBărbulescu, A. (2023). Fractal Characterization of the Mass Loss of Bronze by Erosion–Corrosion in Seawater. Materials, 16(10), 3877. https://doi.org/10.3390/ma16103877






