Modelling of Electro-Viscoelastic Materials through Rate Equations
Abstract
1. Introduction
Notation
2. Balance Equations
Representation Formulae
3. Euclidean Invariance and Objectivity
4. Constraint on the Stress Tensor
5. Thermodynamic Analysis
Constitutive Assumptions and Thermodynamic Restrictions
6. Electroelastic and Hypo-Electroelastic Models
7. Electro-Viscoelastic Models
8. Heat Conduction in Dielectrics
9. Electroelastic Materials with Dielectric Memory
9.1. Dielectrics with Memory
9.2. Ferroelectric Hysteresis
9.3. One-Dimensional Models of Hysteresis
Ferroelectric Soft Materials
10. Dependence on the Gradient of the Electric Field
11. Relation to Other Approaches
12. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Menhert, M.; Hossain, M.; Steinmann, P. A complete thermo-electro-viscoelastic characterization of dielectric elastomers, Part II: Continuum modeling approach. J. Mech. Phys. Solids 2021, 157, 104625. [Google Scholar] [CrossRef]
- Diaz-Calleja, R.; Ginestar, D.; Compañ Moreno, V.; Llovera-Segovia, P.; Burgos-Simón, C.; Cortés, J.C.; Díaz-Boils, J. Viscoelastic effects on the response of electroelastic materials. Polymers 2021, 13, 2198. [Google Scholar] [CrossRef] [PubMed]
- Behera, S.K.; Kumar, D.; Sarangi, S. Modeling of electro-viscoelastic dielectric elastomer: A continuum mechanics approach. Eur. J. Mech./A Solids 2021, 90, 104369. [Google Scholar] [CrossRef]
- Bustamante, R.; Dorfmann, A.; Ogden, R.W. On electric body forces and Maxwell stresses in nonlinearly electroelastic solids. Int. J. Eng. Sci. 2009, 47, 1131–1141. [Google Scholar] [CrossRef]
- Menhert, M.; Hossain, M.; Steinmann, P. On nonlinear thermo-electro-elasticity. Proc. R. Soc. A 2016, 472, 20160170. [Google Scholar] [CrossRef] [PubMed]
- Rajagopal, K.R.; Ruzicka, M. Mathematical modeling of electrorheological materials. Cont. Mech. Thermodyn. 2001, 13, 59–78. [Google Scholar] [CrossRef]
- Giorgi, C.; Morro, A. A thermodynamic approach to rate-type models of elastic-plastic materials. J. Elasticity 2021, 147, 113–148. [Google Scholar] [CrossRef]
- Giorgi, C.; Morro, A. A thermodynamic approach to rate-type models in deformable ferroelectrics. Cont. Mech. Thermodyn. 2021, 33, 727–747. [Google Scholar] [CrossRef]
- Giorgi, C.; Morro, A. Magneto-viscoelastic materials: Memory functionals and rate equations. Materials 2022, 15, 6699. [Google Scholar] [CrossRef]
- Morro, A.; Giorgi, C. Mathematical Modelling of Continuum Physics; Birckhäuser: Cham, Switzerland, 2023. [Google Scholar]
- Steinhausen, R.; Pientschke, C.; Kuvatov, A.Z.; Langhammer, H.T.; Beige, H.; Movchikova, A.A.; Malyshkina, O.V. Modelling and characterization of piezoelectric and polarization gradients. J. Electroceram. 2008, 20, 47–52. [Google Scholar] [CrossRef]
- Giorgi, C.; Morro, A. A thermodynamically-consistent modeling of ferromagnetic hysteresis. Materials 2023, 16, 2882. [Google Scholar] [CrossRef]
- Dorfmann, L.; Ogden, R.W. Nonlinear electroelasticity: Material properties, continuum theory and applications. Proc. R. Soc. A 2017, 473, 20170311. [Google Scholar] [CrossRef]
- Saxena, P.; Vu, D.K.; Steinmann, P. On rate-dependent dissipation effects in electroelasticity. Int. J. Non-Linear Mech. 2014, 62, 1–11. [Google Scholar] [CrossRef]
- Schrade, D.; Müller, R.; Gross, D.; Keip, M.A.; Thai, H.; Schröder, J. An invariant formulation for phase field models in ferroelectrics. Int. J. Solids Struct. 2014, 51, 2144–2156. [Google Scholar] [CrossRef]
- Huang, S.; Qi, L.; Huang, W.; Shu, L.; Zhou, S.; Jiang, X. Flexoelectricity in dielectrics: Materials, structures and generalizations. J. Adv. Dielectr. 2018, 8, 1830002. [Google Scholar] [CrossRef]
- Kaltenbacher, B.; Krejci, P. A thermodynamically consistent phenomenological model for ferroelectric and ferroelastic hysteresis. Z. Amgew. Math. Mech. 2016, 96, 874–891. [Google Scholar] [CrossRef]
- Pasco, Y.; Berry, A. A hybrid analytical/numerical model of piezoelectric stack actuators using a macroscopic nonlinear theory of ferroelectricity and a Preisach model of hysteresis. J. Intell. Mater. Syst. Struct. 2006, 15, 115–141. [Google Scholar] [CrossRef]
- Smith, R.C.; Seelecke, S.; Ounaies, Z.; Smith, J. A free energy model for hysteresis in ferroelectric materials. J. Intell. Mater. Syst. Struct. 2003, 14, 719–737. [Google Scholar] [CrossRef]
- Schröder, J.; Romanovski, H. A thermodynamically consistent mesoscopic model for transversely isotropic ferroelectric ceramics in a coordinate-invariant setting. Arch. Appl. Mech. 2005, 74, 863–877. [Google Scholar] [CrossRef]
- Rosato, D.; Miehe, C. Dissipative ferroelectricity at finite strains—Variational principles, constitutive assumptions and algorithms. Int. J. Eng. Sci. 2014, 74, 162–189. [Google Scholar] [CrossRef]
- Su, Y.; Landis, C.M. Continuum thermodynamics of ferroelctric domain evolution: Theory, finite element implementation, and application to domain wall pinning. J. Mech. Phys. Solids 2007, 55, 280–305. [Google Scholar] [CrossRef]
- Gurtin, M.E. Generalized Ginzburg-Landau and Cahn-Hilliard equations based on a microforce balance. Phys. D 1996, 92, 178–192. [Google Scholar] [CrossRef]
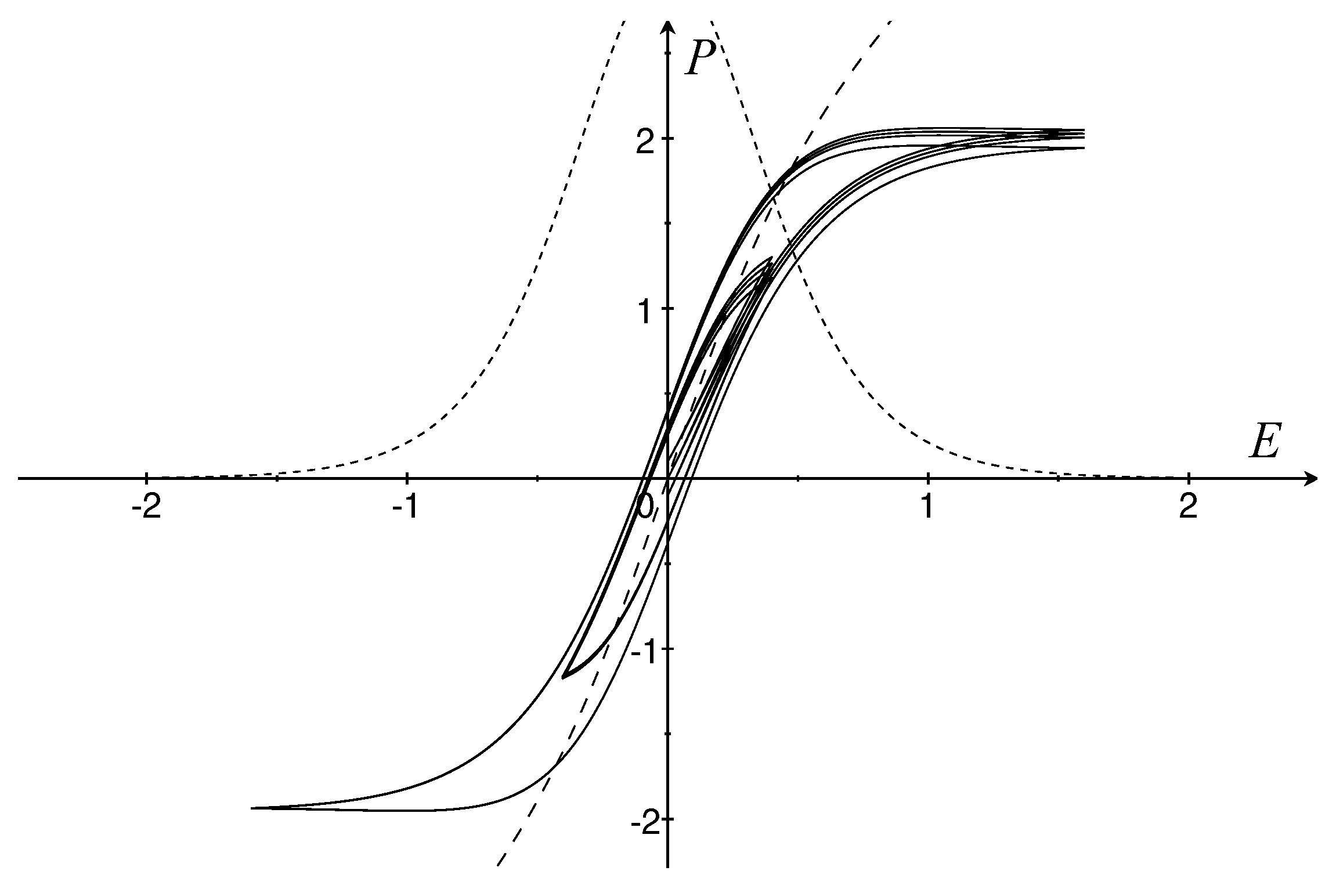
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giorgi, C.; Morro, A. Modelling of Electro-Viscoelastic Materials through Rate Equations. Materials 2023, 16, 3661. https://doi.org/10.3390/ma16103661
Giorgi C, Morro A. Modelling of Electro-Viscoelastic Materials through Rate Equations. Materials. 2023; 16(10):3661. https://doi.org/10.3390/ma16103661
Chicago/Turabian StyleGiorgi, Claudio, and Angelo Morro. 2023. "Modelling of Electro-Viscoelastic Materials through Rate Equations" Materials 16, no. 10: 3661. https://doi.org/10.3390/ma16103661
APA StyleGiorgi, C., & Morro, A. (2023). Modelling of Electro-Viscoelastic Materials through Rate Equations. Materials, 16(10), 3661. https://doi.org/10.3390/ma16103661






