Optimization of Monolayer MoS2 with Prescribed Mechanical Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Optimization Problem Formulation
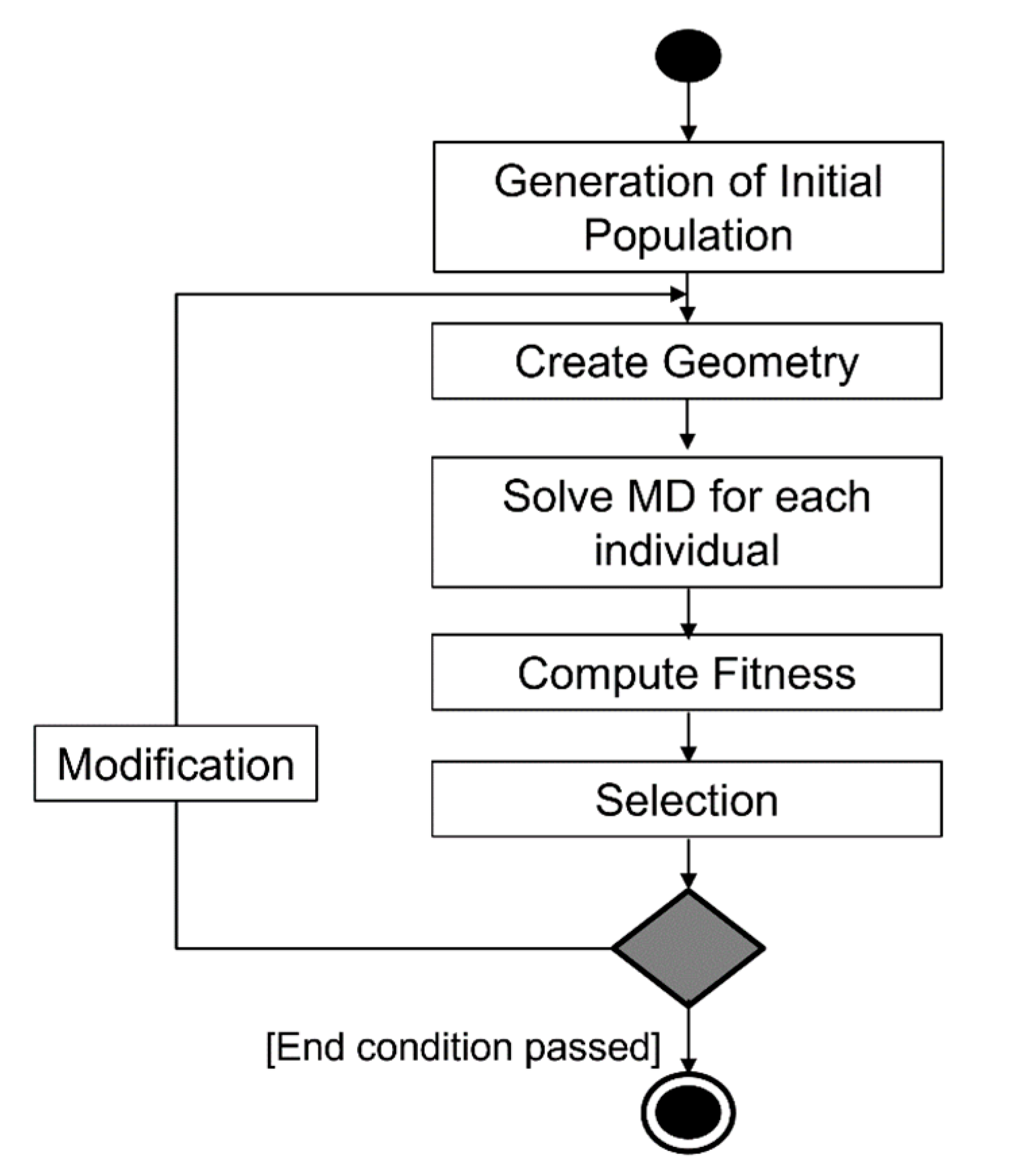
2.2. Evolutionary Optimization
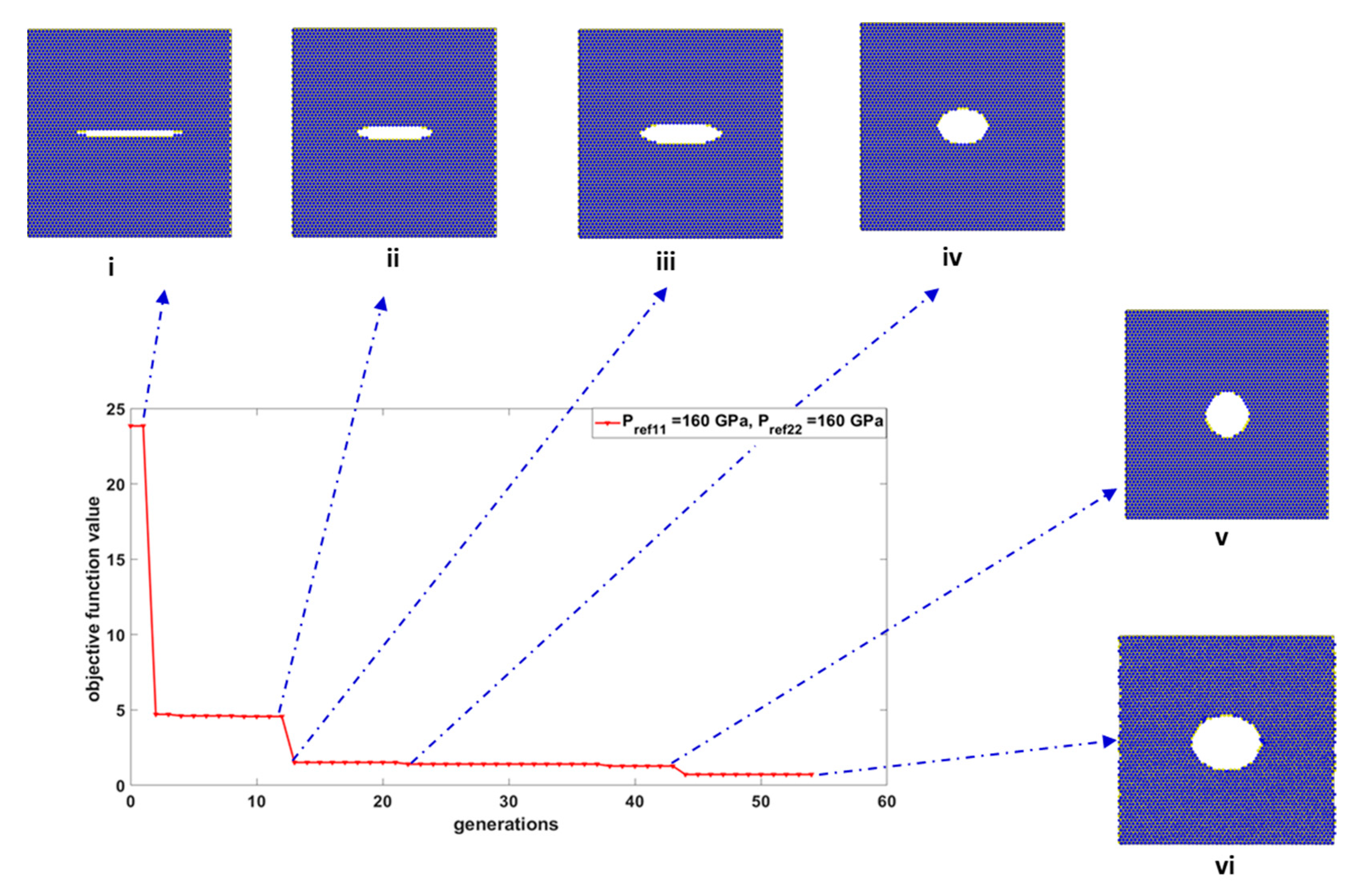
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akhter, M.J.; Kuś, W.; Mrozek, A.; Burczyński, T. Mechanical Properties of Monolayer MoS2 with Randomly Distributed Defects. Materials 2020, 13, 1307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, M.F.; Nazir, G.; Lermolenko, V.M.; Eom, J. Electrical and photo-electrical properties of MoS2 nanosheets with and without an Al2O3 capping layer under various environmental conditions. Sci. Technol. Adv. Mater. 2016, 17, 166–176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Zhu, H. Two-dimensional MoS2: Properties, preparation, and applications. J. Mater. 2015, 1, 33–44. [Google Scholar] [CrossRef] [Green Version]
- Heiranian, M.; Farimani, A.B.; Aluru, N.R. Water desalination with a single-layer MoS2 nanopore. Nat. Commun. 2015, 6, 8616. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Liu, K.; Bulushev, R.D.; Khlybov, S.; Dumcenco, D.; Kis, A.; Radenovic, A. Identification of single nucleotides in MoS2 nanopores. Nat. Nanotechnol. 2015, 10, 1070–1076. [Google Scholar] [CrossRef]
- Yang, T.; Lin, H.; Zheng, X.; Loh, K.P.; Jia, B. Tailoring pores in graphene-based materials: From generations to applications. J. Mater. Chem. A 2017, 5, 16537–16558. [Google Scholar] [CrossRef] [Green Version]
- Macha, M.; Marion, S.; Nandigana, V.V.; Radenovic, A. 2D materials as an emerging platform for nanopore-based power generation. Nat. Rev. Mater. 2019, 4, 588–605. [Google Scholar] [CrossRef]
- Su, S.; Wang, X.; Xue, J. Nanopores in two-dimensional materials: Accurate fabrication. Mater. Horiz. 2021, 8, 1390–1408. [Google Scholar] [CrossRef]
- Graf, M.; Lihter, M.; Thakur, M.; Georgiou, V.; Topolancik, J.; Ilic, B.R.; Liu, K.; Feng, J.; Astier, Y.; Radenovic, A. Fabrication and practical applications of molybdenum disulfide nanopores. Nat. Protoc. 2019, 14, 1130–1168. [Google Scholar] [CrossRef]
- Hong, J.; Hu, Z.; Probert, M.; Li, K.; Lv, D.; Yang, X.; Gu, L.; Mao, N.; Feng, Q.; Xie, L.; et al. Exploring atomic defects in molybdenum disulphide monolayers. Nat. Commun. 2015, 6, 6293. [Google Scholar] [CrossRef] [Green Version]
- Vancsó, P.; Magda, G.Z.; Pető, J.; Noh, J.; Kim, Y.; Hwang, C.; Biró, L.P.; Tapasztó, L. The intrinsic defect structure of exfoliated MoS2 single layers revealed by Scanning Tunneling Microscopy. Sci. Rep. 2016, 6, 29726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.; Robertson, A.; Warner, J.H. Atomic structure of defects and dopants in 2D layered transition metal dichalcogenides. Chem. Soc. Rev. 2018, 47, 6764. [Google Scholar] [CrossRef] [PubMed]
- Mahata, A.; Jiang, J.; Mahapatra, D.R.; Rabczuk, T. Effect of intrinsic structural defects on mechanical properties of single layer MoS2. Nano-Struct. Nano-Objects 2019, 18, 100247. [Google Scholar] [CrossRef]
- Li, Y.; Chen, P.; Zhang, C.; Peng, J.; Gao, F.; Liu, H. Molecular dynamics simulation on the buckling of single-layer MoS2 sheet with defects under uniaxial compression. Comput. Mater. Sci. 2019, 162, 116–123. [Google Scholar] [CrossRef]
- Li, M.; Wan, Y.; Tu, L.; Yang, Y.; Lou, J. The Effect of VMoS3 Point Defect on the Elastic Properties of Monolayer MoS2 with REBO Potentials. Nanoscale Res. Lett. 2016, 11, 155. [Google Scholar] [CrossRef] [Green Version]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Comm. 2022, 271, 10817. [Google Scholar] [CrossRef]
- Burczyński, T.; Kuś, W.; Beluch, W.; Długosz, A.; Poteralski, A.; Szczepanik, M. Intelligent Computing in Optimal Design. In Solid Mechanics and Its Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Kokot, G.; Burczyński, T. Evolutionary Algorithms and Boundary Element Method in Generalized Shape Optimization. J. Theor. Appl. Mech. 2003, 41, 341–364. [Google Scholar]
- Kokot, G.; Orantek, P. The Topology Optimization Using Evolutionary Algorithms. In IUTAM Symposium on Evolutionary Methods in Mechanics. Solid Mechanics and Its Applications 117; Burczyński, T., Osyczka, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 173–186. [Google Scholar] [CrossRef]
- Sigmund, O. Tailoring materials with prescribed elastic properties. Mech. Mater. 1995, 20, 351–368. [Google Scholar] [CrossRef]
- Mrozek, A.; Kuś, W.; Burczyński, T. Searching of stable configurations of nanostructures using computational intelligence methods. Tech. Sci. 2010, 20, 85–97. [Google Scholar]
- Mrozek, A.; Kuś, W.; Burczyński, T. Nano level optimization of graphene allotropes by means of a hybrid parallel evolutionary algorithm. Comput. Mater. Sci. 2015, 106, 161–169. [Google Scholar] [CrossRef]
- Mrozek, A.; Kuś, W.; Burczyński, T. Method For Determining Structures of New Carbon-based 2D Materials with Predefined Mechanical Properties. Int. J. Multiscale Comput. Eng. 2017, 15, 379–394. [Google Scholar] [CrossRef]
- Kandemir, A.; Yapicioglu, H.; Kinaci, A.; CaÇin, T.; Sevik, C. Thermal transport properties of MoS2 and MoSe2 monolayers. Nanotechnology 2016, 27, 55703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, M.; Shirodkar, S.N.; Plech, P.; Kaxiras, E.; Elliott, R.S.; Tadmor, E.B. A force-matching Stillinger-Weber potential for MoS2: Parameterization and Fisher information theory based sensitivity analysis. J. Appl. Phys. 2017, 122, 244301. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—the Open Visualization Tool. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131, 154107. [Google Scholar] [CrossRef] [Green Version]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolutionary Algorithms; Springer: Berlin, Germany, 1996. [Google Scholar]
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Swarm Intelligence; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2001. [Google Scholar]
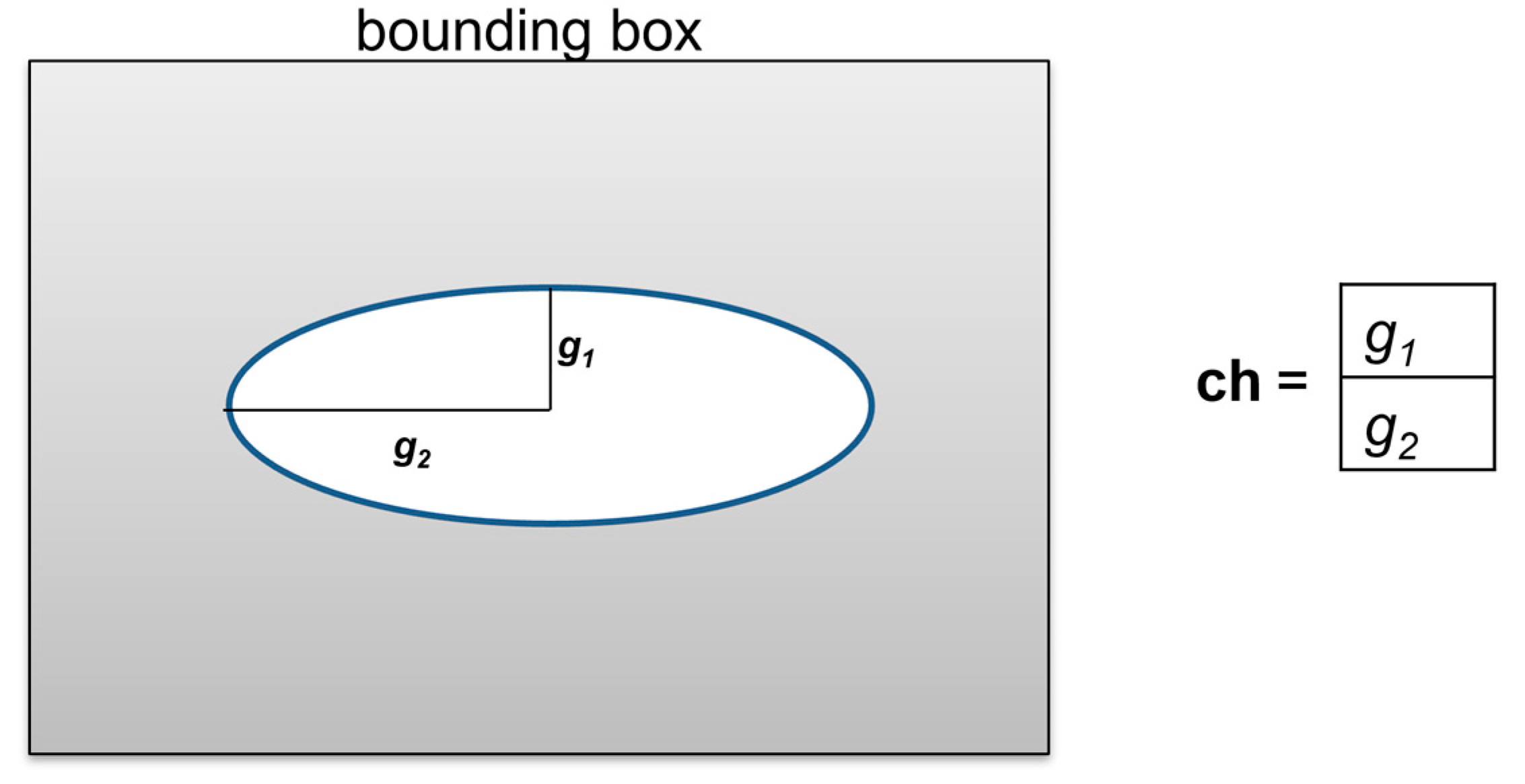
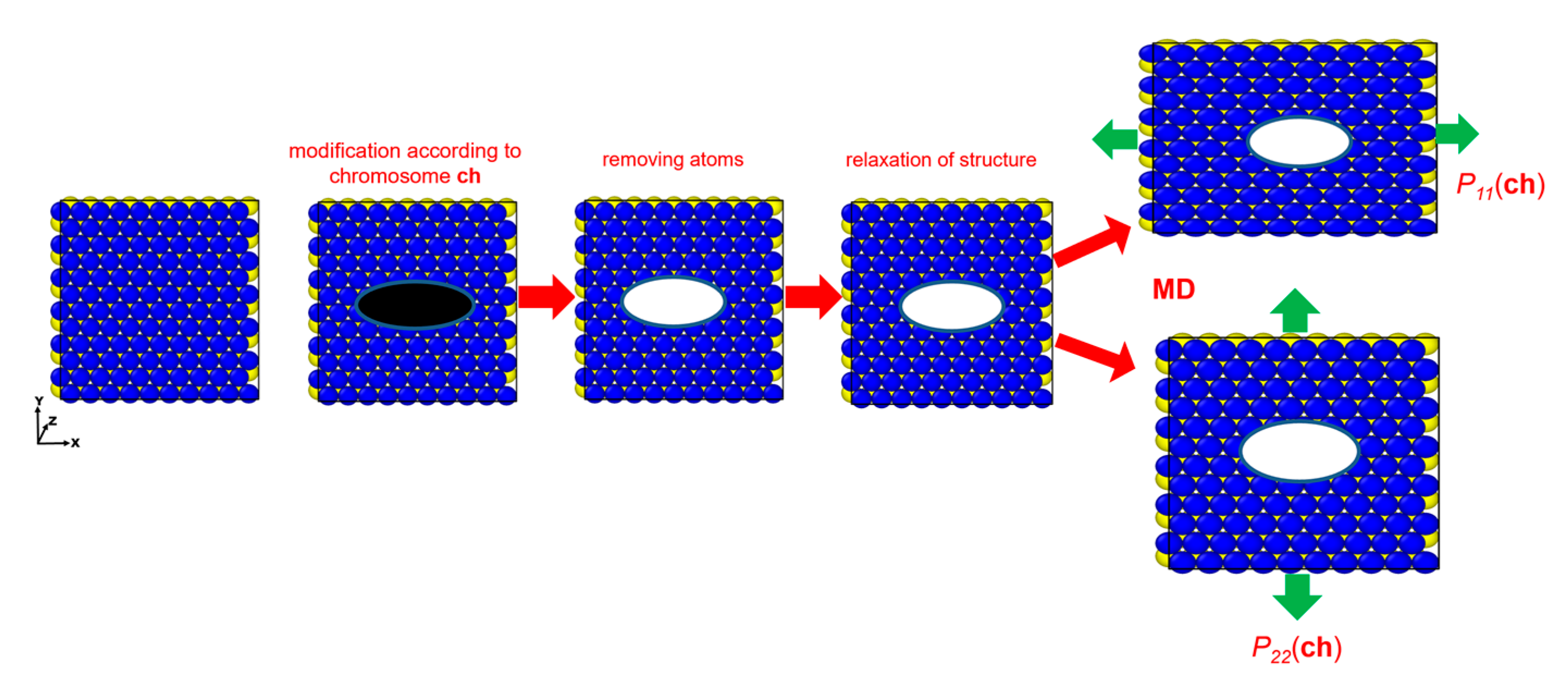
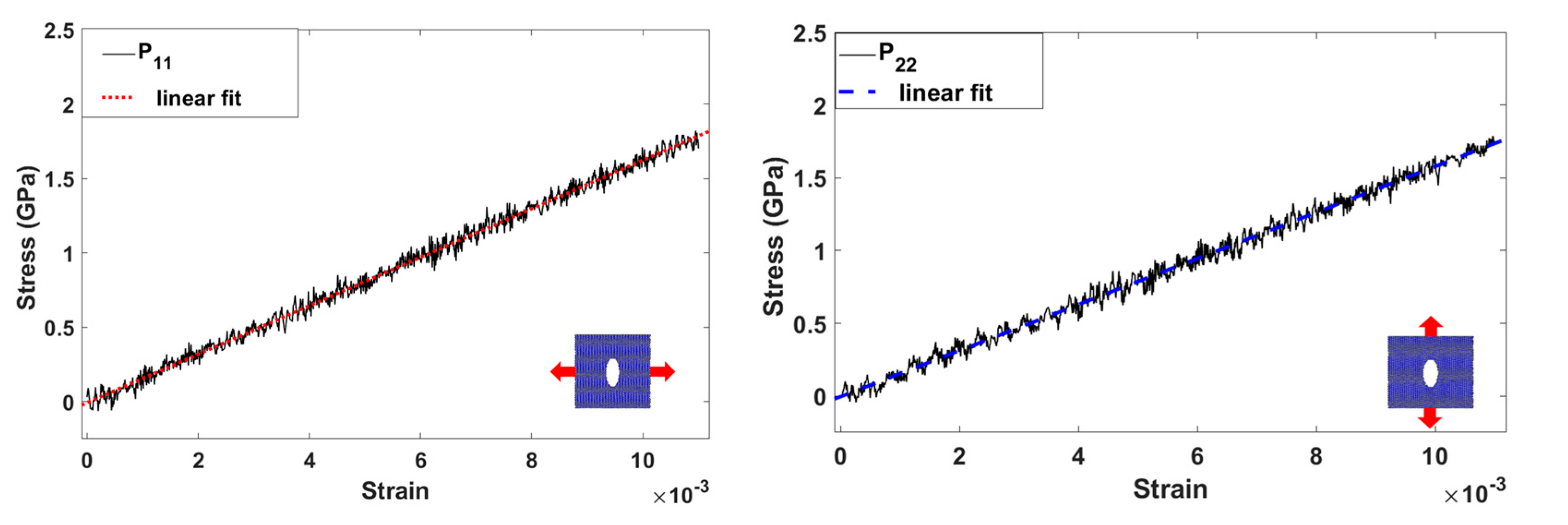
| Case | Pref11 (GPa) | P11 (GPa) | Pref22 (GPa) | P22 (GPa) | g1 (Å) | g2 (Å) | eP11 (%) | eP22 (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 150.0 | 149.2 | 180.0 | 179.5 | 36.35 | 12.19 | 0.5 | 0.3 |
| 2 | 160.0 | 162.6 | 160.0 | 158.0 | 28.12 | 23.15 | 1.6 | 1.3 |
| 3 | 180.0 | 179.5 | 150.0 | 148.0 | 15.35 | 33.44 | 0.3 | 1.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuś, W.; Akhter, M.J.; Burczyński, T. Optimization of Monolayer MoS2 with Prescribed Mechanical Properties. Materials 2022, 15, 2812. https://doi.org/10.3390/ma15082812
Kuś W, Akhter MJ, Burczyński T. Optimization of Monolayer MoS2 with Prescribed Mechanical Properties. Materials. 2022; 15(8):2812. https://doi.org/10.3390/ma15082812
Chicago/Turabian StyleKuś, Wacław, Mohammed Javeed Akhter, and Tadeusz Burczyński. 2022. "Optimization of Monolayer MoS2 with Prescribed Mechanical Properties" Materials 15, no. 8: 2812. https://doi.org/10.3390/ma15082812
APA StyleKuś, W., Akhter, M. J., & Burczyński, T. (2022). Optimization of Monolayer MoS2 with Prescribed Mechanical Properties. Materials, 15(8), 2812. https://doi.org/10.3390/ma15082812








