Broadband Perfect Absorber in the Visible Range Based on Metasurface Composite Structures
Abstract
:1. Introduction
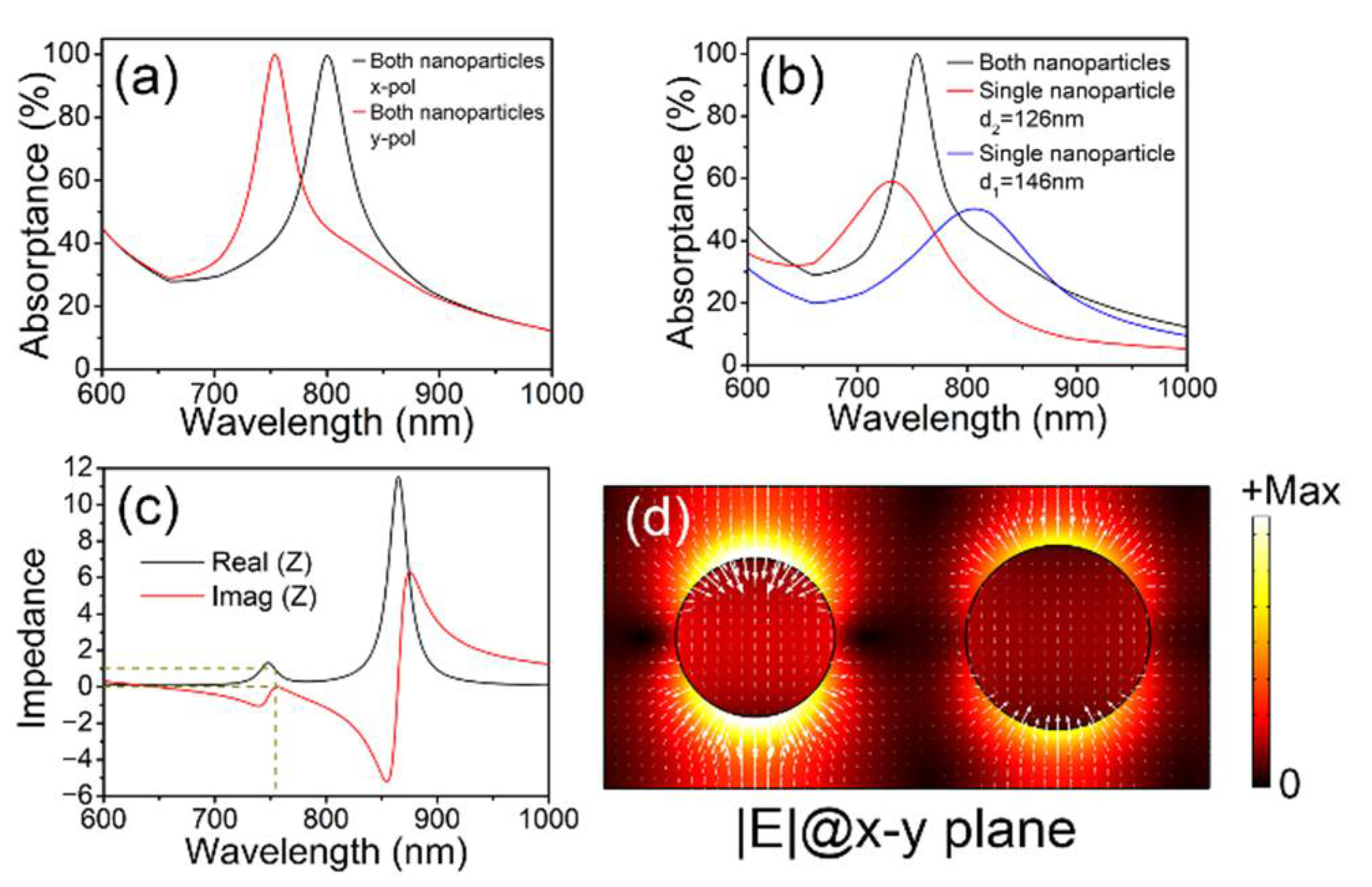
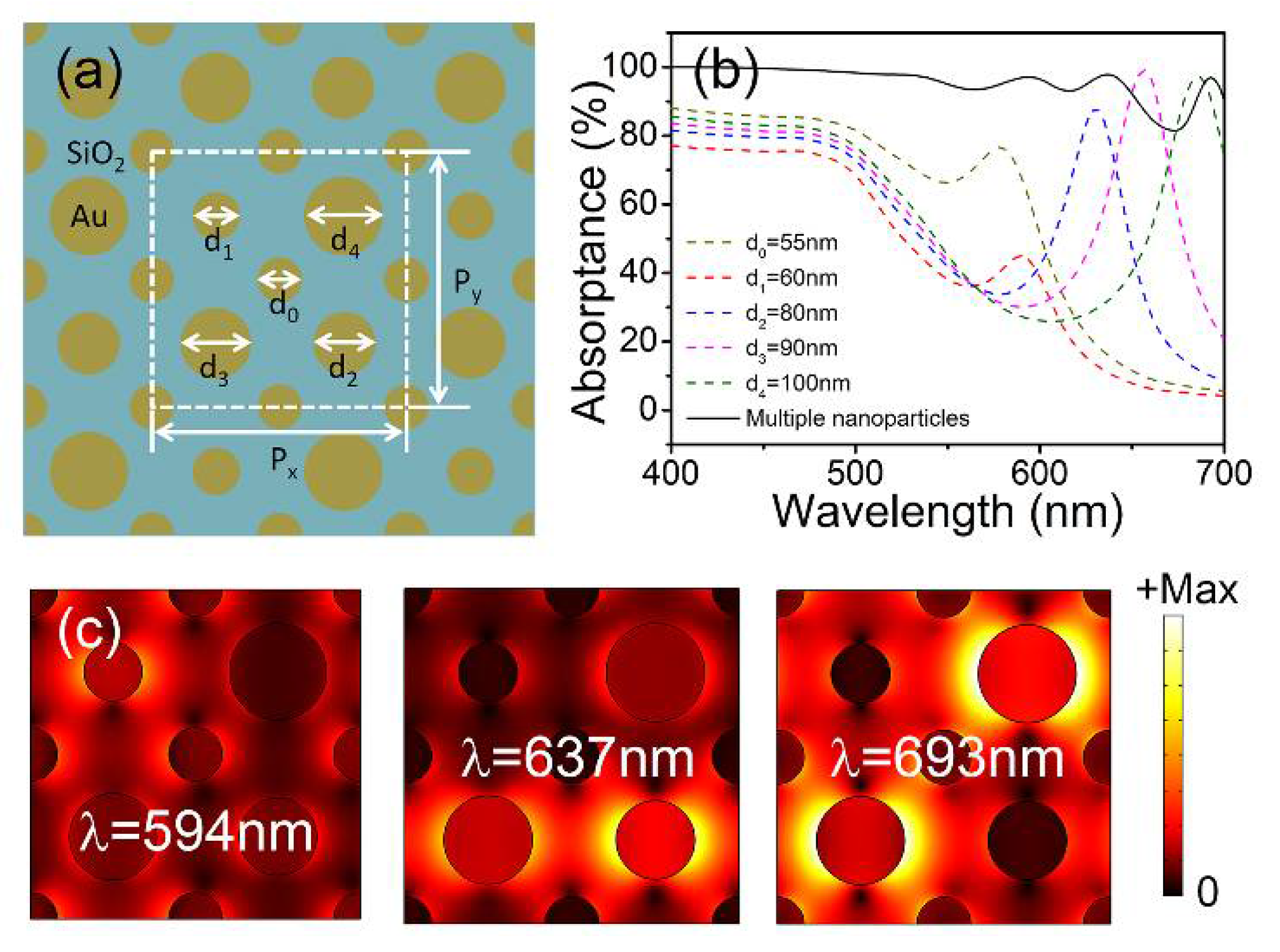
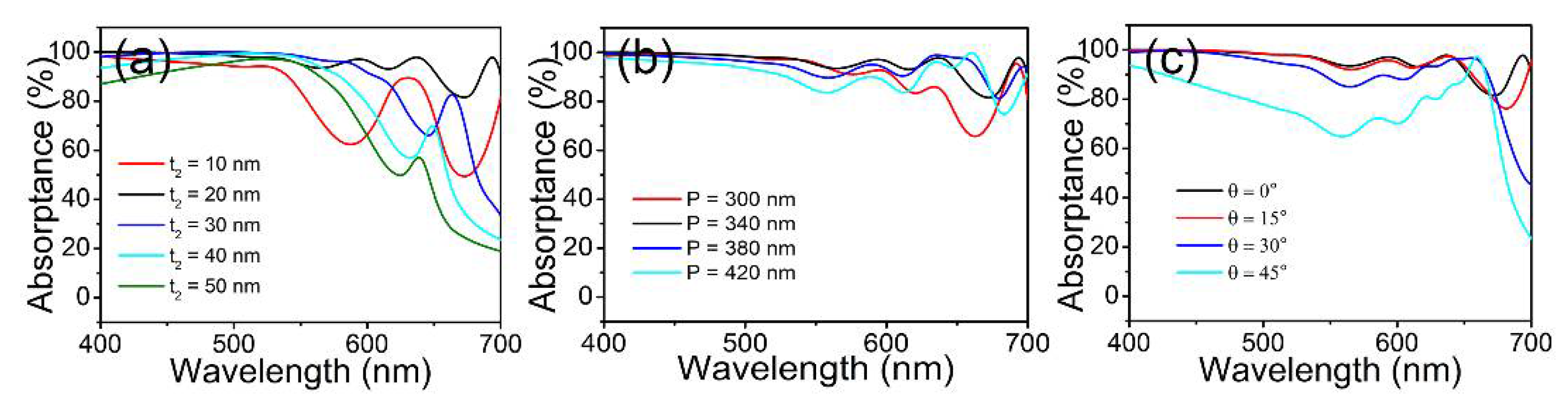
2. Simulation and Discussion
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Patel, S.K.; Charola, S.; Jani, C.; Ladumor, M.; Guo, T. Graphene-based highly efficient and broadband solar absorber. Opt. Mater. 2019, 96, 109330. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Z.; Liu, G.; Pan, P.; Wang, J. Ultra-broadband solar absorbers for high-efficiency thermophotovoltaics. Opt. Express 2020, 28, 36476. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Heo, S.W.; Lee, W.; Inoue, D.; Zhi, J.; Yu, K.; Jinno, H.; Hashizume, D.; Sekino, M.; Yokota, T.; et al. Self-powered ultra-flexible electronics via nano-grating-patterned organic photovoltaics. Nature 2018, 561, 516–521. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.Y.; Wan, Y.; Nordlander, P.; Halas, N.J. Color-Selective and CMOS-Compatible Photodetection Based on Aluminum Plasmonics. Adv. Mater. 2014, 26, 6318–6323. [Google Scholar] [CrossRef] [PubMed]
- Suen, J.Y.; Fan, F.; Montoya, J.; Bingham, C.; Padilla, W.J. Multifunctional metamaterial pyroelectric infrared detectors. Optica 2017, 4, 276–279. [Google Scholar] [CrossRef]
- Talghader, J.J.; Gawarikar, A.S.; Shea, R.P. Spectral selectivity in infrared thermal detection. Light Sci. App. 2012, 1, e24. [Google Scholar] [CrossRef] [Green Version]
- Mcphedran, R.C.; Shadrivov, I.V.; Kuhlmey, B.T.; Kivshar, Y.S. Metamaterials and metaoptics. NPG Asia Mater. 2011, 3, 100–108. [Google Scholar] [CrossRef]
- Landy, N.; Sajuyigbe, S.; Mock, J.; Smith, D.; Padilla, W. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Meng, W.; Zhao, X.; Zhang, J.; Schalch, J.; Xin, Z. A three-dimensional all-metal terahertz metamaterial perfect absorber. Appl. Phys. Lett. 2017, 111, 051101. [Google Scholar] [CrossRef]
- Jia, D.; Xu, J.; Yu, X. Ultra-broadband terahertz absorption using bi-metasurfaces based multiplexed resonances. Opt. Express 2018, 26, 26227–26234. [Google Scholar] [CrossRef]
- Zhou, R.; Jiang, T.; Peng, Z.; Li, Z.; Su, H. Tunable broadband terahertz absorber based on graphene metamaterials and VO2. Opt. Mater. 2021, 114, 110915. [Google Scholar] [CrossRef]
- Liang, Y.; Koshelev, K.; Zhang, F.; Lin, H.; Kivshar, Y. Bound states in the continuum in anisotropic plasmonic metasurfaces. Nano Lett. 2020, 20, 6351–6356. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Wang, Q.; Ding, L. Broadband near-infrared metamaterial absorber based on rainbow trapping effect. Opt. Commun. 2020, 475, 126284. [Google Scholar] [CrossRef]
- Parsamyan, H. Near-Perfect Broadband Infrared Metamaterial Absorber Utilizing Nickel. Appl. Optics 2020, 59, 7504–7509. [Google Scholar] [CrossRef] [PubMed]
- Akselrod, G.M.; Huang, J.; Hoang, T.B.; Bowen, P.T.; Su, L.; Smith, D.R.; Mikkelsen, M.H. Large-Area Metasurface Perfect Absorbers from Visible to Near-Infrared. Adv. Mater. 2015, 27, 7897–8115. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, M.; Chen, L. Polarization-Independent Near-Perfect Absorber in the Visible Regime Based on One-Dimensional Meta-Surface. Plasmonics 2017, 12, 1889–1895. [Google Scholar] [CrossRef]
- Tang, B.; Li, Z.; Palacios, E.; Liu, Z.; Butun, S.; Aydin, K. Chiral-Selective Plasmonic Metasurface Absorbers Operating at Visible Frequencies. IEEE Photonics Technol. Lett. 2017, 29, 295–298. [Google Scholar] [CrossRef]
- Butt, M.; Khonina, S.; Kazanskiy, N.; Piramidowicz, R. Hybrid metasurface perfect absorbers for temperature and biosensing applications. Opt. Mater. 2022, 123, 111906. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, K.; Cheng, Q.; Lu, L.; Li, B.; Song, J.; Luo, Z. Tunable ultra-narrowband near-infrared absorber made of a nanodisk-based metasurface and a phase-change material Ge2Sb2Te5 layer. Appl. Optics. 2020, 59, 6309–6314. [Google Scholar] [CrossRef]
- Park, C.; Lee, S. Narrowband and flexible perfect absorber based on a thin-film nano-resonator incorporating a dielectric overlay. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Fung, K.H.; Xu, J.; Ma, H.; Jin, Y.; He, S.; Fang, N.X. Ultrabroadband light absorption by a sawtooth anisotropic metamaterial slab. Nano Lett. 2012, 12, 1443–1447. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Liu, H.; Jin, Y.; Zhu, L. Ultra-broadband perfect absorber utilizing a multi-size rectangular structure in the UV-MIR range. Results Phys. 2020, 18, 103336. [Google Scholar] [CrossRef]
- Raman, A.P.; Anoma, M.A.; Zhu, L.; Rephaeli, E.; Fana, F. Passive radiative cooling below ambient air temperature under direct sunlight. Nature 2014, 515, 540–544. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Rubin, N.A.; Zaidi, A.; Tamagnone, M.; Capasso, F. Metasurface optics for on-demand polarization transformations along the optical path. Nat. Photonics 2021, 15, 287–296. [Google Scholar] [CrossRef]
- Genevet, P.; Capasso, F. Holographic optical metasurfaces: A review of current progress. Rep. Prog. Phys. 2015, 78, 024401. [Google Scholar] [CrossRef]
- Genevet, P.; Capasso, F.; Aieta, F.; Khorasaninejad, M.; Devlin, R. Recent advances in planar optics: From plasmonic to dielectric metasurfaces. Optica 2017, 4, 139–152. [Google Scholar] [CrossRef]
- Wang, R.; Gong, Q.; Chen, J. Extra-narrowband metallic filters with an ultrathin single-layer metallic grating. Chin. Phys. B 2020, 29, 064215. [Google Scholar] [CrossRef]
- Wen, Y.; Ma, W.; Bailey, J.; Matmon, G.; Yu, X. Broadband Terahertz Metamaterial Absorber Based on Asymmetric Resonators With Perfect Absorption. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 406–411. [Google Scholar] [CrossRef]
- Bouchon, P.; Koechlin, C.; Pardo, F.; HaDar, R.; Pelouard, J.L. Wideband omnidirectional infrared absorber with a patchwork of plasmonic nanoantennas. Opt. Lett. 2012, 37, 1038–1040. [Google Scholar] [CrossRef]
- Khan, A.D.; Khan, A.D.; Khan, S.D.; Noman, M. Light absorption enhancement in tri-layered composite metasurface absorber for solar cell applications. Opt. Mater. 2018, 84, 195–198. [Google Scholar] [CrossRef]
- Liu, F.; Qi, L. A simple two-layer broadband metamaterial absorber for solar cells. Mod. Phys. Lett. 2021, 35, 2150291. [Google Scholar] [CrossRef]
- Jung, J.Y.; Lee, J.; Choi, D.G.; Choi, J.H.; Neikirk, D.P. Wavelength-Selective Infrared Metasurface Absorber for Multispectral Thermal Detection. IEEE Photonics J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Grant, J.; Escorcia-Carranza, I.; Li, C.; Mccrindle, I.J.H.; Gough, J.; Cumming, D.R.S. A monolithic resonant terahertz sensor element comprising a metamaterial absorber and micro-bolometer. Laser Photonics Rev. 2013, 7, 1043–1048. [Google Scholar] [CrossRef]
- Johnson, P.B. Optical Constants of the Noble Metals. Phys. Rev. 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.L.; Starr, T.; Starr, A.; Padilla, W.J. Infrared Spatial and Frequency Selective Metamaterial with Near-Unity Absorbance. Phys. Rev. Lett. 2010, 104, 207403. [Google Scholar] [CrossRef] [Green Version]
- Sievenpiper, D.; Zhang, L.; Broas, R.F.J.; Alexopolous, N.G. High-impedance electromagnetic surfaces with a forbidden frequency band. IEEE T Microw. Theory 1999, 47, 2059–2074. [Google Scholar] [CrossRef] [Green Version]
- Azad, A.; Kort-Kamp, W.; Sykora, M.; Weisse-Bernstein, N.; Luk, T.; Taylor, A.; Dalvit, D.; Chen, H. Metasurface broadband solar absorber. Sci. Rep. 2015, 6, 20347. [Google Scholar] [CrossRef]
- Zheng, M.; Chen, Y.; Liu, Z.; Liu, Y.; Wang, Y.; Liu, P.; Liu, Q.; Bi, K.; Shu, Z.; Zhang, Y.; et al. Kirigami-inspired Multiscale Patterning of Metallic Structures via Predefined Nanotrench Templates. Microsyst. Nanoeng. 2019, 5, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Xiang, Q.; Li, Z.; Wang, Y.; Meng, Y.; Duan, H. “Sketch and Peel” lithography for high-resolution multiscale patterning. Nano Lett. 2016, 16, 3253–3259. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Yue, S.; Zhang, Z.; Hou, Y.; Zhao, H.; Qu, S.; Li, M.; Zhang, Z. Broadband Perfect Absorber in the Visible Range Based on Metasurface Composite Structures. Materials 2022, 15, 2612. https://doi.org/10.3390/ma15072612
Wang R, Yue S, Zhang Z, Hou Y, Zhao H, Qu S, Li M, Zhang Z. Broadband Perfect Absorber in the Visible Range Based on Metasurface Composite Structures. Materials. 2022; 15(7):2612. https://doi.org/10.3390/ma15072612
Chicago/Turabian StyleWang, Ran, Song Yue, Zhe Zhang, Yu Hou, Hongda Zhao, Shitian Qu, Man Li, and Zichen Zhang. 2022. "Broadband Perfect Absorber in the Visible Range Based on Metasurface Composite Structures" Materials 15, no. 7: 2612. https://doi.org/10.3390/ma15072612
APA StyleWang, R., Yue, S., Zhang, Z., Hou, Y., Zhao, H., Qu, S., Li, M., & Zhang, Z. (2022). Broadband Perfect Absorber in the Visible Range Based on Metasurface Composite Structures. Materials, 15(7), 2612. https://doi.org/10.3390/ma15072612





