Phase Field Models for Thermal Fracturing and Their Variational Structures
Abstract
:1. Introduction
2. Thermoelasticity Model
2.1. Formulation of the Problem
2.2. Variational Principle and Energy Equality
2.3. Numerical Experiment
2.3.1. Non-Dimensional Setting
2.3.2. Numerical Setup and Time Discretization
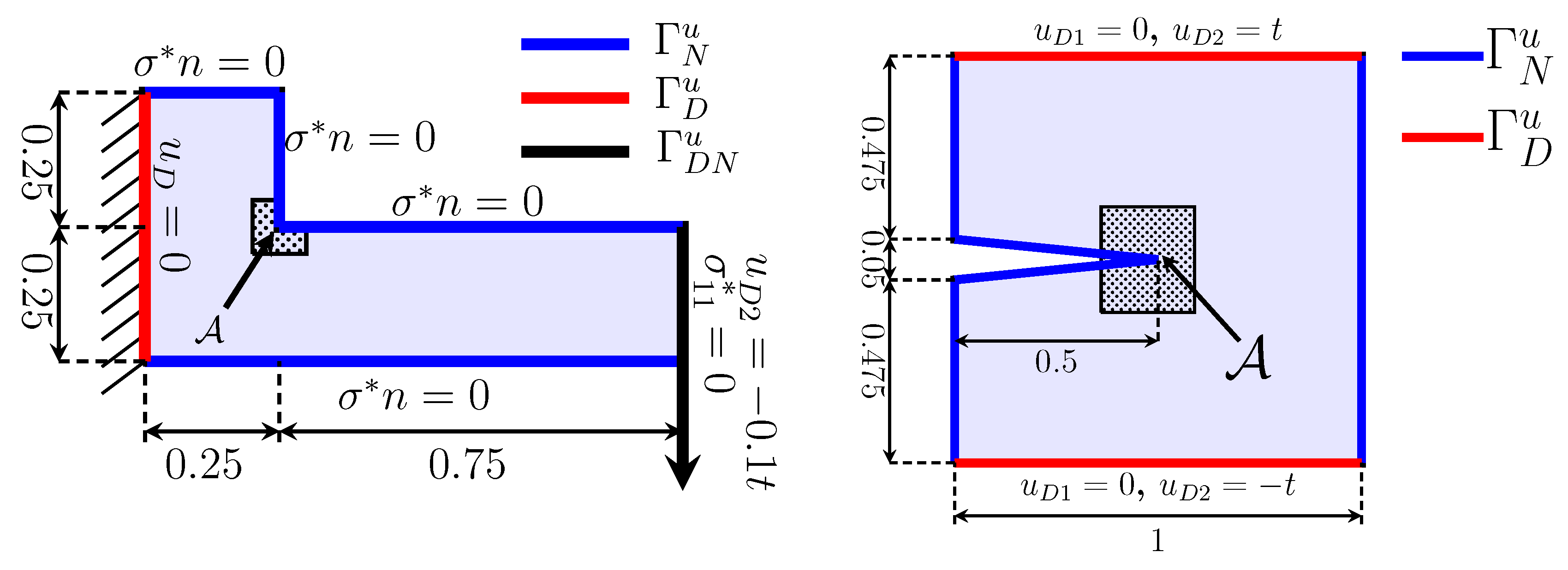
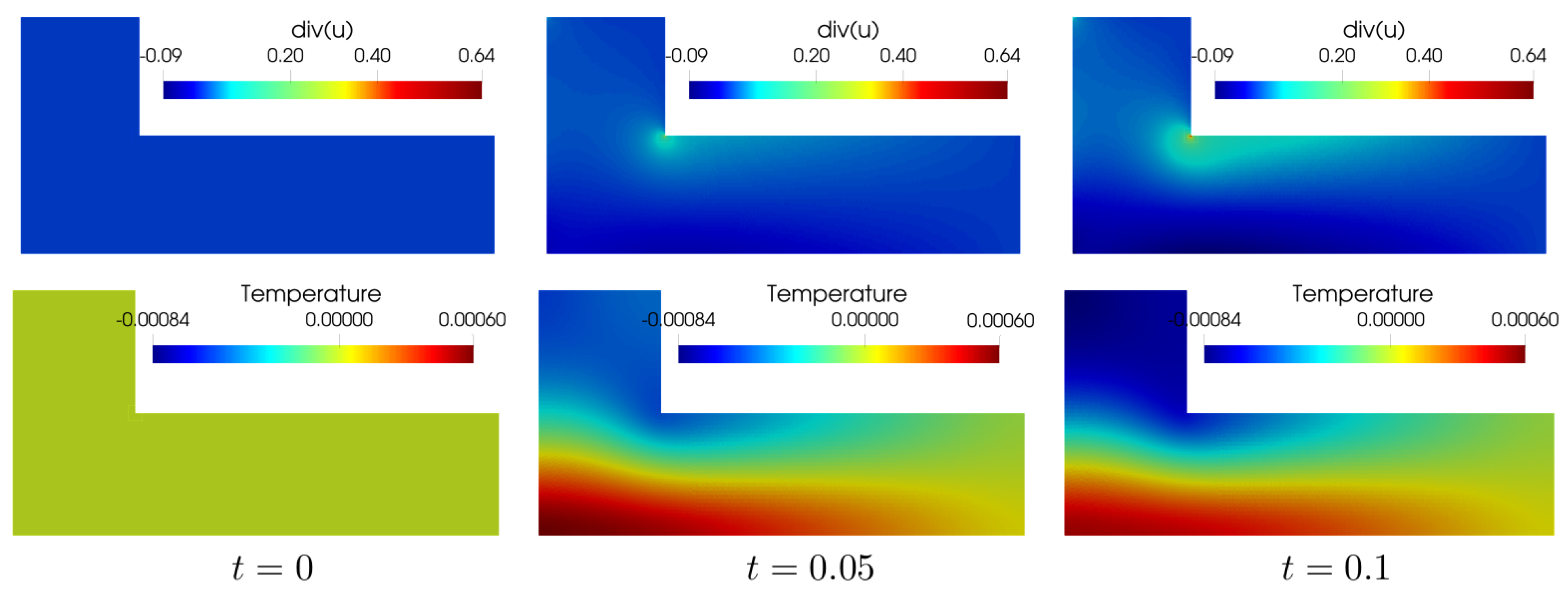
2.3.3. L-Shape Cantilever
2.3.4. Cracked Domain
3. Crack Propagation under Thermal Stress
3.1. Fracturing Phase Field Model (F-PFM)
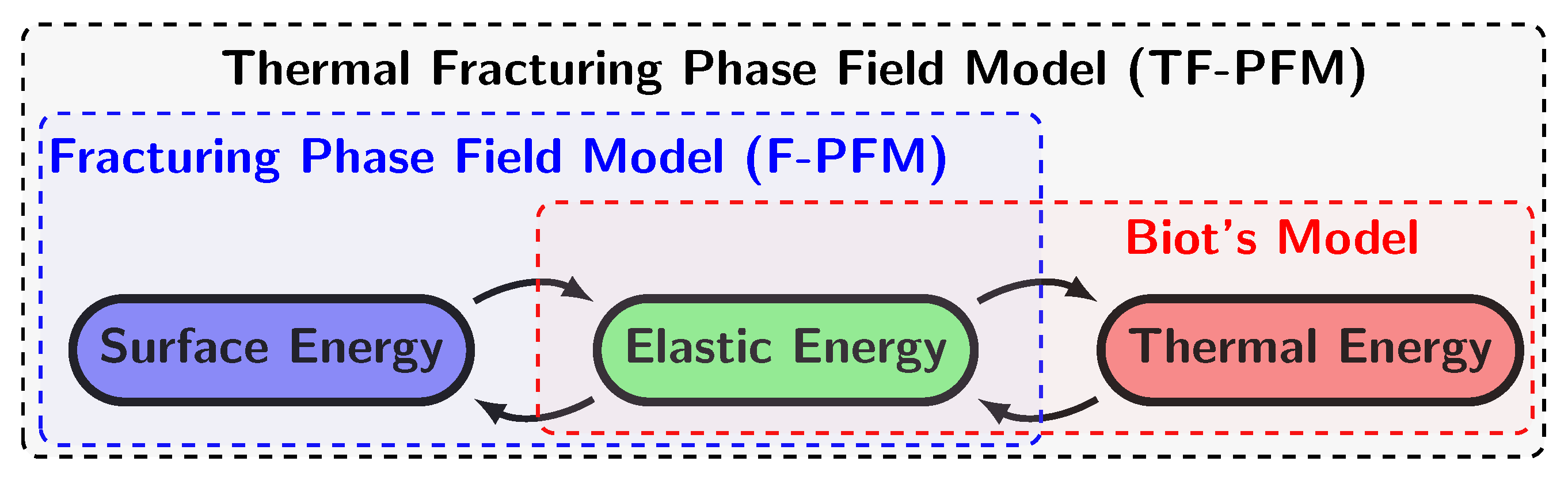
3.2. Thermal Fracturing Phase Field Model 1 (TF-PFM1)
3.3. Thermal Fracturing Phase Field Model 2 (TF-PFM2)
4. Numerical Experiments
4.1. Non-Dimensional Setting
4.2. Time Discretization
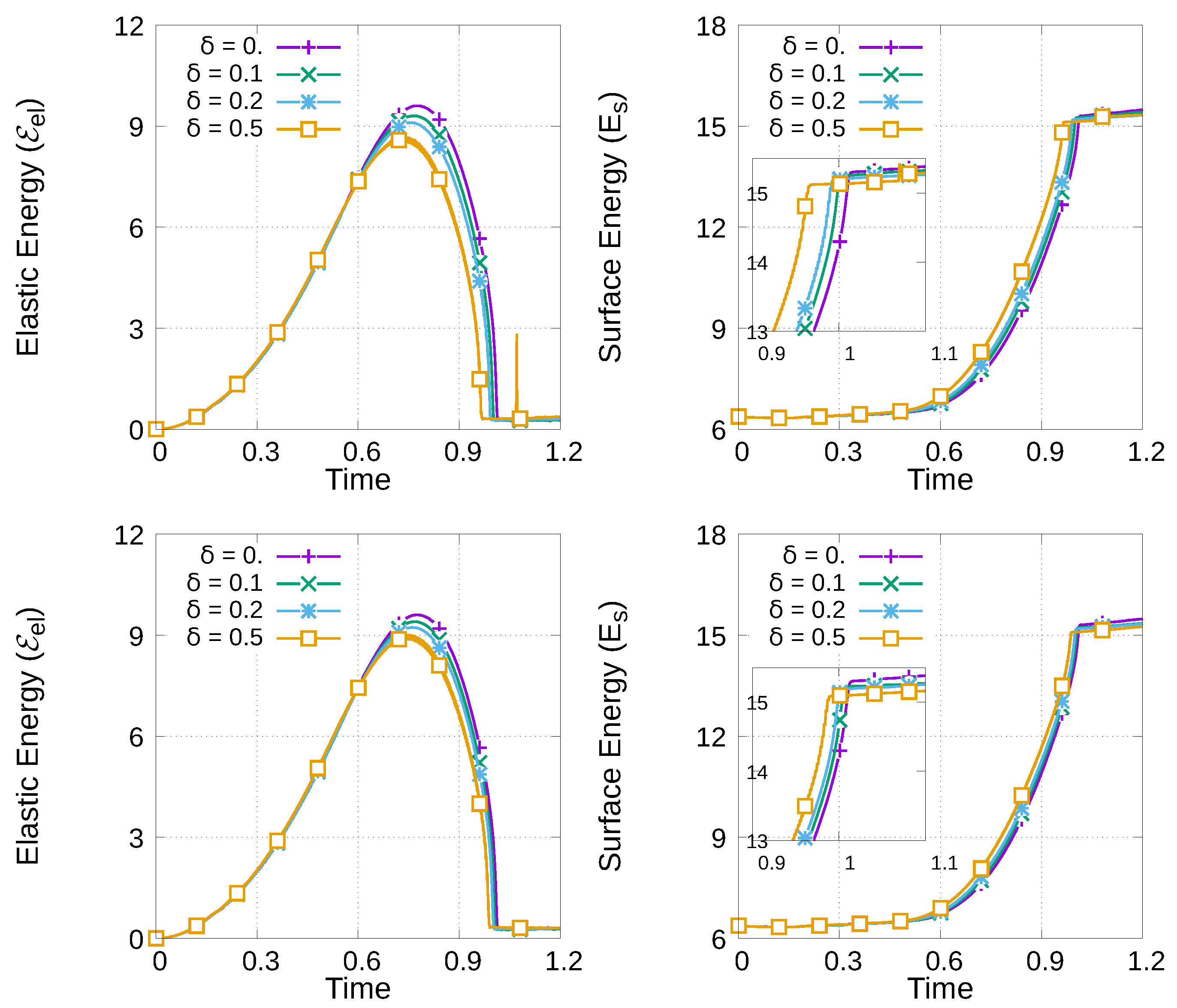
4.3. Thermoelastic Effect on the Crack Speed
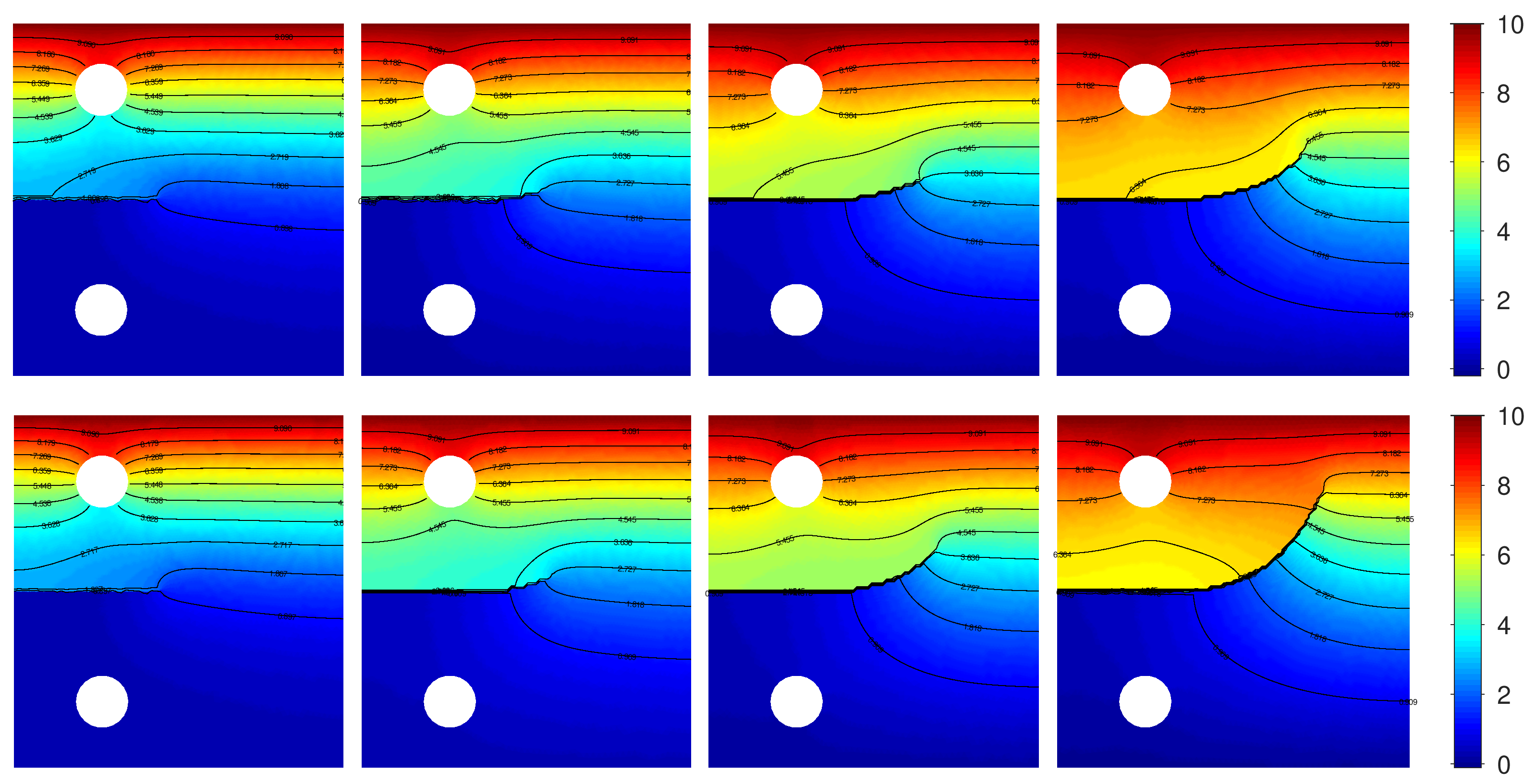
4.4. Thermoelastic Effect on the Crack Path
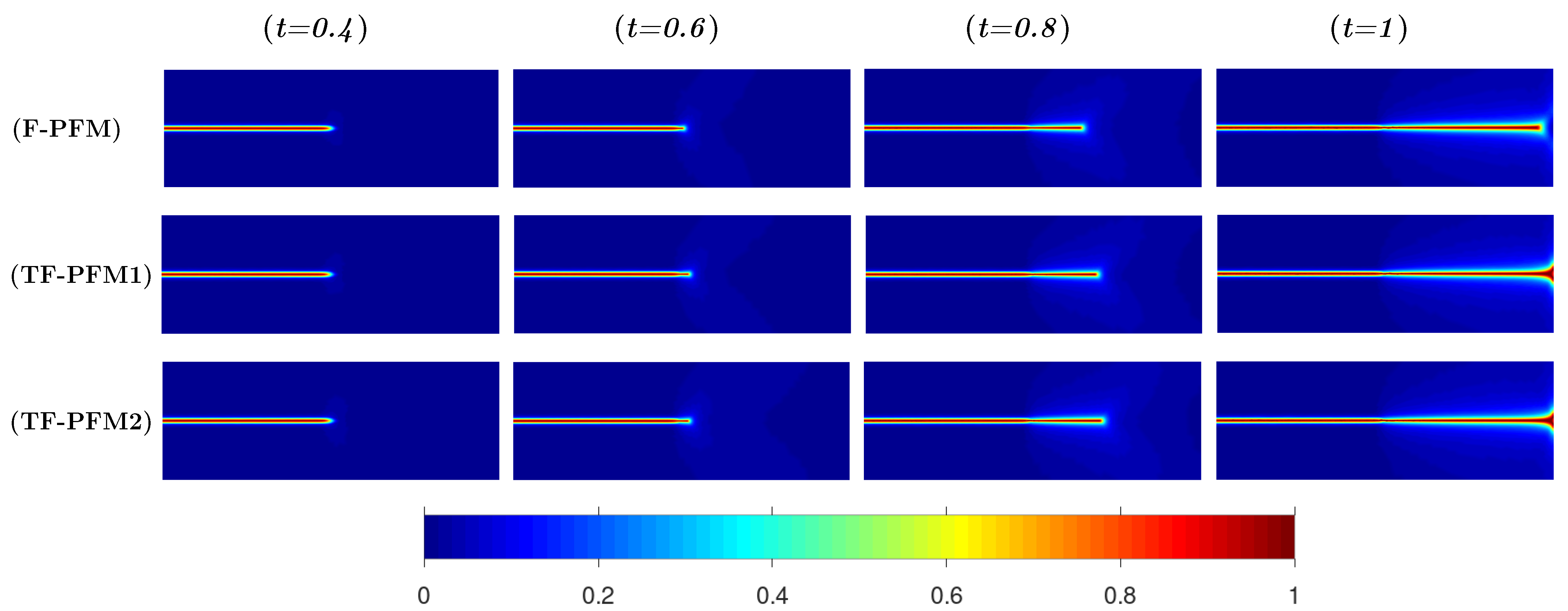
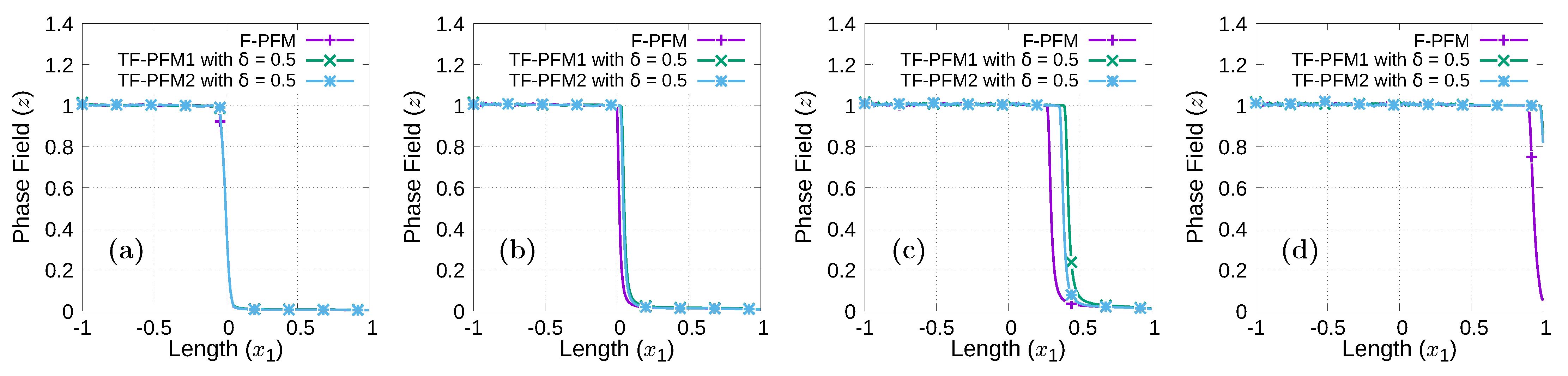
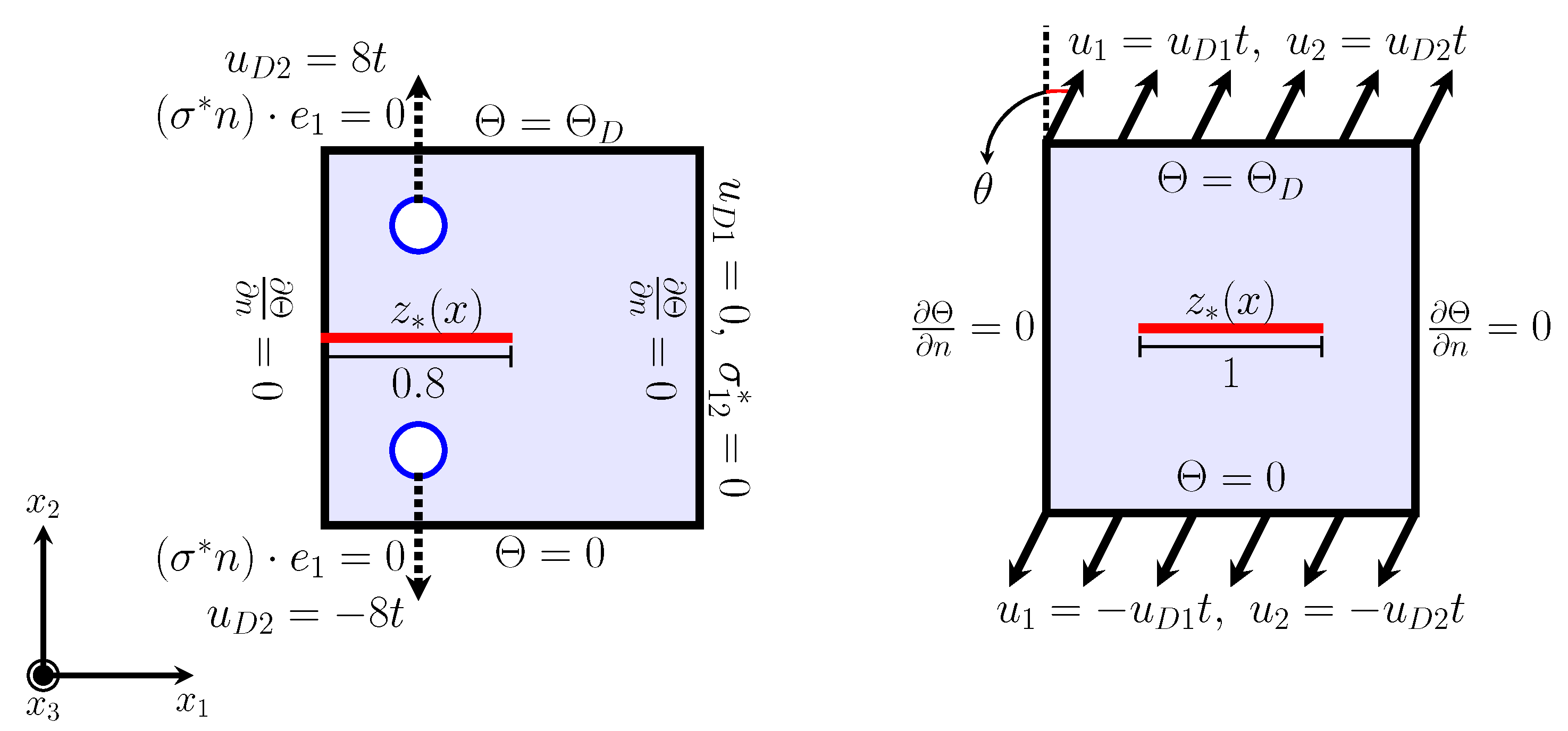
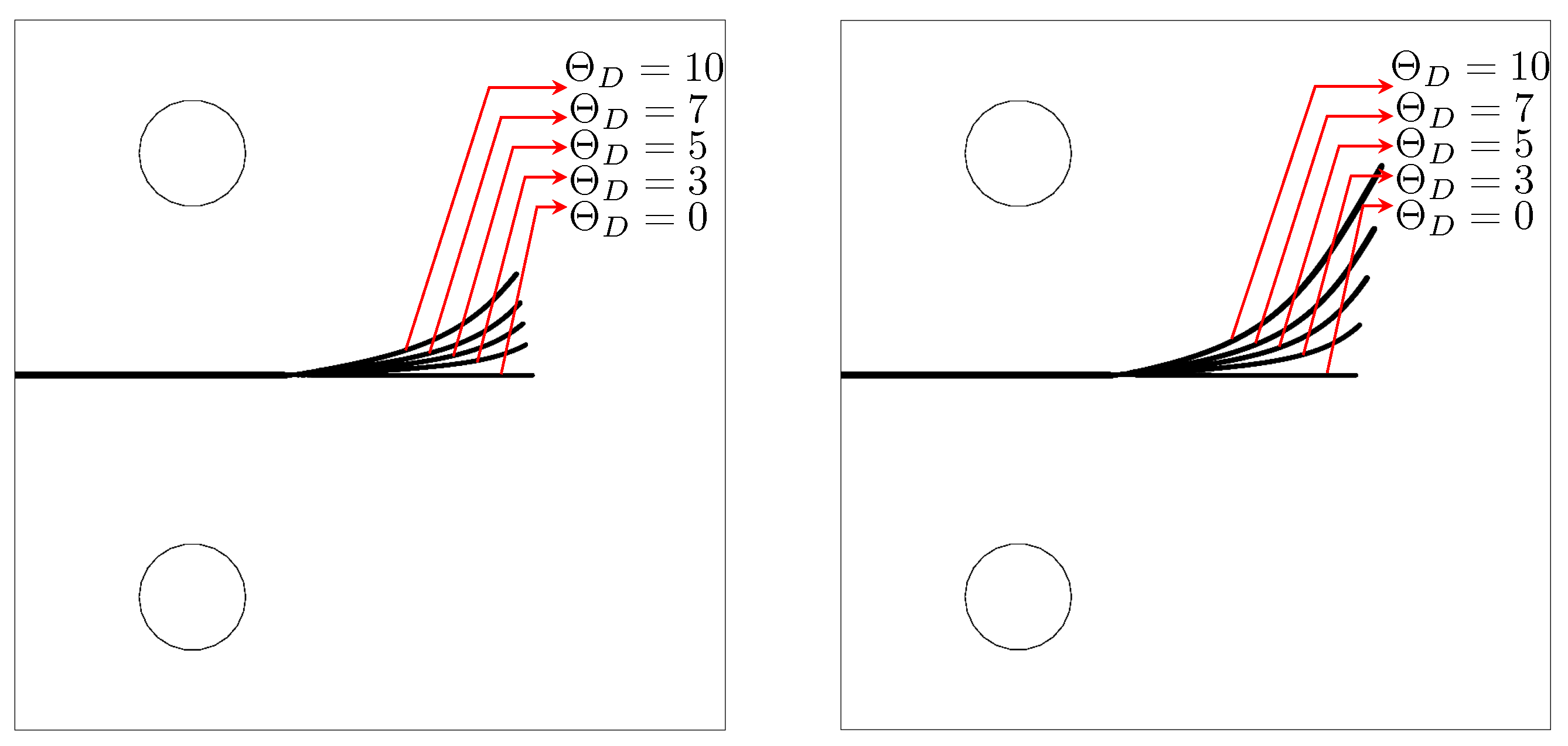
4.4.1. Mode I
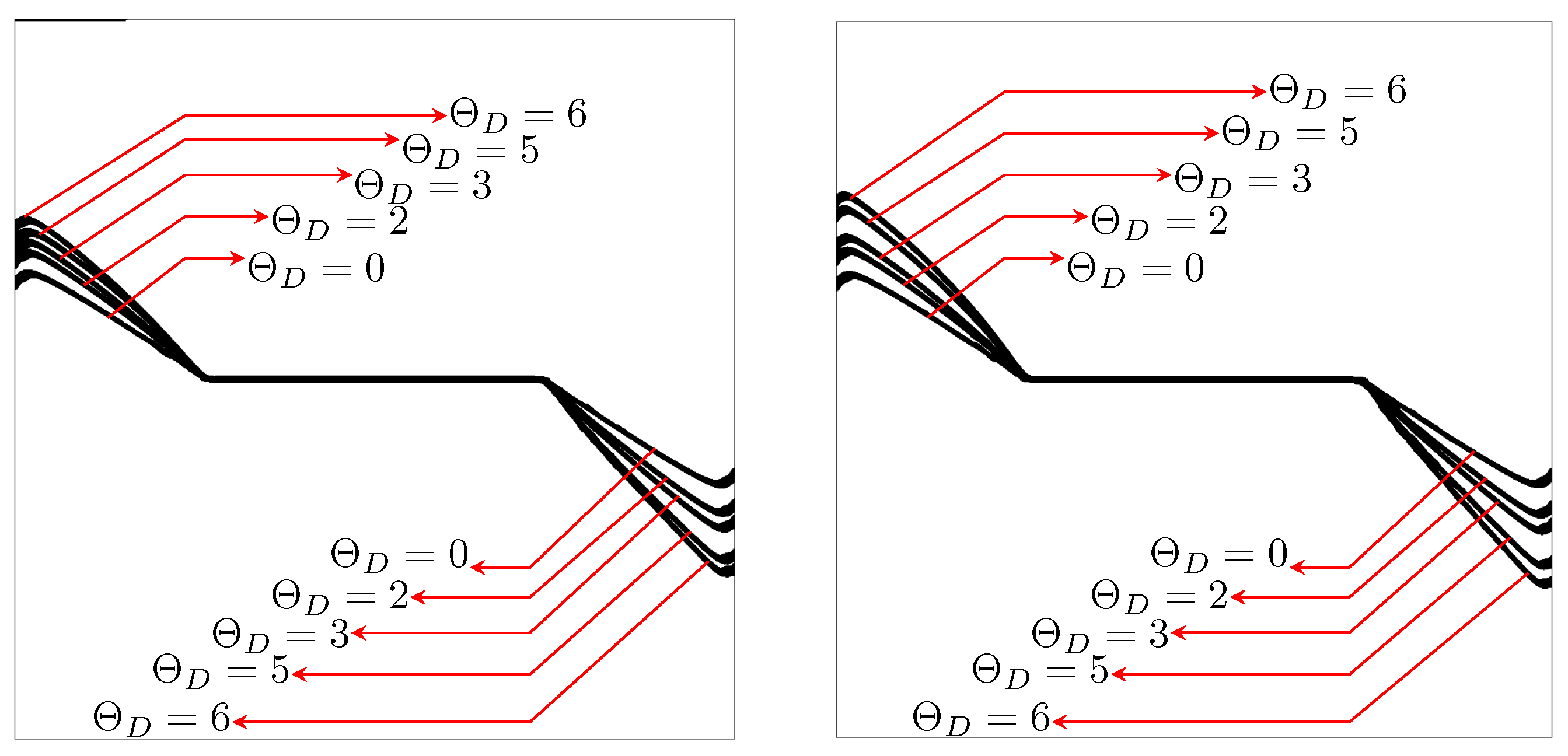
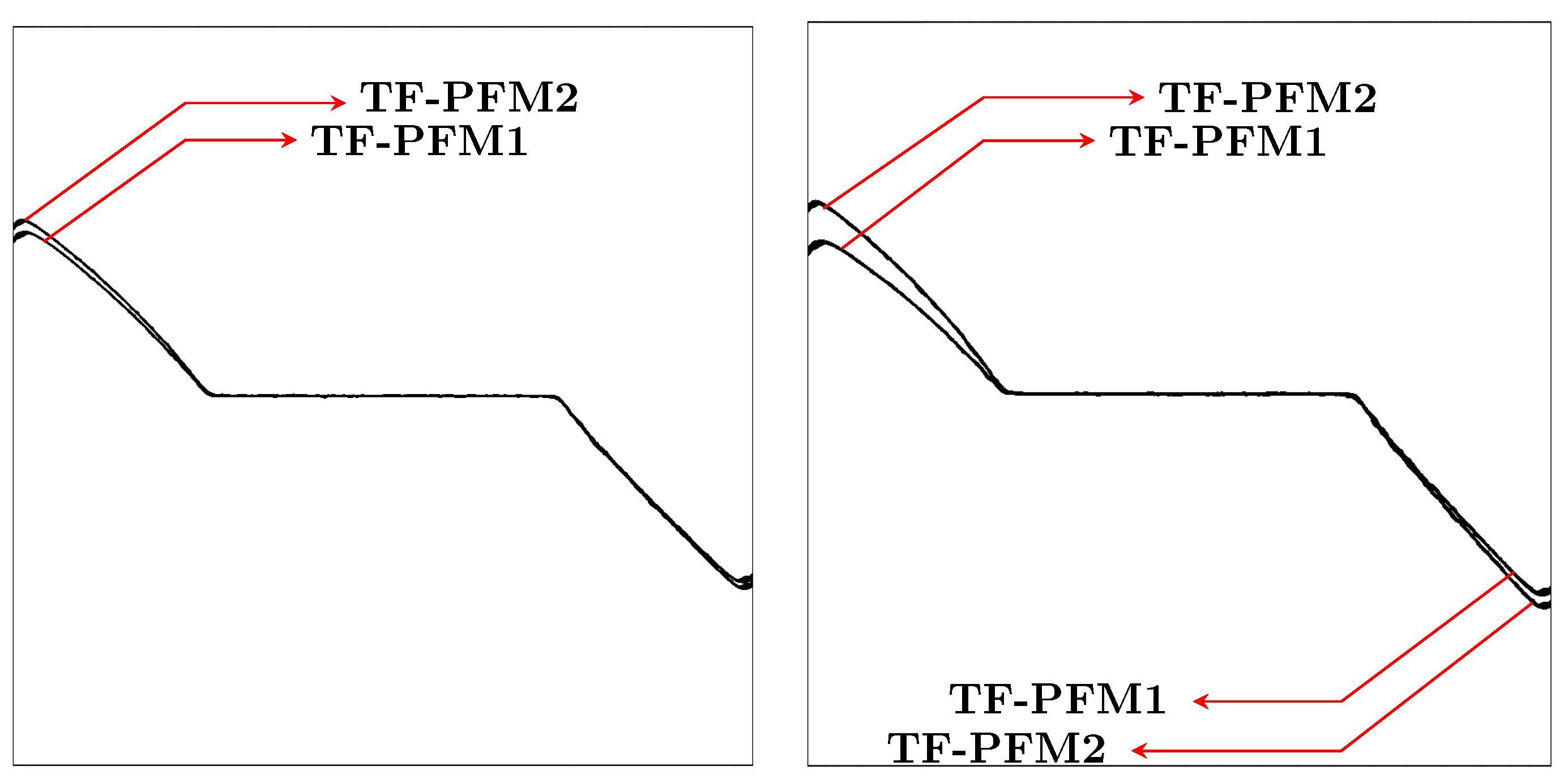
4.4.2. Mode I + II
5. Conclusions and Future Works
- The thermoelastic coupling parameter in TF-PFM1 and TF-PFM2 enhances crack propagation (Figure 10).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Weak Forms
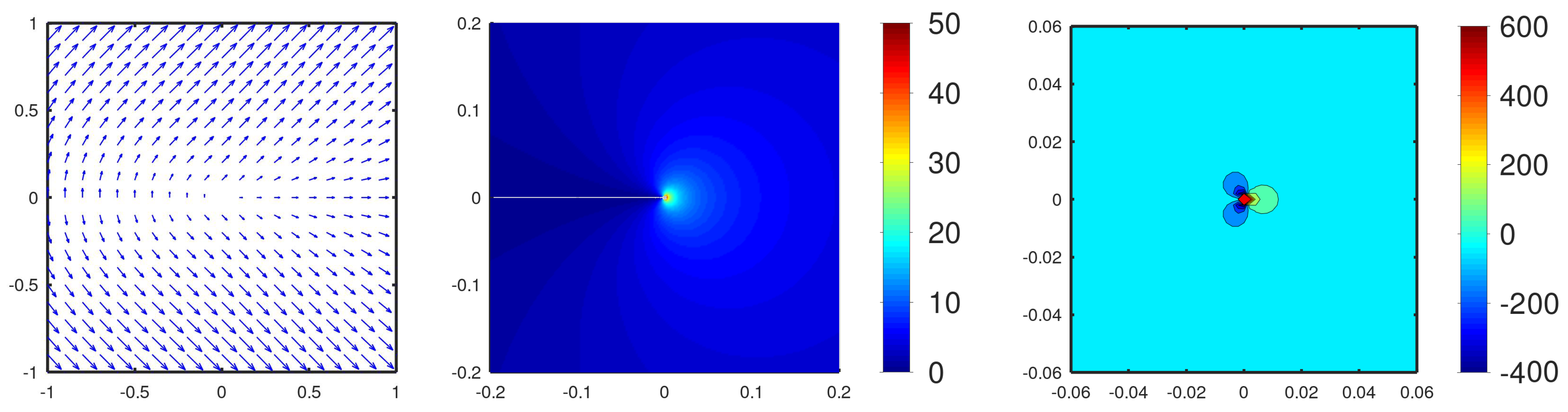
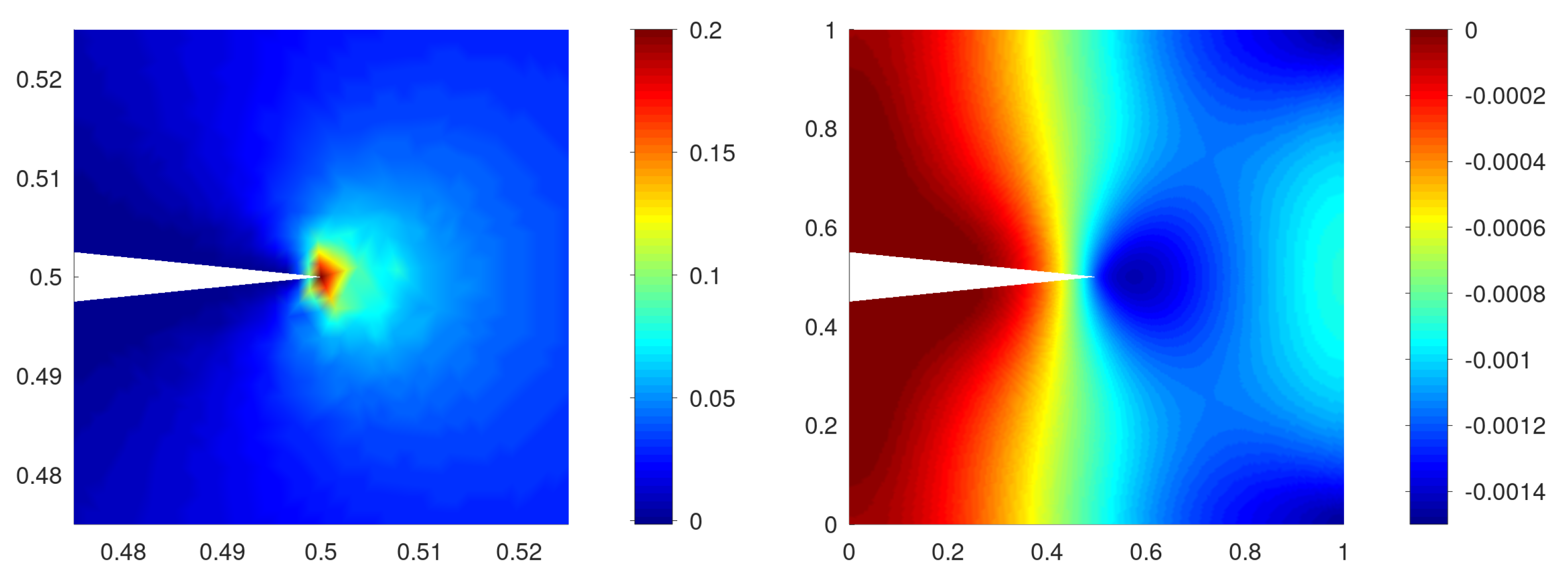
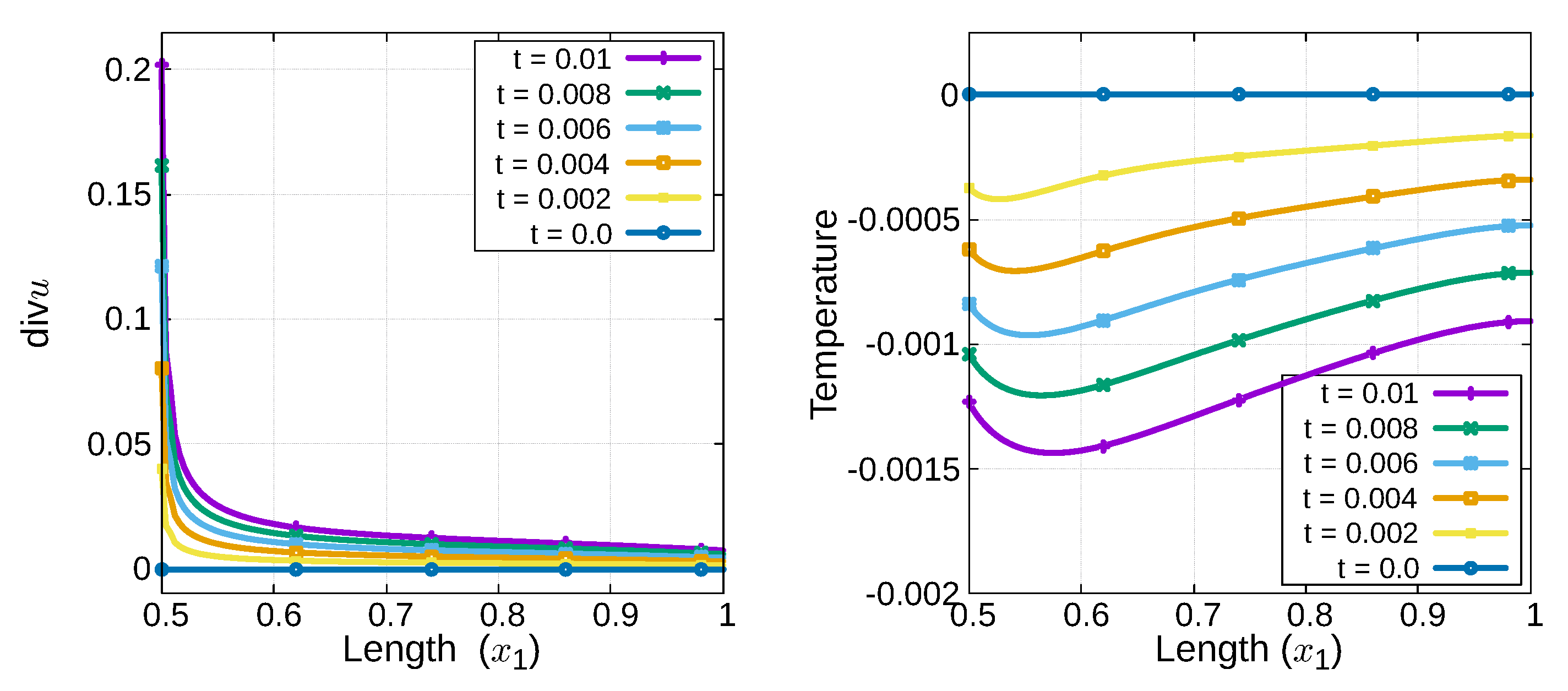
Appendix B. Divergence of u around the Crack Tip
References
- Mackin, T.J.; Noe, S.C.; Ball, K.J.; Bedell, B.C.; Bim-Merle, D.P.; Bingman, M.C.; Bomleny, D.M.; Chemlir, G.J.; Clayton, D.B.; Evans, H.A.; et al. Thermal cracking in disc brakes. Eng. Fail. Anal. 2002, 9, 63–76. [Google Scholar] [CrossRef]
- Nara, Y.; Morimoto, K.; Yoneda, T.; Hiroyoshi, N.; Kaneko, K. Effects of humidity and temperature on subcritical crack growth in sandstone. Int. J. Solids Struct. 2011, 48, 1130–1140. [Google Scholar] [CrossRef] [Green Version]
- Vivekanandan, A.; Ramesh, K. Study of crack interaction effects under thermal loading by digital photoelasticity and finite elements. Exp. Mech. 2020, 60, 295–316. [Google Scholar] [CrossRef]
- Kou, M.; Liu, X.; Tang, S.; Wang, Y. 3D X-ray computed tomography on failure characteristics of rock-like materials under coupled hydro-mechanical loading. Theor. Appl. Fract. Mech. 2019, 104, 102396. [Google Scholar] [CrossRef]
- Louthan, M.R., Jr.; Caskey, G.R., Jr.; Donovan, J.A.; Rawl, D.E., Jr. Hydrogen embrittlement of metals. Mater. Sci. Eng. 1972, 10, 357–368. [Google Scholar] [CrossRef]
- Dwivedi, S.K.; Vishwakarma, M. Hydrogen embrittlement in different materials: A review. Int. J. Hydrogen Energy 2018, 43, 21603–21616. [Google Scholar] [CrossRef]
- Freiman, S.W. Effects of chemical environments on slow crack growth in glasses and ceramics. J. Geophys. Res. Solid Earth 1984, 89, 4072–4076. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Entezari, A.; Filippi, M.; Carrera, E.; Kouchakzadeh, M.A. 3D dynamic coupled thermoelastic solution for constant thickness disks using refined 1D finite element models. Appl. Math. Model. 2018, 60, 273–285. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. A re-examination of the basic postulates of thermomechanics. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 432, 171–194. [Google Scholar]
- Kouchakzadeh, M.A.; Entezari, A. Analytical solution of classic coupled thermoelasticity problem in a rotating disk. J. Therm. Stress. 2015, 38, 1267–1289. [Google Scholar] [CrossRef]
- Zheng, B.J.; Gao, X.W.; Yang, K.; Zhang, C.Z. A novel meshless local Petrov–Galerkin method for dynamic coupled thermoelasticity analysis under thermal and mechanical shock loading. Eng. Anal. Bound. Elem. 2015, 60, 154–161. [Google Scholar] [CrossRef]
- Zhou, F.X.; Li, S.R.; Lai, Y.M. Three-dimensional analysis for transient coupled thermoelastic response of a functionally graded rectangular plate. J. Sound Vib. 2011, 330, 3990–4001. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Karma, A.; Kessler, D.A.; Levine, H. Phase-field model of mode III dynamic fracture. Phys. Rev. Lett. 2001, 87, 045501. [Google Scholar] [CrossRef] [Green Version]
- Francfort, G.A.; Marigo, J.-J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. The Variational Approach to Fracture. J. Elast. 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Bourdin, B. Numerical implementation of the variational formulation of brittle fracture. Interfaces Free Bound. 2007, 9, 411–430. [Google Scholar] [CrossRef] [Green Version]
- Amor, H.; Marigo, J.-J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Takaishi, T.; Kimura, M. Phase field model for mode III crack growth in two-dimensional elasticity. Kybernetika 2009, 45, 605–614. [Google Scholar]
- Miehe, C.; Schaenzel, L.M.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Alfat, S.; Kimura, M.; Firihu, M.Z.; Rahmat. Numerical investigation of shape domain effect to its elasticity and surface energy using adaptive finite element method. AIP Conf. Proc. 2018, 1964, 020011. [Google Scholar]
- Hamdia, K.M.; Msekh, M.A.; Silani, M.; Thai, T.Q.; Budarapu, P.R.; Rabczuk, T. Assessment of computational fracture models using Bayesian method. Eng. Fract. Mech. 2019, 205, 387–398. [Google Scholar] [CrossRef]
- Kimura, M.; Takaishi, T.; Alfat, S.; Nakano, T.; Tanaka, Y. Irreversible phase field models for crack growth in industrial applications: Thermal stress. viscoelasticity, hydrogen embrittlement. SN Appl. Sci. 2021, 3, 1–26. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yvonnet, J.; Bornert, M.; Chateau, C.; Sab, K.; Romani, R.; Roy, R.L. On the choice of parameters in the phase field method for simulating crack initiation with experimental validation. Int. J. Fract. 2016, 197, 213–226. [Google Scholar] [CrossRef]
- Bourdin, B.; Marigo, J.-J.; Maurini, C.; Sicsic, P. Morphogenesis and propagation of complex cracks induced by thermal shocks. Phys. Rev. Lett. 2014, 112, 014301. [Google Scholar] [CrossRef] [Green Version]
- Ai, W.; Augarde, C.E. Thermoelastic fracture modelling in 2D by an adaptive cracking particle method without enrichment functions. Int. J. Mech. Sci. 2019, 160, 343–357. [Google Scholar] [CrossRef]
- Duflot, M. The extended finite element method in thermoelastic fracture mechanics. Int. J. Numer. Methods Eng. 2008, 74, 827–847. [Google Scholar] [CrossRef]
- Nguyen, M.N.; Bui, T.Q.; Nguyen, N.T.; Truong, T.T. Simulation of dynamic and static thermoelastic fracture problems by extended nodal gradient finite elements. Int. J. Mech. Sci. 2017, 134, 370–386. [Google Scholar] [CrossRef]
- Gao, Y.; Oterkus, S. Ordinary state-based peridynamics modelling for fully coupled thermoelastic problems. Contin. Mech. Thermodyn. 2019, 31, 907–937. [Google Scholar] [CrossRef] [Green Version]
- Yamabe-Mitarai, Y.; Kuroda, S.; Motohashi, N.; Matsumoto, H.; Miyamoto, G.; Chandiran, E.; Yoshida, Y.; Itsumi, Y. Effect of forging temperature on microstructure evolution and tensile properties of Ti-17 alloys. Mater. Trans. 2019, 60, 1733–1739. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.C.; Freiman, S.W.; Rice, R.W.; Mecholsky, J.J. Microstructural aspects of crack propagation in ceramics. J. Mater. Sci. 1978, 13, 2659–2670. [Google Scholar] [CrossRef]
- Girault, V.; Raviart, P.A. Finite Element Approximation of the Navier–Stokes Equations; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Anderson, T.L. Fracture Mechanics. In Fundamentals and Applications, 4th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Duvaut, G.; Lions, J.L. Inequalities in Mechanics and Physics; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Ciarlet, P.G. The Finite Element Method for Elliptic Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–266. [Google Scholar] [CrossRef]
- Zehnder, A.T.; Potdar, Y.K.; Bhalla, K. Plasticity induced heating in the fracture and cutting of metals. In Thermomechaninal Fatigue Fracture; Aliabadi, M.H., Ed.; WIT Press: Southampton, UK, 2002; pp. 209–244. [Google Scholar]
- Rusinek, A.; Klepaczko, J.R. Experiments on heat generated during plastic deformation and stored energy for TRIP steels. Mater. Des. 2009, 30, 35–48. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, C.; Gu, L.; Bi, M.; Hou, P.; Zheng, D.; Wang, L. Analysis on surface damage of M50 steel at impact-sliding contacts. Tribol. Int. 2020, 150, 106384. [Google Scholar] [CrossRef]
- Alfat, S.; Kimura, M. A Phase Field Approach for Thermal Fracturing Models in The Maxwell Visco-Elastic Type. In preparation.
- Jaskowiec, J. A model for heat transfer in cohesive cracks. Comput. Struct. 2017, 180, 89–103. [Google Scholar] [CrossRef]
- Giannakeas, I.N.; Papathanasiou, T.K.; Bahai, H. Simulation of thermal shock cracking in ceramics using bond-based peridynamics and FEM. J. Eur. Ceram. Soc. 2018, 38, 3037–3048. [Google Scholar] [CrossRef] [Green Version]




| Type of Energy | Definition | Equation |
|---|---|---|
| Elastic | (8) | |
| Thermoelastic | (10) | |
| Thermal | (11) | |
| Modified elastic | (24) | |
| Modified thermoelastic | (29) | |
| Surface | (25) |
| Model | Strong Form | Energy | Energy Equality |
|---|---|---|---|
| Linear elasticity | (6) | - | |
| Biot’s model | (1) and (2) | (12) | |
| F-PFM | (22a) and (22b) | (27) | |
| TF-PFM1 | (31a) and (31c) | (33) a | |
| TF-PFM2 | (35a) and (35c) | (36) |
| Symbol | Physical Meaning [Unit] | Symbol | Physical Meaning [Unit] |
|---|---|---|---|
| u | Displacement [] | Stress tensor with thermal effect [] | |
| Temperature [] | Strain tensor with thermal effect [-] | ||
| Reference temperature [] | Stress thermal modulus [ · −1] | ||
| z | Damage variable [-] | Thermal conductivity [ · −1 · −1] | |
| Stress tensor [] | Volumetric heat capacity [ · −1 · −3] | ||
| Strain tensor [-] | Coefficient of linear thermal expansion [−1] | ||
| Young’s modulus [] | Thermoelastic coupling parameter [-] | ||
| Poisson ratio [-] | Critical energy release rate a [] | ||
| , | Lamé’s constants b [] | Length scale in F-PFM or TF-PFM [] | |
| t | Time [] | Time regularization parameter in F-PFM or TF-PFM [] |
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Value | 1 | 0.3 | 1. | 0.7 | 0.001 | 0.01 | 5.08 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfat, S.; Kimura, M.; Maulana, A.M. Phase Field Models for Thermal Fracturing and Their Variational Structures. Materials 2022, 15, 2571. https://doi.org/10.3390/ma15072571
Alfat S, Kimura M, Maulana AM. Phase Field Models for Thermal Fracturing and Their Variational Structures. Materials. 2022; 15(7):2571. https://doi.org/10.3390/ma15072571
Chicago/Turabian StyleAlfat, Sayahdin, Masato Kimura, and Alifian Mahardhika Maulana. 2022. "Phase Field Models for Thermal Fracturing and Their Variational Structures" Materials 15, no. 7: 2571. https://doi.org/10.3390/ma15072571
APA StyleAlfat, S., Kimura, M., & Maulana, A. M. (2022). Phase Field Models for Thermal Fracturing and Their Variational Structures. Materials, 15(7), 2571. https://doi.org/10.3390/ma15072571







