Advanced Estimation of Compressive Strength and Fracture Behavior in Ceramic Honeycombs by Polarimetry Measurements of Similar Epoxy Resin Honeycombs
Abstract
:1. Introduction
2. Materials and Methods
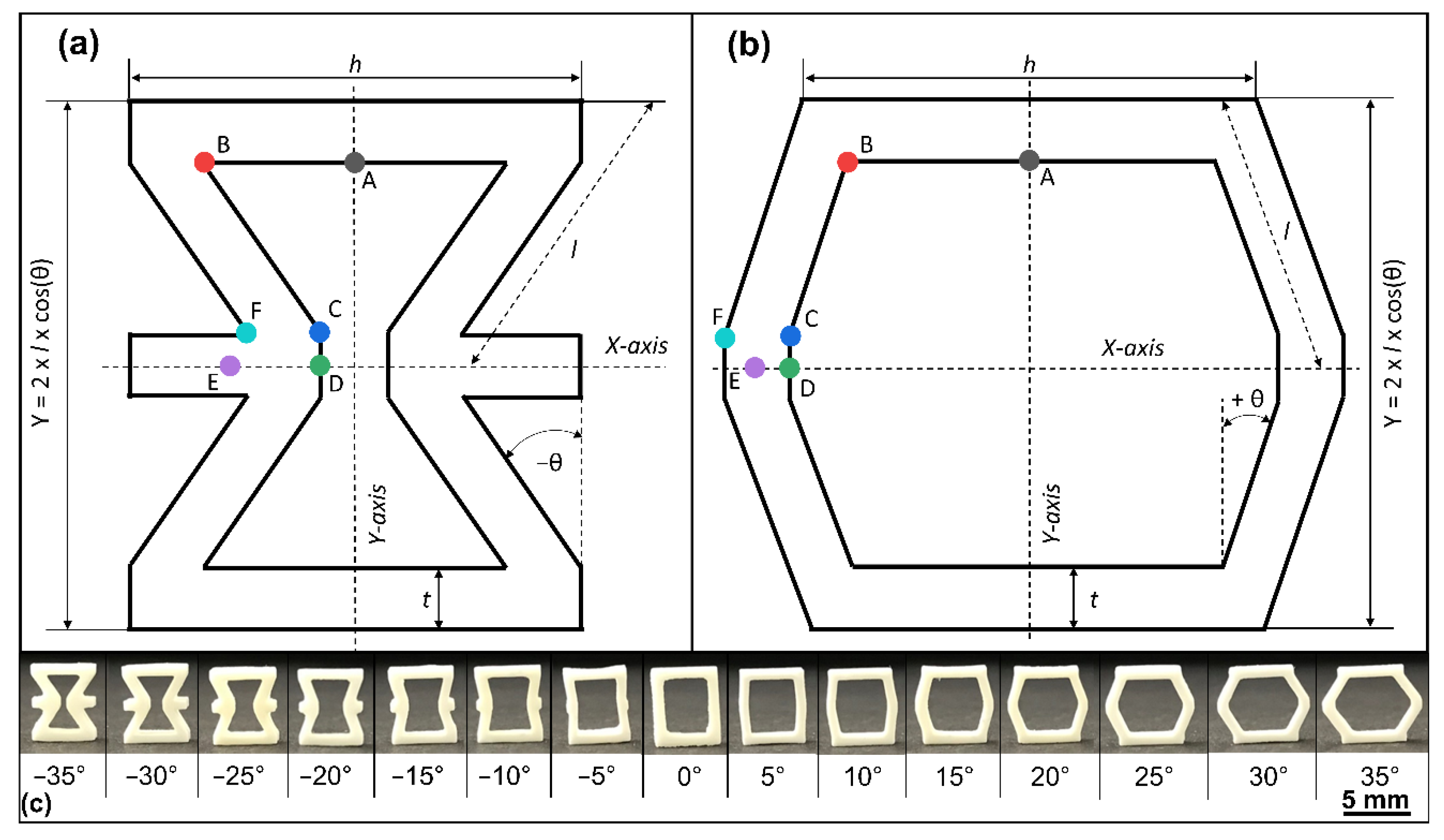
2.1. Sample Preparation
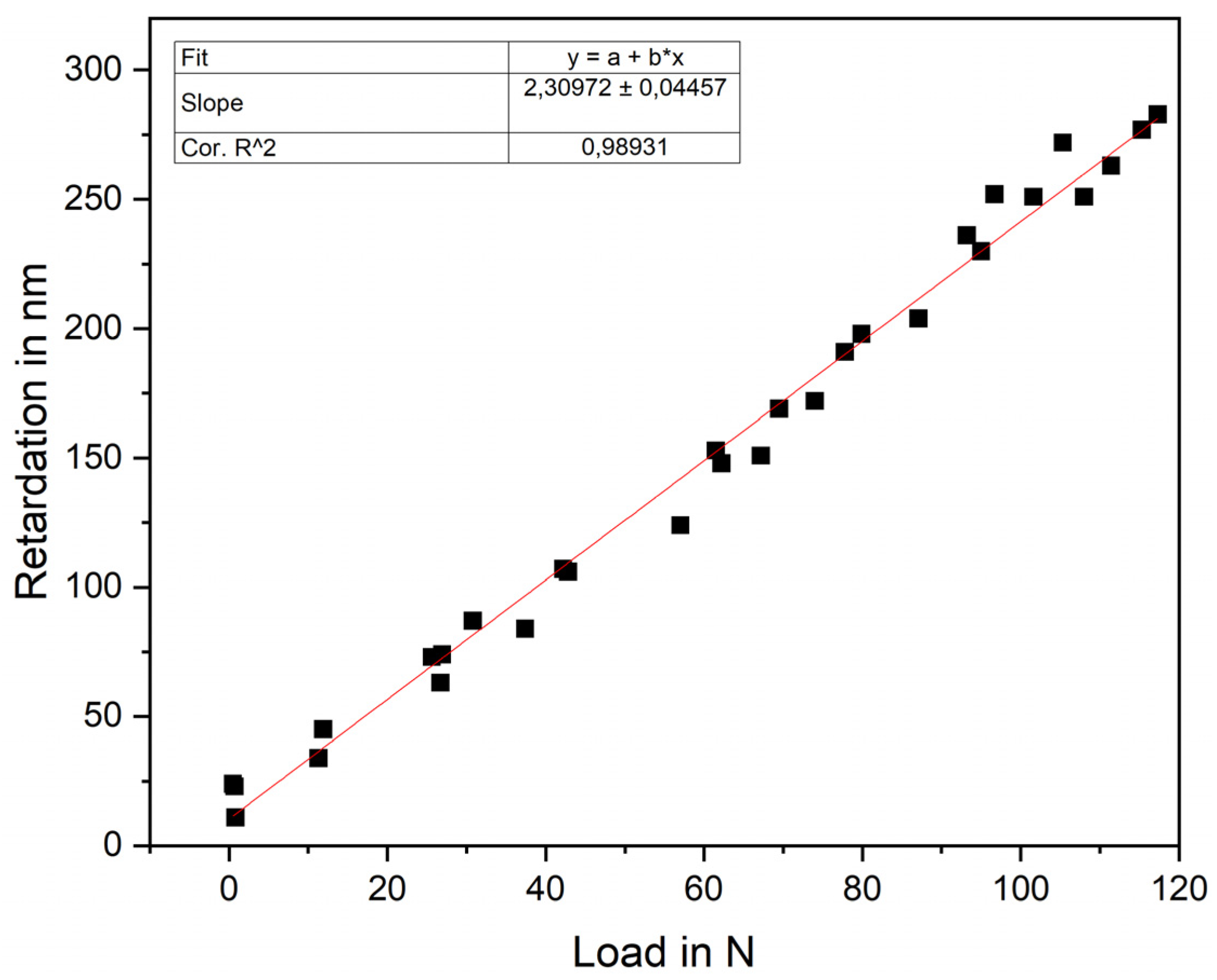
2.2. Characterization
3. Results and Discussion
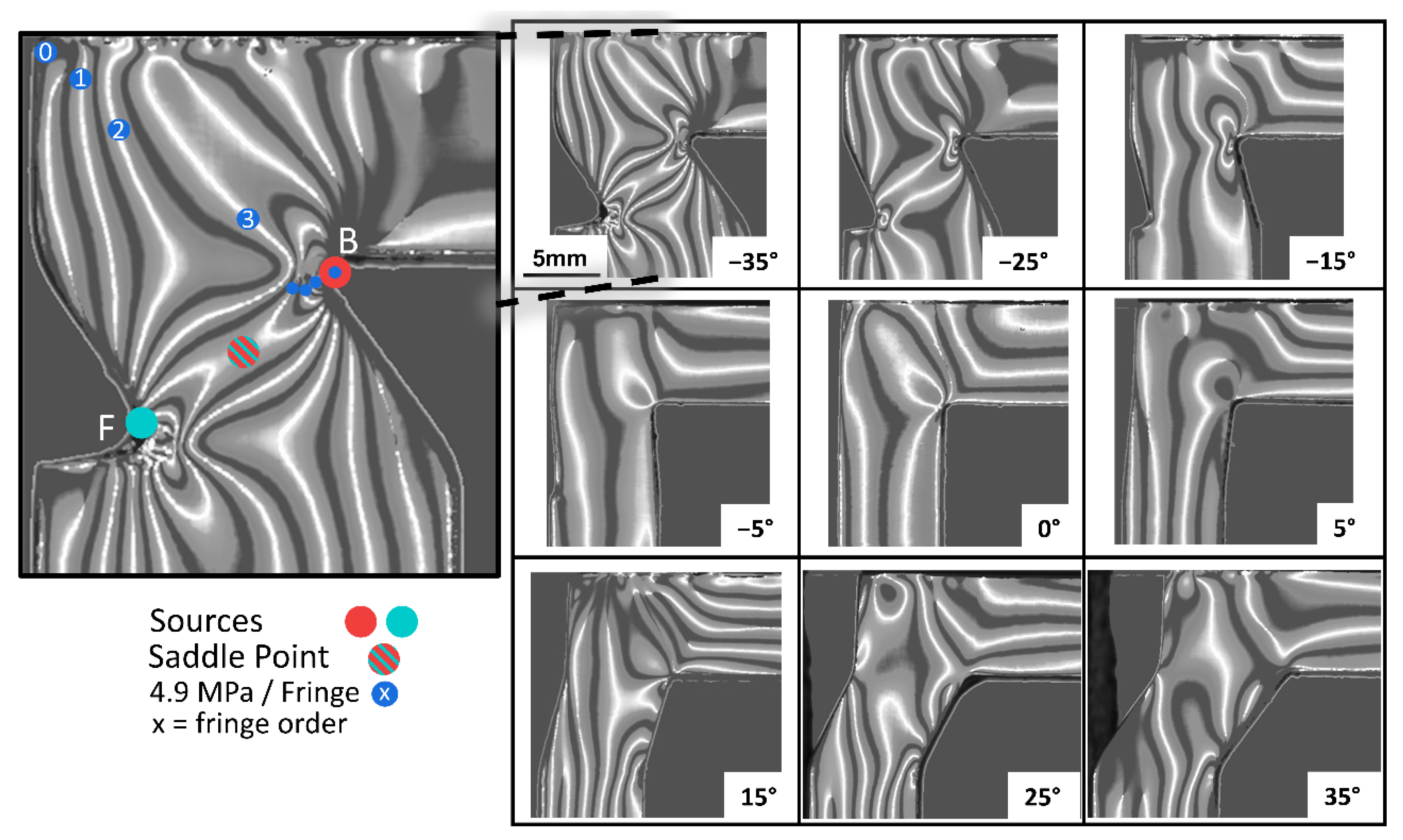
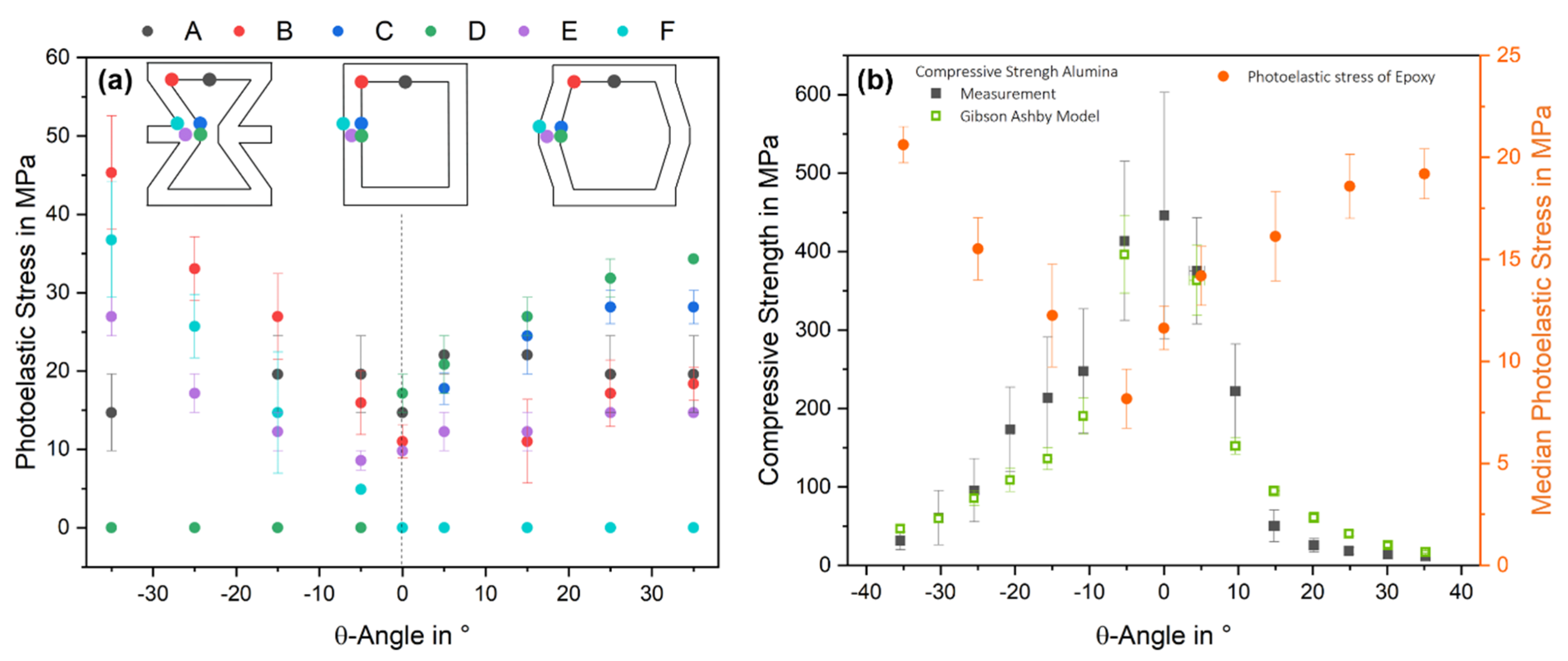
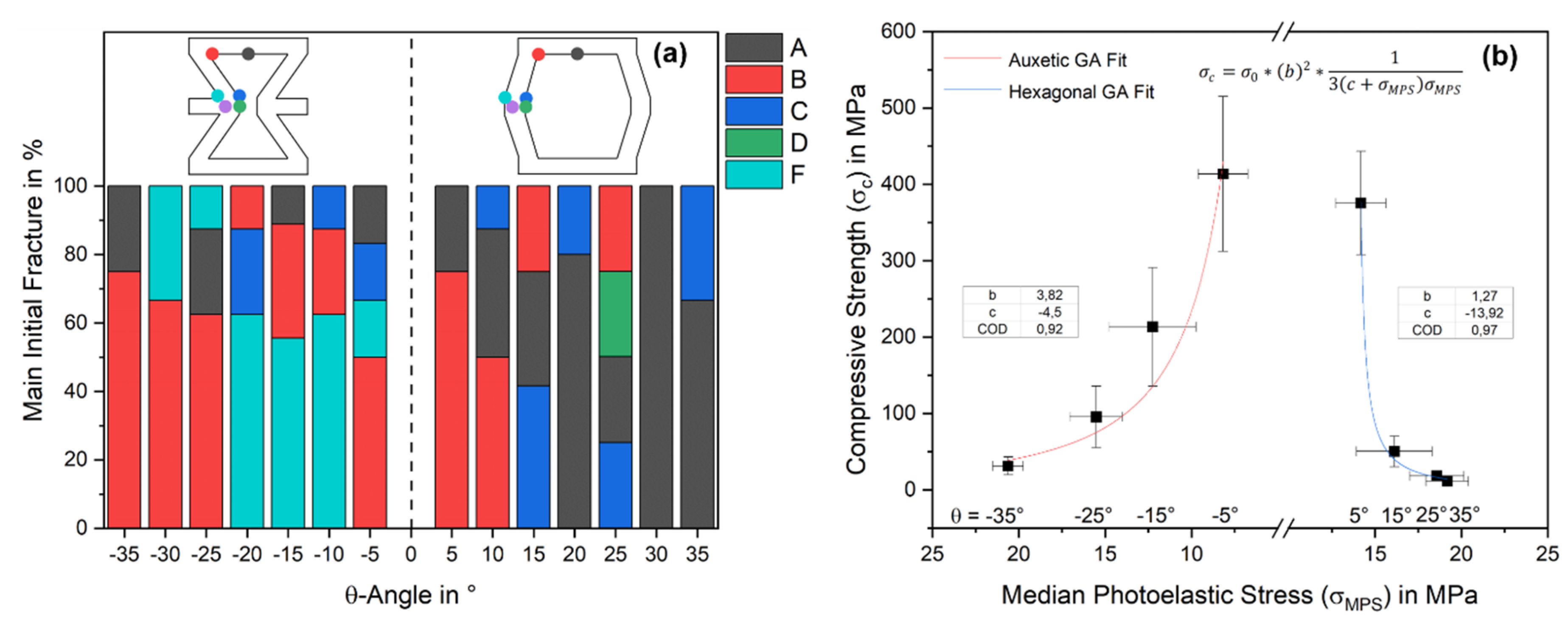
3.1. Influence of the θ-Angle on the Photoelastic Stresses
3.2. Structural Influence on Mechanical Properties
4. Conclusions
- Hexagonal and auxetic honeycomb unit cells were fabricated from epoxy and alumina with an θ-angle of −35 to +35;
- Critical stress points were identified by photoelastic measurements of epoxy, which closely matched those fracture points in the alumina determined by DIC;
- Smaller absolute angles showed more homogeneous stress distributions, which were also reflected in the compressive strengths of the alumina, with a maximum of 446 ± 156 MPa at 0°
- The most important achievement was the correlation of the photoelastic measurement of the epoxy with the compressive strength of the alumina by adapting the model from Gibson and Ashby.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassan, M.R.; Scarpa, F.; Mohamed, N.A. In-plane Tensile Behavior of Shape Memory Alloy Honeycombs with Positive and Negative Poisson’s Ratio. J. Intell. Mater. Syst. Struct. 2009, 20, 897–905. [Google Scholar] [CrossRef]
- Lakes, R. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Yang, W.; Li, Z.-M.; Shi, W.; Xie, B.-H.; Yang, M.-B. Review on auxetic materials. J. Mater. Sci. 2004, 39, 3269–3279. [Google Scholar] [CrossRef]
- Eichhorn, F.; Keppner, F.; Köllner, D.; Fey, T. Deformation Behavior of 2D Composite Cellular Lattices of Ceramic Building Blocks and Epoxy Resin. Adv. Eng. Mater. 2021, 24, 2100536. [Google Scholar] [CrossRef]
- Fey, T.; Eichhorn, F.; Han, G.; Ebert, K.; Wegener, M.; Roosen, A.; Kakimoto, K.; Greil, P. Mechanical and electrical strain response of a piezoelectric auxetic PZT lattice structure. Smart Mater. Struct. 2016, 25, 15017. [Google Scholar] [CrossRef]
- Grima, J.N.; Oliveri, L.; Attard, D.; Ellul, B.; Gatt, R.; Cicala, G.; Recca, G. Hexagonal Honeycombs with Zero Poisson’s Ratios and Enhanced Stiffness. Adv. Eng. Mater. 2010, 12, 855–862. [Google Scholar] [CrossRef]
- Abd El-Sayed, F.K.; Jones, R.; Burgess, I.W. A theoretical approach to the deformation of honeycomb based composite materials. Composites 1979, 10, 209–214. [Google Scholar] [CrossRef]
- Hoffman, G.A. Poisson’s Ratio for Honeycomb Sandwich Cores. J. Aerosp. Sci. 1958, 25, 534–535. [Google Scholar] [CrossRef]
- Masters, I.G.; Evans, K.E. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Balawi, S.; Abot, J.L. The effect of honeycomb relative density on its effective in-plane elastic moduli: An experimental study. Compos. Struct. 2008, 84, 293–299. [Google Scholar] [CrossRef]
- Scarpa, F.; Panayiotou, P.; Tomlinson, G. Numerical and experimental uniaxial loading on in-plane auxetic honeycombs. J. Strain Anal. Eng. Des. 2000, 35, 383–388. [Google Scholar] [CrossRef]
- Bezazi, A.; Scarpa, F.; Remillat, C. A novel centresymmetric honeycomb composite structure. Compos. Struct. 2005, 71, 356–364. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Puga, H.; Meireles, J. Positive, zero and negative Poisson’s ratio non-stochastic metallic cellular solids: Dependence between static and dynamic mechanical properties. Compos. Struct. 2019, 226, 111239. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids; Cambridge University Press: Cambridge, UK, 1997; ISBN 9780521499118. [Google Scholar]
- Mathieu, F.; Hild, F.; Roux, S. Identification of a crack propagation law by digital image correlation. Int. J. Fatigue 2012, 36, 146–154. [Google Scholar] [CrossRef] [Green Version]
- Carroll, J.D.; Abuzaid, W.; Lambros, J.; Sehitoglu, H. High resolution digital image correlation measurements of strain accumulation in fatigue crack growth. Int. J. Fatigue 2013, 57, 140–150. [Google Scholar] [CrossRef]
- Bu, J.; Chen, X.; Hu, L.; Yang, H.; Liu, S. Experimental Study on Crack Propagation of Concrete Under Various Loading Rates with Digital Image Correlation Method. Int. J. Concr. Struct. Mater. 2020, 14, 25. [Google Scholar] [CrossRef]
- Bhosale, A.B.; Prakash, S.S. Crack Propagation Analysis of Synthetic vs. Steel vs. Hybrid Fibre-Reinforced Concrete Beams Using Digital Image Correlation Technique. Int. J. Concr. Struct. Mater. 2020, 14, 57. [Google Scholar] [CrossRef]
- Fey, T.; Götz, M.; Greil, P. Photoelastic Imaging of Residual Stress Distribution in Epoxy Interface Layers of Ceramics with Periodic Building-Block Structure. Adv. Eng. Mater. 2013, 15, 1099–1104. [Google Scholar] [CrossRef]
- Bombolakis, E.G. Photoelastic investigation of brittle crack growth within a field of uniaxial compression. Tectonophysics 1964, 1, 343–351. [Google Scholar] [CrossRef]
- Bradley, W.B.; Kobayashi, A.S. An investigation of propagating cracks by dynamic photoelasticity. Exp. Mech. 1970, 10, 106–113. [Google Scholar] [CrossRef]
- Smith, C.W. Photoelasticity in fracture mechanics. Exp. Mech. 1980, 20, 390–396. [Google Scholar] [CrossRef]
- Kobayashi, T.; Dally, J.W. A system of modified epoxies for dynamic photoelastic studies of fracture. Exp. Mech. 1977, 17, 367–374. [Google Scholar] [CrossRef]
- Patterson, E.A. Digital Photoelasticity: Principles, Practice and Potential. Strain 2002, 38, 27–39. [Google Scholar] [CrossRef]
- Ramesh, K.; Ramakrishnan, V. Digital photoelasticity of glass: A comprehensive review. Opt. Lasers Eng. 2016, 87, 59–74. [Google Scholar] [CrossRef]
- MacKenzie, H.W.; Hand, R.J. Basic Optical Stress Measurement in Glass; Society of Glass Technology: Sheffield, UK, 1999; ISBN 0900682272. [Google Scholar]
- Alsiya, S.; Lekshmi, C.J.; Priya, B.P.J.; Mehta, R.C. Image Processing Algorithm for Fringe Analysis in Photoelasticity. SJET 2016, 4, 325–328. [Google Scholar] [CrossRef]
- Telle, R. Keramik, 7th ed.; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 3-540-63273-5. [Google Scholar]
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mülhaupt, R. Polymers for 3D Printing and Customized Additive Manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. Part B Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- OpenSCAD. Available online: https://openscad.org/ (accessed on 24 January 2022).
- Biggemann, J.; Diepold, B.; Pezoldt, M.; Stumpf, M.; Greil, P.; Fey, T. Automated 3D assembly of periodic alumina-epoxy composite structures. J. Am. Ceram. Soc. 2018, 101, 3864–3873. [Google Scholar] [CrossRef]
- Biggemann, J.; Pezoldt, M.; Stumpf, M.; Greil, P.; Fey, T. Modular ceramic scaffolds for individual implants. Acta Biomater. 2018, 80, 390–400. [Google Scholar] [CrossRef]
- Theocaris, P.S.; Prassianakis, J. Interrelation of mechanical and optical properties of plasticized epoxy polymers. J. Appl. Polym. Sci. 1978, 22, 1725–1734. [Google Scholar] [CrossRef]
- Theocaris, P.S. Viscoelastic properties of epoxy resins derived from creep and relaxation tests at different temperatures. Rheol Acta 1962, 2, 92–96. [Google Scholar] [CrossRef]
- Aben, H.; Ainola, L. Isochromatic fringes in photoelasticity. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2000, 17, 750–755. [Google Scholar] [CrossRef]
- Ramesh, K.; Mangal, S.K. Data acquisition techniques in digital photoelasticity: A review. Opt. Lasers Eng. 1998, 30, 53–75. [Google Scholar] [CrossRef]
- Petersen; Link, R.E.; Gomez, J.T.; Shukla, A.; Sharma, A. Photoelastic Evaluation of Stress Fields and Fracture During Dynamic Splitting Experiments. J. Test. Eval. 2002, 30, 186. [Google Scholar] [CrossRef]
- Hou, X.; Deng, Z.; Zhang, K. Dynamic Crushing Strength Analysis of Auxetic Honeycombs. Acta Mech. Solida Sin. 2016, 29, 490–501. [Google Scholar] [CrossRef]
- Attard, D.; Grima, J.N. Modelling of hexagonal honeycombs exhibiting zero Poisson’s ratio. Phys. Status Solidi 2011, 248, 52–59. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Köllner, D.; Tolve-Granier, B.; Simon, S.; Kakimoto, K.-i.; Fey, T. Advanced Estimation of Compressive Strength and Fracture Behavior in Ceramic Honeycombs by Polarimetry Measurements of Similar Epoxy Resin Honeycombs. Materials 2022, 15, 2361. https://doi.org/10.3390/ma15072361
Köllner D, Tolve-Granier B, Simon S, Kakimoto K-i, Fey T. Advanced Estimation of Compressive Strength and Fracture Behavior in Ceramic Honeycombs by Polarimetry Measurements of Similar Epoxy Resin Honeycombs. Materials. 2022; 15(7):2361. https://doi.org/10.3390/ma15072361
Chicago/Turabian StyleKöllner, David, Bastien Tolve-Granier, Swantje Simon, Ken-ichi Kakimoto, and Tobias Fey. 2022. "Advanced Estimation of Compressive Strength and Fracture Behavior in Ceramic Honeycombs by Polarimetry Measurements of Similar Epoxy Resin Honeycombs" Materials 15, no. 7: 2361. https://doi.org/10.3390/ma15072361
APA StyleKöllner, D., Tolve-Granier, B., Simon, S., Kakimoto, K.-i., & Fey, T. (2022). Advanced Estimation of Compressive Strength and Fracture Behavior in Ceramic Honeycombs by Polarimetry Measurements of Similar Epoxy Resin Honeycombs. Materials, 15(7), 2361. https://doi.org/10.3390/ma15072361






