Characterisation and Comparison of Material Parameters of 3D-Printable Absorbing Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials Used
2.2. Sample Preparation
- a rectangular waveguide resonator;
- a coaxial transmission line;
- a piece of rectangular waveguide.
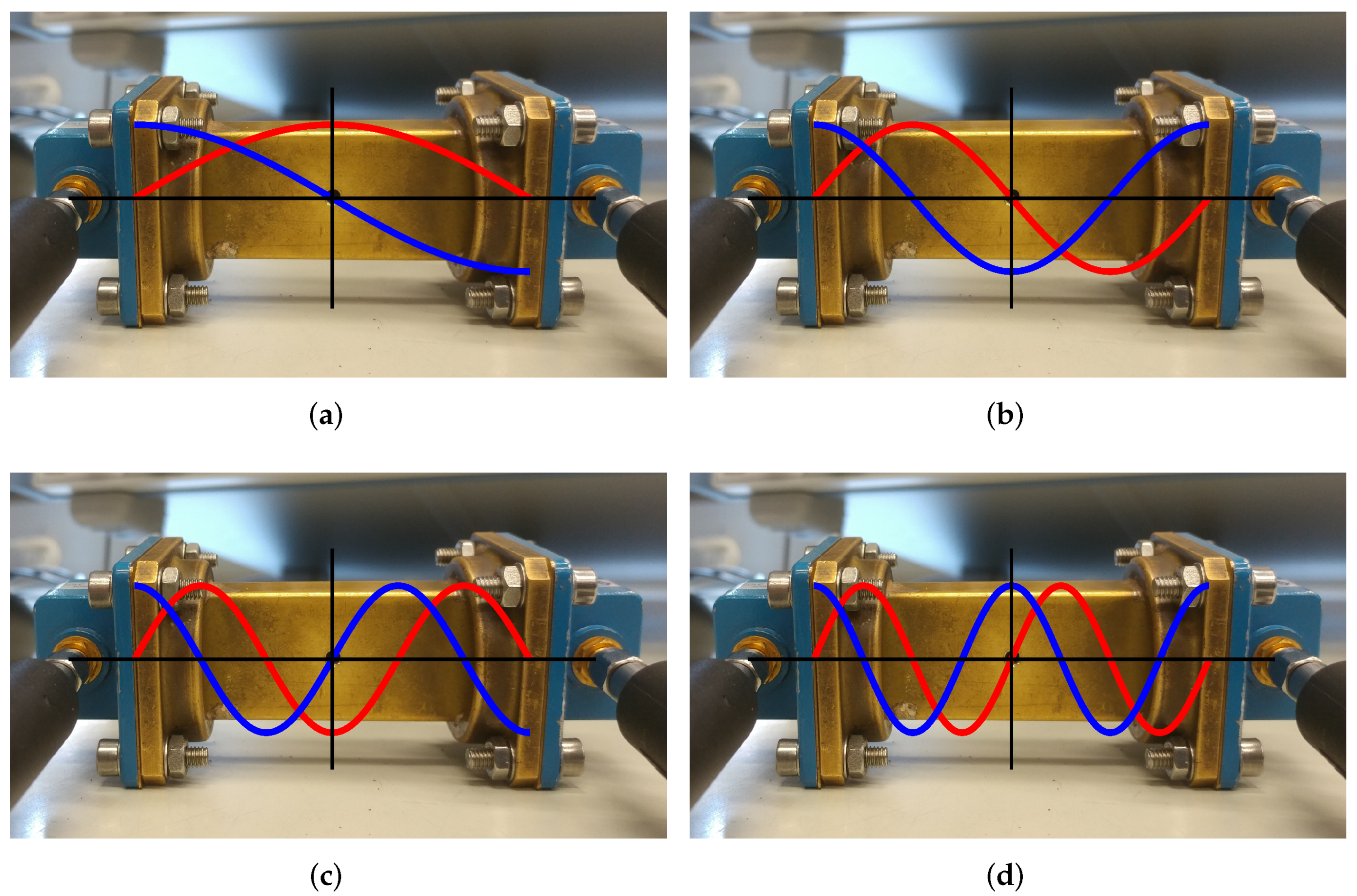
2.2.1. Resonator Samples
2.2.2. Coaxial Samples
2.2.3. Waveguide Samples
2.2.4. Samples for SEM Imaging
2.3. Material Parameter Extraction
2.3.1. Resonator Method
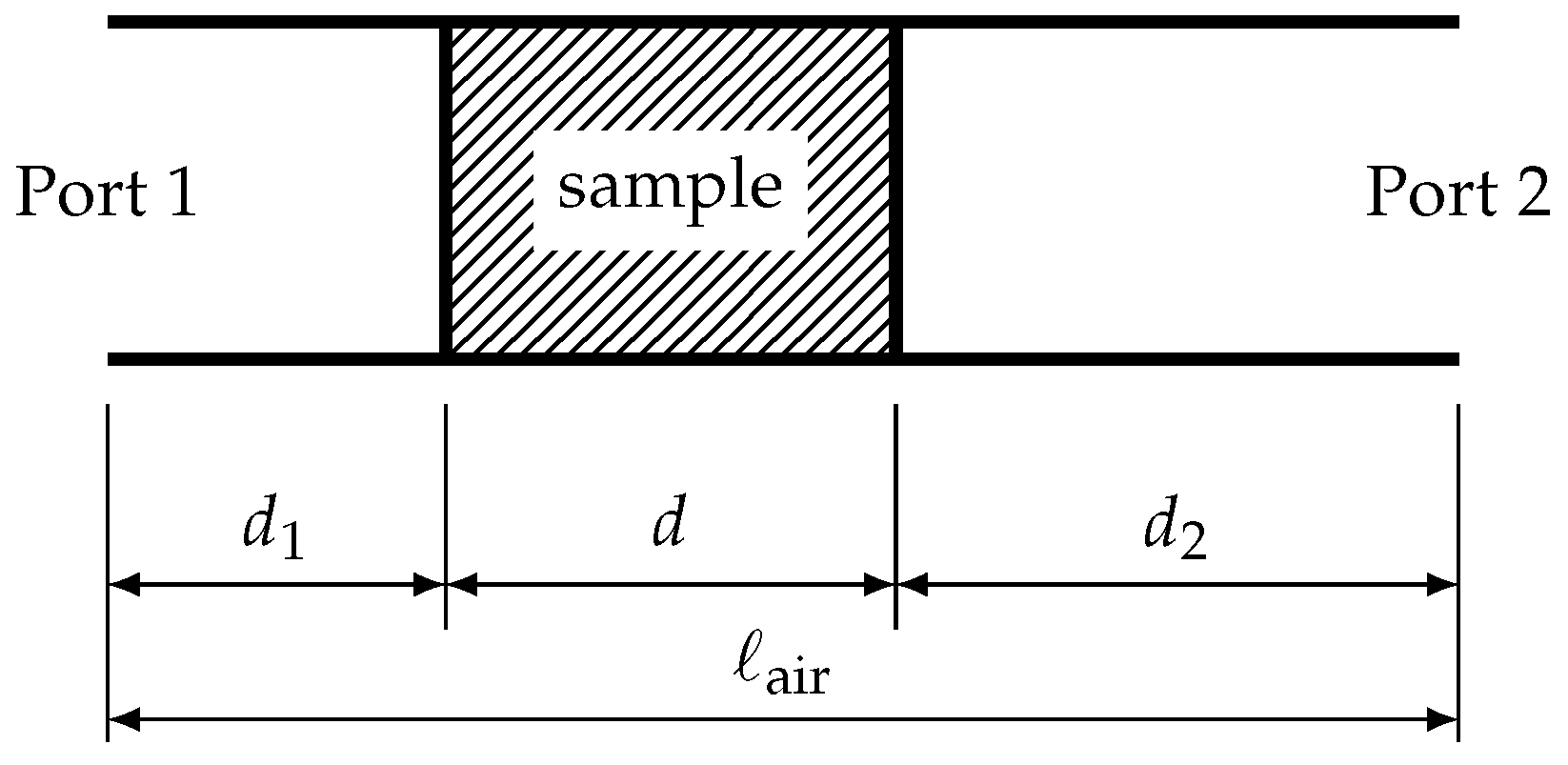
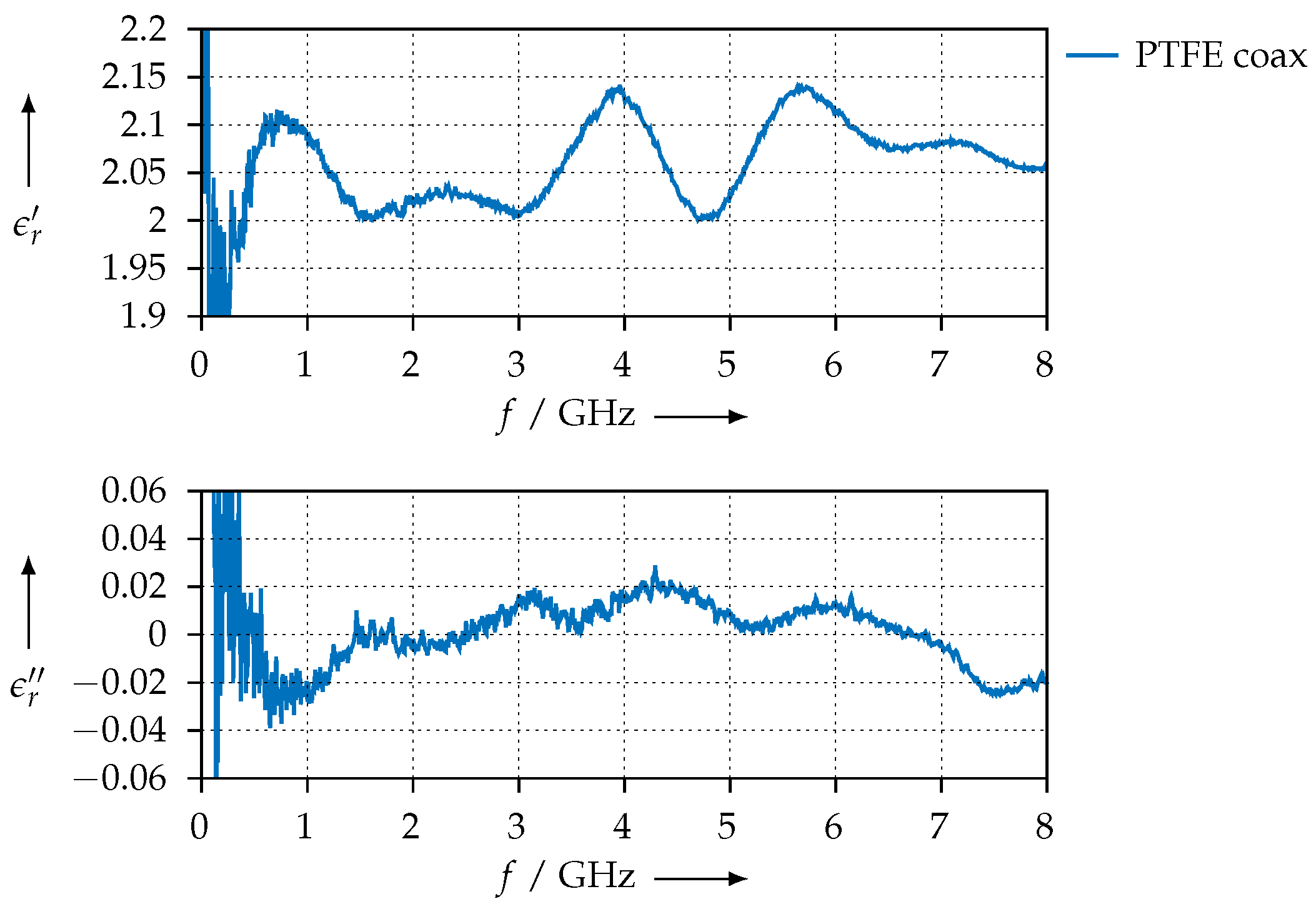
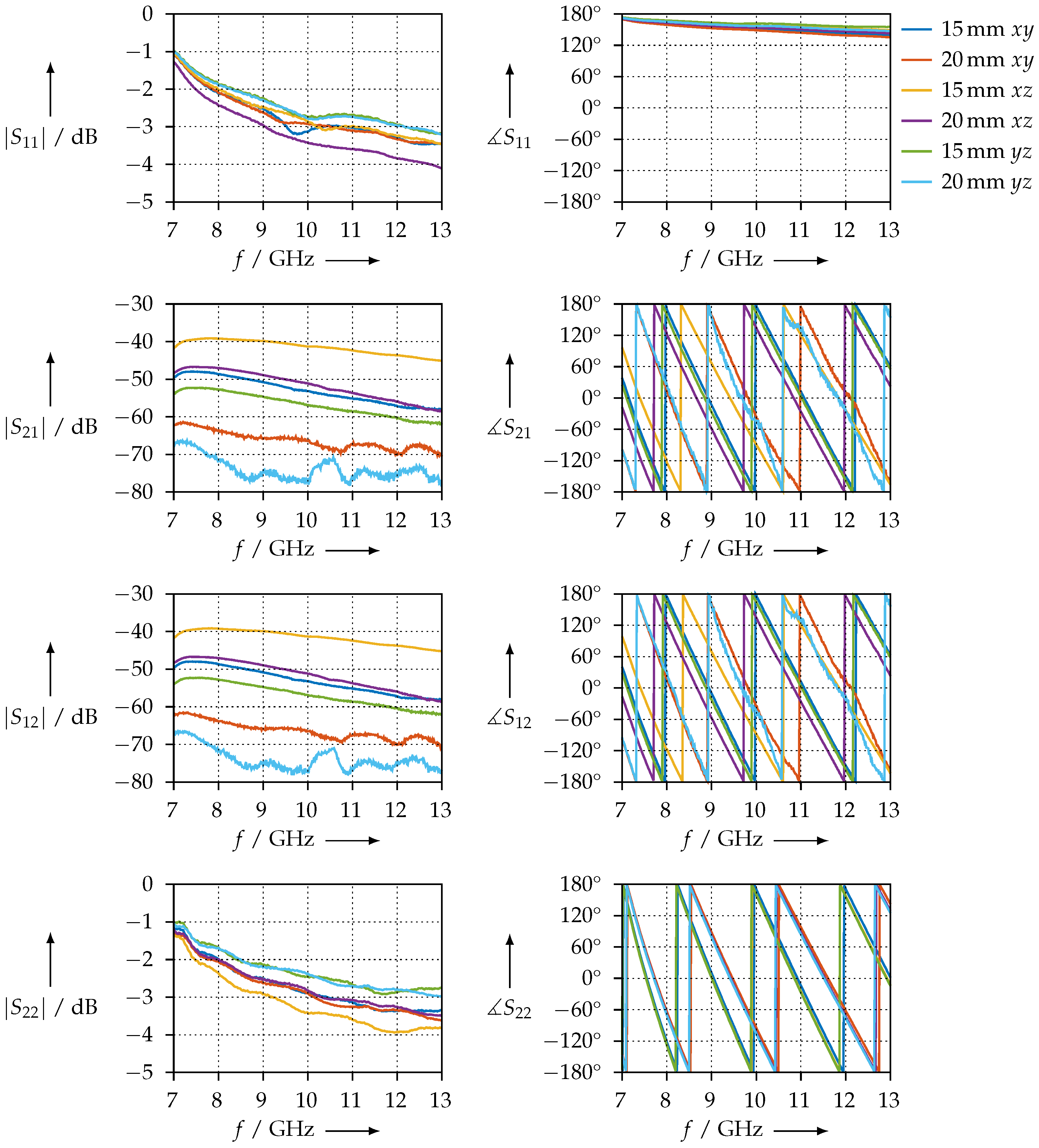
2.3.2. Transmission/Reflection Method
- the magnitude of and should be equal, i.e., the sample should have the same reflection coefficient, no matter the direction from which the waves travel;
- the magnitude and phase of and should be equal, i.e., the transmission through the samples does not depend on the direction.
2.4. Considerations in the Context of Anisotropic Material Parameters
2.5. Overview of Samples Prepared
3. Results
3.1. Microscope Images
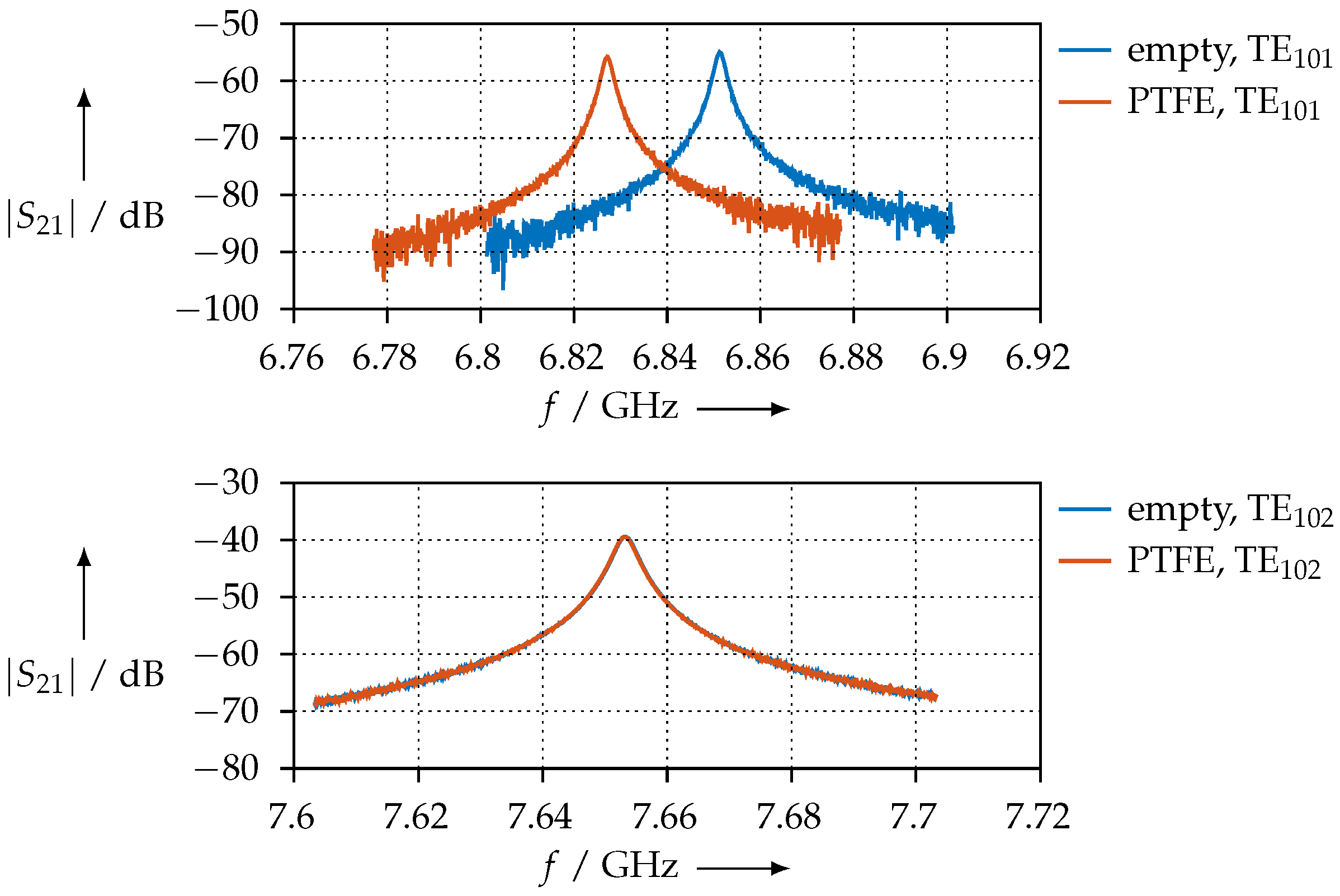
3.2. Resonator Measurements
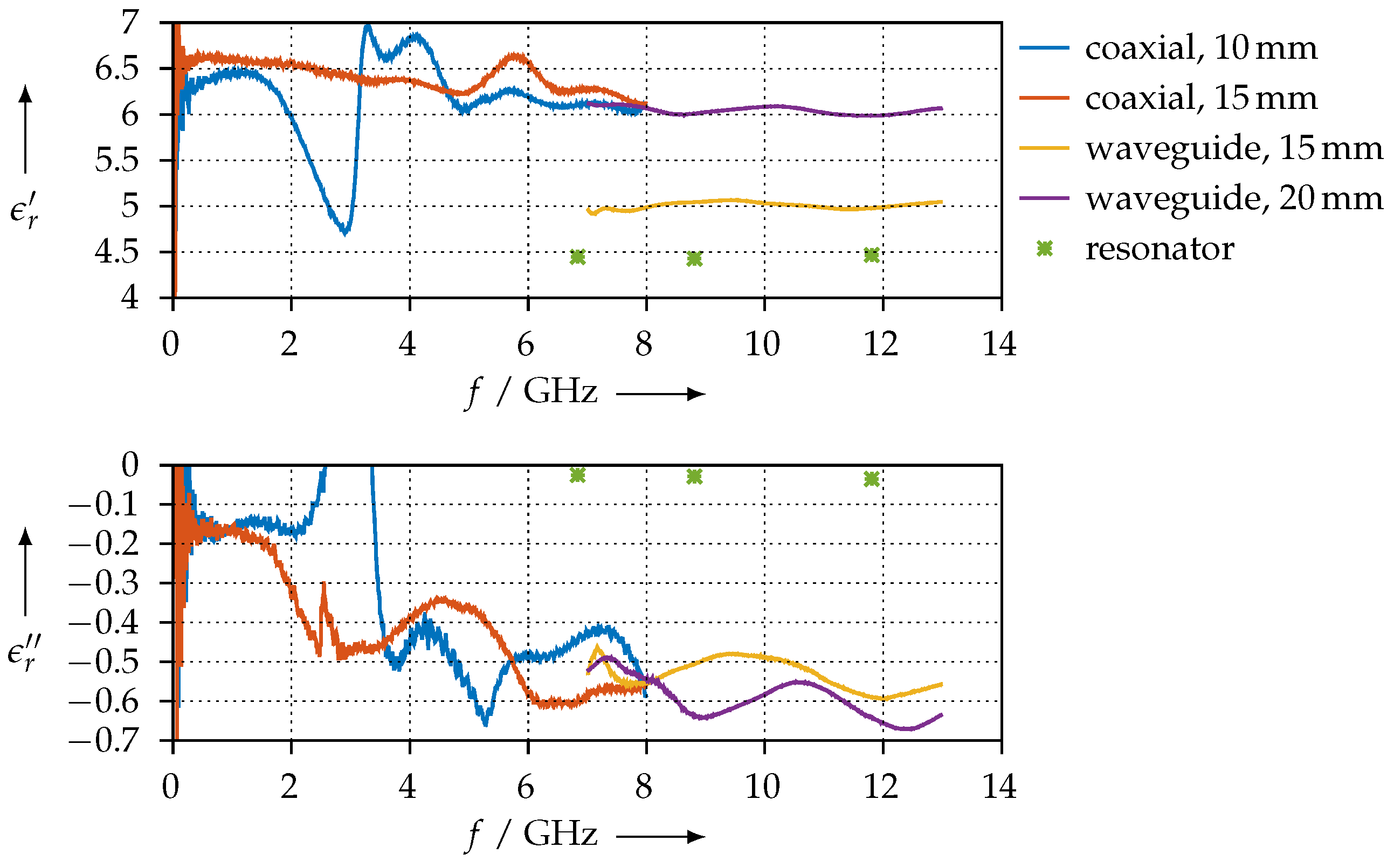
- For the PLA sample, the permittivity we found is close to the literature values; see Section 3.3.1;
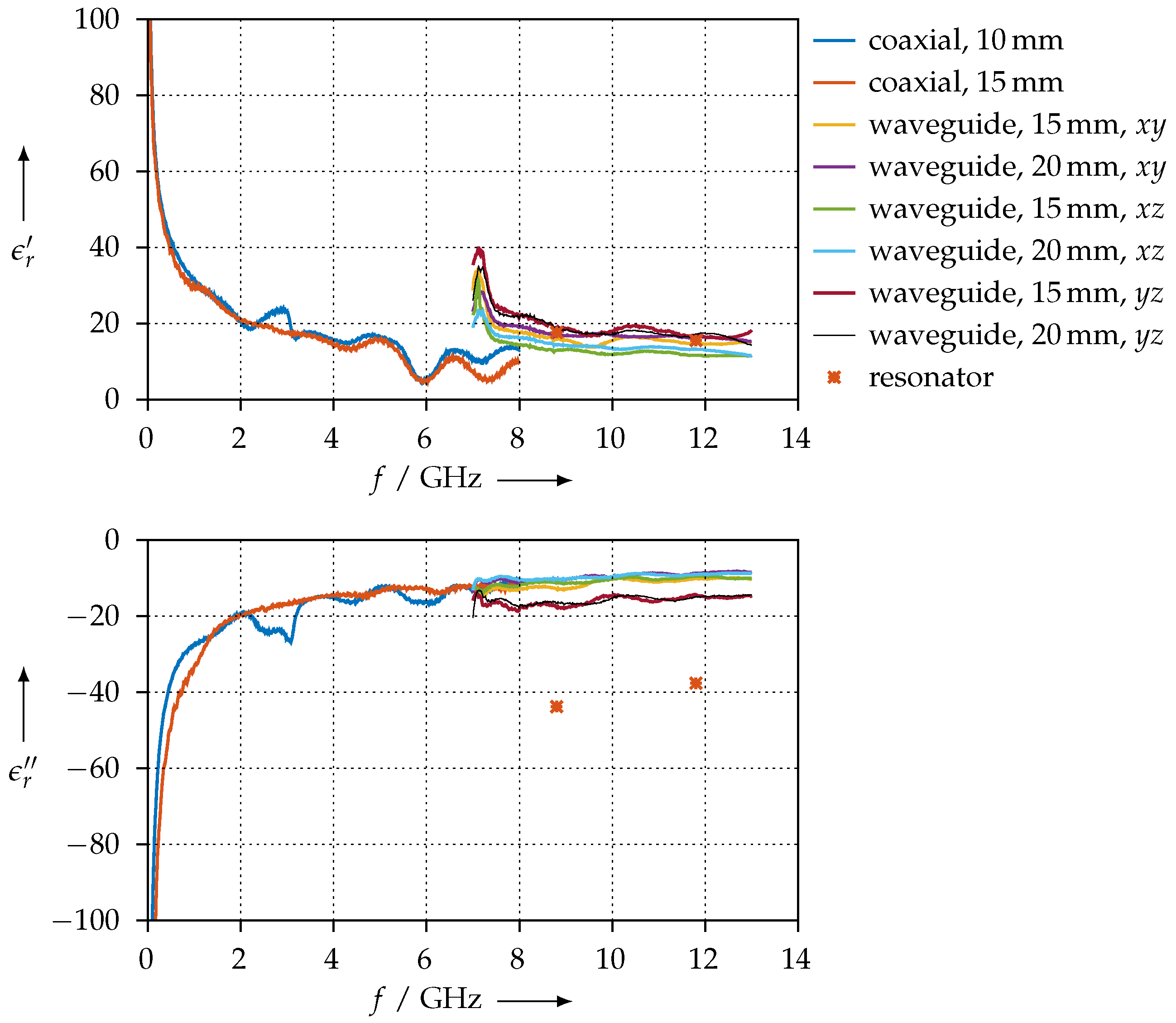
- As the CDP material is PLA with carbon loading, we expect no magnetic effects. Indeed, is close to 1 and is close to 0. Therefore, we can indeed conclude that no magnetic effects are present in this material; the fact that our is different from 1 is likely due to measurement errors. On the other hand, we have two measurements of and , both of which are quite close together. When of CDP is compared to the other materials, we see that the losses of the CDP material are much larger than for all other materials. The losses are so high that we were unable to reliably measure a resonance for the TE mode. Additionally, the difference between the TE and TE is larger when compared to the other materials; the reason for this is the increase in the numeric errors when the and are determined from weak resonances;
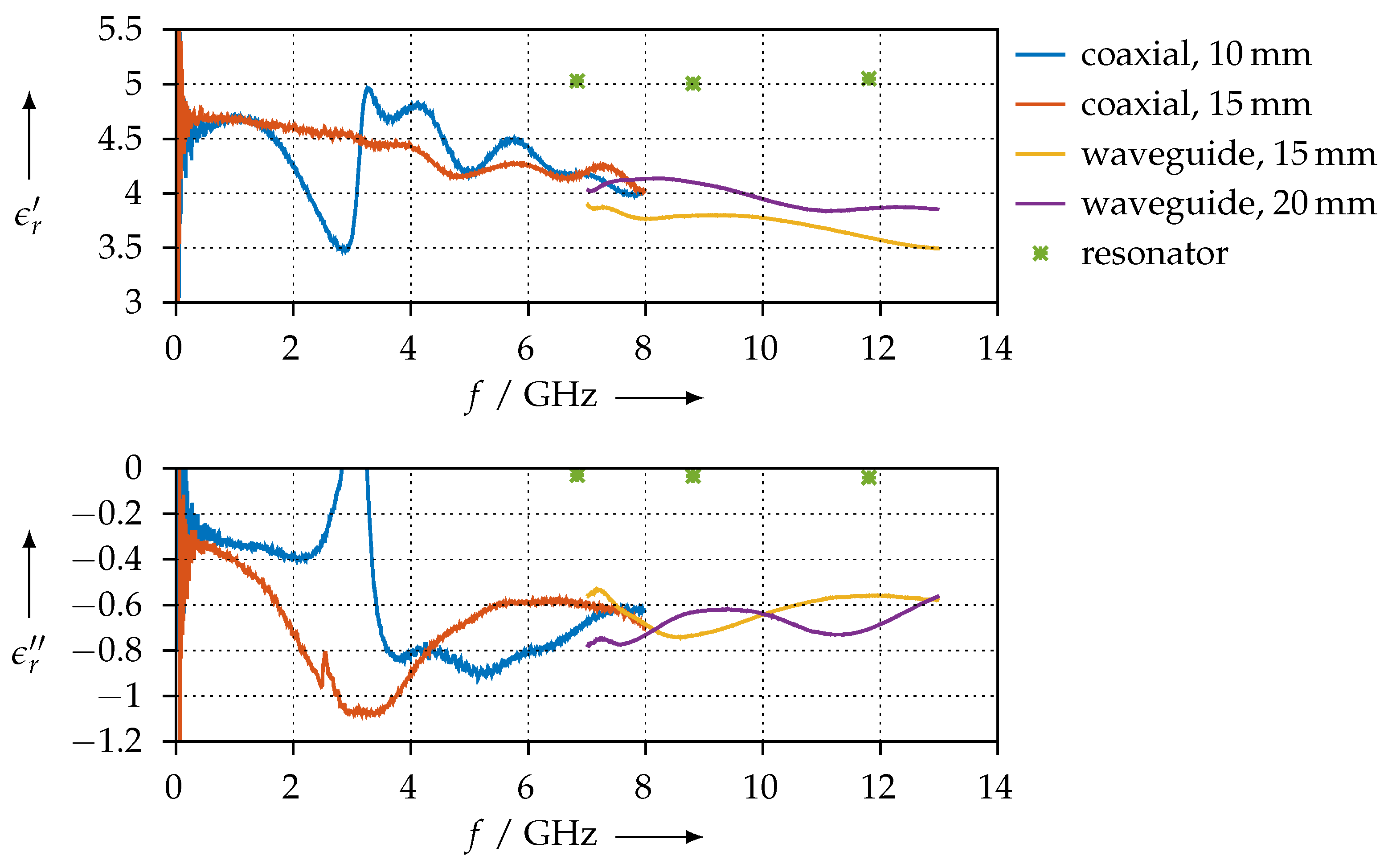
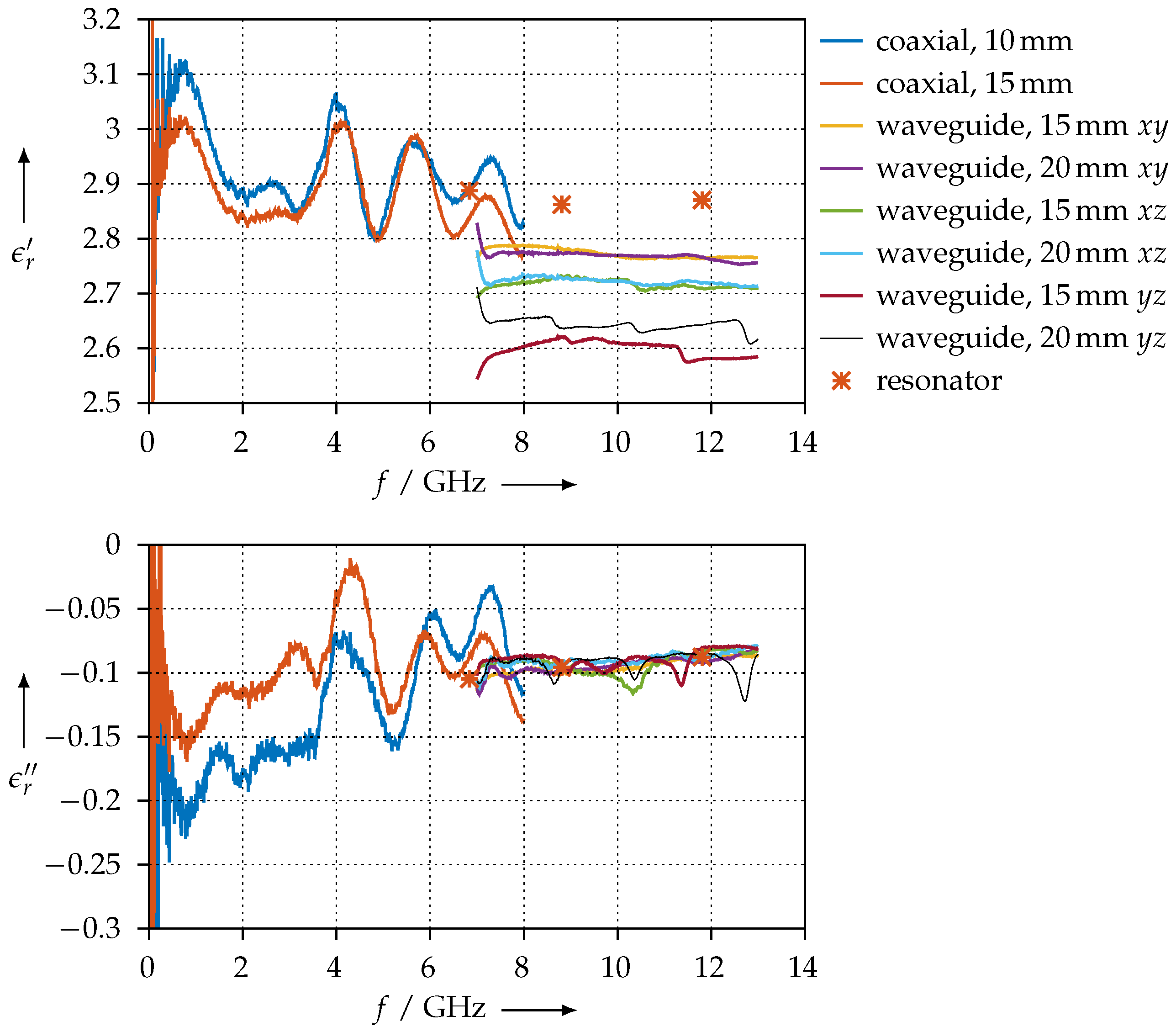
- For the FEP material, we see that the permittivity measurements all agree very well with each other. Since FEP is a PLA matrix which is loaded with iron powder, magnetic effects could be expected to some degree; we see that there is a certain amount of magnetic loss, as is clearly greater than zero. Furthermore, we also see that is slightly smaller than 1, i.e., the material is only slightly magnetic. The order of magnitude for our and is comparable to the one that others report for similar materials [27];
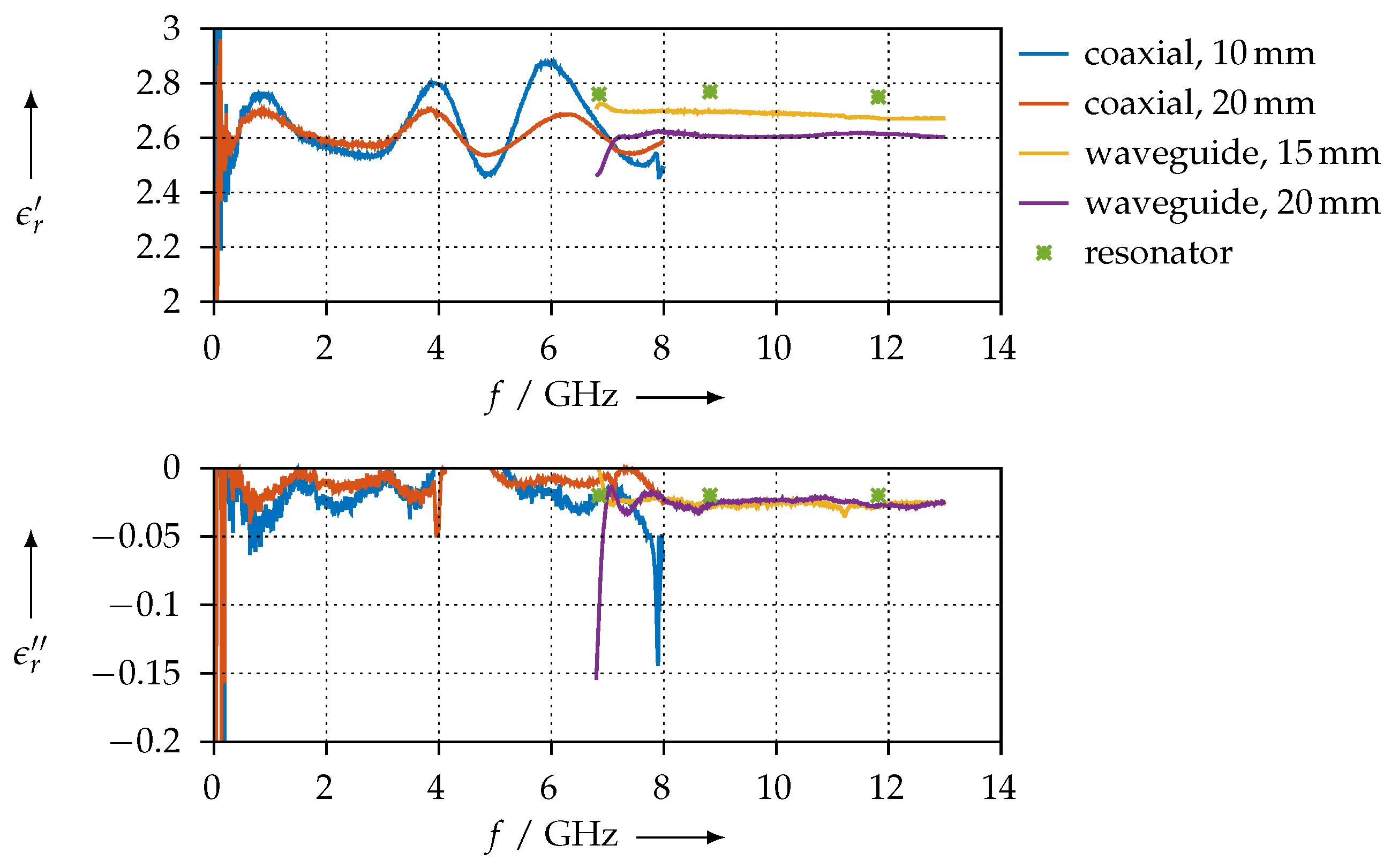
- The SSP material is PLA loaded with stainless steel powder. We can see that is closer to 1 than for the FEP, i.e., magnetic effects are weaker for the SSP material, which makes sense, as stainless steel is generally nonmagnetic or only weakly magnetic compared to iron. Furthermore we also see that the magnetic losses are smaller than for FEP, which is again consistent with the fact that stainless steel has fewer magnetic properties than iron;
- For the KIM material, we see that all permittivity measurements agree well with each other. The permeability is close to 1, from which we conclude that this material is nonmagnetic.
3.3. Permittivity
3.3.1. Pure PLA
3.3.2. FEP Material
- 1.
- We can assume and calculate ;
- 2.
- We can calculate both and at the same time.
3.3.3. SSP Material
3.3.4. SAAB Material
3.3.5. Anisotropic Measurements
4. Discussion
4.1. Measurement Consistency
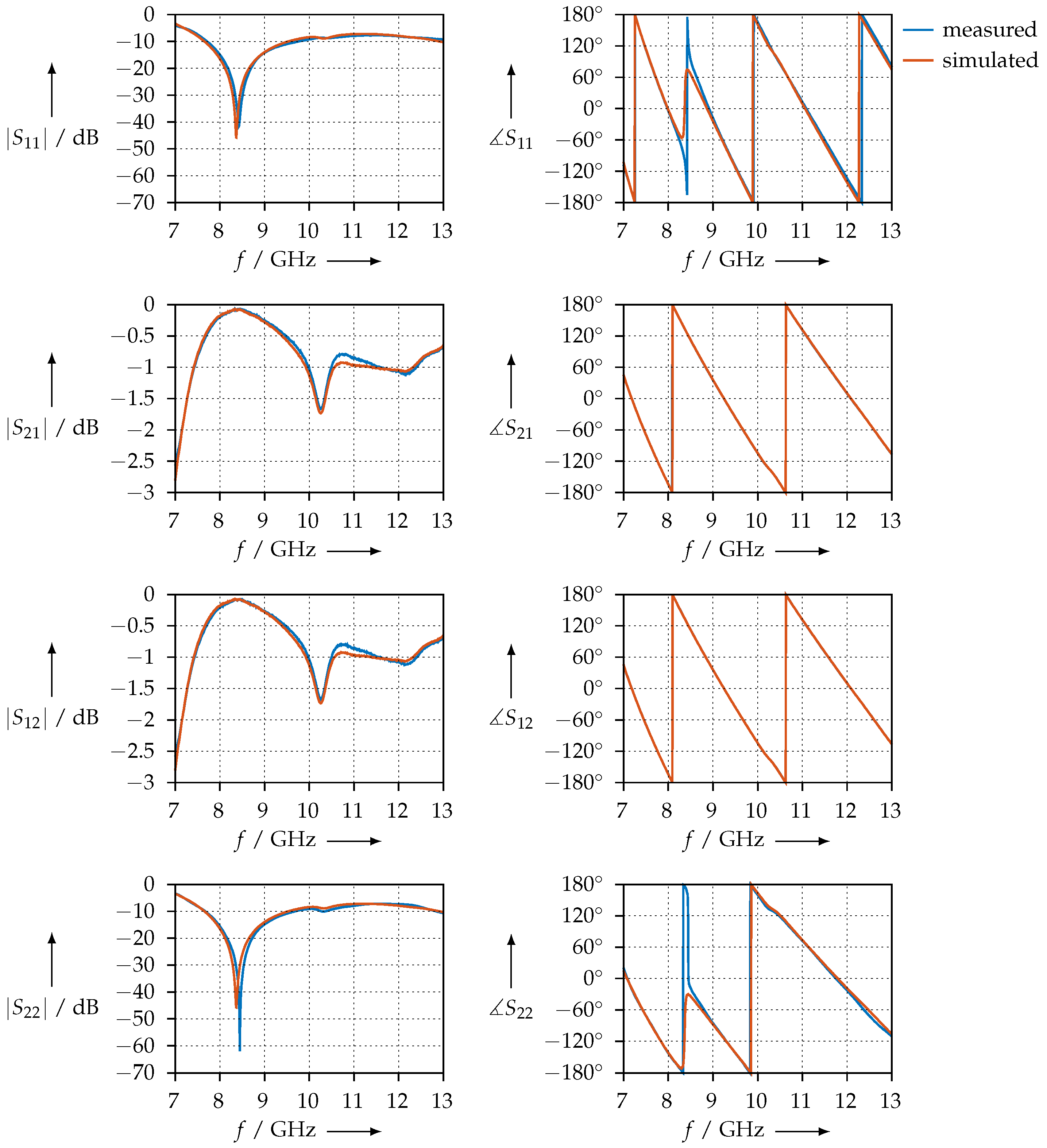
4.2. Agreement of the Methods and Measurement Error Estimation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABS | acrylnitrile butadiene styrene |
| DC | direct current |
| FFF | fused filament fabrication |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MUT | material under test |
| PLA | polylactic acid |
| PTFE | polytetrafluoroethylene |
| RFI | radio frequency interference |
| SEM | scanning electron microscope |
| TE | transverse electric |
| TEM | transverse electromagnetic |
| MSDS | material safety data sheet |
References
- Jacob, K.; Schröder, A.; Murk, A. Design, Manufacturing, and Characterization of Conical Blackbody Targets With Optimized Profile. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 76–84. [Google Scholar] [CrossRef]
- Yagoubov, P.; Murk, A.; Wylde, R.; Bell, G.; Tan, G.H. Calibration loads for ALMA. In Proceedings of the 2011 International Conference on Infrared, Millimeter, and Terahertz Waves, Houston, TX, USA, 2–7 October 2011. [Google Scholar]
- Arbaoui, Y.; Laur, V.; Maalouf, A.; Quéffélec, P.; Passerieux, D.; Delias, A.; Blondy, P. Full 3-D Printed Microwave Termination: A Simple and Low-Cost Solution. IEEE Trans. Microw. Theory Tech. 2016, 64, 271–278. [Google Scholar] [CrossRef]
- Márquez-Segura, E.; Shin, S.; Dawood, A.; Ridler, N.M.; Lucyszyn, S. Microwave Characterization of Conductive PLA and Its Application to a 12 to 18 GHz 3-D Printed Rotary Vane Attenuator. IEEE Access 2021, 9, 84327–84343. [Google Scholar] [CrossRef]
- Kjelgård, K.G.; Wisland, D.T.; Lande, T.S. 3D Printed Wideband Microwave Absorbers using Composite Graphite/PLA Filament. In Proceedings of the European Microwave Conference (EuMC), Madrid, Spain, 23–27 September 2018; pp. 859–862. [Google Scholar]
- Sapritsky, V.; Prokhorov, A. Blackbody Radiometry. Volume 1: Fundamentals; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Zivkovic, I.; Murk, A. Characterization of Magnetically Loaded Microwave Absorbers. Prog. Electromagn. Res. B 2011, 33, 277–289. [Google Scholar] [CrossRef][Green Version]
- Wollack, E.J.; Fixsen, D.J.; Henry, R.; Kogut, A.; Limon, M.; Mirel, P. Electromagnetic and Thermal Properties of a Conductively Loaded Epoxy. Int. J. Infrared Milli. Waves 2008, 29, 51–61. [Google Scholar] [CrossRef]
- Lönnqvist, A.; Tamminen, A.; Mallat, J.; Räisänen, A.V. Monostatic Reflectivity Measurement of Radar Absorbing Materials at 310 GHz. IEEE Trans. Microw. Theory Tech. 2006, 9, 3486–3491. [Google Scholar] [CrossRef]
- Jacob, K.; Schröder, A.; von Werra, L.; Reinhard, F.; Raisin, P.; Murk, A. Radiometric Characterization of a Water-Based Conical Blackbody Calibration Target for Millimeter-Wave Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1688–1696. [Google Scholar] [CrossRef]
- Petroff, M.; Appel, J.; Rostem, K.; Bennet, C.L.; Eimer, J.; Marriage, T.; Ramirez, J.; Wollack, E.J. A 3D-printed broadband millimeter wave absorber. Rev. Sci. Instrum. 2019, 90, 024701. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Yan, L.; Ma, H.; Fan, Y.; Wang, J.; Feng, M.; Qu, S. Electromagnetic wave absorption and compressive behavior of a three-dimensional metamaterial absorber based on 3D printed honeycomb. Sci. Rep. 2018, 8, 4817. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Shang, X.; Ridler, N.M.; Lucyszyn, S. Polymer-Based 3-D Printed 140-220 GHz Low-Cost Quasi-Optical Components and Integrated Subsystem Assembly. IEEE Access 2021, 9, 28020–28038. [Google Scholar] [CrossRef]
- Proto-Pasta Material Safety Datasheets. Available online: https://www.proto-pasta.com/pages/documentation (accessed on 18 January 2022).
- Costa, F.; Borgese, M.; Degiorgi, M.; Monorchio, A. Electromagnetic Characterisation of Materials by Using Transmission/Reflection (T/R) Devices. Electronics 2017, 6, 95. [Google Scholar] [CrossRef]
- Lee, C.; McGhee, J.; Tsipogiannis, C.; Zhang, S.; Cadman, D.; Goulas, A.; Whittaker, T.; Gheisari, R.; Engstrom, D.; Vardaxoglou, J.; et al. Evaluation of Microwave Characterization Methods for Additively Manufactured Materials. Designs 2019, 3, 47. [Google Scholar] [CrossRef]
- Yang, R.B.; Tsay, C.Y.; Hung, D.S.; Liang, W.F.; Yao, Y.D.; Lin, C.K. Complex permittivity and permeability of iron-based composite absorbers measured by cavity perturbation method in X-band frequency range. J. Appl. Phys. 2009, 105, 07A528. [Google Scholar] [CrossRef]
- Harrington, R.F. Time-Harmonic Electromagnetic Fields; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Wypych, G. Handbook of Polymers; Elsevier: Toronto, ON, Canada, 2016. [Google Scholar]
- Middleton, W.M. (Ed.) Reference Data for Engineers: Radio, Electronics, Computer, and Communications, 9th ed.; Newnes: Oxford, UK; Boston, UK, 2002. [Google Scholar]
- EpsiMu–Permeability and Dielectric Permittivity Measurements. Available online: https://www.epsimu.com/ (accessed on 26 November 2021).
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mathew, K.T. Perturbation Theory. In Encyclopedia of RF and Microwave Engineering; Mathew, K.T., Ed.; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Raveendranath, U.; Matthew, K.T. New Cavity Perturbation Technique for Measuring Complex Permeability of Ferrite Materials. Microwave Opt. Technol. Lett. 1998, 18, 241–243. [Google Scholar] [CrossRef]
- Petersan, P.J. Measurement of Resonant Frequency and Quality Factor of Microwave Resonators: Comparison of Methods. J. Appl. Phys. 1998, 84, 3392–3402. [Google Scholar] [CrossRef]
- Baker-Jarvis, J.; Vanzura, E.J.; Kissick, W.A. Improved technique for determining complex permittivity with the transmission/reflection method. IEEE Trans. Microw. Theory Tech. 1990, 38, 1096–1103. [Google Scholar] [CrossRef]
- Guan, X.; Xu, X.; Kuniyoshi, R.; Zhou, H.; Zhu, Y. Electromagnetic and mechanical properties of carbonyl iron powders-PLA composites fabricated by fused deposition modeling. Mater. Res. Express 2018, 5, 115303. [Google Scholar] [CrossRef]
- Zechmeister, J.; Lacik, J. Complex Relative Permittivity Measurement of Selected 3D-Printed Materials up to 10 GHz. In Proceedings of the 2019 Conference on Microwave Techniques (COMITE), Pardubice, Czech Republic, 16–18 April 2019. [Google Scholar]
- Dichtl, C.; Sippel, P.; Krohns, S. Dielectric Properties of 3D Printed Polylactic Acid. Adv. Mater. Sci. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- Kalaš, D.; Šíma, K.; Kadlec, P.; Polanský, R.; Soukup, R.; Řeboun, J.; Hamáček, A. FFF 3D Printing in Electronic Applications: Dielectric and Thermal Properties of Selected Polymers. Polymers 2021, 13, 3702. [Google Scholar] [CrossRef] [PubMed]













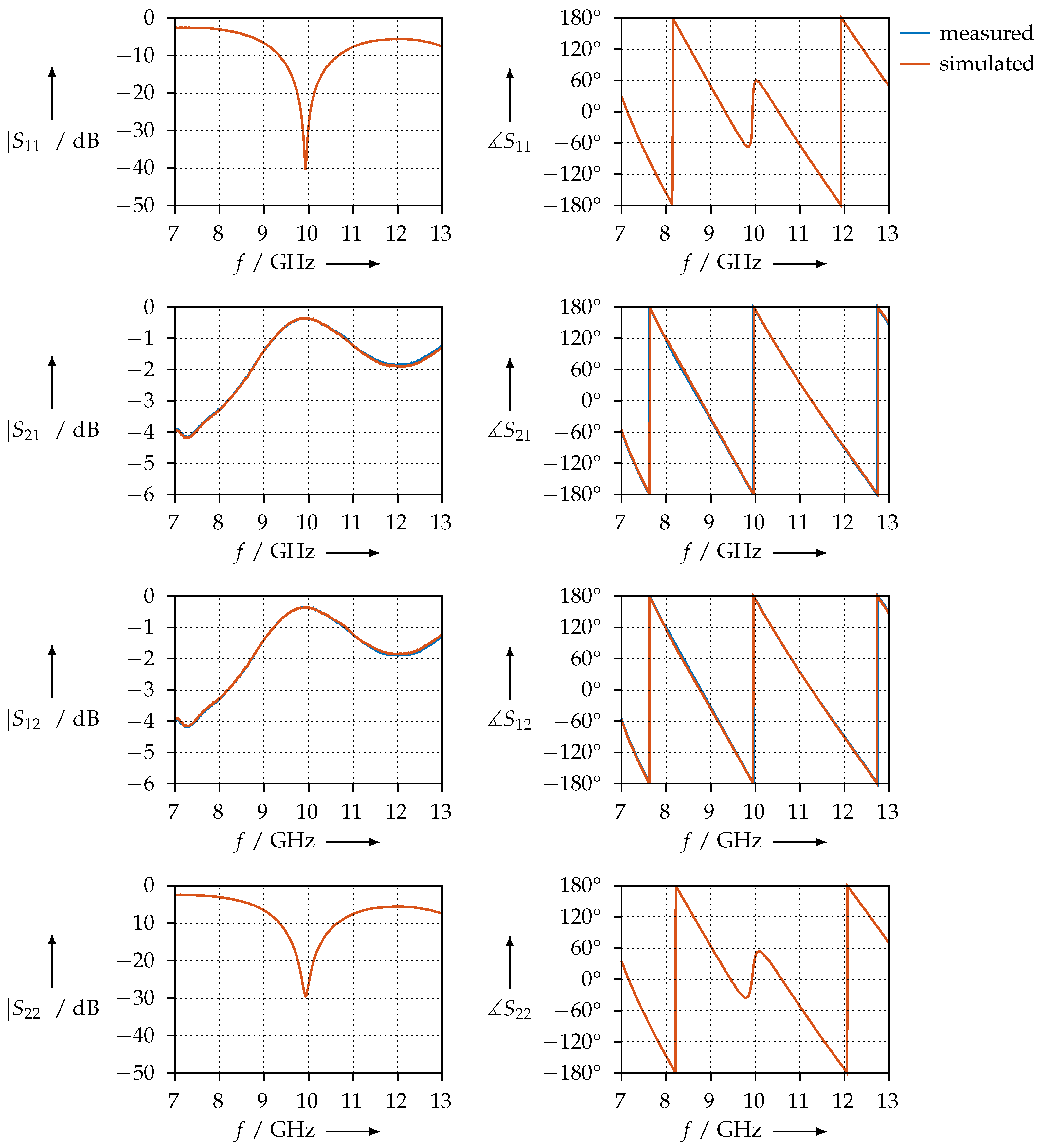



| Abbreviation | Material | Filler | Filler wt% | Matrix |
|---|---|---|---|---|
| PLA | Flashforge PLA standard filament | none | none | PLA |
| CDP | Protopasta CDP12805 | carbon black | <35 | PLA |
| FEP | Protopasta FEP12805 | iron | <45 | PLA |
| SSP | Protopasta SSP12805 | stainless steel | >60 | PLA |
| SAAB | SAAB Barracuda RAM filament | N/A | N/A | N/A |
| KIM | Kimya ABS-ESD Black 3D filament | none | none | ABS |
| Sample | Mode | or (GHz) | or | ||||
|---|---|---|---|---|---|---|---|
| empty | TE | 6.851277 | 2753 | ||||
| empty | TE | 7.653260 | 2052 | ||||
| empty | TE | 8.827069 | 1492 | ||||
| empty | TE | 10.245652 | 1101 | ||||
| empty | TE | 11.82682 | 1286 | ||||
| PTFE | TE | 6.827127 | 2749 | 2.0245 | |||
| PTFE | TE | 7.653156 | 2048 | 1.0070 | |||
| PTFE | TE | 8.796516 | 1487 | 2.0059 | |||
| PTFE | TE | 10.245335 | 1101 | 1.0070 | 0 | ||
| PTFE | TE | 11.785624 | 1280 | 2.0125 |
| Material | Type | Orientation | Length (mm) | Diameter (mm) |
|---|---|---|---|---|
| PLA | waveguide | 15 | ||
| PLA | waveguide | 20 | ||
| PLA | coaxial | — | 10 | |
| PLA | coaxial | — | 20 | |
| PLA | resonator | — | 0.6 | |
| CDP | waveguide | 15 | ||
| CDP | waveguide | 20 | ||
| CDP | waveguide | 15 | ||
| CDP | waveguide | 20 | ||
| CDP | waveguide | 15 | ||
| CDP | waveguide | 20 | ||
| CDP | coaxial | — | 10 | |
| CDP | coaxial | — | 15 | |
| CDP | resonator | — | 30 | 0.4 |
| FEP | waveguide | 15 | ||
| FEP | waveguide | 20 | ||
| FEP | coaxial | — | 10 | |
| FEP | coaxial | — | 15 | |
| FEP | resonator | — | 30 | 0.8 |
| SSP | waveguide | 15 | ||
| SSP | waveguide | 20 | ||
| SSP | coaxial | — | 10 | |
| SSP | coaxial | — | 15 | |
| SSP | resonator | — | 30 | 0.8 |
| SAAB | coaxial | — | 15 | |
| SAAB | coaxial | — | 20 | |
| KIM | waveguide | 15 | ||
| KIM | waveguide | 20 | ||
| KIM | waveguide | 15 | ||
| KIM | waveguide | 20 | ||
| KIM | waveguide | 15 | ||
| KIM | waveguide | 20 | ||
| KIM | coaxial | — | 10 | |
| KIM | coaxial | — | 15 | |
| KIM | resonator | — | 30 | 1.1 |
| Sample | Mode | ||||
|---|---|---|---|---|---|
| PLA | TE | 2.76 | |||
| PLA | TE | 1.01 | 0 | ||
| PLA | TE | 2.77 | |||
| PLA | TE | 1.01 | 0 | ||
| PLA | TE | 2.75 | |||
| CDP | TE | — | — | ||
| CDP | TE | 1.09 | |||
| CDP | TE | 17.63 | |||
| CDP | TE | 1.08 | |||
| CDP | TE | 15.52 | |||
| FEP | TE | 5.03 | |||
| FEP | TE | 0.95 | |||
| FEP | TE | 5.01 | |||
| FEP | TE | 0.93 | |||
| FEP | TE | 5.05 | |||
| SSP | TE | 4.45 | |||
| SSP | TE | 0.96 | |||
| SSP | TE | 4.43 | |||
| SSP | TE | 0.94 | |||
| SSP | TE | 4.47 | |||
| KIM | TE | 2.89 | |||
| KIM | TE | 1.00 | 0 | ||
| KIM | TE | 2.86 | |||
| KIM | TE | 1.00 | 0 | ||
| KIM | TE | 2.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plüss, T.; Zimmer, F.; Hehn, T.; Murk, A. Characterisation and Comparison of Material Parameters of 3D-Printable Absorbing Materials. Materials 2022, 15, 1503. https://doi.org/10.3390/ma15041503
Plüss T, Zimmer F, Hehn T, Murk A. Characterisation and Comparison of Material Parameters of 3D-Printable Absorbing Materials. Materials. 2022; 15(4):1503. https://doi.org/10.3390/ma15041503
Chicago/Turabian StylePlüss, Tobias, Felix Zimmer, Tobias Hehn, and Axel Murk. 2022. "Characterisation and Comparison of Material Parameters of 3D-Printable Absorbing Materials" Materials 15, no. 4: 1503. https://doi.org/10.3390/ma15041503
APA StylePlüss, T., Zimmer, F., Hehn, T., & Murk, A. (2022). Characterisation and Comparison of Material Parameters of 3D-Printable Absorbing Materials. Materials, 15(4), 1503. https://doi.org/10.3390/ma15041503






