Elastodynamic Behaviour of Laminate Structures with Soft Thin Interlayers: Theory and Experiment
Abstract
1. Introduction
2. Mathematical Modelling
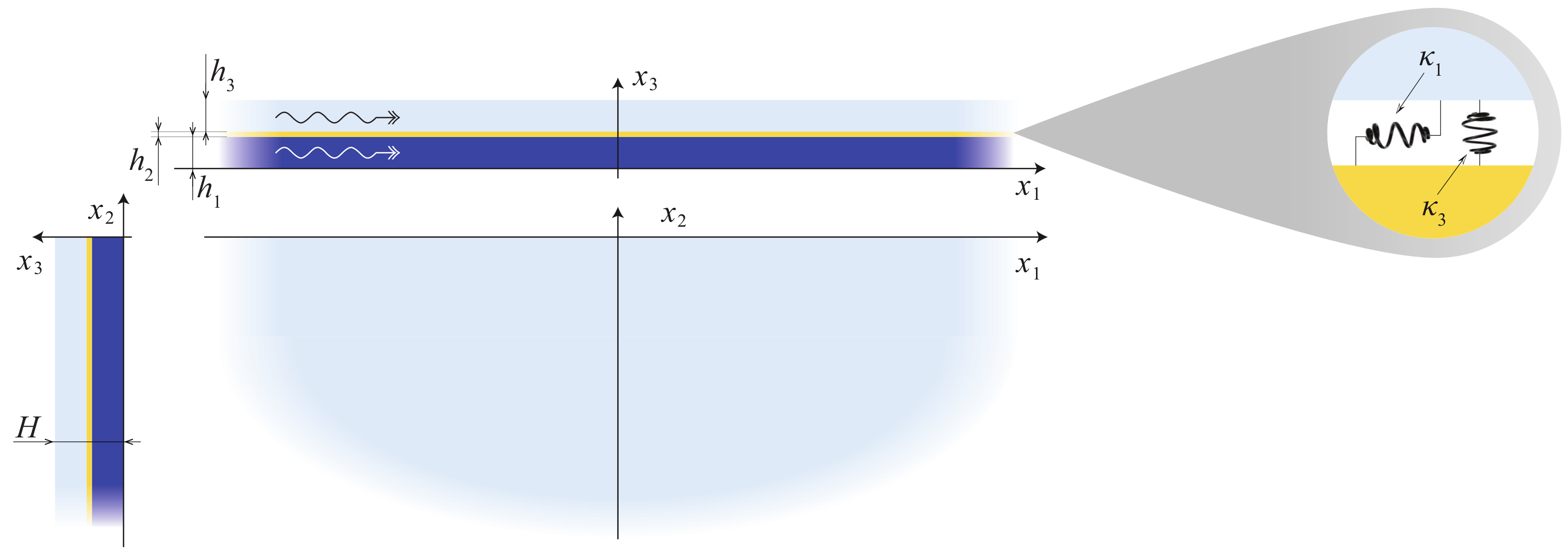
2.1. Exact Statement of Boundary Value Problem
2.2. Modeling of the Film via EBCs
2.3. Thickness Resonance Frequencies
3. Properties of Lamb Waves in Laminates with Soft Interlayer
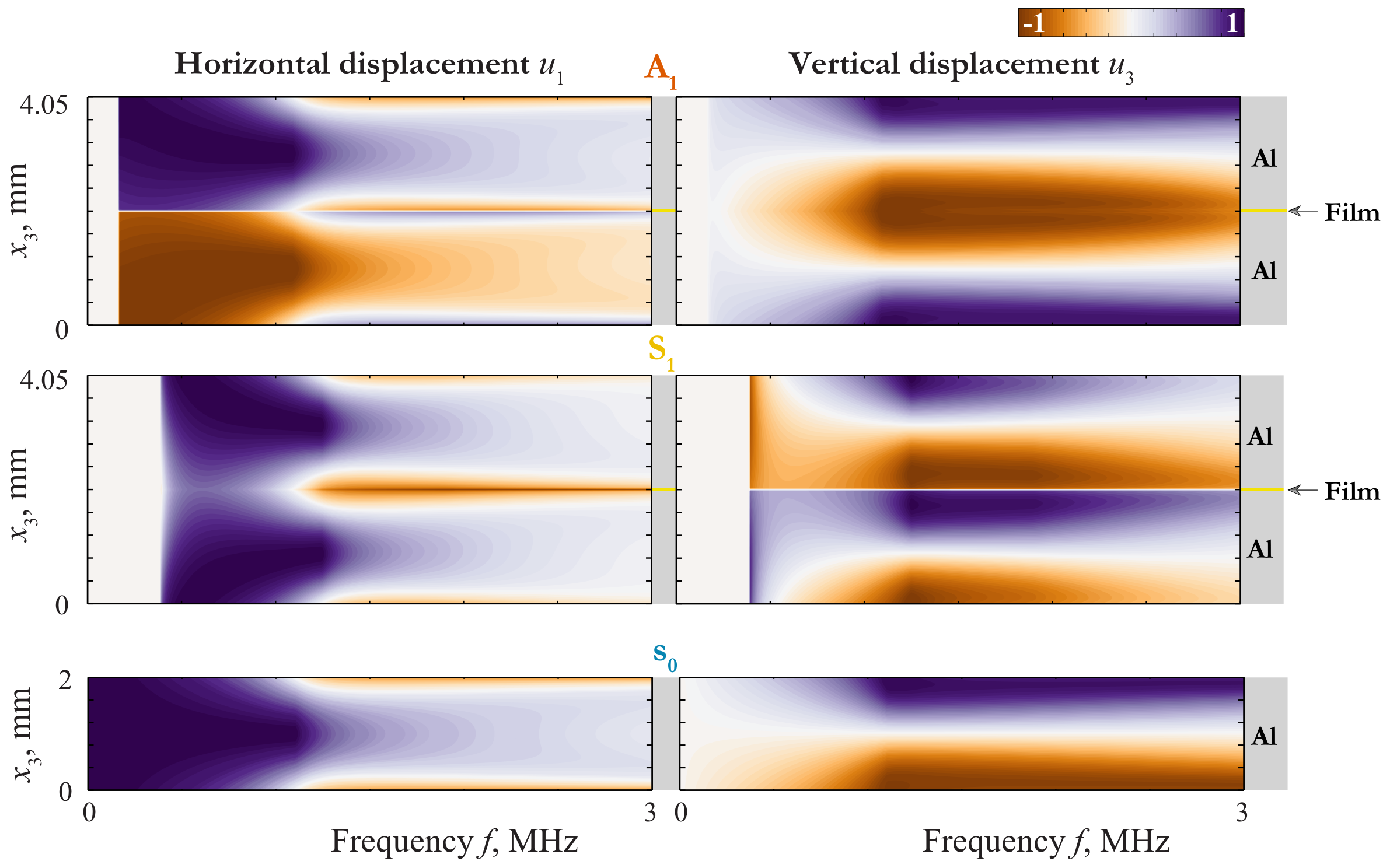
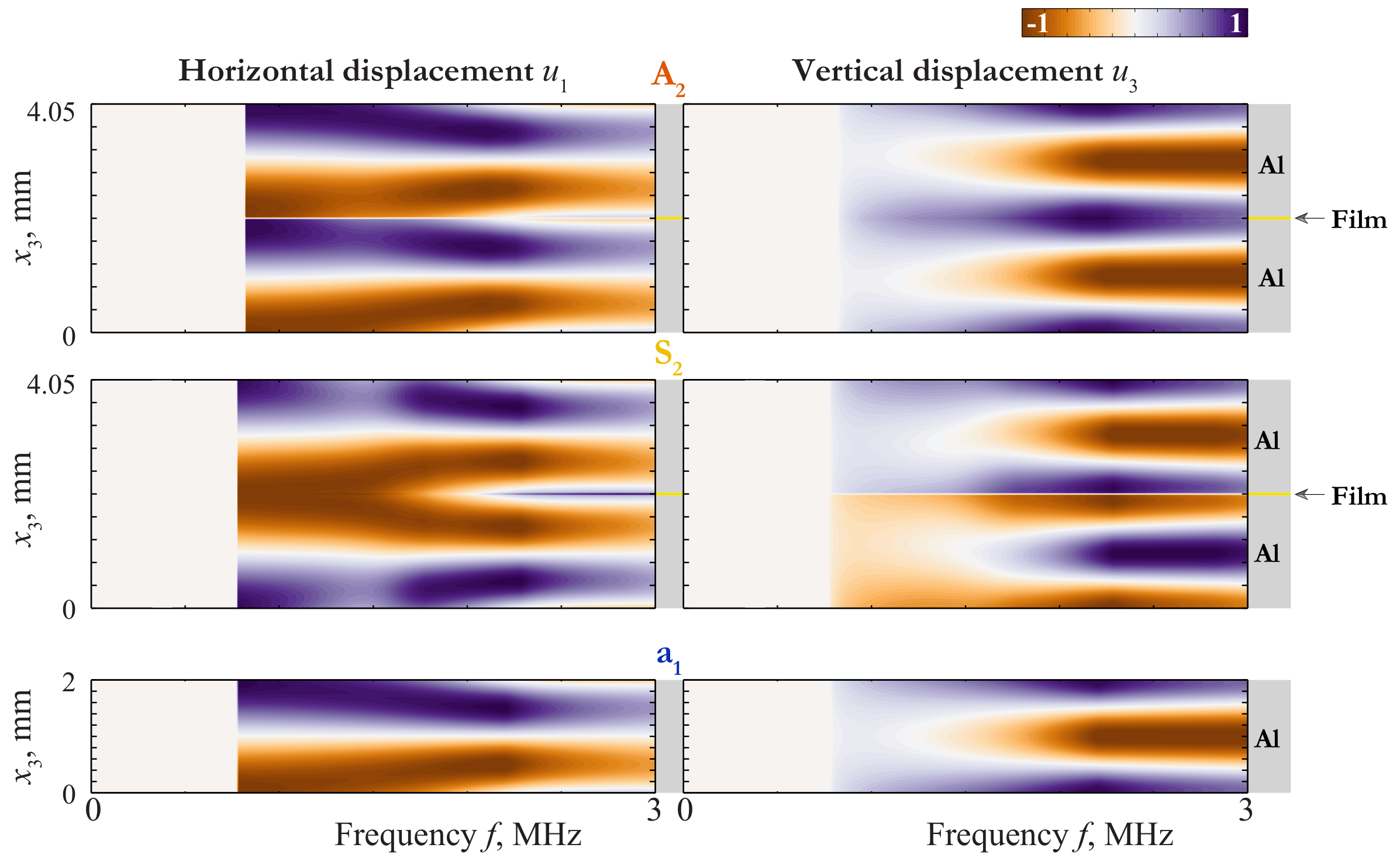
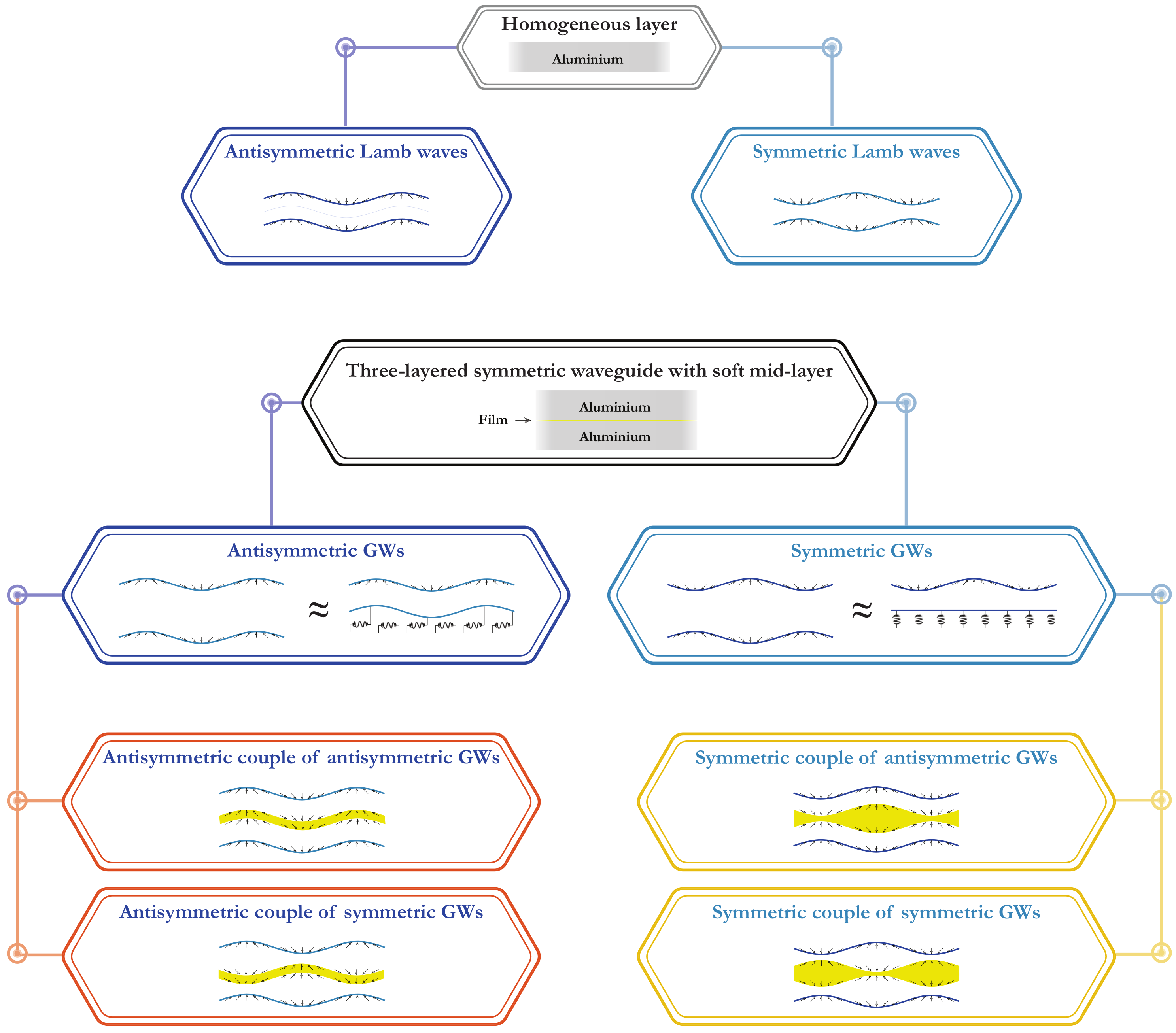
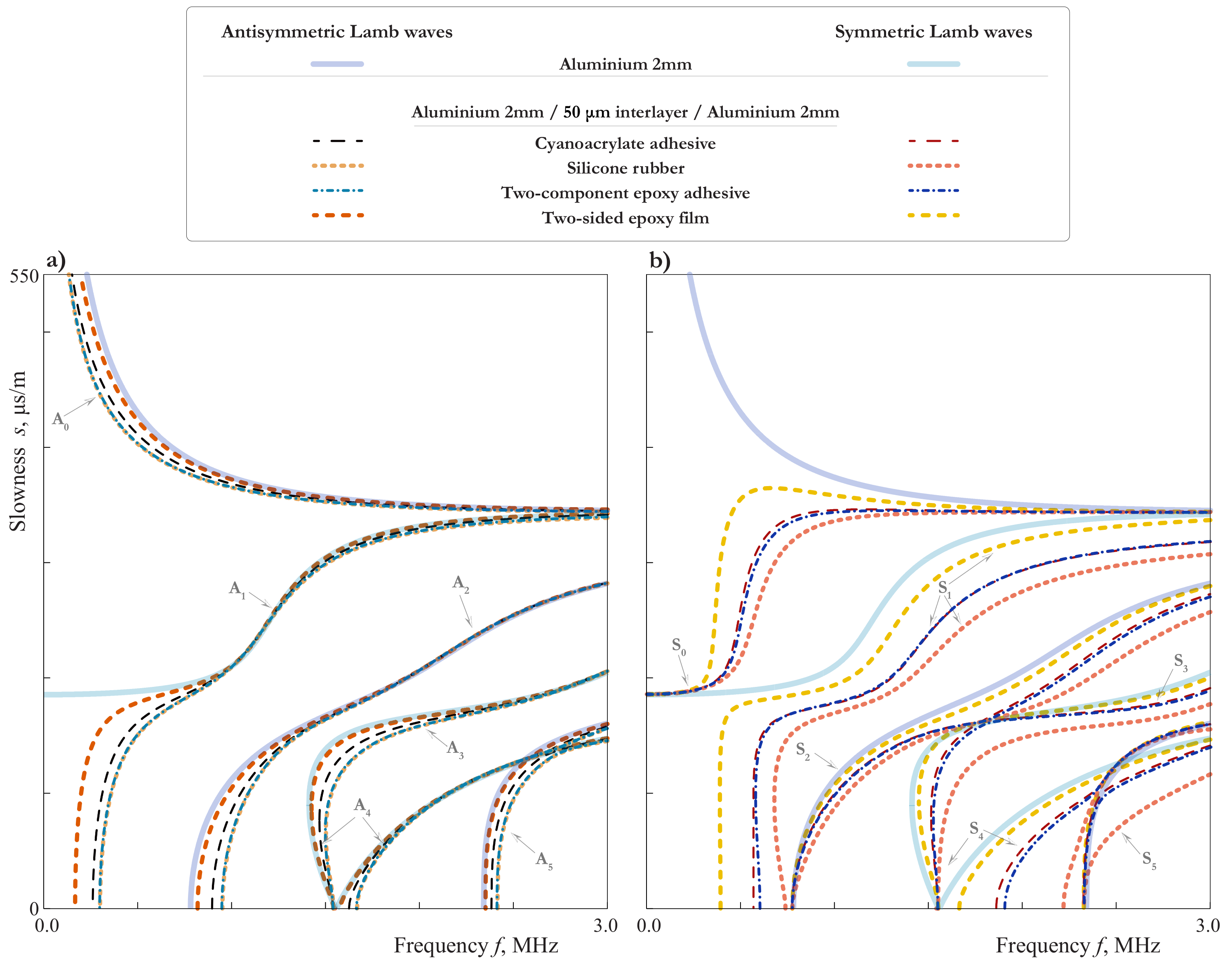
3.1. Main Properties of Dispersion Curves and Vibration Forms
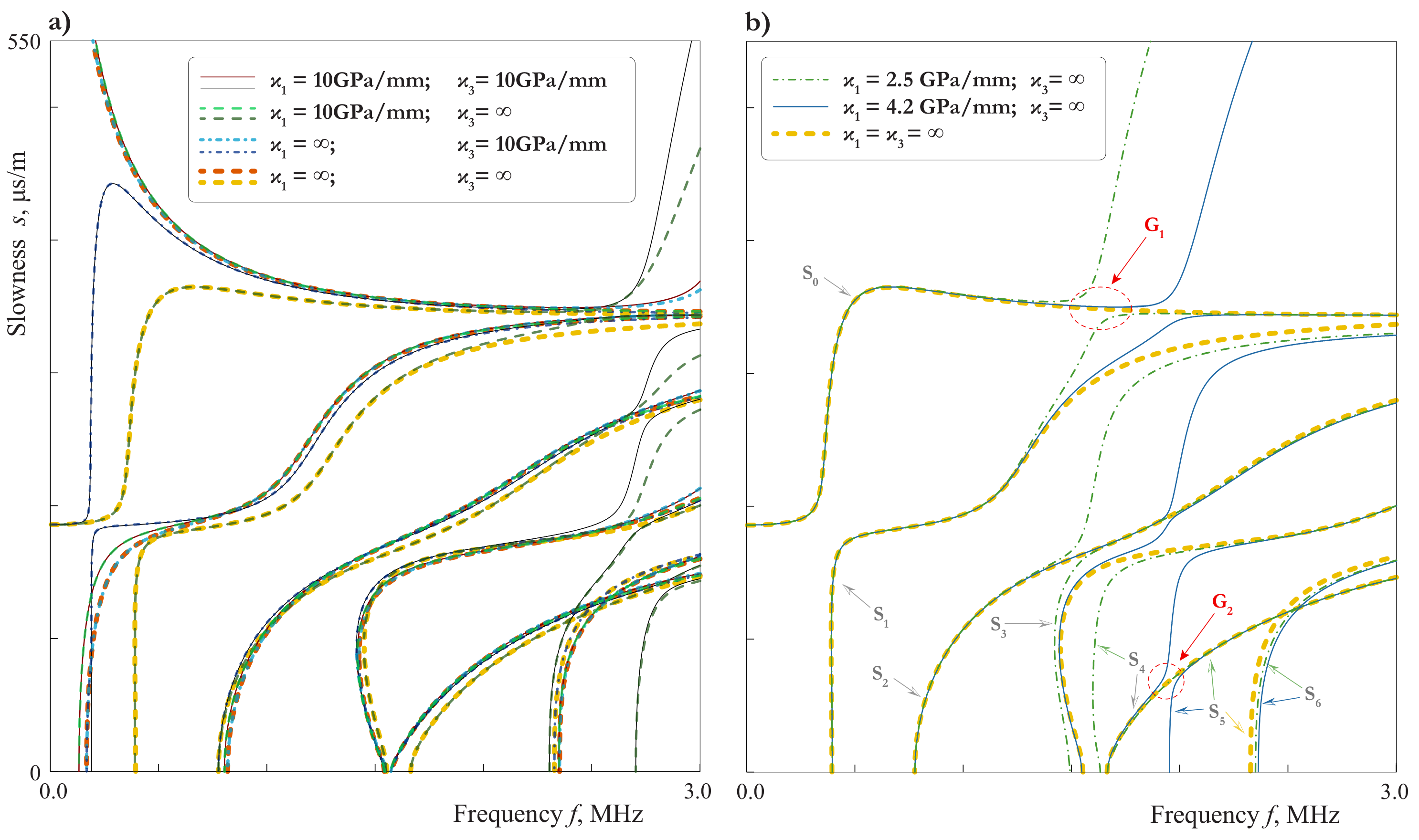
3.2. Influence of the Mechanical Properties of Interlayer
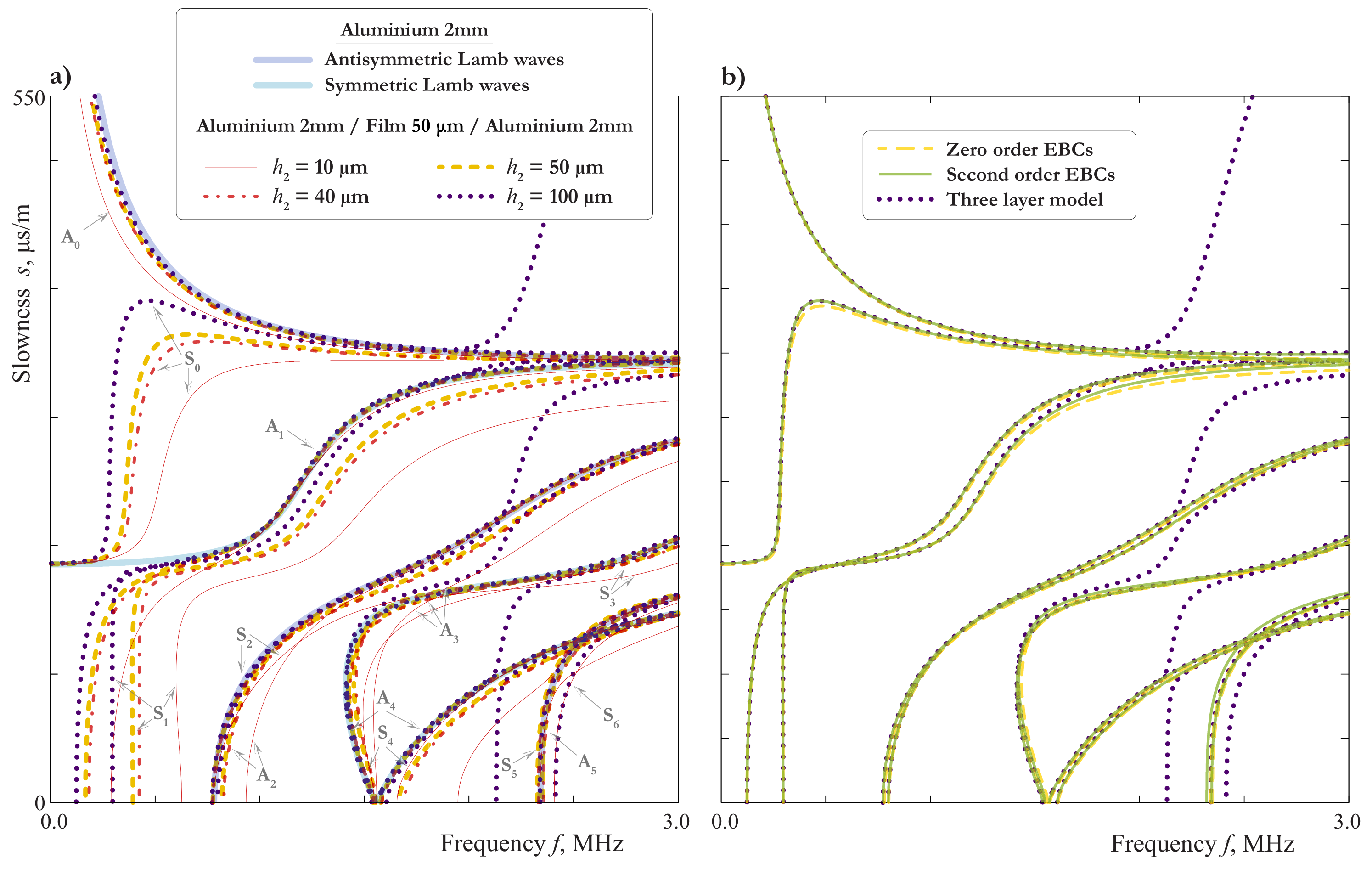
3.3. Influence of the Thickness of Interlayer
3.4. Influence of the Adhesive Bonding or Imperfect Contact
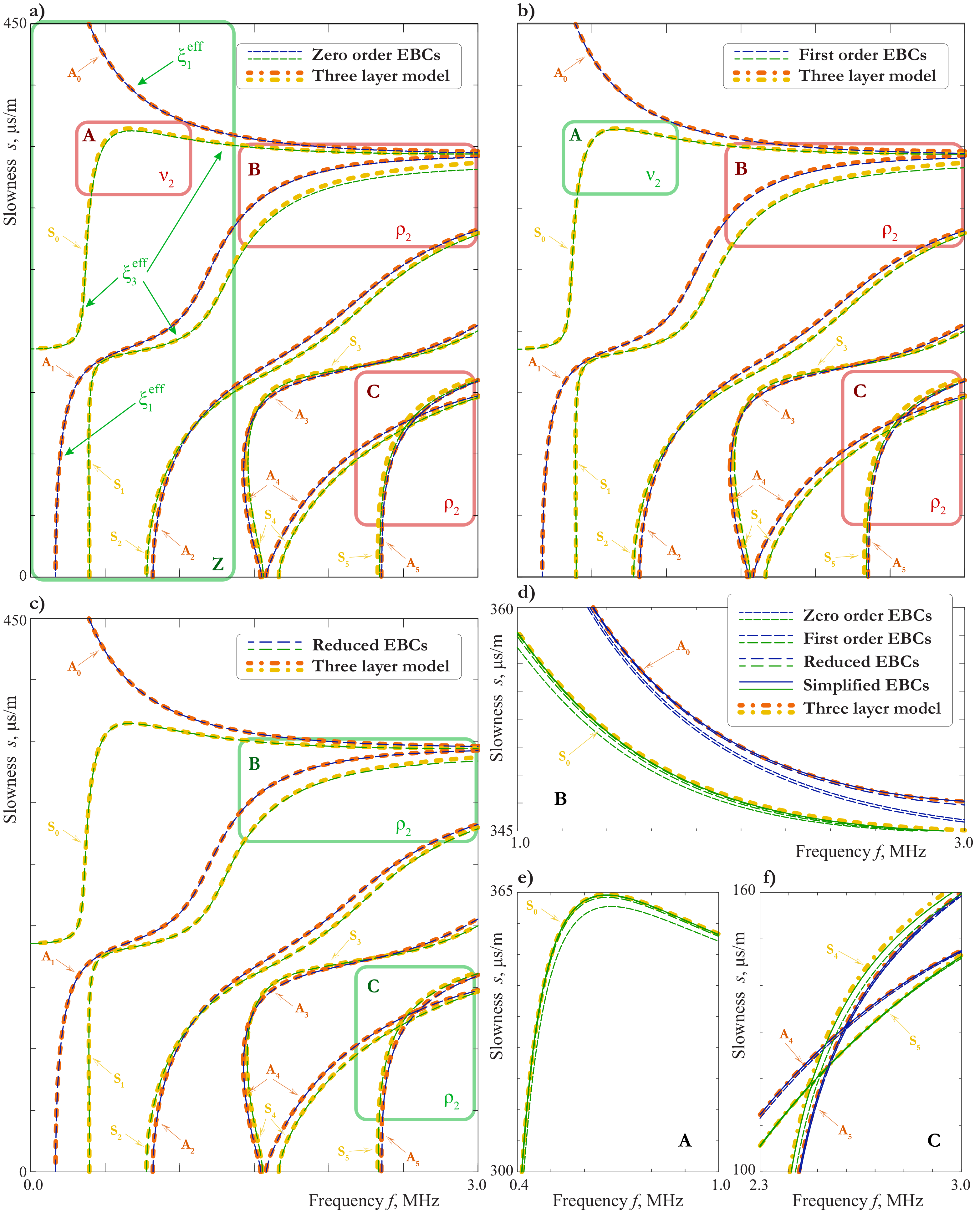
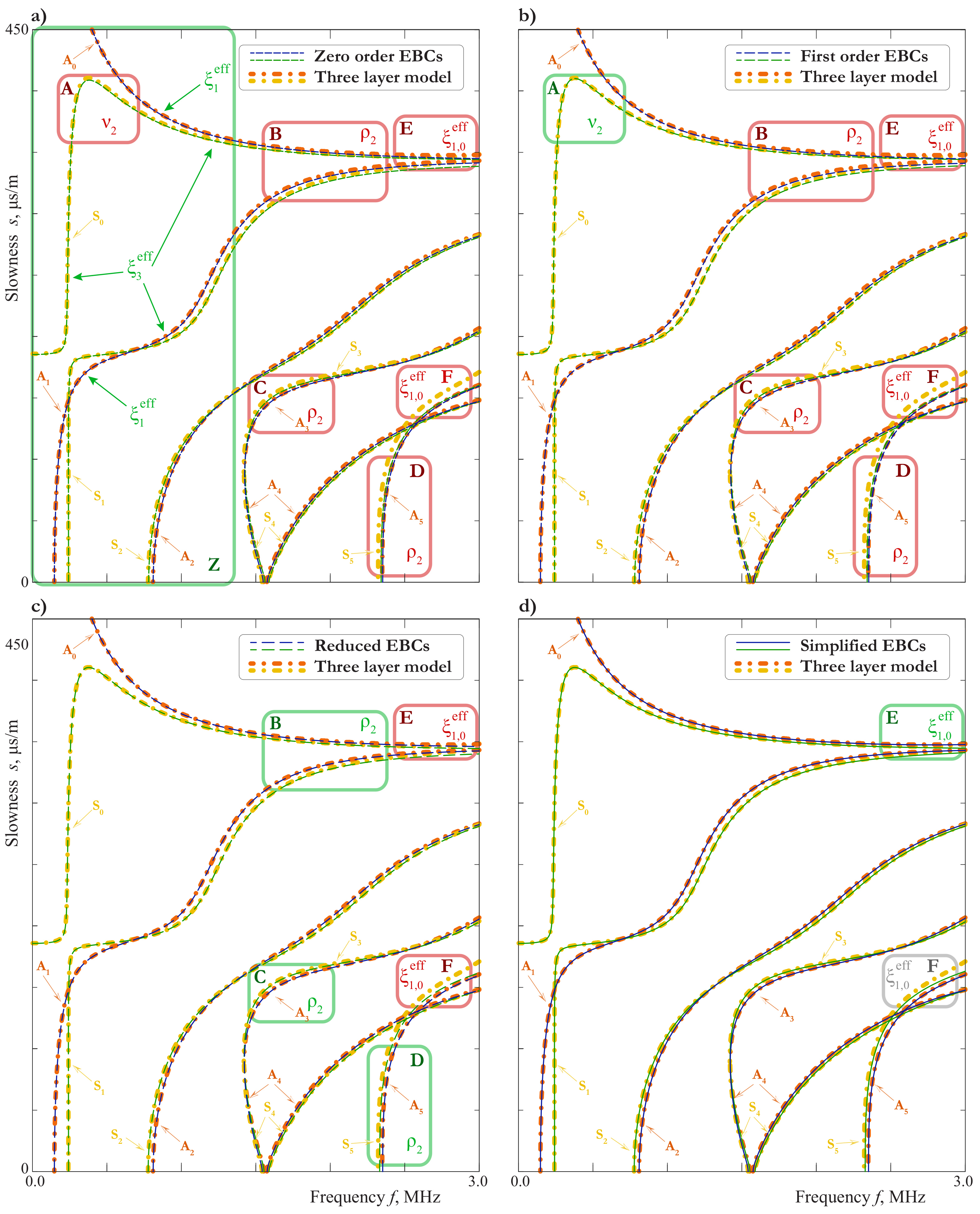
3.5. Analysis of the Influence of the Film Parameters on the Basis of EBCs
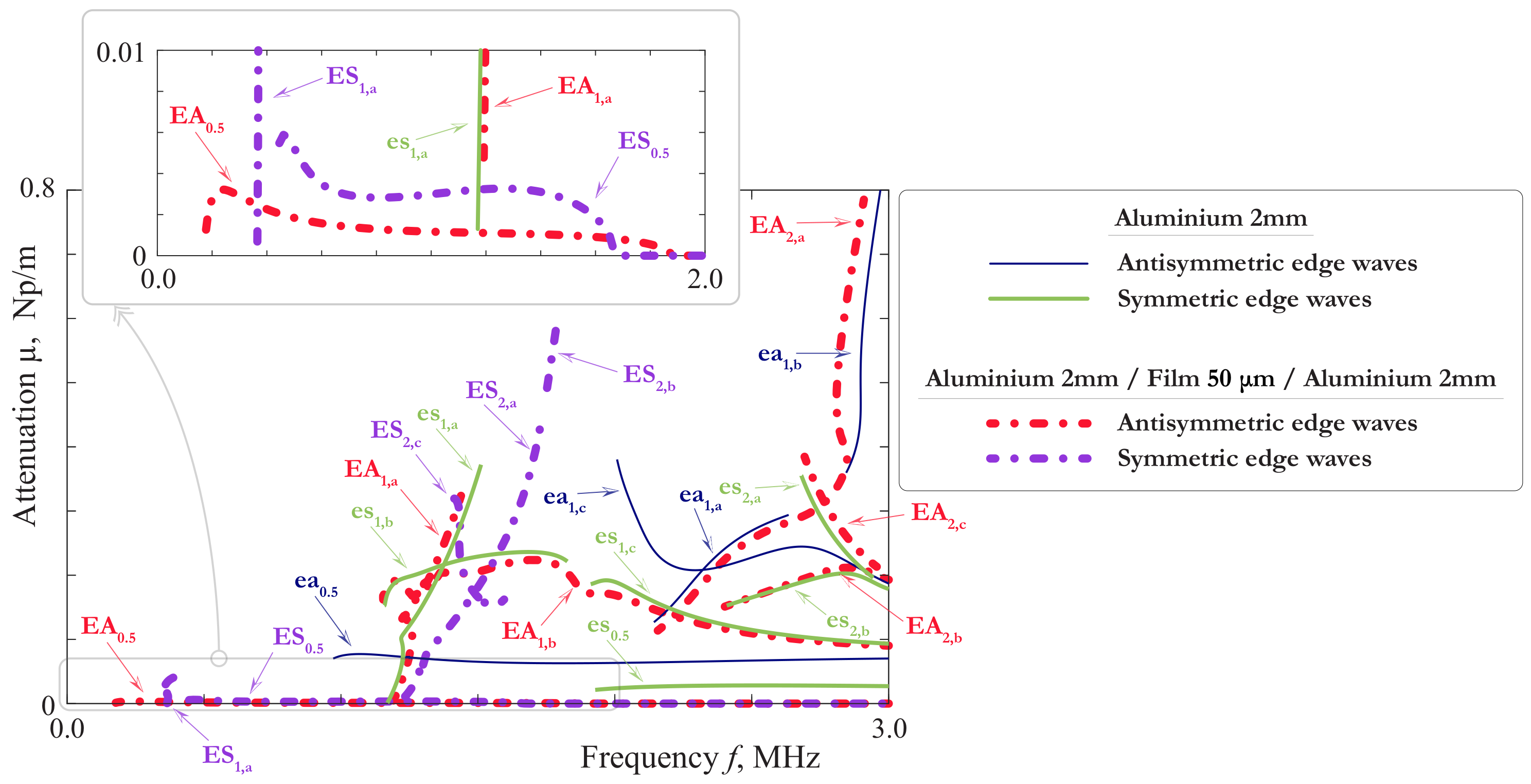
4. Properties of Other Guided Waves in Laminates with Soft Interlayer
5. Comparison: Theory vs. Experiment
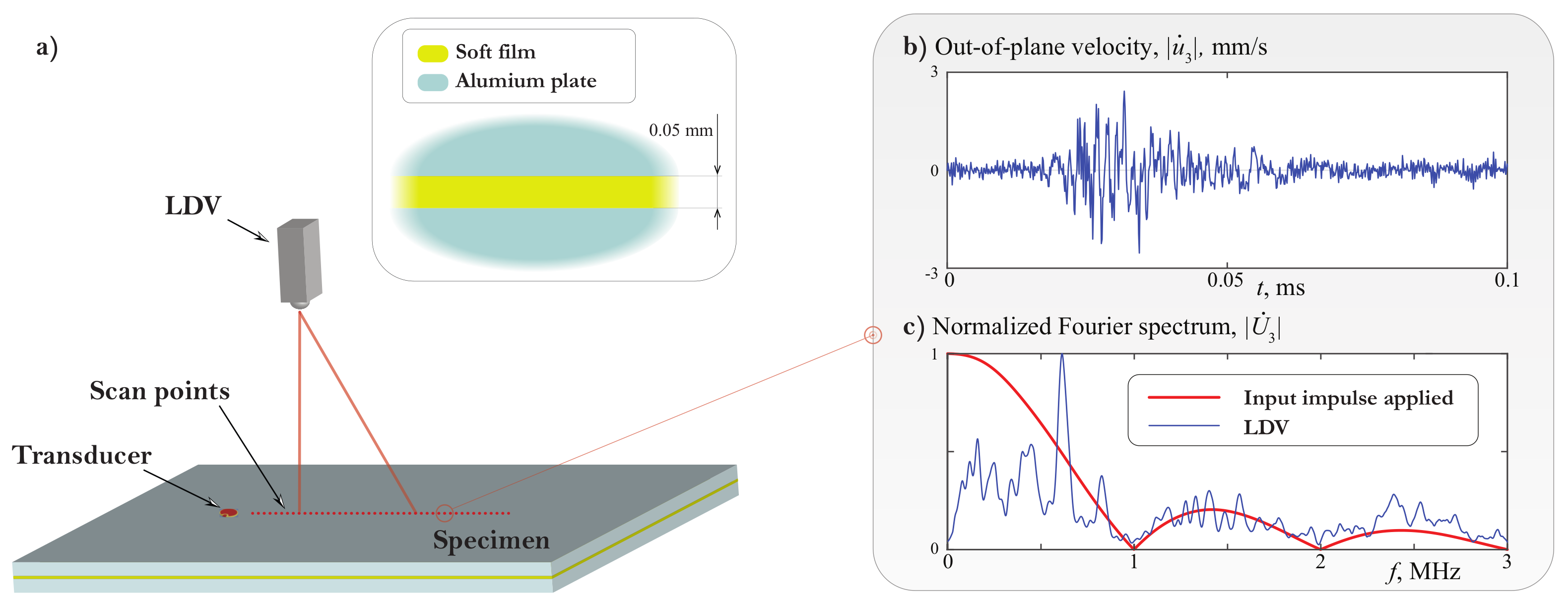
5.1. Experimental Setup
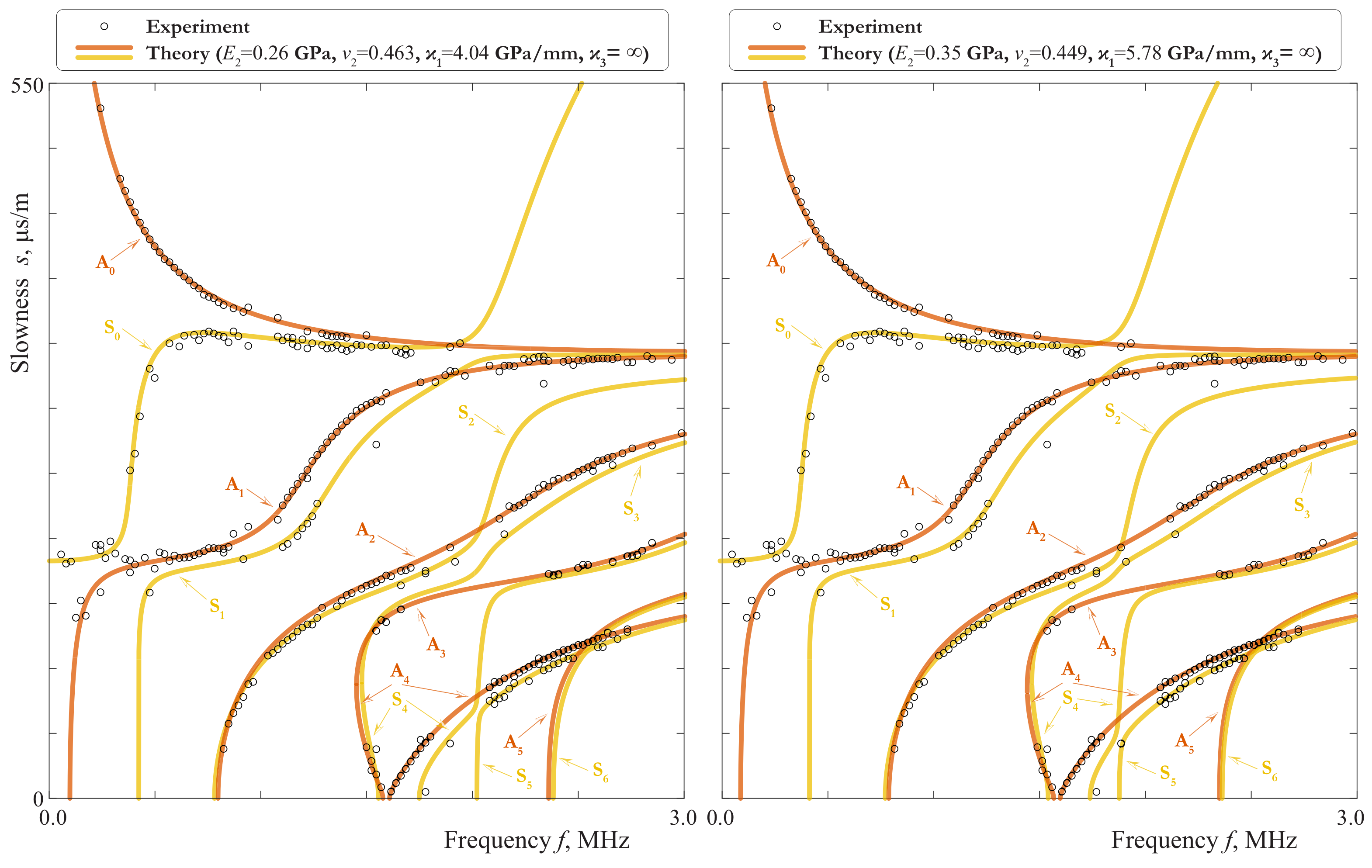
5.2. Analysis of the Experimental Data
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NDT | non-destructive testing |
| SHM | stuctural health monitoring |
| SCs | slowness curves |
| EGWs | elastic guided waves |
| GWs | guided waves |
| LWs | Lamb waves |
| ALW | antisymmetric Lamb wave |
| SLW | symmetric Lamb wave |
| EWs | edge waves |
| BCs | boundary conditions |
| EBCs | effective boundary conditions |
| SBCs | spring-type boundary conditions |
| LDV | laser Doppler vibrometer |
References
- Higgins, A. Adhesive bonding of aircraft structures. Int. J. Adhes. Adhes. 2000, 20, 367–376. [Google Scholar] [CrossRef]
- Barnes, T.; Pashby, I. Joining techniques for aluminium spaceframes used in automobiles: Part II. adhesive bonding and mechanical fasteners. J. Mater. Process. Technol. 2000, 99, 72–79. [Google Scholar] [CrossRef]
- Norville, H.S.; King, K.W.; Swofford, J.L. Behavior and Strength of Laminated Glass. J. Eng. Mech. 1998, 124, 46–53. [Google Scholar] [CrossRef]
- Adams, R.; Drinkwater, B. Nondestructive testing of adhesively-bonded joints. NDT E Int. 1997, 30, 93–98. [Google Scholar] [CrossRef]
- Ramalho, G.M.F.; Lopes, A.M.; da Silva, L.F.M. Structural health monitoring of adhesive joints using Lamb waves: A review. Struct. Control Health Monit. 2022, 29, e2849. [Google Scholar] [CrossRef]
- Goglio, L.; Rossetto, M. Ultrasonic testing of adhesive bonds of thin metal sheets. NDT E Int. 1999, 32, 323–331. [Google Scholar] [CrossRef]
- Huo, S.; Reis, H. Estimation of adhesive bond strength in laminated safety glass using guided mechanical waves: Part I. An energy velocity approach. Insight—Non-Destr. Test. Cond. Monit. 2008, 50, 146–152. [Google Scholar] [CrossRef]
- Gauthier, C.; Ech-Cherif El-Kettani, M.; Galy, J.; Predoi, M.; Leduc, D. Structural adhesive bonding characterization using guided Lamb waves and the vertical modes. Int. J. Adhes. Adhes. 2020, 98, 102467. [Google Scholar] [CrossRef]
- Mehrabi, M.; Soorgee, M.H.; Habibi, H.; Kappatos, V. A novel application of ultrasonic Lamb waves: Studying adhesive effects on the inspection of coating debonding in a three-layer waveguide. Nondestruct. Test. Eval. 2021, 36, 616–636. [Google Scholar] [CrossRef]
- Koodalil, D.; Rajagopal, P.; Balasubramaniam, K. Quantifying adhesive thickness and adhesion parameters using higher-order SH guided waves. Ultrasonics 2021, 114, 106429. [Google Scholar] [CrossRef]
- Nakao, S.; Hayashi, T. Adhesive Bond Imaging by Noncontact Measurements with Single-Sided Access. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2018, 1, 021009. [Google Scholar] [CrossRef]
- Rucka, M.; Wojtczak, E.; Lachowicz, J. Damage Imaging in Lamb Wave-Based Inspection of Adhesive Joints. Appl. Sci. 2018, 8, 522. [Google Scholar] [CrossRef]
- Spytek, J.; Ziaja-Sujdak, A.; Dziedziech, K.; Pieczonka, L.; Pelivanov, I.; Ambrozinski, L. Evaluation of disbonds at various interfaces of adhesively bonded aluminum plates using all-optical excitation and detection of zero-group velocity Lamb waves. NDT E Int. 2020, 112, 102249. [Google Scholar] [CrossRef]
- Ke, Y.T.; Cheng, C.C.; Lin, Y.C.; Huang, C.L.; Hsu, K.T. Quantitative assessment of bonding between steel plate and reinforced concrete structure using dispersive characteristics of lamb waves. NDT E Int. 2019, 102, 311–321. [Google Scholar] [CrossRef]
- Ismaili, N.A.; Chenouni, D.; Lakhliai, Z.; El-kettani, M.E.C.; Morvan, B.; Izbicki, J.L. Determination of epoxy film parameters in a three-layer metal/adhesive/metal structure. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1955–1959. [Google Scholar] [CrossRef]
- Ong, W.; Rajic, N.; Chiu, W.; Rosalie, C. Adhesive material property evaluation for improved Lamb wave simulation. Int. J. Adhes. Adhes. 2016, 71, 28–38. [Google Scholar] [CrossRef]
- Zhu, X.; Li, Y.; Chen, G.; Wang, P.C. Curing-Induced Distortion Mechanism in Adhesive Bonding of Aluminum AA6061-T6 and Steels. J. Manuf. Sci. Eng. 2013, 135, 051007. [Google Scholar] [CrossRef]
- Rudawska, A. The influence of curing conditions on the strength of adhesive joints. J. Adhes. 2020, 96, 402–422. [Google Scholar] [CrossRef]
- Loukkal, A.; Lematre, M.; Bavencoffe, M.; Lethiecq, M. Modeling and numerical study of the influence of imperfect interface properties on the reflection coefficient for isotropic multilayered structures. Ultrasonics 2020, 103, 106099. [Google Scholar] [CrossRef]
- Mezil, S.; Bruno, F.; Raetz, S.; Laurent, J.; Royer, D.; Prada, C. Investigation of interfacial stiffnesses of a tri-layer using Zero-Group Velocity Lamb modes. J. Acoust. Soc. Am. 2015, 138, 3202–3209. [Google Scholar] [CrossRef]
- Fraisse, P.; Schmit, F.; Zarembowitch, A. Ultrasonic inspection of very thin adhesive layers. J. Appl. Phys. 1992, 72, 3264–3271. [Google Scholar] [CrossRef]
- Vlasie, V.; Rousseau, M. Acoustical validation of the rheological models for a structural bond. Wave Motion 2003, 37, 333–349. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Wang, Y.J. Analysis of boundary conditions for elastic wave interaction with an interface between two solids. J. Acoust. Soc. Am. 1991, 89, 503–515. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Wang, Y.J. Equivalent boundary conditions for thin orthotropic layer between two solids: Reflection, refraction, and interface waves. J. Acoust. Soc. Am. 1992, 91, 1875–1887. [Google Scholar] [CrossRef] [PubMed]
- Boström, A.; Bövik, P.; Olsson, P. A comparison of exact first order and spring boundary conditions for scattering by thin layers. J. Nondestruct. Eval. 1992, 11, 175–184. [Google Scholar] [CrossRef]
- Puthillath, P.; Ren, B.; Lissenden, C.J.; Rose, J.L. Guided wave mode pairs for transmissibility in adhesively bonded metal plates. AIP Conf. Proc. 2013, 1511, 199–206. [Google Scholar] [CrossRef]
- Lugovtsova, Y.; Johannesmann, S.; Henning, B.; Prager, J. Analysis of Lamb wave mode repulsion and its implications to the characterisation of adhesive bonding strength. Proc. Meet. Acoust. 2019, 38, 030005. [Google Scholar] [CrossRef]
- Baik, J.M.; Thompson, R.B. Ultrasonic scattering from imperfect interfaces: A quasi-static model. J. Nondestruct. Eval. 1984, 4, 177–196. [Google Scholar] [CrossRef]
- Boström, A.; Wickham, G.R. On the boundary conditions for ultrasonic transmission by partially closed cracks. J. Nondestruct. Eval. 1991, 10, 139–149. [Google Scholar] [CrossRef]
- Lekesiz, H.; Katsube, N.; Rokhlin, S.I.; Seghi, R.R. Effective spring stiffness for a periodic array of interacting coplanar penny-shaped cracks at an interface between two dissimilar isotropic materials. Int. J. Solids Struct. 2013, 50, 2817–2828. [Google Scholar] [CrossRef][Green Version]
- Golub, M.V.; Doroshenko, O.V. Effective spring boundary conditions for modelling wave transmission through a composite with a random distribution of interface circular cracks. Int. J. Solids Struct. 2019, 165, 115–126. [Google Scholar] [CrossRef]
- Glushkov, E.V.; Glushkova, N.V. On the efficient implementation of the integral equation method in elastodynamics. J. Comput. Acoust. 2001, 9, 889–898. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Eremin, A. Forced wave propagation and energy distribution in anisotropic laminate composites. J. Acoust. Soc. Am. 2011, 129, 2923–2934. [Google Scholar] [CrossRef] [PubMed]
- Yokoyama, T.; Shimizu, H. Determination of Impact Shear Strength of Adhesive Bonds with the Split Hopkinson Bar. Trans. Jpn. Soc. Mech. Eng. Ser. A 1997, 63, 2604–2609. [Google Scholar] [CrossRef][Green Version]
- Pan, Y.; Zhu, F.; Fan, J.; Tao, J.; Lin, X.; Wang, F.; Shi, L. Investigation of Mechanical Properties of Silicone/Phosphor Composite Used in Light Emitting Diodes Package. Polymers 2018, 10, 195. [Google Scholar] [CrossRef] [PubMed]
- Goglio, L.; Rezaei, M. Variations in mechanical properties of an epoxy adhesive on exposure to warm moisture. J. Adhes. Sci. Technol. 2014, 28, 1394–1404. [Google Scholar] [CrossRef]
- Golub, M.V.; Doroshenko, O.V.; Wilde, M.V.; Eremin, A.A. Experimental validation of the applicability of effective spring boundary conditions for modelling damaged interfaces in laminate structures. Compos. Struct. 2021, 273, 114141. [Google Scholar] [CrossRef]
- Kaplunov, J.D.; Kossovich, L.Y.; Nolde, E.V. Dynamics of Thin Walled Elastic Bodies; Academic Press: San Diego, CA, USA, 1998; p. 226. [Google Scholar]
- Dai, H.H.; Kaplunov, J.; Prikazchikov, D. A long-wave model for the surface elastic wave in a coated half-space. Proc. R. Soc. A 2010, 466, 3097–3116. [Google Scholar] [CrossRef]
- Kaplunov, J.; Prikazchikov, D.A.; Prikazchikova, L.A. Dispersion of elastic waves in a strongly inhomogeneous three-layered plate. Int. J. Solids Struct. 2017, 113–114, 169–179. [Google Scholar] [CrossRef]
- Kaplunov, J. Asymptotic analysis of an anti-plane dynamic problem for a three-layered strongly inhomogeneous laminate. Math. Mech. Solids 2020, 25, 3–16. [Google Scholar] [CrossRef]
- Lawrie, J.B.; Kaplunov, J.D. Edge waves and resonance on elastic structures: An overview. Math. Mech. Solids 2012, 17, 4–16. [Google Scholar] [CrossRef]
- Wilde, M.V.; Golub, M.V.; Eremin, A.A. Experimental and theoretical investigation of transient edge waves excited by a piezoelectric transducer bonded to the edge of a thick elastic plate. J. Sound Vib. 2019, 441, 26–49. [Google Scholar] [CrossRef]
- Wilde, M.V.; Golub, M.V.; Eremin, A.A. Experimental observation of theoretically predicted spectrum of edge waves in a thick elastic plate with facets. Ultrasonics 2019, 98, 88–93. [Google Scholar] [CrossRef] [PubMed]
- Hughes, J.M.; Mohabuth, M.; Khanna, A.; Vidler, J.; Kotousov, A.; Ng, C.T. Damage detection with the fundamental mode of edge waves. Struct. Health Monit. 2021, 20, 74–83. [Google Scholar] [CrossRef]
- Hughes, J.M.; Mohabuth, M.; Kotousov, A.; Ng, C.T. The fundamental ultrasonic edge wave mode: Propagation characteristics and potential for distant damage detection. Ultrasonics 2021, 114, 106369. [Google Scholar] [CrossRef] [PubMed]
- Neumann, M.N.; Hennings, B.; Lammering, R. Identification and Avoidance of Systematic Measurement Errors in Lamb Wave Observation with One-Dimensional Scanning Laser Vibrometry. Strain 2013, 49, 95–101. [Google Scholar] [CrossRef]
- Schöpfer, F.; Binder, F.; Wöstehoff, A.; Schuster, T.; von Ende, S.; Föll, S.; Lammering, R. Accurate determination of dispersion curves of guided waves in plates by applying the matrix pencil method to laser vibrometer measurement data. CEAS Aeronaut. J. 2013, 4, 61–68. [Google Scholar] [CrossRef]
- Dahmen, S. Influence of volumic fraction of adhesive in elastic and viscous thin bonded Aluminum/Adhesive/Aluminum plate on Lamb modes that have ZGV modes. Ultrasonics 2019, 94, 37–49. [Google Scholar] [CrossRef]
- Budhe, S.; Banea, M.; de Barros, S.; da Silva, L. An updated review of adhesively bonded joints in composite materials. Int. J. Adhes. Adhes. 2017, 72, 30–42. [Google Scholar] [CrossRef]






| Material | Density | Young Modulus | Poisson’s Ratio |
|---|---|---|---|
| E, GPa | |||
| Aluminium | 2700 | 70 | 0.33 |
| Cyanoacrylate adhesive [34] | 1248 | 1.7 | 0.4 |
| Silicone rubber [35] | 1150 | 3.1 | 0.48 |
| Two-component epoxy adhesive [36] | 1345 | 2.75 | 0.35 |
| Two-sided epoxy tape [37] | 930 | 0.5 | 0.4 |
| Material | Eff. Stiffness | Density | Young Modulus | Poisson’s Ratio | |
|---|---|---|---|---|---|
| GPa/mm | , | E, GPa | |||
| Aluminium | – | – | 2715 | 72 | 0.345 |
| Two-sided epoxy tape | 1.1 | 26 | 900 | 0.26–0.35 | –0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilde, M.V.; Golub, M.V.; Eremin, A.A. Elastodynamic Behaviour of Laminate Structures with Soft Thin Interlayers: Theory and Experiment. Materials 2022, 15, 1307. https://doi.org/10.3390/ma15041307
Wilde MV, Golub MV, Eremin AA. Elastodynamic Behaviour of Laminate Structures with Soft Thin Interlayers: Theory and Experiment. Materials. 2022; 15(4):1307. https://doi.org/10.3390/ma15041307
Chicago/Turabian StyleWilde, Maria V., Mikhail V. Golub, and Artem A. Eremin. 2022. "Elastodynamic Behaviour of Laminate Structures with Soft Thin Interlayers: Theory and Experiment" Materials 15, no. 4: 1307. https://doi.org/10.3390/ma15041307
APA StyleWilde, M. V., Golub, M. V., & Eremin, A. A. (2022). Elastodynamic Behaviour of Laminate Structures with Soft Thin Interlayers: Theory and Experiment. Materials, 15(4), 1307. https://doi.org/10.3390/ma15041307








