Effects of Low Temperatures on Flexural Strength of Macro-Synthetic Fiber Reinforced Concrete: Experimental and Numerical Investigation
Abstract
:1. Introduction
2. Experimental Program
2.1. Concrete Mix
2.2. Test Setup and Testing Procedure
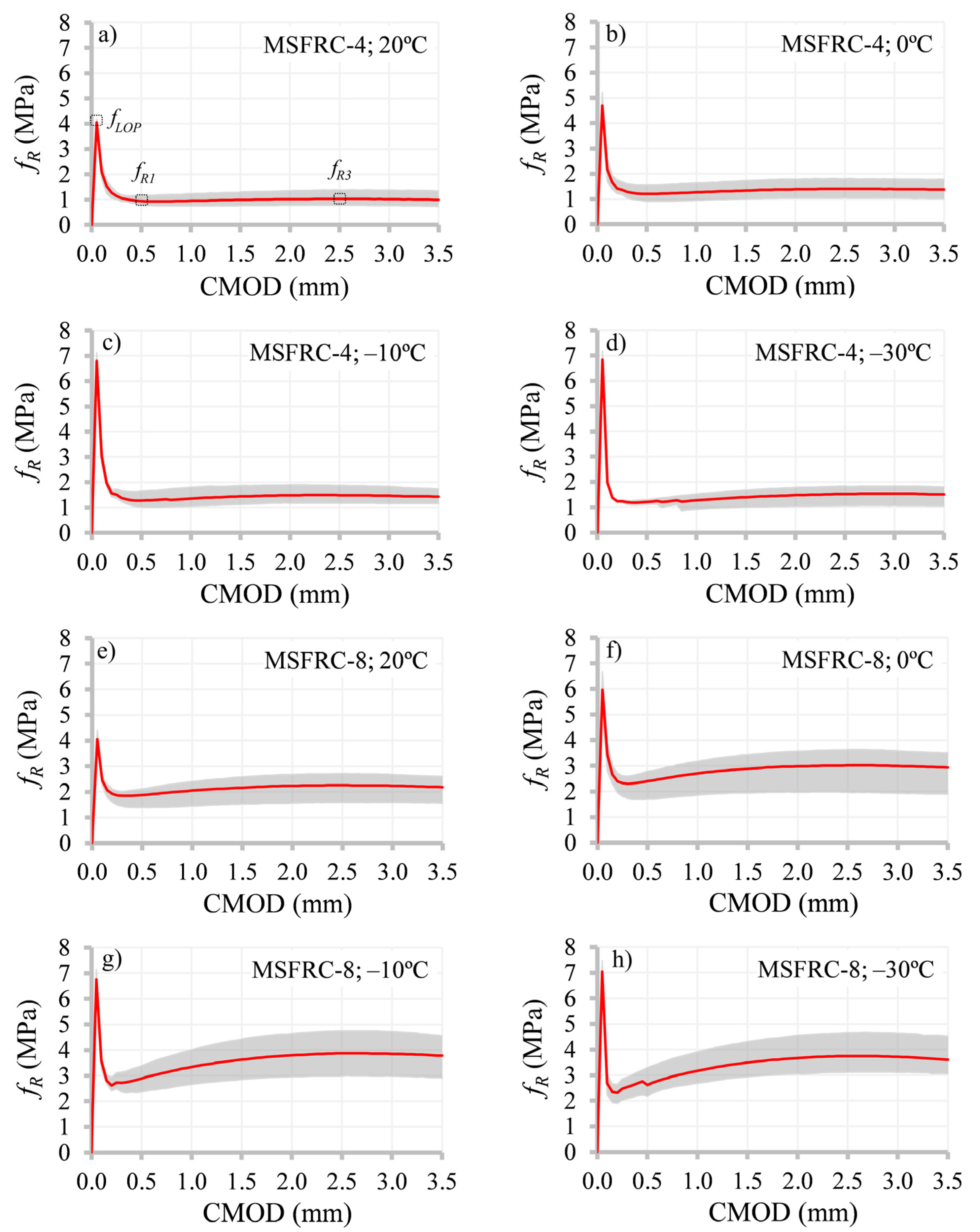
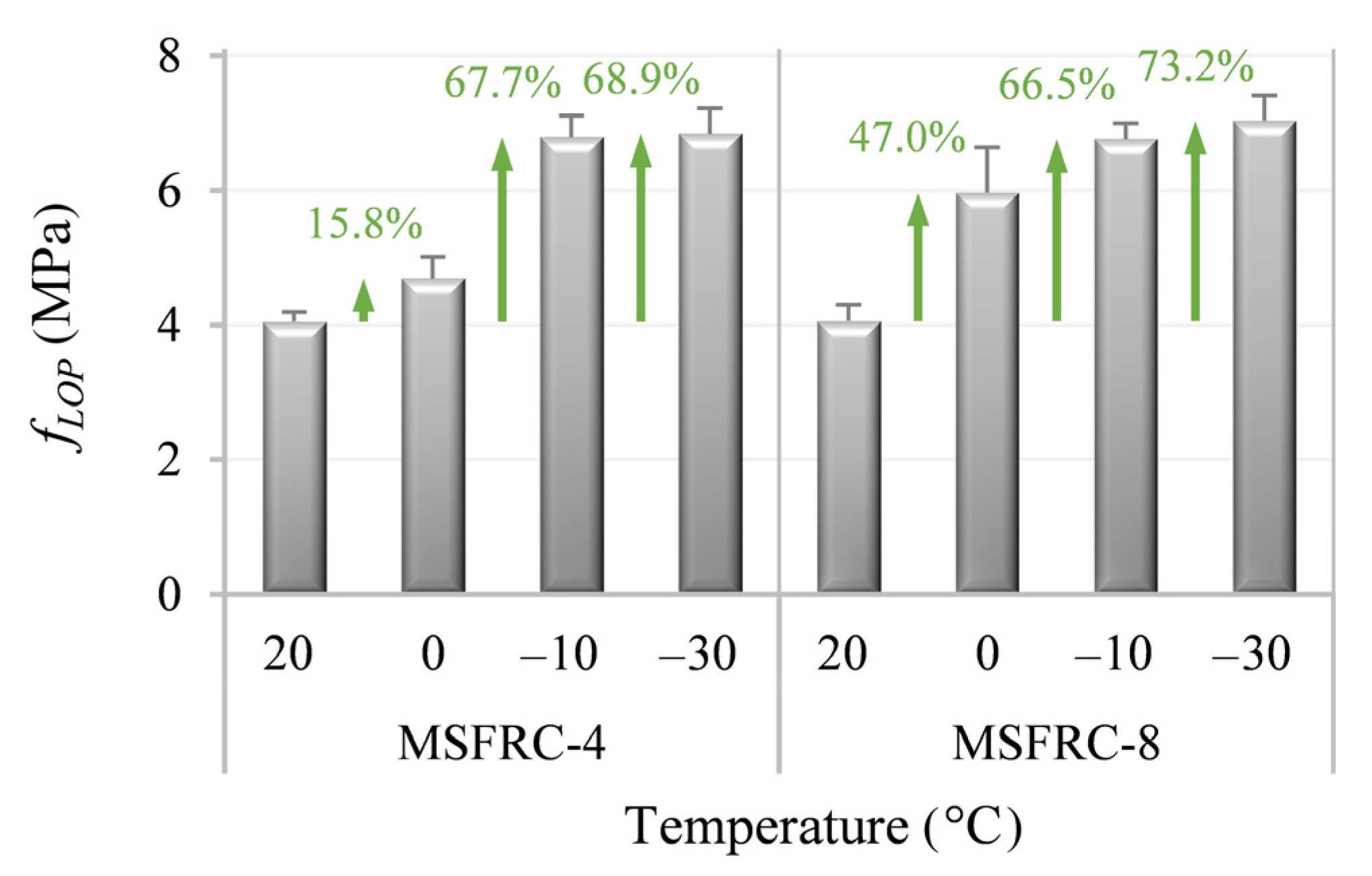
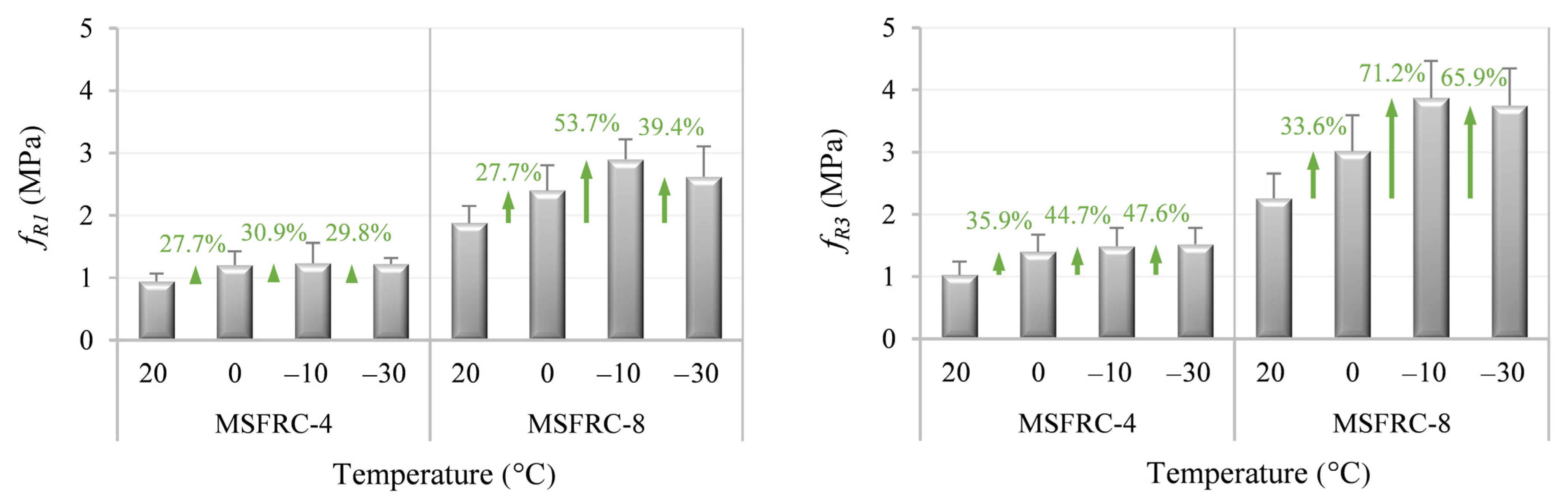
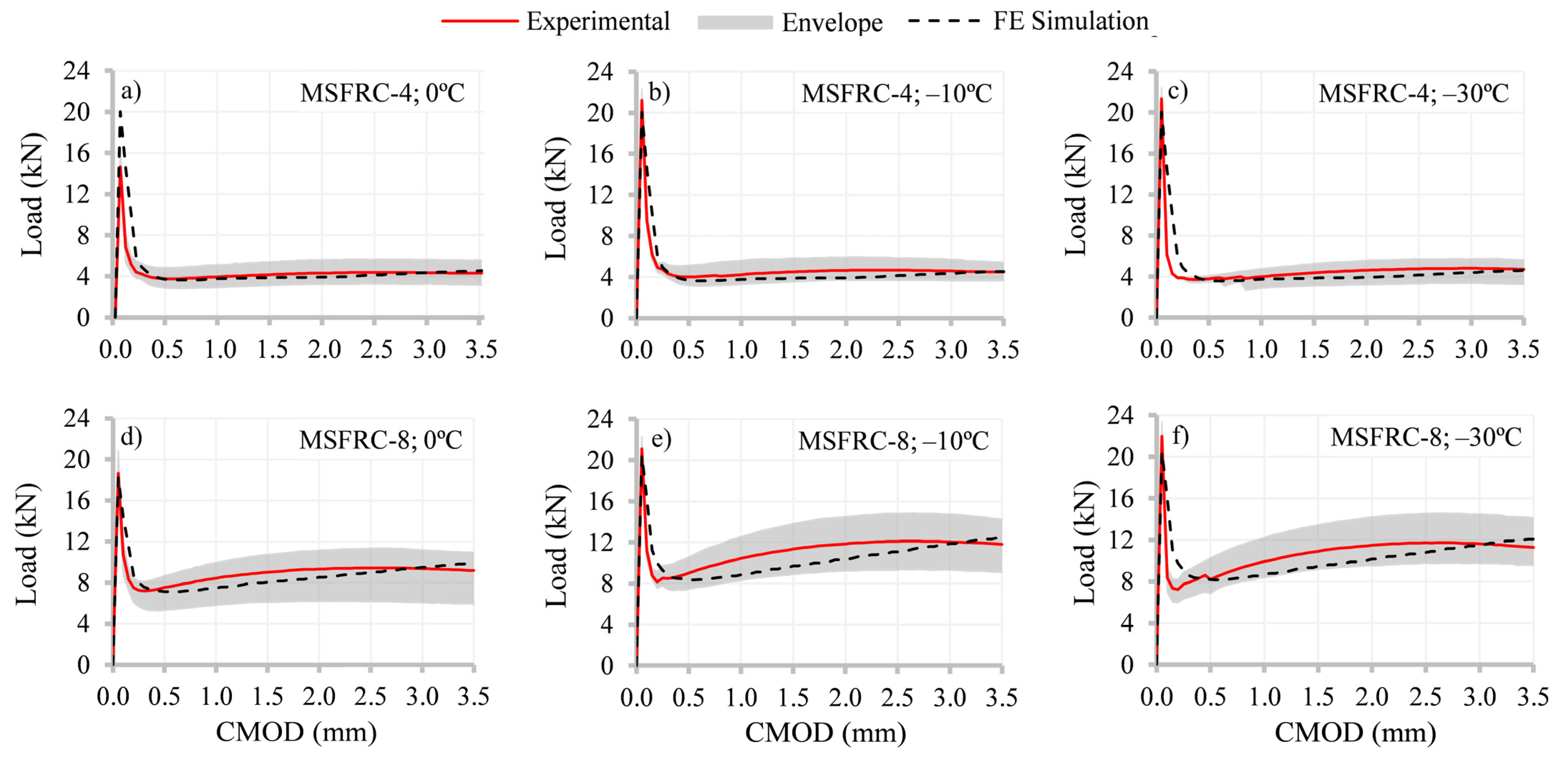
3. Experimental Results and Discussion
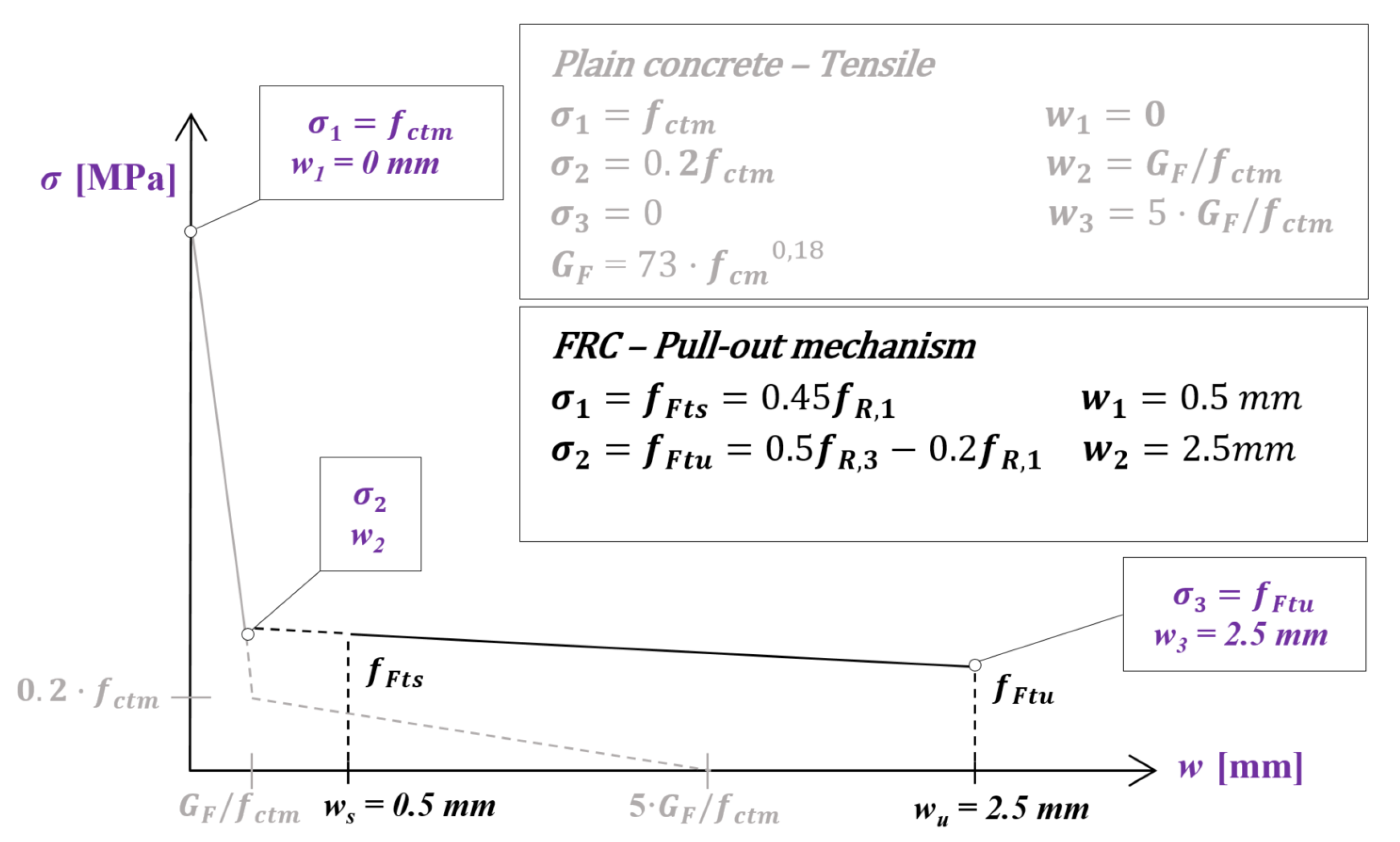
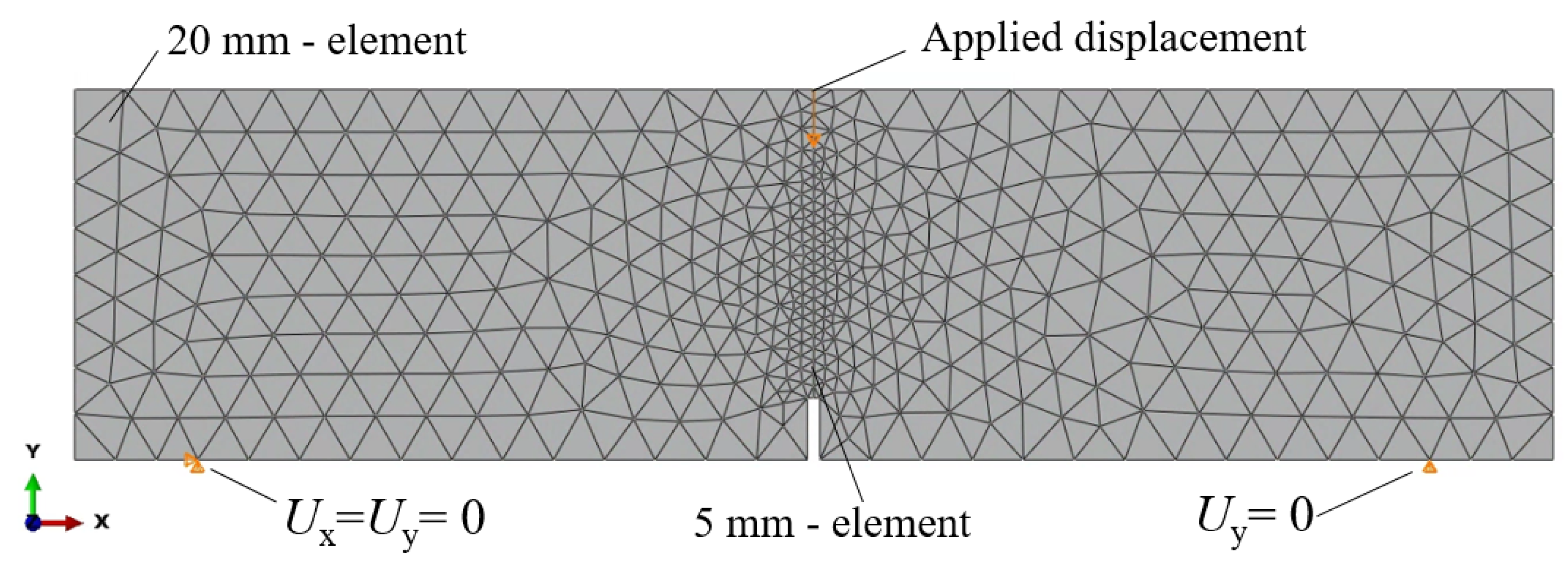
4. Numerical Analysis
5. Conclusions
- Low temperatures led to an increase in the required energy to produce fiber pull-out, and therefore, post-cracking flexural behavior was enhanced: fR1 and fR3 increased to 54% and 71%, respectively, for temperatures below 0 °C.
- A greater increase in fR3 at low temperatures (in comparison with the observed values of fR1) was observed. This could be due to the confinement effect caused by the shrinkage of the matrix embedding the fibers. This effect seemed to lead to a higher fiber bond (higher matrix–fiber friction). This outcome is of paramount importance for design procedures at ultimate conditions.
- The numerical analysis adopting the multi-linear constitutive model that is suggested by the fib Model Code 2010 evidenced a certain overestimation of the real flexural behavior in cases of studied MSFRC prismatic beams. This phenomenon led to the requirement of introducing correction factors to properly simulate the structural response of the elements in question. Importantly, the imposed correction factors (for both fR1 and fR3) were almost identical despite the temperature variation, although the fiber content did have an effect on these values.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fib. Fib Model Code for Concrete Structures 2010; International Federation for Structural Concrete (FIB): Lausanne, Switzerland, 2013; ISBN 9783433030615. [Google Scholar]
- Spanish Ministry of Public Works. Code on Structural Concrete, EHE-08, Permanent Commission of the Concrete; Spanish Ministry of Public Works: Madrid, Spain, 2008. [Google Scholar]
- RILEM. Bending Test: Final Recommendations; RILEM TC-162-TDF. Mater. Struct. 2002, 35, 579–582. [Google Scholar]
- Italian National Research Council CNR. CNR-DT 204/2006 Guide for the Design and Construction of Fiber-Reinforced Concrete Structures; Consiglio Nazionale Delle Ricerche: Rome, Italy, 2006. [Google Scholar]
- DBV. Guide to Good Practice Steel Fibre Concrete; German Society for Concrete and Construction Technology: Berlin, Germany, 2001. [Google Scholar]
- ACI Committee 544. Report on Design and Construction of Steel Fiber-Reinforced Concrete Elevated Slabs; American Concrete Institute: Farmington Hills, MI, USA, 2004; ISBN 9781942727323. [Google Scholar]
- Zollo, R.F. Fiber-reinforced Concrete: An Overview after 30 Years of Development. Cem. Concr. Compos. 1997, 19, 107–122. [Google Scholar] [CrossRef]
- Groli, G.; Pérez, A.; Marchetto, F.; Aríñez, F. Serviceability performance of FRC columns under imposed displacements: An experimental study. Eng. Struct. 2015, 101, 450–464. [Google Scholar] [CrossRef]
- Pujadas, P.; Blanco, A.; de la Fuente, A.; Aguado, A. Cracking behavior of FRC slabs with traditional reinforcement. Mater. Struct. Constr. 2012, 45, 707–725. [Google Scholar] [CrossRef] [Green Version]
- Tiberti, G.; Minelli, F.; Plizzari, G.A.; Vecchio, F.J. Influence of concrete strength on crack development in SFRC members. Cem. Concr. Compos. 2014, 45, 176–185. [Google Scholar] [CrossRef]
- Conforti, A.; Zerbino, R.; Plizzari, G.A. Influence of steel, glass and polymer fibers on the cracking behavior of reinforced concrete beams under flexure. Struct. Concr. 2018, 20, 133–143. [Google Scholar] [CrossRef] [Green Version]
- McMahon, J.A.; Birely, A.C. Service performance of steel fiber reinforced concrete (SFRC) slabs. Eng. Struct. 2018, 168, 58–68. [Google Scholar] [CrossRef]
- Serrano, R.; Cobo, A.; Prieto, M.I.; de las Nieves González, M. Analysis of fire resistance of concrete with polypropylene or steel fibers. Constr. Build. Mater. 2016, 122, 302–309. [Google Scholar] [CrossRef] [Green Version]
- Jin, L.; Zhang, R.; Dou, G.; Du, X. Fire resistance of steel fiber reinforced concrete beams after low-velocity impact loading. Fire Saf. J. 2018, 98, 24–37. [Google Scholar] [CrossRef]
- Khaliq, W.; Kodur, V.; Asce, F. Effectiveness of Polypropylene and Steel Fibers in Enhancing Fire Resistance of High-Strength Concrete Columns. J. Struct. Eng. 2018, 144, 1–12. [Google Scholar] [CrossRef]
- Carlesso, D.M.; de la Fuente, A.; Cavalaro, S.H.P. Fatigue of cracked high performance fiber reinforced concrete subjected to bending. Constr. Build. Mater. 2019, 220, 444–455. [Google Scholar] [CrossRef]
- Germano, F.; Tiberti, G. Post-peak fatigue performance of steel fiber reinforced concrete under flexure. Mater. Struct. 2015, 49(10), 4229–4245. [Google Scholar] [CrossRef]
- Fall, D.; Shu, J.; Rempling, R.; Lundgren, K.; Zandi, K. Two-way slabs: Experimental investigation of load redistributions in steel fibre reinforced concrete. Eng. Struct. 2014, 80, 61–74. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, S.M.F.; Foster, S.J.; Valipour, H. Moment redistribution and post-peak behaviour of lightly reinforced-SFRC continuous slabs. Eng. Struct. 2021, 232, 111834. [Google Scholar] [CrossRef]
- Nogales, A.; Tošić, N.; de la Fuente, A. Rotation and moment redistribution capacity of fibre reinforced concrete beams: Parametric analysis and code compliance. Struct. Concr. 2021. (Online version before inclusion in an issue). [Google Scholar] [CrossRef]
- Venkateshwaran, A.; Tan, K.H. Moment redistribution in continuous steel-fibre-reinforced concrete slabs. Struct. Build. 2020, 173, 161–174. [Google Scholar] [CrossRef]
- Nia, A.A.; Hedayatian, M.; Nili, M.; Sabet, V.A. An experimental and numerical study on how steel and polypropylene fibers affect the impact resistance in fiber-reinforced concrete. Int. J. Impact Eng. 2012, 46, 62–73. [Google Scholar] [CrossRef]
- Teng, T.; Chu, Y.-A.; Chang, F.-A.; Shen, B.-C.; Cheng, D.-S. Development and validation of numerical model of steel fiber reinforced concrete for high-velocity impact. Comput. Mater. Sci. 2008, 42, 90–99. [Google Scholar] [CrossRef]
- Rai, B.; Singh, N.K. Statistical and experimental study to evaluate the variability and reliability of impact strength of steel-polypropylene hybrid fiber reinforced concrete. J. Build. Eng. 2021, 44, 102937. [Google Scholar] [CrossRef]
- Vivas, J.C.; Zerbino, R.; Torrijos, M.; Giaccio, G. A test procedure for evaluating the impact behaviour of fibre reinforced concrete. Mater. Struct. 2021, 54, 208. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Q.; Yuan, Y.; Taerwe, L. Comparison of the structural behavior of reinforced concrete tunnel segments with steel fiber and synthetic fiber addition. Tunn. Undergr. Space Technol. 2020, 103, 103506. [Google Scholar] [CrossRef]
- Conforti, A.; Trabucchi, I.; Tiberti, G.; Plizzari, G.A.; Caratelli, A.; Meda, A. Precast tunnel segments for metro tunnel lining: A hybrid reinforcement solution using macro-synthetic fi bers. Eng. Struct. 2019, 199, 109628. [Google Scholar] [CrossRef]
- De la Fuente, A.; Pujadas, P.; Blanco, A.; Aguado, A. Experiences in Barcelona with the use of fibres in segmental linings. Tunn. Undergr. Sp. Technol. 2012, 27, 60–71. [Google Scholar] [CrossRef] [Green Version]
- Aidarov, S.; Mena, F.; de la Fuente, A. Structural response of a fibre reinforced concrete pile-supported flat slab: Full-scale test. Eng. Struct. 2021, 239, 112292. [Google Scholar] [CrossRef]
- Leporace-Guimil, B.; Mudadu, A.; Conforti, A.; Plizzari, G.A. Influence of fiber orientation and structural-integrity reinforcement on the flexural behavior of elevated slabs. Eng. Struct. 2021, 113583. [Google Scholar] [CrossRef]
- Di Prisco, M.; Colombo, M.; Pourzarabi, A. Biaxial bending of SFRC slabs: Is conventional reinforcement necessary? Mater. Struct. Constr. 2019, 52, 1–15. [Google Scholar] [CrossRef]
- De la Fuente, A.; Aguado, A.; Molins, C.; Armengou, J. Innovations on components and testing for precast panels to be used in reinforced earth retaining walls. Constr. Build. Mater. 2011, 25, 2198–2205. [Google Scholar] [CrossRef]
- Meda, A.; Plizzari, G.A.; Riva, P. Fracture behavior of SFRC slabs on grade. Mater. Struct. Constr. 2004, 37, 405–411. [Google Scholar] [CrossRef]
- Meda, A.; Plizzari, G.A. New design approach for steel fiber-reinforced concrete slabs-on-ground based on fracture mechanics. ACI Struct. J. 2004, 101, 298–303. [Google Scholar] [CrossRef]
- Aidarov, S.; Mena, F.; de la Fuente, A. Self-compacting Steel Fibre Reinforced Concrete: Material Characterization and Real Scale Test up to Failure of a Pile Supported Flat Slab. In Proceedings of the RILEM-fib International Symposium on Fibre Reinforced Concrete, Valencia, Spain, 20–22 September 2021; Springer: Cham, Switzerland, 2021; pp. 702–713. [Google Scholar]
- Alberti, M.G.; Enfedaque, A.; Gálvez, J.C. The effect of fibres in the rheology of self-compacting concrete. Constr. Build. Mater. 2019, 219, 144–153. [Google Scholar] [CrossRef]
- Cavalaro, S.H.P.; Aguado, A. Intrinsic scatter of FRC: An alternative philosophy to estimate characteristic values. Mater. Struct. Constr. 2015, 48, 3537–3555. [Google Scholar] [CrossRef] [Green Version]
- Tiberti, G.; Germano, F.; Mudadu, A.; Plizzari, G.A. An overview of the flexural post-cracking behavior of steel fiber reinforced concrete. Struct. Concr. 2018, 19, 695–718. [Google Scholar] [CrossRef]
- Parmentier, B.; De Grove, E.; Vandewalle, L.; Van Rickstal, F. Dispersion of the mechanical properties of FRC investigated by different bending tests. In Tailor Made Concrete Structures; Taylor & Francis Group: Abingdon, UK, 2008; pp. 507–512. [Google Scholar]
- Amin, A.; Gilbert, R.I. Instantaneous crack width calculation for steel fiber-reinforced concrete flexural members. ACI Struct. J. 2018, 115, 535–543. [Google Scholar] [CrossRef]
- Colombo, M.; Martinelli, P.; di Prisco, M. On the evaluation of the structural redistribution factor in FRC design: A yield line approach. Mater. Struct. 2017, 50, 1–18. [Google Scholar] [CrossRef]
- De la Fuente, A.; Escariz, R.C.; de Figueiredo, A.D.; Aguado, A. Design of macro-synthetic fibre reinforced concrete pipes. Constr. Build. Mater. 2013, 43, 523–532. [Google Scholar] [CrossRef]
- Di Prisco, M.; Martinelli, P.; Parmentier, B. On the reliability of the design approach for FRC structures according to fib Model Code 2010: The case of elevated slabs. Struct. Concr. 2016, 17, 588–602. [Google Scholar] [CrossRef]
- Di Prisco, M.; Plizzari, G.; Vandewalle, L. Fibre reinforced concrete: New design perspectives. Mater. Struct. Constr. 2009, 42, 1261–1281. [Google Scholar] [CrossRef]
- Facconi, L.; Minelli, F. Verification of structural elements made of FRC only: A critical discussion and proposal of a novel analytical method. Eng. Struct. 2017, 131, 530–541. [Google Scholar] [CrossRef]
- Facconi, L.; Plizzari, G.; Minelli, F. Elevated slabs made of hybrid reinforced concrete: Proposal of a new design approach in flexure. Struct. Concr. 2019, 20, 52–67. [Google Scholar] [CrossRef] [Green Version]
- Enfedaque, A.; Alberti, M.G.; Gálvez, J.C.; Domingo, J. Numerical simulation of the fracture behaviour of glass fibre reinforced cement. Constr. Build. Mater. 2017, 136, 108–117. [Google Scholar] [CrossRef]
- Enfedaque, A.; Alberti, M.G.; Galvez, J. Analysis of the Versatility of Multi-Linear Softening Functions Applied in the Simulation of Fracture Behaviour of Fibre-Reinforced Cementitious Materials. Materials 2019, 12, 3656. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Enfedaque, A.; Alberti, M.G.; Galvez, J.; Cabanas, P. Numerical Simulation of the Fracture Behavior of High-Performance Fiber-Reinforced Concrete by Using a Cohesive Crack-Based Inverse Analysis. Materials 2022, 15, 71. [Google Scholar] [CrossRef] [PubMed]
- de Maio, U.; Fantuzzi, N.; Greco, F.; Leonetti, L.; Pranno, A. Failure Analysis of Ultra High-Performance Fiber-Reinforced Concrete Structures Enhanced with Nanomaterials by Using a Diffuse Cohesive Interface Approach. Nanomaterials 2020, 10, 1792. [Google Scholar] [CrossRef] [PubMed]
- Di Prisco, M.; Martinelli, P.; Dozio, D. The structural redistribution coefficient KRd: A numerical approach to its evaluation. Struct. Concr. 2016, 17, 390–407. [Google Scholar] [CrossRef]
- Фoтoграф Сергей Филинин. Available online: https://sergeyfilinin.ru/#portfolio (accessed on 25 December 2021).
- Lee, G.C.; Shih, S.; Chang, K.C. Mechanical Properties of Concrete at Low Temperature. J. Cold Reg. Eng. 1988, 2, 13–24. [Google Scholar] [CrossRef]
- Xie, J.; Yan, J.B. Experimental studies and analysis on compressive strength of normal-weight concrete at low temperatures. Struct. Concr. 2018, 19, 1235–1244. [Google Scholar] [CrossRef]
- Montejo, L.A.; Sloan, J.E.; Kowalsky, M.J.; Hassan, T. Cyclic Response of Reinforced Concrete Members at Low Temperatures. J. Cold Reg. Eng. 2008, 22, 79–102. [Google Scholar] [CrossRef]
- Pigeon, M.; Cantin, R. Flexural properties of steel fiber-reinforced concretes at low temperatures. Cem. Concr. Compos. 1998, 20, 365–375. [Google Scholar] [CrossRef]
- Caballero-Jorna, M.; Roig-Flores, M.; Serna, P. Short-term effects of moderate temperatures on the mechanical properties of steel and macrosynthetic fiber reinforced concretes. In Proceedings of the RILEM-Fib X International Symposium on Fibre Reinforced Concrete BEFIB 2021, Valencia, Spain, 20–22 September 2021; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Richardson, A.; Ovington, R. Temperature related steel and synthetic fibre concrete performance. Constr. Build. Mater. 2017, 153, 616–621. [Google Scholar] [CrossRef]
- CEN. EN 14651; Test Method for Metallic Fibre Concrete. Measuring the Flexural Tensile Strength (Limit of Proportionality (LOP), Residual). European Committee for Standardization: Bruxelles, Belgium, 2007; ISBN 9780580610523.
- CEN. EN 12350-2:2019; Testing Fresh Concrete. Slump Test. European Committee for Standardization: Bruxelles, Belgium, 2019.
- König, G.; Kützing, L. Modelling the increase of ductility of HPC under compressive forces—A fracture mechanical approach. In Proceedings of the Third International RILEM Workshop on High Performance Fiber Reinforced Cement Composites, Mainz, Germany, 16–19 May 1999; RILEM Publications SARL: Bagneux, France, 1999; pp. 251–260. [Google Scholar]
- Mena, F.; Aidarov, S.; de la Fuente, A. Hormigones autocompactantes reforzados con fibras para aplicaciones con alta responsabilidad estructural. Campaña experimental en laboratorio. In Proceedings of the III Congreso de Consultores de Estructuras, Barcelona, Spain, 3–5 April 2019; pp. 1–10. [Google Scholar]
- Bentur, A.; Mindess, S. Fibre Reinforced Cementitious Composites; Taylor & Francis: Abingdon, UK, 2007. [Google Scholar]
- Kim, J.K.; Mai, Y.-W. High strength, high fracture toughness fibre composites with interface control-A review. Compos. Sci. Technol. 1991, 41, 333–378. [Google Scholar] [CrossRef]
- Galeote, E.; Nogales, A.; de la Fuente, A. Analysis of design constitutive model for plastic fibre reinforced concrete through inverse analysis. In Proceedings of the 75th RILEM Week, Merida, Mexico, 29 August–3 September 2021; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Nogales, A.; Galeote, E.; de la Fuente, A. Finite element analysis characterization of macro synthetic fibre reinforced concrete constitutive equation. In Proceedings of the 75th RILEM Week, Merida, Mexico, 29 August–3 September 2021; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Dassault Systèmes Simulia. Abaqus CAE User’s Manual (6.12); Dassault Systèmes: Vélizy-Villacoublay, France, 2012. [Google Scholar]
- Nogales, A.; de la Fuente, A. Elevated Flat Slab of Fibre Reinforced Concrete Non-Linear Simulation up to Failure; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; Volume 36, ISBN 9783030837198. [Google Scholar]



| Materials | MSFRC-4 | MSFRC-8 |
|---|---|---|
| CEM II-A/L 42.5R (kg/m3) | 310 | 310 |
| Coarse aggregate 10/20 (kg/m3) | 690 | 680 |
| Coarse aggregate 4/10 (kg/m3) | 127 | 125 |
| Fine aggregate 0/4 (kg/m3) | 1025 | 1025 |
| Water-cement ratio | 0.58 | 0.58 |
| Additives (% on cement content) | 1.2 | 1.5 |
| Synthetic fibers (kg/m3) | 4 | 8 |
| Property | PPF | Representation |
|---|---|---|
| Material | Transparent polypropylene |  |
| Shape | Embossed monofilament | |
| Diameter (mm) | 0.85 | |
| Length (mm) | 48 | |
| Aspect ratio | 56.5 | |
| Number of fibers per kg | 41,200 | |
| Tensile strength (MPa) | >400 |
| Temperature (°C) | MSFRC-4 | MSFRC-8 | |||||
|---|---|---|---|---|---|---|---|
| fR,EXP (MPa) | fR,NL (Mpa) | fR,NL/fR,EXP | fR,EXP (Mpa) | fR,NL (Mpa) | fR,NL/fR,EXP | ||
| fR1 | 20 | 0.94 | 0.60 | 0.64 | 1.88 | 1.35 | 0.72 |
| 0 | 1.20 | 0.80 | 0.67 | 2.4 | 1.80 | 0.75 | |
| −10 | 1.23 | 0.80 | 0.65 | 2.89 | 2.25 | 0.78 | |
| −30 | 1.22 | 0.80 | 0.66 | 2.83 | 2.25 | 0.80 | |
| fR3 | 20 | 1.03 | 1.03 | 1.00 | 2.26 | 2.40 | 1.06 |
| 0 | 1.40 | 1.60 | 1.14 | 3.02 | 3.20 | 1.06 | |
| −10 | 1.49 | 1.80 | 1.21 | 3.87 | 4.60 | 1.19 | |
| −30 | 1.52 | 1.80 | 1.18 | 3.75 | 4.60 | 1.23 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aidarov, S.; Nogales, A.; Reynvart, I.; Tošić, N.; de la Fuente, A. Effects of Low Temperatures on Flexural Strength of Macro-Synthetic Fiber Reinforced Concrete: Experimental and Numerical Investigation. Materials 2022, 15, 1153. https://doi.org/10.3390/ma15031153
Aidarov S, Nogales A, Reynvart I, Tošić N, de la Fuente A. Effects of Low Temperatures on Flexural Strength of Macro-Synthetic Fiber Reinforced Concrete: Experimental and Numerical Investigation. Materials. 2022; 15(3):1153. https://doi.org/10.3390/ma15031153
Chicago/Turabian StyleAidarov, Stanislav, Alejandro Nogales, Igor Reynvart, Nikola Tošić, and Albert de la Fuente. 2022. "Effects of Low Temperatures on Flexural Strength of Macro-Synthetic Fiber Reinforced Concrete: Experimental and Numerical Investigation" Materials 15, no. 3: 1153. https://doi.org/10.3390/ma15031153
APA StyleAidarov, S., Nogales, A., Reynvart, I., Tošić, N., & de la Fuente, A. (2022). Effects of Low Temperatures on Flexural Strength of Macro-Synthetic Fiber Reinforced Concrete: Experimental and Numerical Investigation. Materials, 15(3), 1153. https://doi.org/10.3390/ma15031153







