A Modified Two-Relaxation Thermoelastic Model for a Thermal Shock of Rotating Infinite Medium
Abstract
1. Introduction
2. Basic Governing Equations
3. Formulation of the Problem
4. Solution of the Problem
5. Boundary Conditions
5.1. Mechanical Conditions
5.2. Thermal Condition
5.3. Traction Free Half-Space
6. Special and Particular Cases
6.1. A Special Case
6.2. Particular Cases
- (a)
- When we put we obtain the reduced equations of the CTE theory.
- (b)
- When we put , and we achieve the equations of the simple LS theory.
- (c)
- The simple GL theory is obtained by putting , and .
- (d)
- If we put , and we achieve the equations of the refined LS theory.
- (e)
- Finally, if we put , and we obtain the refined GL theory.
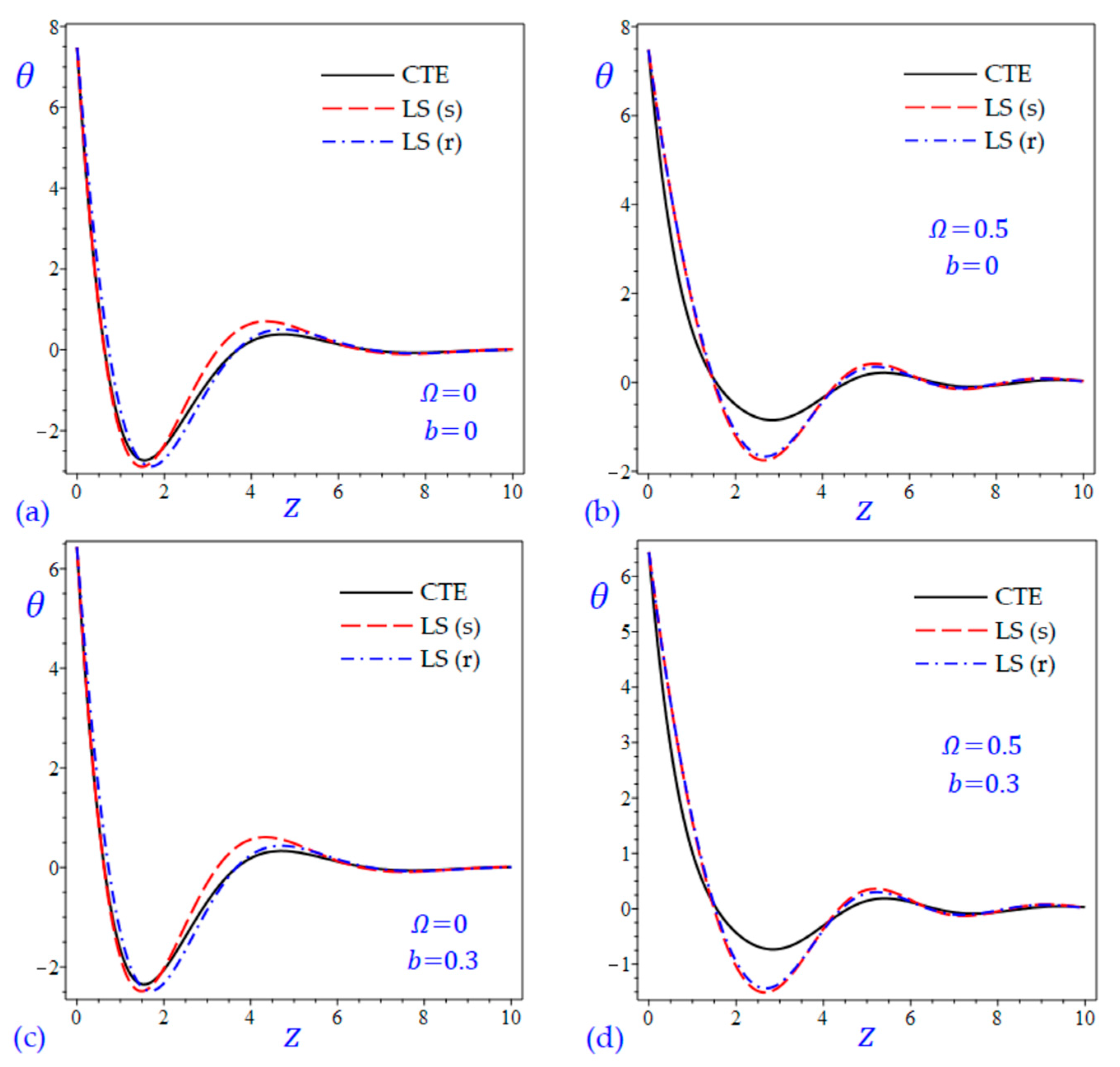
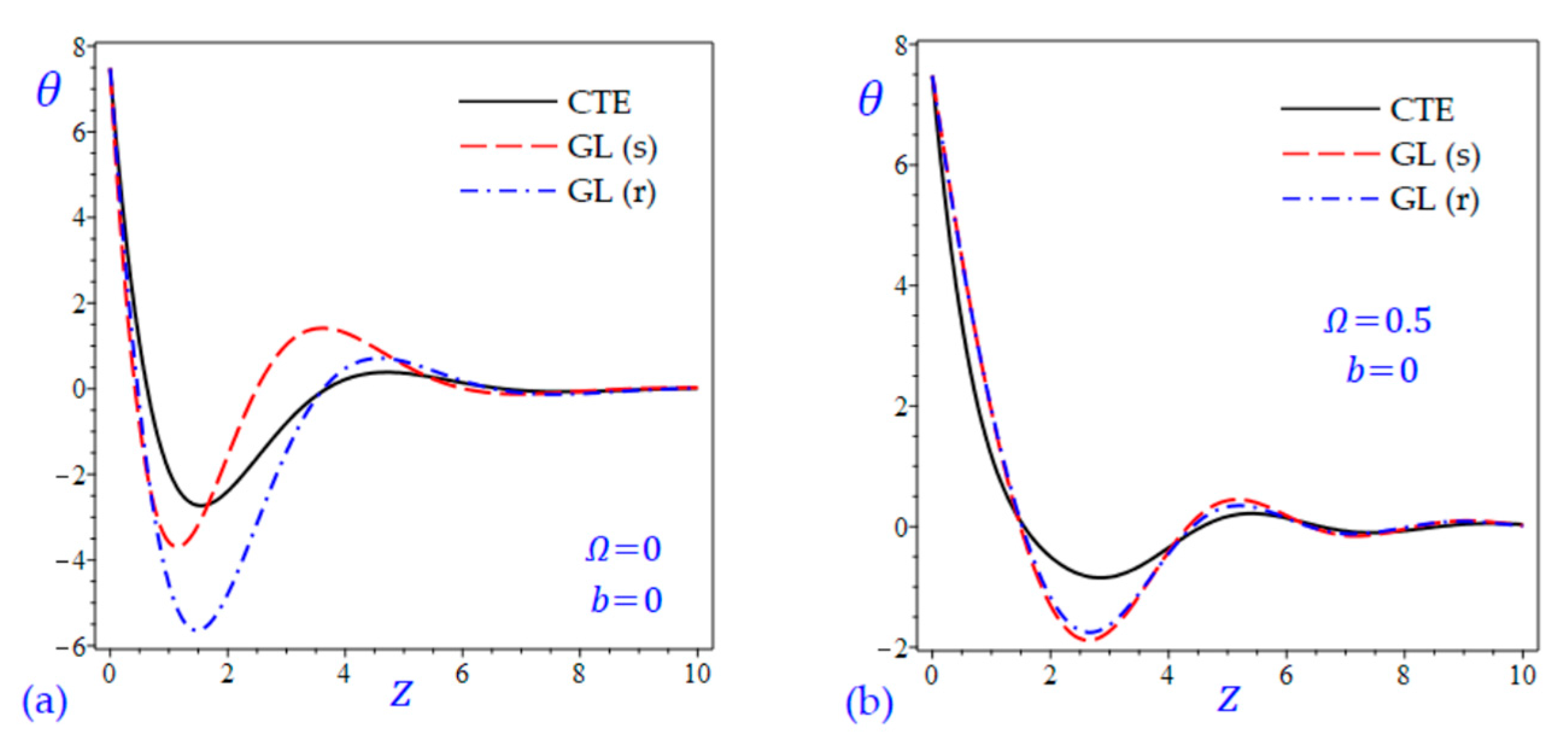
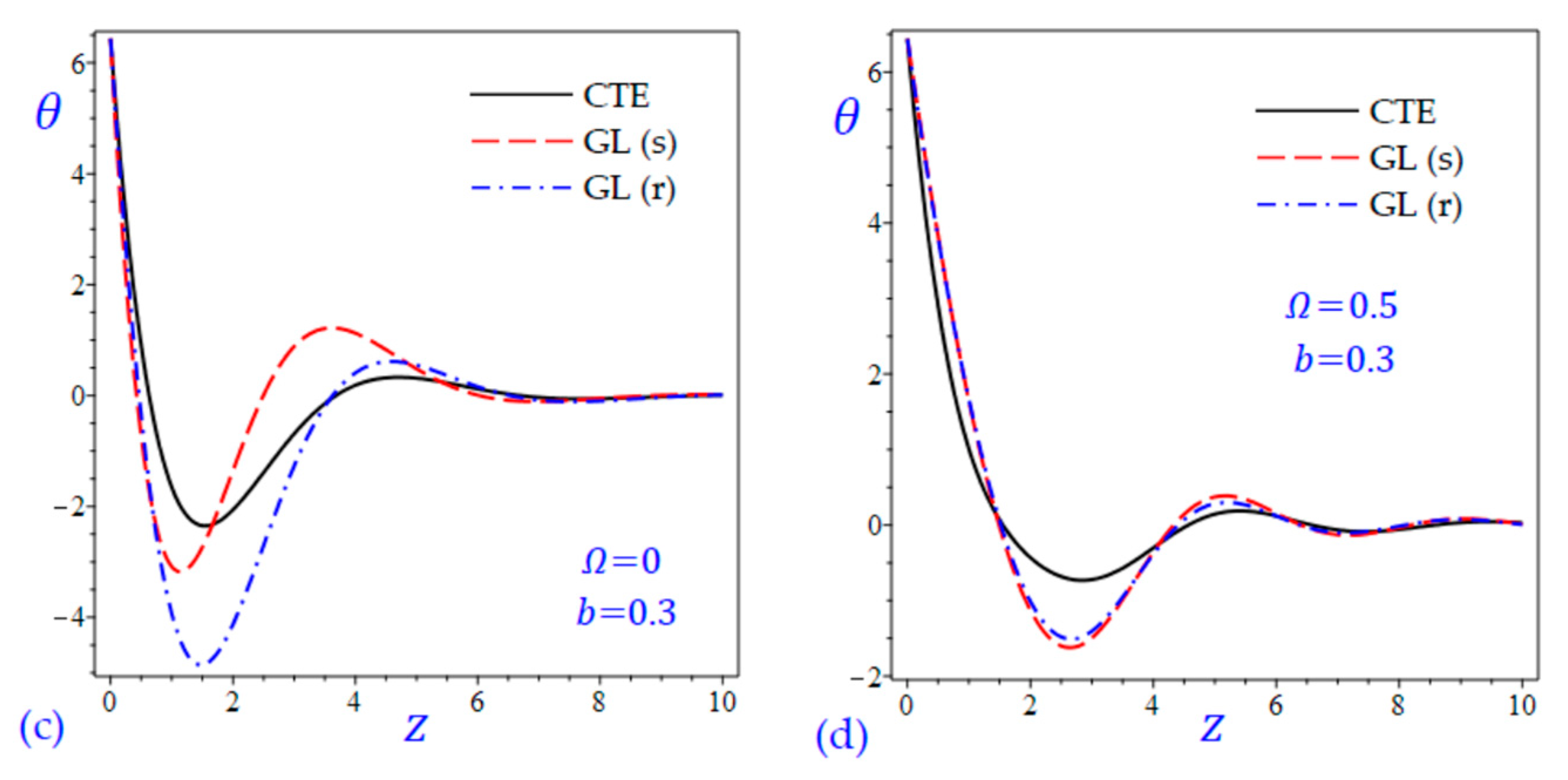
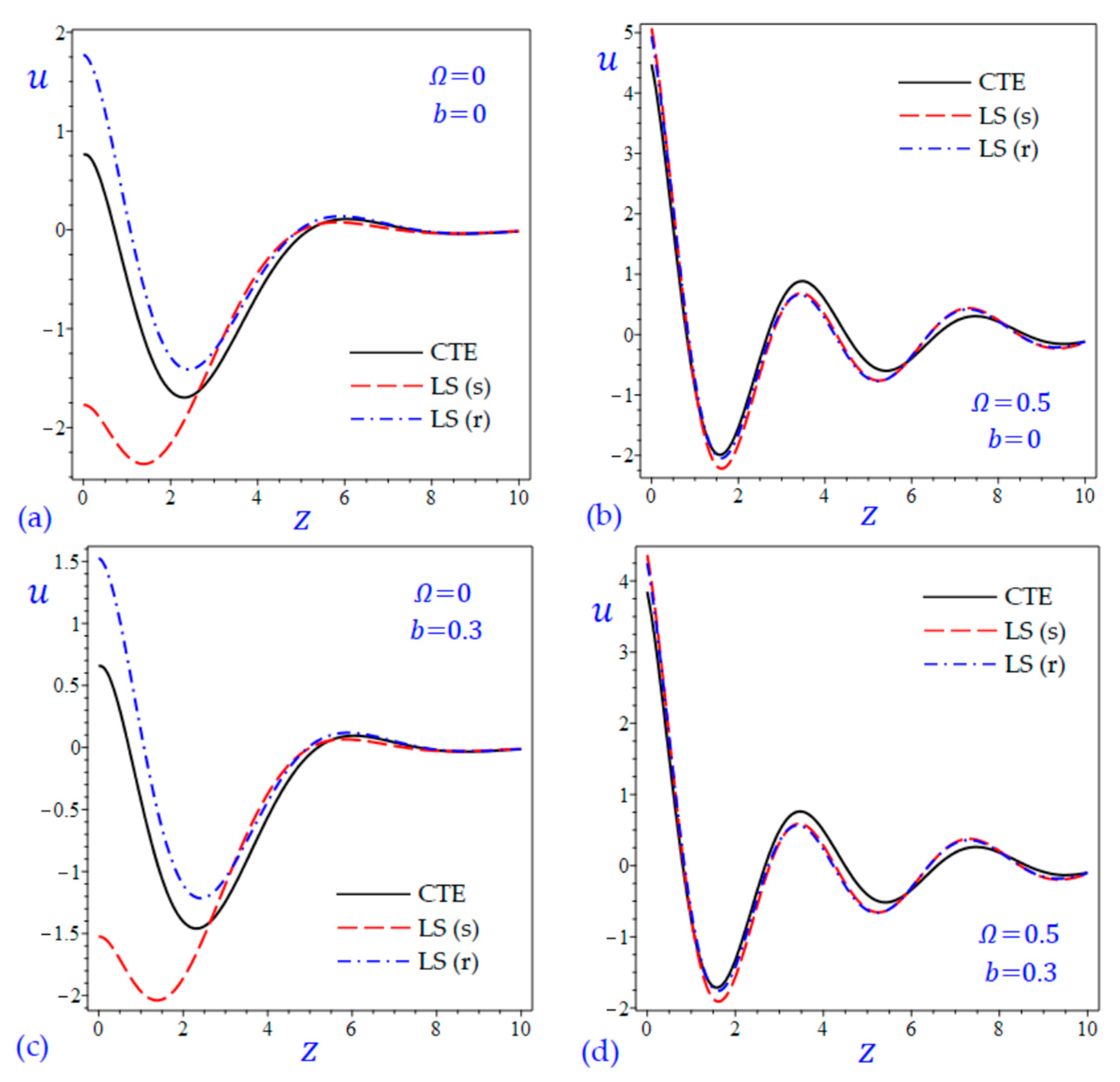
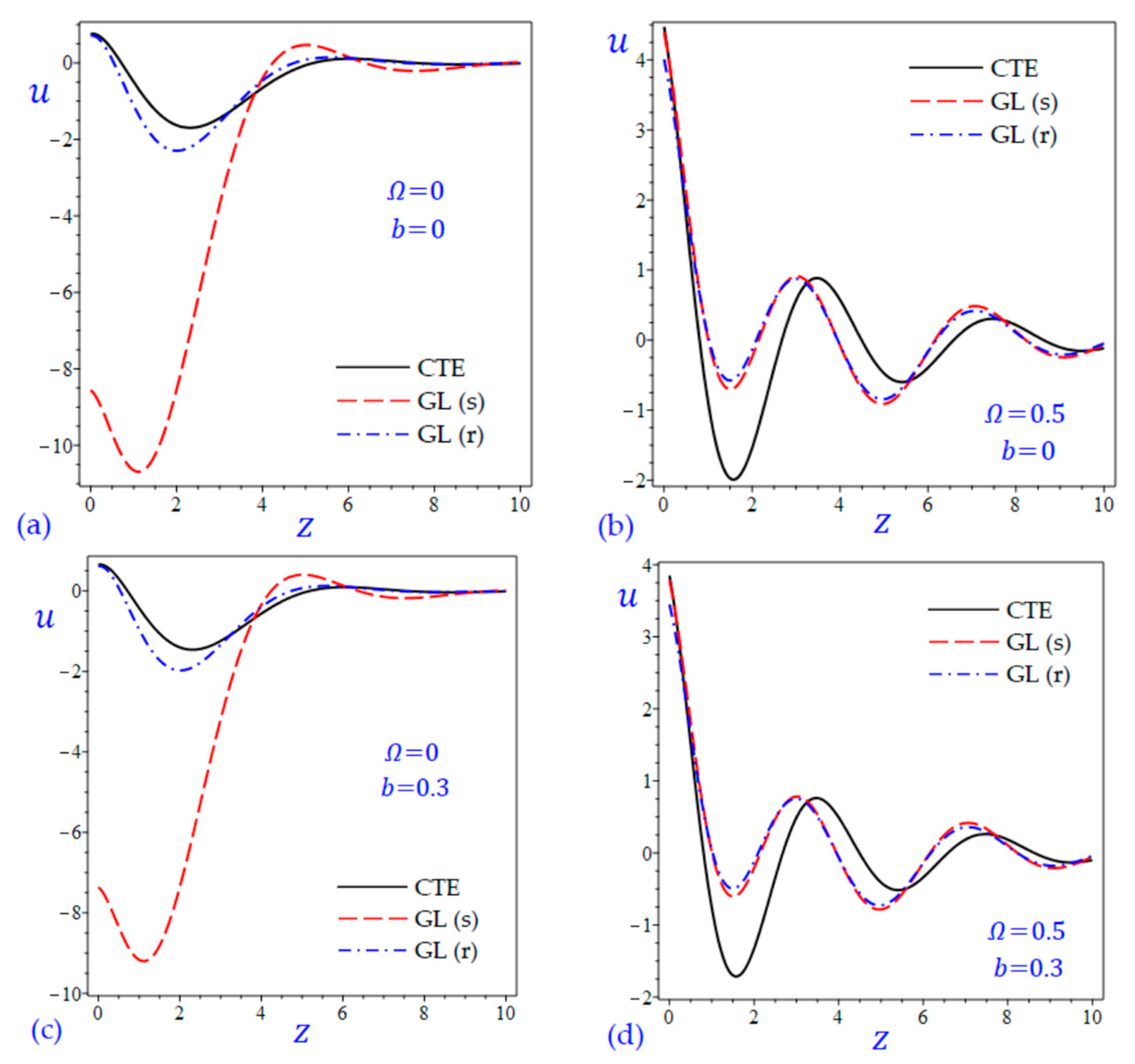
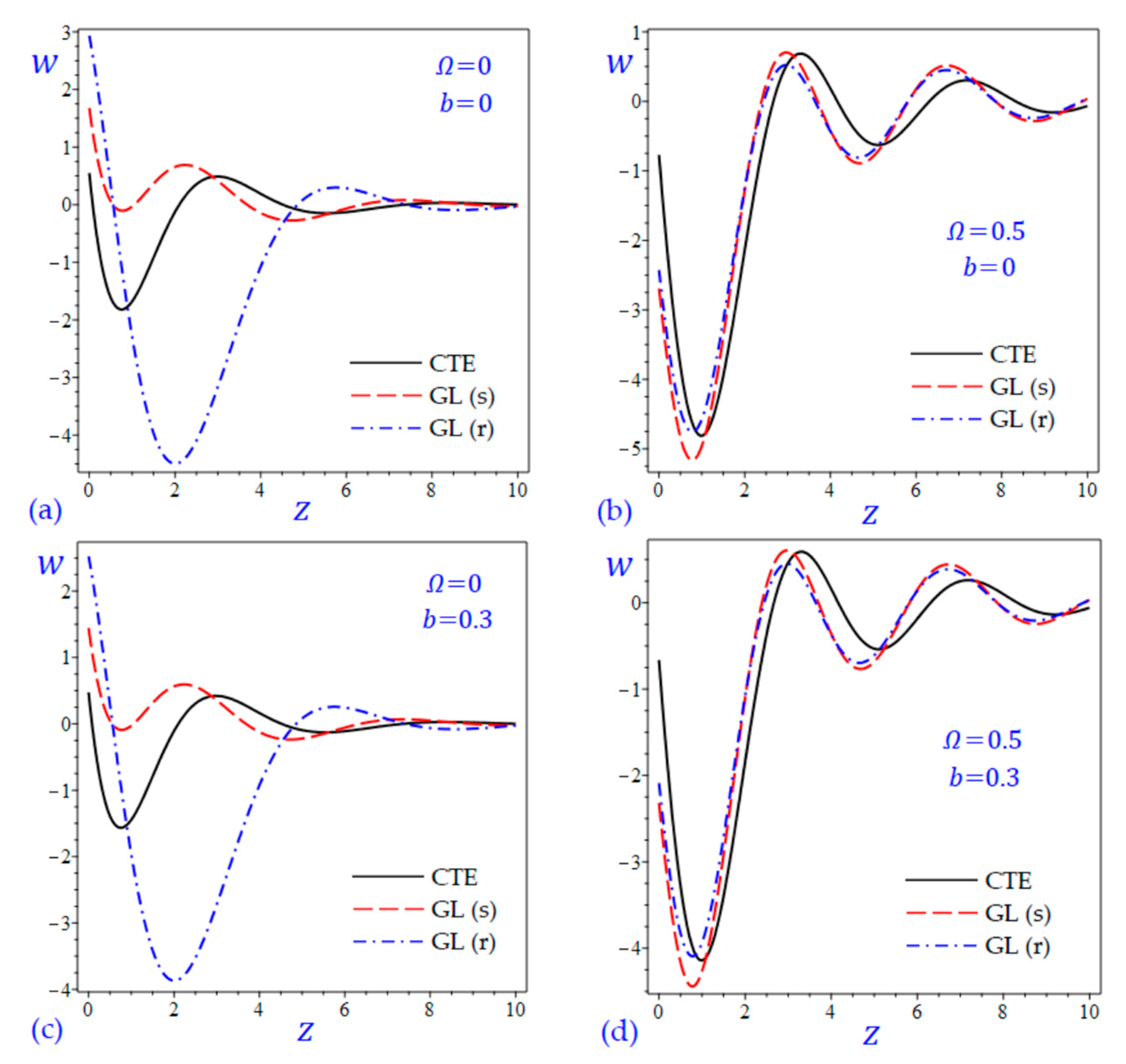
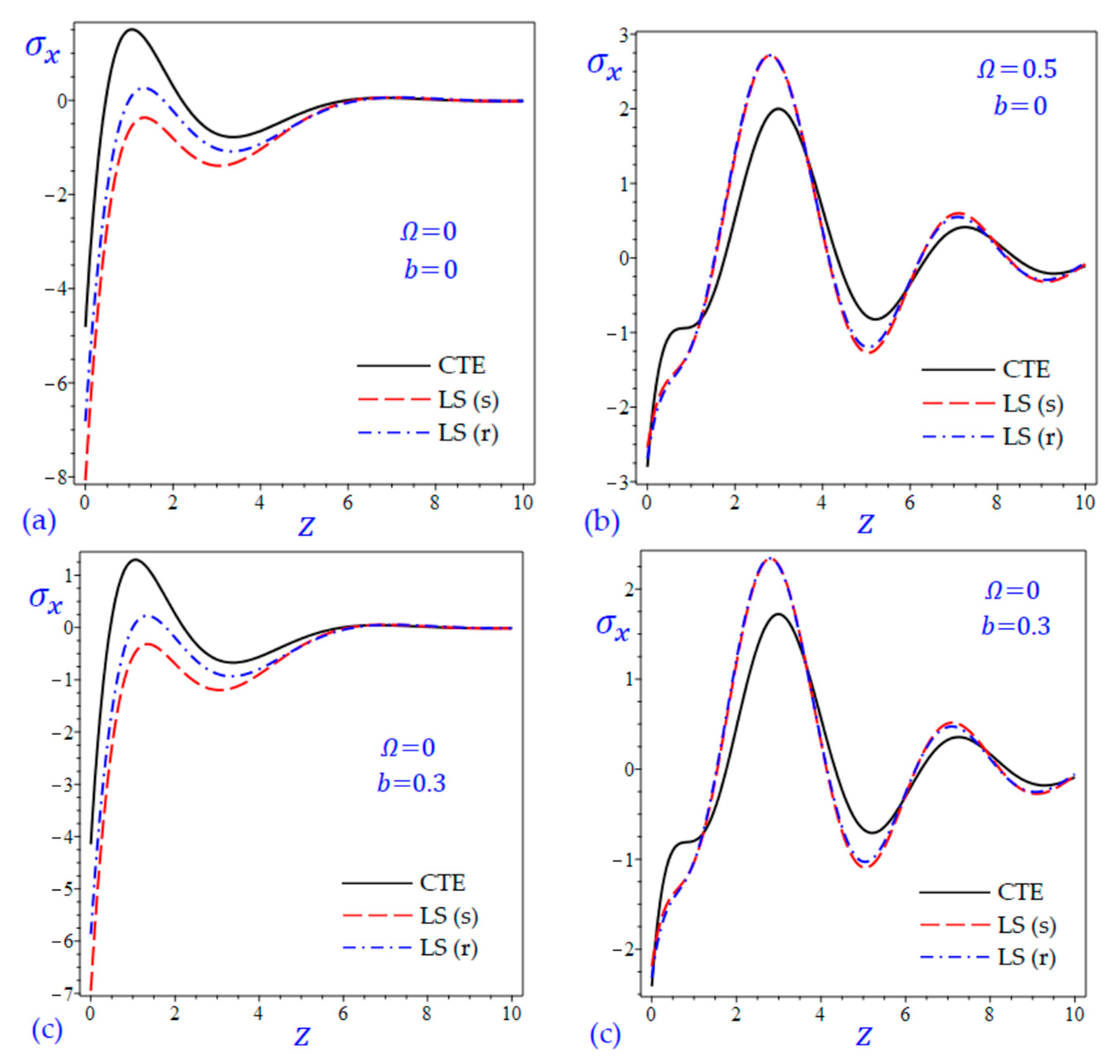
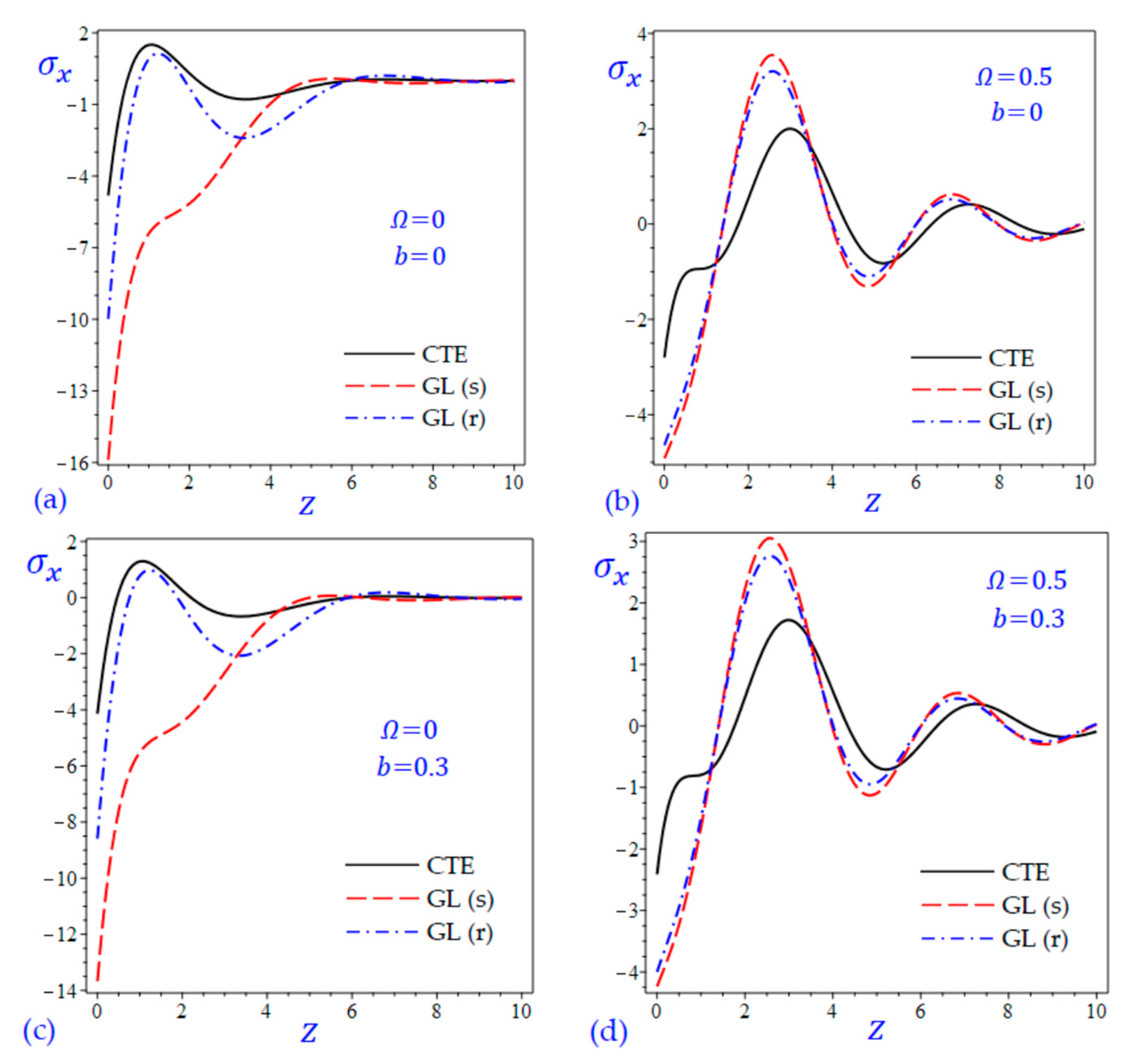
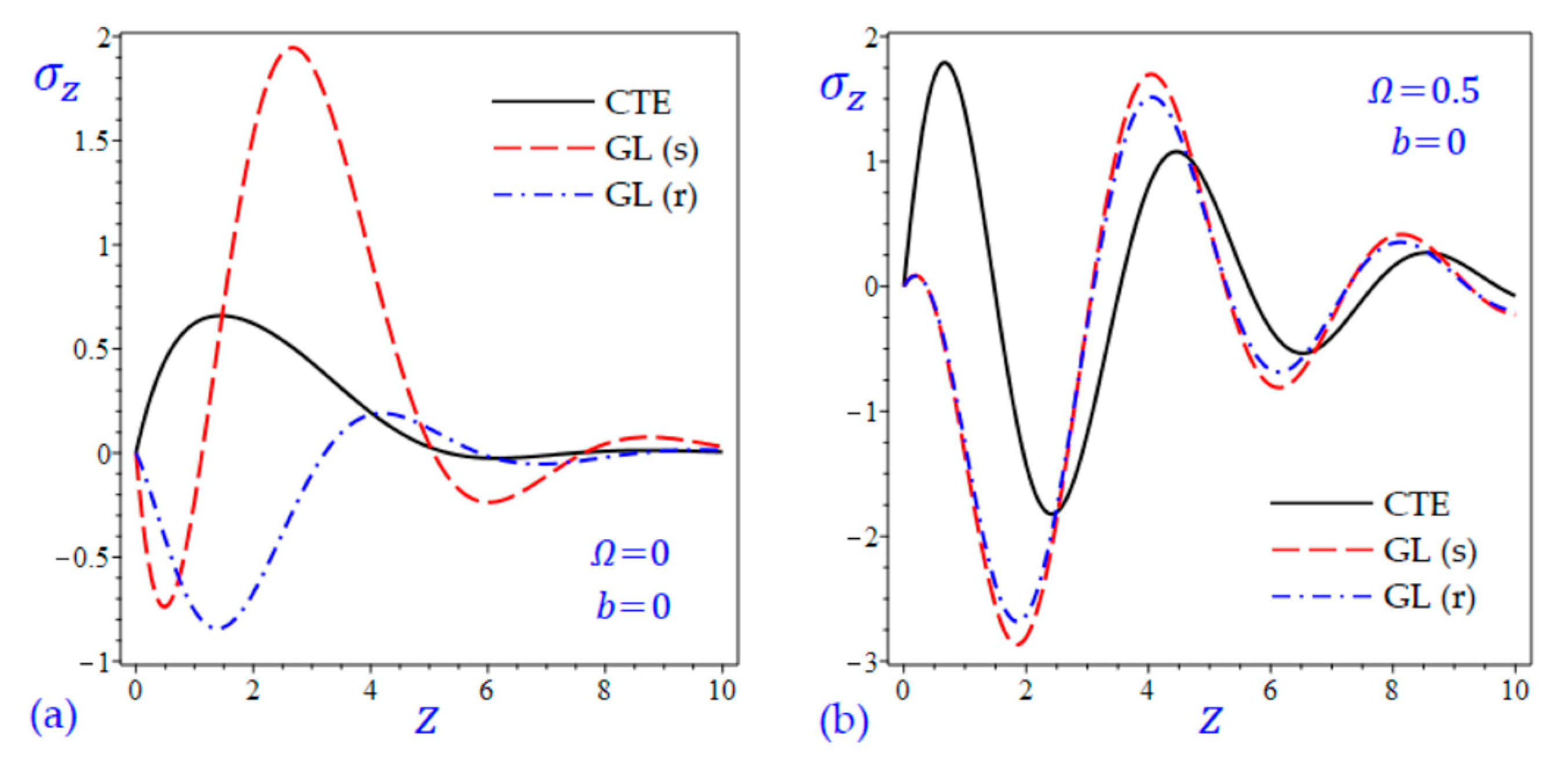
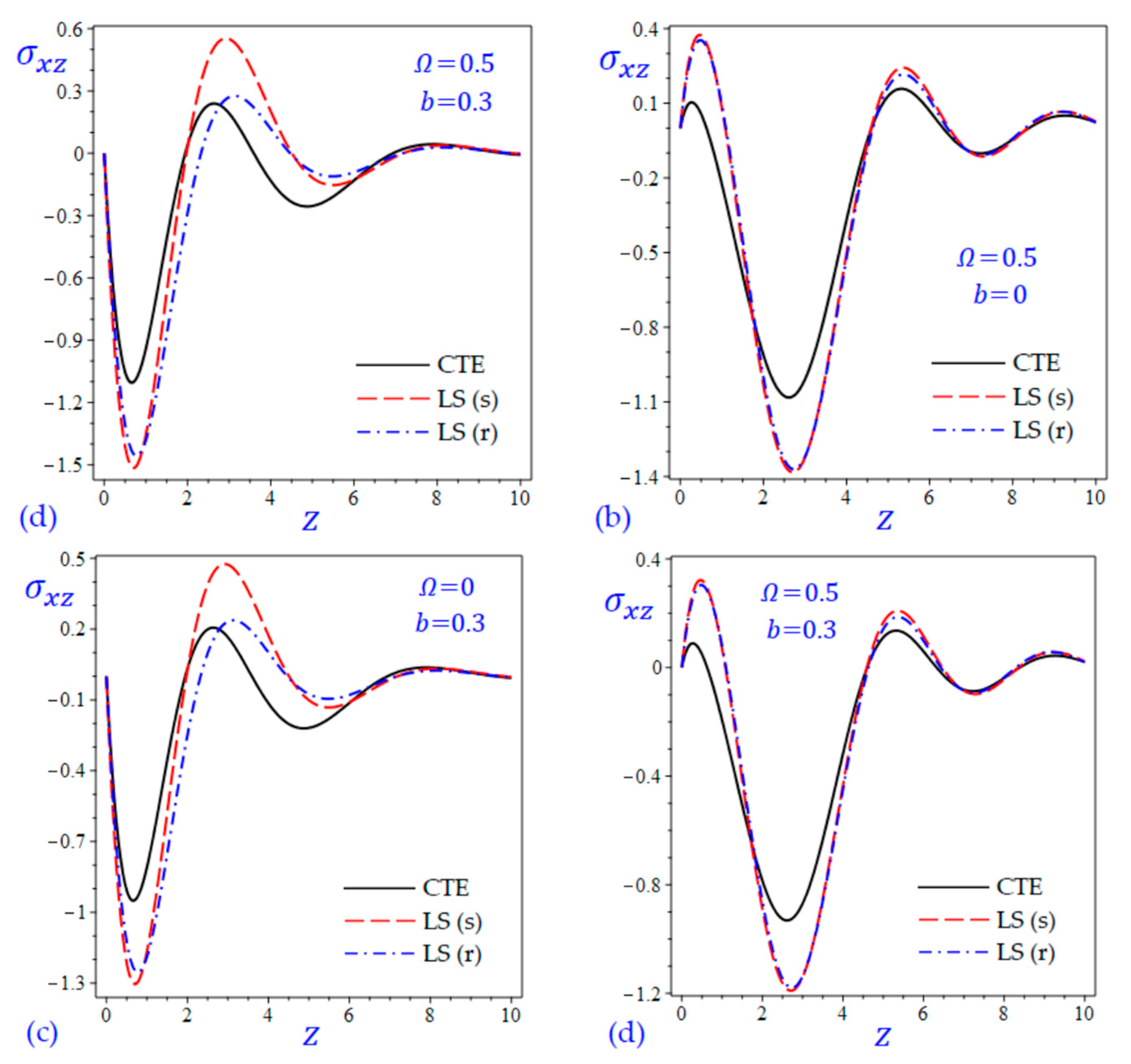
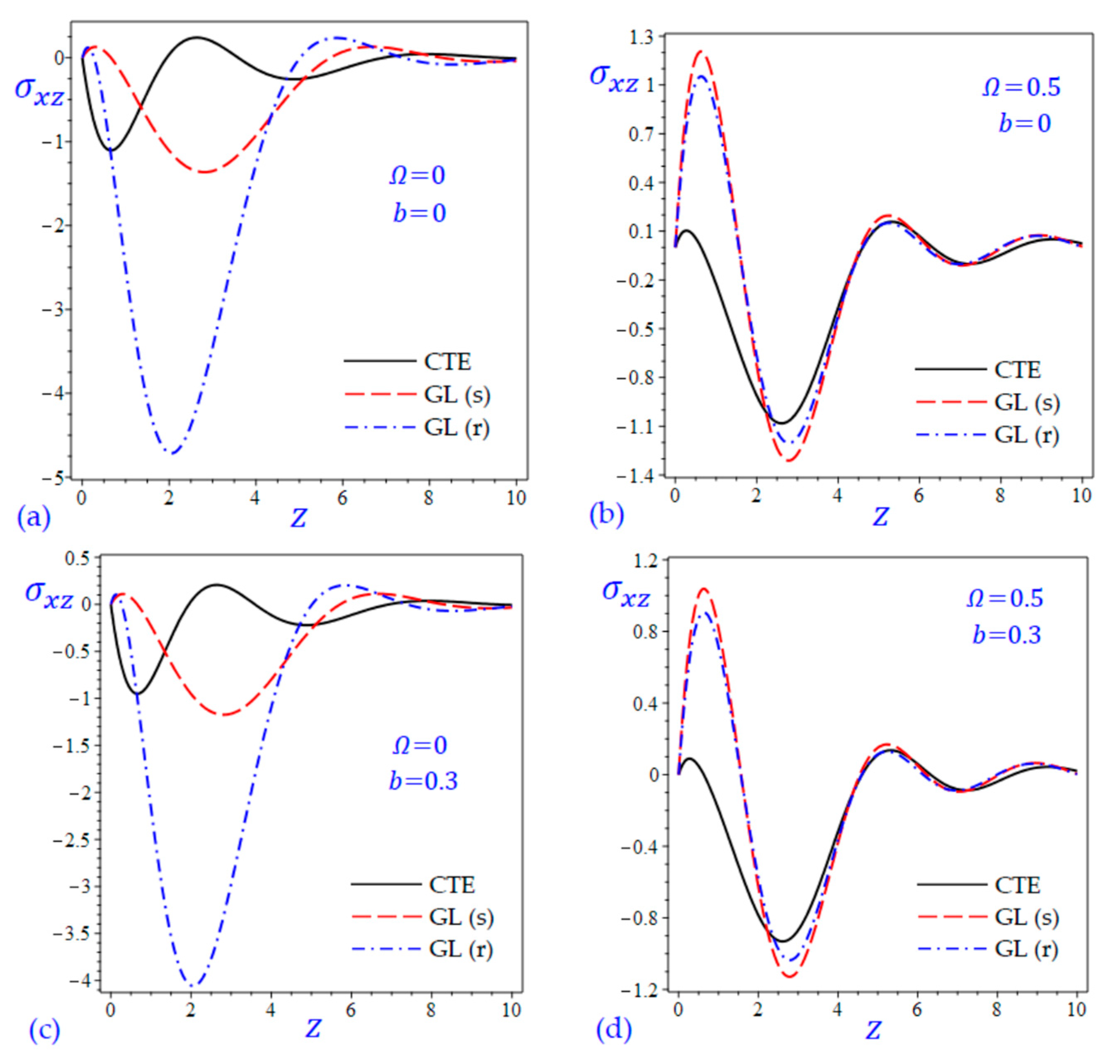
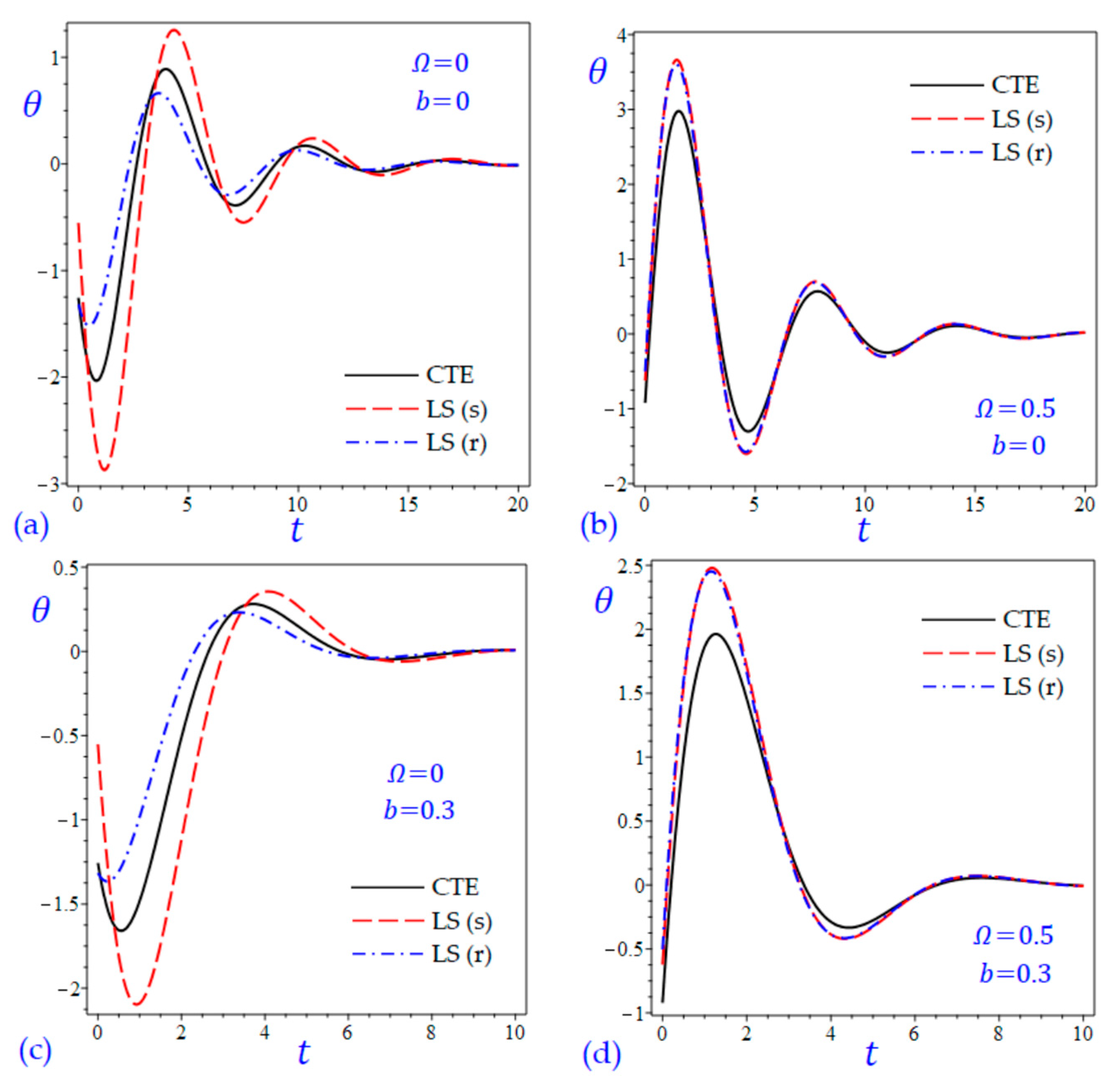
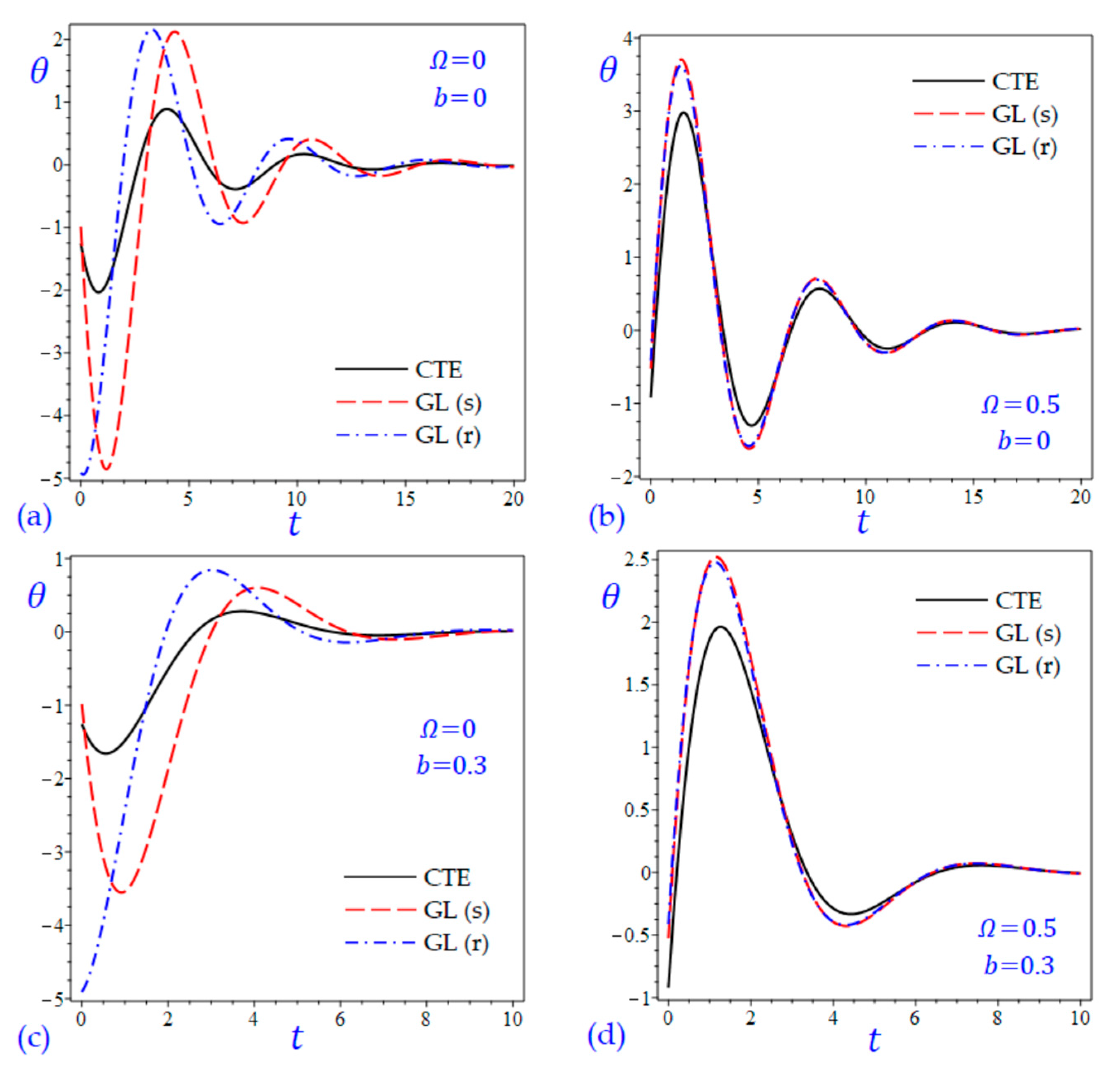
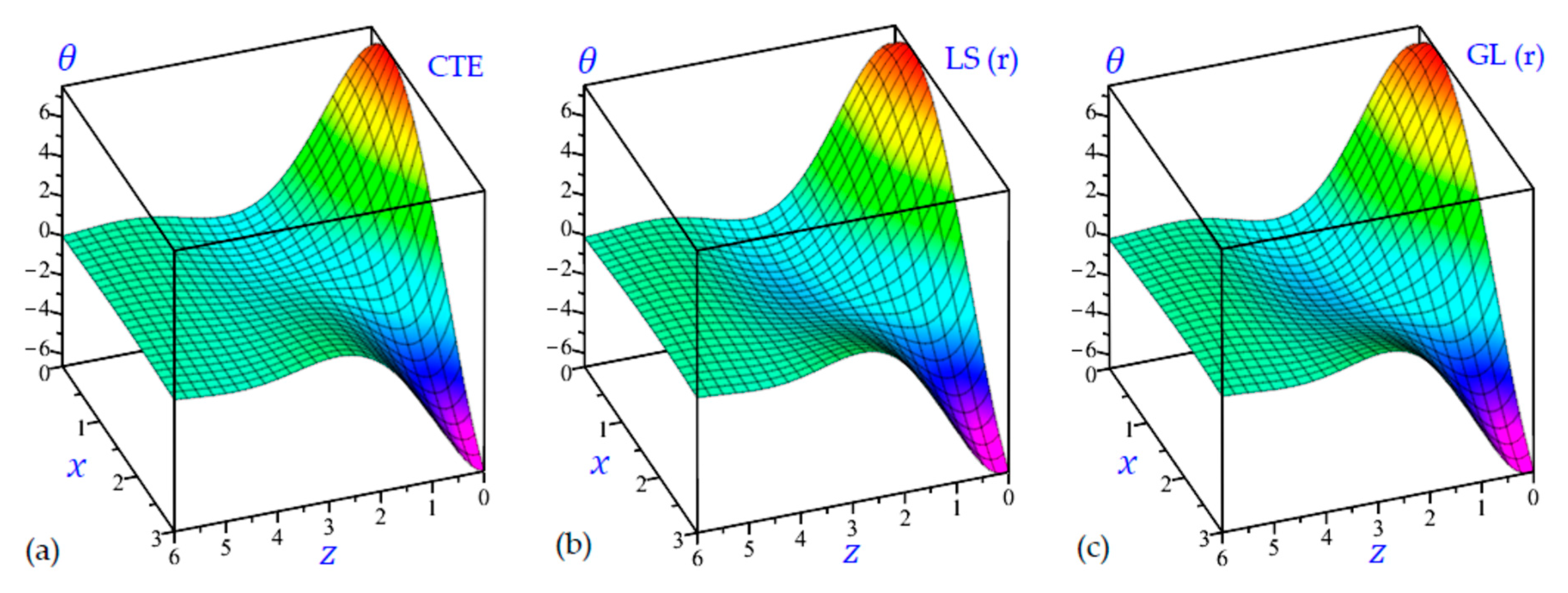
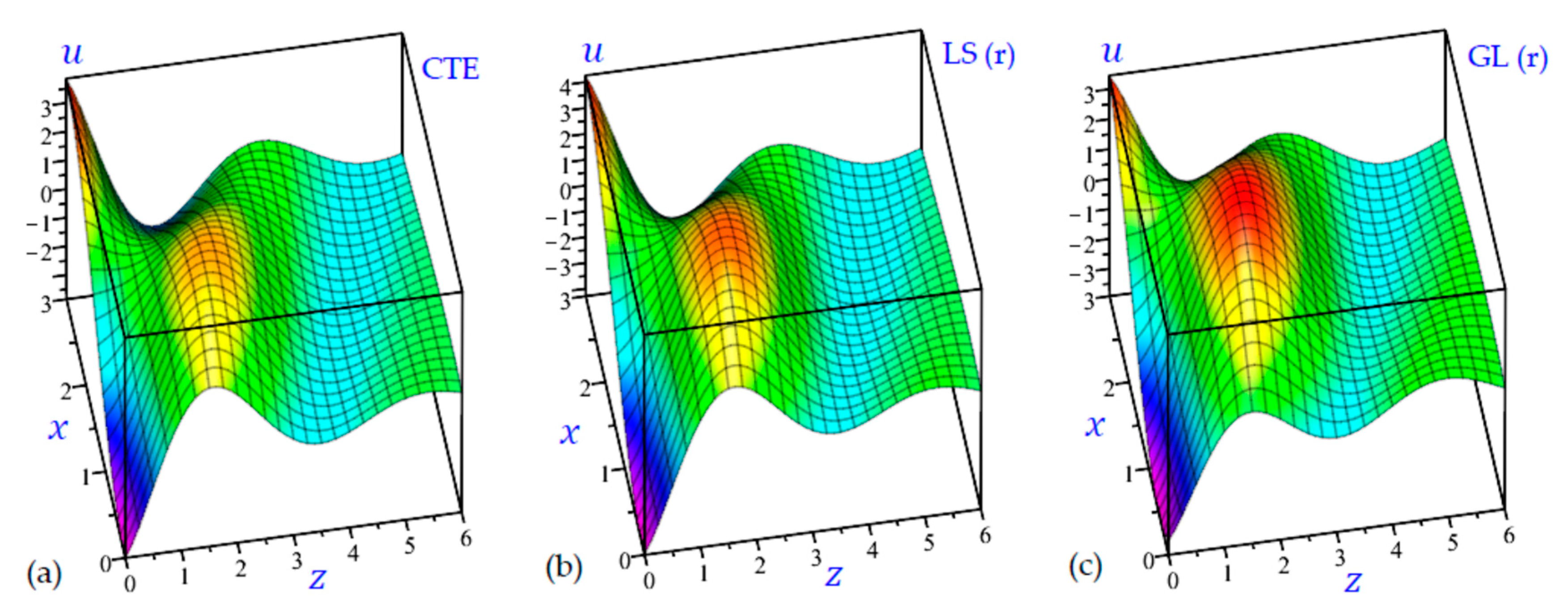
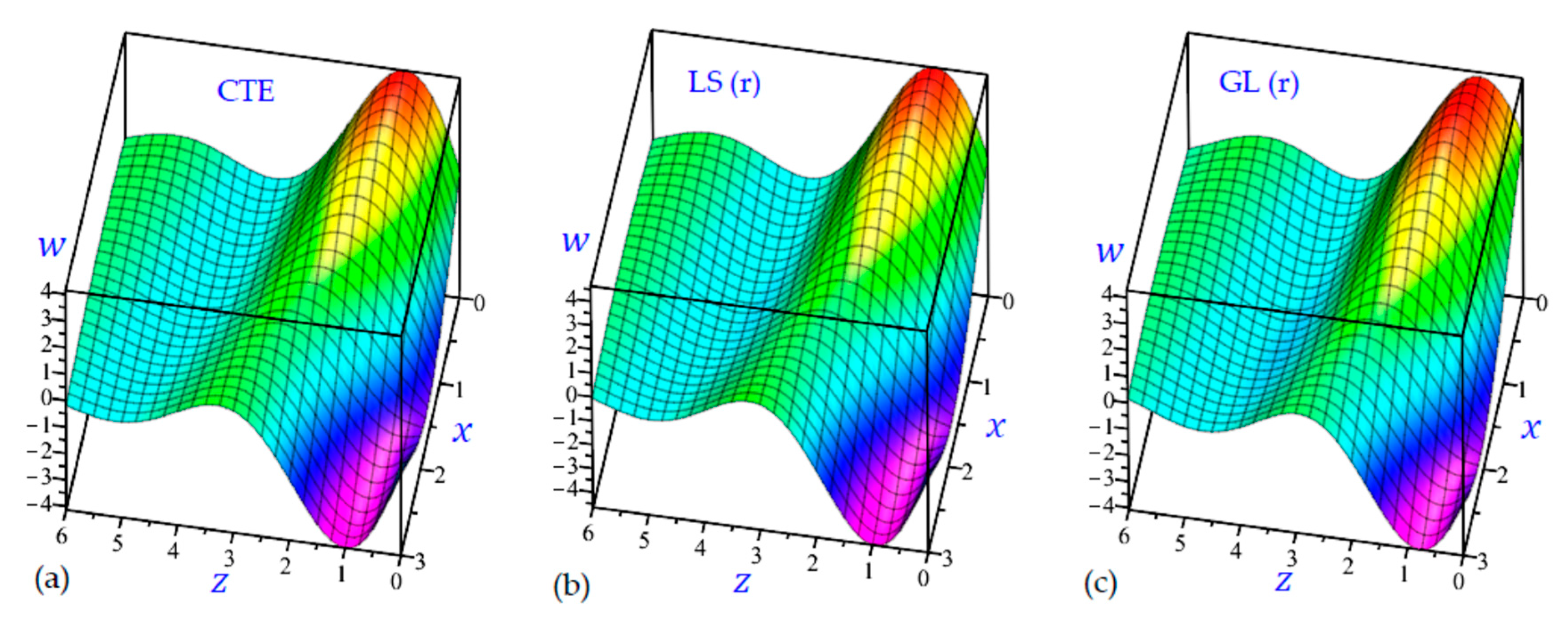
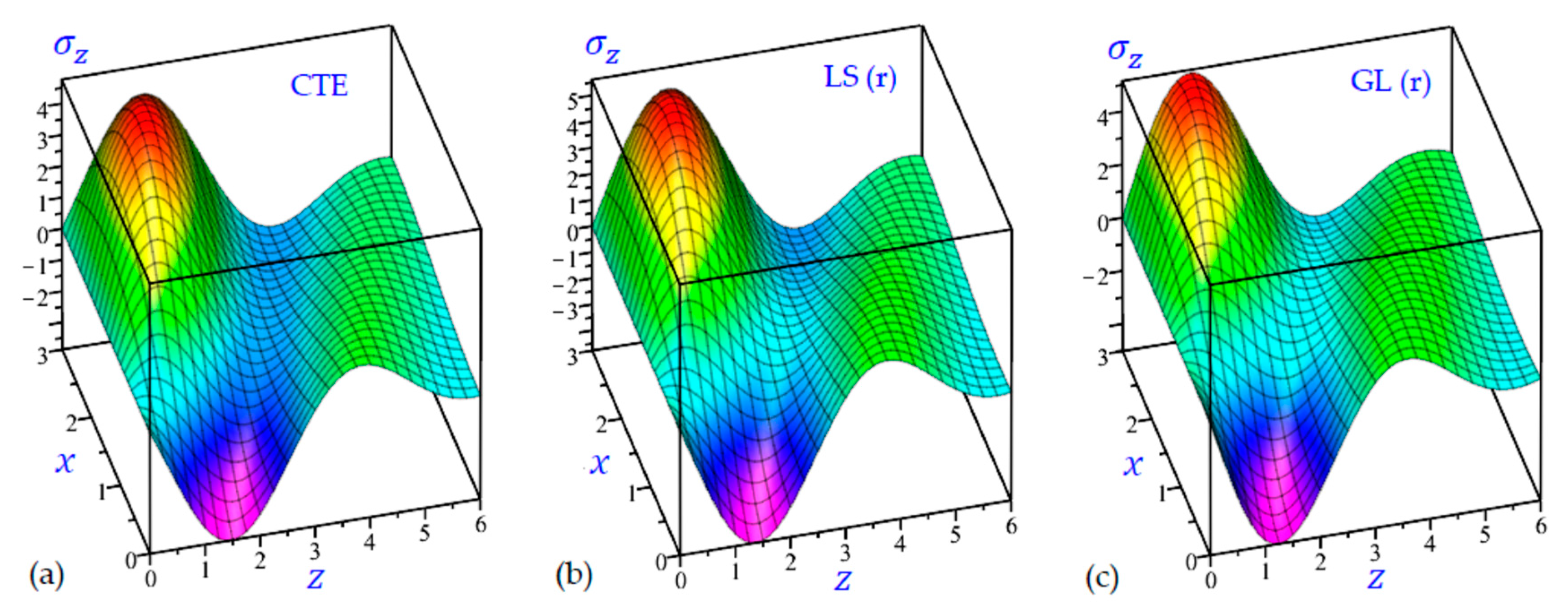
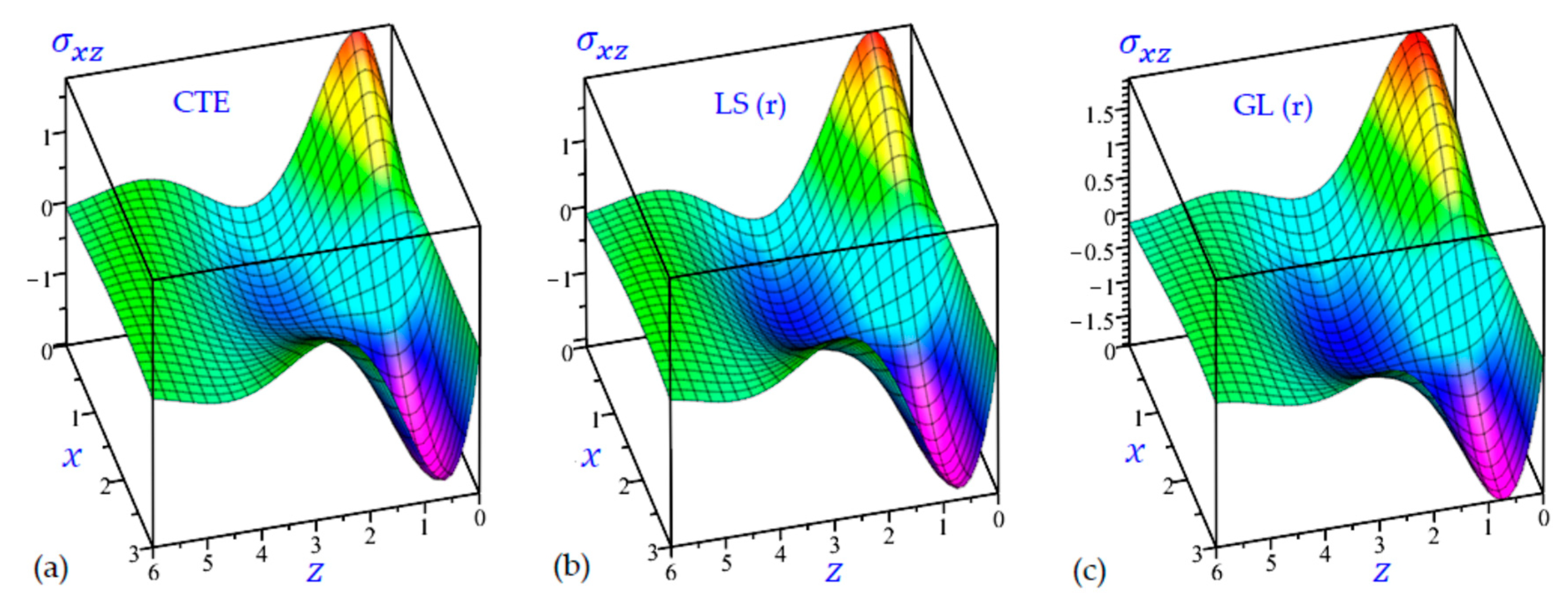
7. Numerical Results and Discussions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Othman, M.I.; Mondal, S. Memory-dependent derivative effect on 2D problem of generalized thermoelastic rotating medium with Lord–Shulman model. Ind. J. Phys. 2020, 94, 1169–1181. [Google Scholar] [CrossRef]
- Kiani, Y. Interaction of thermal and mechanical waves in axisymmetric generalized thermoelasticity of rotating disk. Waves Random Complex Media 2021, 31, 420–434. [Google Scholar] [CrossRef]
- Youssef, H.M.; El-Bary, A.A.; Al-Lehaibi, E.A. Thermal-stress analysis of a damaged solid sphere using hyperbolic two-temperature generalized thermoelasticity theory. Sci. Rep. 2021, 11, 2289. [Google Scholar] [CrossRef]
- Sadeghi, M.; Kiani, Y. Generalized magneto-thermoelasticity of a layer based on the Lord–Shulman and Green–Lindsay theories. J. Therm. Stress. 2022, 45, 319–340. [Google Scholar] [CrossRef]
- Tzou, D.Y. A unified field approach for heat conduction from macro-to micro-scales. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Heydarpour, Y.; Malekzadeh, P.; Gholipour, F. Thermoelastic analysis of FG-GPLRC spherical shells under thermo-mechanical loadings based on Lord-Shulman theory. Compos. B Eng. 2019, 164, 400–424. [Google Scholar] [CrossRef]
- Abd-Alla, A.; Abo-Dahab, S.; Kilany, A. Effect of several fields on a generalized thermoelastic medium with voids in the context of Lord-Shulman or dual-phase-lag models. Mech. Based Des. Struct. Mach. 2022, 50, 3901–3924. [Google Scholar] [CrossRef]
- Abouelregal, A.E. A novel generalized thermoelasticity with higher-order time-derivatives and three-phase lags. Multidiscip. Model. Mater. Struct. 2020, 16, 689–711. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Mashat, D.S.; Allehaibi, A.M. Magneto-Thermoelastic Response in an Unbounded Medium Containing a Spherical Hole via Multi-Time-Derivative Thermoelasticity Theories. Materials 2022, 15, 2432. [Google Scholar] [CrossRef] [PubMed]
- Alibeigloo, A. Three dimensional coupled thermoelasticity solution of sandwich plate with FGM core under thermal shock. Compos. Struct. 2017, 177, 96–103. [Google Scholar] [CrossRef]
- Alibeigloo, A. Coupled thermoelasticity analysis of carbon nano tube reinforced composite rectangular plate subjected to thermal shock. Compos. B Eng. 2018, 153, 445–455. [Google Scholar] [CrossRef]
- Ailawalia, P.; Narah, N.S. Effect of rotation in generalized thermoelastic solid under the influence of gravity with an overlying infinite thermoelastic fluid. Appl. Math. Mech. 2009, 30, 1505–1518. [Google Scholar] [CrossRef]
- Othman, M.I.; Hasona, W.; Abd-Elaziz, E.M. Effect of rotation on micropolar generalized thermoelasticity with two temperatures using a dual-phase lag model. Can. J. Phys. 2014, 92, 149–158. [Google Scholar] [CrossRef]
- Othman, M.I.; Zidan, M.E.; Hilal, M.I. The influence of gravitational field and rotation on thermoelastic solid with voids under Green-Naghdi theory. J. Phys. 2013, 2, 22–34. [Google Scholar]
- Othman, M.I.; Hasona, W.; Abd-Elaziz, E.M. Effect of rotation and initial stress on generalized micropolar thermoelastic medium with three-phase-lag. J. Comput. Theor. Nanosci. 2015, 12, 2030–2040. [Google Scholar] [CrossRef]
- Biswas, S.; Mukhopadhyay, B.; Shaw, S. Effect of rotation in magneto-thermoelastic transversely isotropic hollow cylinder with three-phase-lag model. Mech. Based Des. Struct. Mach. 2019, 47, 234–254. [Google Scholar] [CrossRef]
- Abo-Dahab, S.; Abd-Alla, A.; Alqarni, A. A two-dimensional problem with rotation and magnetic field in the context of four thermoelastic theories. Res. Phys. 2017, 7, 2742–2751. [Google Scholar] [CrossRef]
- Othman, M.I.; Abbas, I.A. Effect of rotation on plane waves at the free surface of a fibre-reinforced thermoelastic half-space using the finite element method. Meccanica 2011, 46, 413–421. [Google Scholar] [CrossRef]
- Zenkour, A.M. Three-dimensional thermal shock plate problem within the framework of different thermoelasticity theories. Compos. Struct. 2015, 132, 1029–1042. [Google Scholar]
- Othman, M.; Song, Y.Q. The effect of rotation on 2-D thermal shock problems for a generalized magneto-thermo-elasticity half-space under three theories. Multidiscip. Model. Mater. Struct. 2009, 5, 43–58. [Google Scholar]
- Tehrani, P.H.; Eslami, M.R. Boundary element analysis of coupled thermoelasticity with relaxation times in finite domain. AIAA J. 2000, 38, 534–541. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Ersoy, H.; Civalek, Ö. Solution of Moore–Gibson–Thompson equation of an unbounded medium with a cylindrical hole. Mathematics 2021, 9, 1536. [Google Scholar] [CrossRef]
- Shakeriaski, F.; Ghodrat, M.; Escobedo-Diaz, J.; Behnia, M. Recent advances in generalized thermoelasticity theory and the modified models: A review. J. Comput. Des. Eng. 2021, 8, 15–35. [Google Scholar] [CrossRef]
- Xiong, Q.-L.; Tian, X.-G. Transient magneto-thermo-elasto-diffusive responses of rotating porous media without energy dissipation under thermal shock. Meccanica 2016, 51, 2435–2447. [Google Scholar] [CrossRef]
- Sharifi, H. Generalized coupled thermoelasticity in an orthotropic rotating disk subjected to thermal shock. J. Therm. Stress. 2022, 45, 695–719. [Google Scholar] [CrossRef]
- Mashat, D.; Zenkour, A.M.; Abouelregal, A. Thermoelastic interactions in a rotating infinite orthotropic elastic body with a cylindrical hole and variable thermal conductivity. Arch. Mech. Eng. 2017, 64, 481–498. [Google Scholar] [CrossRef]
- Abbas, I.A.; Zenkour, A.M. The effect of rotation and initial stress on thermal shock problem for a fiber-reinforced anisotropic half-space using Green-Naghdi theory. J. Comput. Theoret. Nanosci. 2014, 11, 331–338. [Google Scholar] [CrossRef]
- Lotfy, K.; Hassan, W. Effect of rotation for two-temperature generalized thermoelasticity of two-dimensional under thermal shock problem. Math. Probl. Eng. 2013, 2013, 297274. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The size-dependent thermoelastic vibrations of nanobeams subjected to harmonic excitation and rectified sine wave heating. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- Zenkour, A.M. Thermoelastic diffusion problem for a half-space due to a refined dual-phase-lag Green–Naghdi model. J. Ocean Eng. Sci. 2020, 5, 214–222. [Google Scholar] [CrossRef]
- Zenkour, A.M. Wave propagation of a gravitated piezo-thermoelastic half-space via a refined multi-phase-lags theory. Mech. Adv. Mater. Struct. 2020, 27, 1923–1934. [Google Scholar] [CrossRef]
- Kutbi, M.A.; Zenkour, A.M. Refined dual-phase-lag Green–Naghdi models for thermoelastic diffusion in an infinite medium. Waves Random Complex Media 2022, 32, 947–967. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. Refined Lord–Shulman theory for 1D response of skin tissue under ramp-type heat. Materials 2022, 15, 6292. [Google Scholar] [CrossRef] [PubMed]
- Zenkour, A.M. Thermal diffusion of an unbounded solid with a spherical cavity via refined three-phase-lag Green–Naghdi models. Ind. J. Phys. 2022, 96, 1087–1104. [Google Scholar] [CrossRef]
- Zenkour, A.M. On generalized three-phase-lag models in photo-thermoelasticity. Int. J. Appl. Mech. 2022, 14, 2250005. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Mashat, D.S.; Allehaibi, A.M. Thermoelastic coupling response of an unbounded solid with a cylindrical cavity due to a moving heat source. Mathematics 2022, 10, 9. [Google Scholar] [CrossRef]
- Aljadani, M.H.; Zenkour, A.M. Effect of hydrostatic initial stress on a rotating half-space in the context of a two-relaxation power-law model. Mathematics 2022, 10, 4727. [Google Scholar] [CrossRef]
- Biswas, S.; Mukhopadhyay, B.; Shaw, S. Thermal shock response in magneto-thermoelastic orthotropic medium with three-phase-lag model. J. Electromagn. Waves Appl. 2017, 31, 879–897. [Google Scholar] [CrossRef]
- Deswal, S.; Hooda, N. A two-dimensional problem for a rotating magneto-thermoelastic half-space with voids and gravity in a two-temperature generalized thermoelasticity theory. J. Mech. 2015, 31, 639–651. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljadani, M.H.; Zenkour, A.M. A Modified Two-Relaxation Thermoelastic Model for a Thermal Shock of Rotating Infinite Medium. Materials 2022, 15, 9056. https://doi.org/10.3390/ma15249056
Aljadani MH, Zenkour AM. A Modified Two-Relaxation Thermoelastic Model for a Thermal Shock of Rotating Infinite Medium. Materials. 2022; 15(24):9056. https://doi.org/10.3390/ma15249056
Chicago/Turabian StyleAljadani, Maryam H., and Ashraf M. Zenkour. 2022. "A Modified Two-Relaxation Thermoelastic Model for a Thermal Shock of Rotating Infinite Medium" Materials 15, no. 24: 9056. https://doi.org/10.3390/ma15249056
APA StyleAljadani, M. H., & Zenkour, A. M. (2022). A Modified Two-Relaxation Thermoelastic Model for a Thermal Shock of Rotating Infinite Medium. Materials, 15(24), 9056. https://doi.org/10.3390/ma15249056






