Investigation of the Effect of ECAP Parameters on Hardness, Tensile Properties, Impact Toughness, and Electrical Conductivity of Pure Cu through Machine Learning Predictive Models
Abstract
1. Introduction
2. Methodology
2.1. Experimental Procedure
2.2. Machine Learning Approach
2.2.1. Linear Regression
2.2.2. Regression Trees
2.2.3. Ensembles of Regression Trees
2.2.4. Regression Gaussian Process
2.2.5. Support Vector Machine
2.2.6. Artificial Neural Network
3. Results
3.1. Microstructural Evolution
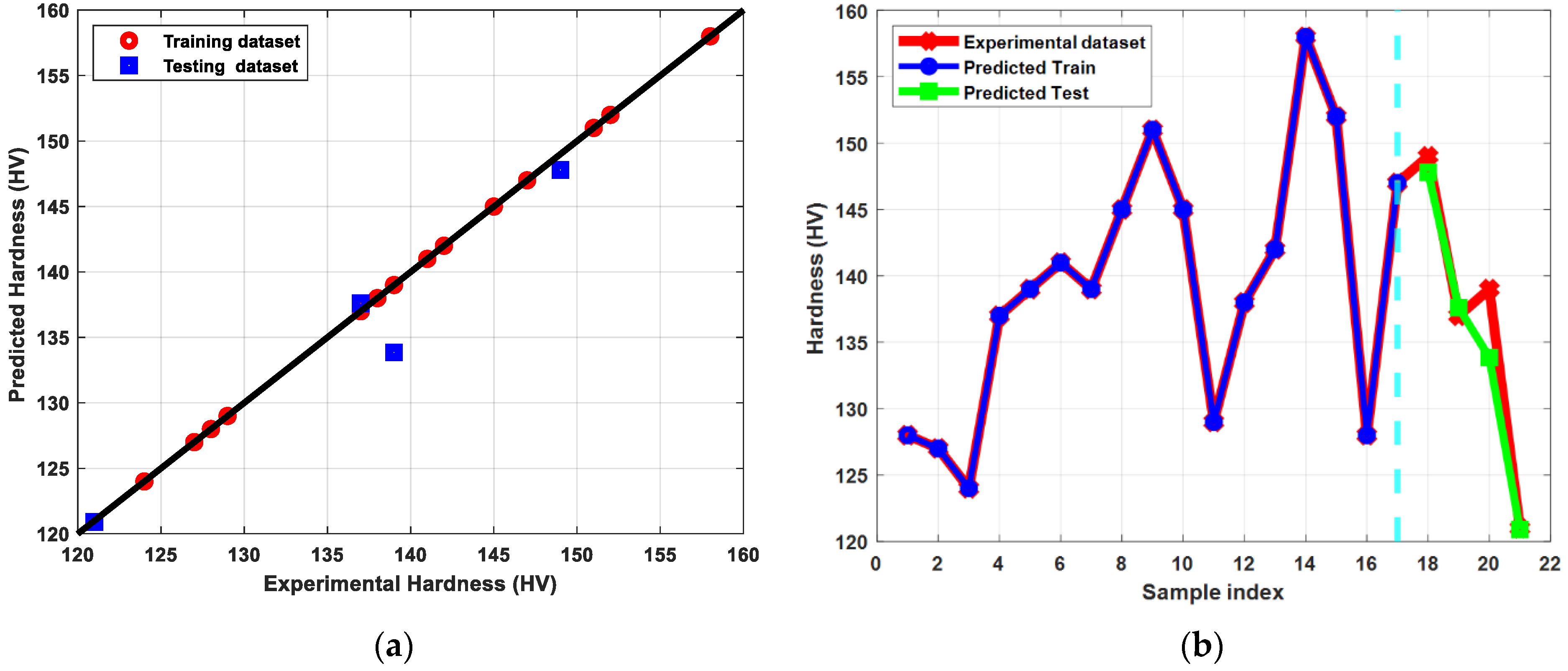
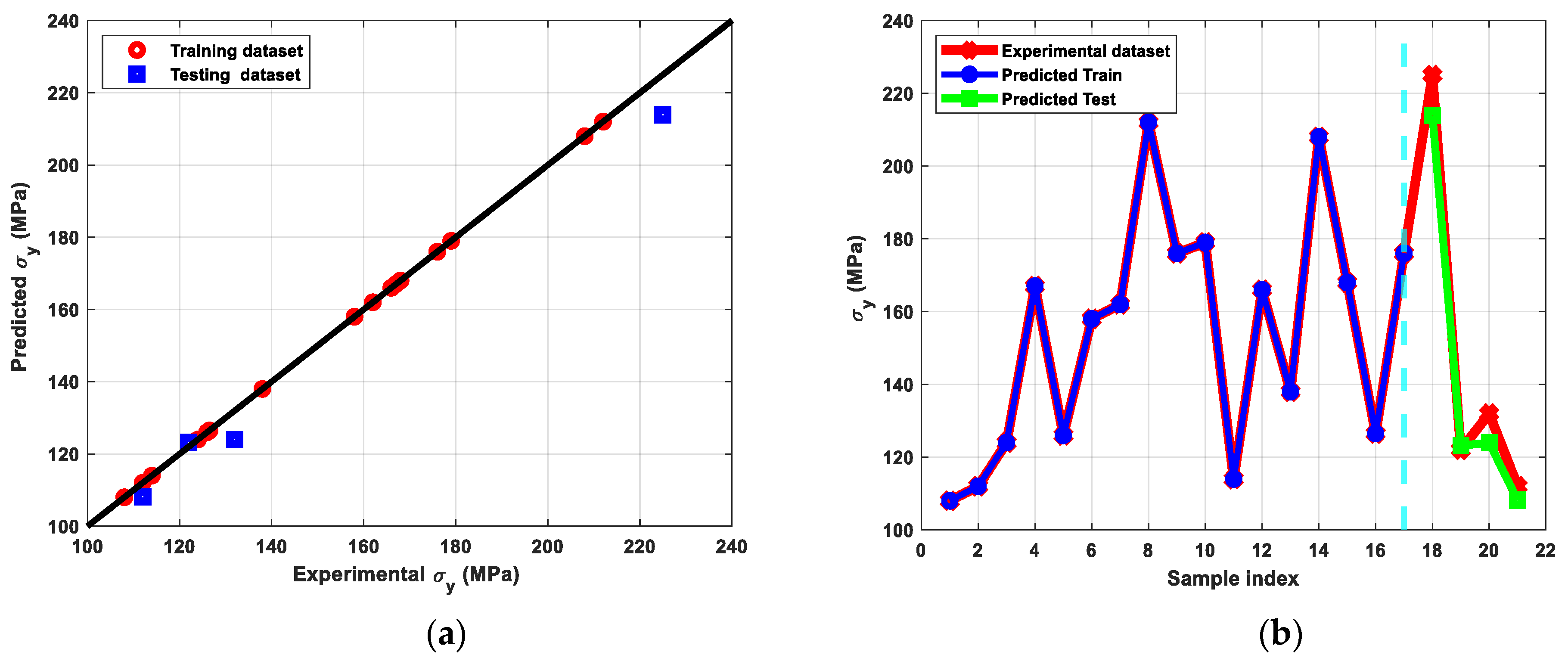
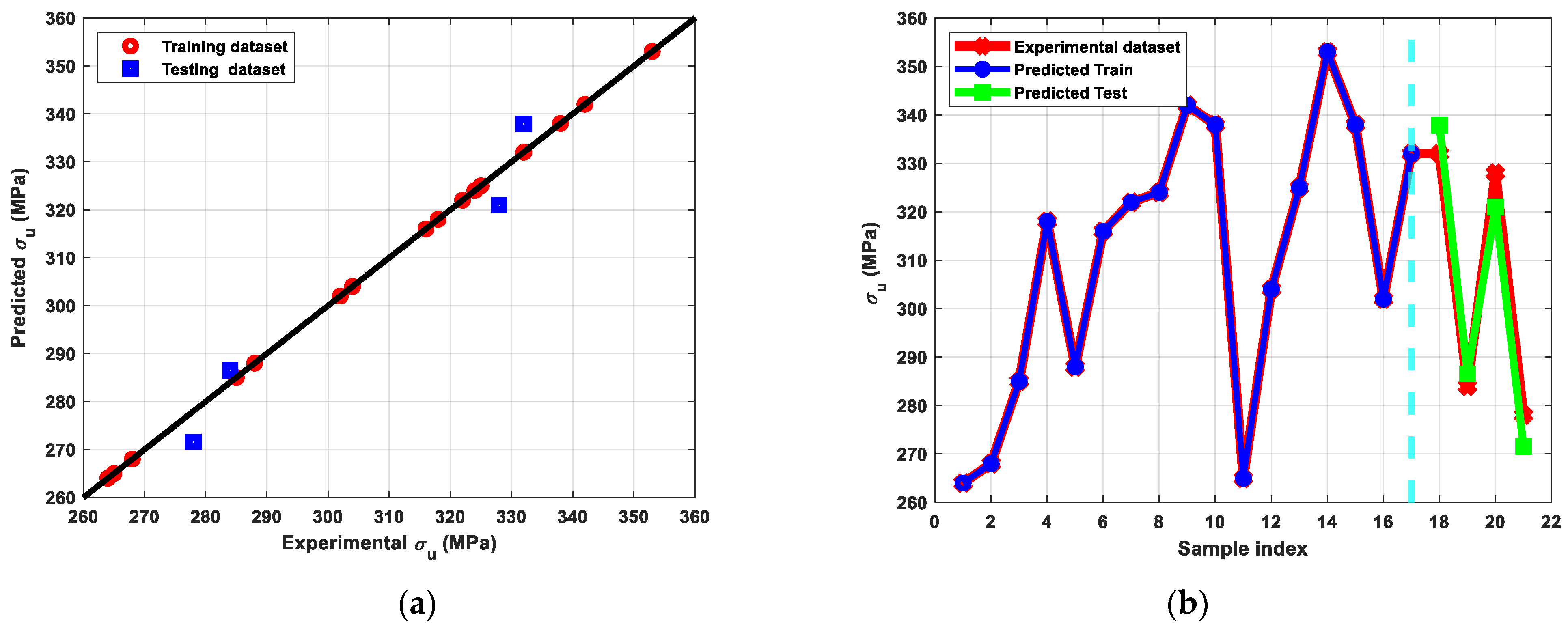
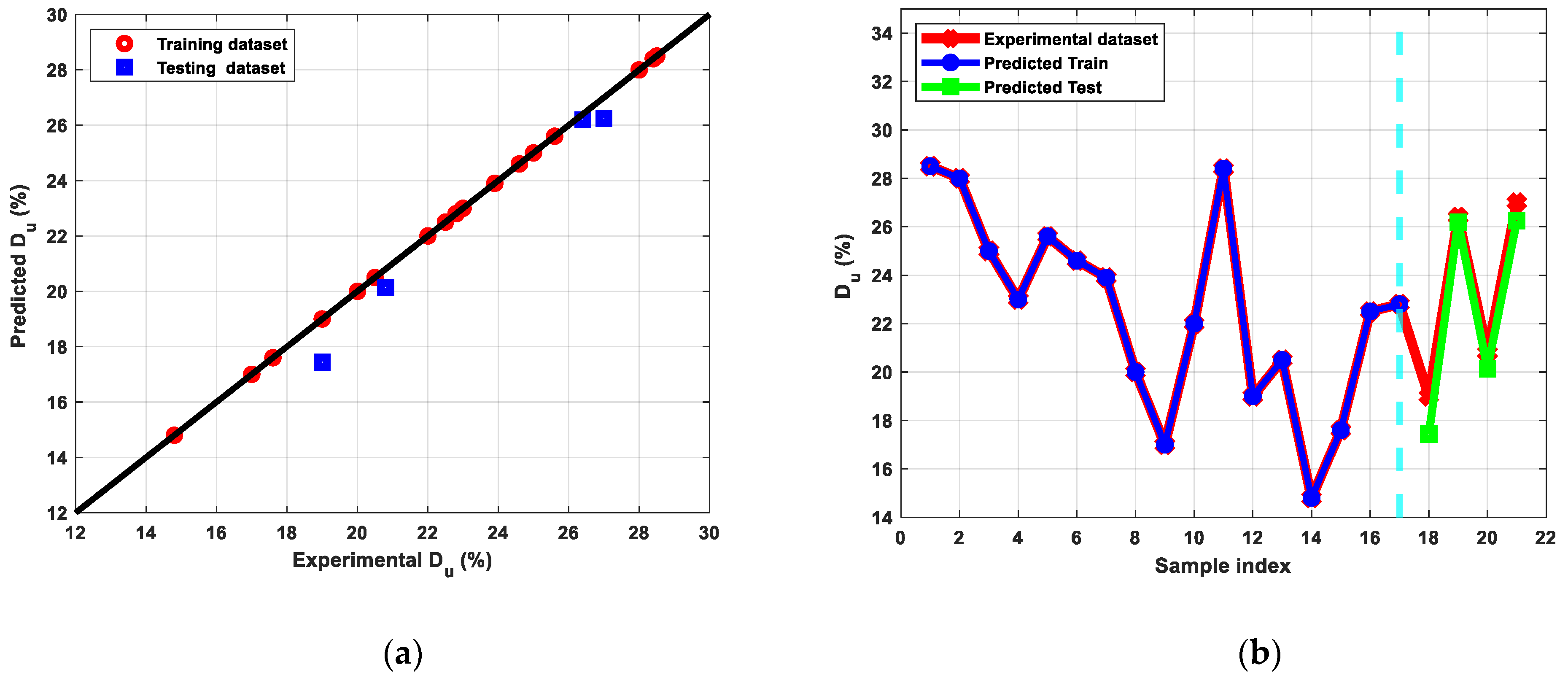
3.2. Analysis of Machine Leaning Approach for Mechanical and Electrical Behaviour
3.3. Effect of ECAP Processing Parameters on Cu Properties
3.3.1. Hardness Distribution
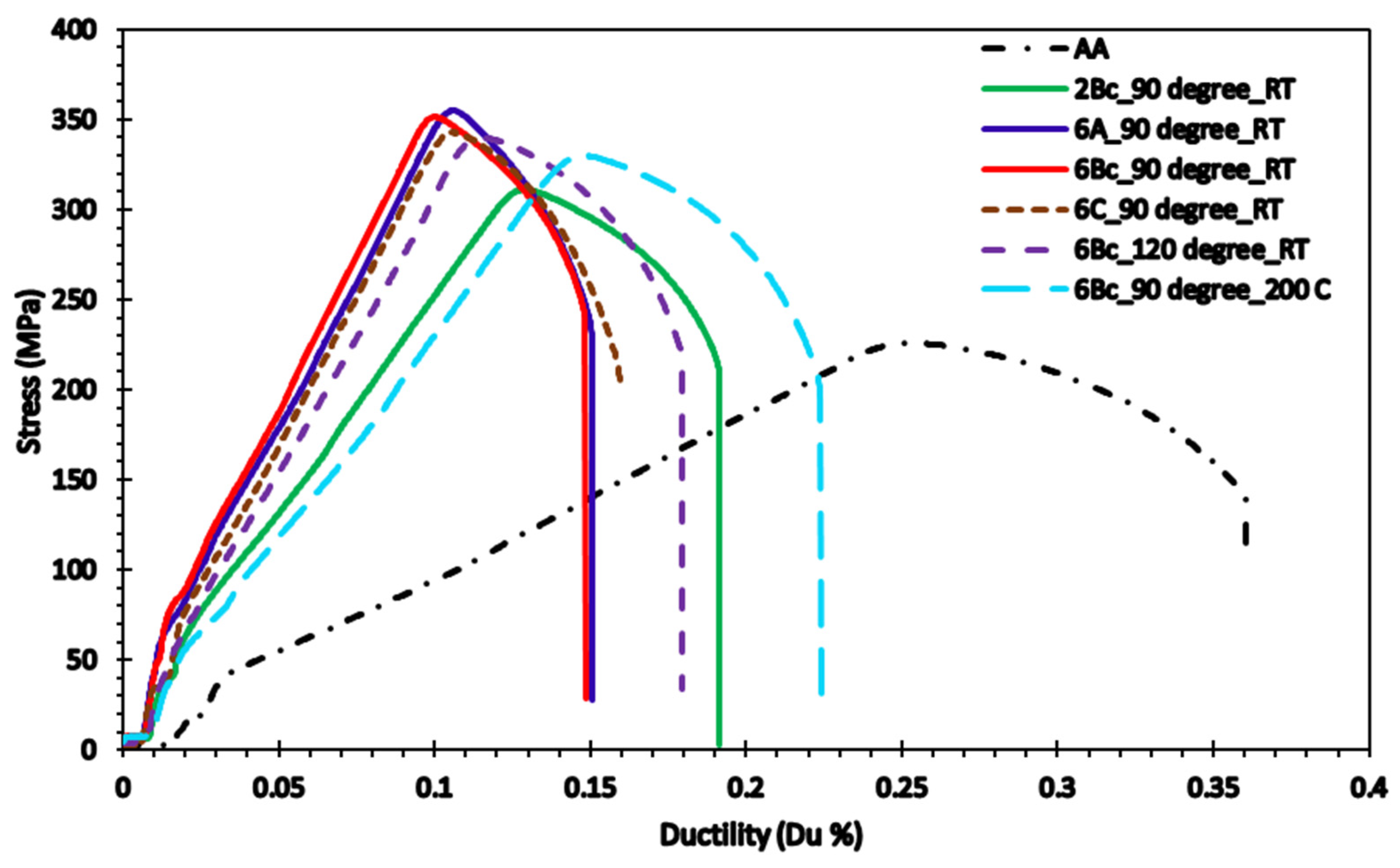
3.3.2. Tensile Properties
3.3.3. Impact Toughness
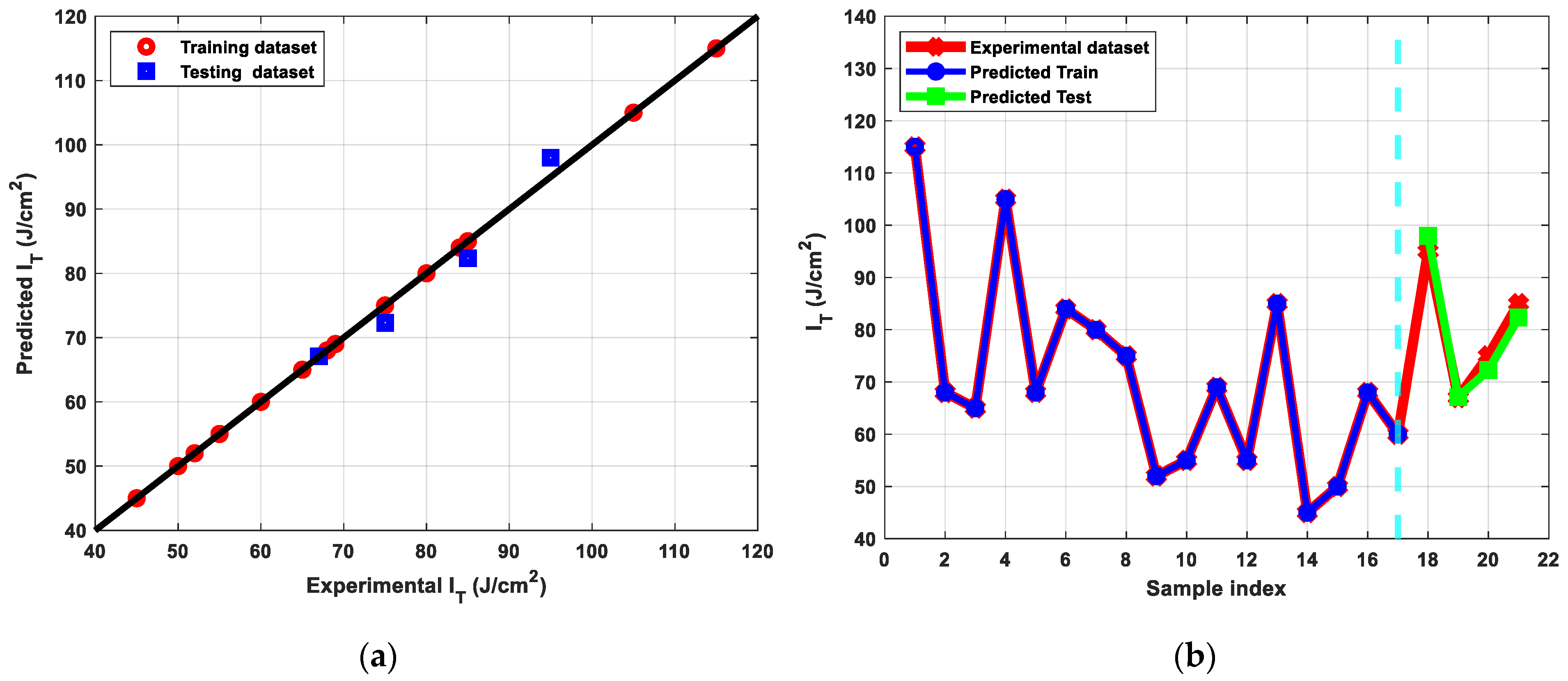
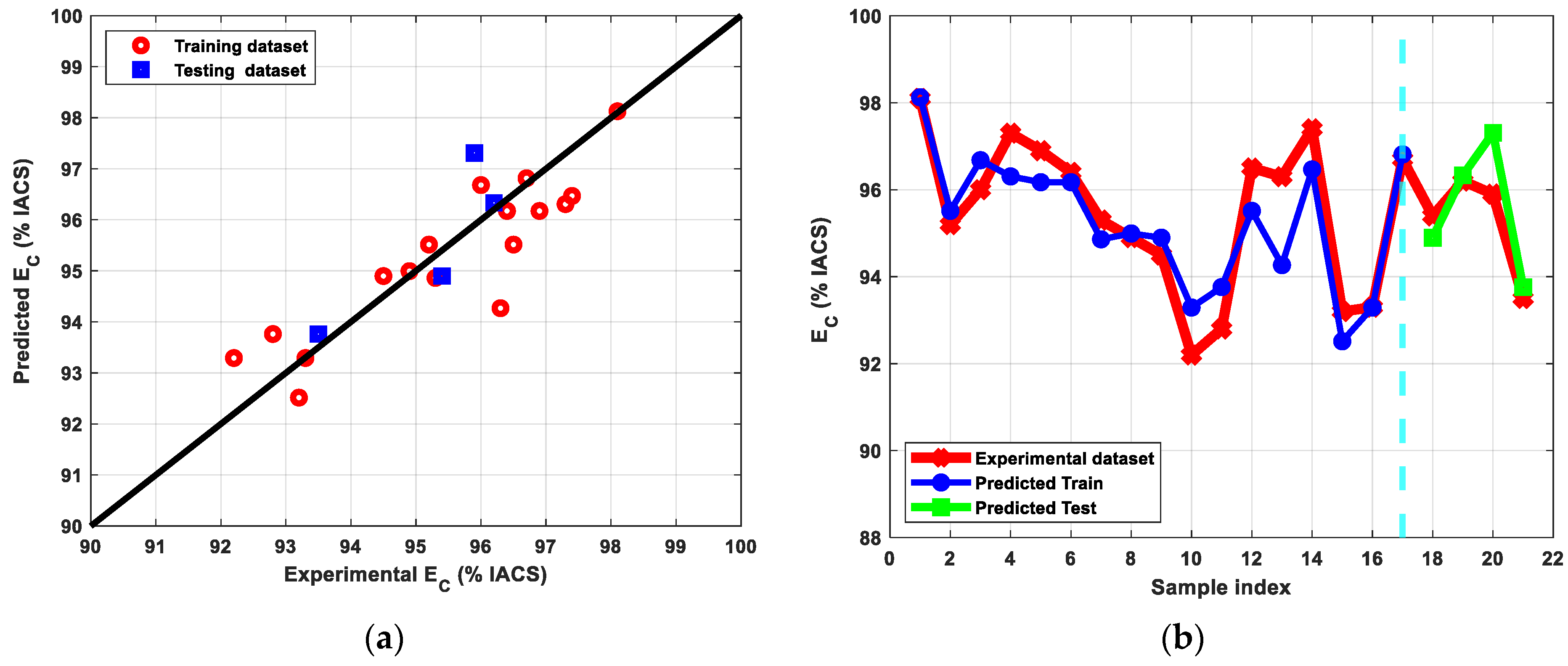
3.3.4. Electrical Conductivity
4. Conclusions
- The 90°-die showed to be more effective in producing a UFG grain structure compared to the 120°-die.
- Route Bc is the most efficient route type in grain refining, resulting in the highest hardness of ECAPed billets.
- ECAP processing at higher temperatures demonstrated a more homogeneous distribution of the hardness.
- 6-Bc processing through the 90°_die at RT resulted in increasing the HV by 72% compared to the AA condition.
- The carefully tuned ANN for hardness outperformed other adopted ML algorithms throughout both training and testing sets with the lowest RMSE and highest R2 values, showing that the prediction values were extremely close to the actual data provided to the model.
- ECAPed billets showed a considerable rise in σy and σu combined with no notable compromise in ductility when compared to AA equivalents.
- Route Bc demonstrated the most reduced ductility and the highest σy when compared to the other route types.
- Processing at 200 °C resulted in increasing the ductility of the ECAPed billets compared to the counterparts processed at RT.
- 6-A processing through the 90°_die at RT resulted in increasing the ultimate tensile strength by 56% compared to the AA condition.
- The ECAP die with a channel angle of 90° is more effective in increasing the tensile strength of the Cu billets.
- The tuned ANN for tensile properties with three hidden layers and the RelU activation function generated the best results among other algorithms, as indicated by the RMSE and R2-scores, with a strong correlation between the actual dataset from the experiments and the predicted dataset.
- The majority of the ECAPed billets showed increased absorbed impact energy compared to the AA.
- Processing ECAP at higher temperatures improved the amount of impact energy that was absorbed.
- The Cu sample processed via 6-Bc utilizing the 90-degree die at 200 °C displayed lesser impact energy than the AA.
- The 120°-die had a larger impact energy than the 90°-die, which may be ascribed to the lesser strain that was applied.
- The ANN generated the best results for impact toughness, surpassing the other algorithms, which were unable to extract valuable information from the input data, while ANN with tuned hyperparameters demonstrated high prediction accuracy.
- ECAP processing can strengthen the Cu billets without a significant effect on their electric conductivity.
- The ANN was able to accurately capture the model’s trend for EC with low RMSE and high R2 values, whereas other algorithms were unable to do so, showing that ANN model inference is appropriate for predicting the EC for new unseen input data under various experimental setting combinations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, M.; Li, Z.; Qiu, W.; Xiao, Z.; Zhao, Z.; Jiang, Y.; Xia, Z.; Huang, H. Development of homogeneity in a Cu-Mg-Ca alloy processed by equal channel angular pressing. J. Alloys Compd. 2019, 820, 153112. [Google Scholar] [CrossRef]
- Abib, K.; Balanos, J.A.M.; Alili, B.; Bradai, D. On the microstructure and texture of Cu-Cr-Zr alloy after severe plastic defor-mation by ECAP. Mater. Charact. 2016, 112, 252–258. [Google Scholar] [CrossRef]
- Alateyah, A.; Ahmed, M.; Zedan, Y.; El-Hafez, H.; Alawad, M.; El-Garaihy, W. Experimental and Numerical Investigation of the ECAP Processed Copper: Microstructural Evolution, Crystallographic Texture and Hardness Homogeneity. Metals 2021, 11, 607. [Google Scholar] [CrossRef]
- Ma, M.; Li, Z.; Qiu, W.; Xiao, Z.; Zhao, Z.; Jiang, Y. Microstructure and properties of Cu–Mg-Ca alloy processed by equal channel angular pressing. J. Alloys Compd. 2019, 788, 50–60. [Google Scholar] [CrossRef]
- Murashkin, M.Y.; Sabirov, I.; Sauvage, X.; Valiev, R.Z. Nanostructured Al and Cu alloys with superior strength and electrical conductivity. J. Mater. Sci. 2016, 51, 33–49. [Google Scholar] [CrossRef]
- Krishna, S.C.; Chawake, N.; Kottada, R.S.; Jha, A.K.; Pant, B.; Venkitakrishnan, P.V. High Strength and Good Ductility in Cu-3Ag-0.5Zr Alloy by Cryo-Rolling and Aging. J. Mater. Eng. Perform. 2016, 26, 350–357. [Google Scholar] [CrossRef]
- Islamgaliev, R.K.; Nesterov, K.M.; Valiev, R.Z. Structure, strength, and electric conductivity of a Cu-Cr copper-based alloy subjected to severe plastic deformation. Phys. Met. Metallogr. 2015, 116, 209–218. [Google Scholar] [CrossRef]
- Král, P.; Dvořák, J.; Kvapilová, M.; Blum, W.; Sklenička, V. The influence of long-term annealing at room temperature on creep behaviour of ECAP-processed copper. Mater. Lett. 2017, 188, 235–238. [Google Scholar] [CrossRef]
- Huang, R.; Zhu, D.; Liao, X.; Yan, Q. Effect of ECAP Process and Subsequent Annealing on Microstructure and Properties of Cu-0.25Se-0.25Te Alloy. J. Electron. Mater. 2020, 49, 2617–2624. [Google Scholar] [CrossRef]
- Bochvar, N.R.; Rybalchenko, O.V.; Shangina, D.V.; Dobatkin, S.V. Effect of equal-channel angular pressing on the precipitation kinetics in Cu-Cr-Hf alloys. Mater. Sci. Eng. A 2019, 757, 84–87. [Google Scholar] [CrossRef]
- Xu, X.; Nie, F.; Zhang, J.; Zheng, W.; Zheng, Y.; Hu, C.; Yang, G. Corrosion and ion release behavior of ultra-fine grained bulk pure copper fabricated by ECAP in Hanks solution as potential biomaterial for contraception. Mater. Lett. 2010, 64, 524–527. [Google Scholar] [CrossRef]
- Jayakumar, P.; Balasubramanian, K.; Tagore, G.R. Recrystallisation and bonding behaviour of ultra fine grained copper and Cu–Cr–Zr alloy using ECAP. Mater. Sci. Eng. A 2012, 538, 7–13. [Google Scholar] [CrossRef]
- Patil, A.; Bontha, S.; Ramesh, M. Effect of ECAP on sliding wear behaviour of Mg-Zn-Gd-Zr alloy. Mater. Today Proc. 2019, 20, 97–102. [Google Scholar] [CrossRef]
- Alateyah, A.; Aljohani, T.; Alawad, M.; El-Hafez, H.; Almutairi, A.; Alharbi, E.; Alhamada, R.; El-Garaihy, B.; El-Garaihy, W. Improved Corrosion Behavior of AZ31 Alloy through ECAP Processing. Metals 2021, 11, 363. [Google Scholar] [CrossRef]
- Alateyah, A.; Alharbi, M.; El-Hafez, H.A.; El-Garaihy, W. The Effect of Equal-Channel Angular Pressing Processing on Microstructural Evolution, Hardness Homogeneity, and Mechanical Properties of Pure Aluminum. SAE Int. J. Mater. Manuf. 2020, 14, 113–125. [Google Scholar] [CrossRef]
- Alateyah, A.; Ahmed, M.M.; Alawad, M.O.; Elkatatny, S.; Zedan, Y.; Nassef, A.; El-Garaihy, W. Effect of ECAP die angle on the strain homogeneity, microstructural evolution, crystallographic texture and mechanical properties of pure magnesium: Numerical simulation and experimental approach. J. Mater. Res. Technol. 2022, 17, 1491–1511. [Google Scholar] [CrossRef]
- El-Shenawy, M.; Ahmed, M.; Nassef, A.; El-Hadek, M.; Alzahrani, B.; Zedan, Y.; El-Garaihy, W. Effect of ECAP on the Plastic Strain Homogeneity, Microstructural Evolution, Crystallographic Texture and Mechanical Properties of AA2xxx Aluminum Alloy. Metals 2021, 11, 938. [Google Scholar] [CrossRef]
- El-Garaihy, W.H.; Alateyah, A.I.; Alawad, M.O.; Aljohani, T.A. Improving the Corrosion Behavior and Mechanical Properties of Biodegradable Mg-Zn-Zr Alloys Through ECAP for Usage in Biomedical Applications. In The Minerals, Metals & Materials Series; Magnesium Technology 2022; Springer: Berlin/Heidelberg, Germany; pp. 259–269. Available online: https://link.springer.com/chapter/10.1007/978-3-030-92533-8_45 (accessed on 5 February 2022).
- Yang, Z.; Ma, A.; Xu, B.; Jiang, J.; Sun, J. Corrosion behavior of AZ91 Mg alloy with a heterogeneous structure produced by ECAP. Corros. Sci. 2021, 187, 109517. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Langdon, T.G. Principles of equal-channel angular pressing as a processing tool for grain refinement. Prog. Mater. Sci. 2006, 51, 881–981. [Google Scholar] [CrossRef]
- Nassef, A.; Samy, S.; El-Garaihy, W.H. Enhancement of mechanical properties for Al-Mg-Si alloy using equal channel angular pressing. Int. J. Chem. Nucl. Mater. Metall. Eng. 2015, 9, 131–136. [Google Scholar]
- El-Garaihy, W.; Rassoul, E.S.M.; Salem, H.G. Consolidation of High Performance AA6061 and AA6061-SiCp Composite Processed by High Pressure Torsion. Mater. Sci. Forum 2014, 783-786, 2623–2628. [Google Scholar] [CrossRef]
- Kong, Y.; Pu, Q.; Jia, Z.; Liu, M.; Roven, H.J.; Jia, J.; Liu, Q. Microstructure and property evolution of Al-0.4Fe-0.15Zr-0.25Er alloy processed by high pressure torsion. J. Alloys Compd. 2020, 824, 153949. [Google Scholar] [CrossRef]
- Bednarczyk, W.; Kawałko, J.; Wątroba, M.; Gao, N.; Starink, M.J.; Bala, P.; Langdon, T.G. Microstructure and mechanical properties of a Zn-0.5Cu alloy processed by high-pressure torsion. Mater. Sci. Eng. A 2020, 776, 139047. [Google Scholar] [CrossRef]
- Salem, H.G.; El-Garaihy, W.H.; Rassoul, E.S.M.A. Influence of high-pressure torsion on the consolidation behaviour and me-chanical properties of AA6061-SiCP composites powders. In Proceedings of the 2012 TMS Annual Meeting and Exhibition, Orlando, FL, USA, 11–15 March 2012; Volume 1, pp. 553–560. [Google Scholar]
- Ghazanlou, S.I.; Eghbali, B.; Petrov, R. Microstructural evolution and strengthening mechanisms in Al7075/graphene nano-plates/carbon nano-tubes composite processed through accumulative roll bonding. Mater. Sci. Eng. A 2021, 807, 140877. [Google Scholar] [CrossRef]
- She, J.; Peng, P.; Tang, A.T.; Zhang, J.Y.; Mao, J.J.; Liu, T.T.; Zhou, S.B.; Wang, Y.; Pan, F.S. Novel on-line twist extrusion process for bulk magnesium alloys. Mater. Des. 2019, 182, 108011. [Google Scholar] [CrossRef]
- El-Garaihy, W.H.; Fouad, D.M.; Salem, H.G. Multi-channel Spiral Twist Extrusion (MCSTE): A Novel Severe Plastic Deformation Technique for Grain Refinement. Met. Mater. Trans. A 2018, 49, 2854–2864. [Google Scholar] [CrossRef]
- Fouad, D.; Moataz, A.; El-Garaihy, W.; Salem, H. Numerical and experimental analysis of multi-channel spiral twist extrusion processing of AA5083. Mater. Sci. Eng. A 2019, 764, 138216. [Google Scholar] [CrossRef]
- Fouad, D.M.; El-Garaihy, W.H.; Ahmed, M.M.Z.; Seleman, M.E.-S.; Salem, H.G. Influence of multi-channel spiral twist extrusion (MCSTE) processing on structural evolution, crystallographic texture and mechanical properties of AA1100. Mater. Sci. Eng. A 2018, 737, 166–175. [Google Scholar] [CrossRef]
- Fouad, D.M.; El-Garaihy, W.H.; Ahmed, M.M.Z.; Albaijan, I.; Seleman, M.M.E.; Salem, H.G. Grain Structure Evolution and Mechanical Properties of Multi-Channel Spiral Twist Extruded AA5083. Metals 2021, 11, 2021. [Google Scholar] [CrossRef]
- Habibi, A.; Ketabchi, M.; Eskandarzadeh, M. Nano-grained pure copper with high-strength and high-conductivity produced by equal channel angular rolling process. J. Mater. Process. Technol. 2011, 211, 1085–1090. [Google Scholar] [CrossRef]
- Molodova, X.; Khorashadizadeh, A.; Gottstein, G.; Winning, M.; Hellmig, R.J. Thermal stability of ECAP processed pure Cu and CuZr. Z. Met. Res. Adv. Tech. 2007, 98, 269–275. [Google Scholar] [CrossRef]
- El-Danaf, E.A.; Soliman, M.S.; Almajid, A.A.; El-Rayes, M.M. Enhancement of mechanical properties and grain size refine-ment of commercial purity aluminum 1050 processed by ECAP. Mater. Sci. Eng. A 2007, 458, 226–234. [Google Scholar] [CrossRef]
- Bagherzadeh, S.; Abrinia, K.; Han, Q. Analysis of plastic deformation behavior of ultrafine-grained aluminum processed by the newly developed ultrasonic vibration enhanced ECAP: Simulation and experiments. J. Manuf. Process. 2020, 50, 485–497. [Google Scholar] [CrossRef]
- Krajňák, T.; Minárik, P.; Stráská, J.; Gubicza, J.; Dluhoš, L.; Máthis, K.; Janeček, M. Influence of temperature of ECAP processing on the microstructure and microhardness of as-cast AX41 alloy. J. Mater. Sci. 2020, 55, 3118–3129. [Google Scholar] [CrossRef]
- Djavanroodi, F.; Omranpour, B.; Sedighi, M. Artificial Neural Network Modeling of ECAP Process. Mater. Manuf. Process. 2013, 28, 276–281. [Google Scholar] [CrossRef]
- Zhao, Q.; Yang, H.; Liu, J.; Zhou, H.; Wang, H.; Yang, W. Machine learning-assisted discovery of strong and con-ductive Cu alloys: Data mining from discarded experiments and physical features. Mater. Des. 2021, 197, 109248. [Google Scholar]
- Hu, M.; Tan, Q.; Knibbe, R.; Wang, S.; Li, X.; Wu, T.; Zhang, M.X. Prediction of mechanical properties of wrought aluminum alloys using feature engineering assisted machine learning approach. Metall. Mater. Trans. A 2021, 52, 2873–2884. [Google Scholar] [CrossRef]
- Taylor, C.D.; Tossey, B.M. High temperature oxidation of corrosion resistant alloys from machine learning. npj Mater. Degrad. 2021, 5, 38. [Google Scholar] [CrossRef]
- El-Shenawy, M.I.; El-Garaihy, W.H.; Elhadek, M.A.; Zaki, M.A.; Nassef, A. Influence of ECAP Parameters on Electrical Conductivity and Hardness of Pure Cu. Port-Said Eng. Res. J. 2022. [Google Scholar] [CrossRef]
- El-Shenawy, M.I.; Elhadek, M.A.; Zaki, M.A.; Nassef, A. Optimization of Equal Channel Angular Pressing Technique Based on Experimental and Finite Element Modeling Approaches. Ph.D. Thesis, Port-Said University, Port-Said, Egypt, 30 November 2022. [Google Scholar]
- Muc, A. Fuzzy approach in modeling static and fatigue strength of composite materials and structures. Neurocomputing 2019, 393, 156–164. [Google Scholar] [CrossRef]
- Jimenez-Martinez, M.; Alfaro-Ponce, M. Effects of synthetic data applied to artificial neural networks for fatigue life prediction in nodular cast iron. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 10. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Blanco, V.; Japón, A.; Puerto, J. A mathematical programming approach to SVM-based classification with label noise. Comput. Ind. Eng. 2022, 172. [Google Scholar] [CrossRef]
- Ahmed, N.I.; Nasrin, F. Reducing Error Rate for Eye-Tracking System by Applying SVM. In Machine Intelligence and Data Science Applications; Springer: New York, NY, USA, 2022; pp. 35–47. [Google Scholar]
- Gu, C.; Tóth, L. The origin of strain reversal texture in equal channel angular pressing. Acta Mater. 2011, 59, 5749–5757. [Google Scholar] [CrossRef]
- Illgen, C.; Frint, P.; Gruber, M.; Volk, W.; Wagner, M.F.-X. Evolution of Grain Refinement in AA5083 Sheet Metal Processed by ECAP. In Light Metals 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 362–369. [Google Scholar] [CrossRef]
- Djavanroodi, F.; Omranpour, B.; Ebrahimi, M.; Sedighi, M. Designing of ECAP parameters based on strain distribution uni-formity. Prog. Nat. Sci. Mater. Int. 2012, 22, 452–460. [Google Scholar] [CrossRef]
- Dalan, F.C.; Andreani, G.F.D.L.; Travessa, D.N.; Faizov, I.A.; Faizova, S.; Cardoso, K.R. Effect of ECAP processing on distribution of second phase particles, hardness and electrical conductivity of Cu–0.81Cr–0.07Zr alloy. Trans. Nonferrous Met. Soc. China 2022, 32, 217–232. [Google Scholar] [CrossRef]
- Wei, K.X.; Chu, Z.Q.; Yang, L.C.; Wei, W.; Du, Q.B.; Alexandrov, I.V.; Hu, J. Performance Evaluation of Electrical Discharge Machining using Ultrafine-Grained Cu Electrodes Processed by Equal Channel Angular Pressing and Deep Cryogenic Treatment. J. Mater. Eng. Perform. 2020, 30, 281–289. [Google Scholar] [CrossRef]
- Wongsa-Ngam, J.; Kawasaki, M.; Langdon, T.G. A comparison of microstructures and mechanical properties in a Cu–Zr alloy processed using different SPD techniques. J. Mater. Sci. 2012, 48, 4653–4660. [Google Scholar] [CrossRef]
- Almenaif, O.; Alhumaydani, Y.; Alnafisah, M.; Aldhalaan, M.; Alateyah, A.; El-Garaihy, W. A Computational Investigation into the Effect of Equal Channel Angular Processing on the Mechanical Properties of Severely Deformed ZK 60 Alloy Validated by Experiments. Am. J. Eng. Appl. Sci. 2020, 13, 296–310. [Google Scholar] [CrossRef]
- Tong, Y.-X.; Wang, Y.; Qian, Z.-M.; Zhang, D.-T.; Li, L.; Zheng, Y.-F. Achieving High Strength and High Electrical Conductivity in a CuCrZr Alloy Using Equal-Channel Angular Pressing. Acta Met. Sin. 2018, 31, 1084–1088. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, J.; Shen, X.; Zhu, R. Cyclic Creep of Ultrafine-Grained Pure Cu Under Cyclic Tension Deformation. J. Mater. Eng. Perform. 2017, 26, 837–842. [Google Scholar] [CrossRef]
- Wang, Y.L.; Lapovok, R.; Wang, J.T.; Qi, Y.S.; Estrin, Y. Thermal behavior of copper processed by ECAP with and without back pressure. Mater. Sci. Eng. A 2015, 628, 21–29. [Google Scholar] [CrossRef]
- Tian, Y.-Z.; Duan, Q.-Q.; Yang, H.-J.; Zou, H.-F.; Yang, G.; Wu, S.-D.; Zhang, Z.-F. Effects of Route on Microstructural Evolution and Mechanical Properties of Cu-8 Wt Pct Ag Alloy Processed by Equal Channel Angular Pressing. Met. Mater. Trans. A 2010, 41, 2290–2303. [Google Scholar] [CrossRef]
- Zhu, C.; Ma, A.; Jiang, J.; Li, X.; Song, D.; Yang, D.; Yuan, Y.; Chen, J. Effect of ECAP combined cold working on mechanical properties and electrical conductivity of Conform-produced Cu–Mg alloys. J. Alloys Compd. 2014, 582, 135–140. [Google Scholar] [CrossRef]
- Ko, Y.G.; Namgung, S.; Lee, B.U.; Shin, D.H. Mechanical and electrical responses of nanostructured Cu–3wt%Ag alloy fabricated by ECAP and cold rolling. J. Alloys Compd. 2010, 504, S448–S451. [Google Scholar] [CrossRef]
- Ni, S.; Jiang, J.; Chen, J.; Song, D.; Ma, A. Microstructure and properties of in-situ synthesized Cu-1 wt% TiC alloy followed by ECAP and post-annealing. Prog. Nat. Sci. Mater. Int. 2016, 26, 643–649. [Google Scholar] [CrossRef]
- Tolaminejad, B.; Dehghani, K. Microstructural characterization and mechanical properties of nanostructured AA1070 aluminum after equal channel angular extrusion. Mater. Des. 2012, 34, 285–292. [Google Scholar] [CrossRef]
- Fang, D.R.; Tian, Y.Z.; Duan, Q.Q.; Wu, S.D.; Zhang, Z.F.; Zhao, N.Q.; Li, J.J. Effects of equal channel angular pressing on the strength and toughness of Al–Cu alloys. J. Mater. Sci. 2011, 46, 5002–5008. [Google Scholar] [CrossRef]
- Jiang, J.; Yuan, T.; Shi, J.; Zhang, L.; Ma, A.; Song, D. Enhanced Impact Toughness at Ambient Temperatures of Ultrafine-Grained Al-26 wt.% Si Alloy Produced by Equal-Channel Angular Pressing. J. Mater. Eng. Perform. 2018, 27, 2131–2137. [Google Scholar] [CrossRef]
- Meyer, L.W.; Hockauf, M.; Zillmann, B.; Schneider, I. Strength, ductility and impact toughness of the magnesium alloy az31b after equal-channel angular pressing. Int. J. Mater. Form. 2009, 2, 61–64. [Google Scholar] [CrossRef]
- Lipińska, M.; Bazarnik, P.; Lewandowska, M. The influence of severe plastic deformation processes on electrical conductivity of commercially pure aluminium and 5483 aluminium alloy. Arch. Civ. Mech. Eng. 2016, 16, 717–723. [Google Scholar] [CrossRef]
- Zhao, N.; Ban, C. Developing a High-Strength Al–Mg–Si Alloy with Improved Electrical Conductivity by a Novel ECAP Route. Met. Mater. Int. 2022, 28, 2513–2528. [Google Scholar] [CrossRef]
- Dalan, F.C.; Andreani, G.F.D.L.; Travessa, D.N.; Faizova, S.; Faizov, I.A.; Cardoso, K.R. Effect of ECAP Processing on Hardness, Electrical Conductivity, and Precipitation Kinetics of the Cu-0.81Cr-0.07Zr Alloy. J. Electron. Mater. 2021, 50, 6171–6182. [Google Scholar] [CrossRef]
- Kumar, S.S.S.; Raghu, T. Electrical Conductivity, Thermal Stability, and Lattice Defect Evolution During Cyclic Channel Die Compression of OFHC Copper. J. Mater. Eng. Perform. 2014, 24, 726–736. [Google Scholar] [CrossRef]
- Ciemiorek, M.; Pawliszak, Ł.; Chromiński, W.; Olejnik, L.; Lewandowska, M. Enhancing the Electrical Conductivity of Electrolytic Tough Pitch Copper Rods Processed by Incremental Equal Channel Angular Pressing. Met. Mater. Trans. A 2020, 51, 3749–3753. [Google Scholar] [CrossRef]
- Cho, K.-J.; Hong, S.I. Modification of microstructure and strength/conductivity properties of Cu-15 Ag in-situ composites by equal-channel angular pressing. Met. Mater. Int. 2012, 18, 355–360. [Google Scholar] [CrossRef]
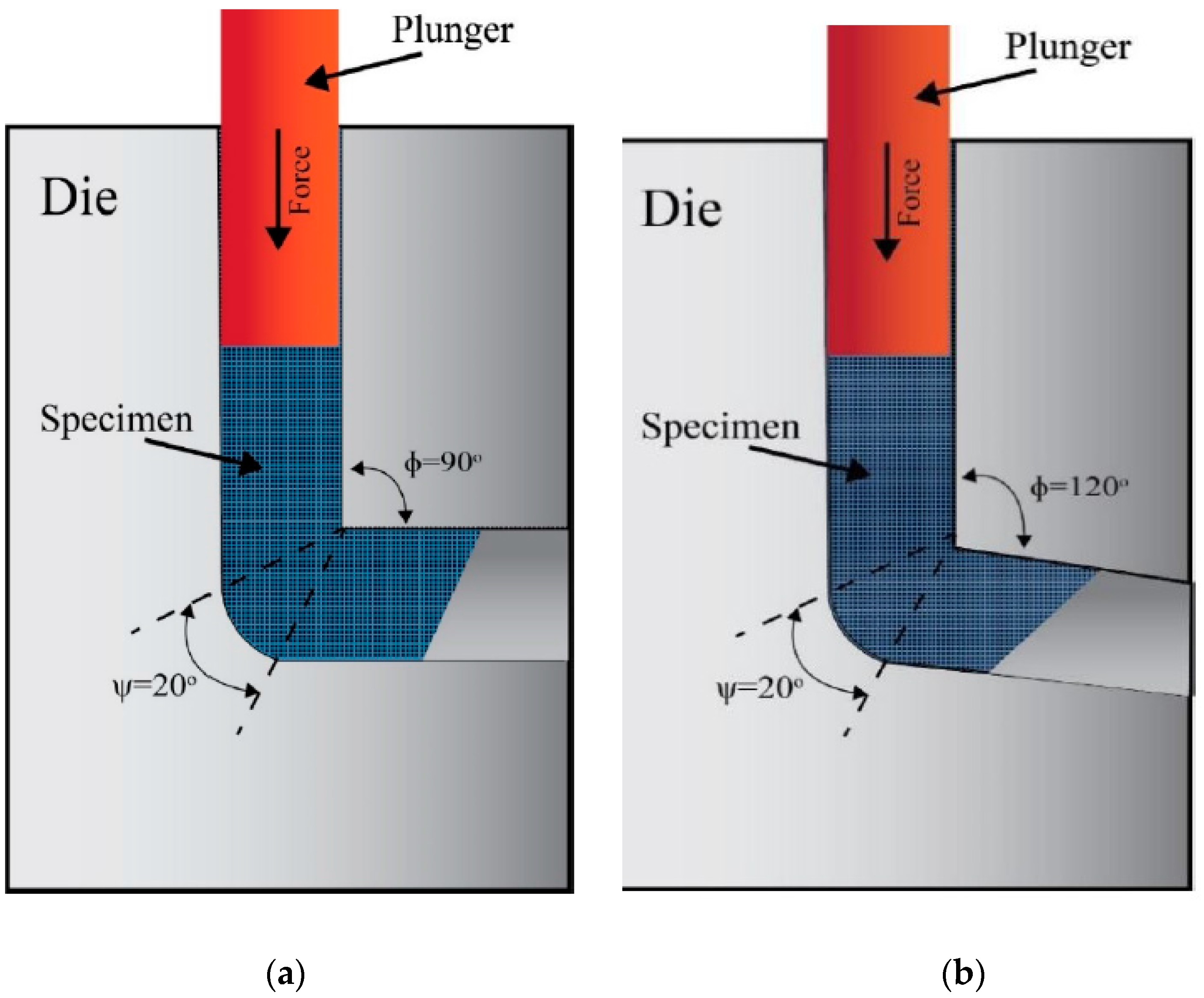
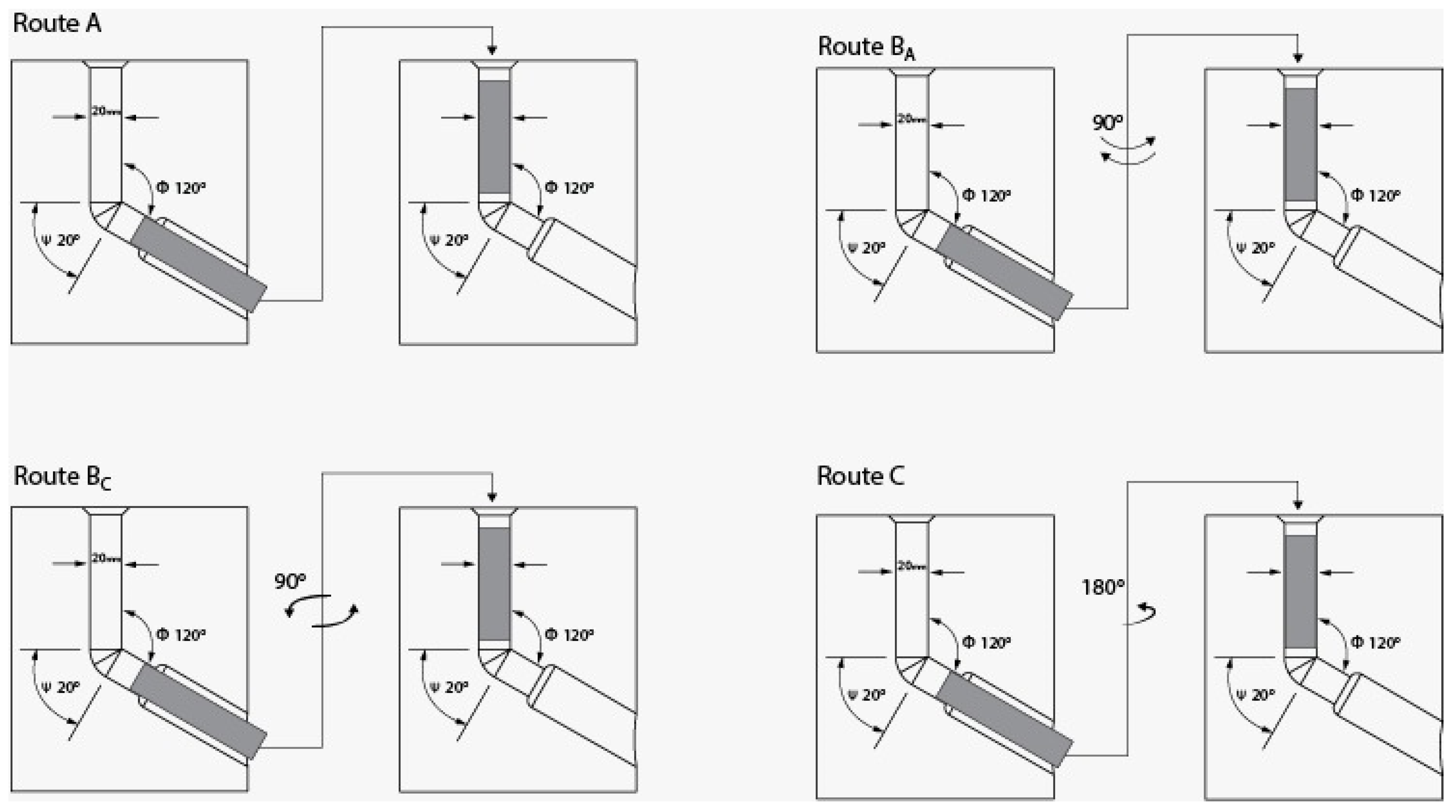

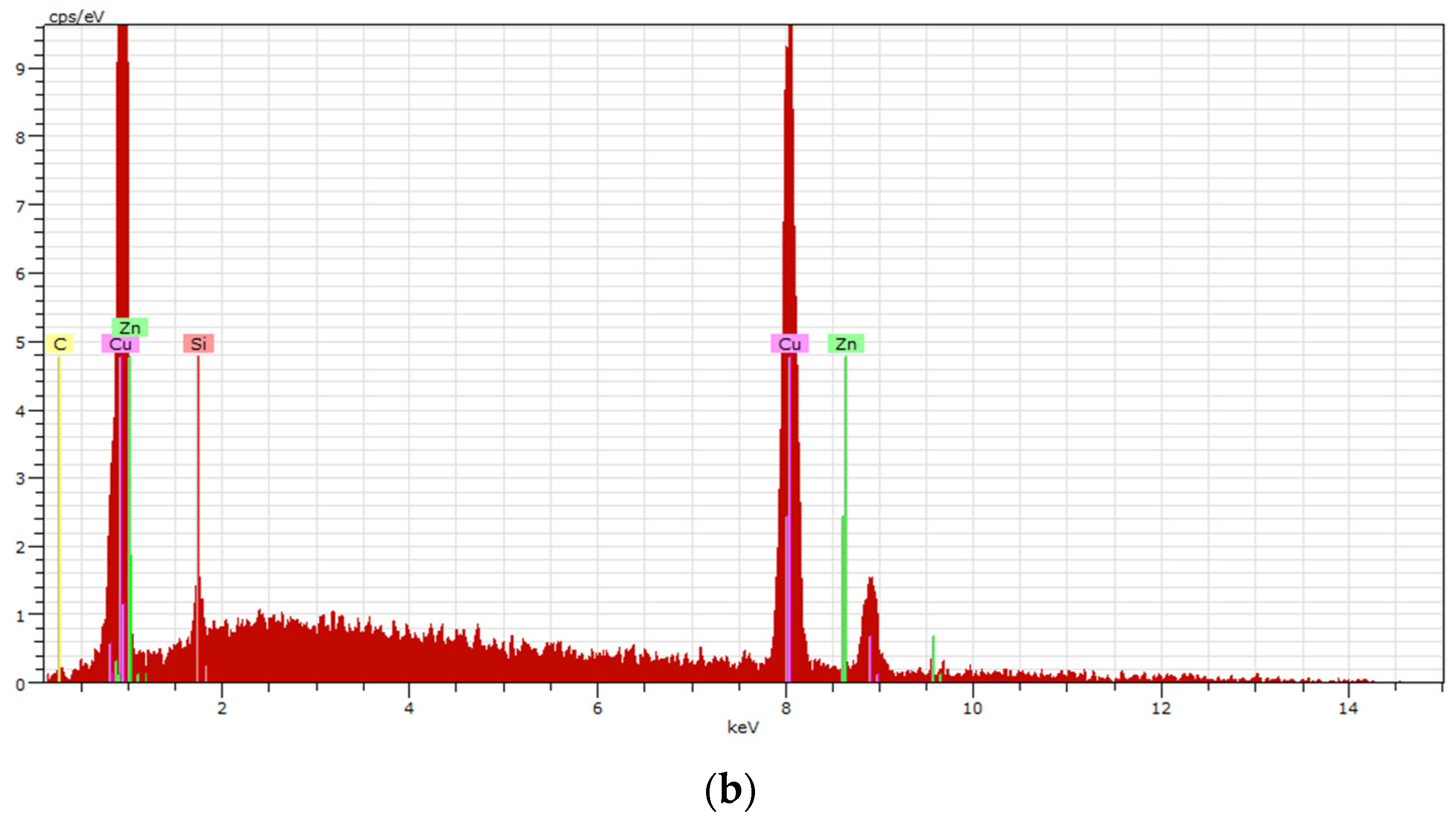





| ECAP Conditions | Symbol | Unit | Conditions Levels | ||
|---|---|---|---|---|---|
| −1 | 0 | 1 | |||
| Number of passes | N | Pass | 2 | 4 | 6 |
| ECAP die angle | φ | ° | 90 | 120 | - |
| Processing temperature | T | K | 298 | 373 | 473 |
| Processing route type | - | - | A | Bc | C |
| Run | ECAP Condition | ECAP Response | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | φ | T | Processing Route Type | Hardness | Tensile Strength | IT (J/cm2) | EC (% IACS) | |||
| (HV) | σy (MPa) | σu (MPa) | Du (%) | |||||||
| AA | 0 | 100 | 82 | 225 | 36 | 60 | 99.4% | |||
| 1 | 2 | 120 | 473 | A | 128 | 108 | 264 | 28.5 | 115 | 98.1% |
| 2 | 2 | 90 | 473 | C | 127 | 112 | 268 | 28 | 68 | 95.2% |
| 3 | 2 | 120 | 298 | C | 124 | 124 | 285 | 25 | 65 | 96% |
| 4 | 6 | 120 | 473 | A | 137 | 167 | 318 | 23 | 105 | 97.3% |
| 5 | 2 | 90 | 373 | A | 139 | 126 | 288 | 25.6 | 68 | 95.4% |
| 6 | 6 | 120 | 473 | C | 141 | 158 | 316 | 24.6 | 84 | 96.9% |
| 7 | 6 | 120 | 473 | C | 139 | 162 | 322 | 23.9 | 80 | 96.4% |
| 8 | 6 | 120 | 298 | C | 145 | 212 | 324 | 20 | 75 | 95.3% |
| 9 | 6 | 120 | 298 | A | 149 | 225 | 332 | 19 | 95 | 94.9% |
| 10 | 2 | 90 | 373 | A | 137 | 122 | 284 | 26.4 | 67 | 94.5% |
| 11 | 4 | 90 | 298 | C | 151 | 176 | 342 | 17 | 52 | 92.2% |
| 12 | 4 | 120 | 373 | C | 139 | 132 | 328 | 20.8 | 75 | 96.2% |
| 13 | 6 | 90 | 473 | Bc | 145 | 179 | 338 | 22 | 55 | 92.8% |
| 14 | 2 | 90 | 473 | C | 129 | 114 | 265 | 28.4 | 69 | 96.5% |
| 15 | 2 | 90 | 298 | Bc | 138 | 166 | 304 | 19 | 55 | 96.3% |
| 16 | 4 | 120 | 373 | A | 142 | 138 | 325 | 20.5 | 85 | 97.4% |
| 17 | 6 | 90 | 298 | A | 158 | 208 | 353 | 14.8 | 45 | 93.2% |
| 18 | 4 | 90 | 298 | C | 152 | 168 | 338 | 17.6 | 50 | 93.3% |
| 19 | 2 | 120 | 298 | A | 128 | 126.5 | 302 | 22.5 | 68 | 96.7% |
| 20 | 2 | 120 | 373 | Bc | 121 | 112 | 278 | 27 | 85 | 95.9% |
| 21 | 6 | 90 | 473 | Bc | 147 | 176 | 332 | 22.8 | 60 | 93.5% |
| Training Set | Testing Set | |||
|---|---|---|---|---|
| ML Algorithm | RMSE (HV) | R2 | RMSE (HV) | R2 |
| Linear regression | 3.29 | 0.87 | 3.77 | 0.86 |
| Regression trees | 4.44 | 0.78 | 7.11 | 0.49 |
| Ensemble of trees | 0.63 | 0.99 | 6.82 | 0.54 |
| Gaussian process regression | 0.62 | 0.99 | 10.45 | 0.08 |
| Fine Gaussian SVR | 3.36 | 0.87 | 3.46 | 0.88 |
| Artificial neural networks | 0.63 | 0.99 | 2.65 | 0.93 |
| Parameter | Training Set | Testing Set | |||
|---|---|---|---|---|---|
| ML Algorithm | RMSE (MPa) | R2 | RMSE (MPa) | R2 | |
| σy | Linear regression | 8.26 | 0.93 | 17.96 | 0.84 |
| Regression trees | 16.87 | 0.71 | 24.09 | 0.72 | |
| Ensemble of trees | 1.72 | 0.99 | 13.79 | 0.91 | |
| Gaussian process regression | 1.65 | 0.99 | 25.74 | 0.67 | |
| Fine Gaussian SVR | 8.99 | 0.86 | 18.31 | 0.83 | |
| Artificial neural networks | 1.65 | 0.99 | 7.14 | 0.96 | |
| Linear regression | 8.65 | 0.89 | 16.44 | 0.55 | |
| Regression trees | 10.96 | 0.84 | 6.91 | 0.92 | |
| Ensemble of trees | 1.85 | 0.99 | 10.09 | 0.83 | |
| σu | Gaussian process regression | 1.68 | 0.99 | 21.22 | 0.26 |
| Fine Gaussian SVR | 9.90 | 0.87 | 16.28 | 0.56 | |
| Artificial neural networks | 1.68 | 0.99 | 5.74 | 0.95 | |
| Linear regression | 1.22 | 0.90 | 2.57 | 0.45 | |
| Regression trees | 2.27 | 0.66 | 1.23 | 0.87 | |
| Ensemble of trees | 0.23 | 0.99 | 1.73 | 0.75 | |
| Du | Gaussian process regression | 0.30 | 0.99 | 3.06 | 0.23 |
| Fine Gaussian SVR | 1.79 | 0.79 | 2.45 | 0.50 | |
| Artificial neural networks | 0.22 | 0.99 | 0.93 | 0.93 | |
| Training Set | Testing Set | |||
|---|---|---|---|---|
| ML Algorithm | RMSE (%) | R2 | RMSE (%) | R2 |
| Linear regression | 7.33 | 0.84 | 10.75 | −0.04 |
| Regression trees | 12.66 | 0.52 | 8.38 | 0.36 |
| Ensemble of trees | 1.57 | 0.99 | 17.11 | −1.64 |
| Gaussian process regression | 1.16 | 0.99 | 11.49 | 0.0048 |
| Fine Gaussian SVR | 7.99 | 0.81 | 11.76 | −0.25 |
| Artificial neural networks | 1.16 | 0.99 | 2.41 | 0.95 |
| Training Set | Testing Set | |||
|---|---|---|---|---|
| ML Algorithm | RMSE (%IACS) | R2 | RMSE (%IACS) | R2 |
| Linear regression | 7.33 | 0.84 | 10.75 | −0.04 |
| Regression trees | 12.66 | 0.52 | 8.38 | 0.36 |
| Ensemble of trees | 1.57 | 0.99 | 17.11 | −1.64 |
| Gaussian process regression | 1.16 | 0.99 | 11.49 | 0.0048 |
| Fine Gaussian SVR | 7.99 | 0.81 | 11.76 | −0.25 |
| Artificial neural networks | 7.99 | 0.81 | 2.41 | 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaban, M.; Alsharekh, M.F.; Alsunaydih, F.N.; Alateyah, A.I.; Alawad, M.O.; BaQais, A.; Kamel, M.; Nassef, A.; El-Hadek, M.A.; El-Garaihy, W.H. Investigation of the Effect of ECAP Parameters on Hardness, Tensile Properties, Impact Toughness, and Electrical Conductivity of Pure Cu through Machine Learning Predictive Models. Materials 2022, 15, 9032. https://doi.org/10.3390/ma15249032
Shaban M, Alsharekh MF, Alsunaydih FN, Alateyah AI, Alawad MO, BaQais A, Kamel M, Nassef A, El-Hadek MA, El-Garaihy WH. Investigation of the Effect of ECAP Parameters on Hardness, Tensile Properties, Impact Toughness, and Electrical Conductivity of Pure Cu through Machine Learning Predictive Models. Materials. 2022; 15(24):9032. https://doi.org/10.3390/ma15249032
Chicago/Turabian StyleShaban, Mahmoud, Mohammed F. Alsharekh, Fahad Nasser Alsunaydih, Abdulrahman I. Alateyah, Majed O. Alawad, Amal BaQais, Mokhtar Kamel, Ahmed Nassef, Medhat A. El-Hadek, and Waleed H. El-Garaihy. 2022. "Investigation of the Effect of ECAP Parameters on Hardness, Tensile Properties, Impact Toughness, and Electrical Conductivity of Pure Cu through Machine Learning Predictive Models" Materials 15, no. 24: 9032. https://doi.org/10.3390/ma15249032
APA StyleShaban, M., Alsharekh, M. F., Alsunaydih, F. N., Alateyah, A. I., Alawad, M. O., BaQais, A., Kamel, M., Nassef, A., El-Hadek, M. A., & El-Garaihy, W. H. (2022). Investigation of the Effect of ECAP Parameters on Hardness, Tensile Properties, Impact Toughness, and Electrical Conductivity of Pure Cu through Machine Learning Predictive Models. Materials, 15(24), 9032. https://doi.org/10.3390/ma15249032










