Impact of the Surface Irregularities of NiFeMo Compacted Powder Particles on Irreversible Magnetization Processes
Abstract
1. Introduction
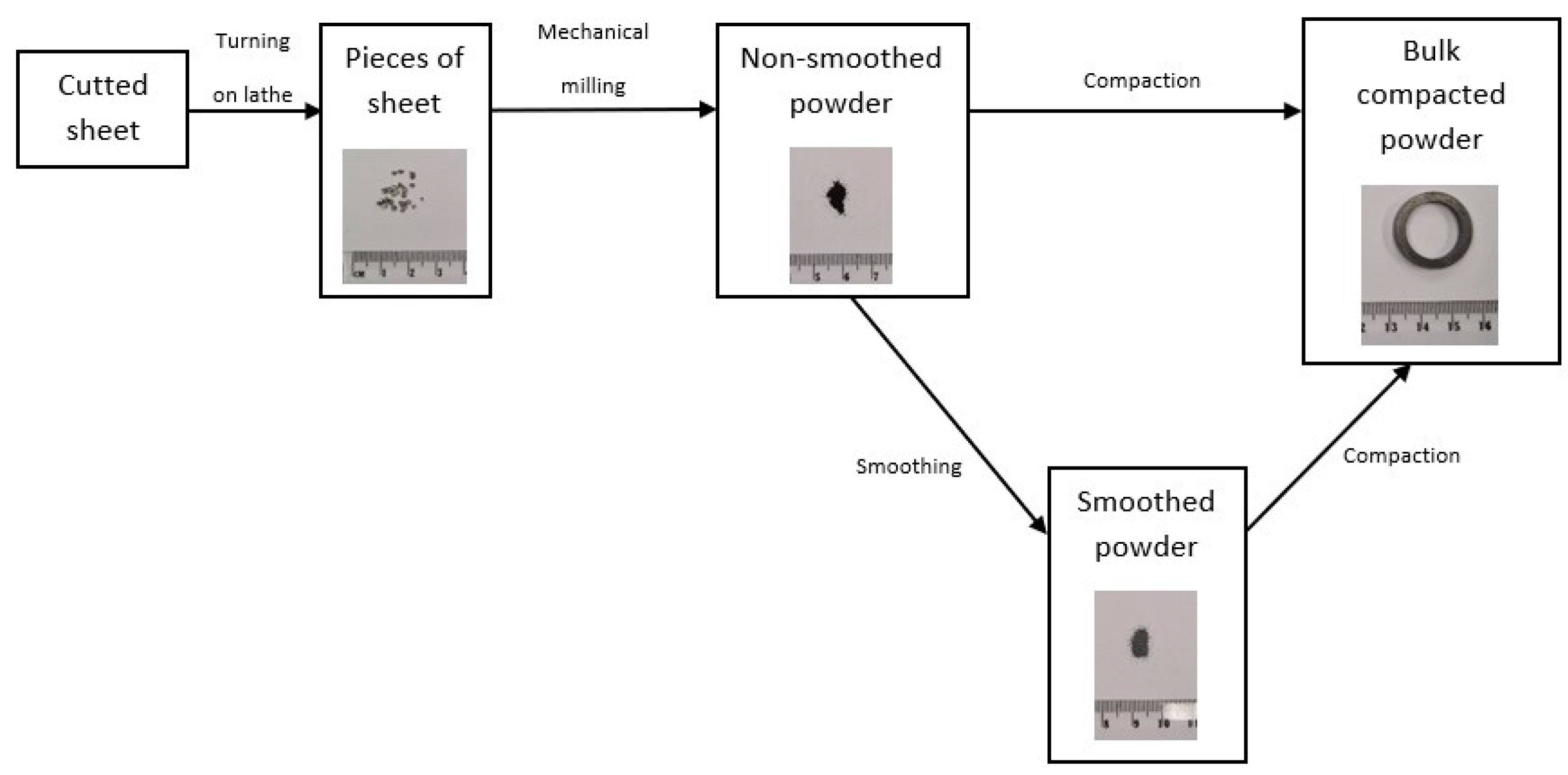
2. Materials and Methods
3. Results and Discussion
3.1. Microstructure
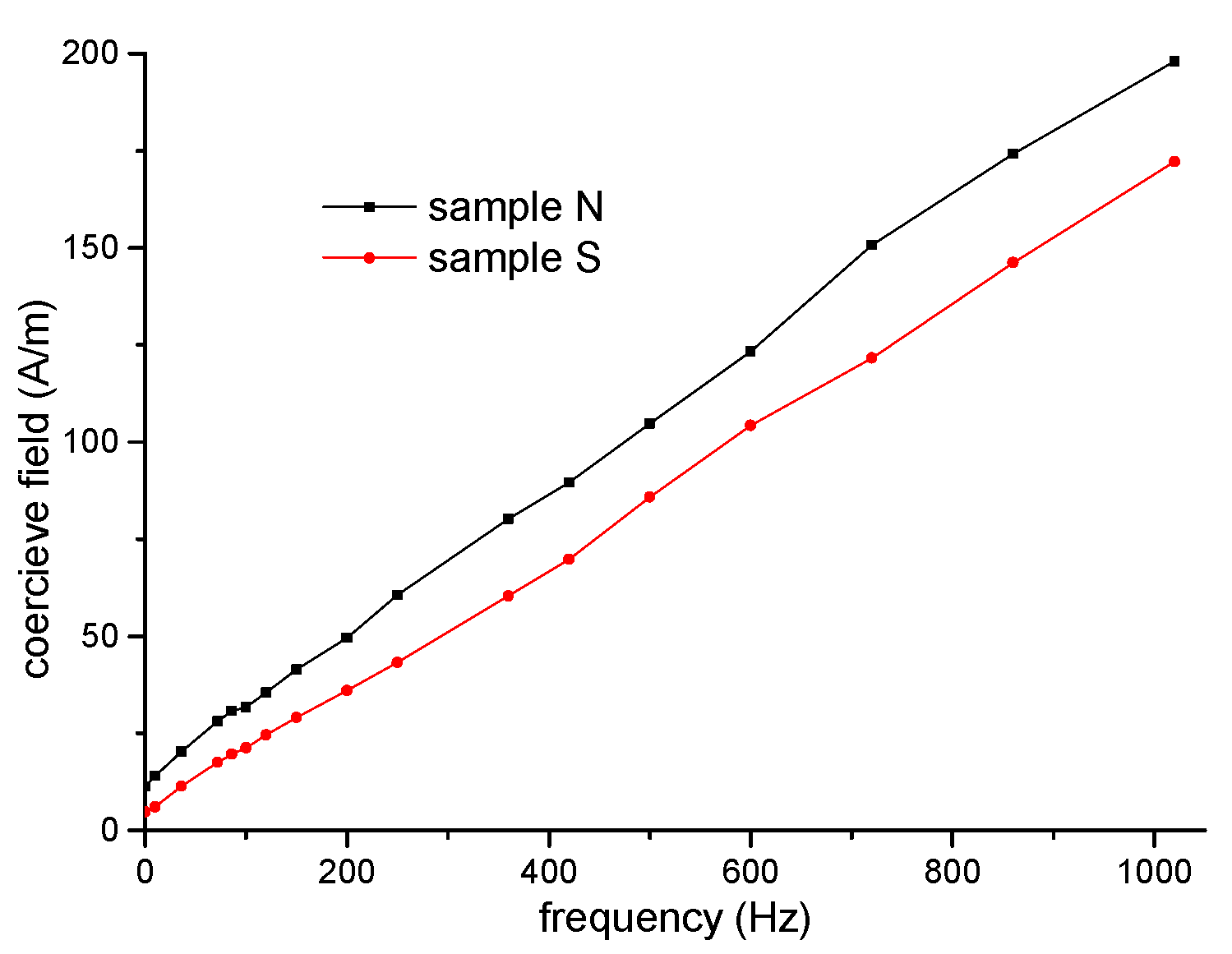
3.2. Coercive Field
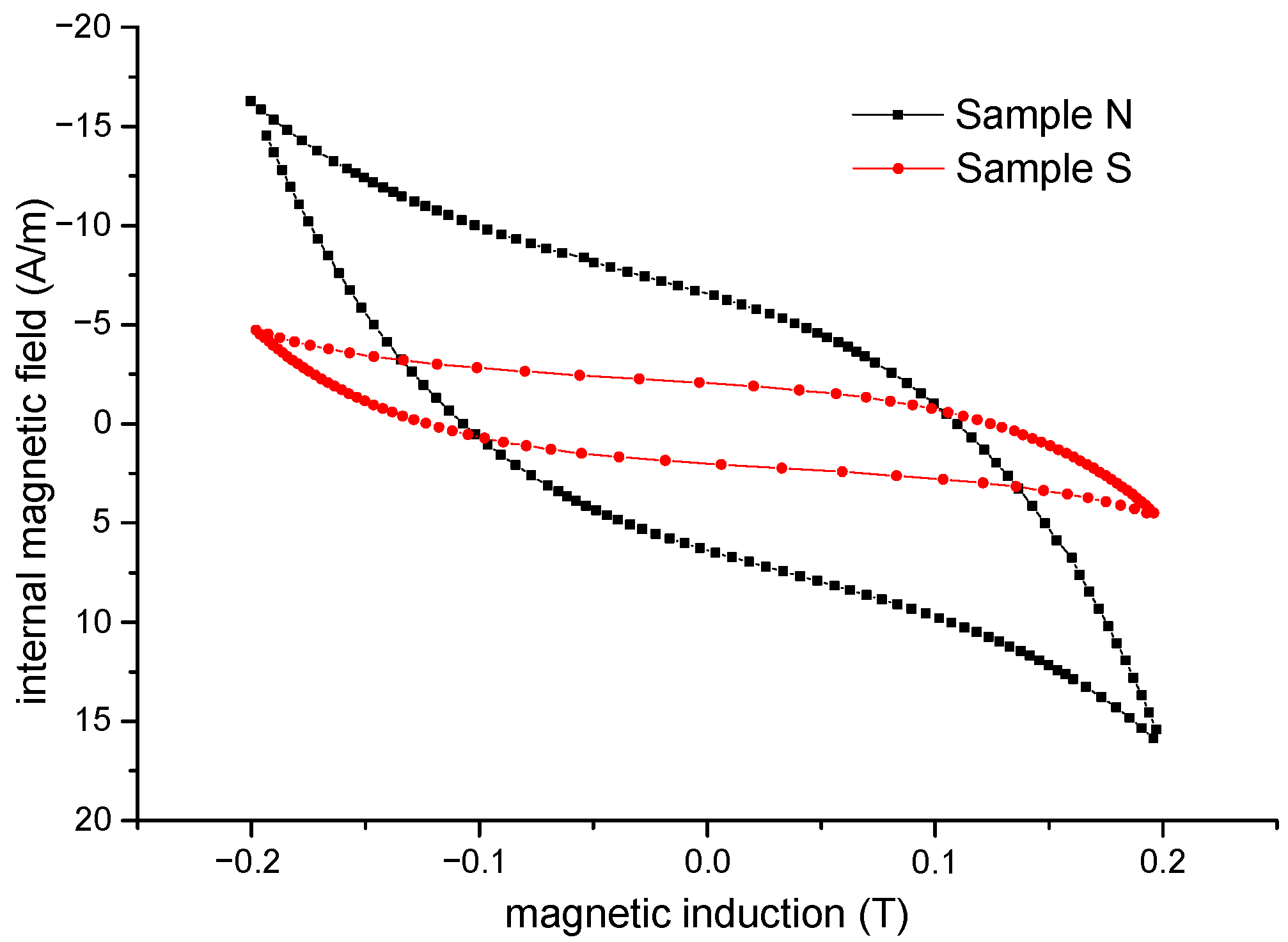
3.3. Hysteresis Loops
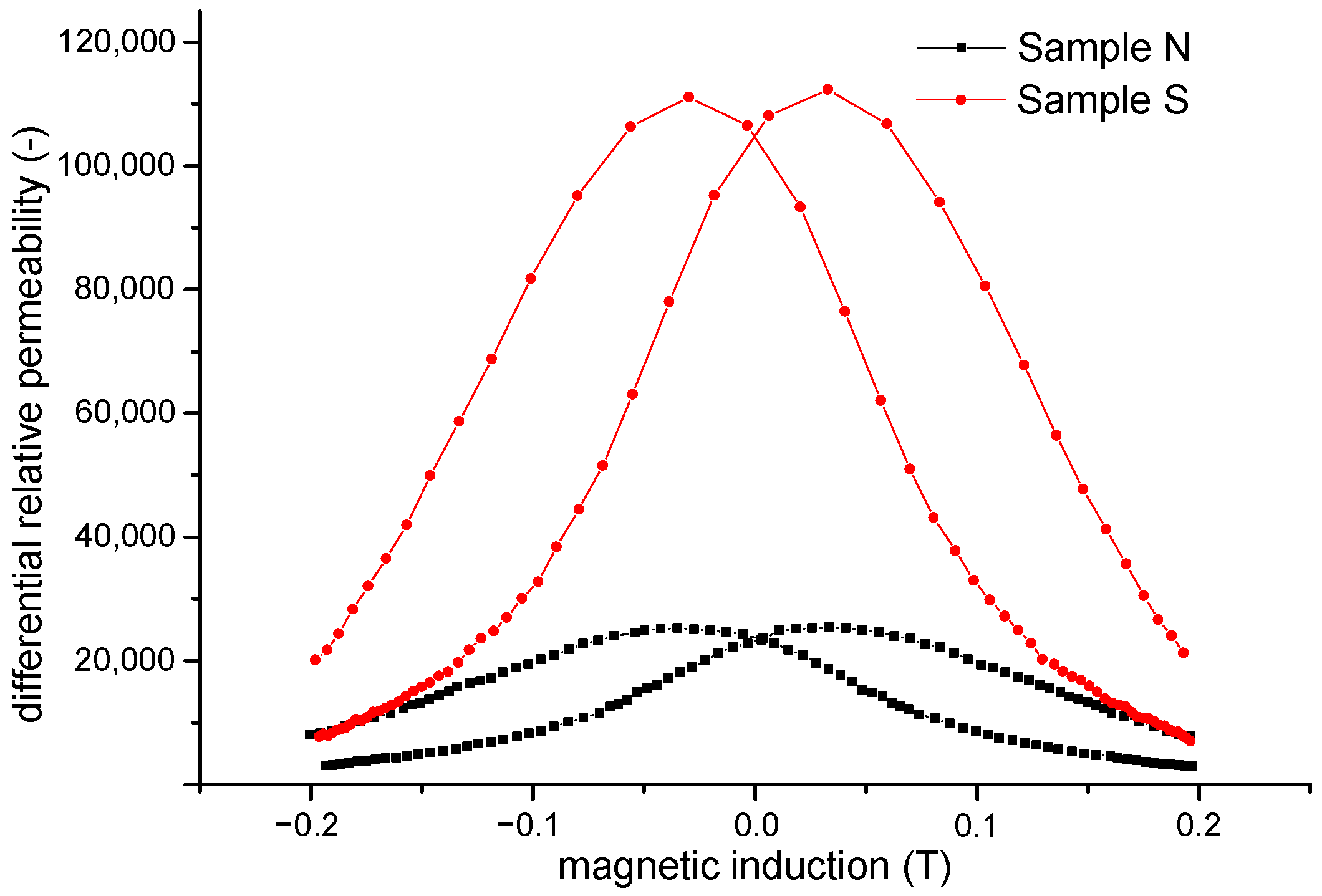
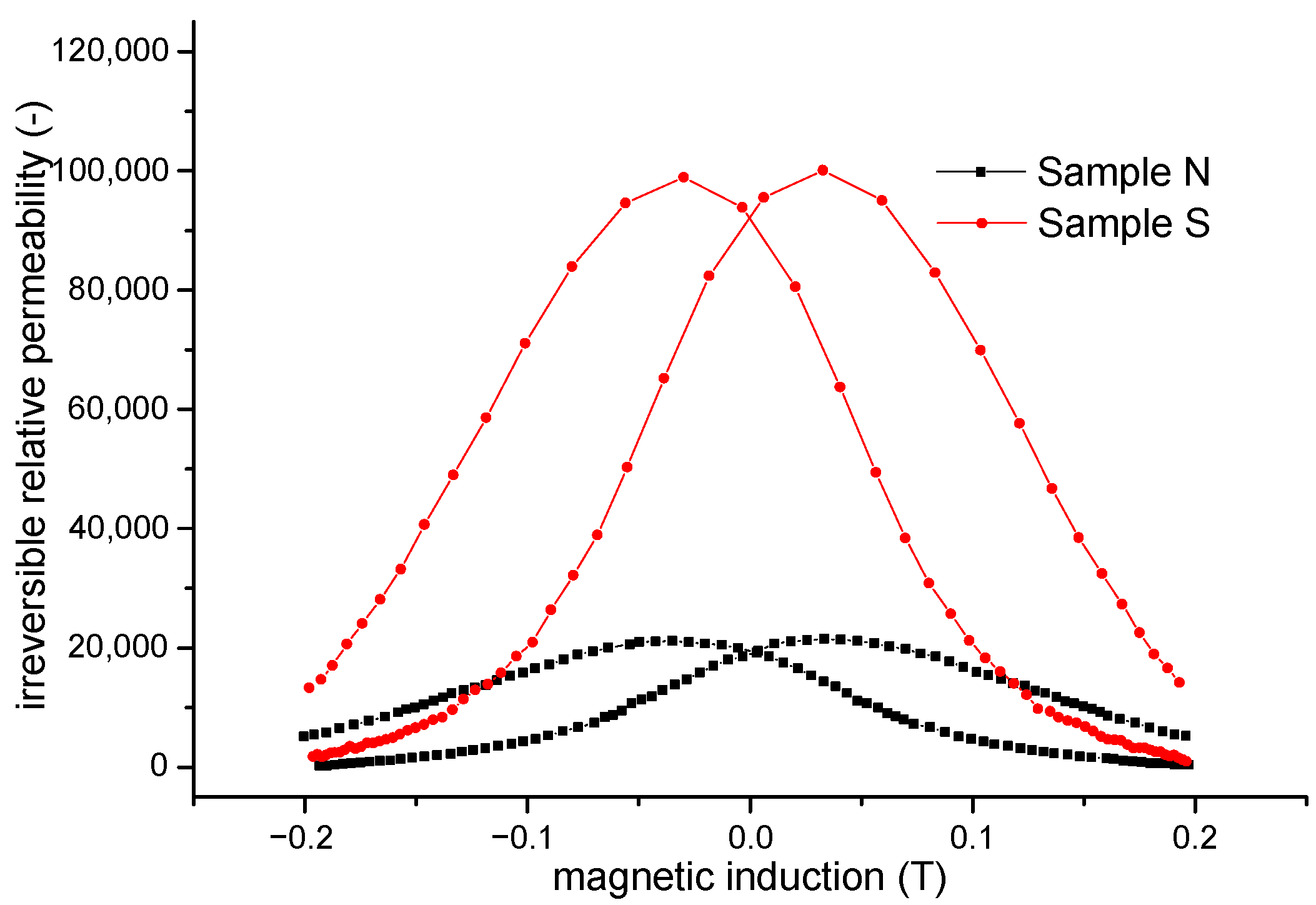
3.4. Permeability
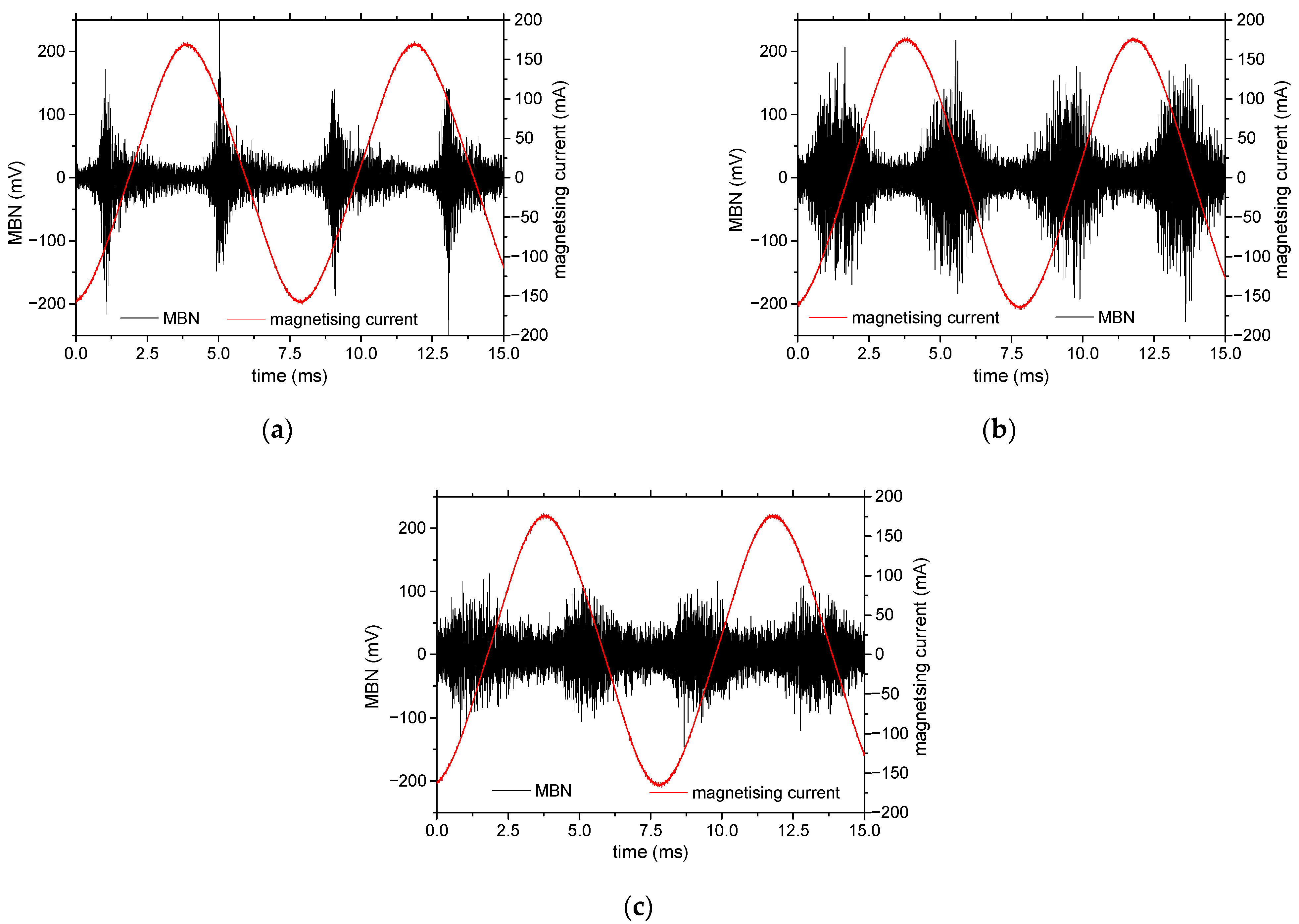
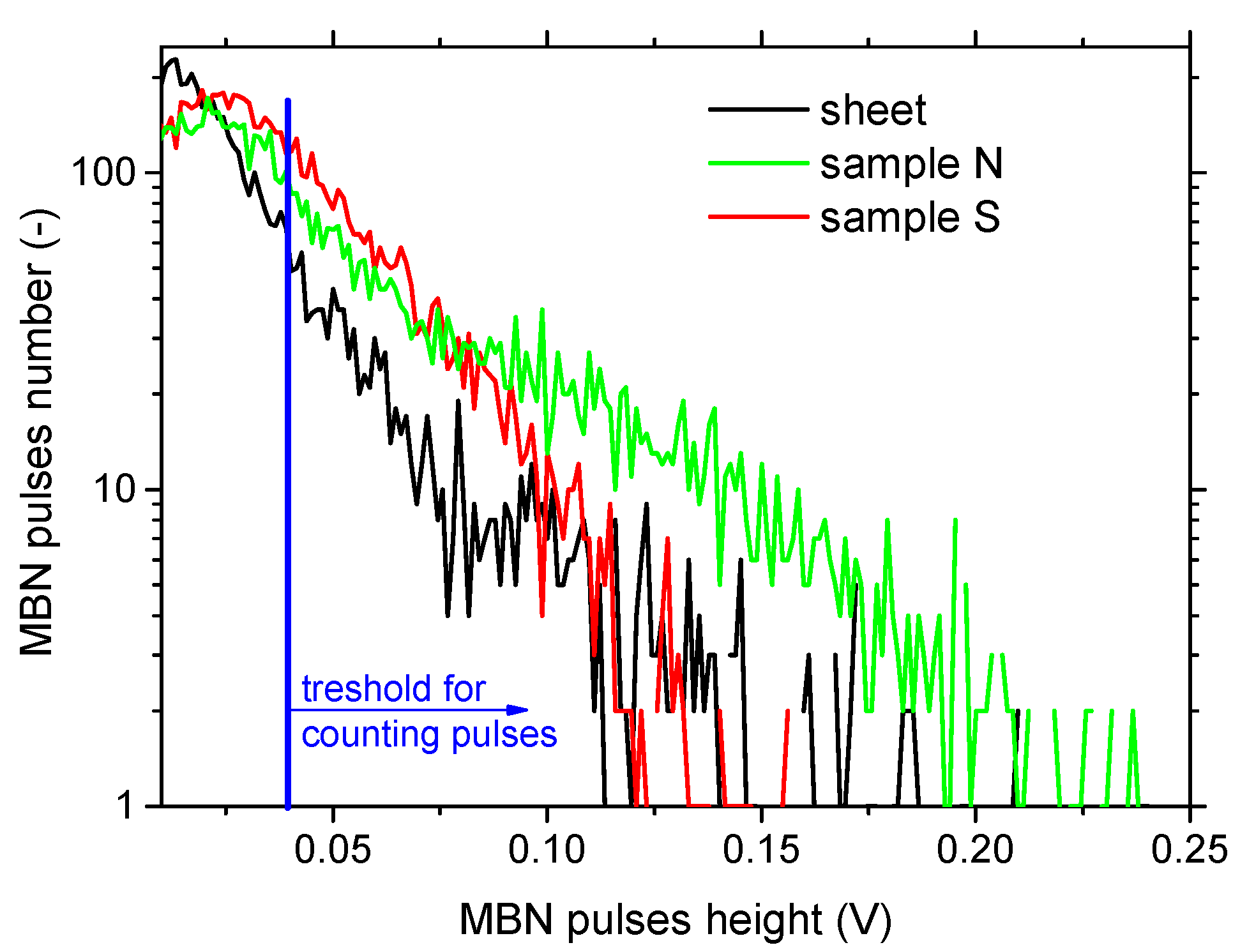
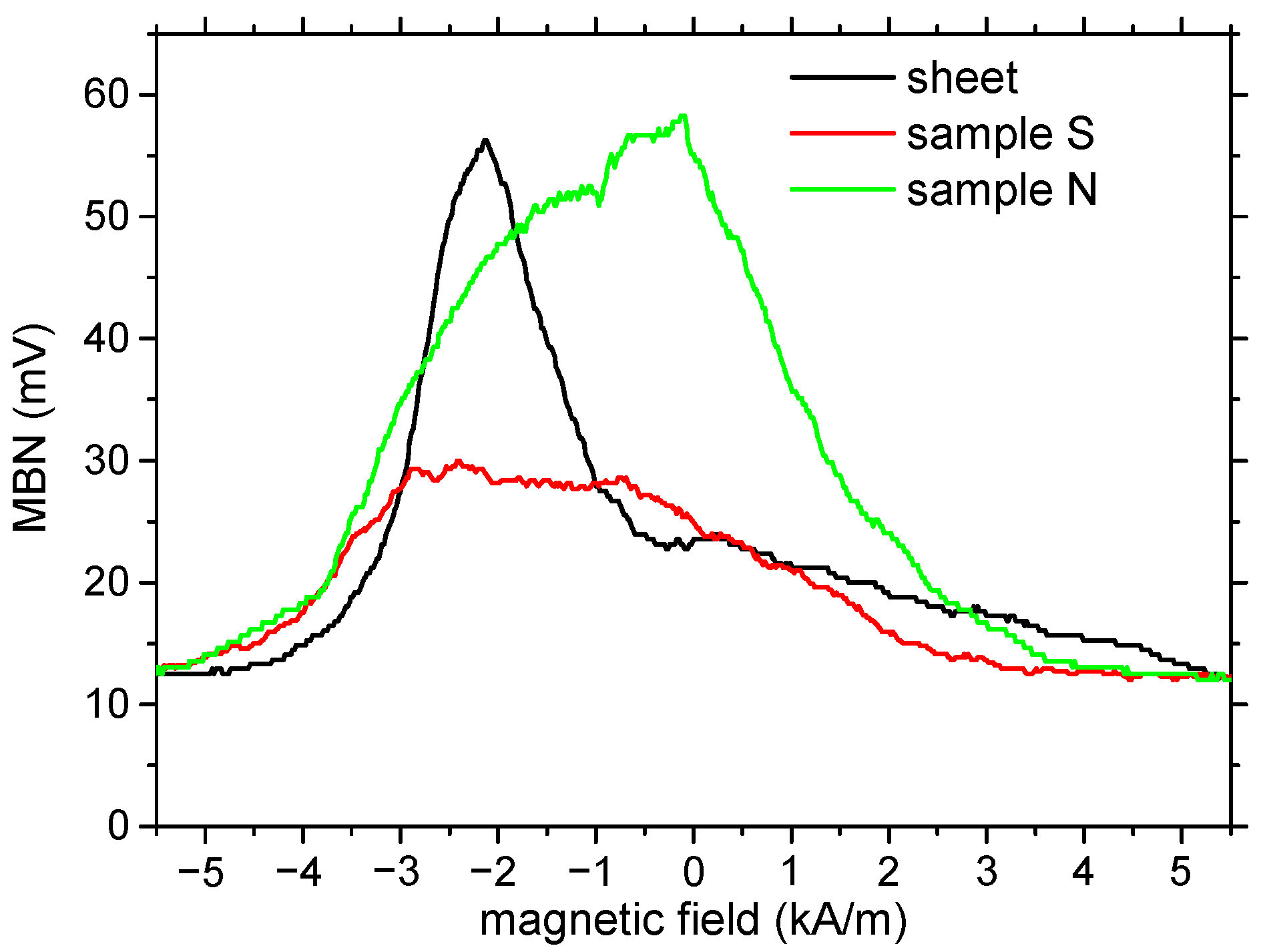
3.5. Magnetic Barkhausen Noise
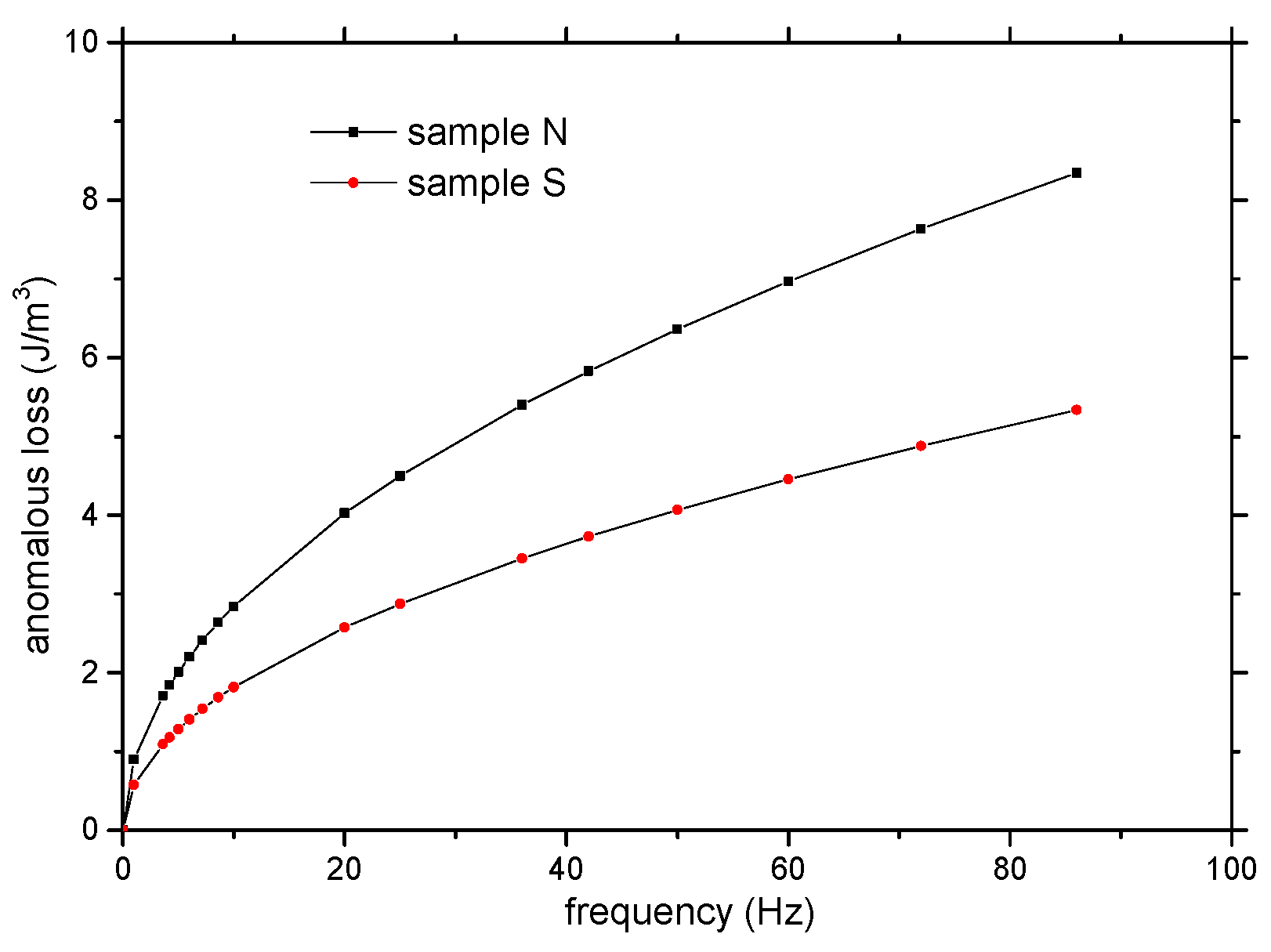
3.6. Losses
4. Conclusions
- The irregular shape of the powder particles of sample N leads to better contact between the particles, but magnetization processes take place more easily in the particles of sample S, where the capture centers for the displacement of the domain walls are reduced.
- There is a lower coercive field in the frequency range from DC to 1 kHz at the maximum induction of 0.2 T for sample S in comparison with sample N.
- There are higher values of differential relative permeability and reversible relative permeability in magnetization reversal in the DC magnetic field at the maximum induction of 0.2 T for sample S in comparison with sample N,
- The lower values of the amplitude of the Barkhausen noise for sample S in comparison with sample N confirms the assumption that a larger number of easily movable domain walls are present over shorter distances in sample S.
- There is lower excess loss in the frequency range from DC to 1 kHz measured at the maximum induction of 0.2 T for sample S in comparison with sample N.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ürge-Vorsatz, D.; Cabeza, L.F.; Serrano, S.; Barreneche, C.; Petrichenko, K. Heating and cooling energy trends and drivers in buildings. Renew. Sustain. Energy Rev. 2015, 41, 85–98. [Google Scholar] [CrossRef]
- Ciemnicka, J.; Prałat, K.; Koper, A.; Makomaski, G.; Majewski, Ł.; Wójcicka, K.; Buczkowska, K.E. Changes in the strength properties and phase transition of gypsum modified with microspheres, aerogel and HEMC polymer. Materials 2021, 14, 3486. [Google Scholar] [CrossRef] [PubMed]
- Powała, K.; Obraniak, A.; Heim, D.; Mrowiec, A. Application of the Hot Wire Method to Measure the Thermal Conductivity Coefficient of a Gypsum Composite. Materials 2022, 15, 6564. [Google Scholar] [CrossRef] [PubMed]
- Gutfleisch, O.; Willard, M.A.; Brück, E. Stronger, Lighter, and More Energy Efficient Magnetic Materials and Devices for the 21st Century. Adv. Mater. 2011, 23, 821–884. [Google Scholar] [CrossRef]
- Silakhori, M.; Naghavi, M.S.; Simon, H.; Metselaar, C.; Meurah, T.; Mahlia, I.; Fauzi, H.; Mehrali, M. Accelerated Thermal Cycling Test of Microencapsulated Paraffin Wax/Polyaniline Made by Simple Preparation Method for Solar Thermal Energy Storage. Materials 2013, 6, 1608–1620. [Google Scholar] [CrossRef]
- Xie, D.Z.; Lin, K.H.; Lin, S.T. Effects of processed parameters on the magnetic performance of a powder magnetic core. J. Magn. Magn. Mater. 2014, 353, 34–40. [Google Scholar] [CrossRef]
- Suryanarayana, C. Mechanical alloying and milling. Prog. Mater. Sci. 2001, 46, 1–184. [Google Scholar] [CrossRef]
- Kollár, P.; Slovenský, P.; Olekšáková, D.; Jakubčin, M.; Birčáková, Z.; Füzer, J.; Bureš, R.; Fáberová, M. Preparation and magnetic properties of NiFeMo powdered compacts of powder elements with smoothed surfaces. J. Magn. Magn. Mater. 2020, 494, 165770. [Google Scholar] [CrossRef]
- Ustinovshikov, Y.; Shabanova, I. A study of microstructures responsible for the emergence of the invar and permalloy effects in Fe/Ni alloys. J. Alloys Compd. 2013, 578, 292–296. [Google Scholar] [CrossRef]
- Olekšáková, D.; Kollár, P.; Jakubčin, M.; Füzer, J.; Tkáč, M.; Slovenský, P.; Bureš, R.; Fáberová, M. Energy loss separation in NiFeMo compacts with smoothed powders according to Landgraf’s and Bertotti’s theories. J. Mater. Sci. 2021, 56, 12835–12844. [Google Scholar] [CrossRef]
- Slovenský, P.; Kollár, P.; Mei, N.; Jakubčin, M.; Zeleňáková, A.; Halama, M.; Walinder, I.O.; Hedberg, Y.S. Mechanical surface smoothing of micron-sized iron powder for improved silica coating performance as soft magnetic composites. Appl. Surf. Sci. 2020, 531, 147340. [Google Scholar] [CrossRef]
- Prashanth, M.; Karunanithi, R.; Rasool Mohideen, S.; Sivasankaran, S.; Vlahović, M. A comparative study on X-ray peak broadening analysis of mechanically alloyed Al2O3 particles dispersion strengthened Al 7017 alloy. Mater. Chem. Phys. 2023, 294, 127015. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Ammar, H.R.; Al-Mufadi, F.A. Continuous hot-compaction behavior of nanostructured FeCrCuMnTi-(V, Zn) high-entropy alloys. Mater. Manuf. Process. S Chem. Phys. 2022, 37, 1122–1131. [Google Scholar] [CrossRef]
- Füzer, J.; Kollár, P.; Olekšáková, D.; Roth, S. AC magnetic properties of the bulk Fe–Ni and Fe–Ni–Mo soft magnetic alloys prepared by warm compaction. J. Alloys Compd. 2009, 483, 557–559. [Google Scholar] [CrossRef]
- Olekšáková, D.; Kollár, P.; Füzer, J. Low Frequency Core Losses Components of FeNiMo Powder Compacted Materials. Acta Phys. Pol. A 2018, 133, 639–641. [Google Scholar] [CrossRef]
- Ma, J.; Qin, M.; Wang, X.; Zhang, L.; Tian, L.; Zhang, X.; Lim, X.; Qu, X. Microstructure and magnetic properties of Fe-79%Ni-4%Mo alloy fabricated by metal injection molding. Powder Technol. 2014, 253, 158–162. [Google Scholar] [CrossRef]
- Batra, R.C. Instability strain and shear band spacing in simple tensile/compressive deformations of thermoviscoplastic materials. Int. J. Impact. Eng. 2007, 34, 448–463. [Google Scholar] [CrossRef]
- Petegem, S.V.; Zimmermann, J.; Van Swygenhoven, H. Yield point phenomenon during strain rate change in nanocrystalline Ni-Fe. Scr. Mater. 2011, 65, 217–220. [Google Scholar]
- Kronmüller, H.; Parkin, S. Micromagnetism 2. In Handbook of Magnetism and Advanced Magnetic Materials; Wiley: New York, NY, USA, 2007; Volume 2. [Google Scholar]
- Chikazumi, S. Physics of Ferromagnetism, 2nd ed.; Oxford Science: Oxford, UK, 1997. [Google Scholar]
- Birčáková, Z.; Kollár, P.; Weidenfeller, B.; Füzer, J.; Fáberová, M.; Bureš, R. Reversible and irreversible DC magnetization processes in the frame of magnetic, thermal and electrical properties of Fe-based composite materials. J. Alloys Compd. 2015, 645, 283–289. [Google Scholar] [CrossRef]
- Blažek, D.; Neslušan, M.; Mičica, M.; Pištora, J. Extraction of Barkhausen noise from the measured raw signal in high-frequency regimes. Measurement 2016, 94, 456–463. [Google Scholar] [CrossRef]
- Alessandro, B.; Beatrice, C.; Bertotti, G.; Montorsi, A. Domain wall dynamics and Barkhausen effect in metallic ferromagnetic materials. II. Experiments. J. Appl. Phys. 1990, 68, 2908. [Google Scholar] [CrossRef]
- Martínez-Ortiz, P.; Pérez-Benitez, J.A.; Espina-Hernández, J.H.; Caleyo, F.; Hallen, J.M. On the estimation of the magnetic easy axis in pipeline steels using magnetic Barkhausen noise. J. Magn. Magn. Mater. 2015, 374, 67–74. [Google Scholar] [CrossRef]
- Shen, T.D.; Harms, U.; Schwarz, R.B. Bulk Fe-based metallic glass with extremely soft ferromagnetic properties. Mater. Sci. Forum 2002, 386, 441–446. [Google Scholar] [CrossRef]
- Bertotti, G. General-properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Bertotti, G.; Fiorillo, F.; Soardo, G.P. The prediction of power losses in soft magnetic-materials. J. Phys. Colloq. 1985, 49, 1915–1919. [Google Scholar] [CrossRef]
- Bertotti, G. Hysteresis in Magnetism. In For Physicists, Materials Scientists, and Engineers, 1st ed.; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]


| Sample | Density a g/cm3 | Coercivity a A/m | DC Losses b J/m−3 | Initial Relative Permeability a | Maximum Relative Permeability a | Excess Loss Coefficient b J·m−3·s1/2 |
|---|---|---|---|---|---|---|
| N | 7.30 | 24.4 | 4.60 | 3400 | 8480 | 0.90 |
| S | 7.15 | 4.80 | 1.54 | 10,850 | 27,700 | 0.58 |
| Conditions of MBN | Values |
|---|---|
| Magnetizing frequency | 125 Hz of sine profile |
| Magnetizing voltage | 6 V |
| Sensor | S1-18-12-01 |
| MBN signal frequency range | From 10 to 150 kHz |
| Sampling frequency | 6.7 MHz |
| Sample | Rms mV | Number of MBN Pulses | PP kA·m−1 | FWHM kA·m−1 |
|---|---|---|---|---|
| Sheet | 23.5 ± 2.5 | 2232 ± 160 | −2.16 ± 0.01 | 1.35 ± 0.07 |
| N | 38.5 ± 3.5 | 5521 ± 267 | −0.65 ± 0.03 | 4.05 ± 0.11 |
| S | 25.0 ± 3.0 | 2920 ± 150 | −2.21 ± 0.01 | 4.40 ± 0.06 |
| Sample | E90 (mV)2 | E180 (mV)2 |
|---|---|---|
| Sheet | 4 | 68 |
| N | 54 | 85 |
| S | 16 | 35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olekšáková, D.; Kollár, P.; Neslušan, M.; Jakubčin, M.; Füzer, J.; Bureš, R.; Fáberová, M. Impact of the Surface Irregularities of NiFeMo Compacted Powder Particles on Irreversible Magnetization Processes. Materials 2022, 15, 8937. https://doi.org/10.3390/ma15248937
Olekšáková D, Kollár P, Neslušan M, Jakubčin M, Füzer J, Bureš R, Fáberová M. Impact of the Surface Irregularities of NiFeMo Compacted Powder Particles on Irreversible Magnetization Processes. Materials. 2022; 15(24):8937. https://doi.org/10.3390/ma15248937
Chicago/Turabian StyleOlekšáková, Denisa, Peter Kollár, Miroslav Neslušan, Miloš Jakubčin, Ján Füzer, Radovan Bureš, and Mária Fáberová. 2022. "Impact of the Surface Irregularities of NiFeMo Compacted Powder Particles on Irreversible Magnetization Processes" Materials 15, no. 24: 8937. https://doi.org/10.3390/ma15248937
APA StyleOlekšáková, D., Kollár, P., Neslušan, M., Jakubčin, M., Füzer, J., Bureš, R., & Fáberová, M. (2022). Impact of the Surface Irregularities of NiFeMo Compacted Powder Particles on Irreversible Magnetization Processes. Materials, 15(24), 8937. https://doi.org/10.3390/ma15248937







