Effect of the Transverse Functional Gradient of the Thin Interfacial Inclusion Material on the Stress Distribution of the Bimaterial under Longitudinal Shear
Abstract
1. Introduction
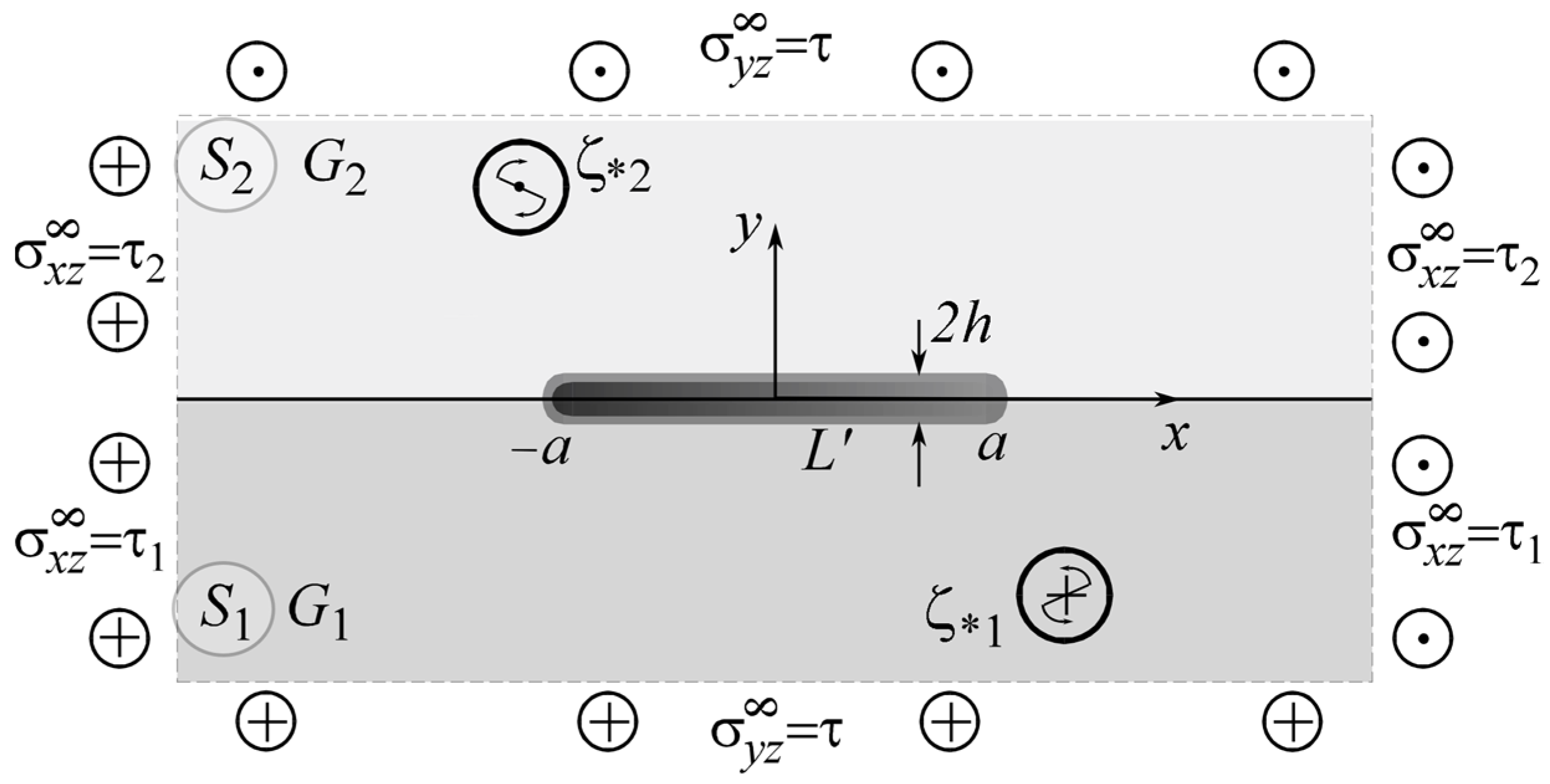
2. Formulation of the Problem
3. Materials and Methods
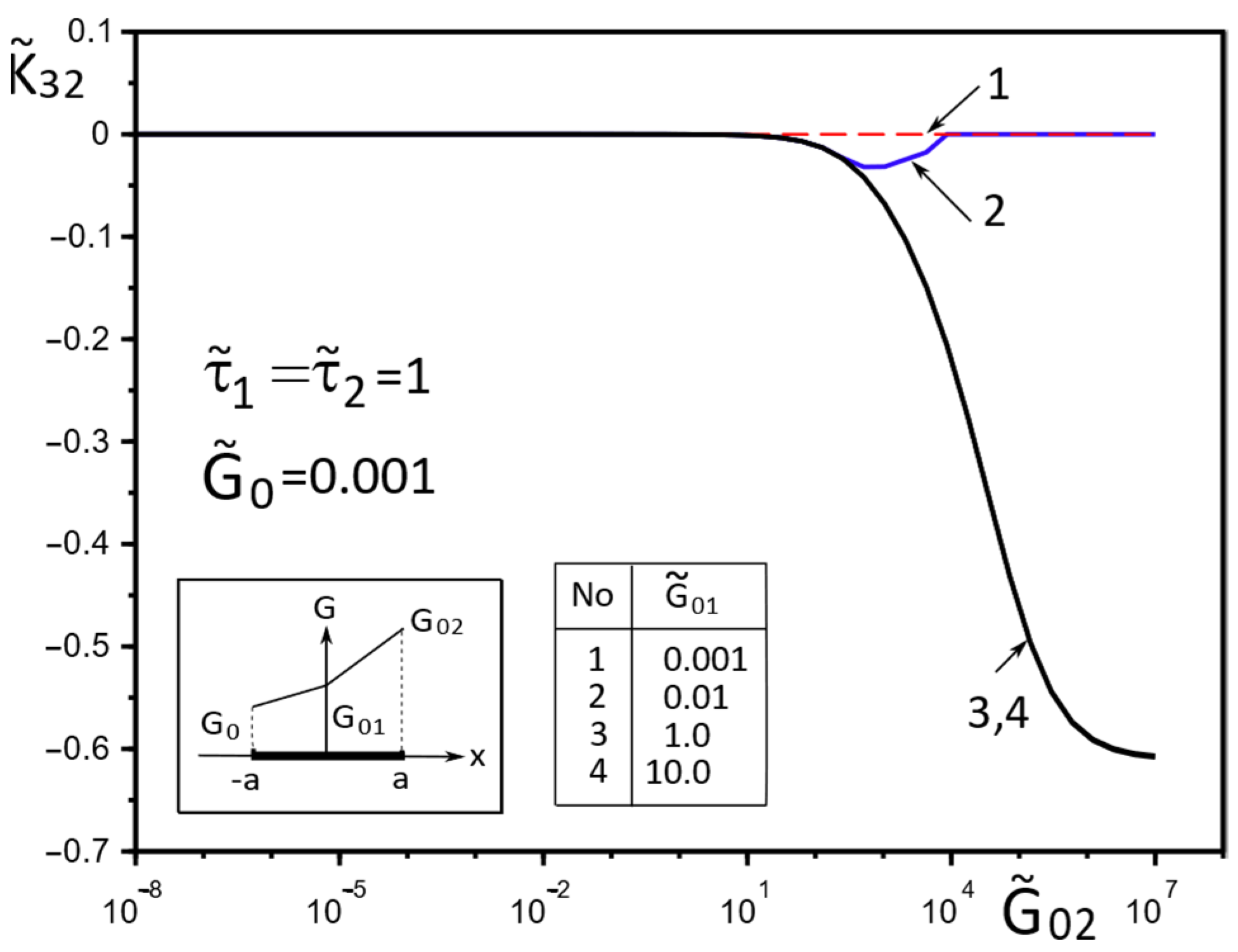
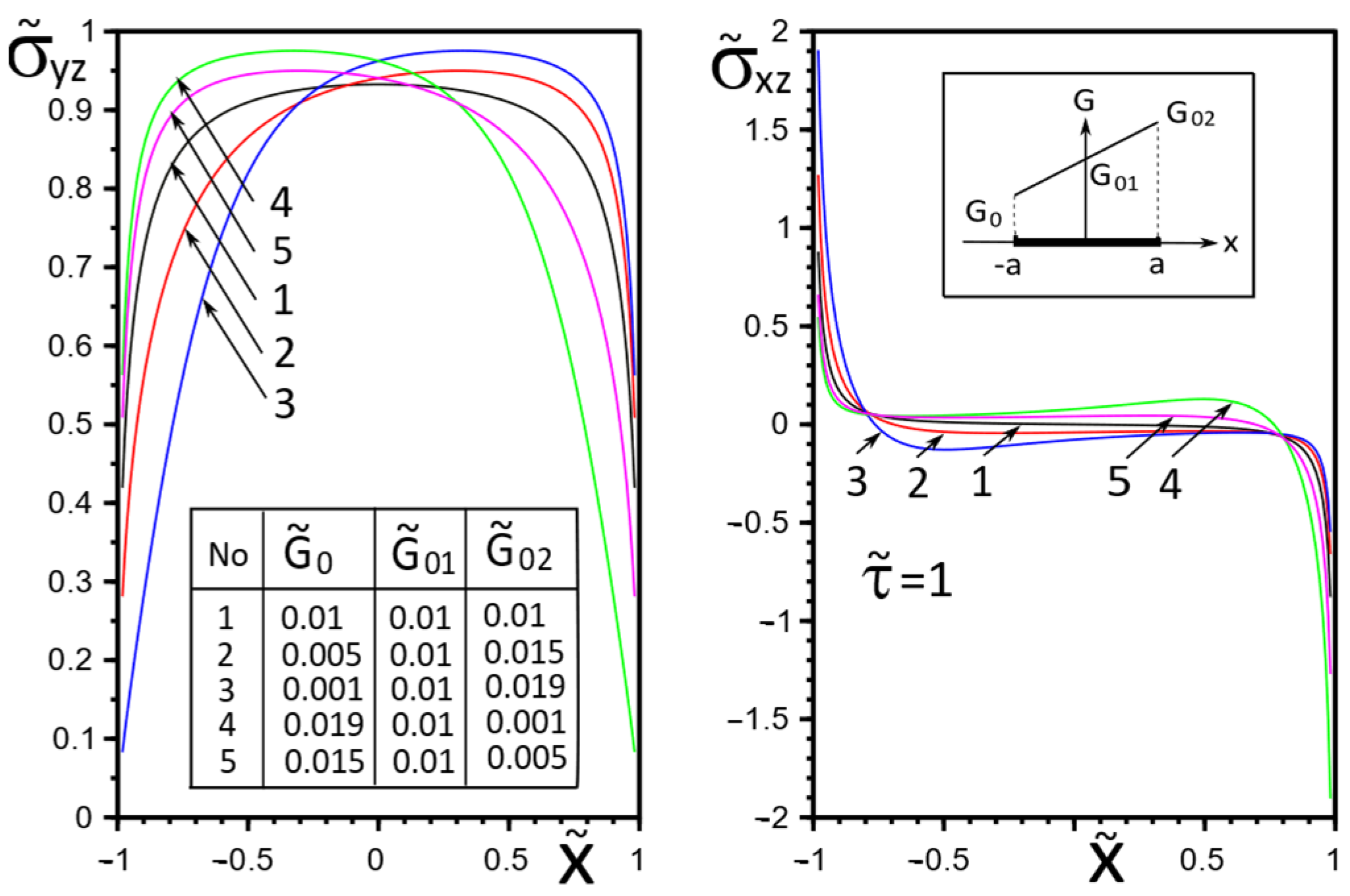
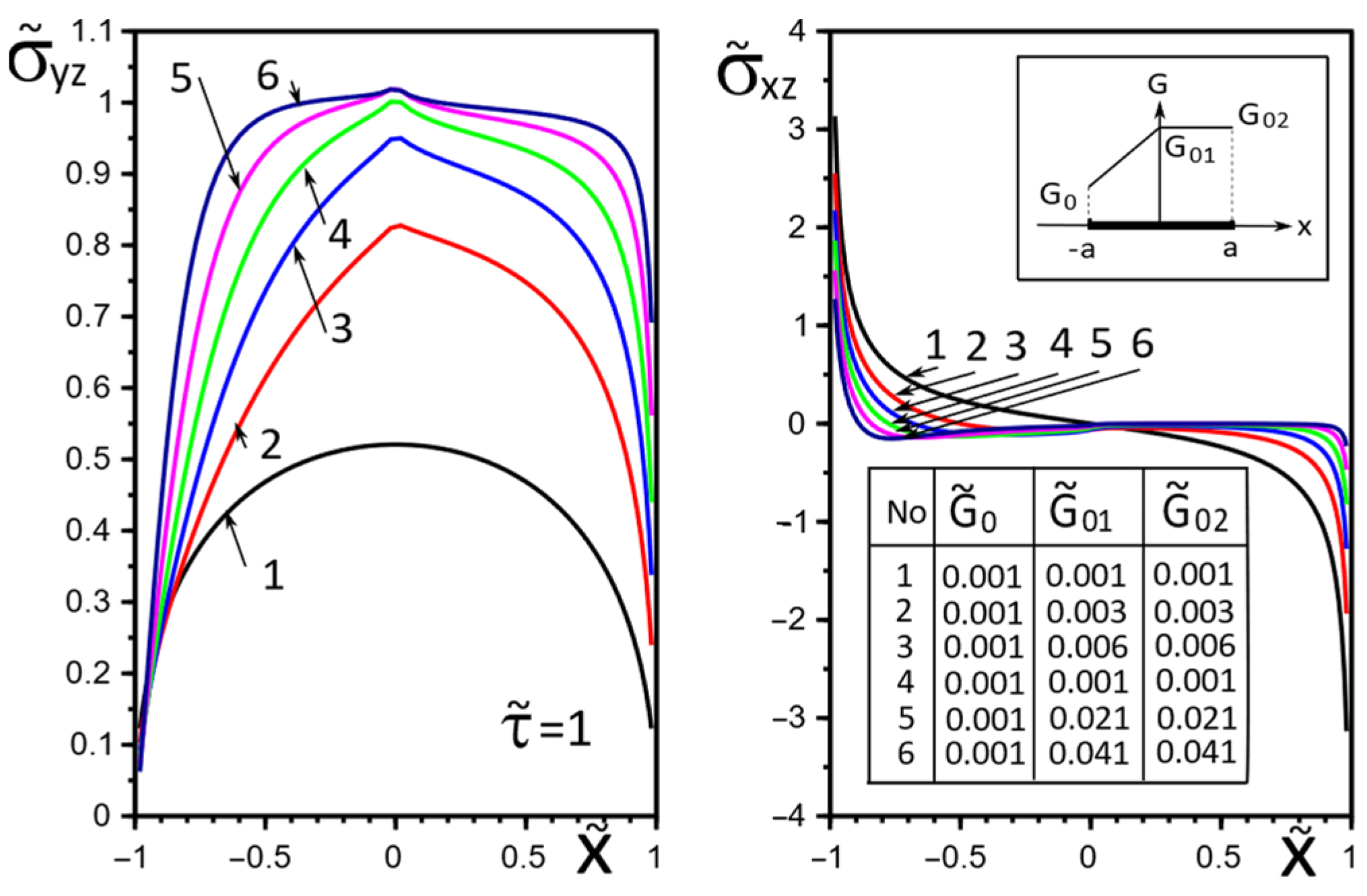
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| FGM | functionally gradient material; |
| GSIF | generalized stress intensity factor; |
| SSS | stress–strain state |
| Cartesian coordinates; | |
| jump functions; | |
| elastic properties of the materials; | |
| half-planes (sections of the solid); | |
| displacement, stresses (components of SSS); | |
| line, modeling the presence of thin inclusion; | |
| magnitudes of concentrated forces and screw dislocations; | |
| , | uniformly distributed in infinity shear stresses. |
References
- Mura, T.; Barnett, D.M. Micromechanics of Defects in Solids. J. Appl. Mech. 1983, 50, 477. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Z. Analytical Micromechanics Models for Elastoplastic Behavior of Long Fibrous Composites: A Critical Review and Comparative Study. Materials 2018, 11, 1919. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Karihaloo, B.L.E.; Duan, H.L. Nano-mechanics or how to extend continuum mechanics to nanoscale. Bull. Pol. Acad. Sci. Tech. Sci. 2007, 55, 133–140. [Google Scholar]
- Zhou, K.; Hoh, H.J.; Wang, X.; Keer, L.M.; Pang, J.H.; Song, B.; Wang, Q.J. A review of recent works on inclusions. Mech. Mater. 2013, 60, 144–158. [Google Scholar] [CrossRef]
- Mencik, J. Mechanics of Components with Treated or Coated Solids; Kluwer Academic Publishing: Dordrecht, The Netherlands, 1996; 360p. [Google Scholar]
- Nemat-Nasser, S.; Hori, M. Micromechanics: Overall Properties of Heterogeneous Materials; North-Holland Series in Applied Mathematics and Mechanics; Elsevier: Amsterdam, The Netherlands, 1993; Volume 37, 687p. [Google Scholar]
- Pasternak, I.; Sulym, H.; Ilchuk, N. Interaction of Physicomechanical Fields in Bodies with Thin Structural Inhomogeneities: A Survey. J. Math. Sci. 2021, 253, 63–83. [Google Scholar] [CrossRef]
- Chen, J. Determination of thermal stress intensity factors for an interface crack in a graded orthotropic coating-substrate structure. Int. J. Fract. 2005, 133, 303–328. [Google Scholar] [CrossRef]
- Johnson, W.S.; Masters, J.; O’Brien, T.K.; Naik, R. Simplified Micromechanical Equations for Thermal Residual Stress Analysis of Coated Fiber Composites. J. Compos. Technol. Res. 1992, 14, 182–186. [Google Scholar] [CrossRef]
- Shevchuk, V.A. Modeling and Computation of Heat Transfer in a System “Body-Multilayer Coating”. Heat Transf. Res. 2006, 37, 412–423. [Google Scholar] [CrossRef]
- Kashtalyan, M.; Menshykova, M. Three-dimensional analysis of a functionally graded coating/substrate system of finite thickness. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2008, 366, 1821–1826. [Google Scholar] [CrossRef]
- Bao, G.; Wang, L. Multiple cracking in functionally graded ceramic/metal coatings. Int. J. Solids Struct. 1995, 32, 2853–2871. [Google Scholar] [CrossRef]
- Zhao, J.; Silberschmidt, V.V. Microstructure-based damage and fracture modelling of alumina coatings. Comput. Mater. Sci. 2005, 32, 620–628. [Google Scholar] [CrossRef]
- Hashin, Z. Thin interphase/imperfect interface in elasticity with application to coated fiber composites. J. Mech. Phys. Solids 2002, 50, 2509–2537. [Google Scholar] [CrossRef]
- Kulchytsky-Zhyhailo, R.; Matysiak, S.J.; Bajkowski, A.S. Semi-analytical solution of three-dimensional thermoelastic problem for half-space with gradient coating. J. Therm. Stress. 2018, 41, 1169–1181. [Google Scholar] [CrossRef]
- Davim, P.; Constantinos, A. (Eds.) Nanocomposites. Materials, Manufacturing and Engineering; Charitidis, Walter de Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2013; 211p. [Google Scholar]
- Kim, C.I.; Schiavone, P.; Ru, C.-Q. The Effects of Surface Elasticity on an Elastic Solid with Mode-III Crack: Complete Solution. Trans. ASME J. Appl. Mech. 2009, 77, 021011. [Google Scholar] [CrossRef]
- Uchida, Y. Properties of functionally graded materials, Manufactured by progressive lamination method for applications. Aichi Inst. Technol. Res. Rep. 2004, 39–B, 39–51. [Google Scholar]
- Ichikawa, K. (Ed.) Functionally Graded Materials in the 21ST Century, A Workshop on Trends and Forecasts; Kluver Academic Publishers: Boston, MA, USA; Dordrecht, The Netherlands; London, UK, 2000; 264p. [Google Scholar]
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Processing and Applications; Materials Technology Series; Springer: Berlin/Heidelberg, Germany, 1999; pp. 247–313. [Google Scholar] [CrossRef]
- Duan, H.; Wang, J.; Huang, Z.; Karihaloo, B. Eshelby formalism for nano-inhomogeneities. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 3335–3353. [Google Scholar] [CrossRef]
- Elperin, T.; Rudin, G. Thermal stresses in a coating–substrate assembly caused by internal heat source. J. Therm. Stress. 2016, 39, 90–102. [Google Scholar] [CrossRef]
- Zhang, N.; Khan, T.; Guo, H.; Shi, S.; Zhong, W.; Zhang, W. Functionally Graded Materials: An Overview of Stability, Buckling, and Free Vibration Analysis. Adv. Mater. Sci. Eng. 2019, 2019, 1354150. [Google Scholar] [CrossRef]
- Li, Y.; Feng, Z.; Hao, L.; Huang, L.; Xin, C.; Wang, Y.; Bilotti, E.; Essa, K.; Zhang, H.; Li, Z.; et al. A Review on Functionally Graded Materials and Structures via Additive Manufacturing: From Multi-Scale Design to Versatile Functional Properties. Adv. Mater. Technol. 2020, 5, 1900981. [Google Scholar] [CrossRef]
- Bishop, A.; Lin, C.Y.; Navaratnam, M.; Rawlings, R.D.; McShane, H.B. A functionally gradient material produced by a powder metallurgical process. J. Mater. Sci. Lett. 1993, 12, 1516–1518. [Google Scholar] [CrossRef]
- Kieback, B.; Neubrand, A.; Riedel, H. Processing techniques for functionally graded materials. Mater. Sci. Eng. A 2003, 362, 81–105. [Google Scholar] [CrossRef]
- Mistler, R.E. High strength alumina substrates produced by a multiple-layer casting technique. Am. Ceram. Soc. Bull. 1973, 52, 850–854. [Google Scholar]
- Sulym, H.T.; Piskozub, I.Z. Nonlinear Deformation of a Thin Interface Inclusion. Mater. Sci. 2018, 53, 600–608. [Google Scholar] [CrossRef]
- Sulym, H.; Piskozub, Y.; Polanski, J. Antiplane Deformation of a Bimaterial with Thin Interfacial Nonlinear Elastic Inclusion. Acta Mech. Autom. 2018, 12, 190–195. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. Soc. Lond. A Math. Phys. Eng. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Sharma, P.; Ganti, S. Size-Dependent Eshelby’s Tensor for Embedded Nano-Inclusions Incorporating Surface/Interface Energies. ASME J. Appl. Mech. 2004, 71, 663–671. [Google Scholar] [CrossRef]
- Benveniste, Y.; Baum, G. An interface model of a graded three-dimensional anisotropic curved interphase. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 463, 419–434. [Google Scholar] [CrossRef]
- Benveniste, Y.; Miloh, T. Imperfect soft and stiff interfaces in two-dimensional elasticity. Mech. Mater. 2001, 33, 309–323. [Google Scholar] [CrossRef]
- Martynyak, R.M.; Serednytska, K.I. Contact Problems of Thermoelasticity for Interface Cracks in Bimaterials; Rastr-7: Lviv, Ukraine, 2017; 168p. [Google Scholar]
- Gurtin, M.E.; Murdoch, A.I. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Steigmann, D.J.; Ogden, R.W. Elastic surface—Substrate interactions. Proc. R. Soc. A Math. Phys. Eng. Sci. 1999, 455, 437–474. [Google Scholar] [CrossRef]
- Sulym, H.T. Bases of Mathematical Theory of Thermo-elastic Equilibrium of Solids Containing Thin Inclusions; Research and Publishing Center of NTSh: L’viv, Ukraine, 2007; 716p, Available online: https://ua1lib.org/book/665574/5c937e (accessed on 19 January 2022). (In Ukrainian)
- Hutsaylyuk, V.; Piskozub, Y.; Piskozub, L.; Sulym, H. Deformation and Strength Parameters of a Composite Structure with a Thin Multilayer Ribbon-like Inclusion. Materials 2022, 15, 1435. [Google Scholar] [CrossRef] [PubMed]
- Piskozub, J.Z. Effect of surface stresses on the tensely deformed state of thin interface microinclusion. Math. Model. Comput. 2021, 8, 69–77. [Google Scholar] [CrossRef]
- Sulim, G.T.; Piskozub, J.Z. Thermoelastic equilibrium of piecewise homogeneous solids with thin inclusions. J. Eng. Math. Spec. Issue Thermomechanics 2008, 61, 315–337. [Google Scholar] [CrossRef]
- Piskozub, Y.; Sulym, H. Effect of Frictional Slipping on the Strength of Ribbon-Reinforced Composite. Materials 2021, 14, 4928. [Google Scholar] [CrossRef] [PubMed]
- Evtushenko, A.A.; Sulim, G.T. Stress concentration near a cavity filled with a liquid. Sov. Mater. Sci. 1981, 16, 546–549. [Google Scholar] [CrossRef]
- Lee, Y.-D.; Erdogan, F. Interface cracking of FGM coatings under steady-state heat flow. Eng. Fract. Mech. 1998, 59, 361–380. [Google Scholar] [CrossRef]
- Martynyak, R.M.; Kryshtafovych, A. Friction contact of two elastic half-planes with local recesses in boundary. J. Frict. Wear 2000, 21, 6–15. [Google Scholar]
- Piskozub, Y.; Sulym, H. Asymptotics of stresses in the vicinity of a thin elastic interphase inclusion. Mater. Sci. 1996, 32, 421–432. [Google Scholar] [CrossRef]
- Sulym, H.; Piskozub, L.; Piskozub, Y.; Pasternak, I. Antiplane Deformation of a Bimaterial Containing an Interfacial Crack with the Account of Friction I. Single Loading. Acta Mech. Autom. 2015, 9, 115–121. [Google Scholar] [CrossRef]
- Sulym, H.; Piskozub, L.; Piskozub, Y.; Pasternak, I. Antiplane Deformation of a Bimaterial Containing an Interfacial Crack with the Account of Friction 2. Repeating and Cyclic Loading. Acta Mech. Autom. 2015, 9, 178–184. [Google Scholar] [CrossRef][Green Version]
- Sulym, H.; Pasternak, I.; Piskozub, L. Longitudinal shear of a bi-material with fractional sliding contact in the interfacial crack. J. Theor. Appl. Mech. 2016, 54, 529–539. [Google Scholar] [CrossRef]
- Yevtushenko, A.; Rozniakowska, M.; Kuciej, M. Transient temperature processes in composite strip and homogeneous foundation. Int. Commun. Heat Mass Transf. 2007, 34, 1108–1118. [Google Scholar] [CrossRef]
- Pasternak, I.M.; Pasternak, R.M.; Sulym, H.T. 2D boundary element analysis of defective thermoelectroelastic bimaterial with thermally imperfect but mechanically and electrically perfect interface. Eng. Anal. Bound. Elem. 2015, 61, 194–206. [Google Scholar] [CrossRef]
- Pasternak, Y.M.; Sulym, H.T.; Piskozub, L.G. Model tonkogo vklyucheniya v usloviyah yego idealnogo i neidealnogo kontaktnogo vzaimodeystviya s okruzhayuschim materialom. In Proceedings of the Trudy VI Mezhdunar. Simp. po Tribofatike MSTF 2010, Minsk, Belarus, 25 October–1 November 2010; BGU: Minsk, Belarus, 2010; Volume 2, Chapter 2. pp. 399–404. [Google Scholar]
- Chen, X.; Liu, Q. Thermal stress analysis of multi-layer thin films and coatings by an advanced boundary element method. Comput. Model. Eng. Sci. 2001, 2, 337–349. [Google Scholar]
- Rodríguez, A.; Calleja, A.; de Lacalle, L.N.L.; Pereira, O.; González, H.; Urbikain, G.; Laye, J. Burnishing of FSW Aluminum Al–Cu–Li Components. Metals 2019, 9, 260. [Google Scholar] [CrossRef]
- Sánchez, A.J.; Egea, A.; Rodríguez, A.; Celentano, D.; Calleja, A.; López de Lacalle, L.N. Joining metrics enhancement when combining FSW and ball-burnishing in a 2050 aluminum alloy. Surf. Coat. Technol. 2019, 367, 327–335. [Google Scholar] [CrossRef]
- Bouhamed, A.; Jrad, H.; Mars, J.; Wali, M.; Gamaoun, F.; Dammak, F. Homogenization of elasto-plastic functionally graded material based on representative volume element: Application to incremental forming process. Int. J. Mech. Sci. 2019, 160, 412–420. [Google Scholar] [CrossRef]
- Chen, Y.Z. Study of multiply-layered cylinders made of functionally graded materials using the transfer matrix method. J. Mech. Mater. Struct. 2011, 6, 641–657. [Google Scholar] [CrossRef][Green Version]
- Jin, Z.-H. An asymptotic solution of temperature field in a strip of a functionally graded material. Int. Commun. Heat Mass Transf. 2002, 29, 887–895. [Google Scholar] [CrossRef]
- Majak, J.; Mikola, M.; Pohlak, M.; Eerme, M.; Karunanidhi, R. Modelling FGM materials. An accurate function approxi-mation algorithms. In Proceedings of the Modern Materials and Manufacturing (MMM 2021), Tallinn, Estonia, 27–29 April 2021; IOP Conference Series: Materials Science and Engineering. 2021; Volume 1140. [Google Scholar]
- Takahashi, M.; Itoh, Y.; Kashiwaya, H. Fabrication and evaluation of W/Cu gradient material by sintering and infiltration technique. In Proceedings of the First International Symposium on Functionally Gradient Materials FGM, Tokyo, Japan, 8–9 October 1990; Functionally Gradient Materials Forum, The Society of Non-Traditional Technology. 1990; pp. 129–134. [Google Scholar]
- El-Borgi, S.; Erdogan, F.; Ben Hatira, F. Stress intensity factors for an interface crack between a functionally graded coating and a homogeneous substrate. Int. J. Fract. 2003, 123, 139–162. [Google Scholar] [CrossRef]
- Erdogan, F.; Wu, B.H. Crack problem in FGM layers under thermal stresses. J. Therm. Stress. 1996, 19, 237–265. [Google Scholar] [CrossRef]
- Wang, B.L.; Mai, Y.W.; Noda, N. Fracture mechanics analysis model for functionally graded materials with arbitrarily dis-tributed properties. Int. J. Fract. 2002, 116, 161–177. [Google Scholar] [CrossRef]
- Yildirim, B.; Dag, S.; Erdogan, F. Three dimensional fracture analysis of FGM coatings under thermomechanical loading. Int. J. Fract. 2005, 132, 371–397. [Google Scholar] [CrossRef]
- Guo, L.-C.; Noda, N.; Ishihara, M. Thermal Stress Intensity Factors for a Normal Surface Crack in a Functionally Graded Coating Structure. J. Therm. Stress. 2007, 31, 149–164. [Google Scholar] [CrossRef]
- Sulym, H.T.; Piskozub, Y.Z. Conditions of contact interaction (a survey). Mat. Metod. Fiz. Mekhanichni Polya 2004, 47, 110–125. [Google Scholar]
- Ding, S.-H.; Li, X. Thermal stress intensity factors for an interface crack in a functionally graded layered structures. Arch. Appl. Mech. 2010, 81, 943–955. [Google Scholar] [CrossRef]
- Kit, G.S. On Analogy between Longitudinal Shear and Stationary Thermal Conductivity of Bodies with Inclusions and Cracks. Dokl. USSR Ser. A 1977, 4, 336–340. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piskozub, Y.; Piskozub, L.; Sulym, H. Effect of the Transverse Functional Gradient of the Thin Interfacial Inclusion Material on the Stress Distribution of the Bimaterial under Longitudinal Shear. Materials 2022, 15, 8591. https://doi.org/10.3390/ma15238591
Piskozub Y, Piskozub L, Sulym H. Effect of the Transverse Functional Gradient of the Thin Interfacial Inclusion Material on the Stress Distribution of the Bimaterial under Longitudinal Shear. Materials. 2022; 15(23):8591. https://doi.org/10.3390/ma15238591
Chicago/Turabian StylePiskozub, Yosyf, Liubov Piskozub, and Heorhiy Sulym. 2022. "Effect of the Transverse Functional Gradient of the Thin Interfacial Inclusion Material on the Stress Distribution of the Bimaterial under Longitudinal Shear" Materials 15, no. 23: 8591. https://doi.org/10.3390/ma15238591
APA StylePiskozub, Y., Piskozub, L., & Sulym, H. (2022). Effect of the Transverse Functional Gradient of the Thin Interfacial Inclusion Material on the Stress Distribution of the Bimaterial under Longitudinal Shear. Materials, 15(23), 8591. https://doi.org/10.3390/ma15238591





