Comparative Measurements and Analysis of the Electrical Properties of Nanocomposites TixZr1−xC+α-Cy (0.0 ≤ x ≤ 1.0)
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
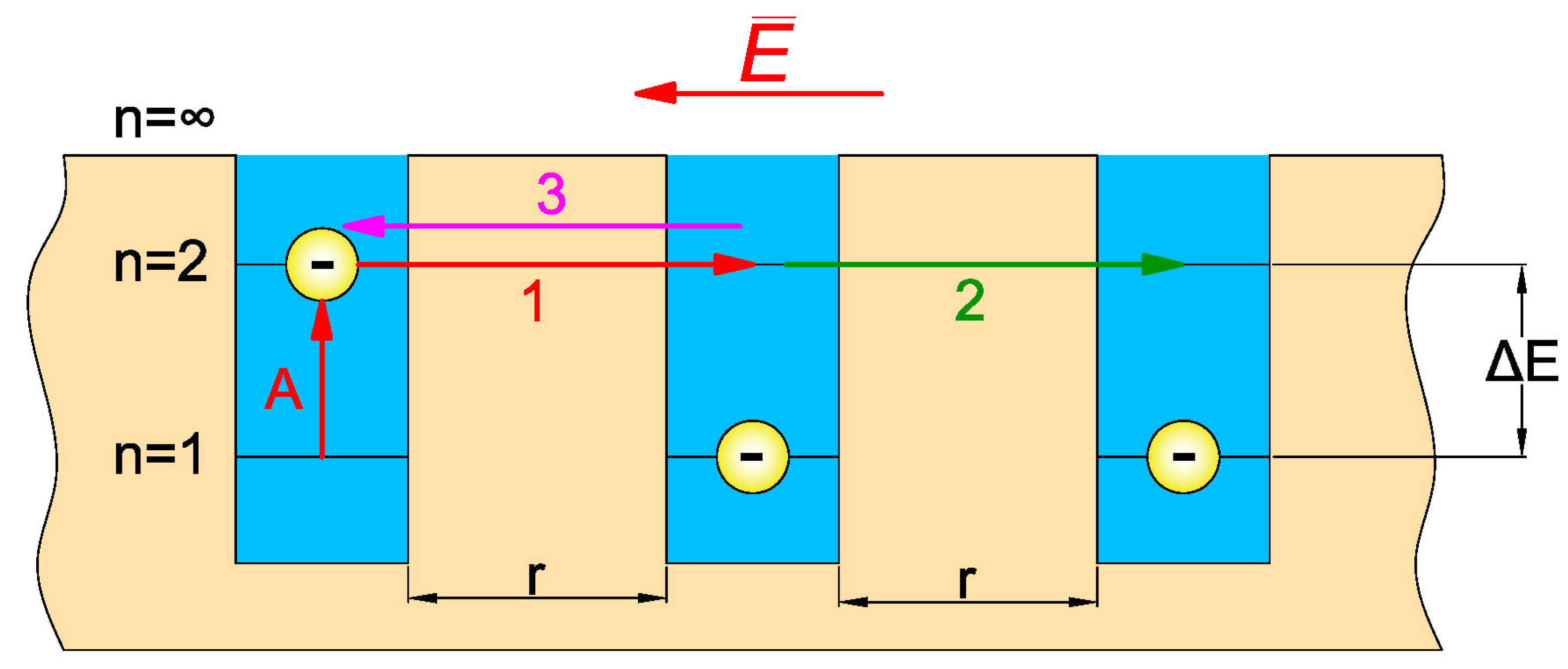
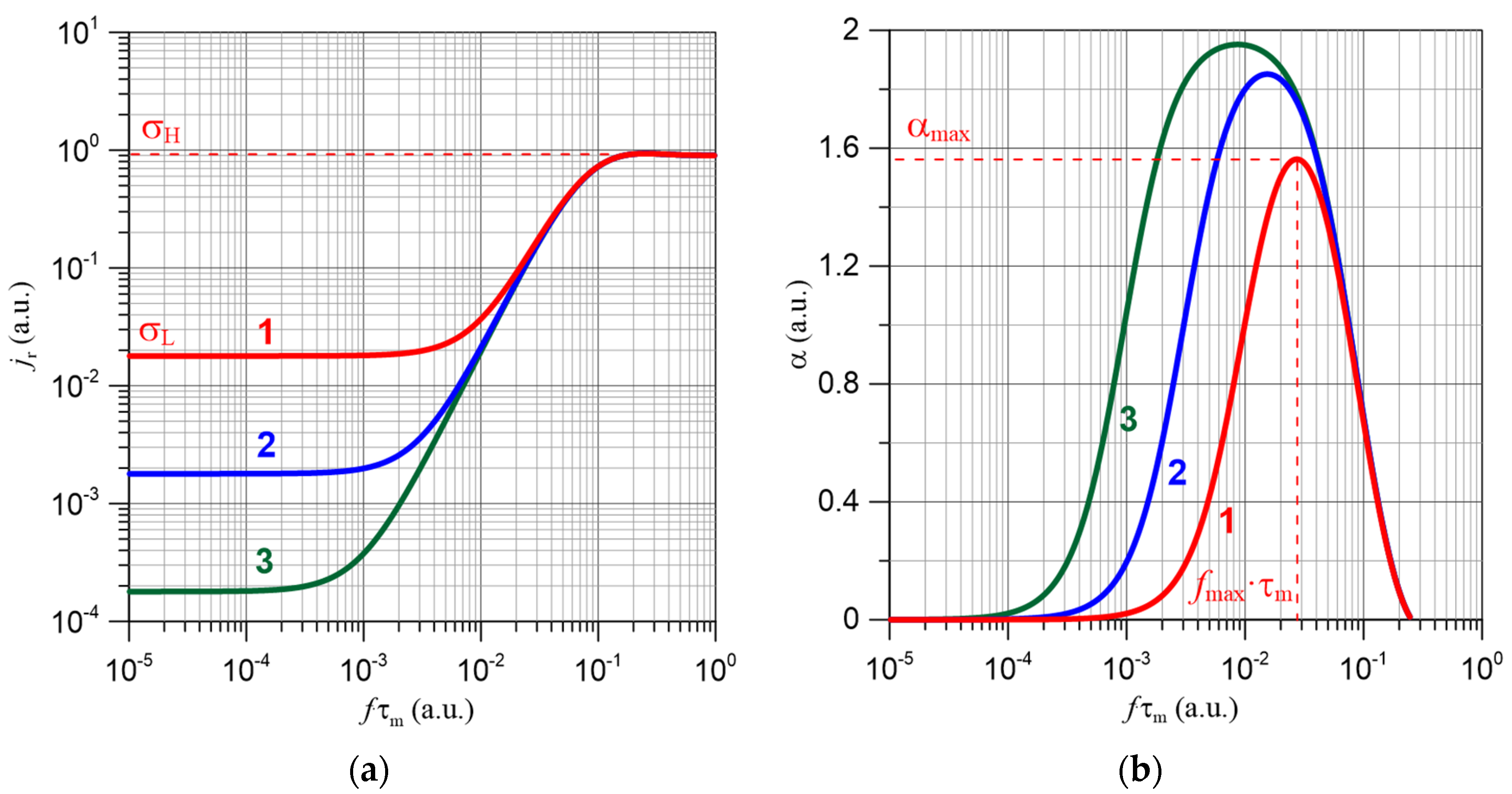
3. Hopping Conductivity of Nanocomposites Considering Quantum Mechanical Electron Tunneling Phenomenon
4. Results and Discussion
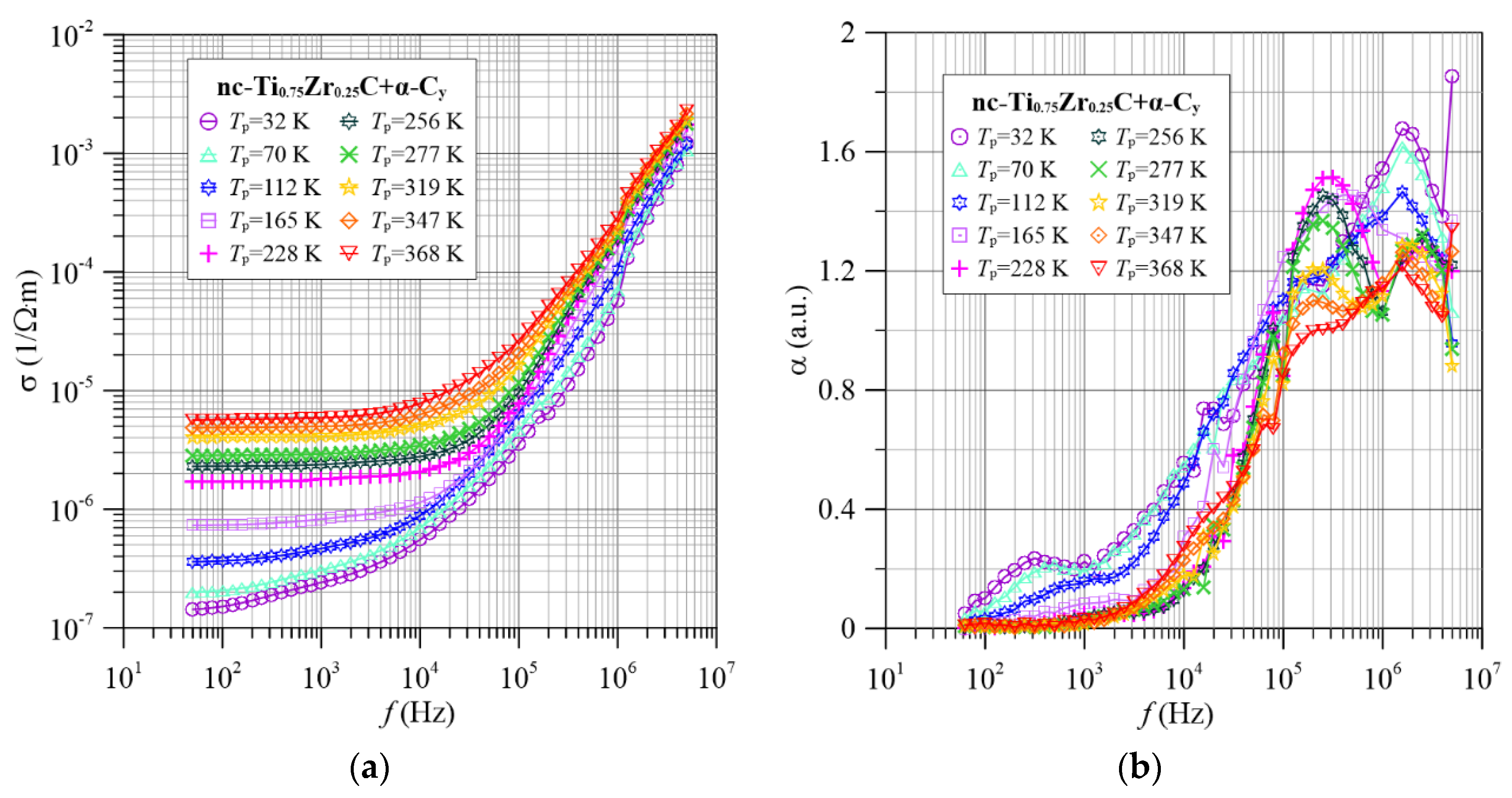
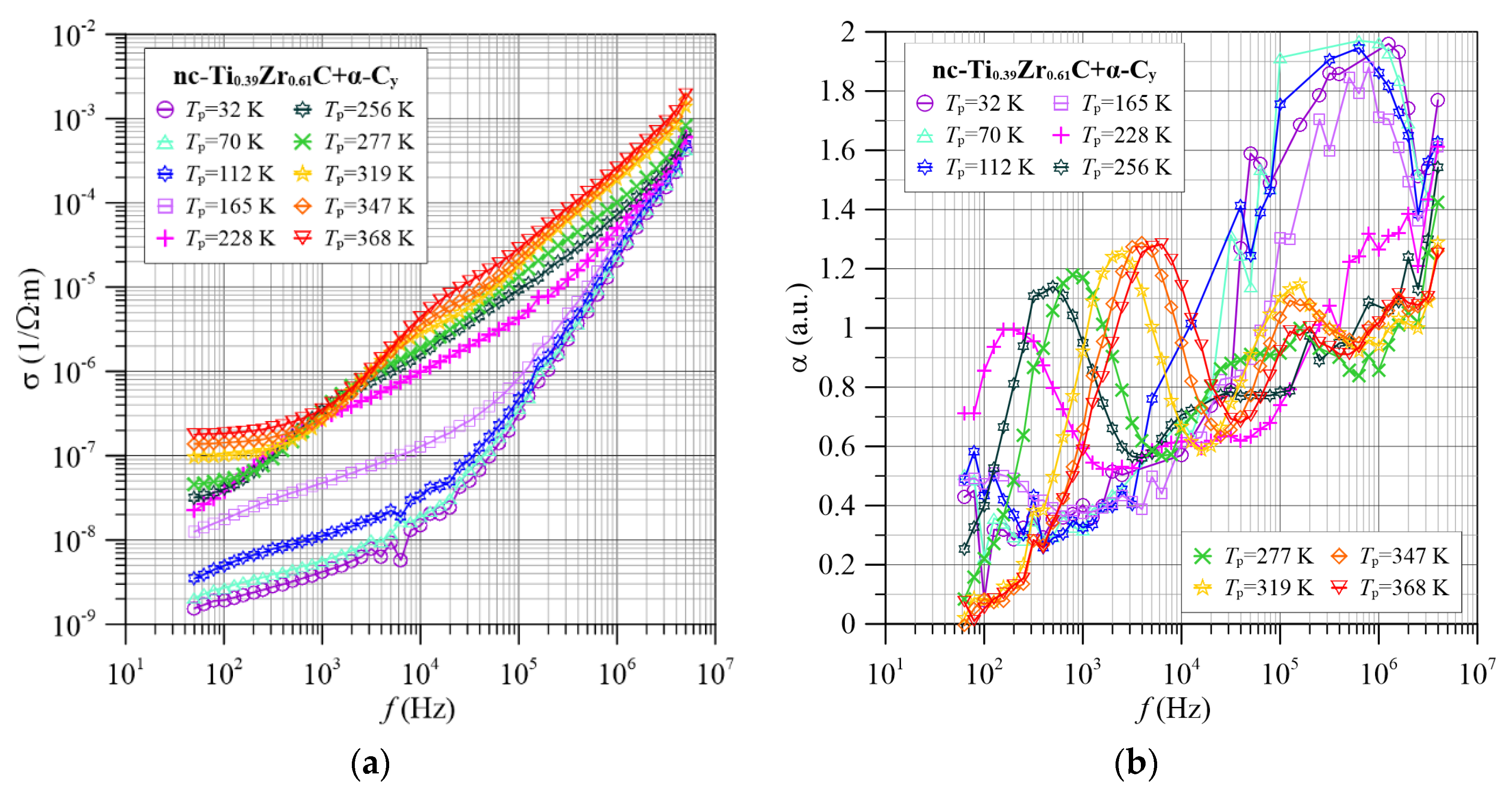
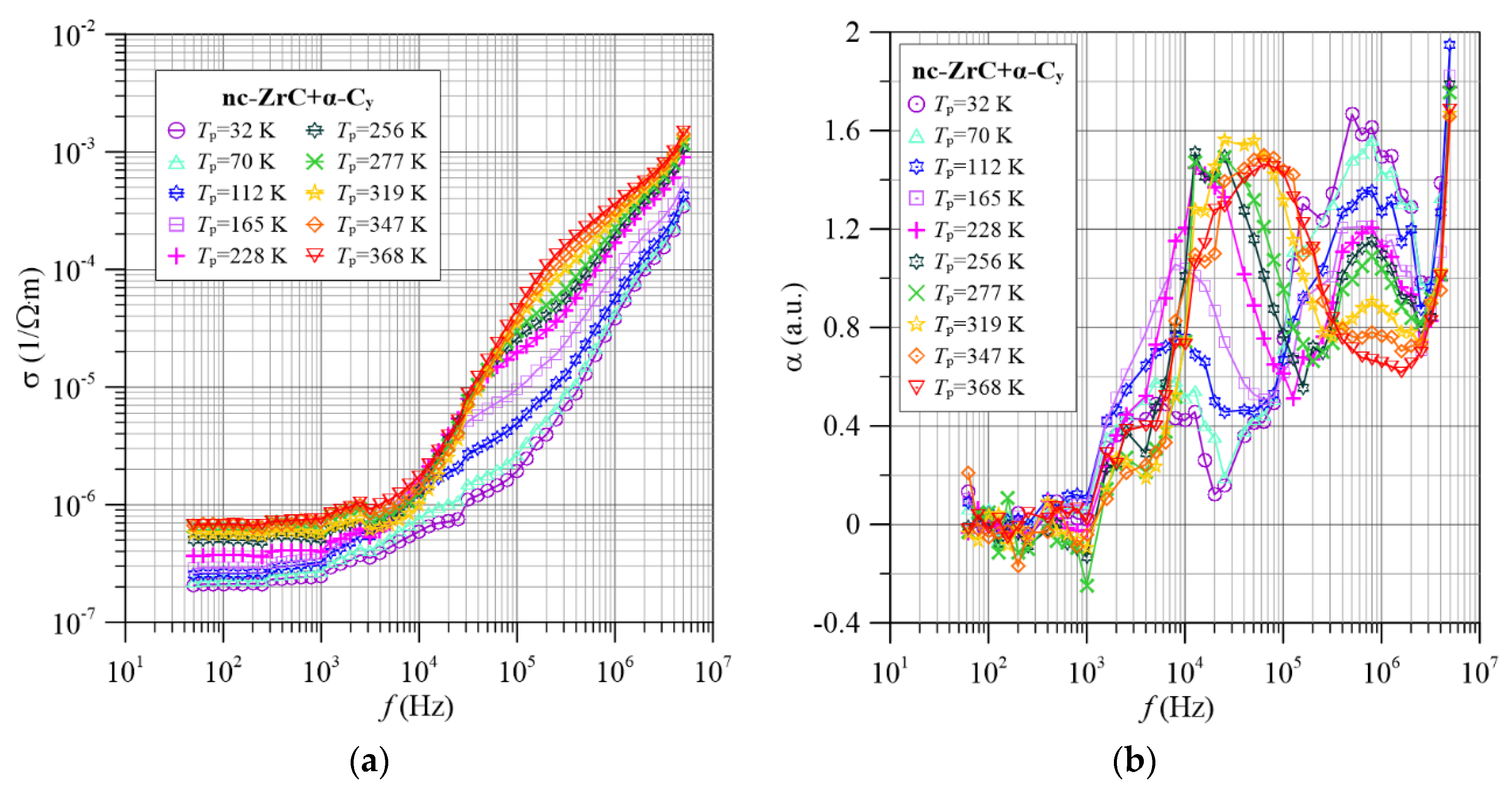
4.1. Frequency-Temperature Dependence of the Conductivity of nc-TixZr1−xC+α-Cy Nanocomposites
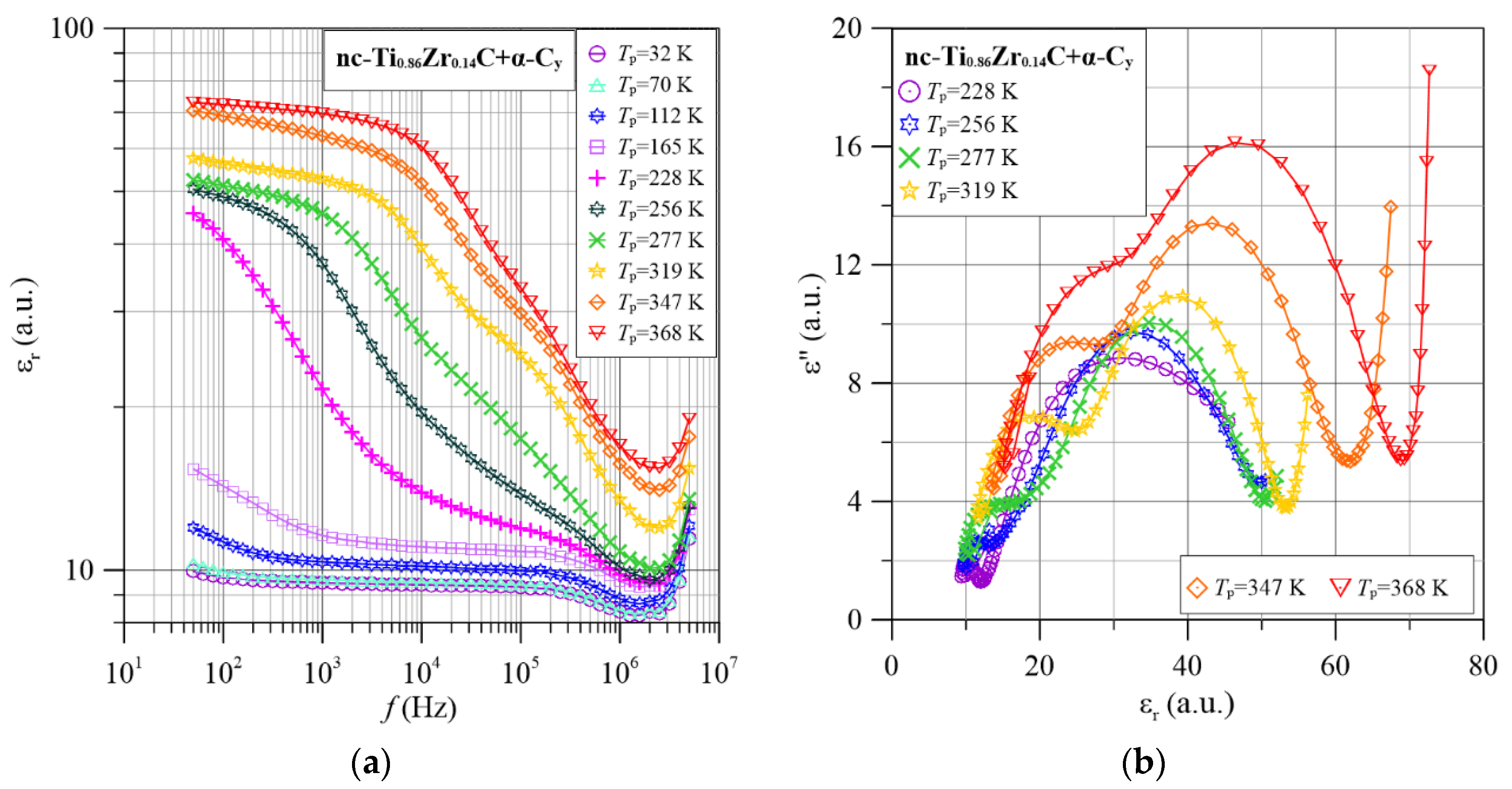
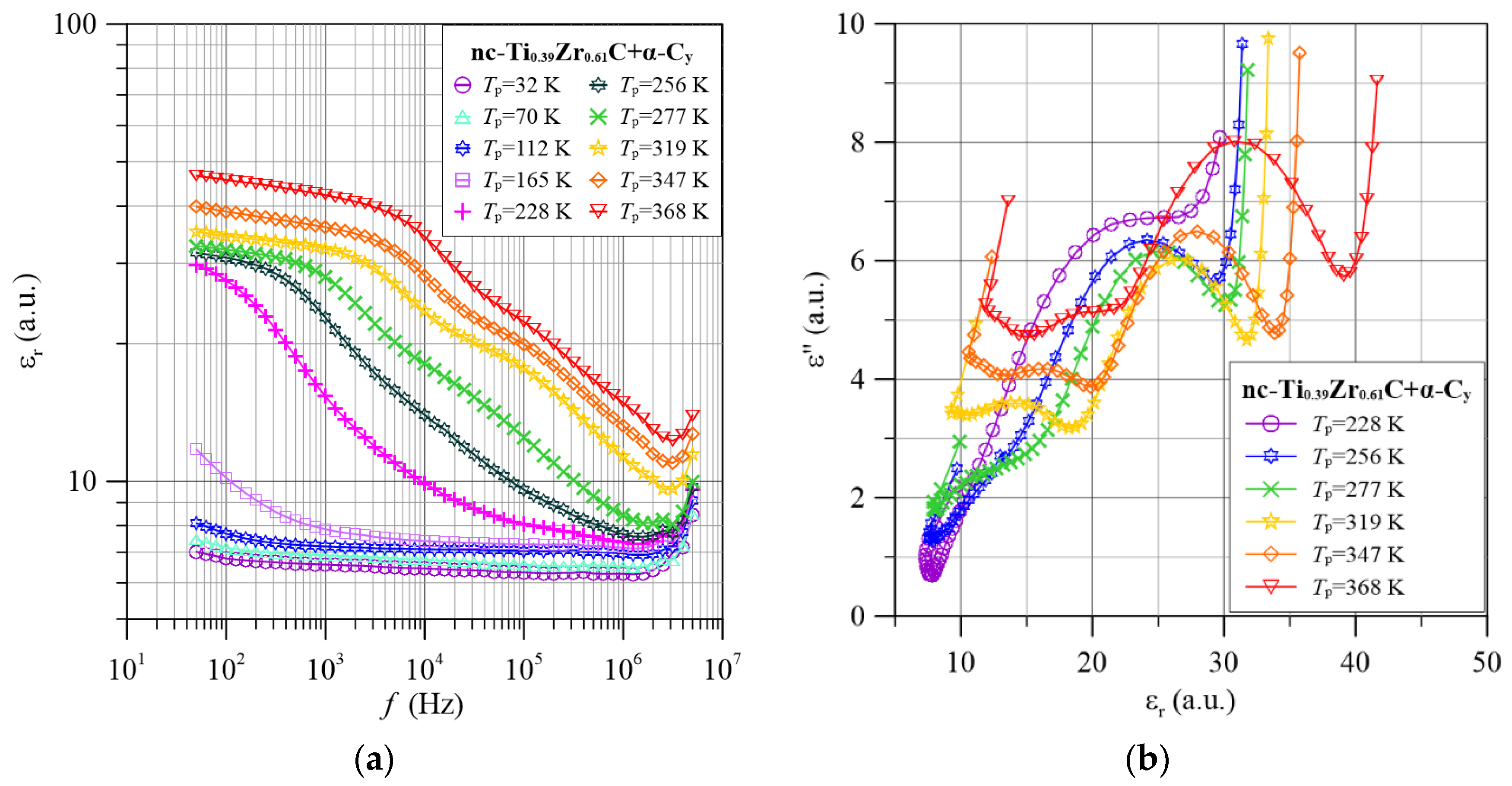
4.2. Frequency-Temperature Dependencies of the Permittivity of TixZr1−xC+α-Cy Nanocomposites
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vilčáková, J.; Sáha, P.; Hausneroná, B.; Quadrat, O. Electrical properties of composites of hard metal carbides in a polymer matrix. Polym. Compos. 2004, 23, 942–946. [Google Scholar] [CrossRef]
- Modine, F.A.; Foegelle, M.D.; Finch, C.B.; Allison, C.Y. Electrical properties of transition-metal carbides of group IV. Phys. Rev. B 1989, 40, 9558. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Naguib, M.; Mochalin, V.N.; Barsoum, M.W.; Gogotsi, Y.; Yu, X.; Nam, K.-W.; Yang, X.-Q.; Kolesnikov, A.I.; Kent, P.R.C. Role of Surface Structure on Li-Ion Energy Storage Capacity of Two-Dimensional Transition-Metal Carbides. J. Am. Chem. Soc. 2014, 136, 6385–6394. [Google Scholar] [CrossRef] [PubMed]
- Eames, C.; Saiful Islam, M. Ion Intercalation into Two-Dimensional Transition-Metal Carbides: Global Screening for New High-Capacity Battery Materials. J. Am. Chem. Soc. 2014, 136, 16270–16276. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhou, A.; Li, L.; Wang, L.; Hu, M.; Li, S.; Gupta, S. Synthesis and characterization of novel Ti3SiC2–cBN composites. Diamond Relat. Mater. 2014, 43, 29–33. [Google Scholar] [CrossRef]
- Rampai, T.; Lang, C.I.; Sigalas, I. Investigation of MAX phase/c-BN composites. Ceram. Int. 2013, 39, 4739–4748. [Google Scholar] [CrossRef]
- Xue, Y.; Qin, J.; Zhang, X.; Ma, M.; He, D.; Liu, R. In situ high pressure synthesis of cBN-based composites. Funct. Mater. Lett. 2014, 7, 14500040. [Google Scholar] [CrossRef]
- Mu, Y.; Guo, J.; Liang, B.; Wang, Q. Rapid fabrication of the Ti3SiC2 bonded diamond composite by spark plasma sintering. Int. J. Refract. Met. Hard Mater. 2011, 29, 397–400. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, L.; Jiang, W.; Chen, L. Effect of TiC content on the microstructure and properties of Ti3SiC2–TiC composites in situ fabricated by spark plasma sintering. Mater. Sci. Eng. A 2008, 487, 137–143. [Google Scholar] [CrossRef]
- Konoplyuk, S.; Abe, T.; Uchimoto, T.; Takagi, T. Synthesis of Ti3SiC2/TiC composites from TiH2/SiC/TiC powders. Mater. Lett. 2005, 59, 2342–2346. [Google Scholar] [CrossRef]
- Dudina, D.V.; Pribytkov, G.A.; Krinitcyn, M.G.; Korchagin, M.A.; Bulina, N.V.; Bokhonov, B.B.; Batraev, I.S.; Rybin, D.K.; Ulianitsky, V.Y. Detonation spraying behavior of TiCx–Ti powders and the role of reactive processes in the coating formation. Ceram. Int. 2016, 42, 690–696. [Google Scholar] [CrossRef]
- Mikhailov, M.M.; Ul’yanitskii, V.Y.; Vlasov, V.A.; Sokolovskiy, A.N.; Lovitskii, A.A. Thermostabilizing BaTiO3 coatings synthesized by detonation spraying method. Surf. Coat. Technol. 2017, 319, 70–75. [Google Scholar] [CrossRef]
- Batraev, I.S.; Ulianitsky, V.Y.; Dudina, D.V. Detonation spraying of copper: Theoretical analysis and experimental studies. Mat. Today: Proceed 2017, 4, 11346–11350. [Google Scholar] [CrossRef]
- Ulianitsky, V.Y.; Batraev, I.S.; Shtertser, A.A.; Dudina, D.V.; Bulina, N.V.; Smurov, I. Detonation spraying behaviour of refractory metals: Case studies for Mo and Ta-based powders. Adv. Powder Tech. 2018, 29, 1859–1864. [Google Scholar] [CrossRef]
- Pogrebnjak, A.; Ivashchenko, V.; Maksakova, O.; Buranich, V.; Konarski, P.; Bondariev, V.; Żukowski, P.; Skrynskyy, P.; Sinelnichenko, A.; Shelest, I.; et al. Comparative measurements and analysis of the mechanical and electrical properties of Ti-Zr-C nanocomposite: Role of stoichiometry. Measurement 2021, 176, 109223. [Google Scholar] [CrossRef]
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef]
- Koyama, M.; Zhang, Z.; Wang, M.; Ponge, D.; Raabe, D.; Tsuzaki, K.; Noguchi, H.; Tasan, C.C. Bone-like crack resistance in hierarchical metastable nanolaminate steels. Science 2017, 355, 1055–1057. [Google Scholar] [CrossRef]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef]
- Kim, S.H.; Kim, H.; Kim, N.J. Brittle intermetallic compound makes ultrastrong low-density steel with large ductility. Nature 2015, 518, 77–79. [Google Scholar] [CrossRef]
- Hofmann, D.C.; Suh, J.Y.; Wiest, A.; Duan, G.; Lind, M.L.; Demetriou, M.D.; Johnson, W.L. Designing metallic glass matrix composites with high toughness and tensile ductility. Nature 2008, 451, 1085–1089. [Google Scholar] [CrossRef] [PubMed]
- Calvert, P. Nanotube composites: A recipe for strength. Nature 1999, 399, 210–211. [Google Scholar] [CrossRef]
- Zhan, G.D.; Kuntz, J.D.; Wan, J.; Mukherjee, A.K. Single-wall carbon nanotubes as attractive toughening agents in alumina-based nanocomposites. Nat. Mater. 2003, 2, 38–42. [Google Scholar] [CrossRef] [PubMed]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef] [PubMed]
- Yeh, J.W. Progres recents dans les alliages a haute entropie. Ann. Chim. Sci. Mater. 2006, 31, 633–648. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Chang, Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Pogrebnjak, A.D.; Bagdasaryan, A.A.; Yakushchenko, I.V.; Beresnev, V.M. The structure and properties of high-entropy alloys and nitride coatings based on them. Russ. Chem. Rev. 2014, 83, 1027–1061. [Google Scholar] [CrossRef]
- Florea, R.M.; Florea, O.B.; Baltatescu, O.; Soare, V.; Chelariu, R.; Carcea, I. High entropy alloys. J. Optoelectron. Adv. Mater. 2013, 15, 761–767. [Google Scholar]
- Gao, M.C. Progress in High Entropy Alloys. JOM 2013, 67, 2251–2253. [Google Scholar] [CrossRef]
- Pogrebnjak, A.D.; Yakushchenko, I.V.; Bagdasaryan, A.A.; Bondar, O.V.; Krause-Rehberg, R.; Abadias, G.; Chartier, P.; Oyoshi, K.; Takeda, Y.; Beresnev, V.M.; et al. Microstructure, physical and chemical properties of nanostructured (Ti–Hf–Zr–V–Nb)N coatings under different deposition conditions. Mater. Chem. Phys. 2014, 147, 1079–1091. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Kozak, R.; Sologubenko, A.; Steurer, W. Single-phase high-entropy alloys–An overview. Z. Kristallogr. 2015, 230, 55–68. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. High entropy alloys. Materials Science and Technology 2015, 31, 1139–1141. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, Q.; Lu, J.; Liu, C.; Yang, Y. High-entropy alloy: Challenges and prospects. Mater. Today 2016, 19, 349–362. [Google Scholar] [CrossRef]
- Pickering, E.J.; Jones, N.G. High-entropy alloys: A critical assessment of their founding principles and future prospects. Int. Mater. Rev. 2016, 61, 183–202. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Toth, L. Transition Metal Carbides and Nitrides; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Rakhadilov, B.K.; Maksakov, O.V.; Buitkenov, D.B.; Kylyshkanov, M.K.; Pogrebnjak, A.D.; Antypenko, V.P.; Konoplianchenko, Y.V. Structural-phase and tribo-corrosion properties of composite Ti3SiC2/TiC MAX-phase coatings: An experimental approach to strengthening by thermal annealing. Appl. Phys. A-Mater. Sci. Process. 2022, 128, 145. [Google Scholar] [CrossRef]
- Lagos, M.A.; Pellegrini, C.; Agote, I.; Azurmendi, N.; Barcena, J.; Parco, M.; Silvestroni, L.; Zoli, L.; Sciti, D. Ti3SiC2-Cf composites by spark plasma sintering: Processing, microstructure and thermo-mechanical properties. J. Eur. Ceram. Soc. 2019, 39, 2824–2830. [Google Scholar] [CrossRef]
- Mott, N.F. Metal-Insulator Transitions; Taylor and Francis: London, UK, 1974. [Google Scholar]
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials, 2nd ed.; Clarendon Press: Oxford, NY, USA, 1979; Available online: http://www.worldcat.org/title/electronic-processes-in-non-crystalline-materials/oclc/5452575 (accessed on 17 October 2018).
- Sarkar, D.K.; Brassard, D.; El Khakania, M.A. Single-electron tunneling at room temperature in Ti𝑥Si1−𝑥O2 nanocomposite thin films. Appl. Phys. Lett. 2005, 87, 253108. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, J.; Du, L.; Zhang, M. Effect of resonant tunneling modulation on ZnO/In2O3 heterojunction nanocomposite in efficient detection of NO2 gas at room temperature. Sensors and Actuators B Chemical 2021, 329, 129230. [Google Scholar] [CrossRef]
- Grimaldi, C.; Cattani, M.; Salvadori, M.C. Dimensional effects on the tunneling conductivity of gold-implanted nanocomposite films. J. Appl. Phys. 2015, 117, 125302. [Google Scholar] [CrossRef]
- Ravich, Y.I.; Nemov, S.A. Hopping conduction via strongly localized impurity states of indium in PbTe and its solid solutions. Semiconductors 2002, 36, 1–20. [Google Scholar] [CrossRef]
- Satou, H.; Sakata, H. DC Hopping conduction in Fe2O3–MgO–TeO2 glasses. Mater. Chem. Phys. 2000, 65, 186–191. [Google Scholar] [CrossRef]
- El-Desoky, M.M. DC conductivity and hopping mechanism in V2O5–B2O3–BaO glasses. Phys. Status Solidi A Appl. Mat. 2003, 195, 422–428. [Google Scholar] [CrossRef]
- Papathanassiou, A.N.; Grammatikakis, J.; Sakkopoulos, S.; Vitoratos, E.; Dalas, E. Localized and long-distance charge hopping in fresh and thermally aged conductive copolymers of polypyrrole and polyaniline studied by combined TSDC and dc conductivity. J. Phys. Chem. Solids 2002, 63, 1771–1778. [Google Scholar] [CrossRef]
- Pramanik, M.H.A.; Butcher, P.N.; Cox, I.D. The d.c. conductivity of chalcogenide films due to the correlated barrier hopping mechanism. Philos. Mag. B 1983, 47, 437–443. [Google Scholar] [CrossRef]
- Svito, I.; Fedotova, J.A.; Milosavljević, M.; Zhukowski, P.; Koltunowicz, T.N.; Saad, A.; Kierczynski, K.; Fedotov, A.K. Influence of sputtering atmosphere on hopping conductance in granular nanocomposite (FeCoZr)x(Al2O3)1−x films. J. Alloys Compd. 2014, 615 (Suppl. S1), S344–S347. [Google Scholar] [CrossRef]
- Kołtunowicz, T.N.; Zhukowski, P.; Fedotova, V.V.; Saad, A.M.; Fedotov, A.K. Hopping Conductance in Nanocomposites (Fe0.45Co0.45Zr0.10)x(Al2O3)1−x Manufactured by Ion-Beam Sputtering of Complex Target in Ar+O2 Ambient. Acta Phys. Pol. A 2011, 120, 39–42. [Google Scholar] [CrossRef]
- Żukowski, P.; Kołtunowicz, T.; Partyka, J.; Fedotova, Y.A.; Larkin, A.V. Hopping conductivity of metal-dielectric nanocomposites produced by means of magnetron sputtering with the application of oxygen and argon ions. Vacuum 2009, 83 (Suppl. S1), S280–S283. [Google Scholar] [CrossRef]
- Svito, I.; Fedotov, A.K.; Koltunowicz, T.N.; Zhukowski, P.; Kalinin, Y.; Sitnikov, A.; Czarnacka, K.; Saad, A. Hopping of electron transport in granular Cux(SiO2)1−x nanocomposite films deposited by ion-beam sputtering. J. Alloys Compd. 2014, 615 (Suppl. S1), S371–S374. [Google Scholar] [CrossRef]
- Pierson, H. Handbook of Refractory Carbides and Nitrides; Noyes Publications: Park Ridge, NJ, USA, 1996. [Google Scholar]
- Koltunowicz, T.N. Test Station for Frequency-Domain Dielectric Spectroscopy of Nanocomposites and Semiconductors. J. Appl. Spectrosc. 2015, 82, 653–658. [Google Scholar] [CrossRef]
- Koltunowicz, T.N.; Gałaszkiewicz, P.; Kierczynski, K.; Rogalski, P.; Okal, P.; Pogrebnjak, A.D.; Buranich, V.; Pogorielov, M.; Diedkova, K.; Zahorodna, V.; et al. Investigation of AC Electrical Properties of MXene-PCL Nanocomposites for Application in Small and Medium Power Generation. Energies 2021, 14, 7123. [Google Scholar] [CrossRef]
- Kołtunowicz, T.N.; Bondariev, V.; Żukowski, P.; Fedotova, J.A.; Fedotov, A.K. AC electrical resonances in nanocomposites with partly oxidized FeCoZr grains embedded in CaF2 ceramic matrix–effects of annealing. J. Alloys Compd. 2020, 819, 153361. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M.; Pitaevskiiĭ, L.P. Electrodynamics of Continuous Media; Pergamon Press: Oxford, UK, 1984. [Google Scholar]
- Żukowski, P.; Kołtunowicz, T.; Partyka, J.; Węgierek, P.; Komarov, F.F.; Mironov, A.M.; Butkievith, N.; Freik, D. Dielectric properties and model of hopping conductivity of GaAs irradiated by H+ ions. Vacuum 2007, 81, 1137–1140. [Google Scholar] [CrossRef]
- Zukowski, P.; Koltunowicz, T.N.; Boiko, O.; Bondariev, V.; Czarnacka, K.; Fedotova, J.A.; Fedotov, A.K.; Svito, I.A. Impedance model of metal-dielectric nanocomposites produced by ion-beam sputtering in vacuum conditions and its experimental verification for thin films of (FeCoZr)x(PZT)(100-x). Vacuum 2015, 120, 37–43. [Google Scholar] [CrossRef]
- Żukowski, P.; Kierczyński, K.; Kołtunowicz, T.N.; Rogalski, P.; Subocz, J. Application of elements of quantum mechanics in analysing AC conductivity and determining the dimensions of water nanodrops in the composite of cellulose and mineral oil. Cellulose 2019, 26, 2969–2985. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory, 3rd ed.; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Żukowski, P.; Rogalski, P.; Kierczyński, K.; Kołtunowicz, T.N. Precise Measurements of the Temperature Influence on the Complex Permittivity of Power Transformers Moistened Paper-Oil Insulation. Energies 2021, 14, 5802. [Google Scholar] [CrossRef]
- Nowak, R. Statystyka dla Fizyków; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2002. [Google Scholar]
- Koltunowicz, T.N.; Zukowski, P.; Boiko, O.; Saad, A.; Fedotova, J.A.; Fedotov, A.K.; Larkin, A.; Kasiuk, J. AC Hopping Conductance in Nanocomposite Films with Ferromagnetic Alloy Nanoparticles in a PbZrTiO3 Matrix. J. Electron. Mater. 2015, 44, 2260–2268. [Google Scholar] [CrossRef]
- Zukowski, P.; Kierczynski, K.; Koltunowicz, T.N.; Rogalski, P.; Subocz, J.; Korenciak, D. AC conductivity measurements of liquid-solid insulation of power transformers with high water content. Measurement 2020, 165, 108194. [Google Scholar] [CrossRef]
- Jonscher, A.K. Dielectric Relaxation in Solids; Chelsea Dielectrics Press: London, UK, 1983. [Google Scholar]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics, I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics II. Direct Current Characteristics. J. Chem. Phys. 1942, 10, 98–105. [Google Scholar] [CrossRef]
- Davidson, D.W.; Cole, R.H. Dielectric relaxation in glycerol, propylene glycol, and n-propanol. J. Chem. Phys. 1951, 19, 1484–1490. [Google Scholar] [CrossRef]
- Davidson, D.W. Dielectric relaxation in liquids: I. The representation of relaxation behavior. Can. J. Chem. 1961, 39, 571–594. [Google Scholar] [CrossRef]
- Havriliak, S.J.; Havriliak, S.J. Dielectric and Mechanical Relaxation in Materials: Analysis, Interpretation and Application to Polymers; Hanser Publishers: Munich, Germany, 1997. [Google Scholar]
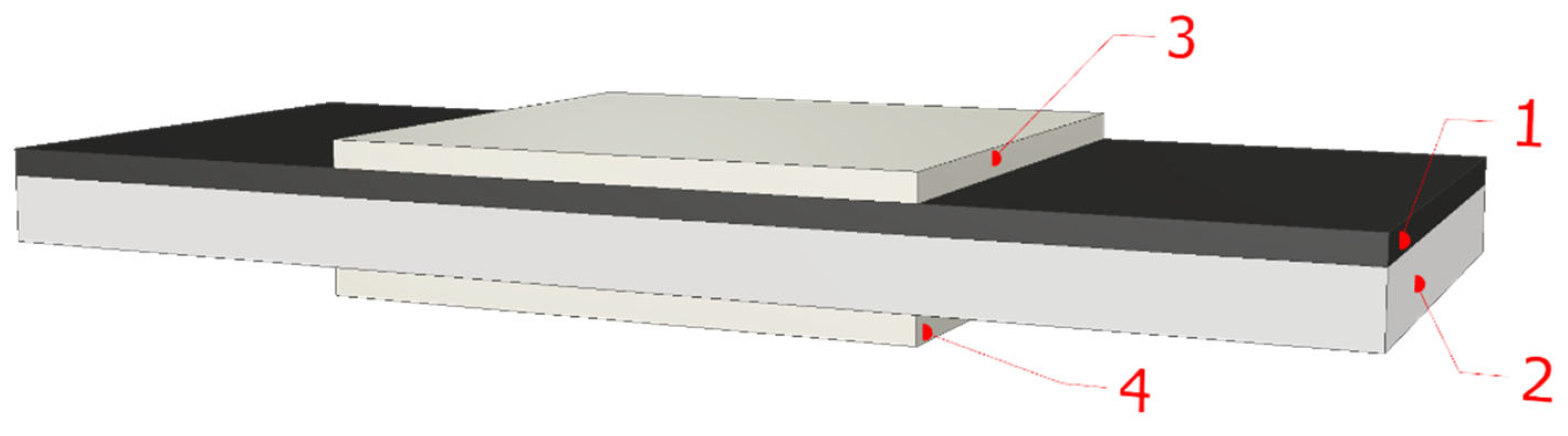


| Sample Number | Target Composition | Real Sample Composition and Structure | Surplus C, a.u. | Thickness, µm | Grain Size L, nm | Thickness of the Carbon Coating on the Nanoparticles Surface, nm |
|---|---|---|---|---|---|---|
| 1 | Ti; C | nc-TiC+α-C1.25 | 1.25 | 0.984 | 18 ± 2 | 0.3–0.5 |
| 2 | Ti0.75+Zr0.25; C | nc-Ti0.86Zr0.14C+α-C2.62 | 2.62 | 1.165 | 9 ± 2 | |
| 3 | Ti0.5+Zr0.5; C | nc-Ti0.75Zr0.25C+α-C0.95 | 0.95 | 1.097 | 11 ± 2 | |
| 4 | Ti0.25+Zr0.75; C | nc-Ti0.39Zr0.61C+α-C0.21 | 0.21 | 1.132 | 15 ± 2 | |
| 5 | Zr; C | nc-ZrC+α-C0.20 | 0.20 | 1.015 | 20 ± 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żukowski, P.; Gałaszkiewicz, P.; Bondariev, V.; Okal, P.; Pogrebnjak, A.; Kupchishin, A.; Ruban, A.; Pogorielov, M.; Kołtunowicz, T.N. Comparative Measurements and Analysis of the Electrical Properties of Nanocomposites TixZr1−xC+α-Cy (0.0 ≤ x ≤ 1.0). Materials 2022, 15, 7908. https://doi.org/10.3390/ma15227908
Żukowski P, Gałaszkiewicz P, Bondariev V, Okal P, Pogrebnjak A, Kupchishin A, Ruban A, Pogorielov M, Kołtunowicz TN. Comparative Measurements and Analysis of the Electrical Properties of Nanocomposites TixZr1−xC+α-Cy (0.0 ≤ x ≤ 1.0). Materials. 2022; 15(22):7908. https://doi.org/10.3390/ma15227908
Chicago/Turabian StyleŻukowski, Paweł, Piotr Gałaszkiewicz, Vitali Bondariev, Paweł Okal, Alexander Pogrebnjak, Anatolyi Kupchishin, Anatolyi Ruban, Maksym Pogorielov, and Tomasz N. Kołtunowicz. 2022. "Comparative Measurements and Analysis of the Electrical Properties of Nanocomposites TixZr1−xC+α-Cy (0.0 ≤ x ≤ 1.0)" Materials 15, no. 22: 7908. https://doi.org/10.3390/ma15227908
APA StyleŻukowski, P., Gałaszkiewicz, P., Bondariev, V., Okal, P., Pogrebnjak, A., Kupchishin, A., Ruban, A., Pogorielov, M., & Kołtunowicz, T. N. (2022). Comparative Measurements and Analysis of the Electrical Properties of Nanocomposites TixZr1−xC+α-Cy (0.0 ≤ x ≤ 1.0). Materials, 15(22), 7908. https://doi.org/10.3390/ma15227908







