Finite Element Modelling of Corrosion-Damaged RC Beams Strengthened Using the UHPC Layers
Abstract
1. Introduction
- The first one involves using a spring element to transfer tension between rebar and concrete. This approach is useful in 2D modeling, where only two nodes represent steel bars as truss elements. The nonlinearity of spring elements can be specified by inserting the experimental load against the displacement relationship. Li et al. [32] employed the 1D interface element, a translator in ABAQUS, to conduct a numerical analysis to study the behavior of corroded RC seawalls representing the bond by the element having two nodes linking the concrete and the steel reinforcement bars. Xiaoming and Hongqiang [33] utilized the spring interface parts to simulate the bond behavior between corroded bars and concrete. However, the results were not validated against experimental test results. Ou and Nguyen [34], Hanjari et al. [35], Kallias and Imran Rafiq [36], and Coronelli and Gambarova [37] used interface components to model the rebars-concrete bond behavior in 2D finite element modeling for corroded bars in RC members under flexure. Other researchers, for example, Kallias and Imran Rafiq [36], Val and Chernin [38], and Murcia-Delso and Shing [39], used four-noded interface elements to simulate the bond strength in ABAQUS.
- The second approach to simulate the loss of bond strength between steel bars and concrete consists of modifying the properties of concrete and steel. To demonstrate the bond interaction between steel bars and concrete, Ziari and Kianoush [40] adjusted the characteristics of concrete in contact with the reinforcing bars in a small region, known as the bond zone, in which the tensile strength and fracture energy of concrete elements were lowered. Dehestani and Mousavi [41] investigated the bond interaction by adding the equivalent strain due to the bond slip to the strain of the steel bars.
- The third approach simulates the connection as an interaction between three-dimensional surfaces of concrete and steel, as proposed by Amleh and Ghosh [42] for finite element modeling of corroded and non-corroded RC members using the results of the pullout tests. This approach can be applied to 3D concrete and steel models in ABAQUS utilizing the mechanical contact property for simulating the tangential and normal behavior of concrete and steel bars contacting surfaces. Biondini and Vergani [43] and Almassri et al. [44] performed 3D FEM on corroded RC beams without considering the loss of bond. German and Pamin [45] performed 2D and 3D FEM of corroded steel bars with corrosion product (rust) modeled as an interface element (COH2D4 elements) in the nonlinear FEM software using ABAQUS.
2. Experimental Program
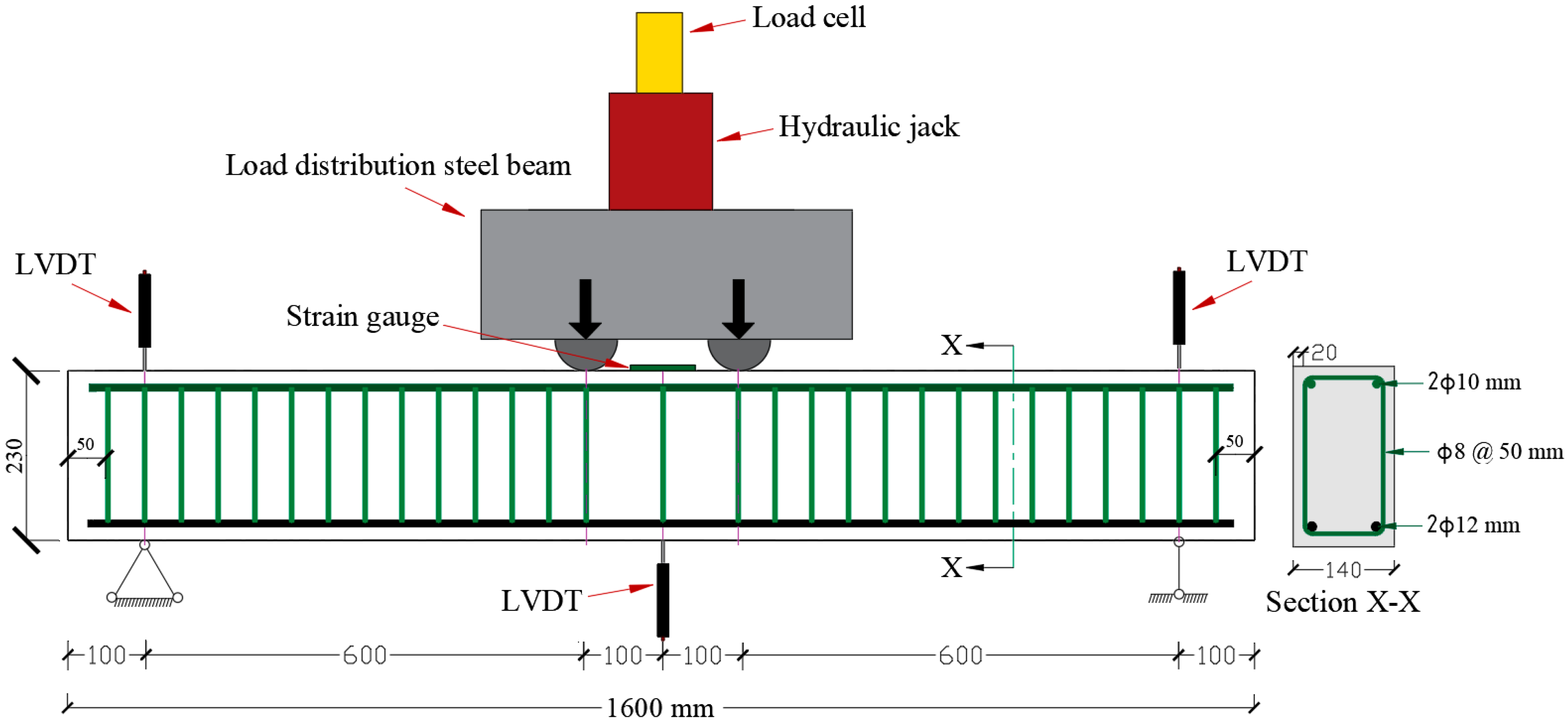
2.1. RC Beam Specimens
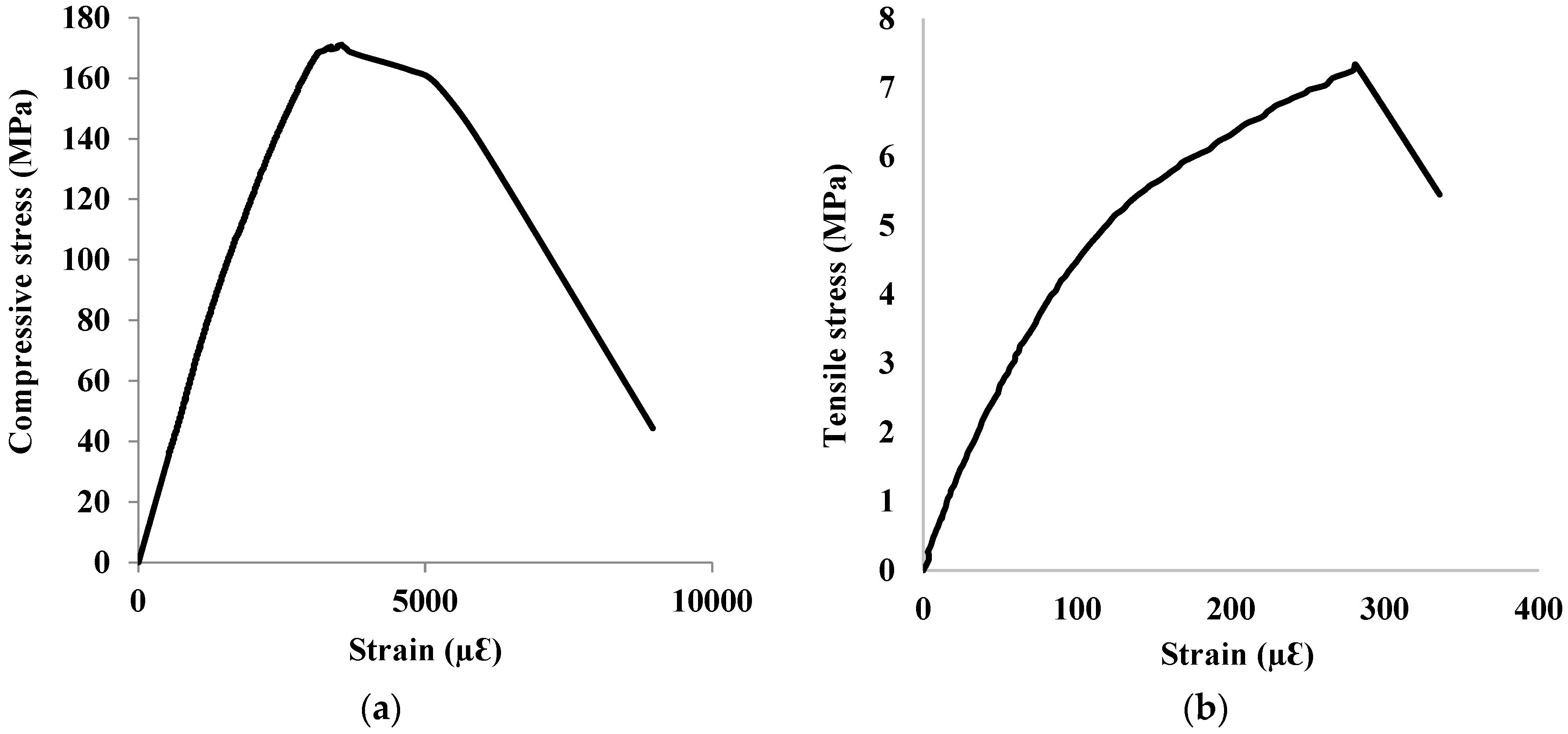
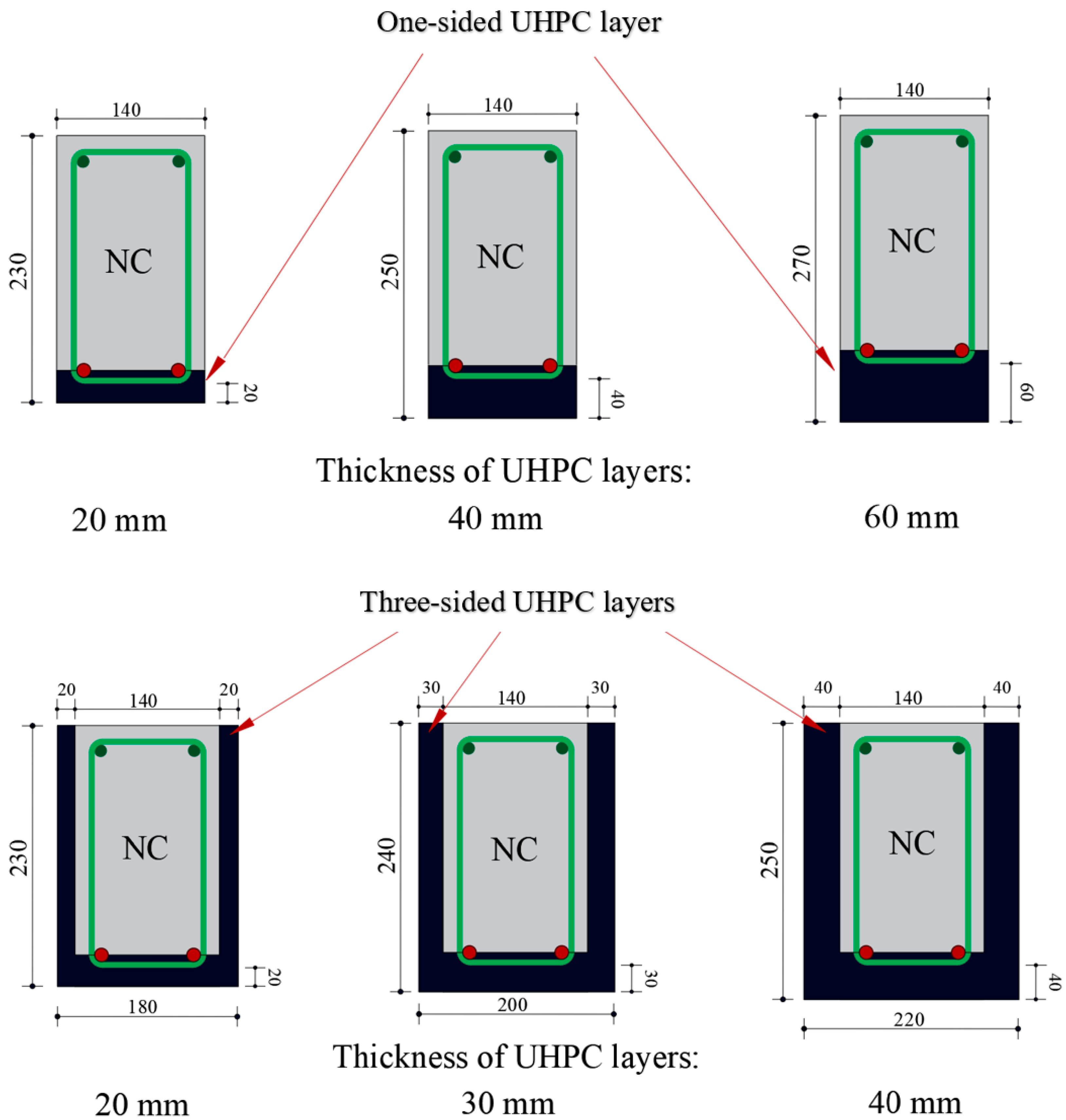
2.2. UHPC Strengthening: Properties, Configurations, and Bond Strength
3. Finite Element Simulation
3.1. Concrete Damage Plasticity Model (CDPM)
- The dilation angle is defined in the p-q plane at high confining pressure (Ψ).
- The parameter of eccentricity (ϵ).
- The initial ratio of equi-biaxial compressive yielding stress to the initial uniaxial compressive yielding stress (.
- The ratio of the tensile to the compressive meridian defines the shape of the yield surface in the deviatory plane (K).
- Parameter of viscosity.
3.2. Bond Simulation of Corroded Bars Using Cohesive Surface Bonding Approach
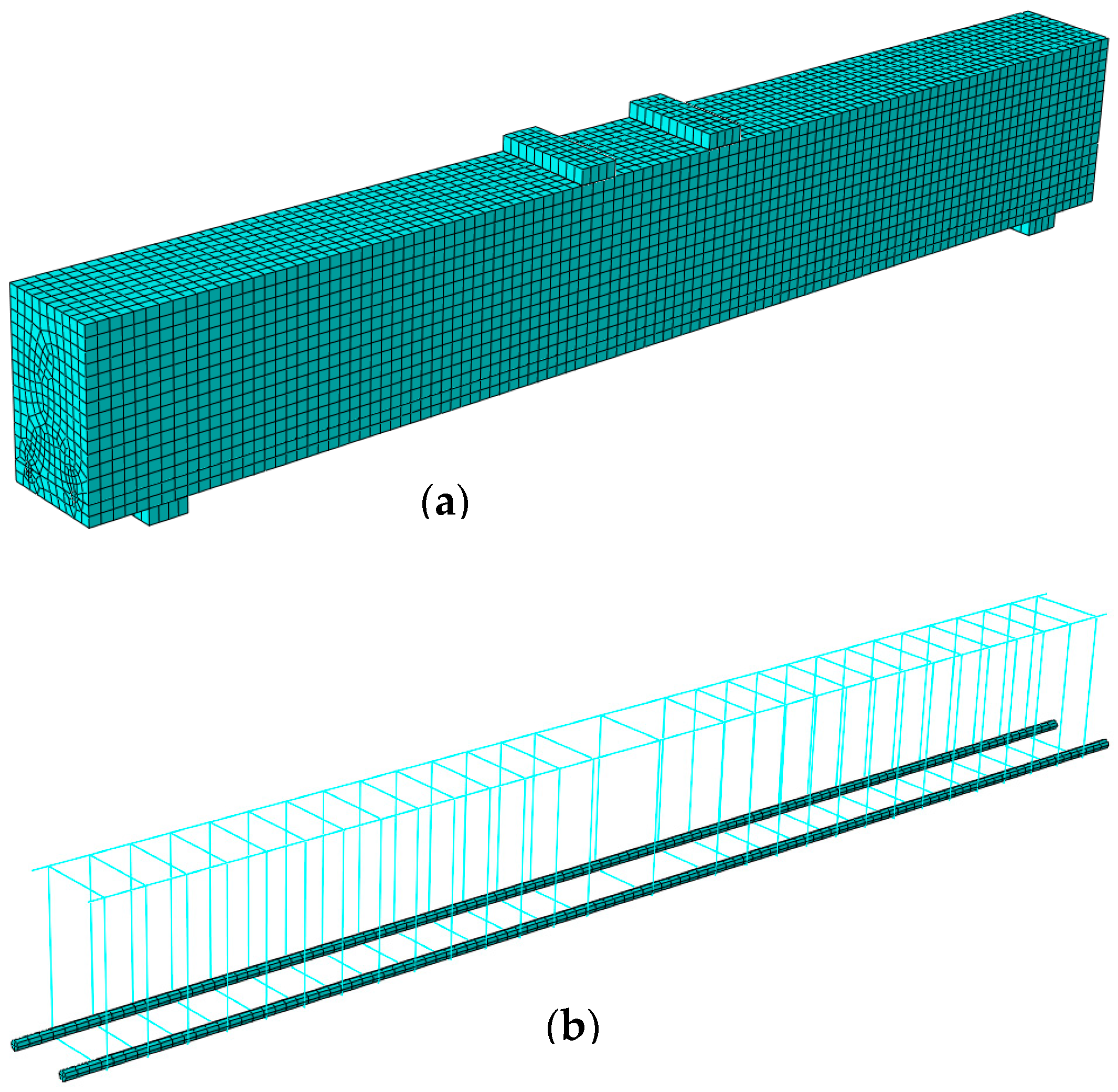
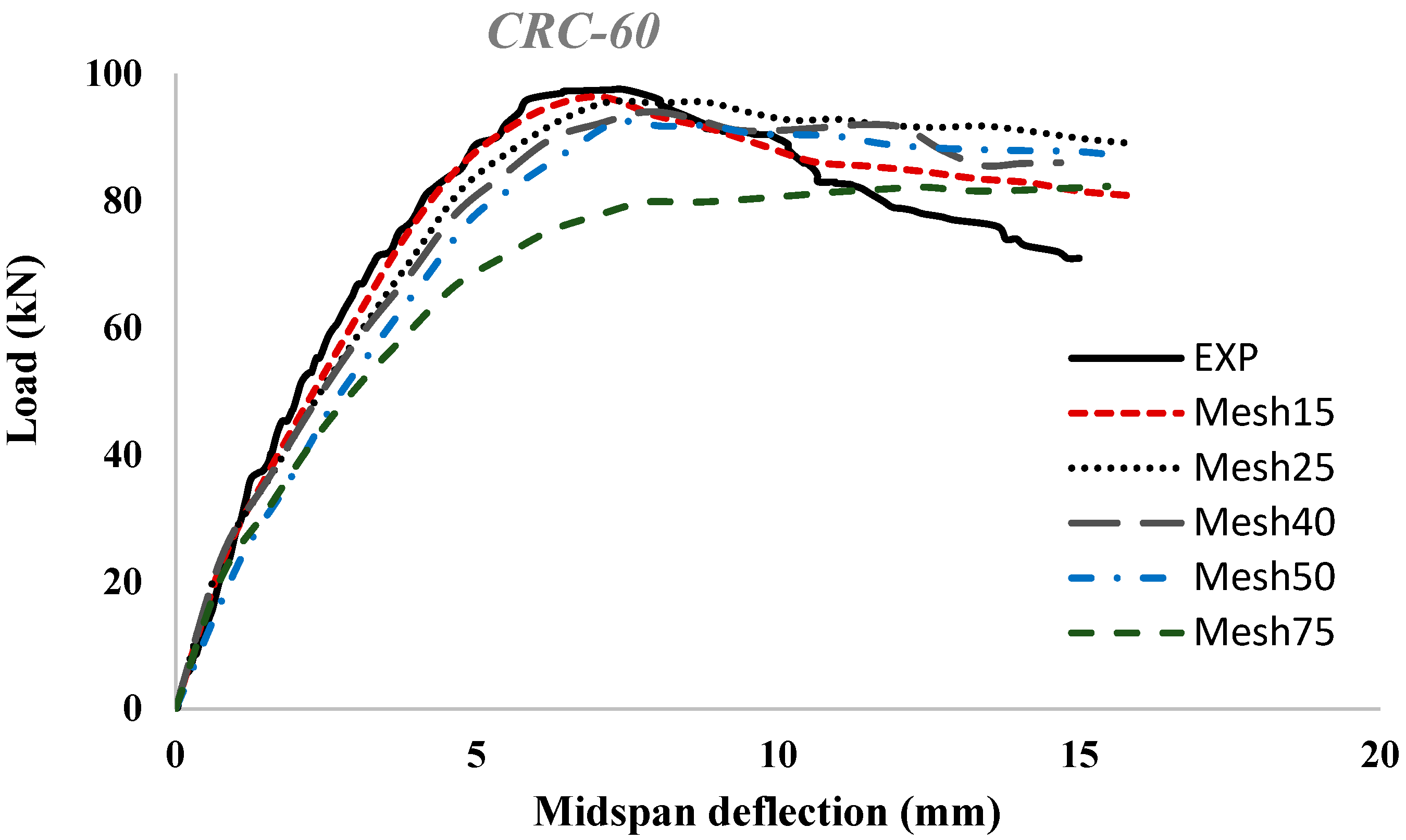
3.3. Elements Type and Meshing
3.4. Finite Element Modeling of Corroded Steel Bars
3.5. Model Constraints
3.5.1. Tie Constraint
3.5.2. Embedded Region Constraint
3.6. Analysis of FEM
3.7. Loading, Boundary Conditions, and Monitoring Points
4. Results and Discussion
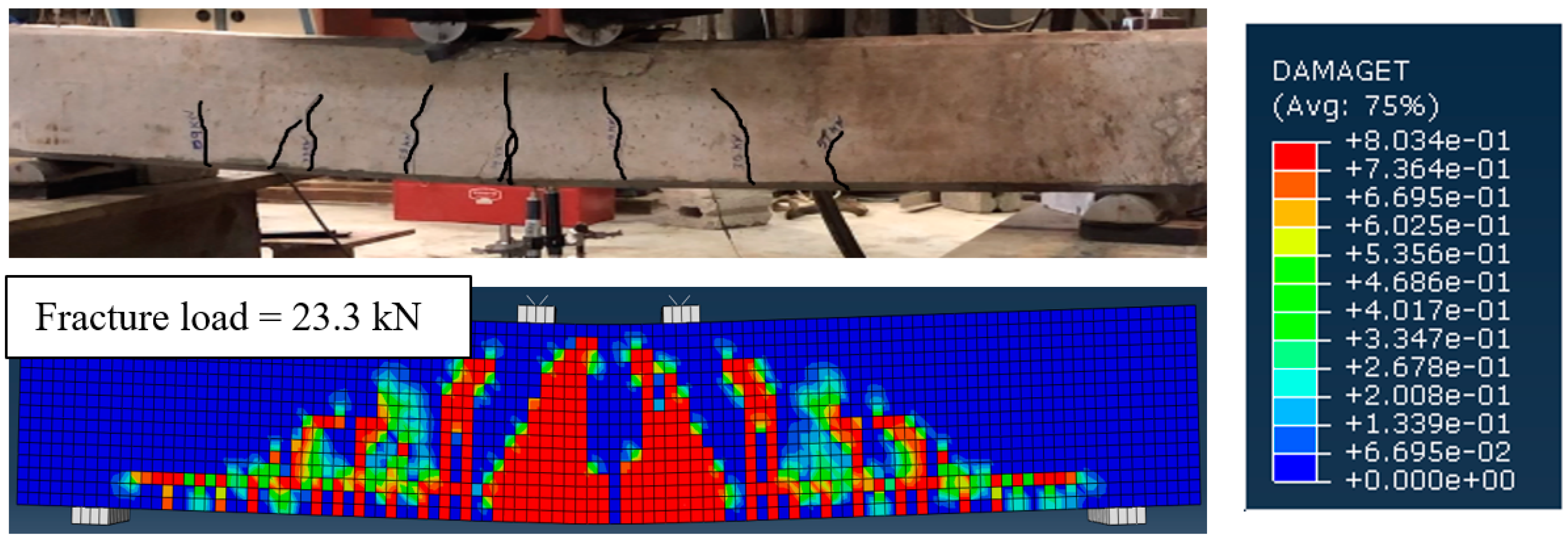
4.1. Crack Patterns at Failure
4.1.1. Uncorroded Un-Strengthened RC Beam (Control Specimen)
4.1.2. Corroded Un-Strengthened and Strengthened RC Beams
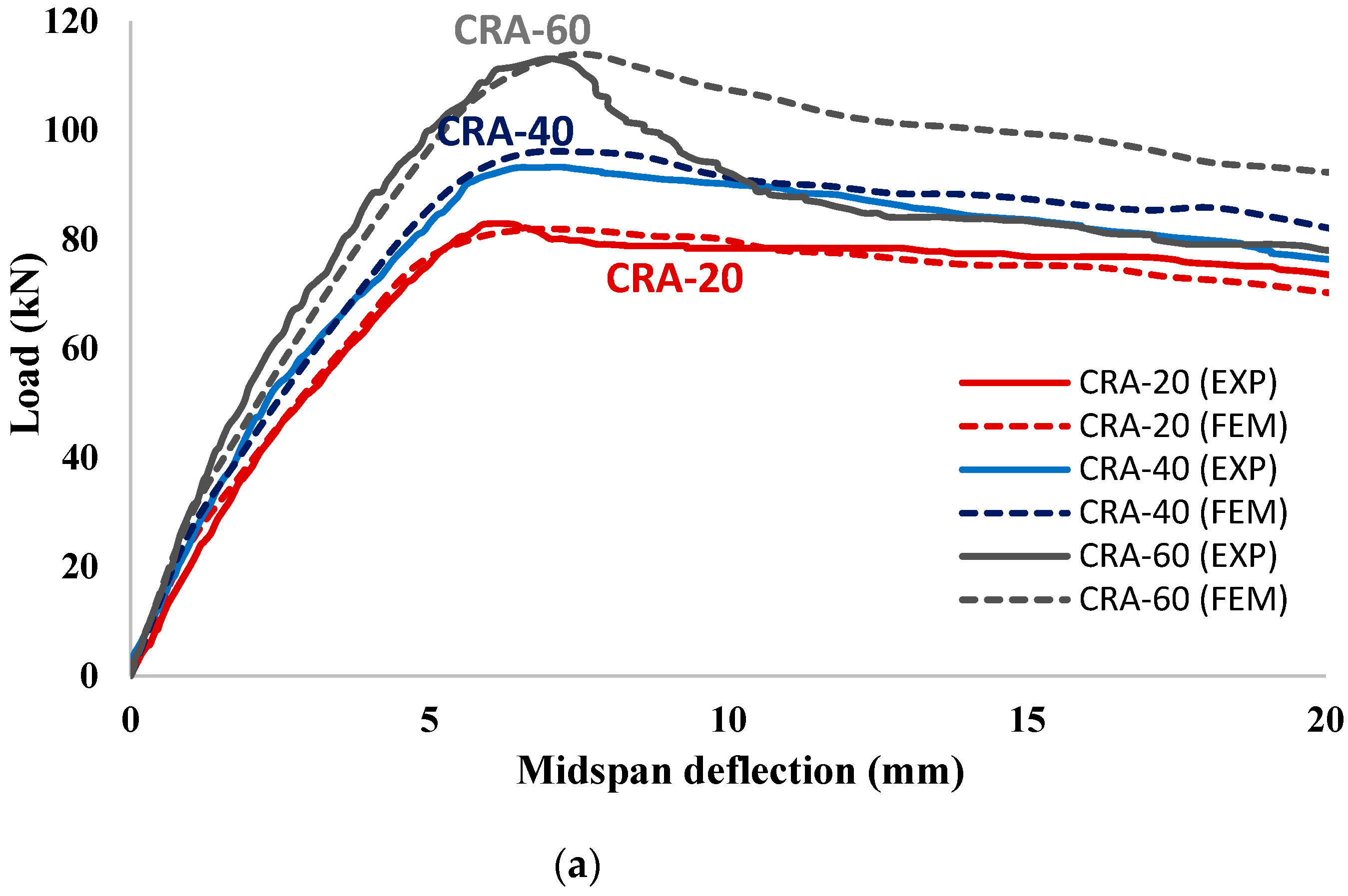
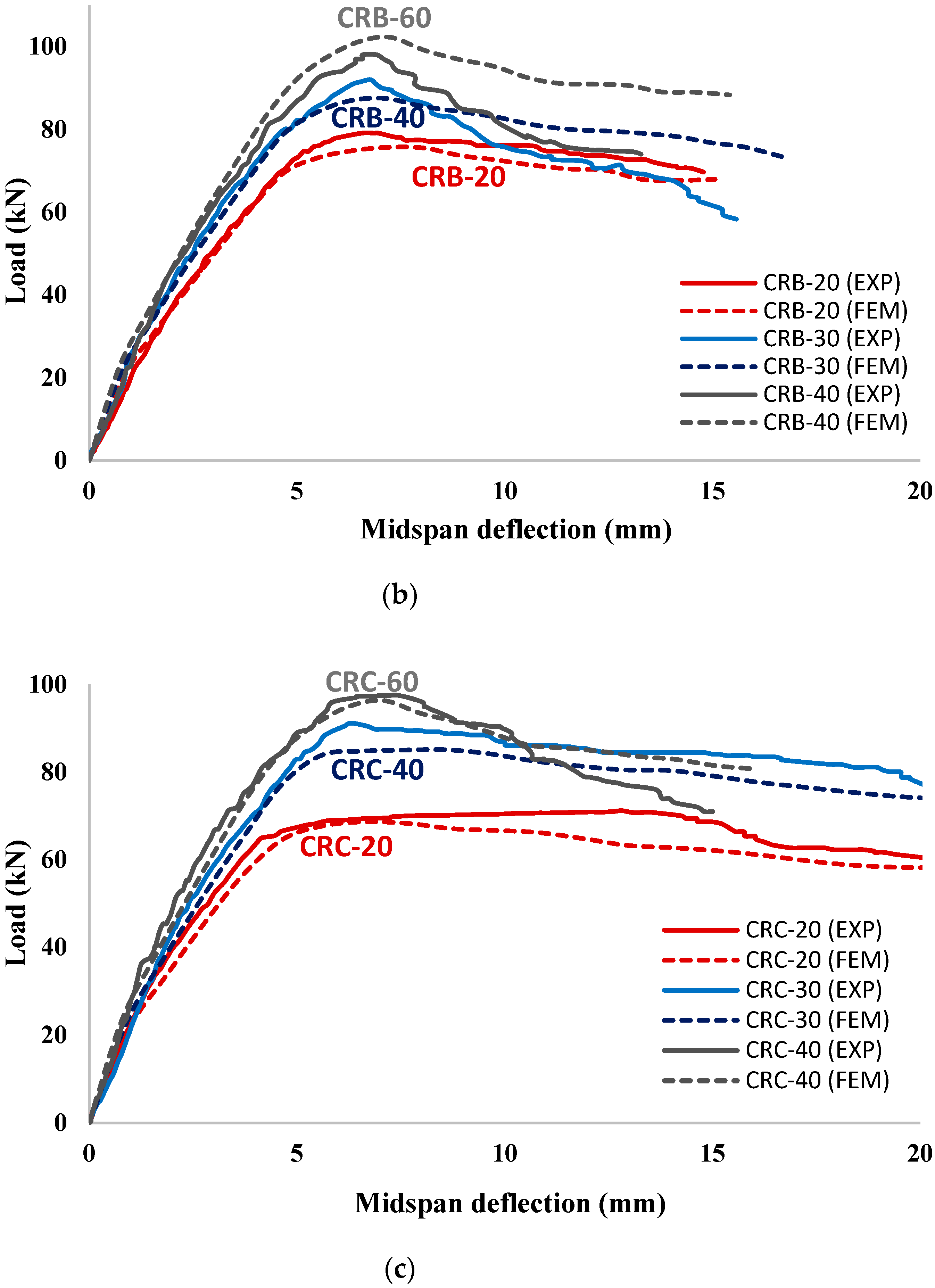
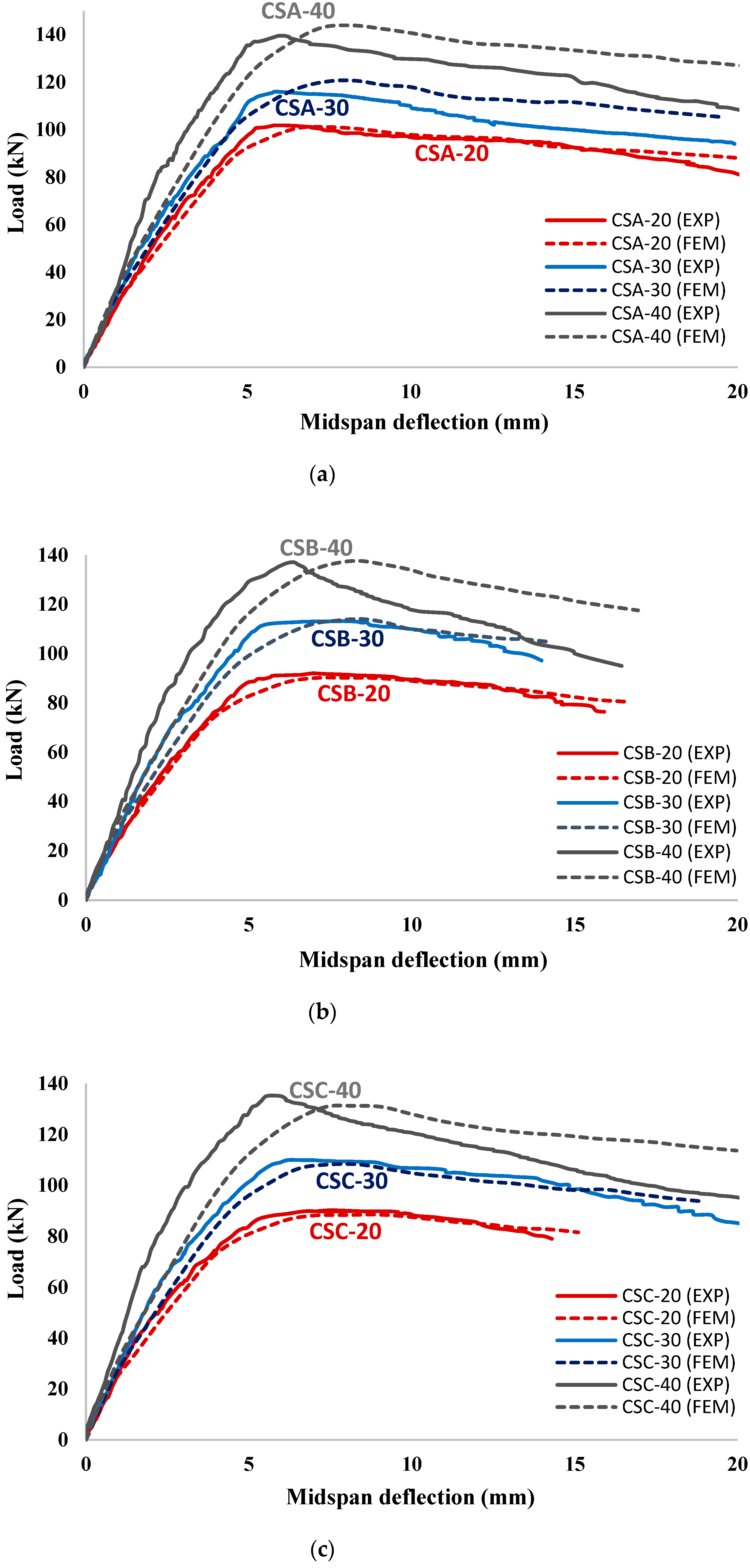
4.2. Load—Deflection Behavior
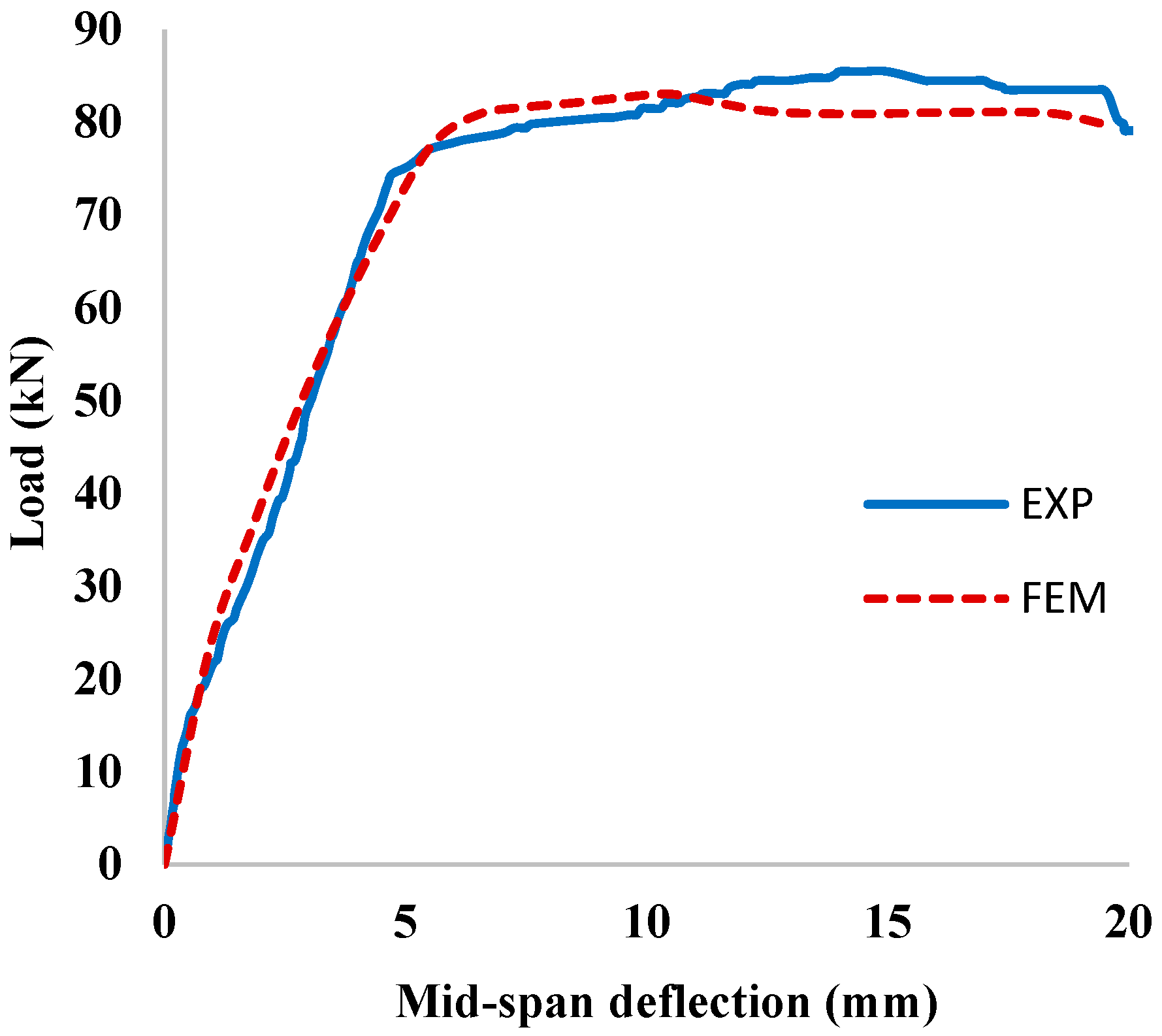
4.2.1. Uncorroded Un-Strengthened RC Beam (Control Specimen)
4.2.2. Corroded Un-Strengthened RC Beams
4.2.3. Corroded Strengthened RC Beams
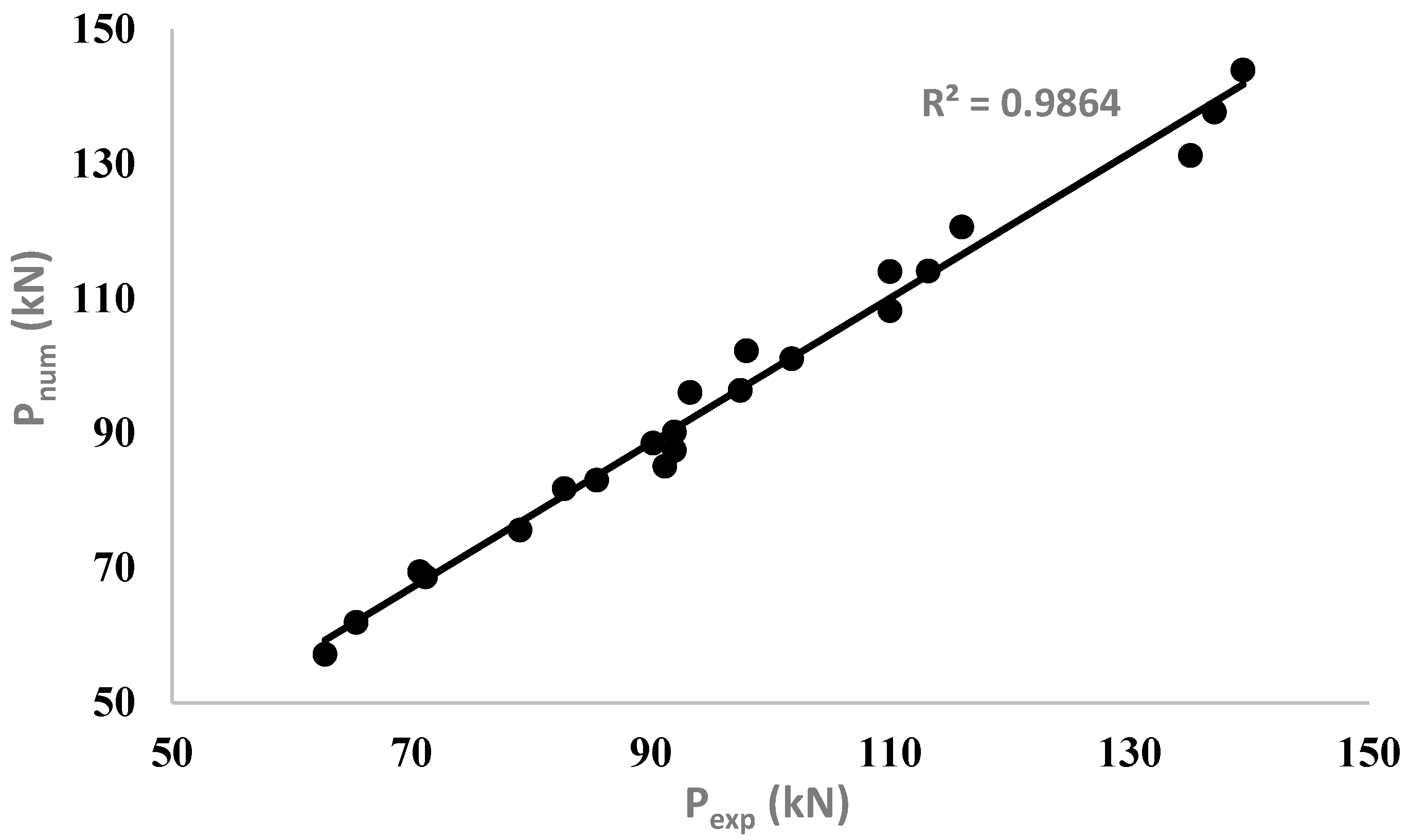
4.3. Ultimate Load (Flexural Strength)
5. Parametric Study
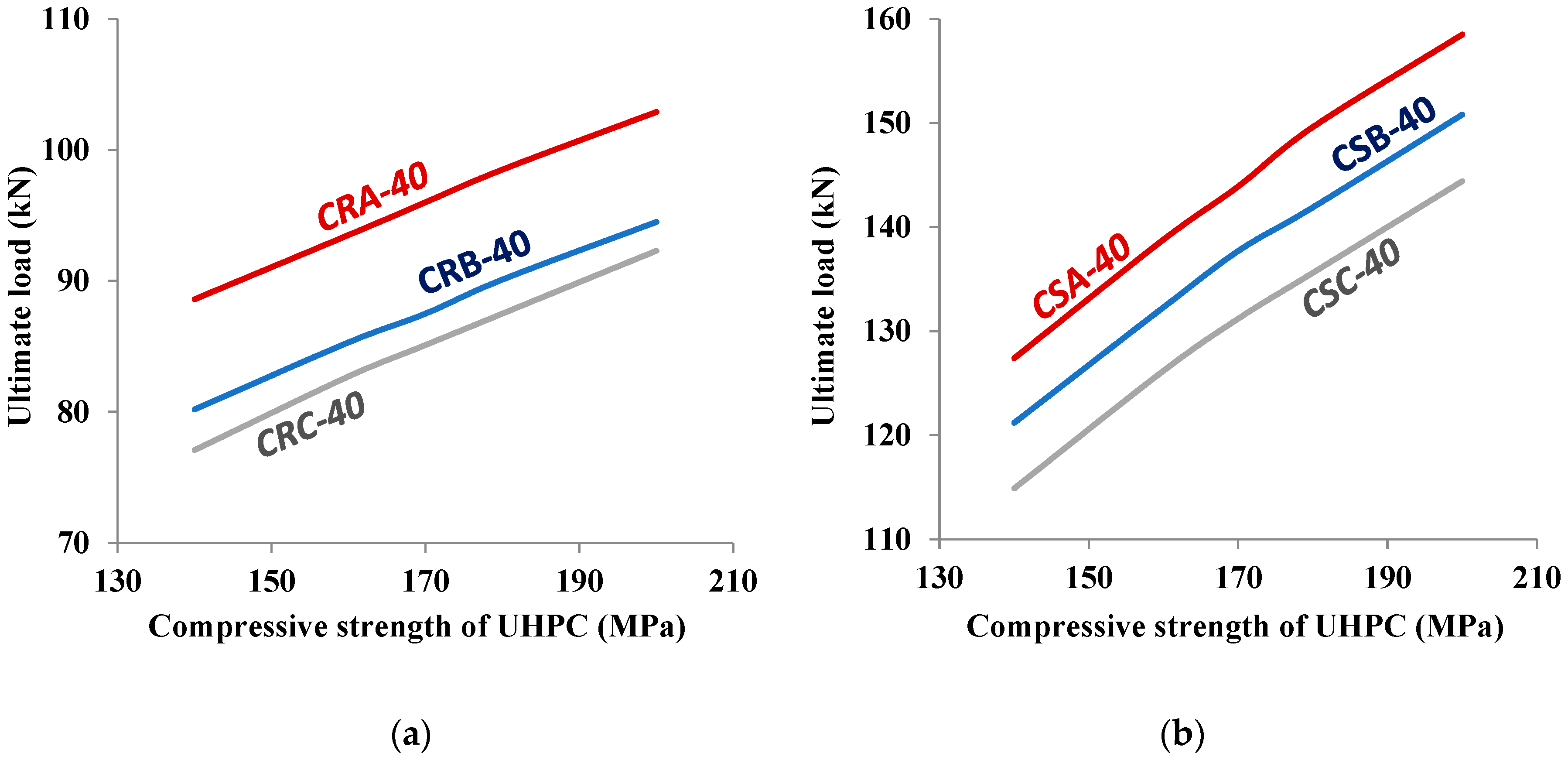
5.1. Effect of Varying the Compressive Strength of UHPC
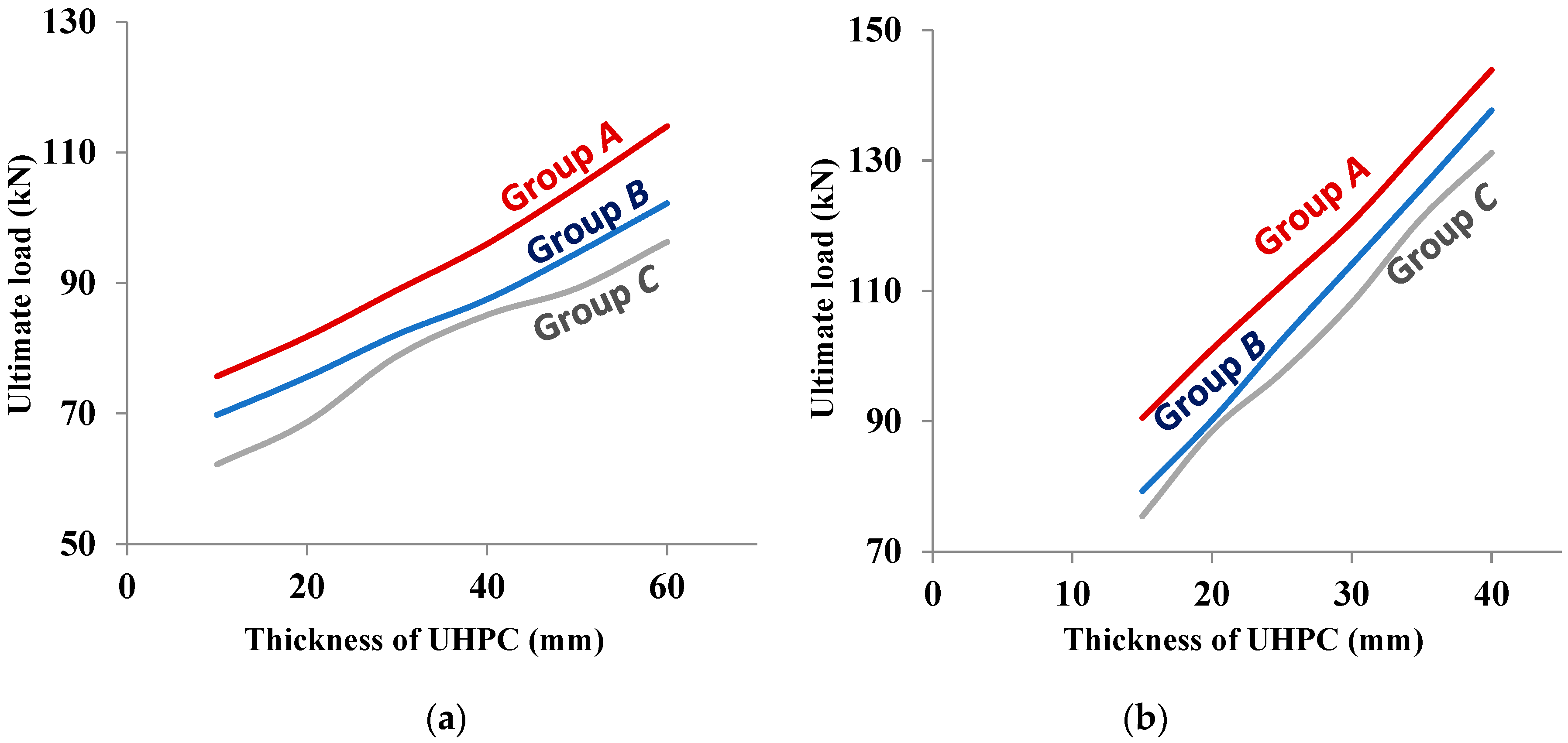
5.2. Effect of Varying the Thickness of UHPC Layers
6. Conclusions
- (1)
- The adoption of CDPM for simulating the normal concrete (used to cast the RC beams) and UHPC (for strengthening the corroded RC beams) and the selection of a cohesive surface bonding approach to simulate the bond between the corroded reinforcing bars and surrounding concrete were found to be appropriate in developing the FEMs, as evidenced by the high accuracy of the FEMs in simulating the flexural behavior of the corroded strengthened RC beams.
- (2)
- The FEMs developed in the present study can capture the flexural behavior of the corroded RC beams strengthened using layers of UHPC with a high degree of accuracy, including crack pattern, ultimate strength, and failure mode. The accuracy of the developed FEMs was confirmed through the comparison of the results obtained experimentally with the corresponding results predicted using the FEMs.
- (3)
- Parametric studies were carried out using the validated FEMs by varying the compressive strength and thickness of UHPC layers. The results of the parametric studies indicated that the flexural strength of corroded strengthened RC beams increases significantly with the increase in the compressive strength and thickness of UHPC layers and decreased significantly with the increase in the degree of reinforcement corrosion.
- (4)
- The proposed FEMs can be utilized to select the optimum thickness of the UHPC layers to achieve the desired ultimate load-carrying capacity of the corroded RC beam for given degrees of reinforcement corrosion, UHPC layer configurations, and the compressive strength of UHPC.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yi, W.J.; Kunnath, S.K.; Sun, X.D.; Shi, C.J.; Tang, F.J. Fatigue Behavior of Reinforced Concrete Beams with Corroded Steel Reinforcement. ACI Struct. J. 2010, 107, 526–533. [Google Scholar] [CrossRef]
- Torres-Acosta, A.A.; Navarro-Gutierrez, S.; Terán-Guillén, J. Residual Flexure Capacity of Corroded Reinforced Concrete Beams. Eng. Struct. 2007, 29, 1145–1152. [Google Scholar] [CrossRef]
- Vidal, T.; Castel, A.; François, R. Corrosion Process and Structural Performance of a 17 Year Old Reinforced Concrete Beam Stored in Chloride Environment. Cem. Concr. Res. 2007, 37, 1551–1561. [Google Scholar] [CrossRef]
- Almusallam, A.A. Effect of Degree of Corrosion on the Properties of Reinforcing Steel Bars. Constr. Build. Mater. 2001, 15, 361–368. [Google Scholar] [CrossRef]
- Fernandez, I.; Bairán, J.M.; Marí, A.R. Corrosion Effects on the Mechanical Properties of Reinforcing Steel Bars. Fatigue and σ-ε Behavior. Constr. Build. Mater. 2015, 101, 772–783. [Google Scholar] [CrossRef]
- Du, Y.G.; Clarkt, L.A.; Chan, A.H.C. Effect of Corrosion on Ductility of Reinforcing Bars. Mag. Concr. Res. 2005, 57, 407–419. [Google Scholar] [CrossRef]
- Cairns, J.; Plizzari, G.A.; Du, Y.; Law, D.W.; Franzoni, C. Mechanical Properties of Corrosion-Damaged Reinforcement. ACI Mater. J. 2005, 102, 256. [Google Scholar] [CrossRef]
- Almusallam, A.A.; Al-Gahtani, A.S.; Aziz, A.R. Rasheeduzzafar Effect of Reinforcement Corrosion on Bond Strength. Constr. Build. Mater. 1996, 10, 123–129. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, Z.; Wang, L.; Zhang, J. Experimental Investigation of Corrosion Effect on Bond Behavior between Reinforcing Bar and Concrete. Constr. Build. Mater. 2017, 152, 240–249. [Google Scholar] [CrossRef]
- Yalciner, H.; Eren, O.; Sensoy, S. An Experimental Study on the Bond Strength between Reinforcement Bars and Concrete as a Function of Concrete Cover, Strength and Corrosion Level. Cem. Concr. Res. 2012, 42, 643–655. [Google Scholar] [CrossRef]
- Siddika, A.; Mamun, M.A.; Alyousef, R.; Amran, Y.H.M. Strengthening of Reinforced Concrete Beams by Using Fiber-Reinforced Polymer Composites: A Review. J. Build. Eng. 2019, 25, 100798. [Google Scholar] [CrossRef]
- Masoud, S.; Soudki, K.; Topper, T. CFRP-Strengthened and Corroded RC Beams under Monotonic and Fatigue Loads. J. Compos. Constr. 2001, 5, 228–236. [Google Scholar] [CrossRef]
- Dong, J.F.; Wang, Q.Y.; Guan, Z.W. Structural Behaviour of RC Beams Externally Strengthened with FRP Sheets under Fatigue and Monotonic Loading. Eng. Struct. 2012, 41, 24–33. [Google Scholar] [CrossRef]
- Meng, W.; Khayat, K.H. Improving Flexural Performance of Ultra-High-Performance Concrete by Rheology Control of Suspending Mortar. Compos. Part B Eng. 2017, 117, 26–34. [Google Scholar] [CrossRef]
- Zadeh, D.B.; Bahari, A.; Tirandaz, F. Ultra-high performance concrete. In Proceedings of the Excellence in Concrete Construction through Innovation-International Conference on Concrete Construction, London, UK, 9–10 September 2008. [Google Scholar]
- Shafieifar, M.; Farzad, M.; Azizinamini, A. Experimental and Numerical Study on Mechanical Properties of Ultra High Performance Concrete (UHPC). Constr. Build. Mater. 2017, 156, 402–411. [Google Scholar] [CrossRef]
- Abbas, S.; Nehdi, M.L.; Saleem, M.A. Ultra-High Performance Concrete: Mechanical Performance, Durability, Sustainability and Implementation Challenges. Int. J. Concr. Struct. Mater. 2016, 10, 271–295. [Google Scholar] [CrossRef]
- Ahmad, S.; Hakeem, I.; Maslehuddin, M. Development of an Optimum Mixture of Ultra-High Performance Concrete. Eur. J. Environ. Civ. Eng. 2016, 20, 1106–1126. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Hussein, H.H.; Chen, G. Flexural Strengthening of Reinforced Concrete Beams or Slabs Using Ultra-High Performance Concrete (UHPC): A State of the Art Review. Eng. Struct. 2020, 205, 110035. [Google Scholar] [CrossRef]
- Bastien-Masse, M.; Brühwiler, E. Ultra high performance fiber reinforced concrete for strengthening and protecting bridge deck slabs. In Bridge Maintenance, Safety, Management and Life Extension, Proceedings of the 7th International Conference of Bridge Maintenance, Safety and Management, IABMAS 2014, Shanghai, China, 7–11 July 2014; CRC Press-Taylor & Francis Group: Boca Raton, FL, USA, 2014; pp. 2176–2182. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Zhu, Y.; Shao, X. Experimental Study on Flexural Behavior of Damaged Reinforced Concrete (RC) Beam Strengthened by Toughness-Improved Ultra-High Performance Concrete (UHPC) Layer. Compos. Part B Eng. 2020, 186, 107834. [Google Scholar] [CrossRef]
- Al-Osta, M.A. Shear Behaviour of RC Beams Retrofitted Using UHPFRC Panels Epoxied to the Sides. Comput. Concr. 2019, 24, 37–49. [Google Scholar] [CrossRef]
- Bahraq, A.A.; Al-Osta, M.A.; Ahmad, S.; Al-Zahrani, M.M.; Al-Dulaijan, S.O.; Rahman, M.K. Experimental and Numerical Investigation of Shear Behavior of RC Beams Strengthened by Ultra-High Performance Concrete. Int. J. Concr. Struct. Mater. 2019, 13, 1–19. [Google Scholar] [CrossRef]
- Lampropoulos, A.P.; Paschalis, S.A.; Tsioulou, O.T.; Dritsos, S.E. Strengthening of Reinforced Concrete Beams Using Ultra High Performance Fibre Reinforced Concrete (UHPFRC). Eng. Struct. 2016, 106, 370–384. [Google Scholar] [CrossRef]
- Hussein, L.; Amleh, L. Structural Behavior of Ultra-High Performance Fiber Reinforced Concrete-Normal Strength Concrete or High Strength Concrete Composite Members. Constr. Build. Mater. 2015, 93, 1105–1116. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Crack Band Theory for Fracture of Concrete. Matériaux Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Tao, Y.; Chen, J.F. Concrete Damage Plasticity Model for Modeling FRP-to-Concrete Bond Behavior. J. Compos. Constr. 2015, 19, 04014026. [Google Scholar] [CrossRef]
- Sadouki, H.; Denarié, E.; Brühwiler, E. Validation of a FEA Model of Structural Response of RC-Cantilever Beams Strengthened with a (R-) UHPFRC Layer. Constr. Build. Mater. 2017, 140, 100–108. [Google Scholar] [CrossRef]
- Al-Osta, M.A.; Isa, M.N.; Baluch, M.H.; Rahman, M.K. Flexural Behavior of Reinforced Concrete Beams Strengthened with Ultra-High Performance Fiber Reinforced Concrete. Constr. Build. Mater. 2017, 134, 279–296. [Google Scholar] [CrossRef]
- Ramachandra Murthy, A.; Karihaloo, B.L.; Priya, D.S. Flexural Behavior of RC Beams Retrofitted with Ultra-High Strength Concrete. Constr. Build. Mater. 2018, 175, 815–824. [Google Scholar] [CrossRef]
- Jankowiak, T.; Lodygowski, T. Identification of Parameters of Concrete Damage Plasticity Constitutive Model. Found. Civ. Environ. Eng. 2005, 6, 53–69. [Google Scholar]
- Li, C.Q.; Yang, S.T.; Saafi, M. Numerical Simulation of Behavior of Reinforced Concrete Structures Considering Corrosion Effects on Bonding. J. Struct. Eng. 2014, 140, 04014092. [Google Scholar] [CrossRef]
- Xiaoming, Y.; Hongqiang, Z. Finite Element Investigation on Load Carrying Capacity of Corroded RC Beam Based on Bond-Slip. Jordan J. Civ. Eng. 2012, 6, 134–146. [Google Scholar]
- Ou, Y.C.; Nguyen, N.D. Plastic Hinge Length of Corroded Reinforced Concrete Beams. ACI Struct. J. 2014, 111, 1049–1058. [Google Scholar] [CrossRef]
- Hanjari, K.Z.; Kettil, P.; Lundgren, K. Analysis of Mechanical Behavior of Corroded Reinforced Concrete Structures. ACI Struct. J. 2011, 108, 532–541. [Google Scholar] [CrossRef]
- Kallias, A.N.; Imran Rafiq, M. Finite Element Investigation of the Structural Response of Corroded RC Beams. Eng. Struct. 2010, 32, 2984–2994. [Google Scholar] [CrossRef]
- Coronelli, D.; Gambarova, P. Structural Assessment of Corroded Reinforced Concrete Beams: Modeling Guidelines. J. Struct. Eng. 2004, 130, 1214–1224. [Google Scholar] [CrossRef]
- Val, D.V.; Chernin, L. Serviceability Reliability of Reinforced Concrete Beams with Corroded Reinforcement. J. Struct. Eng. 2009, 135, 896–905. [Google Scholar] [CrossRef]
- Murcia-Delso, J.; Benson Shing, P. Bond-Slip Model for Detailed Finite-Element Analysis of Reinforced Concrete Structures. J. Struct. Eng. 2015, 141, 04014125. [Google Scholar] [CrossRef]
- Ziari, A.; Kianoush, M.R. Finite-Element Parametric Study of Bond and Splitting Stresses in Reinforced Concrete Tie Members. J. Struct. Eng. 2014, 140, 04013106. [Google Scholar] [CrossRef]
- Dehestani, M.; Mousavi, S.S. Modified Steel Bar Model Incorporating Bond-Slip Effects for Embedded Element Method. Constr. Build. Mater. 2015, 81, 284–290. [Google Scholar] [CrossRef]
- Amleh, L.; Ghosh, A. Modeling the Effect of Corrosion on Bond Strength at the Steel-Concrete Interface with Finite-Element Analysis. Can. J. Civ. Eng. 2006, 33, 673–682. [Google Scholar] [CrossRef]
- Biondini, F.; Vergani, M. Deteriorating Beam Finite Element for Nonlinear Analysis of Concrete Structures under Corrosion. Struct. Infrastruct. Eng. 2015, 11, 519–532. [Google Scholar] [CrossRef]
- Almassri, B.; Al Mahmoud, F.; Francois, R. Behaviour of Corroded Reinforced Concrete Beams Repaired with NSM CFRP Rods, Experimental and Finite Element Study. Compos. Part B Eng. 2016, 92, 477–488. [Google Scholar] [CrossRef]
- German, M.; Pamin, J. FEM Simulations of Cracking in RC Beams Due to Corrosion Progress. Arch. Civ. Mech. Eng. 2015, 15, 1160–1172. [Google Scholar] [CrossRef]
- El Maaddawy, T.A.; Soudki, K.A. Effectiveness of Impressed Current Technique to Simulate Corrosion of Steel Reinforcement in Concrete. J. Mater. Civ. Eng. 2003, 15, 41–47. [Google Scholar] [CrossRef]
- ASTM Standard E8/E8M-13a; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2013.
- ASTM G1-90 ASTM G1; Standard Practice for Preparing, Cleaning, and Evaluation Corrosion Test Specimens. ASTM: West Conshohocken, PA, USA, 2003.
- ASTM C150/C150M-17; Standard Specification for Portland Cement. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM C39/C39M; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTMC496/C496M-17; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2017.
- Al-Madani, M.K.; Al-Osta, M.A.; Ahmad, S.; Khalid, H.R.; Al-Huri, M. Interfacial Bond Behavior between Ultra High Performance Concrete and Normal Concrete Substrates. Constr. Build. Mater. 2022, 320, 126229. [Google Scholar] [CrossRef]
- ACI Committee 546 2014; ACI 546R-14: Guide to Concrete Repair. American Concrete Institute: Farmington Hills, MI, USA, 2014. [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A Plastic-Damage Model for Concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Abaqus, A. 6.13 Analysis User’s Manual; SIMULIA: Providence, IR, USA, 2013. [Google Scholar]
- Birtel, V.; Mark, P. Parameterised Finite Element Modelling of RC Beam Shear Failure. In Proceedings of the Ababqus User’s Conference, Boston, MA, USA, 23–25 May 2006; Volume 14, pp. 95–108. [Google Scholar]
- Rodríguez Soler, J.; Martinez Cutillas, F.J.; Marti Rodriguez, J. Concrete constitutive model, calibration and applications. In Proceedings of the 2013 SIMULIA Community Conference (SCC), Vienna, Austria, 21–24 May 2013. [Google Scholar]
- Chaudhari, S.V.; Chakrabarti, M.A. Modeling of Concrete for Nonlinear Analysis Using Finite Element Code ABAQUS. Int. J. Comput. Appl. 2012, 44, 14–18. [Google Scholar]
- Bahraq, A.A.; Al-Osta, M.A.; Khan, M.I.; Ahmad, S. Numerical and Analytical Modeling of Seismic Behavior of Beam-Column Joints Retrofitted with Ultra-High Performance Fiber Reinforced Concrete. Structures 2021, 32, 1986–2003. [Google Scholar] [CrossRef]
- Al-Osta, M.A.; Al-Sakkaf, H.A.; Sharif, A.M.; Ahmad, S.; Baluch, M.H. Finite Element Modeling of Corroded RC Beams Using Cohesive Surface Bonding Approach. Comput. Concr. 2018, 22, 167–182. [Google Scholar] [CrossRef]
- El Maaddawy, T.; Soudki, K.; Topper, T. Analytical Model to Predict Nonlinear Flexural Behavior of Corroded Reinforced Concrete Beams. ACI Struct. J. 2005, 102, 550. [Google Scholar]
- Soh, C.K.; Chiew, S.P.; Dong, Y.X. Damage Model for Concrete-Steel Interface. J. Eng. Mech. 1999, 125, 979–983. [Google Scholar] [CrossRef]
- Mercan, B. Modeling and Behavior of Prestressed Concrete Spandrel Beams; University of Minnesota: Minneapolis, MN, USA, 2011; ISBN 1124768254. [Google Scholar]
- Al-Osta, M.A. Exploitation of Ultrahigh-Performance Fibre-Reinforced Concrete for the Strengthening of Concrete Structural Members. Adv. Civ. Eng. 2018, 2018, 8678124. [Google Scholar] [CrossRef]



| Specimen’s ID | Actual Mass Loss % | Strengthening Configuration | Thickness of UHPC Layer (mm) |
|---|---|---|---|
| UU | 0 | No strengthening | 0 |
| CUA | 9.8 | 0 | |
| CUB | 17.4 | No strengthening | 0 |
| CUC | 20.8 | 0 | |
| CRA-20 | 10 | 20 | |
| CRA-40 | 10.8 | 1-sided | 40 |
| CRA-60 | 11.8 | 60 | |
| CRB-20 | 18.1 | 20 | |
| CRB-40 | 17.8 | 1-sided | 40 |
| CRB-60 | 18.3 | 60 | |
| CRC-20 | 22.1 | 20 | |
| CRC-40 | 20.8 | 1-sided | 40 |
| CRC-60 | 22.6 | 60 | |
| CSA-20 | 10.2 | 20 | |
| CSA-30 | 9.5 | 3-sided | 30 |
| CSA-40 | 9.1 | 40 | |
| CSB-20 | 17.5 | 20 | |
| CSB-30 | 16.7 | 3-sided | 30 |
| CSB-40 | 16.8 | 40 | |
| CSC-20 | 21.2 | 20 | |
| CSC-30 | 22.3 | 3-sided | 30 |
| CSC-40 | 20.9 | 40 |
| Input Parameter | Normal Concrete | UHPC |
|---|---|---|
| Mass density (kg/m3) | 2400 | 2500 |
| Young modulus (GPa) | 33 | 46 |
| Poisson ratio | 0.19 | 0.20 |
| Ψ (°) | 36 | 36 |
| ϵ | 0.1 | 0.1 |
| 1.16 | 1.16 | |
| K | 0.667 | 0.667 |
| Parameter of viscosity | 0 | 0 |
| Beam’s ID | (MPa) | (mm) | (N/mm3) | (N/mm3) |
|---|---|---|---|---|
| CRA-20 | 8.95 | 0.396 | 22.58 | 2258.00 |
| CRA-40 | 8.87 | 0.397 | 22.37 | 2236.82 |
| CRA-60 | 8.78 | 0.397 | 22.10 | 2209.62 |
| CRB-20 | 8.16 | 0.403 | 20.22 | 2021.86 |
| CRB-40 | 8.19 | 0.403 | 20.31 | 2031.36 |
| CRB-60 | 8.14 | 0.404 | 20.16 | 2015.51 |
| CRC-20 | 7.77 | 0.411 | 18.91 | 1891.15 |
| CRC-40 | 7.89 | 0.408 | 19.34 | 1934.39 |
| CRC-60 | 7.72 | 0.412 | 18.74 | 1874.36 |
| CSA-20 | 8.93 | 0.397 | 22.53 | 2252.75 |
| CSA-30 | 9.00 | 0.396 | 22.71 | 2270.96 |
| CSA-40 | 9.03 | 0.396 | 22.79 | 2279.23 |
| CSB-20 | 8.22 | 0.403 | 20.41 | 2040.81 |
| CSB-30 | 8.30 | 0.402 | 20.66 | 2065.76 |
| CSB-40 | 8.29 | 0.402 | 20.63 | 2062.66 |
| CSC-20 | 7.85 | 0.409 | 19.21 | 1921.16 |
| CSC-30 | 7.75 | 0.411 | 18.84 | 1884.44 |
| CSC-40 | 7.93 | 0.407 | 19.48 | 1947.56 |
| Beam ID | Experimentally | Numerically | Difference (%) |
|---|---|---|---|
| UU | 85.5 | 83.0 | −2.9 |
| CUA | 70.7 | 69.5 | −1.7 |
| CUB | 65.4 | 61.9 | −5.4 |
| CUC | 62.8 | 57.2 | −8.9 |
| CRA-20 | 82.8 | 81.8 | −1.2 |
| CRA-40 | 93.3 | 96.0 | 2.9 |
| CRA-60 | 110.0 | 114.0 | 3.6 |
| CRB-20 | 79.1 | 75.6 | −4.4 |
| CRB-40 | 92.0 | 87.5 | −4.9 |
| CRB-60 | 98.0 | 102.2 | 4.3 |
| CRC-20 | 71.2 | 68.7 | −3.5 |
| CRC-40 | 91.2 | 85.1 | −6.7 |
| CRC-60 | 97.5 | 96.4 | −1.1 |
| CSA-20 | 101.8 | 101.1 | −0.7 |
| CSA-30 | 116.0 | 120.6 | 4.0 |
| CSA-40 | 139.5 | 143.9 | 3.2 |
| CSB-20 | 92.0 | 90.2 | −2.0 |
| CSB-30 | 113.2 | 114.1 | 0.8 |
| CSB-40 | 137.1 | 137.7 | 0.4 |
| CSC-20 | 90.2 | 88.5 | −1.9 |
| CSC-30 | 110.0 | 108.2 | −1.6 |
| CSC-40 | 135.1 | 131.2 | −2.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Huri, M.A.; Al-Osta, M.A.; Ahmad, S. Finite Element Modelling of Corrosion-Damaged RC Beams Strengthened Using the UHPC Layers. Materials 2022, 15, 7606. https://doi.org/10.3390/ma15217606
Al-Huri MA, Al-Osta MA, Ahmad S. Finite Element Modelling of Corrosion-Damaged RC Beams Strengthened Using the UHPC Layers. Materials. 2022; 15(21):7606. https://doi.org/10.3390/ma15217606
Chicago/Turabian StyleAl-Huri, Mohammed A., Mohammed A. Al-Osta, and Shamsad Ahmad. 2022. "Finite Element Modelling of Corrosion-Damaged RC Beams Strengthened Using the UHPC Layers" Materials 15, no. 21: 7606. https://doi.org/10.3390/ma15217606
APA StyleAl-Huri, M. A., Al-Osta, M. A., & Ahmad, S. (2022). Finite Element Modelling of Corrosion-Damaged RC Beams Strengthened Using the UHPC Layers. Materials, 15(21), 7606. https://doi.org/10.3390/ma15217606





