Study on the Crack Propagation of Stiff-Thin-Film-on-Soft-Substrate Structures under Biaxial Loading
Abstract
1. Introduction
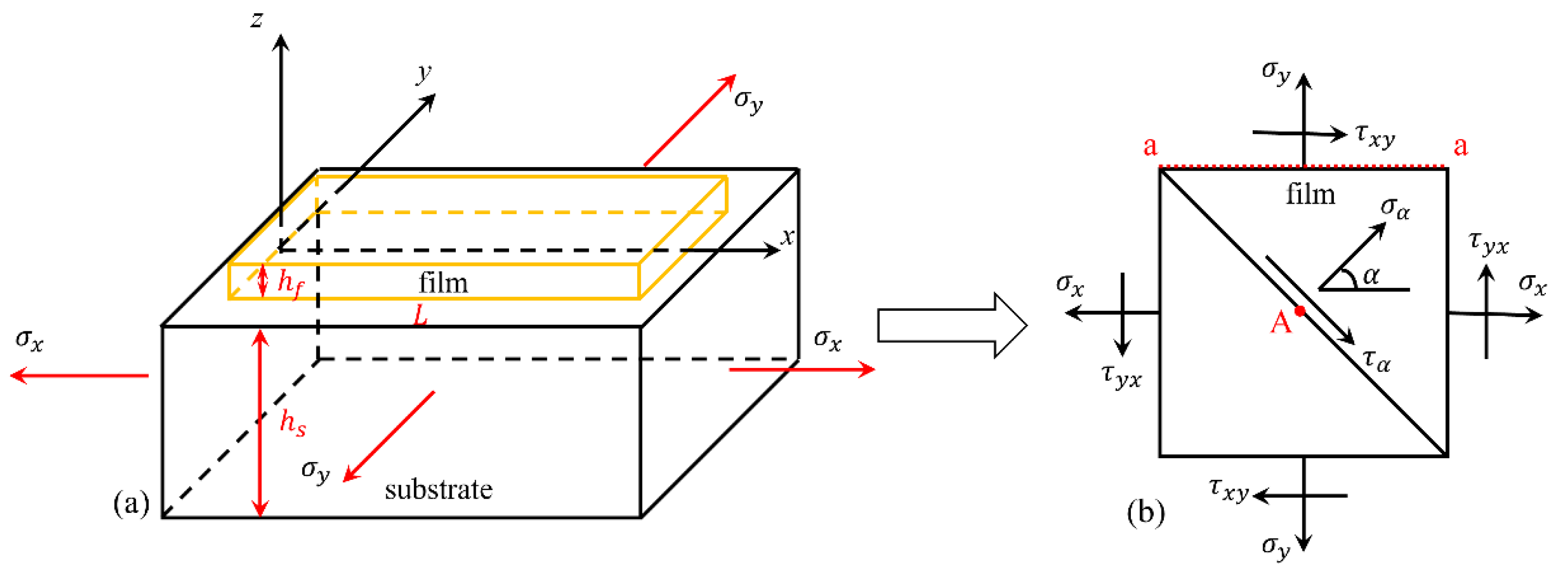
2. Theoretical Model
3. Finite Element and Experimental Verification
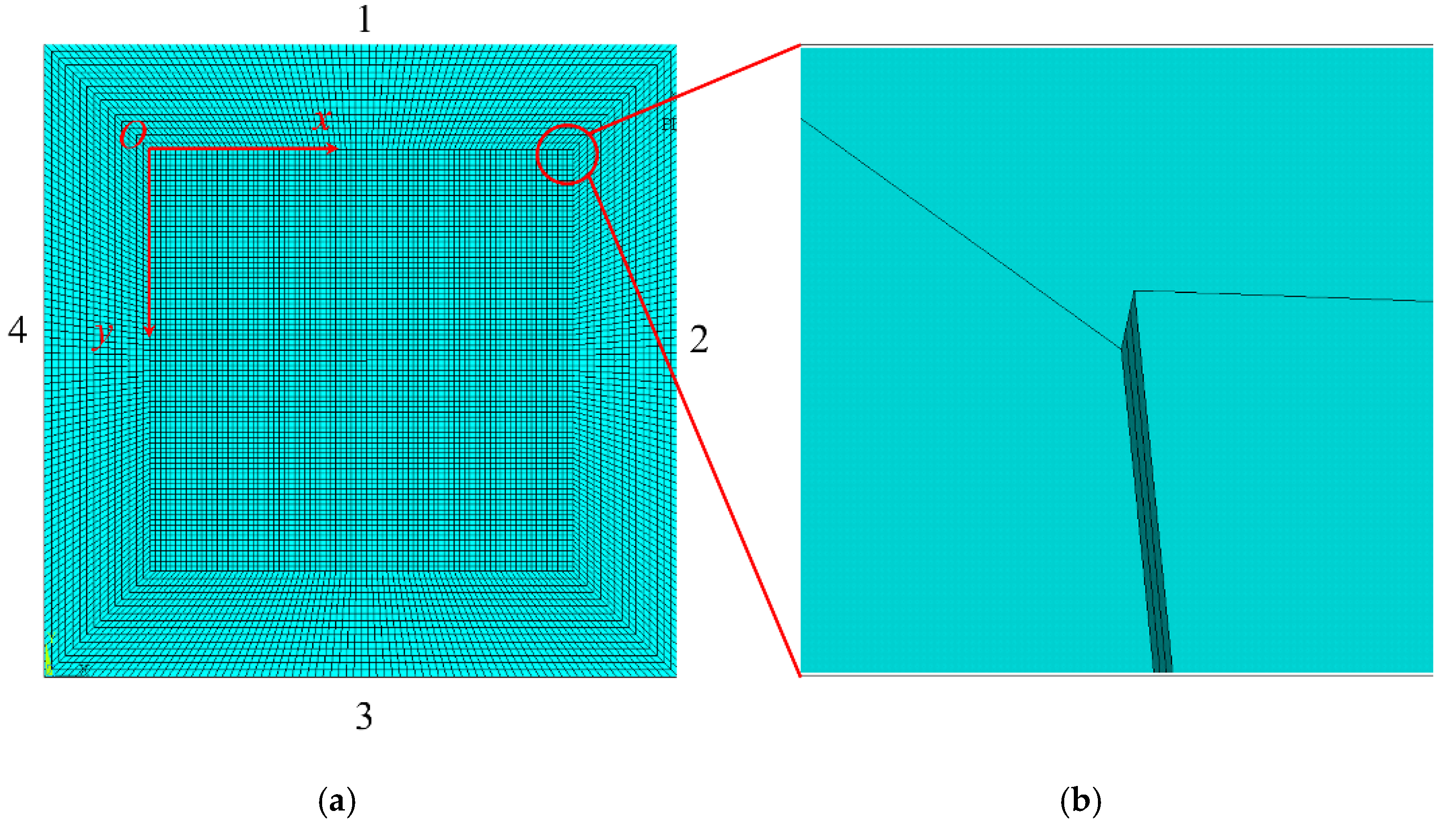
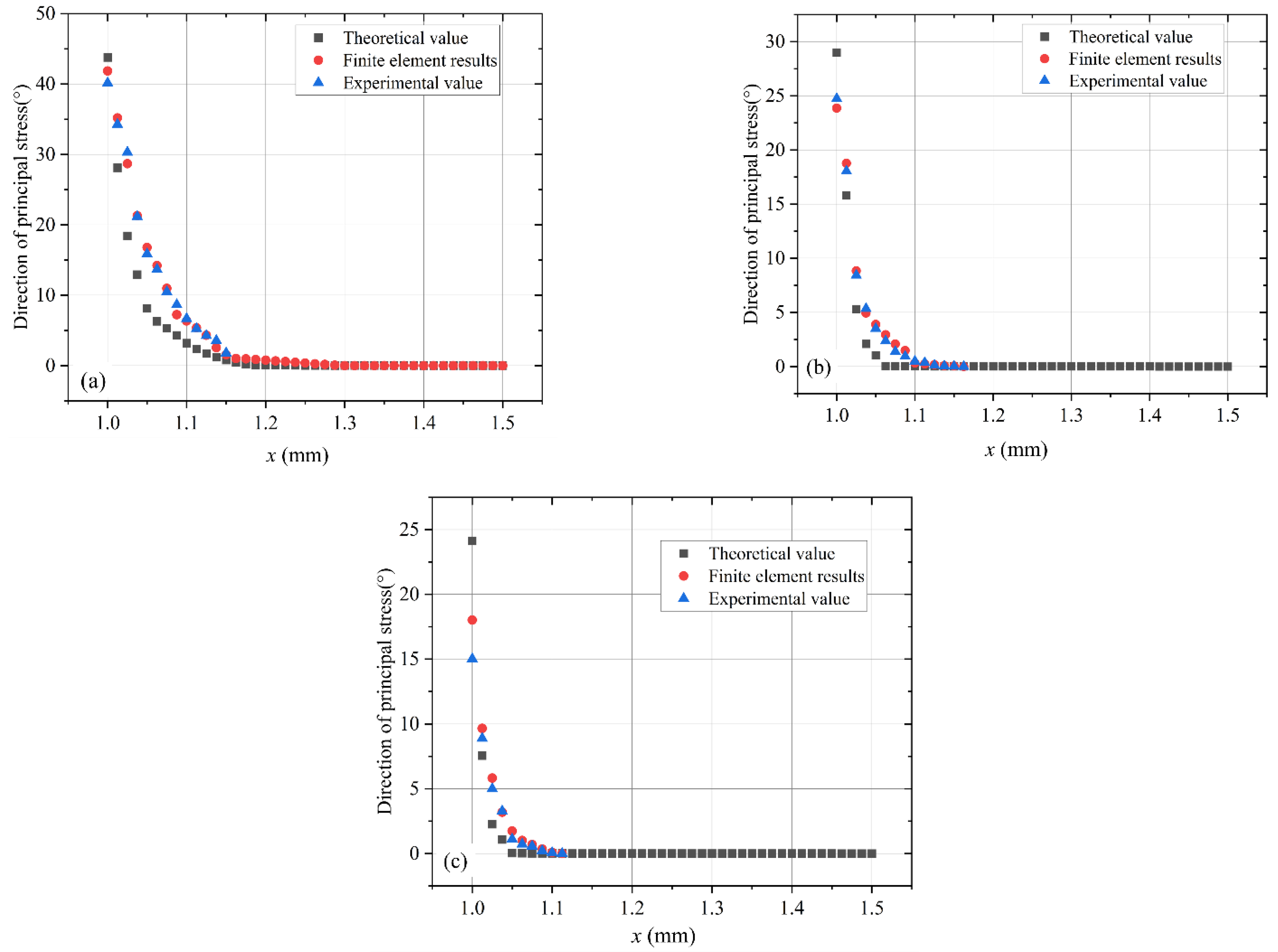
3.1. Finite Element Simulation Results
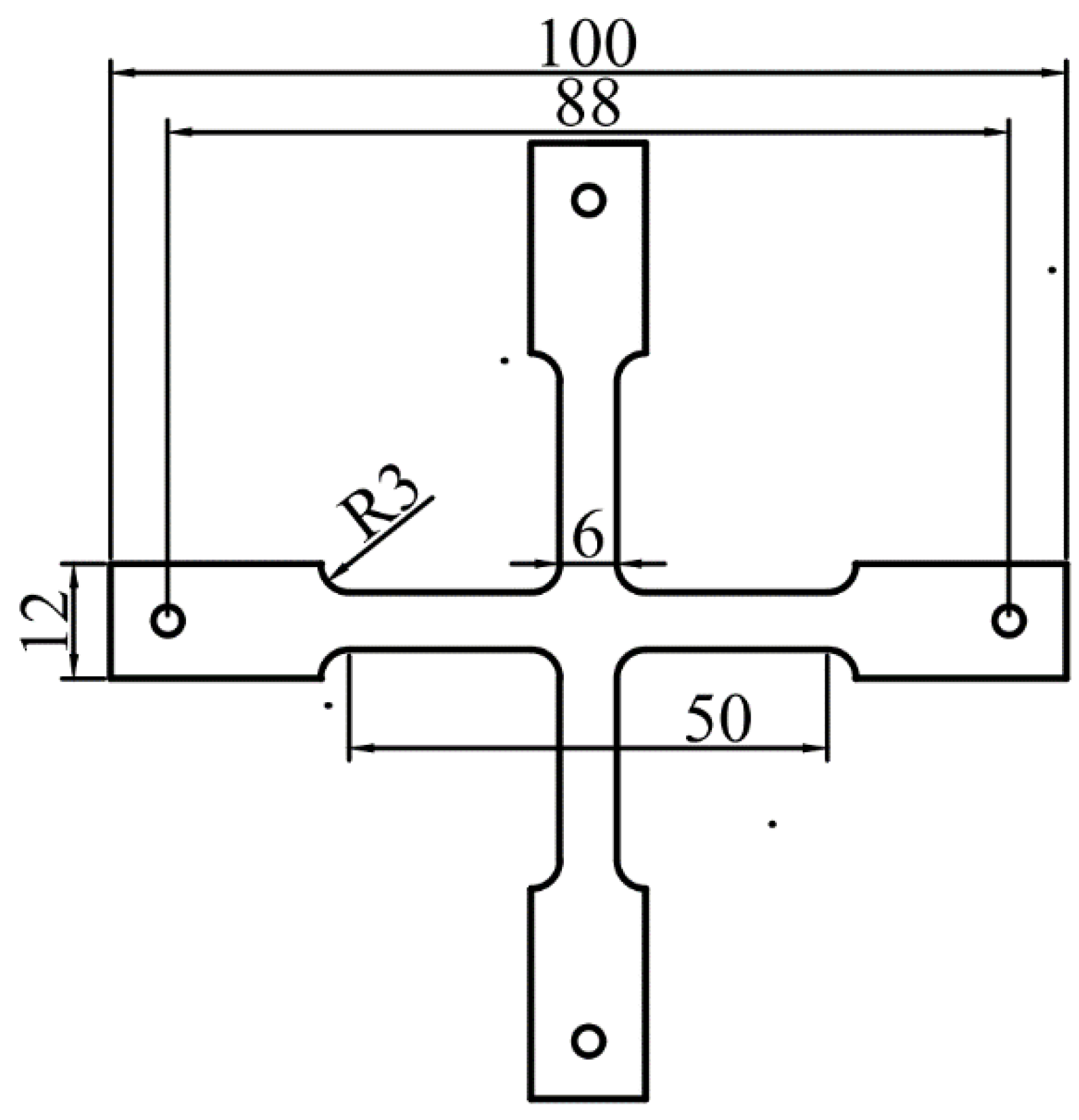
3.2. Experimental Verification
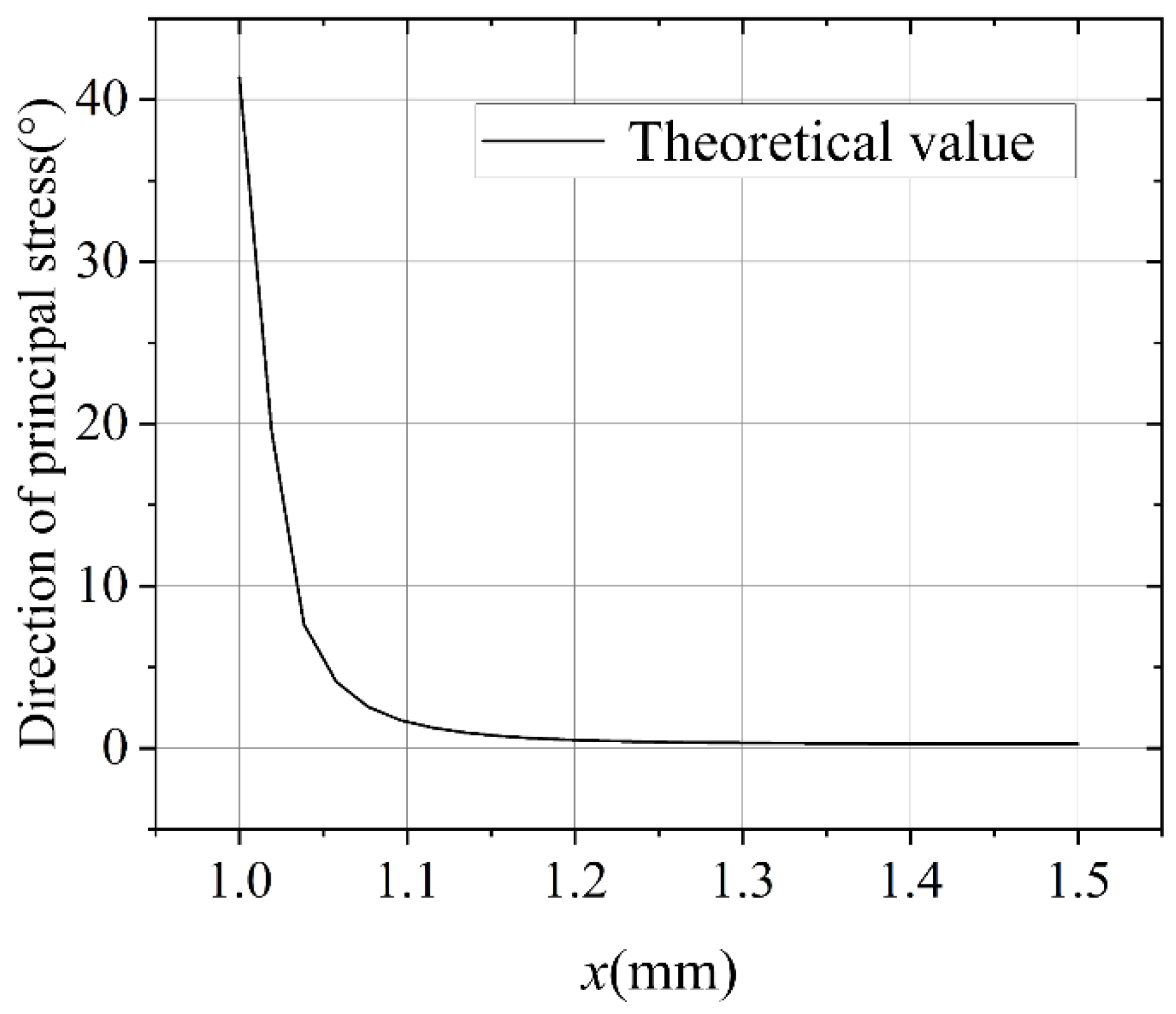
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thouless, M.D. Crack Spacing in Brittle Films on Elastic Substrates. J. Am. Ceram. Soc. 2010, 73, 2144–2146. [Google Scholar] [CrossRef]
- Mcguigan, A. An elastic-plastic shear lag model for fracture of layered coatings. Thin Solid Film. 2003, 424, 219–223. [Google Scholar] [CrossRef]
- Zhang, X.C.; Xu, B.S.; Wang, H.D.; Wu, Y.X. Analyses of interfacial stresses and normal stresses within an elongated film strip/substrate system. Thin Solid Film. 2006, 515, 2251–2256. [Google Scholar] [CrossRef]
- Yin, H.M.; Prieto-Muñoz, P.A. Stress transfer through fully bonded interface of layered materials. Mech. Mater. 2013, 62, 69–79. [Google Scholar] [CrossRef]
- Liu, Y.J.; Yin, H.M. Elastic thermal stresses in a hollow circular overlay/substrate system. Mech. Res. Commun. 2014, 55, 10–17. [Google Scholar] [CrossRef]
- Li, L.A.; Li, R.J.; Wang, S.B.; Wang, Z.Y.; Li, T.; Li, C.W. Stress analysis of film-on-substrate structure under tensile loads. Mech. Mater. 2018, 120, 1–14. [Google Scholar] [CrossRef]
- Xue, Z.; Hutchinson, J.W. Neck retardation and enhanced energy absorption in metal–elastomer bilayers. Mech. Mater. 2007, 39, 473–487. [Google Scholar] [CrossRef]
- Jia, Z.; Li, T. Necking limit of substrate-supported metal layers under biaxial in-plane loading. Int. J. Plast. 2013, 51, 65–79. [Google Scholar] [CrossRef]
- Bettaieb, M.B.; Abed-Meraim, F. Investigation of localized necking in substrate-supported metal layers: Comparison of bifurcation and imperfection analyses. Int. J. Plast. 2015, 65, 168–190. [Google Scholar] [CrossRef]
- Hu, Z.L.; Lee, K.Y.; Li, X.F. Crack in an elastic thin-film with surface effect. Int. J. Eng. Sci. 2018, 123, 158–173. [Google Scholar] [CrossRef]
- Jones, C.; Greene, R. Pulled in different directions. Mater. World 2001, 9, 19–21. [Google Scholar]
- Xiuli, X. In-situ CLSM characterization of deformation and fracture behavior of (Cu, Cr) metal thin films on flexible substrates. Surf. Topogr. Metrol. Prop. 2022, 10, 025001. [Google Scholar]
- Galliot, C.; Luchsinger, R.H. A simple model describing the non-linear biaxial tensile behaviour of PVC-coated polyester fabrics for use in finite element analysis. Compos. Struct. 2009, 90, 438–447. [Google Scholar] [CrossRef]
- Upadhyay, M.V.; Panzner, T.; Van Petegem, S.; Van Swygenhoven, H. Stresses and Strains in Cruciform Samples Deformed in Tension. Exp. Mech. 2017, 57, 905–920. [Google Scholar] [CrossRef]
- Djaziri, S.; Thiaudière, D.; Geandier, G.; Renault, P.O.; Le Bourhis, E.; Goudeau, P.; Castelnau, O.; Faurie, D. Controlled biaxial deformation of nanostructured W/Cu thin films studied by X-ray diffraction. Surf. Coat. Technol. 2010, 205, 1420–1425. [Google Scholar] [CrossRef]
- Djaziri, S.; Faurie, D.; Le Bourhis, E.; Goudeau, P.; Renault, P.O.; Mocuta, C.; Thiaudière, D.; Hild, F. Deformation modes of nanostructured thin film under controlled biaxial deformation. Thin Solid Film. 2013, 530, 30–34. [Google Scholar] [CrossRef]
- Van Do, T.; Hong Doan, D.; Chi Tho, N.; Dinh Duc, N. Thermal Buckling Analysis of Cracked Functionally Graded Plates. Int. J. Struct. Stab. Dyn. 2022, 22, 2250089. [Google Scholar] [CrossRef]
- Cong, P.H.; Thom, D.V.; Duc, D.H. Phase field model for fracture based on modified couple stress. Eng. Fract. Mech. 2022, 269, 108534. [Google Scholar] [CrossRef]
- Doan, D.H.; Van Do, T.; Nguyen, N.X.; Van Vinh, P.; Trung, N.T. Multi-phase-field modelling of the elastic and buckling behaviour of laminates with ply cracks. Appl. Math. Model. 2021, 94, 68–86. [Google Scholar] [CrossRef]
- Kim, B.C.; Matsuoka, T.; Moraes, C.; Huang, J.; Thouless, M.D.; Takayama, S. Guided fracture of films on soft substrates to create micro/nano-feature arrays with controlled periodicity. Sci. Rep. 2013, 3, 3027. [Google Scholar] [CrossRef]
- Huang, J.; Kim, B.C.; Takayama, S.; Thouless, M.D. The control of crack arrays in thin films. J. Mater. Sci. 2014, 49, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Amjadi, M.; Turan, M.; Clementson, C.P.; Sitti, M. Parallel Microcracks-based Ultrasensitive and Highly Stretchable Strain Sensors. Acs Appl. Mater. Interfaces 2016, 8, 5618. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.W.; Kang, D.; Pikhitsa, P.V.; Lee, T.; Kim, S.M.; Lee, G.; Tahk, D.; Choi, M. Ultra-sensitive Pressure sensor based on guided straight mechanical cracks. Sci. Rep. 2017, 7, 40116. [Google Scholar] [CrossRef]
- Hearn, E.J. Mechanics of Materials 2, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Liu, M.; Yu, S.; He, L.; Ni, Y. Recent progress on crack pattern formation in thin films. Soft Matter 2022, 18, 5906–5927. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, J.; Lee, S.; Wooh, S.; Yoon, H.; Char, K. Cracking of Colloidal Films to Generate Rectangular Fragments. Langmuir ACS J. Surf. Colloids 2022, 38, 4935–4941. [Google Scholar] [CrossRef] [PubMed]
- Elsayed, I.A.; Afify, A.S. Controlling the Surface Morphology of ZnO Nano-Thin Film Using the Spin Coating Technique. Materials 2022, 15, 6178. [Google Scholar] [CrossRef] [PubMed]





| Category | Item Type | Young’s Modulus | Poisson’s Ratio | Thickness |
|---|---|---|---|---|
| Film | Chromium | 290 GPa | 0.12 | 100 nm |
| Substrate | Polyimide | 2.5 GPa | 0.33 | 125 μm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, L.; Li, C.; Wang, Z.; Wang, S.; Xue, X. Study on the Crack Propagation of Stiff-Thin-Film-on-Soft-Substrate Structures under Biaxial Loading. Materials 2022, 15, 7421. https://doi.org/10.3390/ma15217421
Li J, Li L, Li C, Wang Z, Wang S, Xue X. Study on the Crack Propagation of Stiff-Thin-Film-on-Soft-Substrate Structures under Biaxial Loading. Materials. 2022; 15(21):7421. https://doi.org/10.3390/ma15217421
Chicago/Turabian StyleLi, Jun, Linan Li, Chuanwei Li, Zhiyong Wang, Shibin Wang, and Xiuli Xue. 2022. "Study on the Crack Propagation of Stiff-Thin-Film-on-Soft-Substrate Structures under Biaxial Loading" Materials 15, no. 21: 7421. https://doi.org/10.3390/ma15217421
APA StyleLi, J., Li, L., Li, C., Wang, Z., Wang, S., & Xue, X. (2022). Study on the Crack Propagation of Stiff-Thin-Film-on-Soft-Substrate Structures under Biaxial Loading. Materials, 15(21), 7421. https://doi.org/10.3390/ma15217421





