Prediction of Resistance Spot Welding Quality Based on BPNN Optimized by Improved Sparrow Search Algorithm
Abstract
:1. Introduction
- (1)
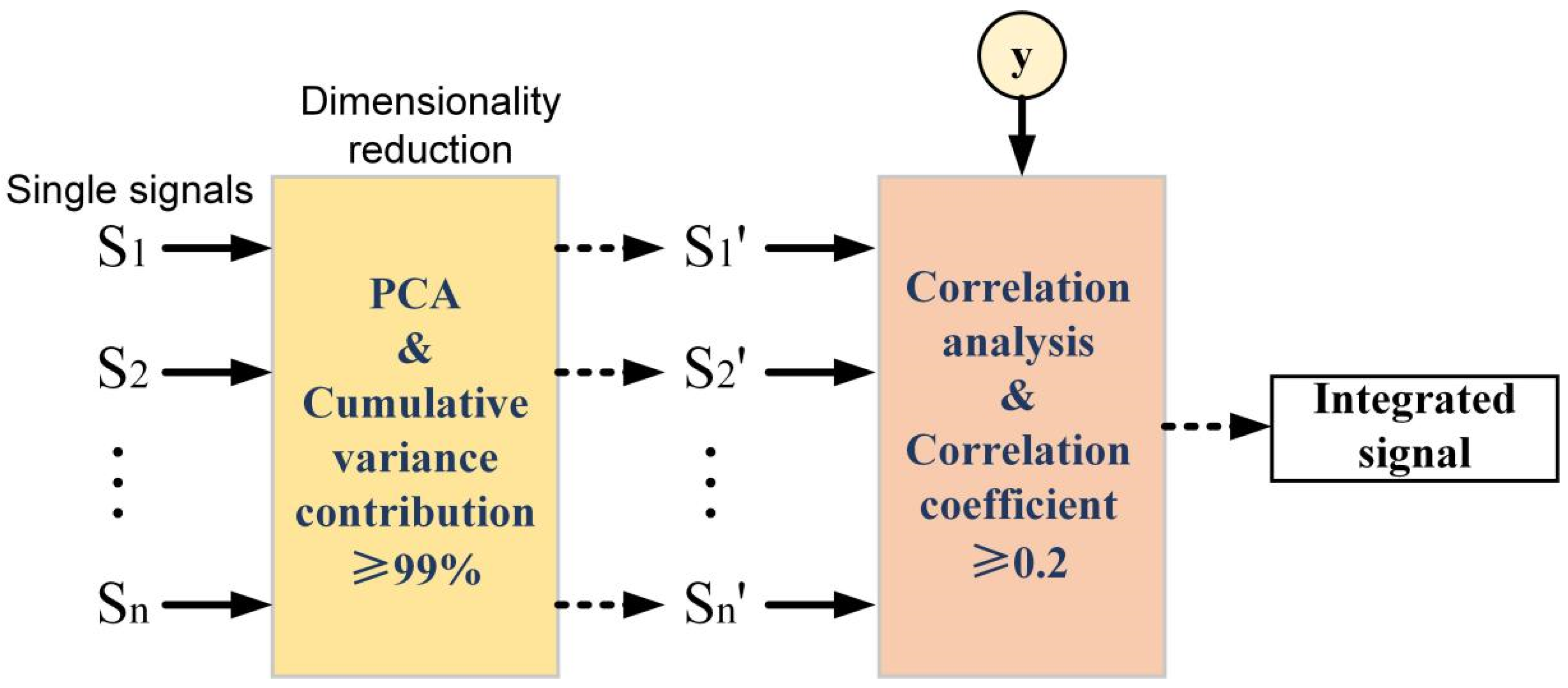
- This paper proposes a method of multi-signal fusion to obtain the integrated signal. First, the correlation analysis is carried out on the data of multiple RSW process signals after principal component analysis (PCA) dimension reduction. The data related to the button diameter are extracted and combined to realize multi-signal fusion. Further, the integrated signal is used to build the RSW prediction model, which contributes a lot to efficient quality monitoring.
- (2)
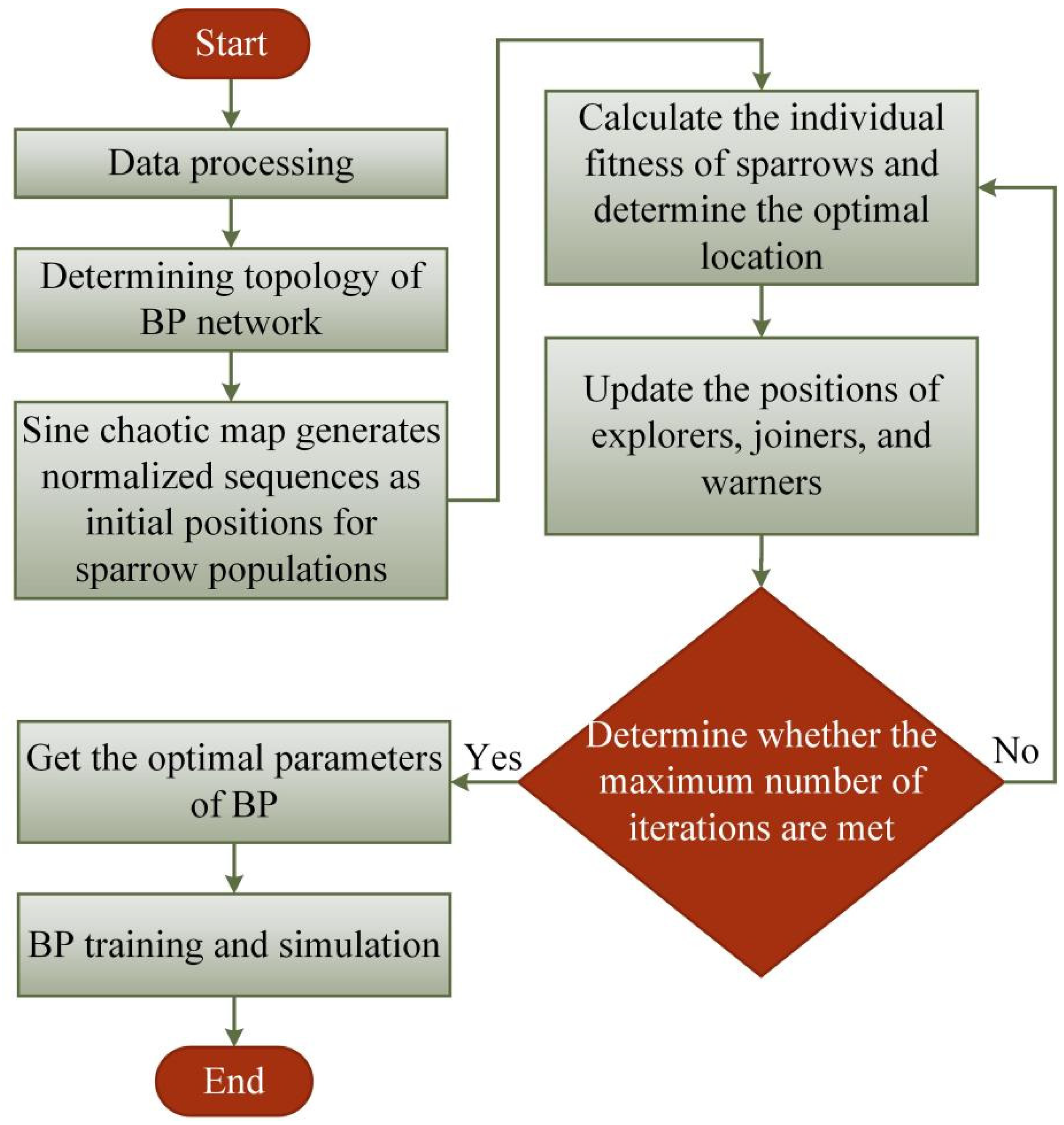
- For the first time, the emerging intelligent algorithm SSA is adopted to optimize a BPNN for the prediction of the RSW quality. Based on model output, Sine-SSA is used to optimize the weights and thresholds of the BPNN and to construct a Sine-SSA-BP prediction model to predict the button diameter.
2. Experimental
3. Results and Discussion
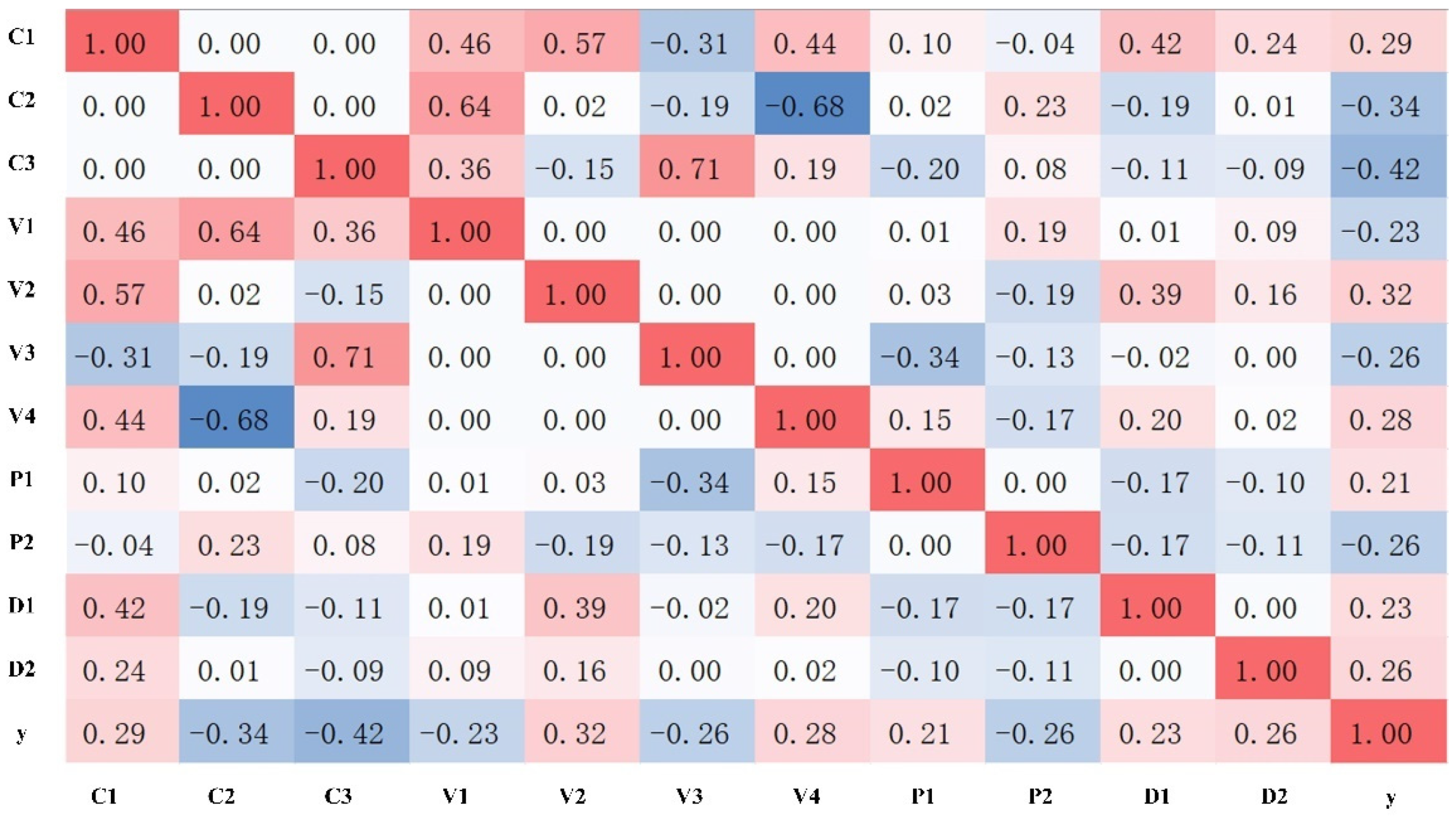
3.1. Signal Analysis
3.2. Multi-Signal Fusion
3.3. Sine-SSA-BP Approach
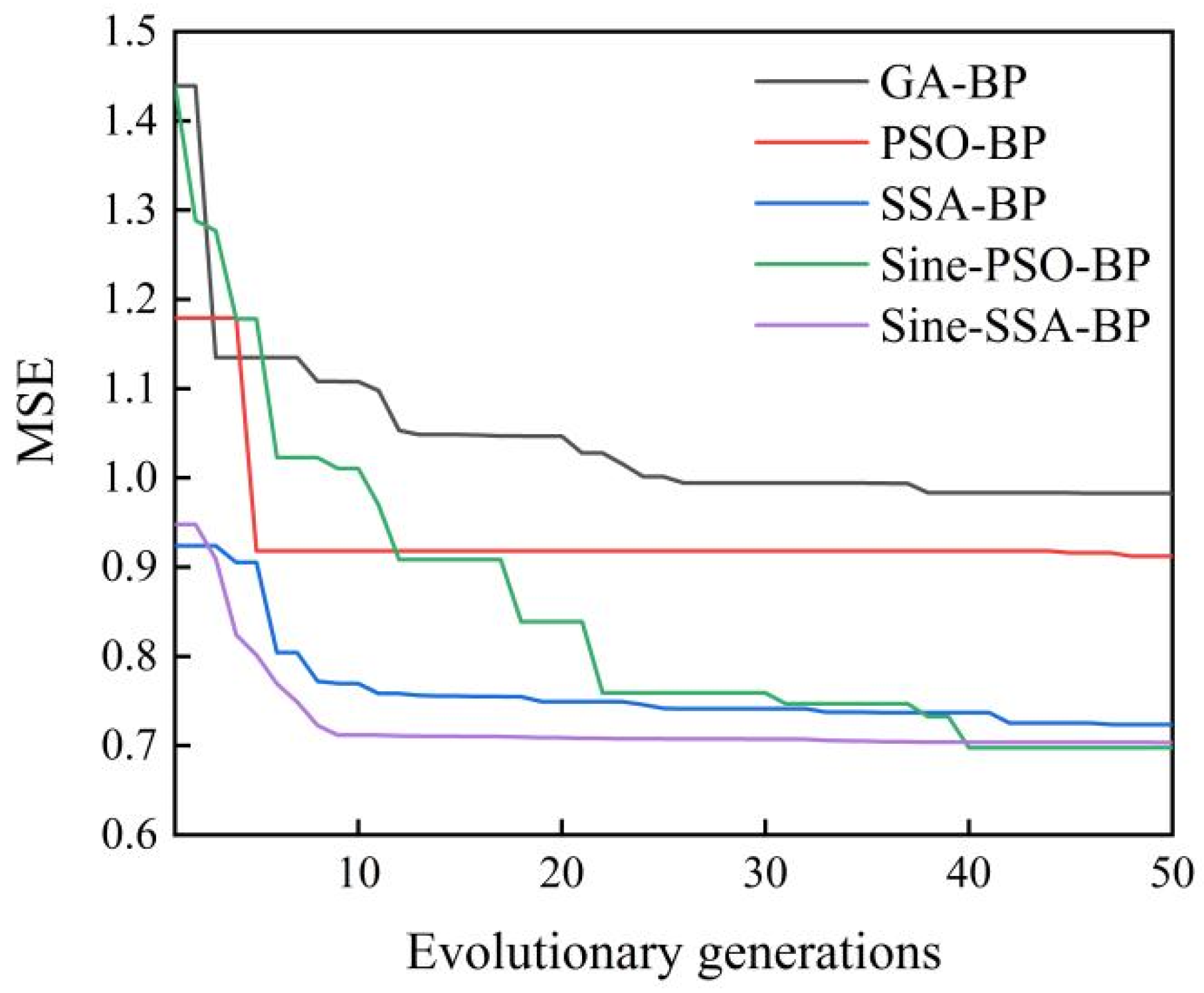
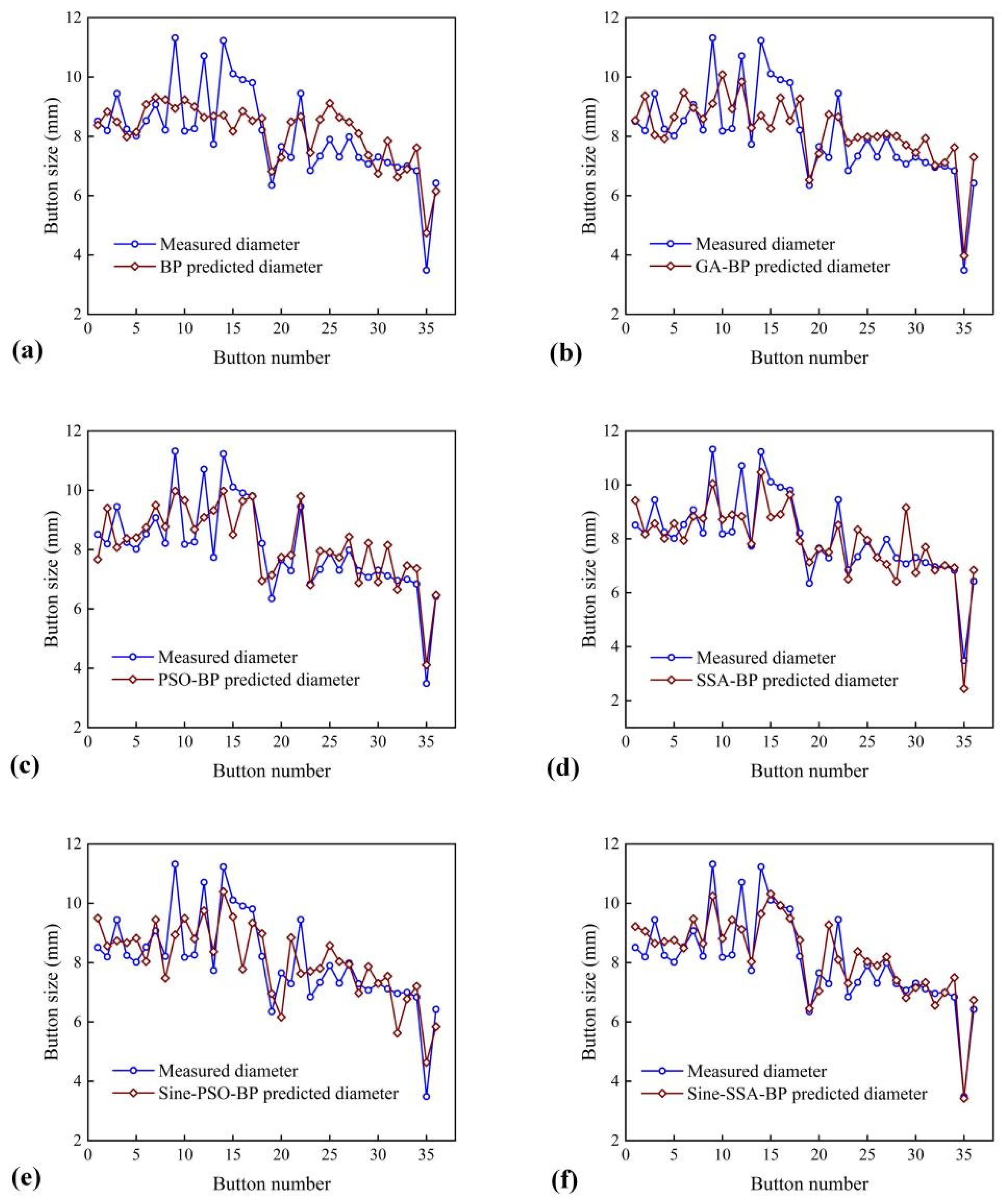
3.4. Comparative Analysis
4. Conclusions
- Under the experimental conditions of this study, compared with a single signal, the integrated signal after multi-signal fusion can more accurately predict the button quality of RSW. Combined with the Sine-SSA-BP model, the best prediction effect is obtained. Moreover, abnormal spot welds are successfully predicted, which is critical for welding quality control.
- The introduction of the sine map can improve the ability of finding the global optimal value of the SSA. The problem of the local optimal solution is avoided. Sine SSA makes it easier and faster to converge to the global optimal MSE value.
- Sine-SSA is used to optimize the weights and thresholds of a BP neural network, thus predicting the quality of spot welds. The prediction results show that compared with the other models, the Sine-SSA-BP model has better prediction accuracy and is more suitable for the prediction of RSW quality.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| RSW | Resistance Spot Welding |
| ANN | Artificial Neural Network |
| BPNN | Backpropagation Neural Network |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| SSA | Sparrow Search Algorithm |
| PCA | Principal Component Analysis |
| MFDC | Medium-Frequency Direct Current |
| RMS | Root Mean Square |
| MAE | Mean Absolute Error |
| MSE | Mean Square Error |
| RMSE | Root-Mean-Square Error |
| R2 | R-square |
References
- Luo, Y.; Li, J.; Wu, W. Nugget quality prediction of resistance spot welding on aluminium alloy based on structure borne acoustic emission signals. Sci. Technol. Weld. Join. 2013, 18, 301–306. [Google Scholar] [CrossRef]
- Shen, Y.; Xia, Y.; Li, H.; Zhou, L.; Li, Y.; Pan, H. A Novel Expulsion Control Strategy With Abnormal Condition Adaptability for Resistance Spot Welding. J. Manuf. Sci. Eng. 2021, 143, 111009–111021. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Chen, G.; Zhang, X. Monitoring and intelligent control of electrode wear based on a measured electrode displacement curve in resistance spot welding. Meas. Sci. Technol. 2007, 18, 867–876. [Google Scholar] [CrossRef]
- Baskoro, A.S.; Amat, M.A.; Arifardi, M.F. Investigation Effect of ECR’s Thickness and Initial Value of Resistance Spot Welding Simulation using 2-Dimensional Thermo-Electric Coupled. Jt. J. Nov. Carbon Resour. Sci. Green Asia Strategy 2021, 8, 821–828. [Google Scholar] [CrossRef]
- Arinez, J.F.; Chang, Q.; Gao, R.X. Artificial Intelligence in Advanced Manufacturing: Current Status and Future Outlook. J. Manuf. Sci. Eng. 2020, 142, 110804–110820. [Google Scholar] [CrossRef]
- Chang, Y.; Yue, J.; Guo, R.; Liu, W.; Li, L. Penetration Quality Prediction of Asymmetrical Fillet Root Welding Based on Optimized BP Neural Network. J. Manuf. Process. 2020, 50, 247–254. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Y.; Liang, D. Performances of regression model and artificial neural network in monitoring welding quality based on power signal. J. Mater. Res. Technol. 2020, 9, 1231–1240. [Google Scholar] [CrossRef]
- Wan, X.; Wang, Y.; Zhao, D. Quality evaluation in small-scale resistance spot welding by electrode voltage recognition. Sci. Technol. Weld. Join. 2016, 21, 358–365. [Google Scholar] [CrossRef]
- Wan, X.; Wang, Y.; Zhao, D.; Huang, Y.; Yin, Z. Weld quality monitoring research in small scale resistance spot welding by dynamic resistance and neural network. Measurement 2017, 99, 120–127. [Google Scholar] [CrossRef]
- Chen, G.; Sheng, B.; Luo, R. A parallel strategy for predicting the quality of welded joints in automotive bodies based on machine learning. J. Manuf. Syst. 2022, 62, 636–649. [Google Scholar] [CrossRef]
- Panza, L.; Maddis, M.D.; Spena, P.R. Use of electrode displacement signals for electrode degradation assessment in resistance spot welding. J. Manuf. Process. 2022, 76, 93–105. [Google Scholar] [CrossRef]
- Pouraliakbar, H.; Khalaj, G.; Jandaghi, M.R. Study on the correlation of toughness with chemical composition and tensile test results in microalloyed API pipeline steels. J. Min. Metall. B Metall. 2015, 51, 173–178. [Google Scholar] [CrossRef]
- Pashazadeh, H.; Gheisari, Y.; Hamedi, M. Statistical modeling and optimization of resistance spot welding process parameters using neural networks and multi-objective genetic algorithm. J. Intell. Manuf. 2016, 27, 549–559. [Google Scholar] [CrossRef]
- Hamidinejad, S.M.; Kolahan, F.; Kokabi, A.H. The modeling and process analysis of resistance spot welding on galvanized steel sheets used in car body manufacturing. J. Mater. Des. 2012, 34, 759–767. [Google Scholar] [CrossRef]
- Shojaeefard, M.H.; Behnagh, R.A.; Akbari, M. Modelling and Pareto optimization of mechanical properties of friction stir welded AA7075/AA5083 butt joints using neural network and particle swarm algorithm. Mater. Design 2013, 44, 190–198. [Google Scholar] [CrossRef]
- Katherasan, D.; Elias, J.V.; Sathiya, P. Simulation and parameter optimization of flux cored arc welding using artificial neural network and particle swarm optimization algorithm. J. Intell. Manuf. 2014, 25, 67–76. [Google Scholar] [CrossRef]
- Khoshaim, A.B.; Moustafa, E.B.; Bafakeeh, O.; Elsheikh, A. An Optimized Multilayer Perceptrons Model Using Grey Wolf Optimizer to Predict Mechanical and Microstructural Properties of Friction Stir Processed Aluminum Alloy Reinforced by Nanoparticles. Coatings 2021, 11, 1476. [Google Scholar] [CrossRef]
- Abushanab, W.S.; Elaziz, M.A.; Ghandourah, E.; Moustafa, E.B.; Elsheikh, A. A new fine-tuned random vector functional link model using Hunger games search optimizer for modeling friction stir welding process of polymeric materials. J. Mater. Res. Technol. 2021, 14, 1482–1493. [Google Scholar] [CrossRef]
- Moustafa, E.B.; Hammad, A.; Elsheikh, A. A new optimized artificial neural network model to predict thermal efficiency and water yield of tubular solar still. Case Stud. Therm. Eng. 2022, 30, 101750. [Google Scholar] [CrossRef]
- Khoshaim, A.B.; Elsheikh, A.; Moustafa, E.B.; Basha, M.; Mosleh, A.O. Prediction of residual stresses in turning of pure iron using artificial intelligence-based methods. J. Mater. Res. Technol. 2021, 11, 2181–2194. [Google Scholar] [CrossRef]
- Elsheikh, A.; Elaziz, M.A.; Ramesh, B.; Egiza, M.; Al-qaness, M.A. Modeling of drilling process of GFRP composite using a hybrid random vector functional link network/parasitism-predation algorithm. J. Mater. Res. Technol. 2021, 14, 298–311. [Google Scholar] [CrossRef]
- Elsheikh, A.; Elaziz, M.A.; Das, S.R.; Muthuramalingam, T.; Lu, S. A new optimized predictive model based on political optimizer for eco-friendly MQL-turning of AISI 4340 alloy with nano-lubricants. J. Manuf. Process. 2021, 67, 562–578. [Google Scholar] [CrossRef]
- Elsheikh, A.; Elaziz, M.A.; Vendan, A. Modeling ultrasonic welding of polymers using an optimized artificial intelligence model using a gradient-based optimizer. Weld. World 2022, 66, 27–44. [Google Scholar] [CrossRef]
- Elsheikh, A.; Muthuramalingam, T.; Shanmugan, S.; Ibrahim, A.; Ramesh, B.; Khoshaim, A.B.; Moustafa, E.B.; Bedairi, B.; Panchal, H.; Sathyamurthy, R. Fine-tuned artificial intelligence model using pigeon optimizer for prediction of residual stresses during turning of Inconel 718. J. Mater. Res. Technol. 2021, 15, 3622–3634. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2021, 8, 22–34. [Google Scholar] [CrossRef]
- Liu, Y. Study on prediction model of coal gangue subgrade settlement based on SSA-SVR. J. Hebei Univ. Geosci. 2021, 44, 99–104. [Google Scholar] [CrossRef]
- Liu, D.; Wei, X.; Wang, W. Short-term wind power prediction based on SSA-ELM. Smart Power 2021, 49, 53–59. [Google Scholar] [CrossRef]
- Hu, J.; Liu, H.; Bi, J.; Li, Y.; Ao, S.; Luo, Z. Quality prediction of aluminum alloy resistance spot welding with shunting by introducing spacing factor. Weld. Int. 2022. [Google Scholar] [CrossRef]
- Yi, S.; Lai, Z.; He, Z. Joint sparse principal component analysis. Pattern Recognit. 2017, 61, 524–536. [Google Scholar] [CrossRef]
- Lyu, X.; Mu, X.; Zhang, J. Chaos sparrow search optimization algorithm. J. Beijing Univ. Aeronaut Astronaut 2021, 47, 1712–1720. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, J.; Zhu, X. A novel chaos optimization algorithm Multimed. Tools Appl. 2017, 76, 17405–17436. [Google Scholar] [CrossRef]






| Materials | Si | Fe | Cu | Mg | V | Mn | Zr | Zn | Ti | Ag | Li | Al |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2219 | 0.06 | 0.17 | 6.3 | 0.02 | 0.1 | 0.31 | 0.15 | 0.02 | 0.07 | - | - | Bal. |
| 5A06 | 0.06 | 0.13 | 0.03 | 6.4 | - | 0.6 | - | 0.02 | 0.05 | - | - | Bal. |
| Materials | Tensile Strength (MPa) | Yield Strength (MPa) | Elongation (%) |
|---|---|---|---|
| 2219 | 455 | 366 | 13.5 |
| 5A06 | 356 | 187 | 20.5 |
| Assembly Condition | Gap (mm) | Spacing (mm) | Number of Replica |
|---|---|---|---|
| 1 | 0.1 | 50 | 15 |
| 2 | 0.2 | 50 | 15 |
| 3 | 0.3 | 50 | 15 |
| 4 | 0.4 | 50 | 15 |
| 5 | 0.5 | 50 | 15 |
| 6 | 0.6 | 50 | 15 |
| 7 | 0.8 | 50 | 15 |
| 8 | 1.0 | 50 | 15 |
| 9 | 1.5 | 50 | 15 |
| 10 | 0 | 10 | 15 |
| 11 | 0 | 15 | 15 |
| 12 | 0 | 20 | 15 |
| 13 | 0 | 25 | 15 |
| 14 | 0 | 30 | 15 |
| 15 | 0 | 35 | 15 |
| 16 | 0 | 40 | 15 |
| 17 | 0 | 45 | 15 |
| 18 | 0 | 50 | 15 |
| Total | 270 | ||
| Signals | Predictive Models | Evaluation Indicators | |||
|---|---|---|---|---|---|
| MAE | MSE | RMSE | R2 | ||
| Integrated signal | BP | 0.9805 | 1.6618 | 1.272 | 0.2464 |
| Sine-SSA-BP | 0.6889 | 0.7763 | 0.8719 | 0.6482 | |
| Current | BP | 0.9805 | 1.6455 | 1.2702 | 0.2791 |
| Sine-SSA-BP | 0.7404 | 0.9708 | 0.9788 | 0.5634 | |
| Voltage | BP | 1.0436 | 1.7738 | 1.3097 | 0.2436 |
| Sine-SSA-BP | 0.789 | 1.0404 | 1.009 | 0.5532 | |
| RMS Power | BP | 1.4859 | 3.5598 | 1.8669 | −0.5524 |
| Sine-SSA-BP | 1.05 | 1.7958 | 1.3246 | 0.2373 | |
| Displacement | BP | 0.9375 | 1.7942 | 1.3257 | 0.1957 |
| Sine-SSA-BP | 0.6814 | 0.788 | 0.8826 | 0.6324 | |
| Prediction Models | Evaluation Indicators | |||
|---|---|---|---|---|
| MAE | MSE | RMSE | R2 | |
| BP | 0.9805 | 1.6618 | 1.272 | 0.2464 |
| GA-BP | 0.8336 | 1.172 | 1.077 | 0.4762 |
| PSO-BP | 0.8011 | 1.0517 | 1.0194 | 0.5402 |
| SSA-BP | 0.6869 | 0.8099 | 0.8908 | 0.6458 |
| Sine-PSO-BP | 0.7754 | 1.0237 | 0.991 | 0.5728 |
| Sine-SSA-BP | 0.6889 | 0.7763 | 0.8719 | 0.6482 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Bi, J.; Liu, H.; Li, Y.; Ao, S.; Luo, Z. Prediction of Resistance Spot Welding Quality Based on BPNN Optimized by Improved Sparrow Search Algorithm. Materials 2022, 15, 7323. https://doi.org/10.3390/ma15207323
Hu J, Bi J, Liu H, Li Y, Ao S, Luo Z. Prediction of Resistance Spot Welding Quality Based on BPNN Optimized by Improved Sparrow Search Algorithm. Materials. 2022; 15(20):7323. https://doi.org/10.3390/ma15207323
Chicago/Turabian StyleHu, Jianming, Jing Bi, Hanwei Liu, Yang Li, Sansan Ao, and Zhen Luo. 2022. "Prediction of Resistance Spot Welding Quality Based on BPNN Optimized by Improved Sparrow Search Algorithm" Materials 15, no. 20: 7323. https://doi.org/10.3390/ma15207323
APA StyleHu, J., Bi, J., Liu, H., Li, Y., Ao, S., & Luo, Z. (2022). Prediction of Resistance Spot Welding Quality Based on BPNN Optimized by Improved Sparrow Search Algorithm. Materials, 15(20), 7323. https://doi.org/10.3390/ma15207323









