A Theoretical Investigation into the Homo- and Hetero-leptic Cu(I) Phosphorescent Complexes Bearing 2,9-dimethyl-1,10-phenanthroline and bis [2-(diphenylphosphino)phenyl]ether Ligand
Abstract
1. Introduction
2. Computation Methods
3. Results and Discussion
3.1. Geometric and Electronic Structures
3.2. Natural Population Analysis
3.3. Ionization Energy (IP) and Electron Affinity (EA) and Reorganization Energy
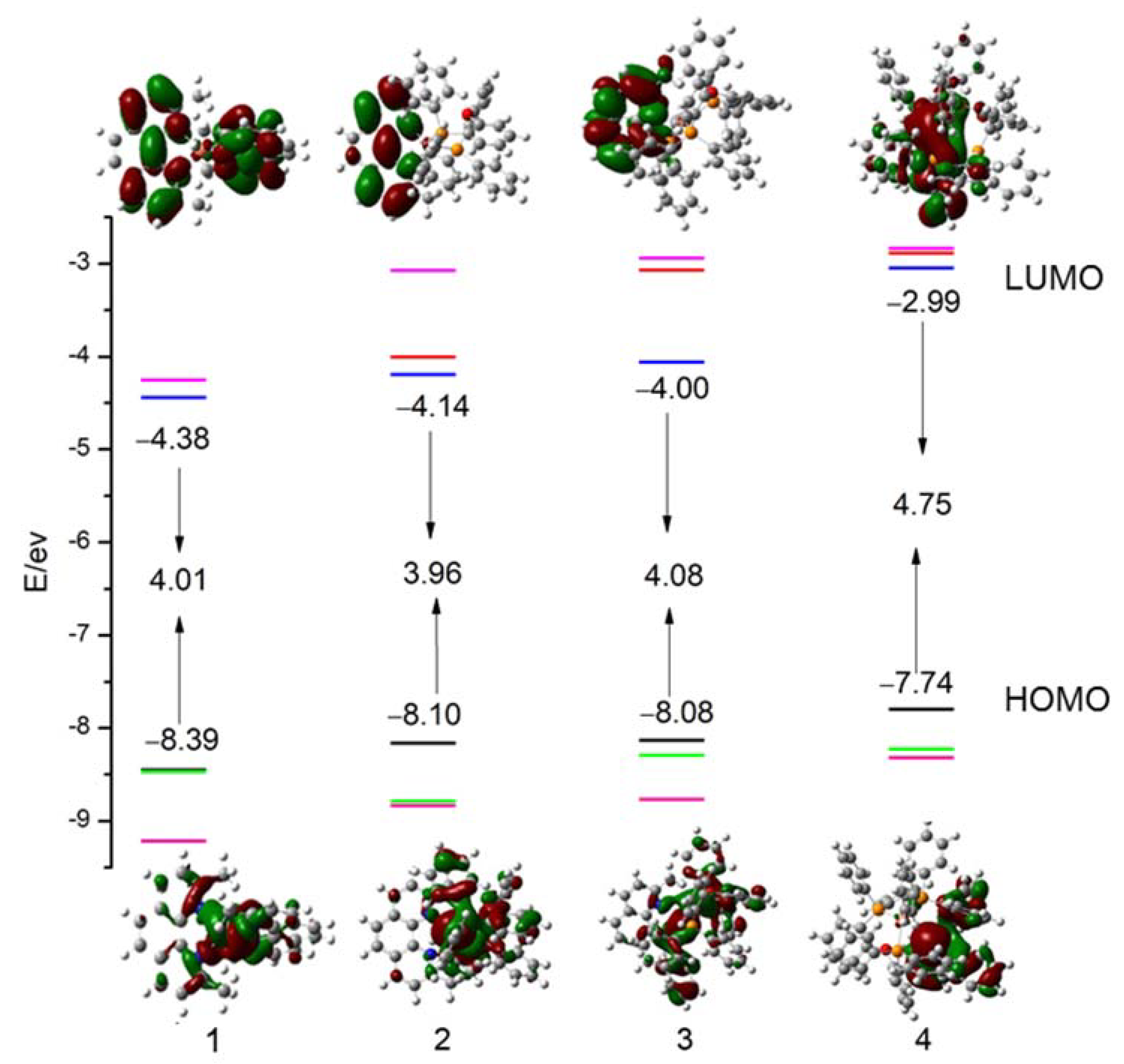
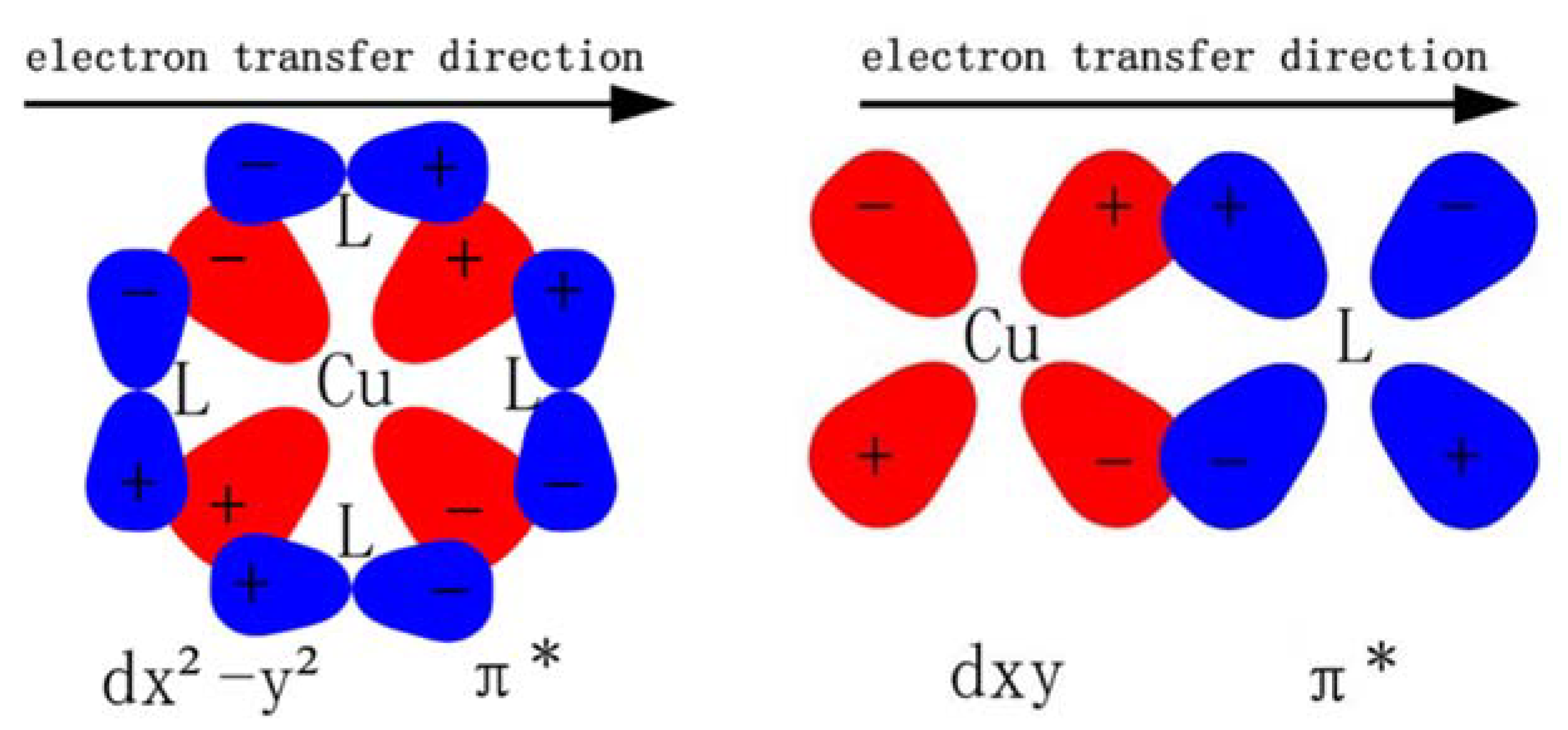
3.4. Frontier Molecular Orbitals
3.5. Absorption and Emission Spectra in PCM Solvent
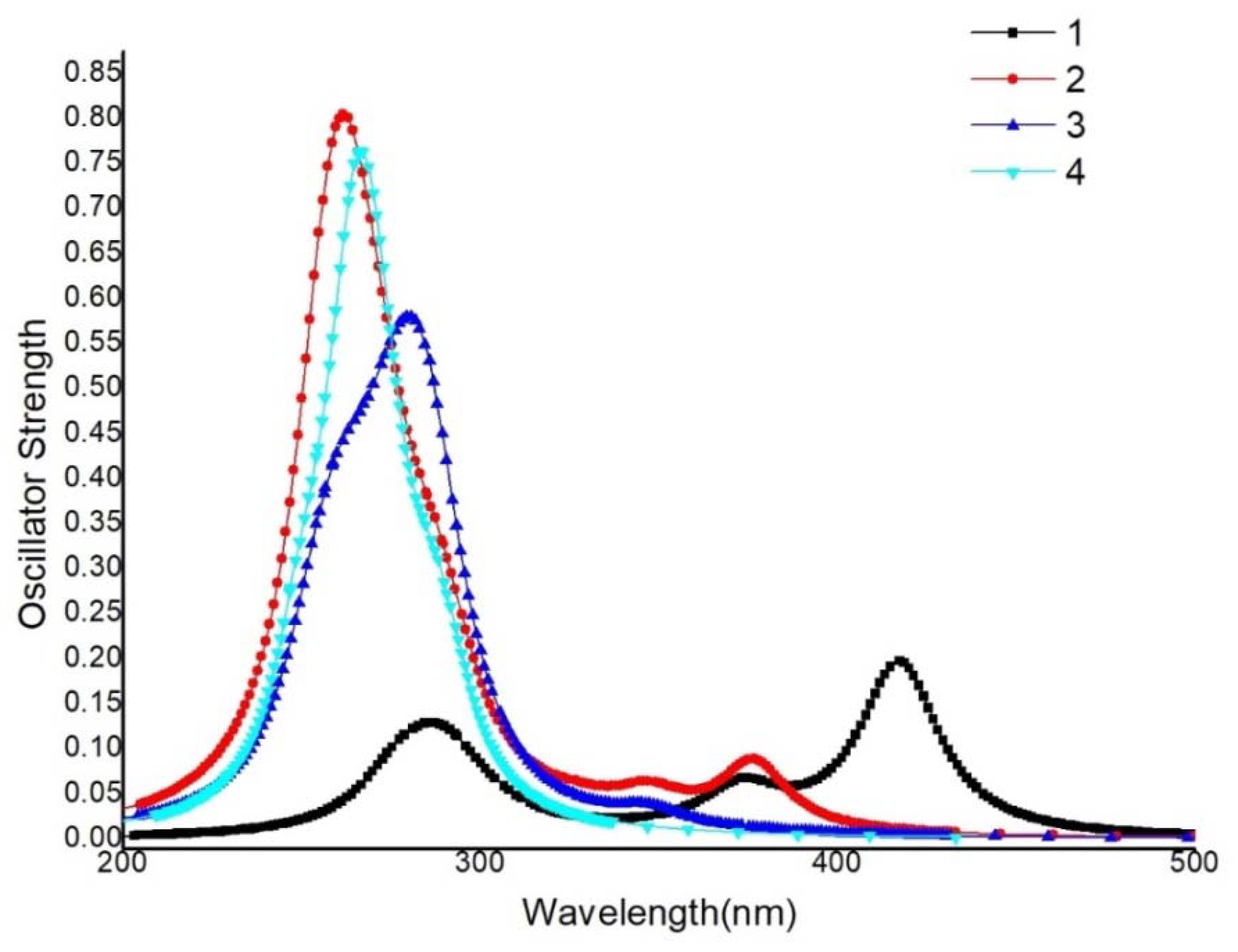
3.5.1. Absorption Spectra
3.5.2. Phosphorescent Spectrum
3.6. The Quantum Yields ()
3.6.1. Radiative Decay
3.6.2. Non-Radiative Decay
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chi, Y.; Chou, P.T. Transition-metal phosphors with cyclometalating ligands: Fundamentals and applications. Chem. Soc. Rev. 2010, 39, 638–655. [Google Scholar] [CrossRef]
- Arena, G.; Calogero, G.; Campagna, S.; Monsù Scolaro, L.; Ricevuto, V.; Romeo, R. Synthesis, Characterization, Absorption Spectra, and Luminescence Properties of Organometallic Platinum(II) Terpyridine Complexes. Inorg. Chem. 1998, 37, 2763–2769. [Google Scholar] [CrossRef] [PubMed]
- Tung, Y.-L.; Wu, P.-C.; Liu, C.-S.; Chi, Y.; Yu, J.-K.; Hu, Y.-H.; Chou, P.-T.; Peng, S.-M.; Lee, G.-H.; Tao, Y.; et al. Highly Efficient Red Phosphorescent Osmium(II) Complexes for OLED Applications. Organometallics 2004, 23, 3745–3748. [Google Scholar] [CrossRef]
- Osawa, M.; Hoshino, M.; Akita, M.; Wada, T. Synthesis and Characterization of Phenanthrylphosphine Gold Complex: Observation of Au-Induced Blue-Green Phosphorescence at Room Temperature. Inorg. Chem. 2005, 44, 1157–1159. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Thavasi, V.; Mhaisalkar, S.G.; Ramakrishna, S. Novel hollow mesoporous 1D TiO2 nanofibers as photovoltaic and photocatalytic materials. Nanoscale 2012, 4, 1707–1716. [Google Scholar] [CrossRef]
- Xu, W.; Schmidt, R.; Whaley, M.; Demas, J.N.; DeGraff, B.A.; Karikari, E.K.; Famer, B.A. Oxygen sensors based on luminescence quenching: Interactions of pyrene with the polymer supports. Anal. Chem. 1995, 67, 3172–3180. [Google Scholar] [CrossRef]
- Kim, Y.I.; Salim, S.; Huq, M.J.; Mallouk, T.E. Visible-light photolysis of hydrogen iodide using sensitized layered semiconductor particles. J. Am. Chem. Soc. 1991, 113, 9561–9563. [Google Scholar] [CrossRef]
- Gafney, H.D. Spectral, photophysical and photochemical properties of Ru(bpy)32+ on porous vycor glass. Coord. Chem. Rev. 1990, 104, 113–141. [Google Scholar] [CrossRef]
- Yersin, H.; Rausch, A.F.; Czerwieniec, R.; Hofbeck, T.; Fischer, T. The triplet state of organo-transition metal compounds. Triplet harvesting and singlet harvesting for efficient OLEDs. Coord. Chem. Rev. 2011, 255, 2622–2652. [Google Scholar] [CrossRef]
- Barbieri, A.; Accorsi, G.; Armaroli, N. Luminescent complexes beyond the platinum group: The d10 avenue. Chem. Commun. 2008, 19, 2185–2193. [Google Scholar] [CrossRef] [PubMed]
- Osawa, M.; Hoshino, M.; Hashimoto, M.; Kawata, I.; Igawa, S.; Yashima, M. Application of three-coordinate copper(I) complexes with halide ligands in organic light-emitting diodes that exhibit delayed fluorescence. Dalton Trans. 2015, 44, 8369–8378. [Google Scholar] [CrossRef]
- Chakkaradhari, G.; Belyaev, A.A.; Karttunen, A.J.; Sivchik, V.; Tunik, S.P.; Koshevoy, I.O. Alkynyl triphosphine copper complexes: Synthesis and photophysical studies. Dalton Trans. 2015, 44, 13294–13304. [Google Scholar] [CrossRef]
- Gneuss, T.; Leitl, M.J.; Finger, L.H.; Rau, N.; Yersin, H.; Sundermeyer, J. A new class of luminescent Cu(I) complexes with tripodal ligands-TADF emitters for the yellow to red color range. Dalton Trans. 2015, 44, 8506–8520. [Google Scholar] [CrossRef] [PubMed]
- Sandroni, M.; Kayanuma, M.; Rebarz, M.; Akdas-Kilig, H.; Pellegrin, Y.; Blart, E.; Le Bozec, H.; Daniel, C.; Odobel, F. Heteroleptic diimine copper(I) complexes with large extinction coefficients: Synthesis, quantum chemistry calculations and physico-chemical properties. Dalton Trans. 2013, 42, 14628–14638. [Google Scholar] [CrossRef] [PubMed]
- Penfold, T.J.; Karlsson, S.; Capano, G.; Lima, F.A.; Rittmann, J.; Reinhard, M.; Rittmann-Frank, M.H.; Braem, O.; Baranoff, E.; Abela, R.; et al. Solvent-Induced Luminescence Quenching: Static and Time-Resolved X-Ray Absorption Spectroscopy of a Copper(I) Phenanthroline Complex. J. Phys. Chem. A 2013, 117, 4591–4601. [Google Scholar] [CrossRef]
- Moudam, O.; Kaeser, A.; Delavaux-Nicot, B.; Duhayon, C.; Holler, M.; Accorsi, G.; Armaroli, N.; Séguy, I.; Navarro, J.; Destruel, P.; et al. Electrophosphorescent homo- and heteroleptic copper(i) complexes prepared from various bis-phosphine ligands. Chem. Commun. 2007, 29, 3077–3079. [Google Scholar] [CrossRef]
- Kaeser, A.; Mohankumar, M.; Mohanraj, J.; Monti, F.; Holler, M.; Cid, J.-J.; Moudam, O.; Nierengarten, I.; Karmazin-Brelot, L.; Duhayon, C.; et al. Heteroleptic Copper(I) Complexes Prepared from Phenanthroline and Bis-Phosphine Ligands. Inorg. Chem. 2013, 52, 12140–12151. [Google Scholar] [CrossRef] [PubMed]
- Cuttell, D.G.; Kuang, S.-M.; Fanwick, P.E.; McMillin, D.R.; Walton, R.A. Simple Cu(I) Complexes with Unprecedented Excited-State Lifetimes. J. Am. Chem. Soc. 2002, 124, 6–7. [Google Scholar] [CrossRef] [PubMed]
- Evans, R.C.; Douglas, P.; Winscom, C.J. Coordination complexes exhibiting room-temperature phosphorescence: Evaluation of their suitability as triplet emitters in organic light emitting diodes. Coord. Chem. Rev. 2006, 250, 2093–2126. [Google Scholar] [CrossRef]
- Bergmann, L.; Braun, C.; Nieger, M.; Bräse, S. The coordination- and photochemistry of copper(i) complexes: Variation of N^N ligands from imidazole to tetrazole. Dalton Trans. 2018, 47, 608–621. [Google Scholar] [CrossRef] [PubMed]
- Femoni, C.; Muzzioli, S.; Palazzi, A.; Stagni, S.; Zacchini, S.; Monti, F.; Accorsi, G.; Bolognesi, M.; Armaroli, N.; Massi, M.; et al. New tetrazole-based Cu(i) homo- and heteroleptic complexes with various P^P ligands: Synthesis, characterization, redox and photophysical properties. Dalton Trans. 2013, 42, 997–1010. [Google Scholar] [CrossRef] [PubMed]
- Saito, K.; Arai, T.; Takahashi, N.; Tsukuda, T.; Tsubomura, T. A series of luminescent Cu(i) mixed-ligand complexes containing 2,9-dimethyl-1,10-phenanthroline and simple diphosphine ligands. Dalton Trans. 2006, 37, 4444–4448. [Google Scholar] [CrossRef]
- Iwamura, M.; Takeuchi, S.; Tahara, T. Substituent effect on the photoinduced structural change of Cu(i) complexes observed by femtosecond emission spectroscopy. Phys. Chem. Chem. Phys. 2014, 16, 4143–4154. [Google Scholar] [CrossRef] [PubMed]
- Mohankumar, M.; Holler, M.; Meichsner, E.; Nierengarten, J.-F.; Niess, F.; Sauvage, J.-P.; Delavaux-Nicot, B.; Leoni, E.; Monti, F.; Malicka, J.M.; et al. Heteroleptic Copper(I) Pseudorotaxanes Incorporating Macrocyclic Phenanthroline Ligands of Different Sizes. J. Am. Chem. Soc. 2018, 140, 2336–2347. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Fox, Gaussian 09, Revision A.02; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Ross, R.B.; Ermler, W.C. Ab initio calculations including relativistic effects for diatomic silver, diatomic gold, silver-gold (AgAu), silver hydride (AgH), and gold hydride (AuH). J. Phys. Chem. 1985, 89, 5202–5206. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. Accuracy of AH n equilibrium geometries by single determinant molecular orbital theory. Mol. Phys. 1974, 27, 209–214. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef] [PubMed]
- Autschbach, J.; Patchkovskii, S.; Ziegler, T.; van Gisbergen, S.J.A.; Jan Baerends, E. Chiroptical properties from time-dependent density functional theory. II. Optical rotations of small to medium sized organic molecules. J. Chem. Phys. 2002, 117, 581–592. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, Q.; Shiota, Y.; Nakagawa, T.; Kuwabara, K.; Yoshizawa, K.; Adachi, C. Computational Prediction for Singlet- and Triplet-Transition Energies of Charge-Transfer Compounds. J. Chem. Theory Comput. 2013, 9, 3872–3877. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Schultz, N.E.; Zhao, Y.; Truhlar, D.G. Density Functionals for Inorganometallic and Organometallic Chemistry. J. Phys. Chem. A 2005, 109, 11127–11143. [Google Scholar] [CrossRef] [PubMed]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Reiher, M.; Salomon, O.; Artur Hess, B. Reparameterization of hybrid functionals based on energy differences of states of different multiplicity. Theor. Chem. Acc. 2001, 107, 48–55. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Accurate excitation energies from time-dependent density functional theory: Assessing the PBE0 model for organic free radicals. Chem. Phys. Lett. 1999, 314, 152–157. [Google Scholar] [CrossRef]
- Boese, A.D.; Martin, J.M.L. Development of density functionals for thermochemical kinetics. J. Chem. Phys. 2004, 121, 3405–3416. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06 functionals and 12 other functionals. Theor. Chem. Acc. 2008, 119, 525. [Google Scholar] [CrossRef]
- Sheng-Zhi, H.; Zhao-Hui, Z.; Khi-Rui, T. Average van der Waals Radii of Atoms in Crystals. Acta Phys. Chim. Sin. 2003, 19, 1073–1077. [Google Scholar] [CrossRef]
- Venkateswaran, R.; Balakrishna, M.S.; Mobin, S.M.; Tuononen, H.M. Copper(I) Complexes of Bis(2-(diphenylphosphino)phenyl) Ether: Synthesis, Reactivity, and Theoretical Calculations. Inorg. Chem. 2007, 46, 6535–6541. [Google Scholar] [CrossRef] [PubMed]
- The PyMOL Molecular Graphics System, Version 1.6.0.0; Schrodinger LLC: New York, NY, USA, 2010.
- Tang, C.W.; VanSlyke, S.A. Organic electroluminescent diodes. Appl. Phys. Lett. 1987, 51, 913–915. [Google Scholar] [CrossRef]
- Qin, L.; Zhang, Q.; Sun, W.; Wang, J.; Lu, C.; Cheng, Y.; Wang, L. Novel luminescent iminephosphine complex of copper(i) with high photochemical and electrochemical stability. Dalton Trans. 2009, 43, 9388–9391. [Google Scholar] [CrossRef]
- Krylova, V.A.; Djurovich, P.I.; Conley, B.L.; Haiges, R.; Whited, M.T.; Williams, T.J.; Thompson, M.E. Control of emission colour with N-heterocyclic carbene (NHC) ligands in phosphorescent three-coordinate Cu(i) complexes. Chem. Commun. 2014, 50, 7176–7179. [Google Scholar] [CrossRef]
- Siddique, Z.A.; Yamamoto, Y.; Ohno, T.; Nozaki, K. Structure-Dependent Photophysical Properties of Singlet and Triplet Metal-to-Ligand Charge Transfer States in Copper(I) Bis(diimine) Compounds. Inorg. Chem. 2003, 42, 6366–6378. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Hong, G.; Dai, D.; Li, L.; Dolg, M. The Beijing four-component density functional program package (BDF) and its application to EuO, EuS, YbO and YbS. Theor. Chem. Acc. 1997, 96, 75–83. [Google Scholar] [CrossRef]
- Liu, W.; Wang, F.; Li, L. The Beijing Density Functional (BDF) Program Package: Methodologies and Applications. J. Theor. Comput. Chem. 2003, 2, 257–272. [Google Scholar] [CrossRef]
- Freed, K.F. Influence of Frequency Shifts on Electron Transfer Processes. J. Phys. Chem. B 2003, 107, 10341–10343. [Google Scholar] [CrossRef]
- Tong, G.S.M.; Chow, P.K.; To, W.-P.; Kwok, W.-M.; Che, C.-M. A Theoretical Investigation into the Luminescent Properties of d8-Transition-Metal Complexes with Tetradentate Schiff Base Ligands. Chem. A Eur. J. 2014, 20, 6433–6443. [Google Scholar] [CrossRef]
- Brunschwig, B.S.; Sutin, N. Rate-Constant Expressions for Nonadiabatic Electron-Transfer Reactions. Comments Inorg. Chem. 1987, 6, 209–235. [Google Scholar] [CrossRef]

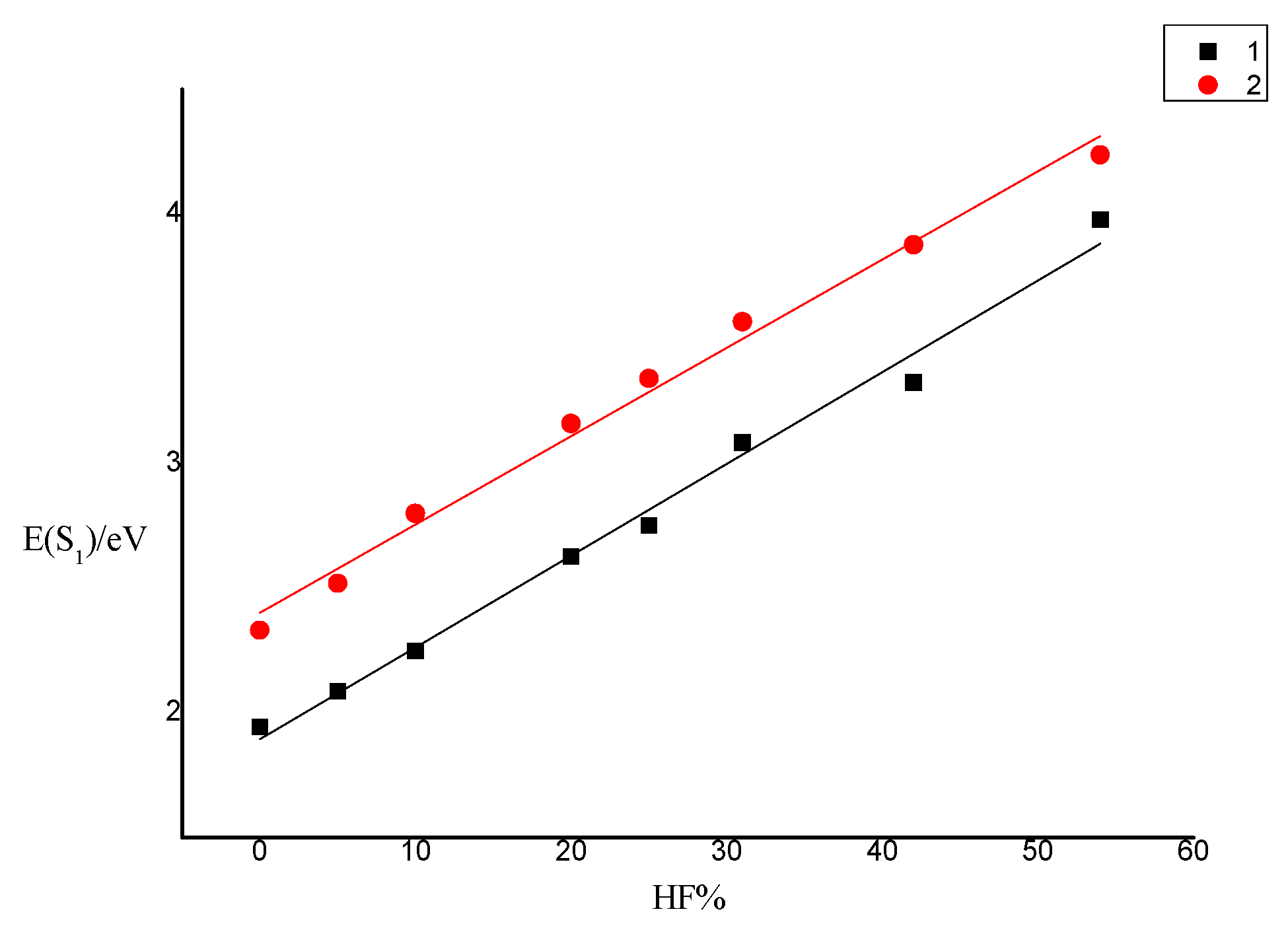
| BLYP (0%) | MPWLY P1M (5%) | TPSSH (10%) | B3LYP (20%) | PBE0 (25%) | MPW1 B95 (31%) | BMK (42%) | M06-2x (54%) | |
|---|---|---|---|---|---|---|---|---|
| HF% | 0 | 5 | 10 | 20 | 25 | 31 | 42 | 54 |
| 1 E(S1)/eV | 1.9432 | 2.0863 | 2.2468 | 2.6259 | 2.7508 | 3.0825 | 3.3242 | 3.9777 |
| 2 E(S1)/eV | 2.3308 | 2.5202 | 2.7997 | 3.1605 | 3.3400 | 3.5679 | 3.8770 | 4.2369 |
| Complex | S0 | T1 | S0-T1 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Cu | Ligand 1 | Ligand 2 | Cu | Ligand 1 | Ligand 2 | Cu | Ligand 1 | Ligand 2 | |
| 1 | 0.5615 | 0.2193 | 0.2193 | 0.5617 | 0.2192 | 0.2192 | 0.0002 | 0.0001 | 0.0001 |
| 2 | 0.3633 | 0.2262 | 0.4105 | 0.3677 | 0.1973 | 0.4350 | 0.0044 | 0.0289 | −0.0245 |
| 3 | 0.2257 | 0.3217 | 0.4526 | 0.3076 | 0.2809 | 0.4116 | 0.0819 | 0.0408 | 0.0410 |
| 4 | 0.5070 | 0.2919 | 0.2011 | 0.5149 | 0.2939 | 0.1918 | 0.0079 | −0.0020 | 0.0093 |
| IP (v) | IP (a) | HEP | EA (v) | EA (a) | EEP | λhole | λelectron | |
|---|---|---|---|---|---|---|---|---|
| 1 | 9.55 | 9.16 | 8.88 | 3.28 | 3.37 | 3.45 | 0.67 | 0.16 |
| 2 | 9.03 | 8.70 | 8.42 | 2.94 | 3.18 | 3.41 | 0.61 | 0.46 |
| 3 | 8.94 | 8.55 | 8.16 | 2.83 | 3.08 | 3.33 | 0.77 | 0.50 |
| 4 | 8.81 | 8.34 | 7.72 | 2.18 | 2.33 | 2.51 | 1.09 | 0.33 |
| Electronic Transition | Configuration (%) | Assignment | ||
|---|---|---|---|---|
| 1 | T1→S0 | 782.9/730expt | H→L (98.0) | MLNLNCT |
| H→L+4 (2.0) | MLNLNCT | |||
| 2 | T1→S0 | 612.7/570expt | H→L (92.5) | MLNCT/LPLNCT |
| H−1→L (2.9) | MLNCT/LPLNCT | |||
| 3 | T1→S0 | 725.7/608expt | H→L (72.0) | MLNCT/LPLNCT |
| H−4→L (19.5) | MLNCT/LPLNCT | |||
| H−3→L (4.5) | MLNCT/LPLNCT | |||
| 4 | T1→S0 | 647.3 | H→L (89.8) | LP1LP2CT |
| E(T1) (cm−1) | krx (s−1) | kry (s−1) | krz (s−1) | kravg (s−1) | krexp (s−1) | |
|---|---|---|---|---|---|---|
| 1 | 12,773 | 2074 | 142 | 2075 | 1430 | 4444 |
| 2 | 16,322 | 12,413 | 16,300 | 12,413 | 13,708 | 10,490 |
| 3 | 13,780 | 3302 | 10,239 | 3302 | 5614 | 17,143 |
| 4 | 15,450 | 10,506 | 47 | 10,506 | 7020 | 0 |
| <T1|SOC|S0>2 | ΔE00 | λ1 | μ1 | μ2 | nM1 | nM2 | λM | λL | λ | Slf | SM | S | knr | knr (expt) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.014 | 17,781 | 2141 | −2011 | 185 | 12 | 11 | 783 | 2735 | 3518 | 41.14 | 0.53 | 0.4176 | 2.8 × 10−5 | |
| 2 | 4777 | 20,997 | 2977 | −712 | 567 | 12 | 11 | 1378 | 3073 | 4451 | 33.96 | 0.93 | 34.89 | 9469.6 | 5.94 × 104 |
| 3 | 1603 | 19,243 | 13,769 | 442 | 853 | 3 | 3 | 2267 | 13,447 | 15,714 | 254.28 | 1.55 | 255.82 | 1.2 × 1011 | 1.41 × 106 |
| 4 | 497 | 25,918 | 12,409 | 416 | 1119 | 9 | 8 | 1371 | 12,182 | 13,553 | 66.62 | 0.97 | 69.59 | 8.8 × 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, L.; Wang, Y.-Y.; He, T.-F.; Zou, L.-Y.; Guo, J.-F.; Ren, A.-M. A Theoretical Investigation into the Homo- and Hetero-leptic Cu(I) Phosphorescent Complexes Bearing 2,9-dimethyl-1,10-phenanthroline and bis [2-(diphenylphosphino)phenyl]ether Ligand. Materials 2022, 15, 7253. https://doi.org/10.3390/ma15207253
Shen L, Wang Y-Y, He T-F, Zou L-Y, Guo J-F, Ren A-M. A Theoretical Investigation into the Homo- and Hetero-leptic Cu(I) Phosphorescent Complexes Bearing 2,9-dimethyl-1,10-phenanthroline and bis [2-(diphenylphosphino)phenyl]ether Ligand. Materials. 2022; 15(20):7253. https://doi.org/10.3390/ma15207253
Chicago/Turabian StyleShen, Lu, Yu-Yang Wang, Teng-Fei He, Lu-Yi Zou, Jing-Fu Guo, and Ai-Min Ren. 2022. "A Theoretical Investigation into the Homo- and Hetero-leptic Cu(I) Phosphorescent Complexes Bearing 2,9-dimethyl-1,10-phenanthroline and bis [2-(diphenylphosphino)phenyl]ether Ligand" Materials 15, no. 20: 7253. https://doi.org/10.3390/ma15207253
APA StyleShen, L., Wang, Y.-Y., He, T.-F., Zou, L.-Y., Guo, J.-F., & Ren, A.-M. (2022). A Theoretical Investigation into the Homo- and Hetero-leptic Cu(I) Phosphorescent Complexes Bearing 2,9-dimethyl-1,10-phenanthroline and bis [2-(diphenylphosphino)phenyl]ether Ligand. Materials, 15(20), 7253. https://doi.org/10.3390/ma15207253







