Selected Problems of Random Free Vibrations of Rectangular Thin Plates with Viscoelastic Dampers
Abstract
:1. Introduction
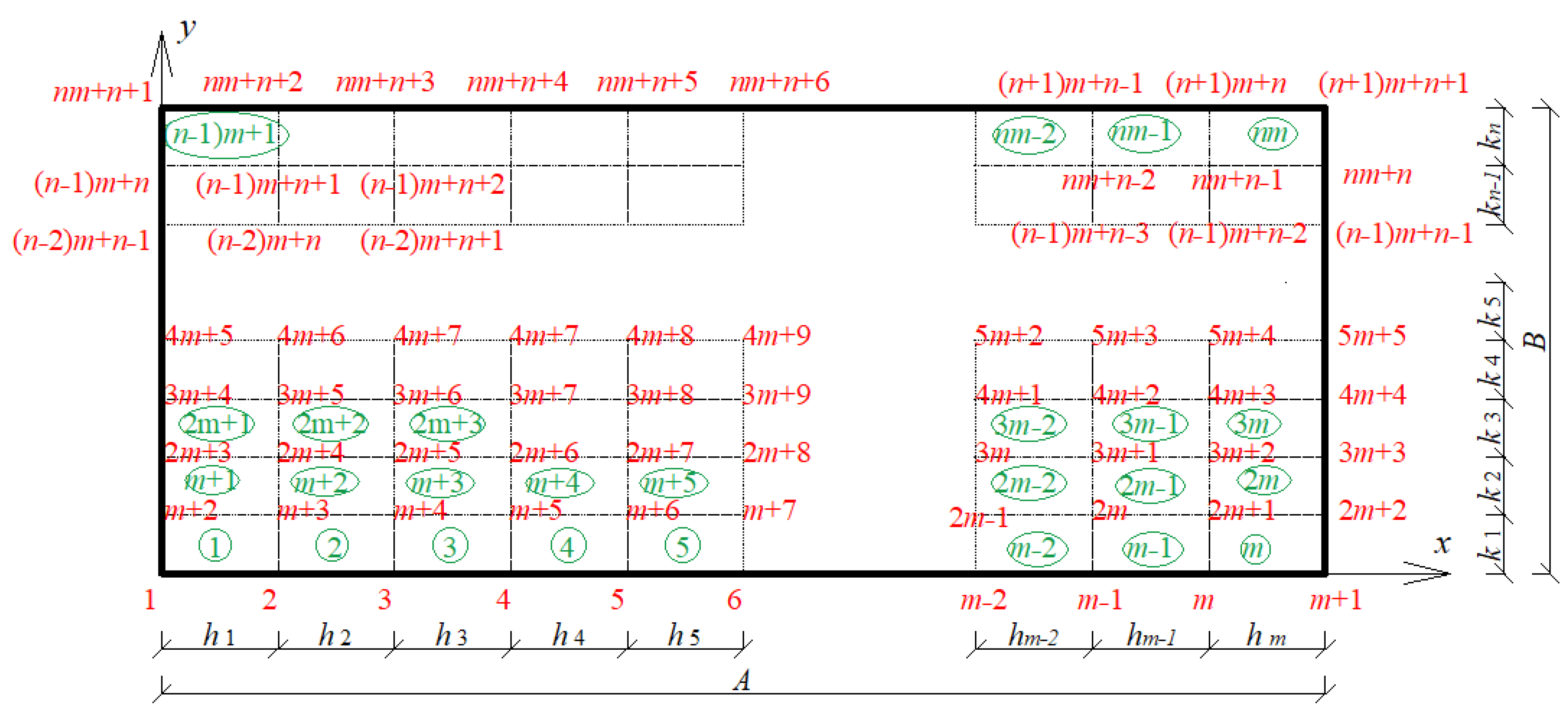
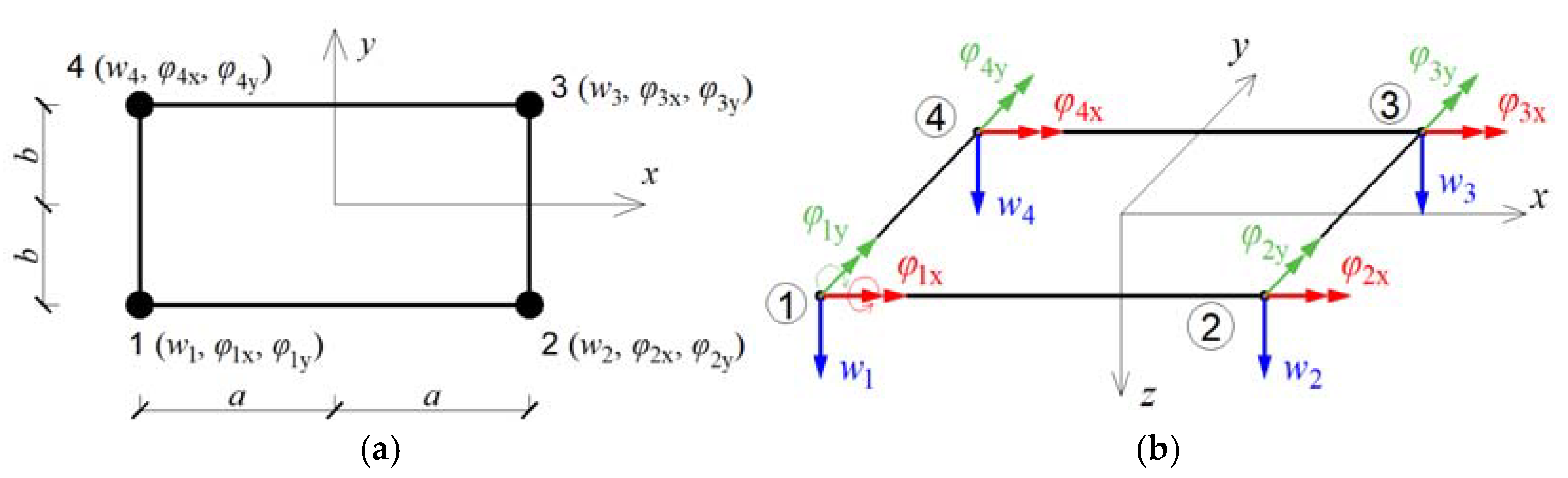
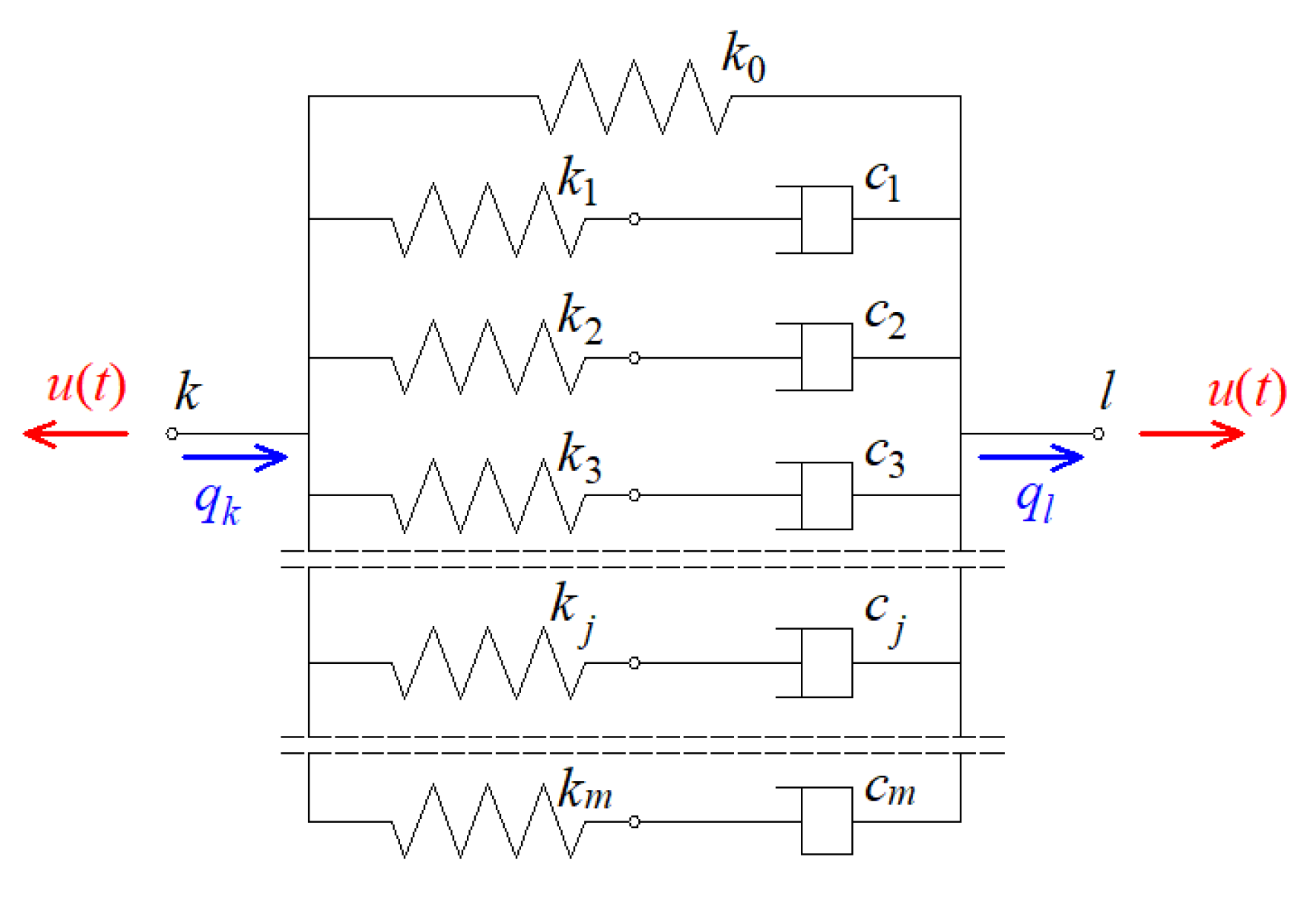
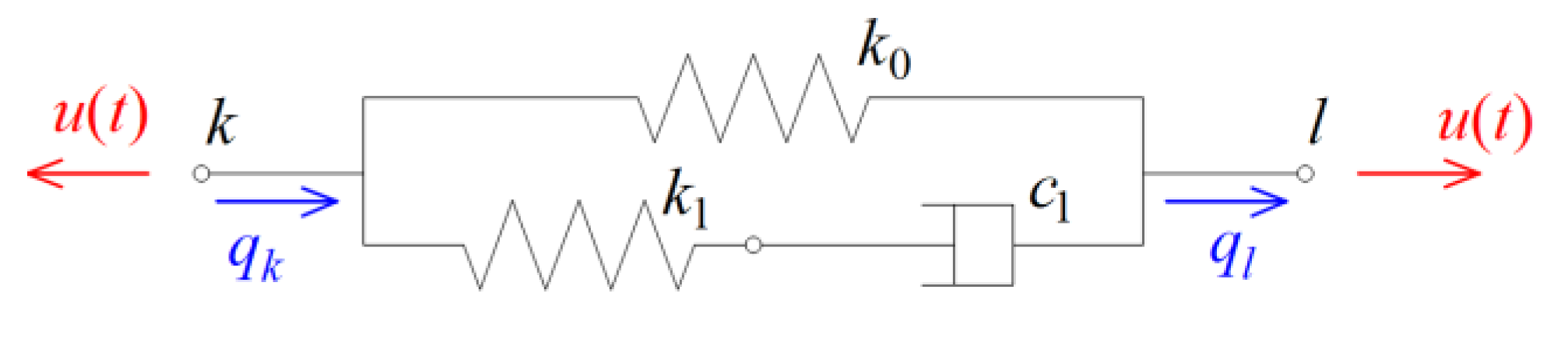
2. Eigenvibration Analysis Methodology
3. Sensitivity and Uncertainty Analyses
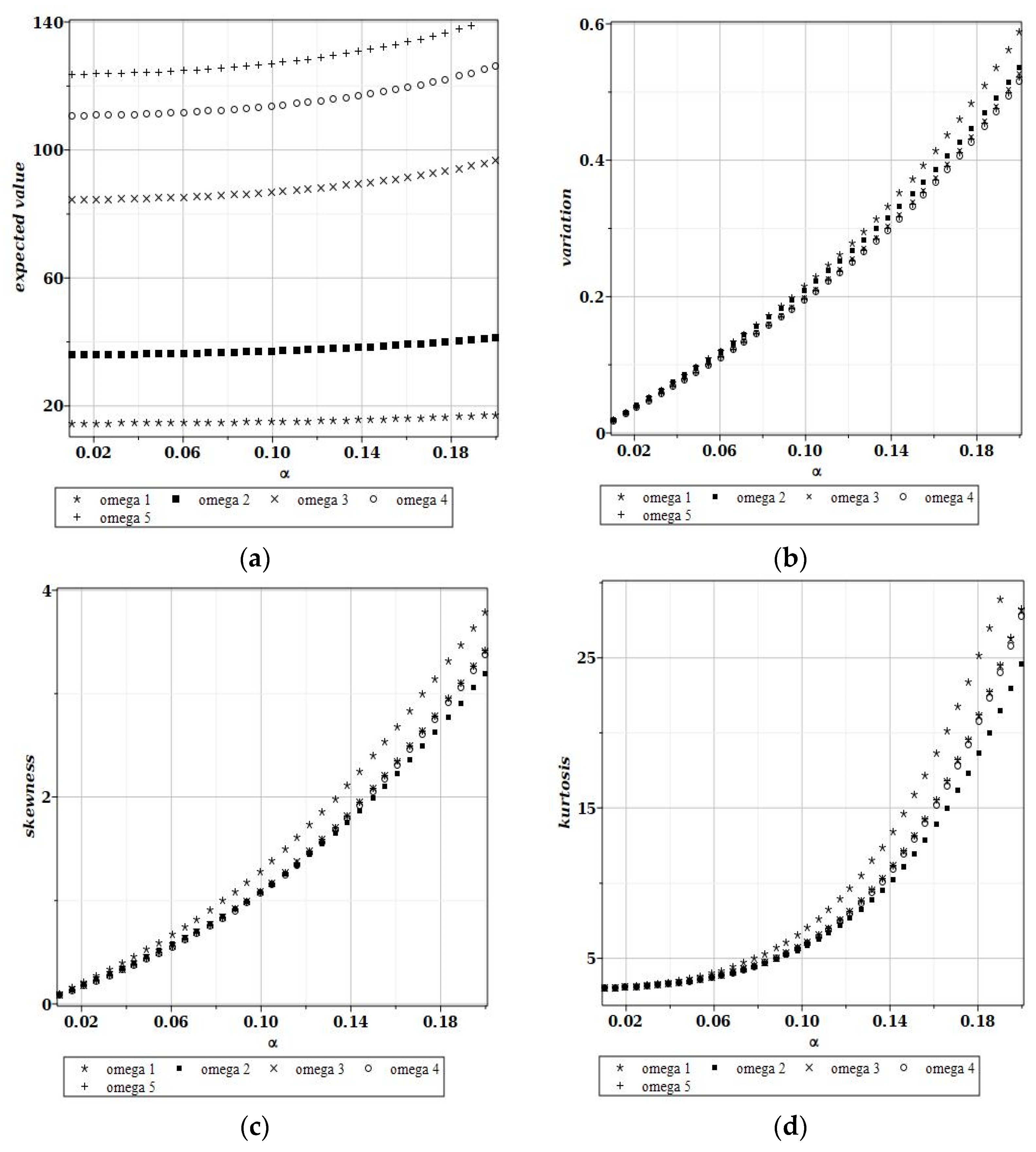
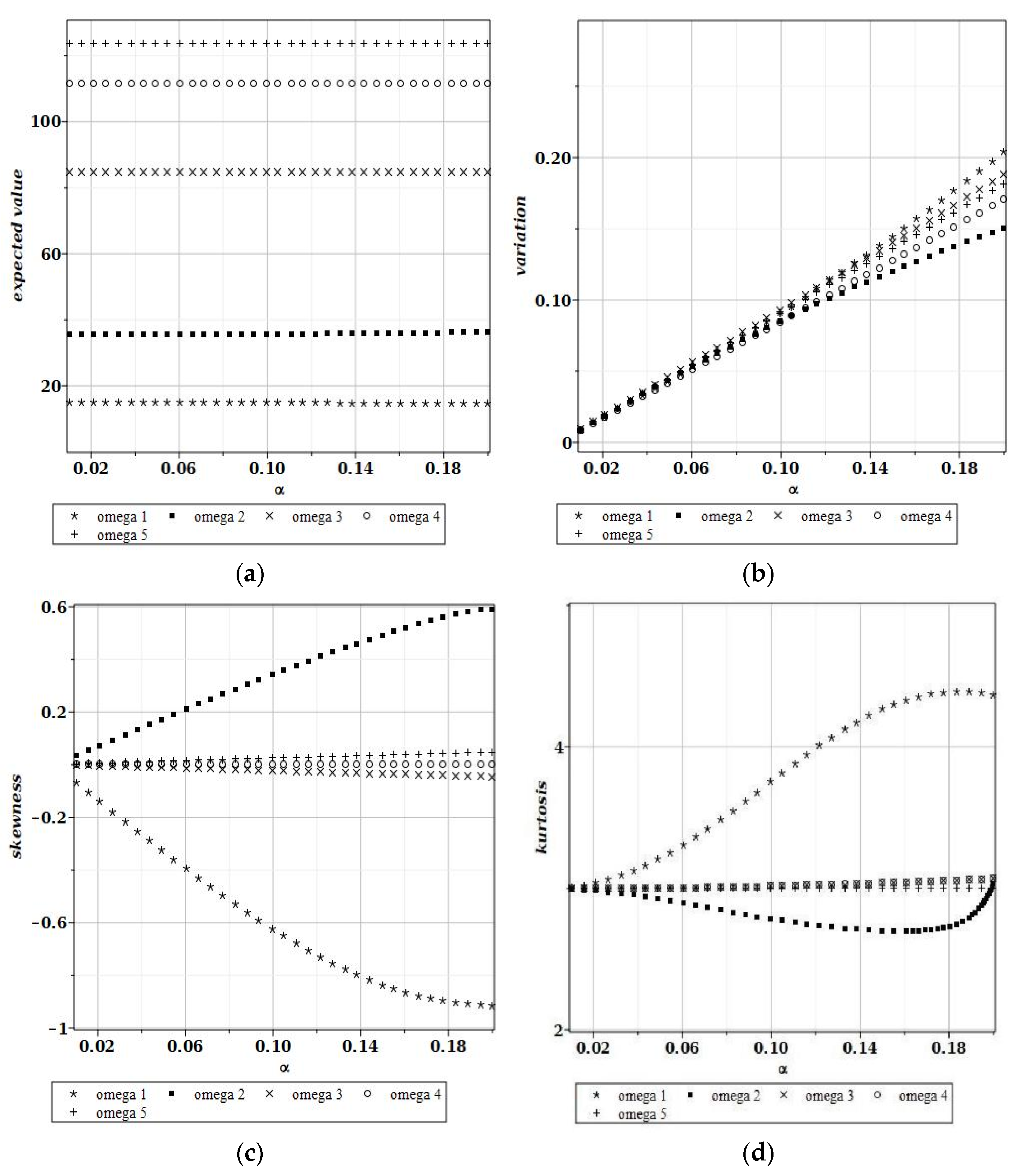
4. Numerical Experiment
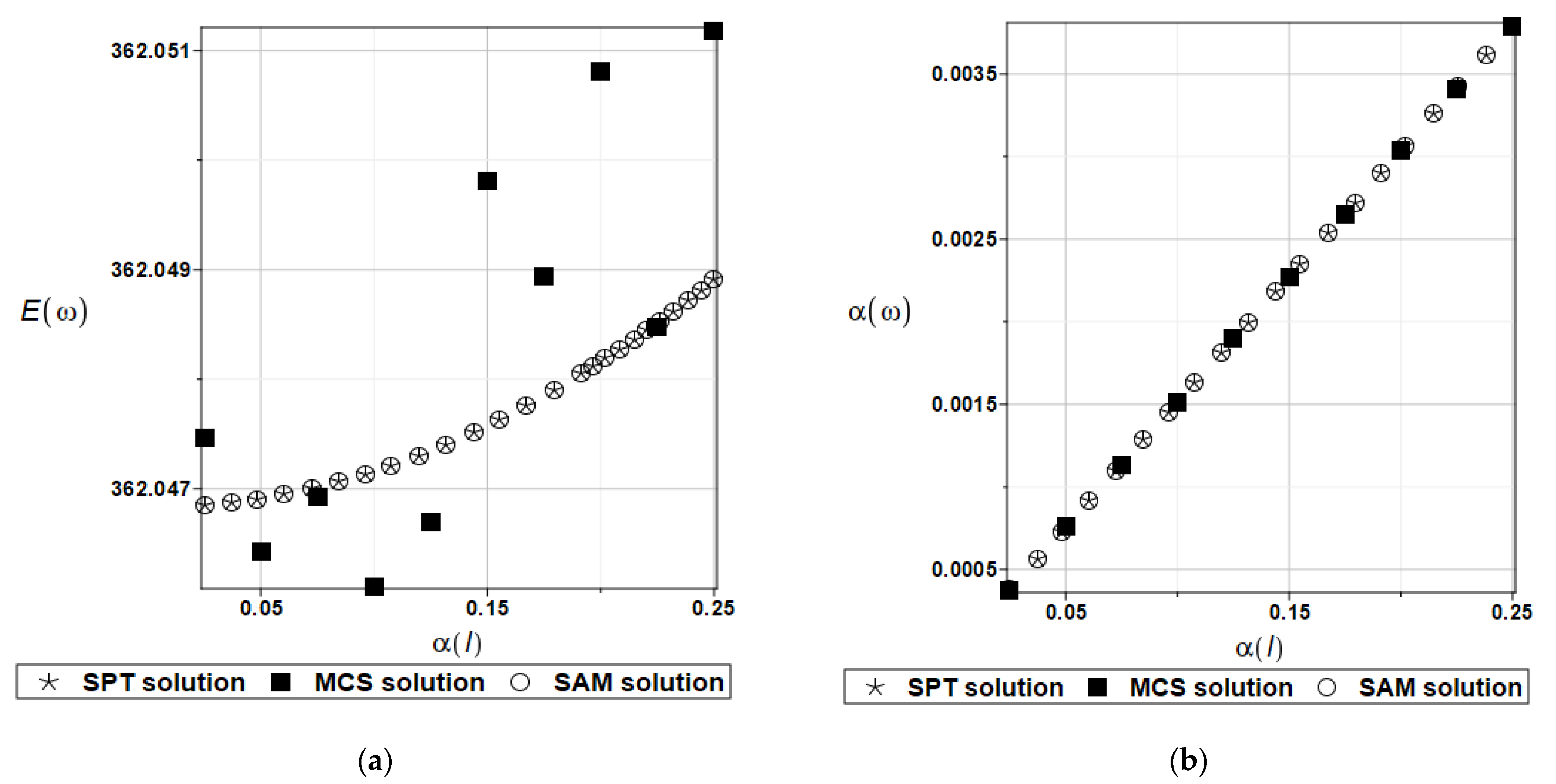
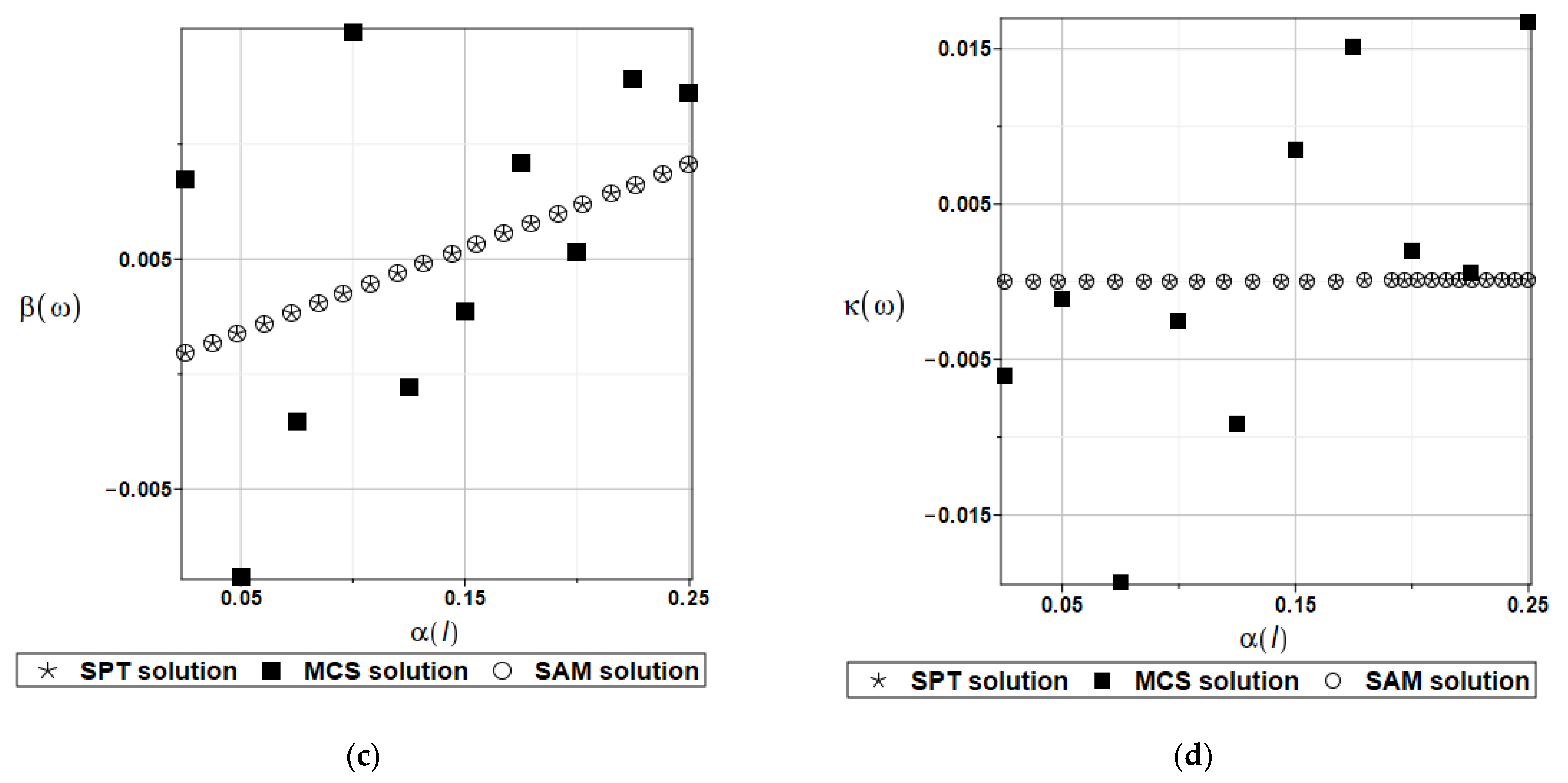
5. Comparative Analysis—Results Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kamiński, M.M. The Stochastic Perturbation Method for Computational Mechanics, 1st ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; ISBN 978-0-470-77082-5. [Google Scholar]
- Kamiński, M. On iterative scheme in determination of the probabilistic moments of the structural response in the stochastic perturbation-based Finite Element Method. Int. J. Numer. Methods Eng. 2015, 104, 1038–1060. [Google Scholar] [CrossRef]
- Arregui-Mena, J.D.; Margetts, L.; Mummery, P.M. Practical Application of the Stochastic Finite Element Method. Arch. Computat. Method. Eng. 2014, 23, 171–190. [Google Scholar] [CrossRef]
- Han, J.-G.; Ren, W.-X.; Huang, Y. A wavelet-based stochastic finite element method of thin plate bending. Appl. Math. Model. 2007, 31, 181–193. [Google Scholar] [CrossRef]
- Chandra, S.; Sepahvand, K.; Matsagar, V.A.; Marburg, S. Stochastic dynamic analysis of composite plate with random temperature increment. Compos. Struct. 2019, 226, 111159. [Google Scholar] [CrossRef]
- Hoi, C.-K.; Noh, H.-C. Stochastic finite element analysis of plate structures by weighted integral method. Struct. Eng. Mech. 1996, 4, 703–715. [Google Scholar]
- Mestrovic, M. Stochastic Finite Element Analysis of Plates, Theories of Plates and Shells Critical Review and New Application. In Proceedings of the Euromech Colloqium 444, Bremen, Germany, 22–25 September 2002. [Google Scholar]
- Zhu, L.; Yan, B.; Wang, Y.; Dun, Y.; Ma, J.; Li, C. Inspection of blade profile and machining deviation analysis based on sample points optimization and NURBS knot insertion. Thin-Walled Struct. 2021, 162, 107540. [Google Scholar] [CrossRef]
- Lewandowski, R. Non-Linear Free Vibrations of Beams by the Finite Element and Continuation Methods. J. Sound Vib. 1994, 170, 577–593. [Google Scholar] [CrossRef]
- Lewandowski, R.; Pawlak, Z. Dynamic analysis of frames with viscoelastic dampers modeled by rheological models with fractional derivatives. J. Sound Vib. 2011, 330, 923–936. [Google Scholar] [CrossRef]
- Lewandowski, R.; Bartkowiak, A.; Maciejewski, H. Dynamic analysis of frames with viscoelastic dampers: A comparison of damper models. Struct. Eng. Mech. 2012, 41, 113–137. [Google Scholar] [CrossRef]
- Lu, L.-Y.; Lin, G.-L.; Shih, M.-H. An experimental study on a generalized Maxwell model for nonlinear viscoelastic dampers used in seismic isolation. Eng. Struct. 2012, 34, 111–123. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamics of Structures; Computers & Structures, Inc.: Berkeley, CA, USA, 1995. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method. Linear Static and Dynamic Finite Element Analysis; Prentice Hall: Hoboken, NJ, USA, 1987. [Google Scholar]
- García-Barruetabeña, J.; Cortés, F.; Abete, J.M.; Fernández, P.; Lamela, M.J.; Fernández-Canteli, A. Experimental characterization and modelization of the relaxation and complex moduli of a flexible adhesive. Mater. Des. 2011, 32, 2783–2796. [Google Scholar] [CrossRef]
- Lewandowski, R.; Przychodzki, M. Influence of temperature on dynamic properties of frames with viscoelastic dampers. J. Civ. Eng. Environ. Archit. 2016, 33, 431–438. (In Polish) [Google Scholar]
- Kamiński, M. On Shannon entropy computations in selected plasticity problems. Int. J. Numer. Methods Eng. 2021, 122, 5128–5143. [Google Scholar] [CrossRef]
- Bredow, R.; Kamiński, M. Structural safety of the steel hall under dynamic excitation using the relative probabilistic entropy concept. Materials 2022, 15, 3587. [Google Scholar] [CrossRef] [PubMed]


| Design Variable Name | Design Variable | Normalized Sensitivity Gradient |
|---|---|---|
| Plate length | [m] | –1.908109 |
| Thickness of the plate | [m] | 1.136478 |
| Young’s modulus | [N/m2] | 0.473791 |
| Poisson ratio | [–] | 0.0669623 |
| Density | [kg/m3] | –0.584767 |
| Stiffness parameter of the damper’s Kelvin element | [N/m] | 0.0109382 |
| Stiffness parameter of the damper’s Maxwell element | [N/m] | –0.0708819 |
| Viscosity parameter of the damper’s Maxwell element | [Ns/m] | 0.164465 |
| Reference temperature | [°C] | 0.0189089 |
| Ambient temperature | [°C] | –0.0295390 |
| SAM | SPT | MCS | |
|---|---|---|---|
| 0.025 | 362.046846366682 | 362.046846366682 | 362.047466435600 |
| 0.050 | 362.046908966730 | 362.046908966730 | 362.046431550698 |
| 0.075 | 362.047013300146 | 362.047013300146 | 362.046932076133 |
| 0.100 | 362.047159366940 | 362.047159366940 | 362.046112284009 |
| 0.125 | 362.047347167119 | 362.047347167119 | 362.046692036114 |
| 0.150 | 362.047576700696 | 362.047576700696 | 362.049805913200 |
| 0.175 | 362.047847967686 | 362.047847967686 | 362.048943295710 |
| 0.200 | 362.048160968106 | 362.048160968106 | 362.050809955170 |
| 0.225 | 362.048515701978 | 362.048515701978 | 362.048477124862 |
| 0.250 | 362.048912169324 | 362.048912169324 | 362.051187451775 |
| SAM | SPT | MCS | |
|---|---|---|---|
| 0.025 | 0.00037913840232059 | 0.00037913840225768 | 0.00037820668516146 |
| 0.050 | 0.00075827679791607 | 0.00075827679779030 | 0.00075890901680434 |
| 0.075 | 0.00113741518006143 | 0.00113741517987277 | 0.00113579512680720 |
| 0.100 | 0.00151655354203154 | 0.00151655354178001 | 0.00151584644876523 |
| 0.125 | 0.00189569187710127 | 0.00189569187678686 | 0.00189866159120374 |
| 0.150 | 0.00227483017854541 | 0.00227483017816811 | 0.00227385578919360 |
| 0.175 | 0.00265396843963868 | 0.00265396843919851 | 0.00265356938565002 |
| 0.200 | 0.00303310665365575 | 0.00303310665315269 | 0.00303502740231922 |
| 0.225 | 0.00341224481387114 | 0.00341224481330523 | 0.00340377236370069 |
| 0.250 | 0.00379138291355934 | 0.00379138291293050 | 0.00378941244520895 |
| SAM | SPT | MCS | |
|---|---|---|---|
| 0.025 | 15.1020303938680 | 15.1020303938679 | 55.8307084247803 |
| 0.050 | 15.0750528266381 | 15.0750528266359 | 56.6189485257520 |
| 0.075 | 15.0309030518086 | 15.0309030517976 | –182.896206992036 |
| 0.100 | 14.9708003252100 | 14.9708003252100 | 59.6193578514476 |
| 0.125 | 14.8964516050049 | 14.8964516049194 | 61.9339027954595 |
| 0.150 | 14.8100515516881 | 14.8100515515109 | 64.6258515558037 |
| 0.175 | 14.7142825280868 | 14.7142825277585 | 68.1357033688504 |
| 0.200 | 14.6123145993600 | 14.6123145988000 | 72.1942549445554 |
| 0.225 | 14.5078055329993 | 14.5078055321022 | 76.9222494795175 |
| 0.250 | 14.4049007988281 | 14.4049007974609 | 82.4482857143314 |
| SAM | SPT | MCS | |
|---|---|---|---|
| 0.025 | 0.021690206735279 | 0.021690206646010 | 0.09677329520225 |
| 0.050 | 0.043860569753305 | 0.043860569571128 | 0.19522123484153 |
| 0.075 | 0.066951757180877 | 0.066951756898434 | –0.10707504128592 |
| 0.100 | 0.091326253488526 | 0.091326253094581 | 0.39417790477171 |
| 0.125 | 0.117231393179819 | 0.117231392659076 | 0.49988129568701 |
| 0.150 | 0.144765615806037 | 0.144765615138953 | 0.60551075944427 |
| 0.175 | 0.173850845320013 | 0.173850844482707 | 0.71407533547204 |
| 0.200 | 0.204216713685934 | 0.204216712650311 | 0.82487834596053 |
| 0.225 | 0.235407286078469 | 0.235407284812828 | 0.93330578277003 |
| 0.250 | 0.266829037072705 | 0.266829035543292 | 1.05206621395503 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamiński, M.; Lenartowicz, A.; Guminiak, M.; Przychodzki, M. Selected Problems of Random Free Vibrations of Rectangular Thin Plates with Viscoelastic Dampers. Materials 2022, 15, 6811. https://doi.org/10.3390/ma15196811
Kamiński M, Lenartowicz A, Guminiak M, Przychodzki M. Selected Problems of Random Free Vibrations of Rectangular Thin Plates with Viscoelastic Dampers. Materials. 2022; 15(19):6811. https://doi.org/10.3390/ma15196811
Chicago/Turabian StyleKamiński, Marcin, Agnieszka Lenartowicz, Michał Guminiak, and Maciej Przychodzki. 2022. "Selected Problems of Random Free Vibrations of Rectangular Thin Plates with Viscoelastic Dampers" Materials 15, no. 19: 6811. https://doi.org/10.3390/ma15196811
APA StyleKamiński, M., Lenartowicz, A., Guminiak, M., & Przychodzki, M. (2022). Selected Problems of Random Free Vibrations of Rectangular Thin Plates with Viscoelastic Dampers. Materials, 15(19), 6811. https://doi.org/10.3390/ma15196811









