1. Introduction
Vibration and noise are correlated with each other and have become important factors in the manufacturing industry, affecting product quality, reducing operational accuracy, and shortening product life [
1,
2]. Modal control of acoustic structures is an indispensable task for avoiding resonance and reducing noise. There are several modal control schemes for porous acoustic structures. Among them, the structural fundamental frequency is widely used for its simple modeling, efficient solution, and stable optimization. From the structural design perspective, the fundamental frequency of porous acoustic structures according to practical working conditions can be optimized and adjusted to avoid resonance, reduce noise, and improve the stability of the acoustic system [
3]. This study aims to raise the structural fundamental frequency by devising a unique type of porous acoustic metamaterial. Metamaterials are a type of artificial materials/structures involving novel geometric shapes and extraordinary physical properties [
4,
5]. The macroproperties of metamaterials significantly depend on the innovative design structure rather than the physical properties of the constituent materials [
6,
7]. The frequency-response analyses of different acoustic metamaterials have been extensively studied by various scholars. Various frequency response design models for acoustic–structure interaction (ASI) systems were established by Yoon et al. [
8] and Vicente et al. [
9] to obtain the corresponding acoustic metamaterial. The boundary interface description, coupling interface assignment, and local modal problems were also solved in these design processes. Moreover, the vibration and noise reduction effects of these optimized structures in practical applications were verified via multiple engineering cases, illustrating the necessity of frequency response analysis for acoustic metamaterials. In this study, a frequency modulation acoustic metamaterial (FMAM), which is a porous acoustic metamaterial with better vibration and noise reduction performance, was designed to reduce the level of structural response and avoid resonance.
It is difficult to complete a complex model description of porous acoustic metamaterials using conventional acoustic materials. Therefore, this study improves the traditional optimization design method and proposes a full-cycle interactive progressive (FIP) design scheme for porous acoustic metamaterials [
10,
11]. FIP design is a full-cycle optimization method that seeks the optimal design in a gradient and interactively adjusts the design direction [
12]. It includes three parts: topology optimization based on the ASI system, parametric optimization based on the surrogate model (SM), and experimental analysis of the frequency response based on the closed acoustic box. An ASI system-based topology optimization provides an innovative initial structure for the FIP scheme of porous acoustic metamaterials [
13,
14]. Topology optimization is a powerful tool to optimize the material distribution within a given design domain, so as to achieve the best structure performance under some design constraints. There are many methods that have been established for topology optimization, e.g., the homogenization method [
15,
16], solid isotropic material with penalization (SIMP) [
17,
18,
19], evolutionary structural optimization (ESO) [
20], level set method (LSM) [
21,
22,
23,
24], and so on. Most of the topology optimization formulations can be efficiently solved by gradient-based algorithms [
25,
26,
27] or intelligent optimization algorithms [
28,
29].
Structural deformation in an ASI system is generally non-linear, while a linear deformation is an ideal situation. However, there is insufficient research on topology optimization based on non-linear finite elements, mainly due to the lack of optimization methods and calculation power. Recently, with the rapid development of hardware computing capabilities, an increasing number of scholars have extended traditional topology optimization methods to non-linear fields [
30,
31]. Singh et al. [
32] observed non-linear acoustics to have the potential to identify damages in composite structures that are difficult to detect using conventional linear ultrasonic methods and presented a rapid approach to model the non-linear behavior caused by closed delamination. Additionally, a few parametric studies have been performed to investigate the effects of various parameters related to the non-linear phenomenon. Some experiments were conducted by Zhang et al. [
33] with a focused transducer working in pulse-echo mode, and the measured amplitudes of non-linear waves reflected upon water–air and water–aluminum/steel interfaces conformed with the simulated results to help advance applications using pulse-echo non-linear acoustics.
Parametric optimization based on the SM includes the core stage of the FIP design. The SM is a data-driven analysis model that can approximate the implicit relationship between design variables, objective functions, and constraints [
34]. It can effectively reduce the calculation costs and improve the design efficiency of parametric optimization. The calculation result by using SMs is recognized to have a very high accuracy [
35,
36]. Extensive investigation of SMs has enabled prevalent use of this model in actual engineering optimization designs. Li et al. [
37] proposed a multisampling point sequence global optimization algorithm based on the Kriging model, whose numerical and simulation examples verify its effectiveness and practicability. Topology and parametric optimizations with the application of response surface method was implemented for the optimal design of a jig reinforcement structure by Cho et al. [
38] to minimize the total jig weight while securing the dimensional precision of a foamed urethane case. Lin et al. [
39] proposed two-stage artificial neural network-based hole image interpretation techniques to develop a fully automated configuration optimization system with improved template variety and recognition reliability.
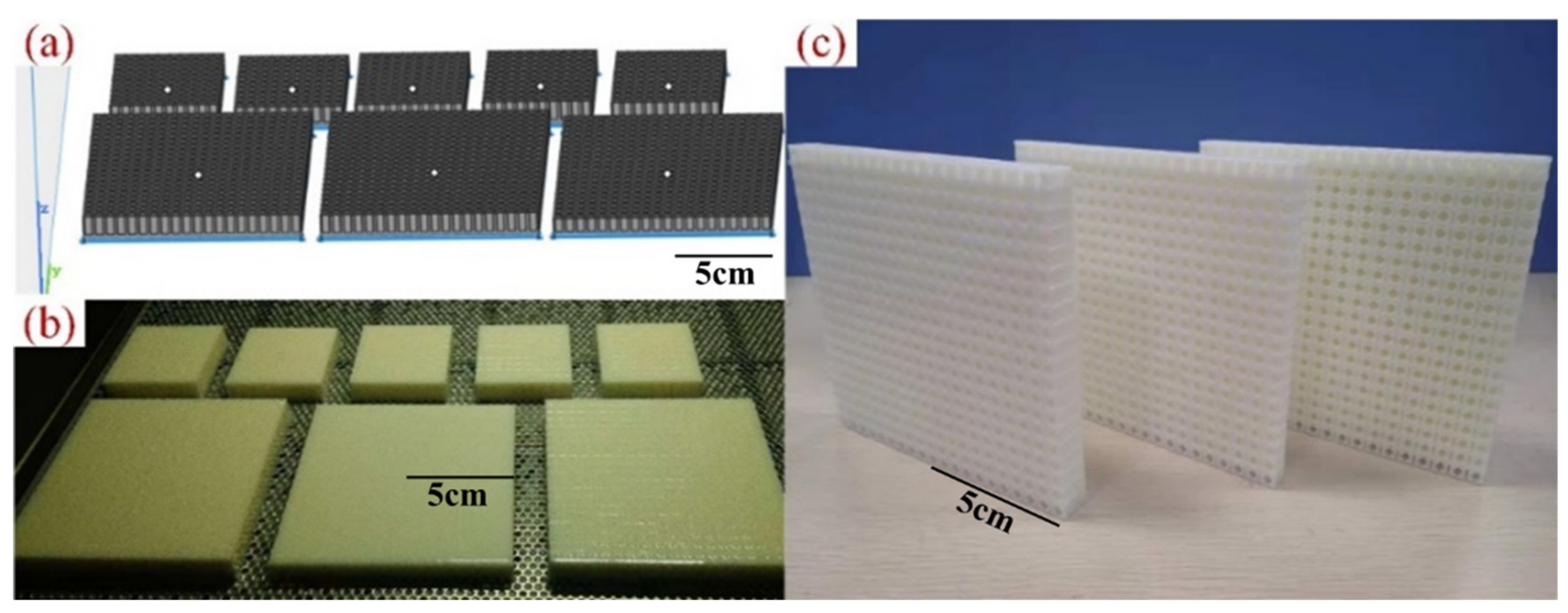
The experimental analysis of the frequency response based on the closed acoustic box includes a verification analysis of the FIP design. It is also necessary to ensure the effectiveness of the optimization results. This process conducts a simulation analysis under practical working conditions and avoids excessive simulation and application deviations. Moreover, the porous acoustic metamaterial unit cell obtained using parametric optimization is distinguished by its complex structure and small macroscopic size. Traditional processing methods are unable to satisfy manufacturing requirements. Based on the additive manufacturing method, our method realizes high-precision manufacturing of optimized structures while the size and shape accuracy satisfy the subsequent experimental requirements.
This study proposes an FIP design method for the fundamental frequency maximization of an FMAM structure. FIP design method can seek the optimal design in a gradient and interactively adjust the design direction to complete a complex model description of porous acoustic metamaterials. FMAM is designed to improve the acoustic and vibration characteristics, avoid resonance, and reduce the level of structural response of acoustic metamaterials effectively. Modal acoustic characteristics of FMAM are studied through a closed acoustic box based on the ASI system. The remainder of this paper is organized as follows:
Section 2 introduces the application background and theories of the frequency modulation process of FMAM.
Section 3 completes the topology optimization with the design goal of maximizing the fundamental frequency and obtaining the initial FMAM configuration.
Section 4 establishes the three-dimensional FMAM model based on the above-mentioned two-dimensional initial configuration and performs parametric optimization based on the SM. Moreover, feedback adjustments were performed to strengthen the parametric optimization effect.
Section 5 describes the construction of a closed ASI box to study the modal and acoustic characteristics of FMAM.
Section 6 summarizes the content of this study. All acronyms are given in the Abbreviations.
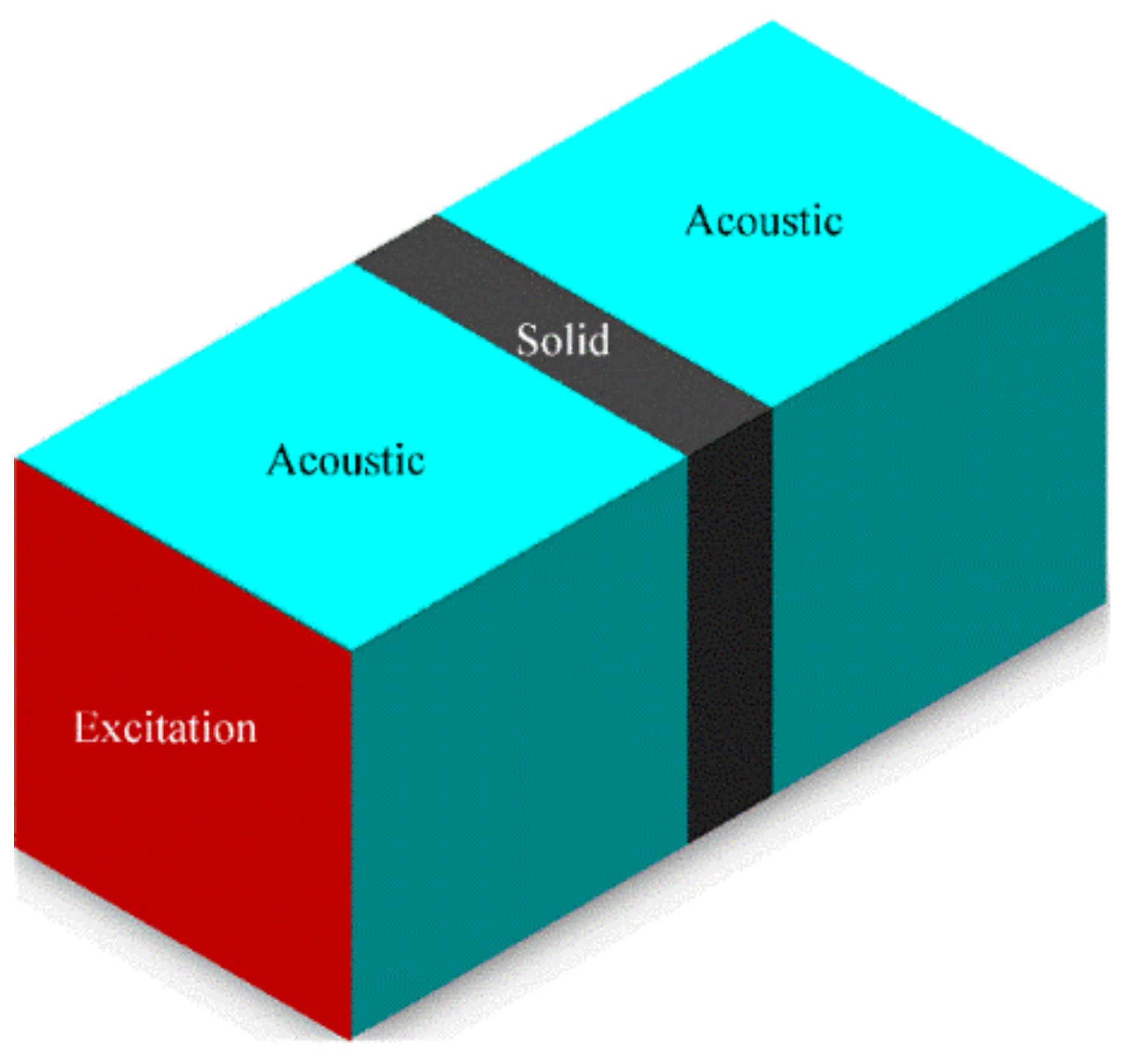
2. Research Problems on FMAM
Noise is a primary form of external excitation in acoustic structures. To ensure a healthy and effective working environment, acoustic insulation and noise reduction materials are worth researching. In particular, if the frequency of an external excitation is close to the natural frequency of the acoustic structure, the amplitude of the acoustic structure increases sharply. Strong vibrations inevitably lead to the aggravation of noise, affecting the overall vibration and noise reduction performance of the acoustic structure.
In this study, FMAM was designed using a straightforward optimization design method to avoid resonance. In previous studies, the shape or size of some structures was optimized to change their natural frequency while they were bound to a single initial structure. The rigidity and mass distribution of some structures were improved to change their natural frequency; however, it was difficult to satisfy the practical requirements for high-dimensional complex structures [
40,
41,
42]. Considering the characteristics of the previous design methods, the FIP design method was used in this study to investigate the natural frequency of acoustic metamaterials.
There are several objective functions for the FIP design method to control the natural frequency of porous acoustic metamaterials such as maximizing the fundamental frequency, minimizing the difference between the natural frequency of any specified order and a given frequency, and maximizing the gap between adjacent natural frequencies. Among the above optimization objectives of the natural frequency, the optimization model with the maximum fundamental frequency was adopted because of its convenience such as stable iteration and rapid convergence. Therefore, maximization of the fundamental frequency of the porous acoustic metamaterial is used as the objective function in the FIP design method.
When a plane wave with finite amplitude propagates in an ideal fluid medium with no viscous loss, the motion and continuity equations of a non-linear medium considering the one-dimensional propagation along the
direction are expressed, respectively, as follows [
43]:
where
represents the particle velocity, which can be obtained from the acoustic wave power,
denotes the acoustic pressure, and
indicates the medium density. At this instant, the non-linear term
has almost the same order of magnitude as the other terms.
In an ideal medium, the particle velocity
and sound velocity
are both single-valued functions of density
for adiabatic processes. Substituting these into Equations (1) and (2), we obtain
The left-hand side of the above formula represents
, which is the derivative of the constant
, and
is the derivative of the constant
. However, the value of
can only be determined by
. Regardless of whether the value is constant for
or
, there is no difference in the derivative of
. So:
From Equation (3), we can get:
where
is the acoustic speed and
. From Equation (5), we obtain
Using this formula, the general relationship between the particle velocity
, density increment
, and acoustic pressure
can be determined. Integrating Equation (6) into
, we obtain
where
represents the total pressure generated by the acoustic wave motion and
denotes the maximum value of the pressure changes, i.e., the maximum value of the acoustic pressure. For plane continuous sound waves, the external sound pressure matrix
on the ASI interface can be obtained using Equation (7). According to the above-mentioned equations, the steady-state boundary equations of the acoustic pressure and displacement at the boundary nodes of the acoustic field are as follows:
On the interface
between the solid structure and air, the external acoustic pressure matrix
and solid internal elastic force matrix
satisfy the balance equation of the coupling interface, which is expressed as follows:
where
and
represent the normal vectors of air and the solid structures acting on the coupling interface, respectively. From the stiffness matrix, mass matrix, and elastic constitutive relationship, the equilibrium equation of the ASI model can be obtained as follows:
where
,
,
, and
represent the total pressure, overall stiffness matrix, and overall displacement matrix, respectively, generated by the large-amplitude acoustic wave motion of the optimized model. Equation (10) is an implicit equation of the structural natural frequency
, and is the main constraint condition for subsequent topology optimization. For a continuous structure system with
n degrees of freedom,
n continuous natural frequencies exist. Among them, the low-order natural frequency, particularly the first-order natural frequency (i.e., the fundamental frequency), is highly significant for analyzing the dynamic characteristics of the structure.
Owing to the non-linear characteristics of the ASI system, the analysis and solution of the natural frequency
must also use the aforementioned non-linear analysis method. The non-linear finite element method was used to analyze the structural frequency response. The nonlinear boundary element method was used to address the problem of acoustic propagation in the coupling boundary and limited acoustic field. In the coupled physical field,
is the closed area of a single structural field,
is a type of boundary of
(each point has a uniquely determined tangent plane), and
is another type of boundary
(a piecewise smooth surface with finite edges). The velocity potential function
was introduced to derive the general equation for the boundary element [
44,
45]. The corresponding governing equations for the potential function
at different positions in the coupled physical field are expressed as follows:
where
. According to the Gaussian divergence theorem and Green’s formula, the weighted residual value of the weight function
is
The boundary integral equation is established to move any point of
in the space region to the boundary region for integration. Therefore, the boundary near the point of
changes from a whole sphere to two hemispheres (
and
). The radius of the ball
is very small. Equation (12) can be transformed into
After the boundary integral equation is discretized by elements including the meshing and discretization of the integral within the domain, the matrix form of the boundary integral equation of the displacement rate is expressed as follows:
where
and
represent the kernel and interpolation shape functions of the basic solution, respectively. Matrix
is obtained from the volume fraction of the inelastic strain.
,
, and
represent the displacement rate of the boundary node, surface force rate, and strain rate of the node in the domain, respectively. The stress integral equation in the domain is
Substituting the boundary conditions into Equation (14), it can be rewritten as
where
Correspondingly, Equation (15) can be rewritten as:
Substituting Equation (16) into Equation (18), we obtain:
The load factors for solving the nonlinear boundary element are required to solve the load increment problem. Equations (16) and (18) can be rewritten as
where
represents the structural strain rate of the basic incremental step,
denotes the incremental structural strain rate, and
and
indicate the load factors of the adjacent loading step. By setting
and
, the boundary node stress is obtained. The load factor of the elastic loading step is then obtained by calculating the equivalent stress of the node:
where the maximum equivalent stress
is equal to the yield limit of uniaxial tension. Subsequent incremental iterative calculations were performed based on the load factor. According to the expressions for the boundary integral and displacement rates, the weak singular integral of type
can be obtained as follows:
The second-order tightly supported radial basis function
is used for interpolation, and we obtain:
where
is the position coordinate of the interpolation control point
,
is the expansion coefficient of the corresponding control point, and r is the support radius defined in Euclidean space.
reflects the influence range of the basis function at the control point
. Combining Equations (22) and (23) yields
where
and
are the interpolation and displacement vectors, respectively [
46,
47].
6. Conclusions
To prevent the porous acoustic structures in the ASI system from resonating and affecting its vibration and noise reduction performance, this study executed an FIP design of the structural fundamental frequency of porous acoustic metamaterials. First, a frequency response model of the solid structure in the ASI system was established. Subsequently, the FIP method was used to obtain the FMAM with better vibration and noise reduction performance based on the goal of maximizing the fundamental frequency of the solid structure. In particular, the constraints of the surficial acoustic pressure were considered in the optimization model of the structural fundamental frequency. Based on the deviation of the results of parametric optimization from the actual requirements, feedback adjustments were made to strengthen the parametric optimization effect. Finally, the modal acoustic characteristics of FMAM were studied using a closed acoustic box based on the ASI system. The design effect of the FIP method on the vibration and noise reduction performance of the FMAM was verified. The following conclusions were drawn:
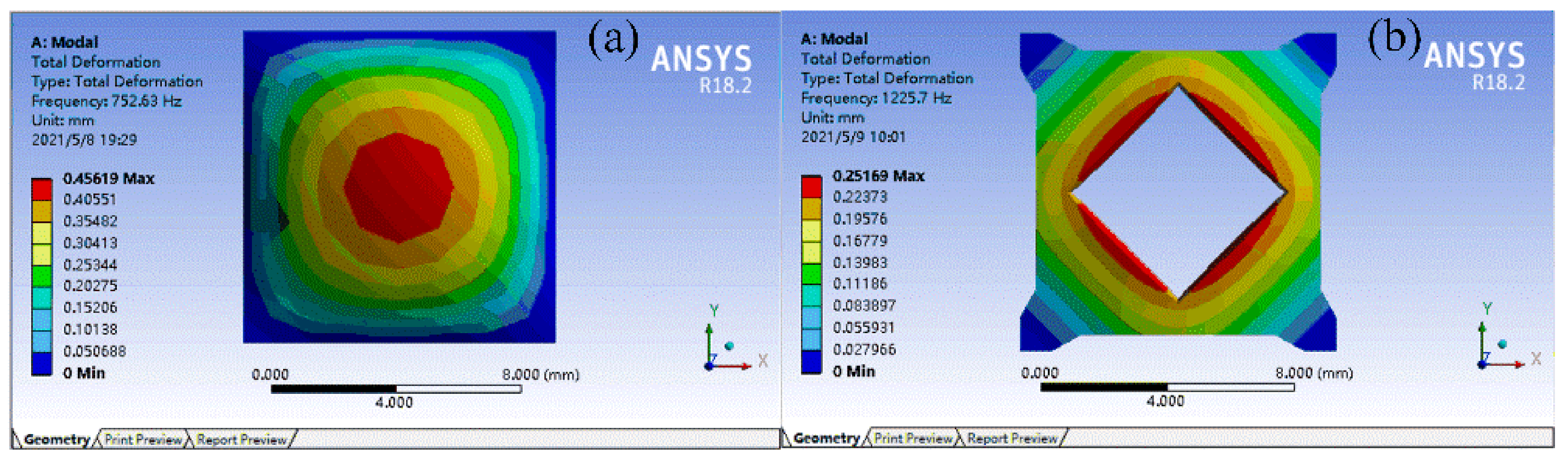
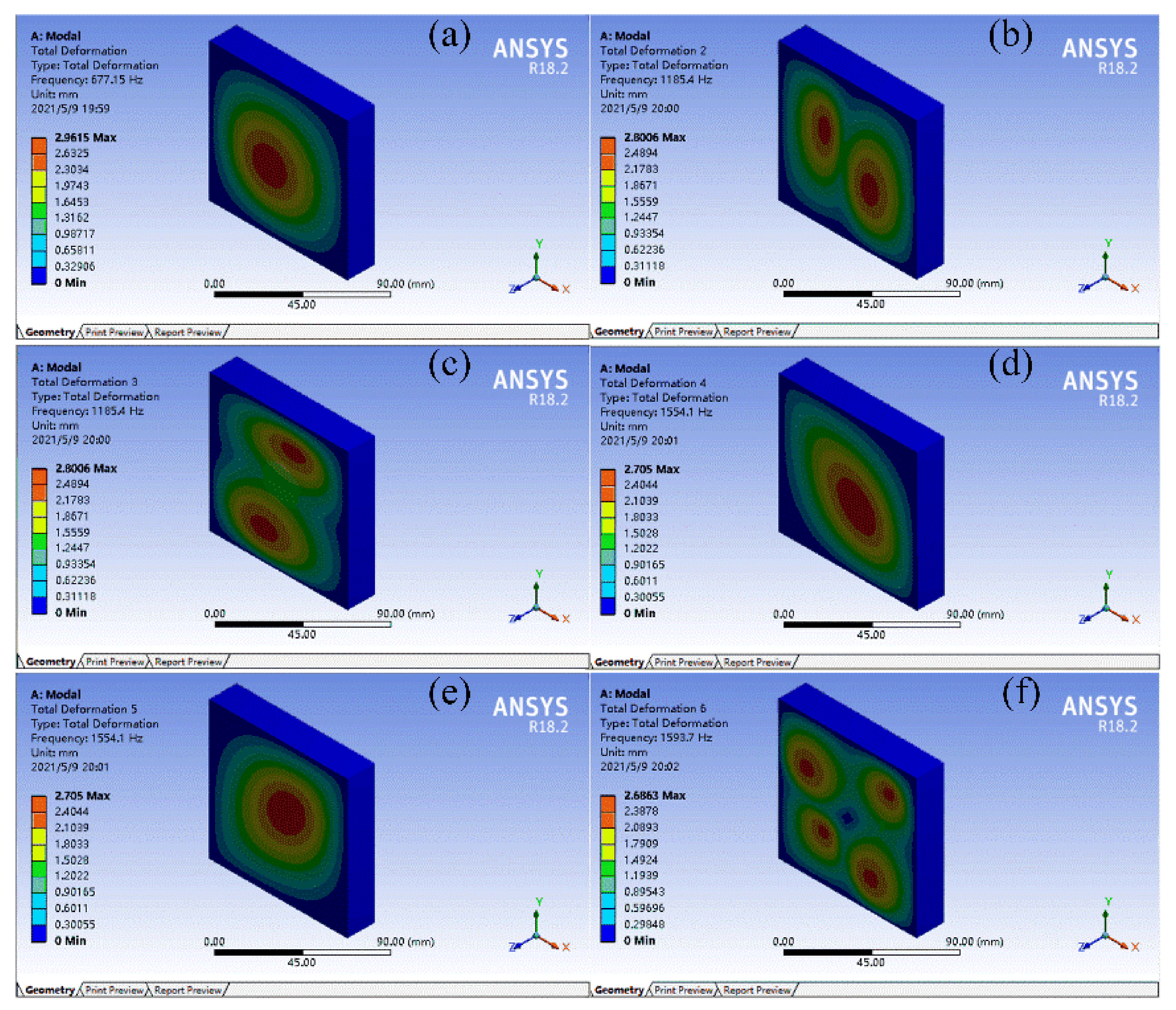
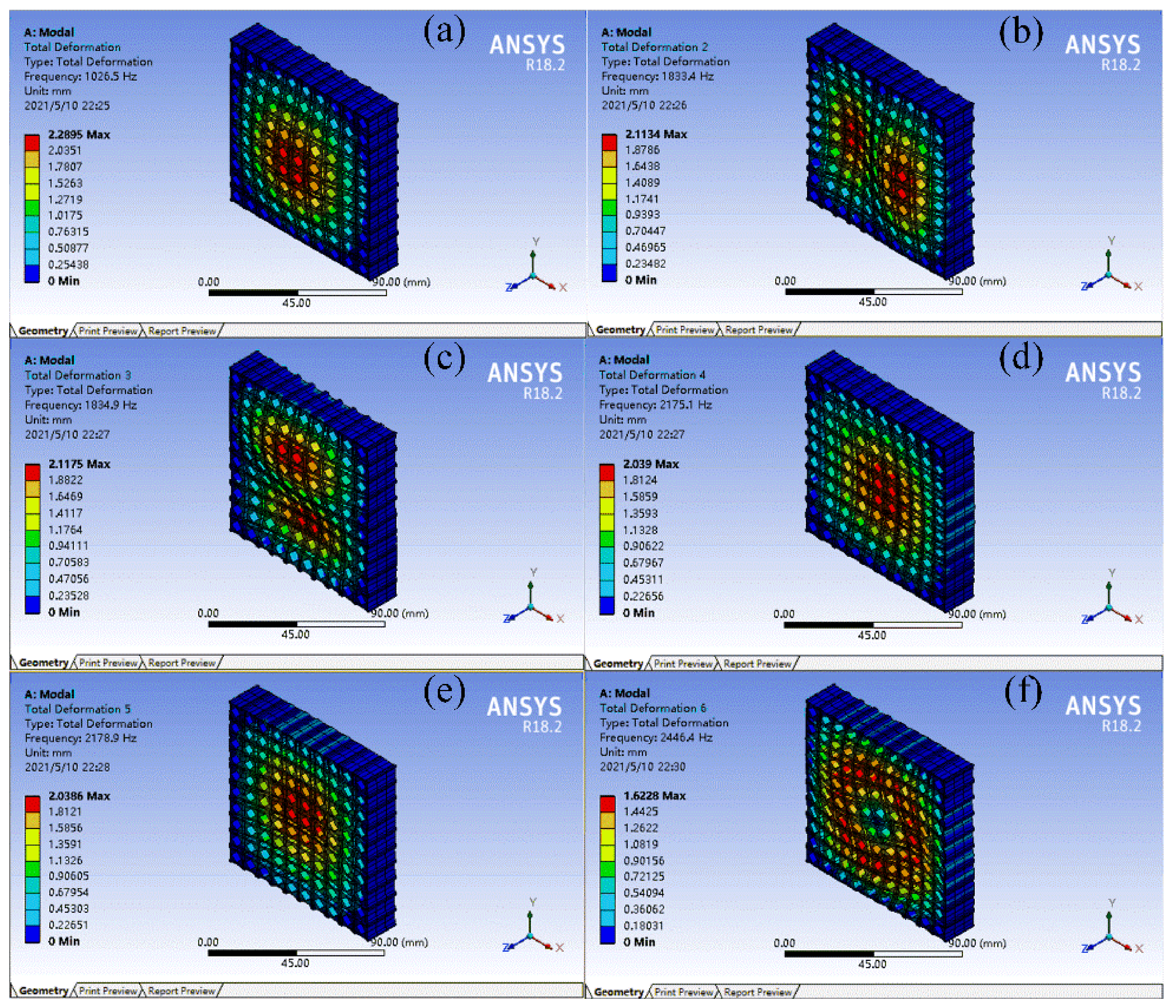
The FMAM obtained using topology optimization increased the natural frequency (from 750 to 1210 Hz) and reduced the maximum amplitude. The change rate was also relatively large (the change rate of the first three natural frequency is 51.6%, 54.67%, and 54.79%, respectively; the change rate of the first three maximum amplitude is −22.69%, −24.54%, and −24.39%, respectively). However, the first three natural frequencies of FMAM (1026.5, 1833.4, and 1834.9 Hz, respectively) still could not avoid the mid-low frequency noise distribution range [500 Hz, 2000 Hz]. Therefore, the fundamental structural frequency required to be further improved through subsequent parametric optimization.
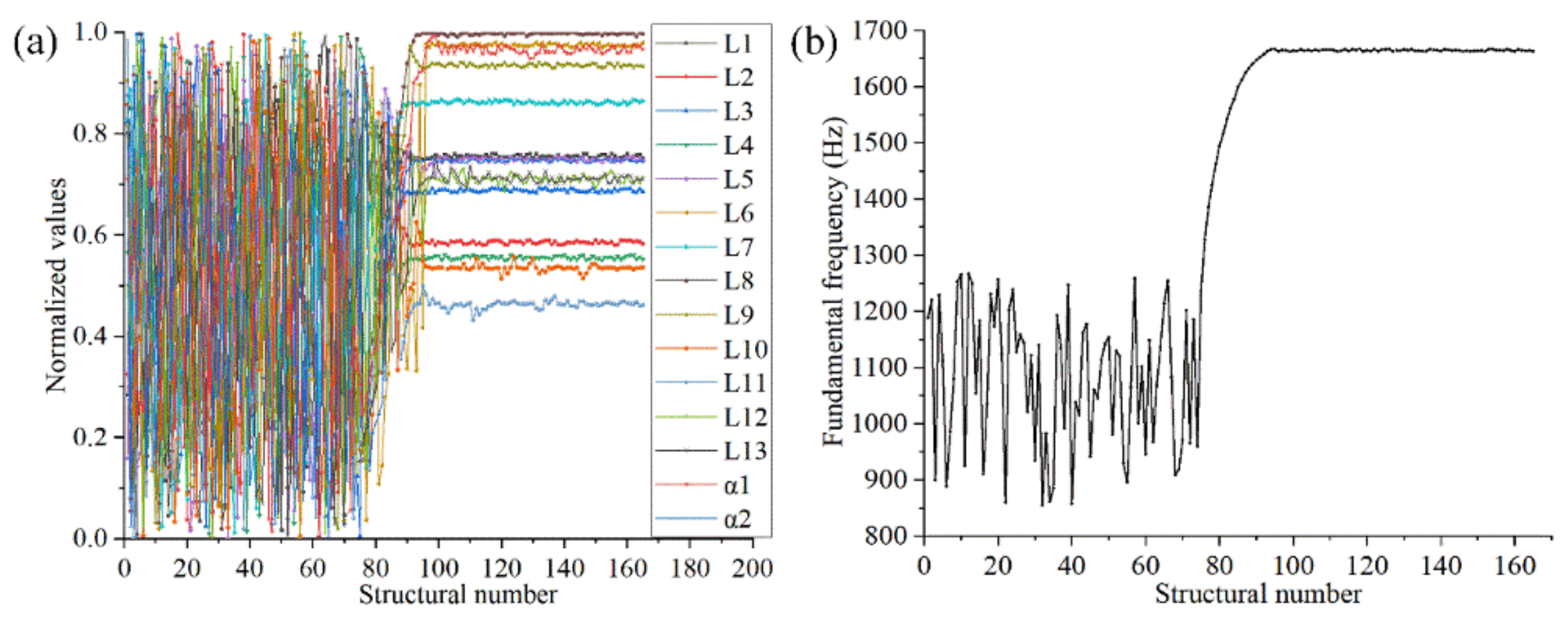
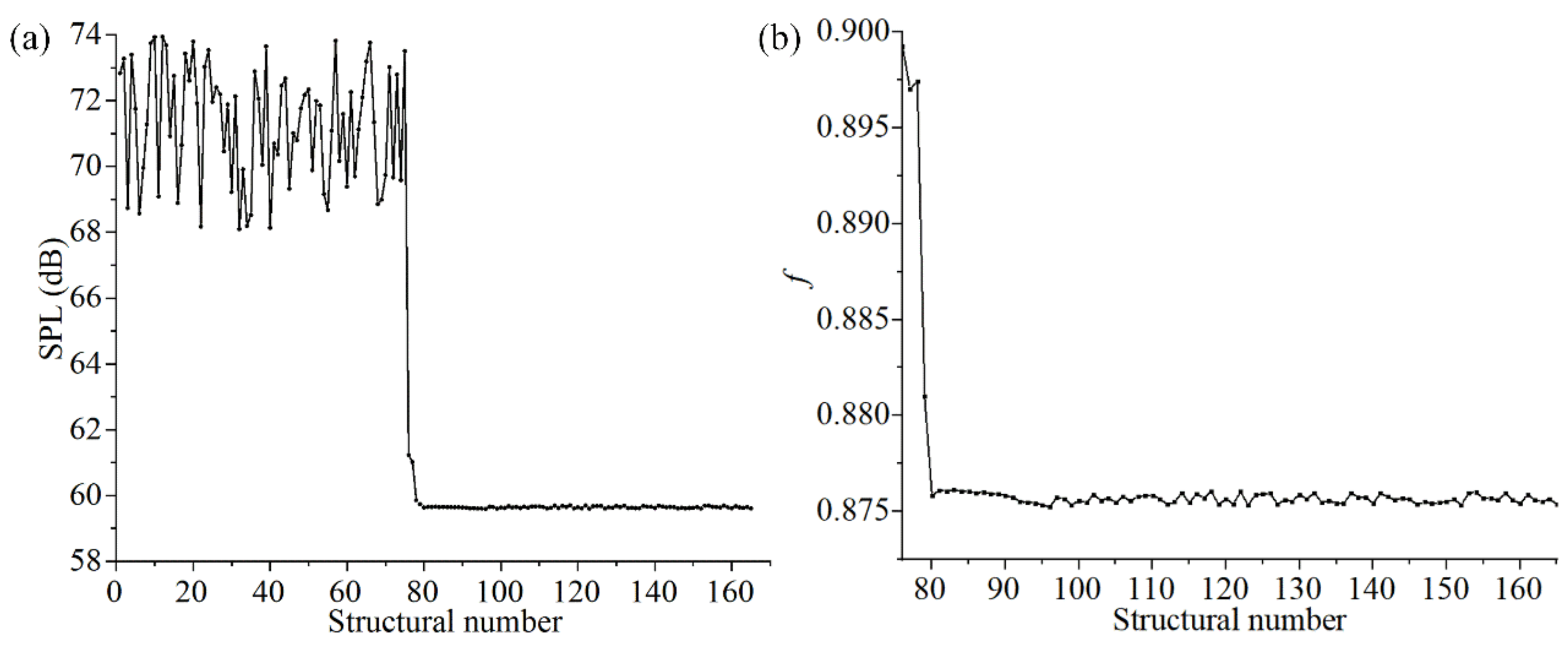
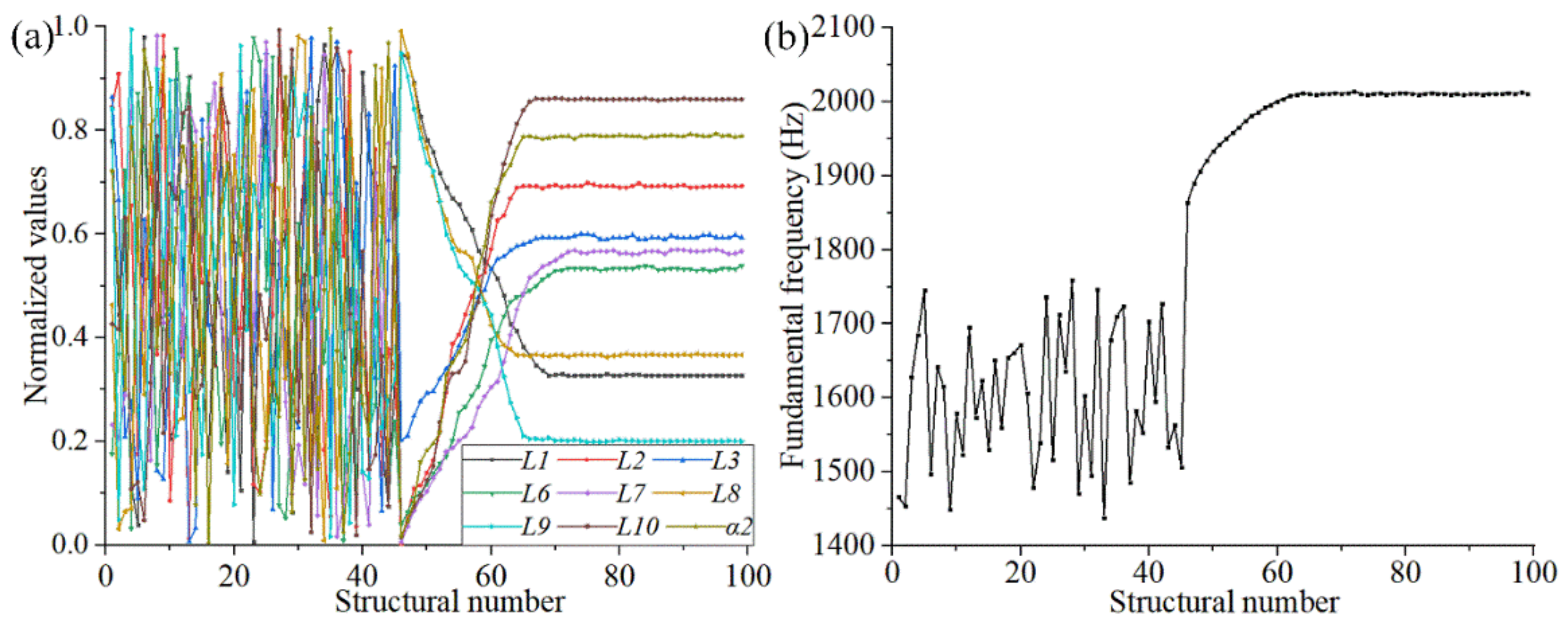
After parametric optimization, the fundamental frequency of the FMAM was 1662.4 Hz, an increase of 61.59%. However, a feedback adjustment was triggered due to the result of the parametric optimization being too far from the design goal. The fundamental frequency of the structure after the second optimization was 2011 Hz, and the entire modal frequency distribution interval completely avoided the mid-to low-frequency noise distribution range.
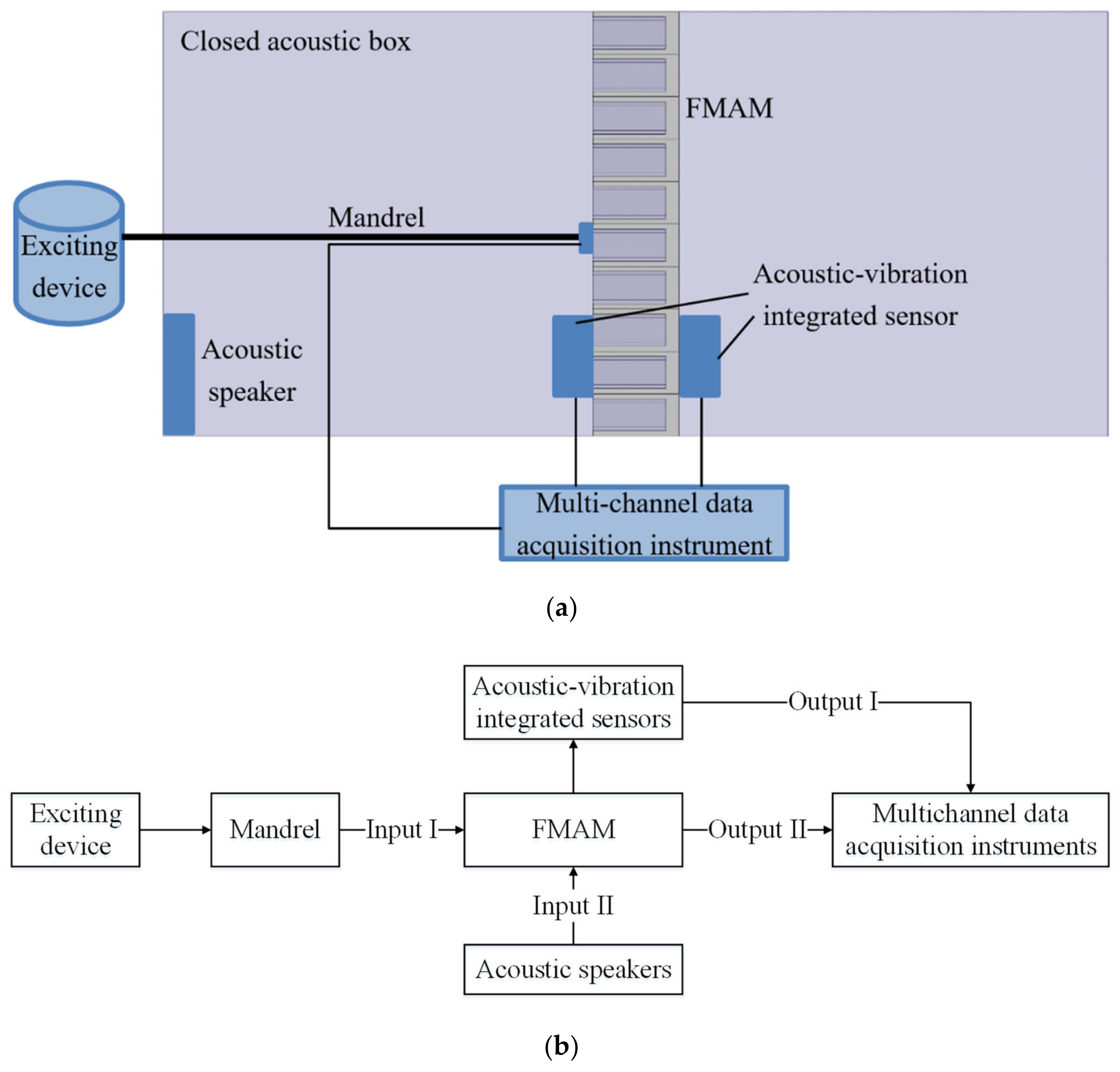
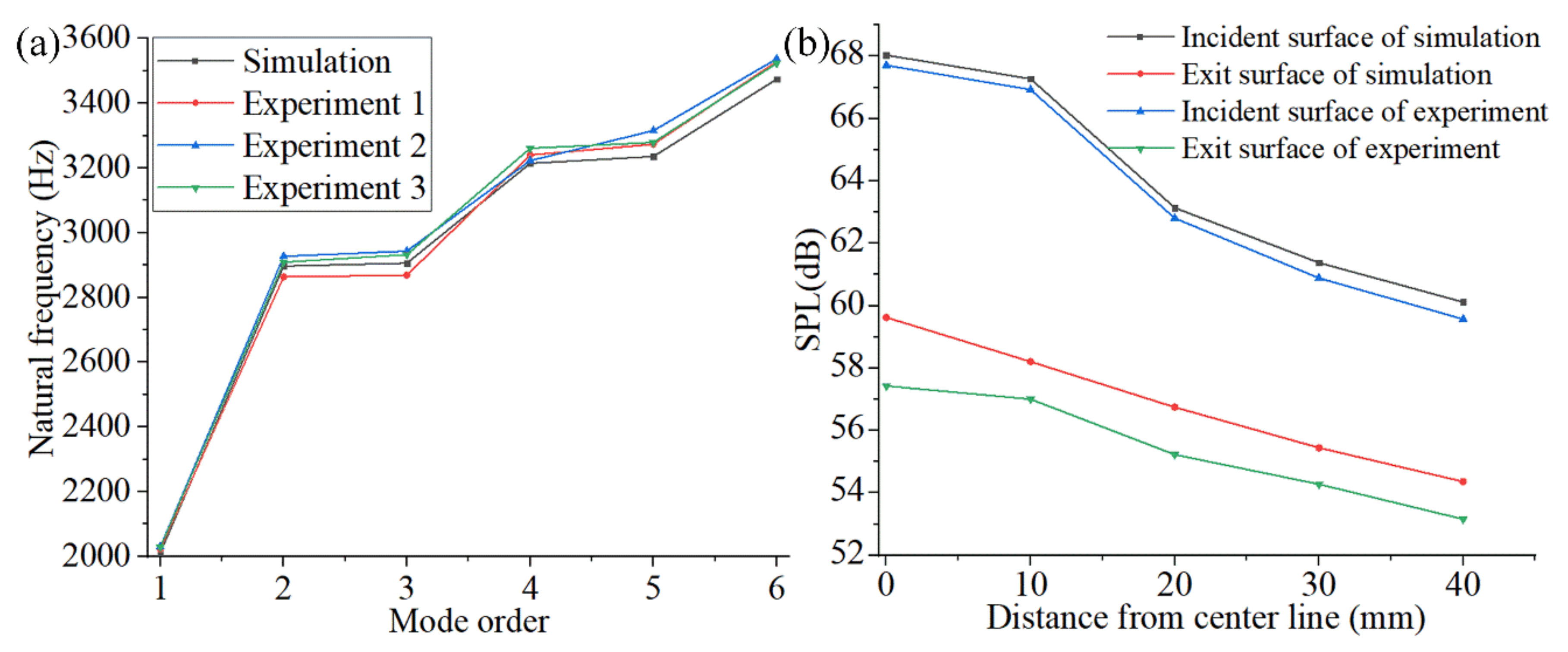
The modal acoustic experiment of the FMAM was performed using a closed acoustic box. The experiment measured that the FMAM reached a resonance state at 2010 Hz with an amplitude of 1.513 mm, consistent with the simulation results. This result illustrated the effectiveness of the FIP method in designing the fundamental frequencies of porous acoustic metamaterials.
In the future, this method can be extended to solve design problem with the mid and high frequency ranges. Moreover, the problem with multiple resonances is also worth an investigation. It is also noted that the parametric modelling is a heuristic step. Further attempts to avoid this step and automate the whole process can be regarded as a future work.