Temperature Field Measurement of Photovoltaic Module Based on Fiber Bragg Grating Sensor Array
Abstract
:1. Introduction
- (1)
- The contact measurement method based on thermal resistance, thermocouples, and other electrical sensors: To avoid the shadow of the sensor, the electrical sensor is usually placed on the surface of the photovoltaic cell backplane for temperature measurement. Bohorquez et al. [6] used a DS18B20 digital temperature sensor to measure the temperature of photovoltaic facilities. The sensor was calibrated and compared with a Pt100 thermal resistance sensor. The deviation between the developed system and the system based on the standard Pt100 was less than ±0.4 °C. Martínez et al. [7] used a single bus digital temperature sensor to measure the temperature of photovoltaic facilities.
- (2)
- The noncontact measurement method based on visible light and infrared imaging: Tsanakas et al. [8] collected the infrared thermal image of a photovoltaic array for image processing, and selected the Canny edge detection operator to identify the hot spot effect module. Bu et al. [9] established an experimental system of pulse electric infrared thermal imaging (PEIT). The results showed that the PEIT algorithm could effectively detect the defects of photovoltaic cells. For obtaining a large field of view of the photovoltaic array image, Mao et al. [10] proposed an automatic splicing algorithm for infrared photovoltaic images based on a fast robust feature detection operator. It performs the full-automatic splicing process from image sequence to panorama. Niazi et al. [11] used the texture and gradient histogram features of photovoltaic module thermal images for classification; the machine learning algorithm was trained to detect hot spots on photovoltaic panels.
- (3)
- The measurement method based on the electrical characteristics of a photovoltaic module. Kim et al. [12] proposed an active hot spot detection method. The results showed that the hot spot in a single cell can increase the capacitance and DC impedance. Ma et al. [13] proposed a hot spot fault diagnosis method based on the photovoltaic module I–V curve. Ghanbari [14] detected the shading hot spot effect by calculating the equivalent DC impedance (EDCI) of a photovoltaic module. Wang et al. [15] proposed an improved fast R-CNN infrared hot spot image detection method. It improved the recognition accuracy of hot spots. Jia [16] proposed a multisensor fault detection and location method based on an improved BP neural network.
2. Photovoltaic Module Temperature Field Analysis
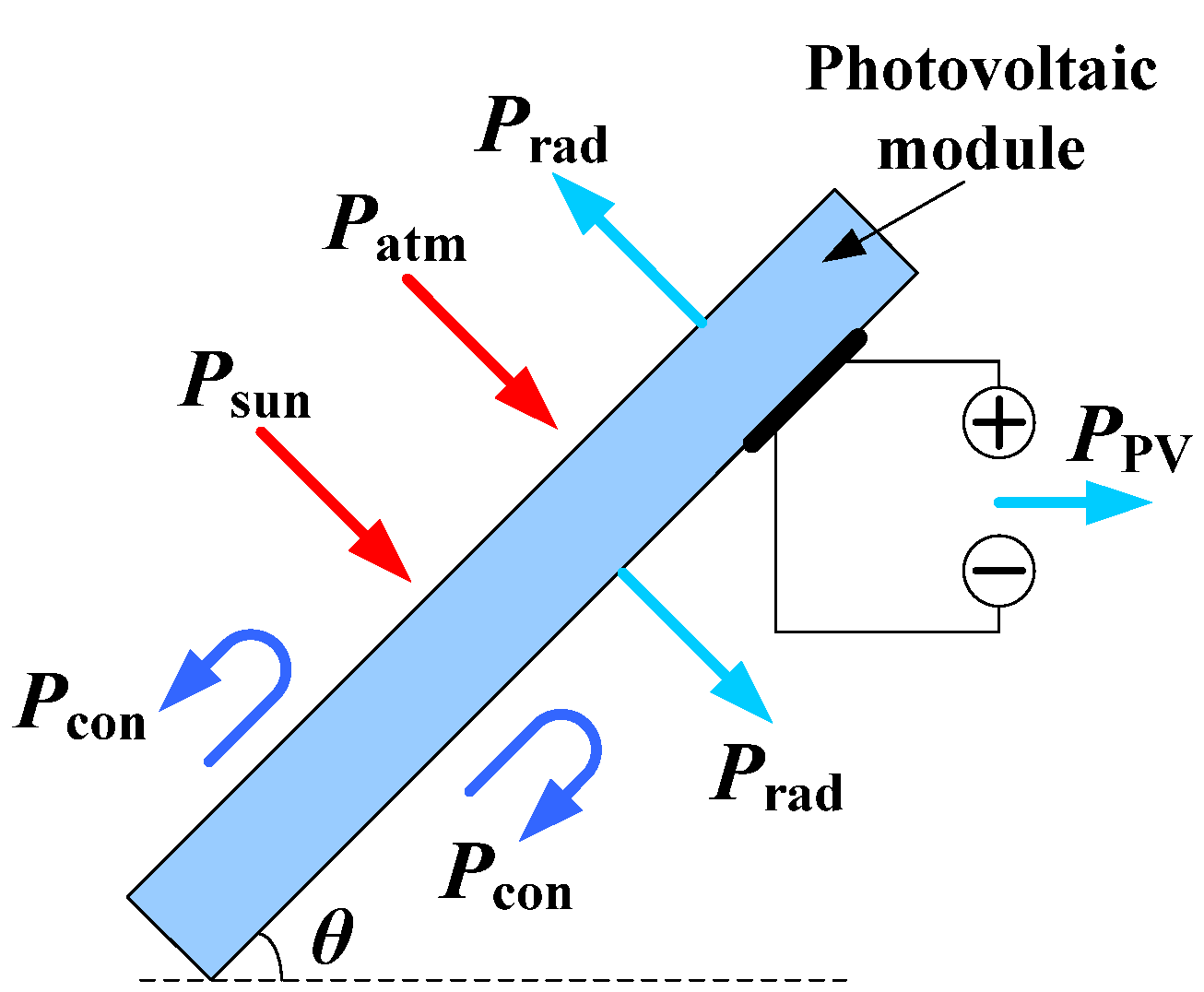
2.1. Energy Input and Output of a Photovoltaic Module
2.2. Photovoltaic Module Temperature Model
2.3. Analysis of Spatial Temperature Field of Photovoltaic Module
3. Temperature Detection Mechanism of FBG Sensor Array
3.1. FBG Temperature Sensing Principle
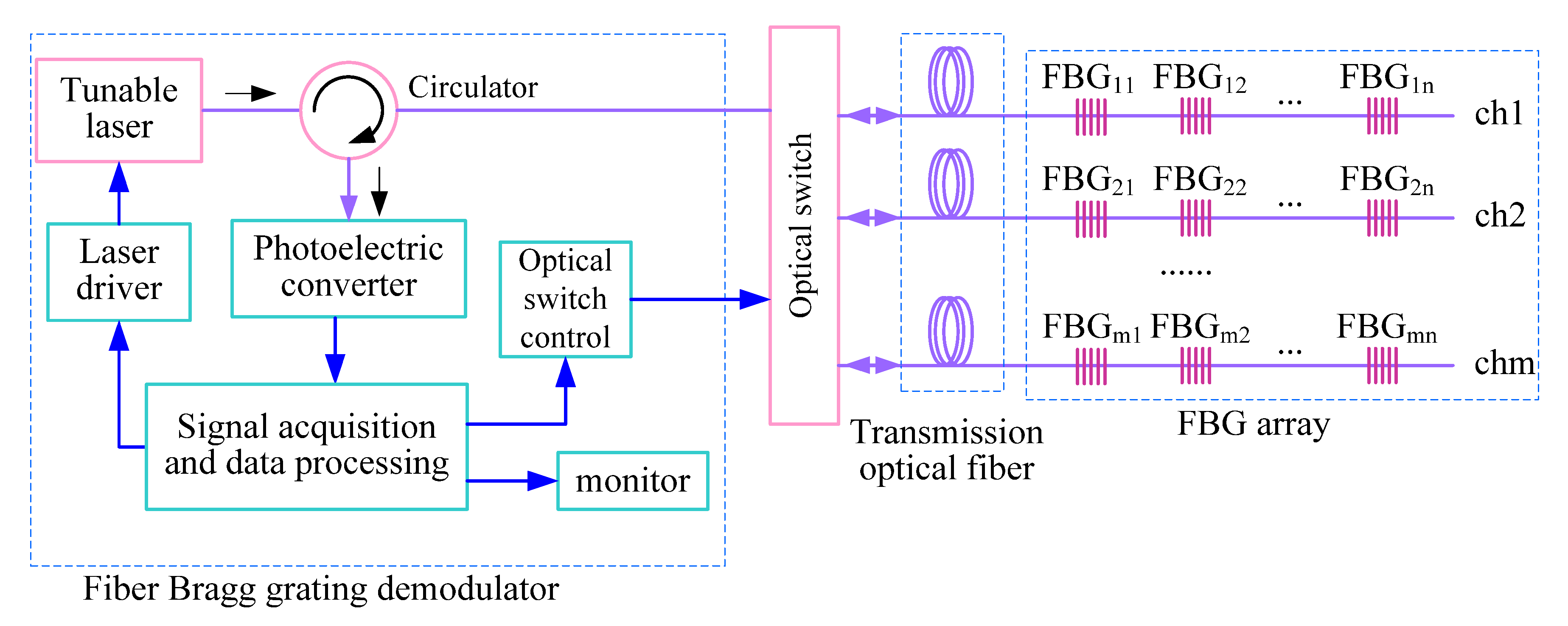
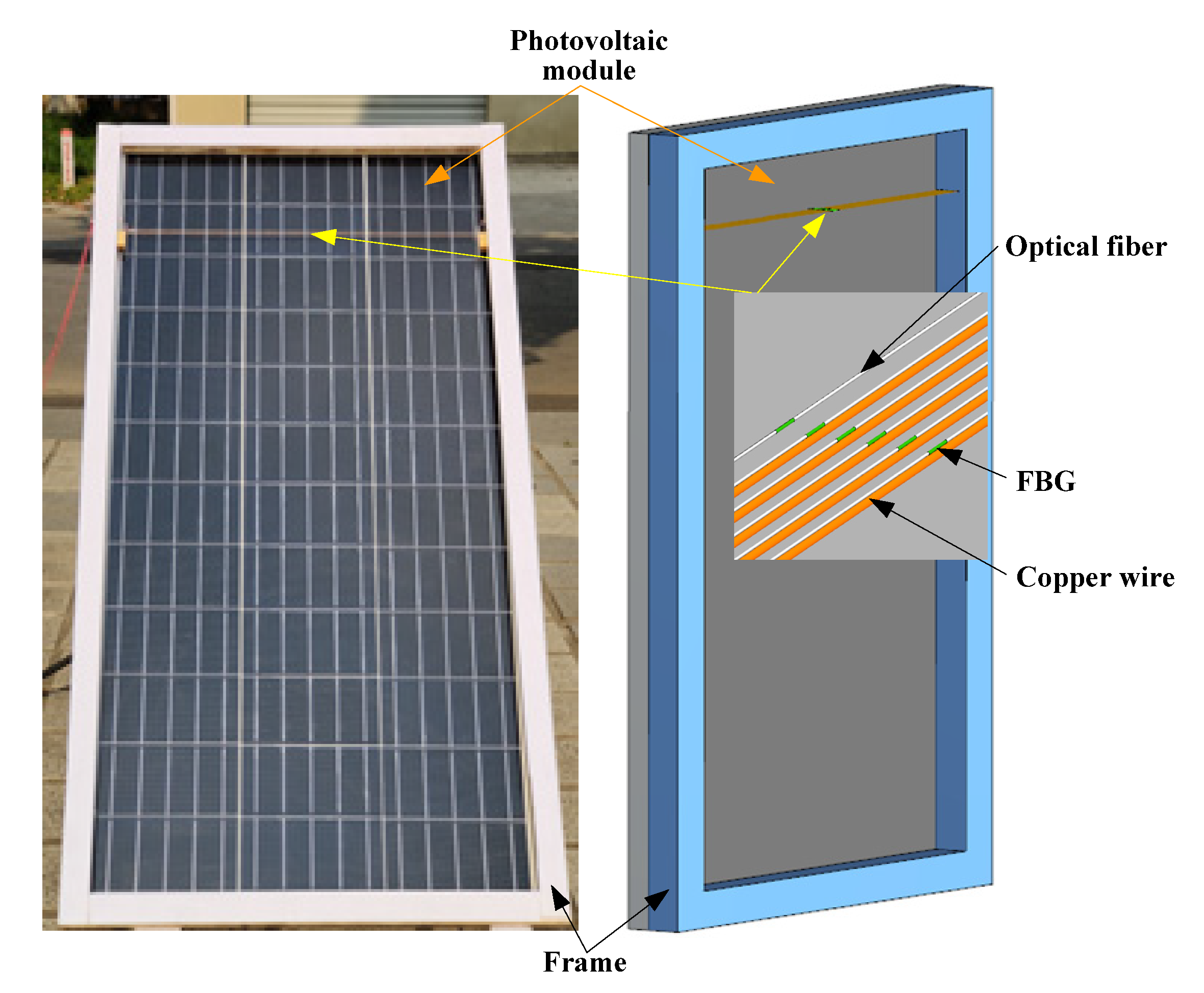
3.2. Temperature Measurement System Based on FBG Array
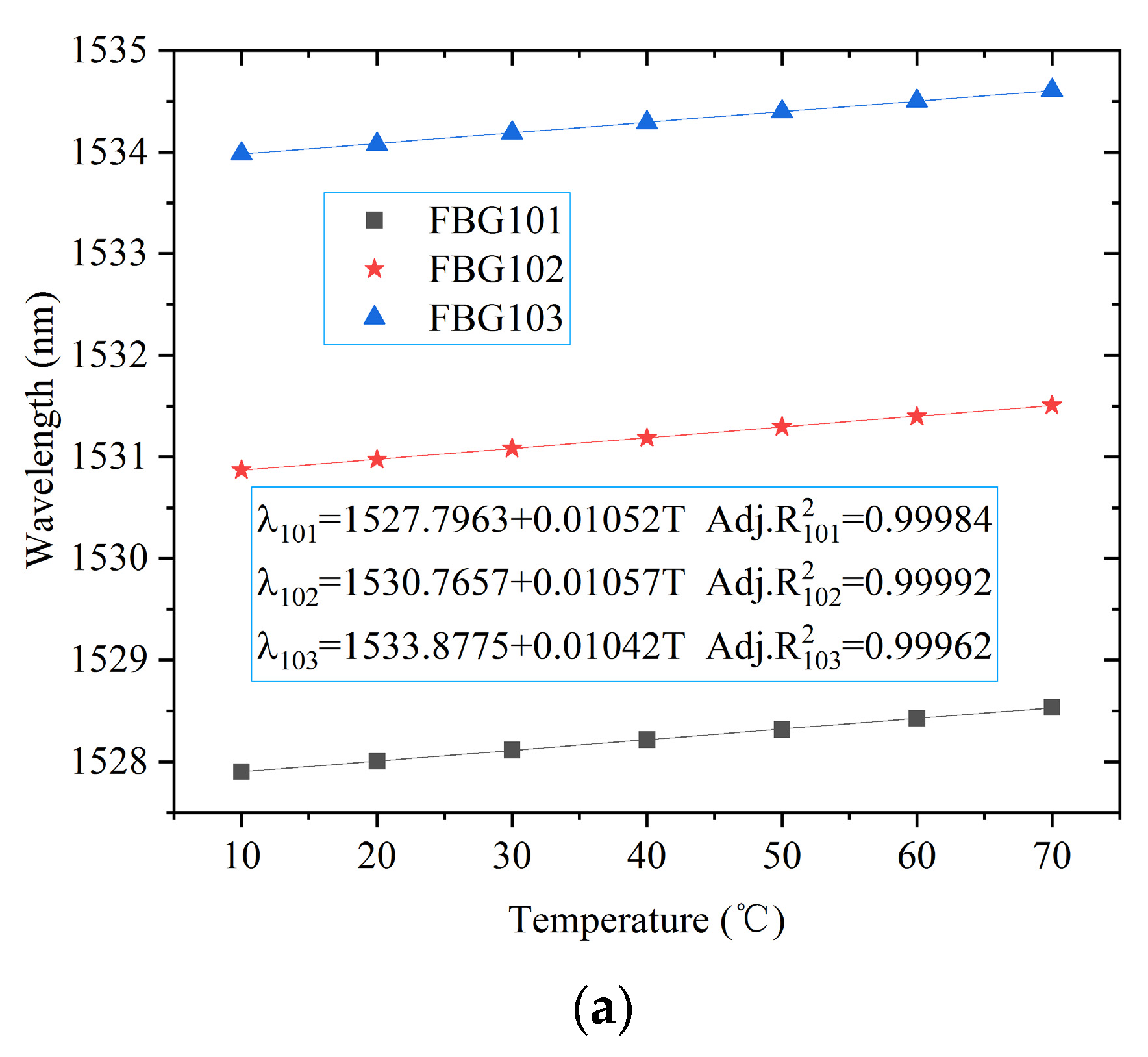
4. Experimental Equipment and FBG Calibration
5. Experiment and Result Analysis
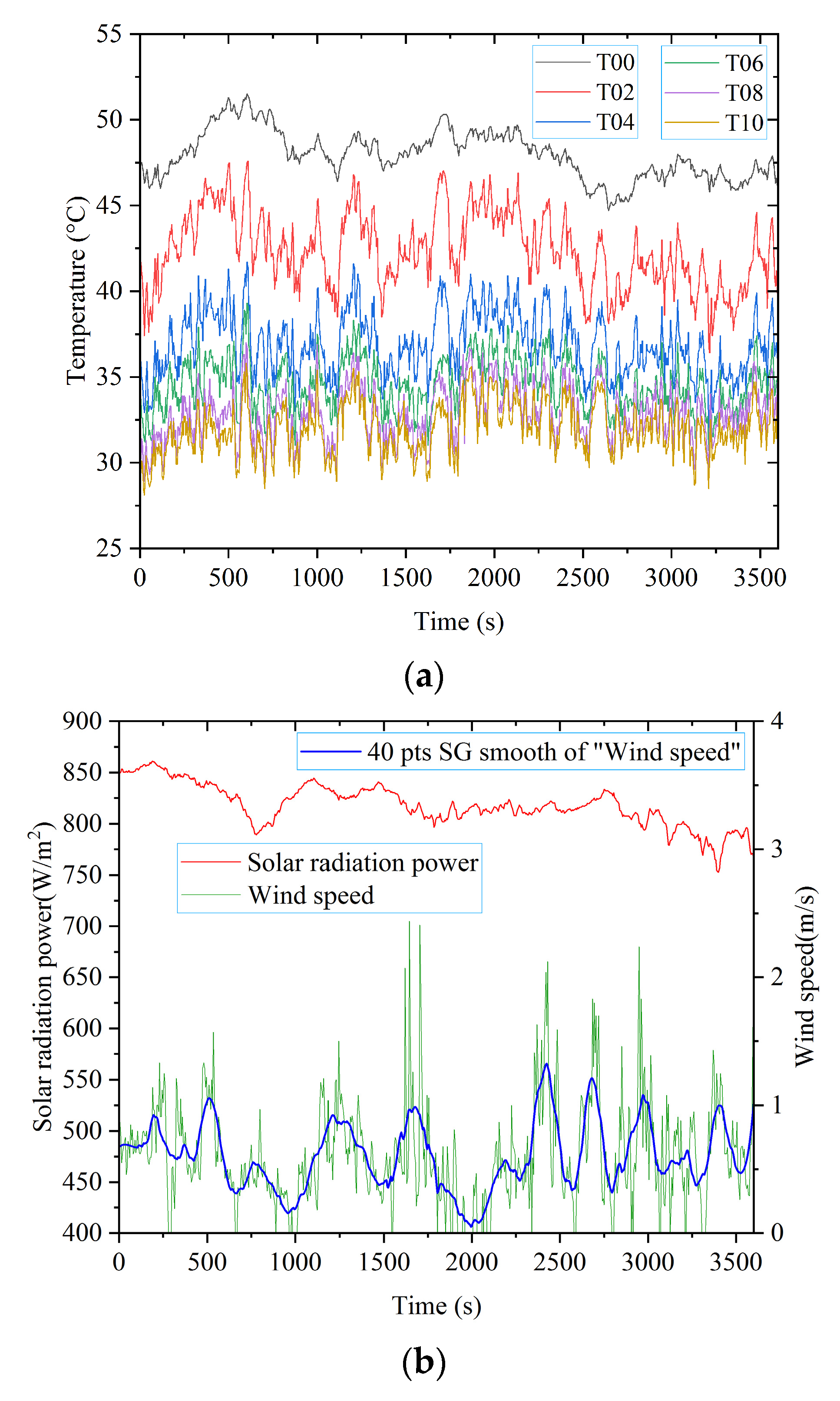
5.1. Surface Temperature Measurement of Photovoltaic Module
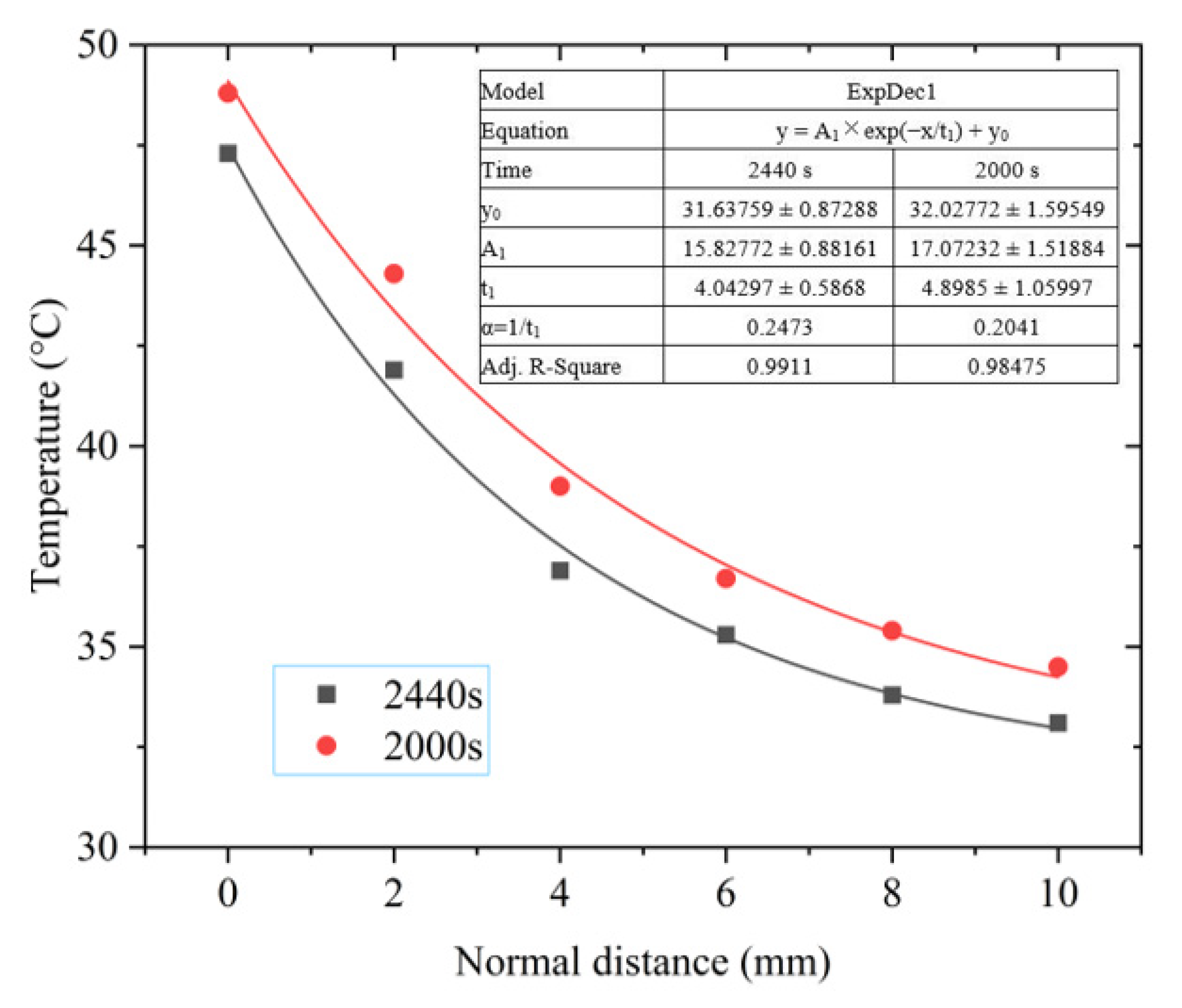
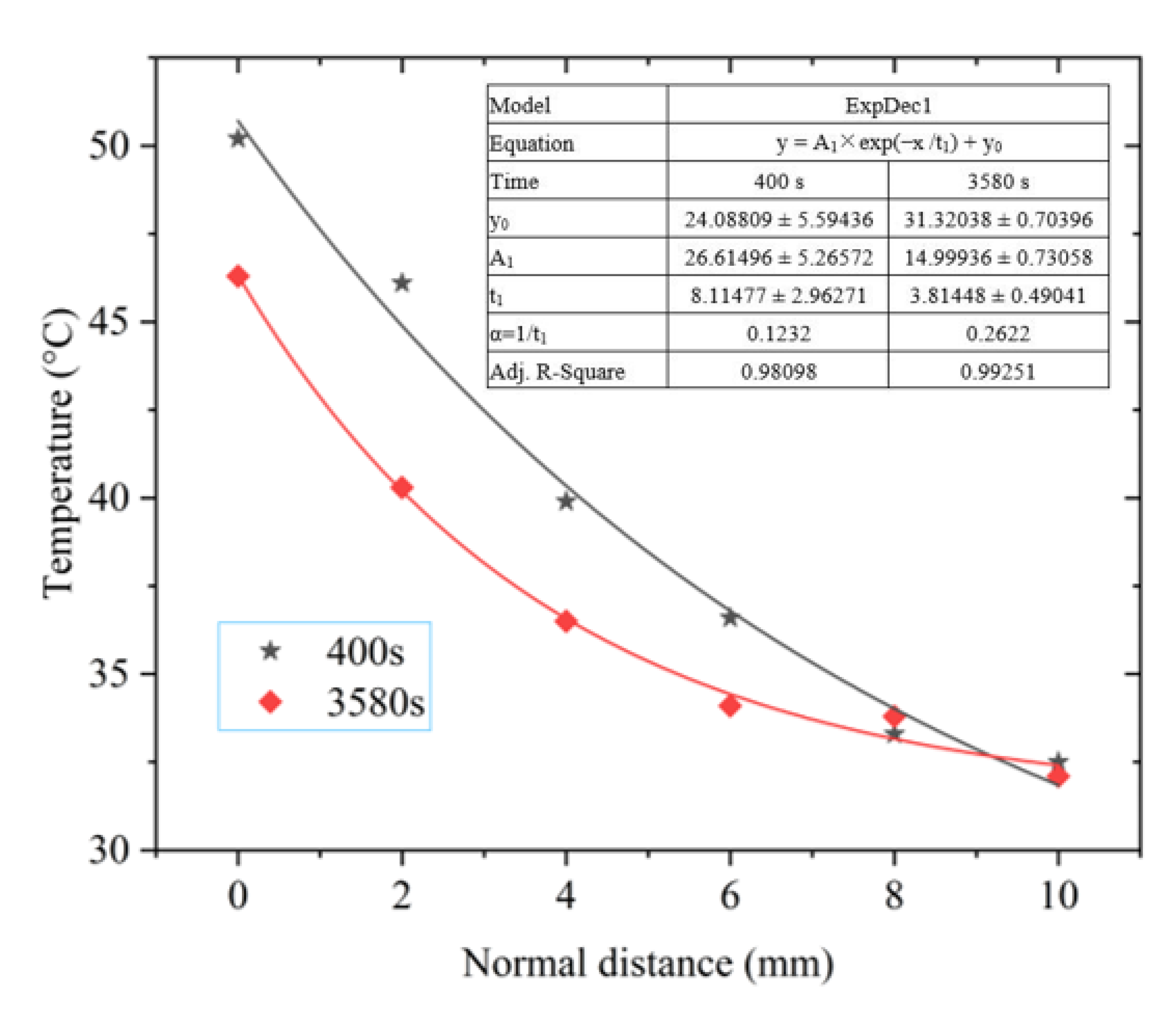
5.2. Measurement and Result Analysis of Spatial Temperature Field Near the Surface of Photovoltaic Module
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Wang, C.; Dai, B.; Yu, J.; Wang, L.; Sun, Y. Recent development and advance of solar photovoltaic materials and photothermal conversion materials. J. Chin. Ceram. Soc. 2017, 45, 1555–1568. [Google Scholar]
- Geisemeyer, I.; Fertig, F.; Warta, W.; Rein, S.; Schubert, M.C. Prediction of silicon PV module temperature for hot spots and worst case partial shading situations using spatially resolved lock-in thermography. Sol. Energy Mater. Sol. Cells 2014, 120 Pt A, 259–269. [Google Scholar] [CrossRef]
- Zhang, Z.; Shan, L.; Wang, L.; Wu, J.; Quan, P. Study on case analysis and effect factors of hot spot fault for photovoltaic module. Acta Energ. Sol. Sin. 2017, 38, 271–278. [Google Scholar]
- Xiao, L.; He, Y.; Peng, Y.; Liu, J.; Li, L. Theory and experiment study on temperature effects on photovoltaic cell conversion characteristics. Electr. Meas. Instrum. 2014, 51, 62–66. [Google Scholar]
- Singh, G.K. Solar power generation by PV (photovoltaic) technology: A review. Energy 2013, 53, 1–13. [Google Scholar] [CrossRef]
- Bohorquez, M.A.M.; Gomez, J.M.E.; Marquez, J.M.A. A new and inexpensive temperature-measuring system: Application to photovoltaic solar facilities. Sol. Energy 2009, 83, 883–890. [Google Scholar] [CrossRef]
- Martínez, M.A.; Andújar, J.M.; Enrique, J.M. Temperature Measurement in PV Facilities on a Per-Panel Scale. Sensors 2014, 14, 13308–13323. [Google Scholar] [CrossRef]
- Tsanakas, J.A.; Chrysostomou, D.; Botsaris, P.N.; Gasteratos, A. Fault diagnosis of photovoltaic modules through image processing and canny edge detection on field thermographic measurements. Int. J. Sustain. Energy 2015, 34, 351–372. [Google Scholar] [CrossRef]
- Bu, C.; Liu, T.; Li, R.; Liu, G.; Tang, Q. Infrared thermography detection and images sequence processing for defects in photovoltaic cells. Acta Opt. Sin. 2021, 42, 0711002. [Google Scholar]
- Mao, X.; Li, Y. Infrared image stitching of UAV in fault detection of photovoltaic array. Acta Energ. Sol. Sin. 2020, 41, 262–269. [Google Scholar]
- Niazi, K.A.K.; Akhtar, W.; Khan, H.A.; Yang, Y.; Athar, S. Hotspot diagnosis for solar photovoltaic modules using a Naïve Bayes classifier. Sol. Energy 2019, 190, 34–43. [Google Scholar] [CrossRef]
- Kim, K.A.; Seo, G.S.; Cho, B.H.; Krein, T.P. Photovoltaic Hot-Spot Detection for Solar Panel Substrings Using AC Parameter Characterization. IEEE Trans. Power Electron. 2015, 31, 1121–1130. [Google Scholar] [CrossRef]
- Ma, M.; Liu, H.; Yun, P.; Liu, F. Rapid diagnosis of hot spot failure of crystalline silicon PV module based on I–V curve. Microelectron. Reliab. 2019, 100–101, 113402. [Google Scholar] [CrossRef]
- Ghanbari, T. Permanent partial shading detection for protection of photovoltaic modules against hot spotting. IET Renew. Power Gener. 2016, 11, 123–131. [Google Scholar] [CrossRef]
- Wang, D.; Li, C.; Li, M.; Zhang, T.; Zhu, R. Solar photovoltaic modules hot spot detection based on deep convolutional neural networks. Acta Energ. Sol. Sin. 2022, 43, 412–417. [Google Scholar]
- Jia, R.; Li, Y.; Zhang, H.; Han, J. Multi-sensor fault detection and positioning method of photovoltaic array based on improved BP neural network. Acta Energ. Sol. Sin 2018, 1, 110–116. [Google Scholar]
- Zhao, N.; Lin, Q.; Yao, K.; Zhang, F.; Tian, B.; Chen, F.; Jiang, Z. Simultaneous Measurement of Temperature and Refractive Index Using High Temperature Resistant Pure Quartz Grating Based on Femtosecond Laser and HF Etching. Materials 2021, 14, 1028. [Google Scholar] [CrossRef]
- Kim, H.; Kang, D.; Kim, M.; Jung, M.H. Microwave Curing Characteristics of CFRP Composite Depending on Thickness Variation Using FBG Temperature Sensors. Materials 2020, 13, 1720. [Google Scholar] [CrossRef]
- Shafighfard, T.; Mieloszyk, M. Model of the Temperature Influence on Additively Manufactured Carbon Fibre Reinforced Polymer Samples with Embedded Fibre Bragg Grating Sensors. Materials 2022, 15, 222. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Wang, J.; Li, F. A High Spatial Resolution FBG Sensor Array for Measuring Ocean Temperature and Depth. Photonic Sens. 2020, 10, 57–66. [Google Scholar] [CrossRef]
- Kumar, J.; Prakash, O.; Agrawal, S.K.; Mahakud, R.; Mokhariwale, A.; Dixit, S.K.; Nakhee, S.V. Distributed fiber Bragg grating sensor for multipoint temperature monitoring up to 500 °C in high-electromagnetic interference environment. Opt. Eng. 2016, 55, 090502. [Google Scholar] [CrossRef]
- Kokhanovskiy, A.; Shabalov, N.; Dostovalov, A.; Wolf, A. Highly Dense FBG Temperature Sensor Assisted with Deep Learning Algorithms. Sensors 2021, 21, 6188. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Wang, F.; Feng, F.; Wei, B. Hot Spot Detection of Photovoltaic Module Based on Distributed Fiber Bragg Grating Sensor. Sensors 2022, 22, 4951. [Google Scholar] [CrossRef]
- Ross, R.G.; Smokler, M.I. Flat-plate solar array project final Report. In Engineering Sciences and Reliability; Jet Propulsion Lab. Publication: Pasadena, CA, USA, 1986; Volume VI, No. 86-31. [Google Scholar]
- Skoplaki, E.; Boudouvis, A.G.; Palyvos, J.A. A simple correlation for the operating temperature of photovoltaic modules of arbitrary mounting. Sol. Energy Mater. Sol. Cells 2008, 92, 1393–1402. [Google Scholar] [CrossRef]
- Mattei, M.; Notton, G.; Cristofari, C.; Muselli, M.; Poggi, P. Calculation of the polycrystalline PV module temperature using a simple method of energy balance. Renew. Energy 2006, 31, 553–567. [Google Scholar] [CrossRef]
- Trinuruk, P.; Sorapipatana, C.; Chenvidhya, D. Estimating operating cell temperature of BIPV modules in Thailand. Renew. Energy 2009, 34, 2515–2523. [Google Scholar] [CrossRef]
- Faiman, D. Assessing the outdoor operating temperature of photovoltaic modules. Prog. Photovolt. Res. Appl. 2008, 16, 307–315. [Google Scholar] [CrossRef]
- Muzathik, A.M. Photovoltaic modules operating temperature estimation using a simple correlation. Int. J. Energy Eng. 2014, 4, 151–158. [Google Scholar]
- Wang, C.; Yang, A.; Li, J.; Si, Z. Experimental study on effect of multi-factor coupling on the surface temperature of photovoltaic module. Acta Energ. Sol. Sin. 2019, 40, 112–118. [Google Scholar]
- Duan, C.; Ruan, J.; Deng, Y.; Quan, Y. Study on equivalent method of boundary radiation-convection heat transfer for transformer temperature field calculation. Electr. Mach. Control. 2020, 24, 120–129. [Google Scholar]
- Shi, Z.; Cheng, Y.; Han, J.; Du, Z.; Yue, X. Preliminary study of heat transfer performance of semi-transparent PV window with different indoor airflow distribution. Acta Energ. Sol. Sin. 2017, 38, 1612–1619. [Google Scholar]
- Hassanian, R.; Riedel, M.; Helgadottir, A.; Yeganeh, N.; Unnthorsson, R. Implicit Equation for Photovoltaic Module Temperature and Efficiency via Heat Transfer Computational Model. Thermo 2022, 2, 39–55. [Google Scholar] [CrossRef]
- Yang, Y. Networking technology of the distributed large capacity fiber grating. Opt. Tech. 2019, 45, 712–717, 736. [Google Scholar]




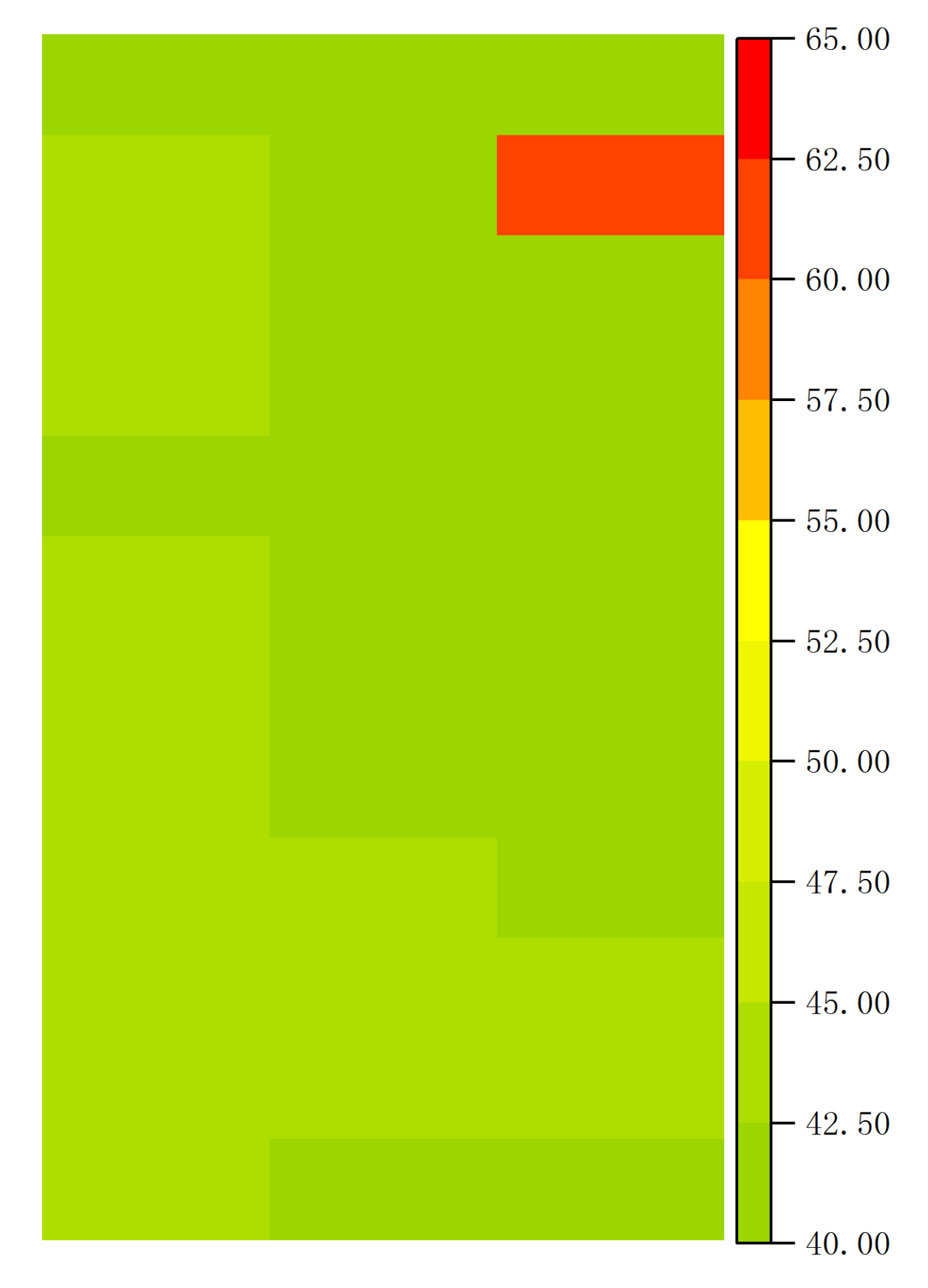
| Cell Number | Temperature (°C) | Cell Number | Temperature (°C) | Cell Number | Temperature (°C) |
|---|---|---|---|---|---|
| 1 | 42.24 | 13 | 42.36 | 25 | 40.06 |
| 2 | 42.95 | 14 | 42.30 | 26 | 60.38 |
| 3 | 42.80 | 15 | 42.46 | 27 | 40.26 |
| 4 | 42.71 | 16 | 41.54 | 28 | 40.48 |
| 5 | 42.42 | 17 | 41.92 | 29 | 41.45 |
| 6 | 42.56 | 18 | 42.21 | 30 | 41.86 |
| 7 | 42.59 | 19 | 41.85 | 31 | 41.79 |
| 8 | 42.67 | 20 | 41.91 | 32 | 41.74 |
| 9 | 43.13 | 21 | 42.56 | 33 | 42.47 |
| 10 | 43.12 | 22 | 42.79 | 34 | 42.56 |
| 11 | 43.16 | 23 | 43.10 | 35 | 42.87 |
| 12 | 42.76 | 24 | 42.40 | 36 | 42.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Feng, F.; Wang, F.; Wei, B. Temperature Field Measurement of Photovoltaic Module Based on Fiber Bragg Grating Sensor Array. Materials 2022, 15, 5324. https://doi.org/10.3390/ma15155324
Li G, Feng F, Wang F, Wei B. Temperature Field Measurement of Photovoltaic Module Based on Fiber Bragg Grating Sensor Array. Materials. 2022; 15(15):5324. https://doi.org/10.3390/ma15155324
Chicago/Turabian StyleLi, Guoli, Fei Feng, Fang Wang, and Bo Wei. 2022. "Temperature Field Measurement of Photovoltaic Module Based on Fiber Bragg Grating Sensor Array" Materials 15, no. 15: 5324. https://doi.org/10.3390/ma15155324
APA StyleLi, G., Feng, F., Wang, F., & Wei, B. (2022). Temperature Field Measurement of Photovoltaic Module Based on Fiber Bragg Grating Sensor Array. Materials, 15(15), 5324. https://doi.org/10.3390/ma15155324






