A Simulation and an Experimental Study of Space Harpoon Low-Velocity Impact, Anchored Debris
Abstract
:1. Introduction
2. Impact Experiment
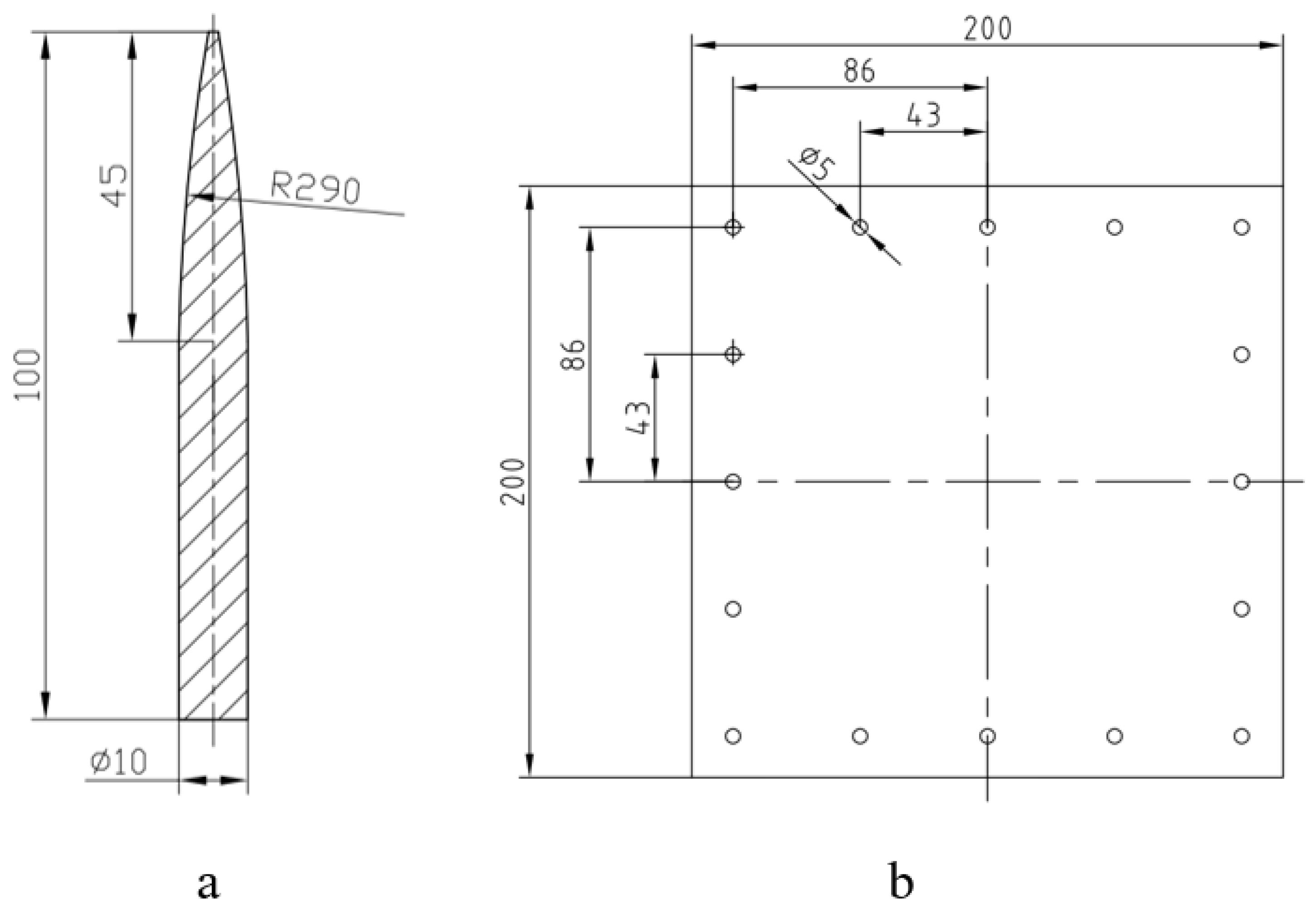
2.1. Harpoon and Target Plate Model
2.2. Experimental Work
2.3. Experimental Results and Analysis
3. Numerical Simulation
3.1. Harpoon–Target Plate Material Model and Equation of State
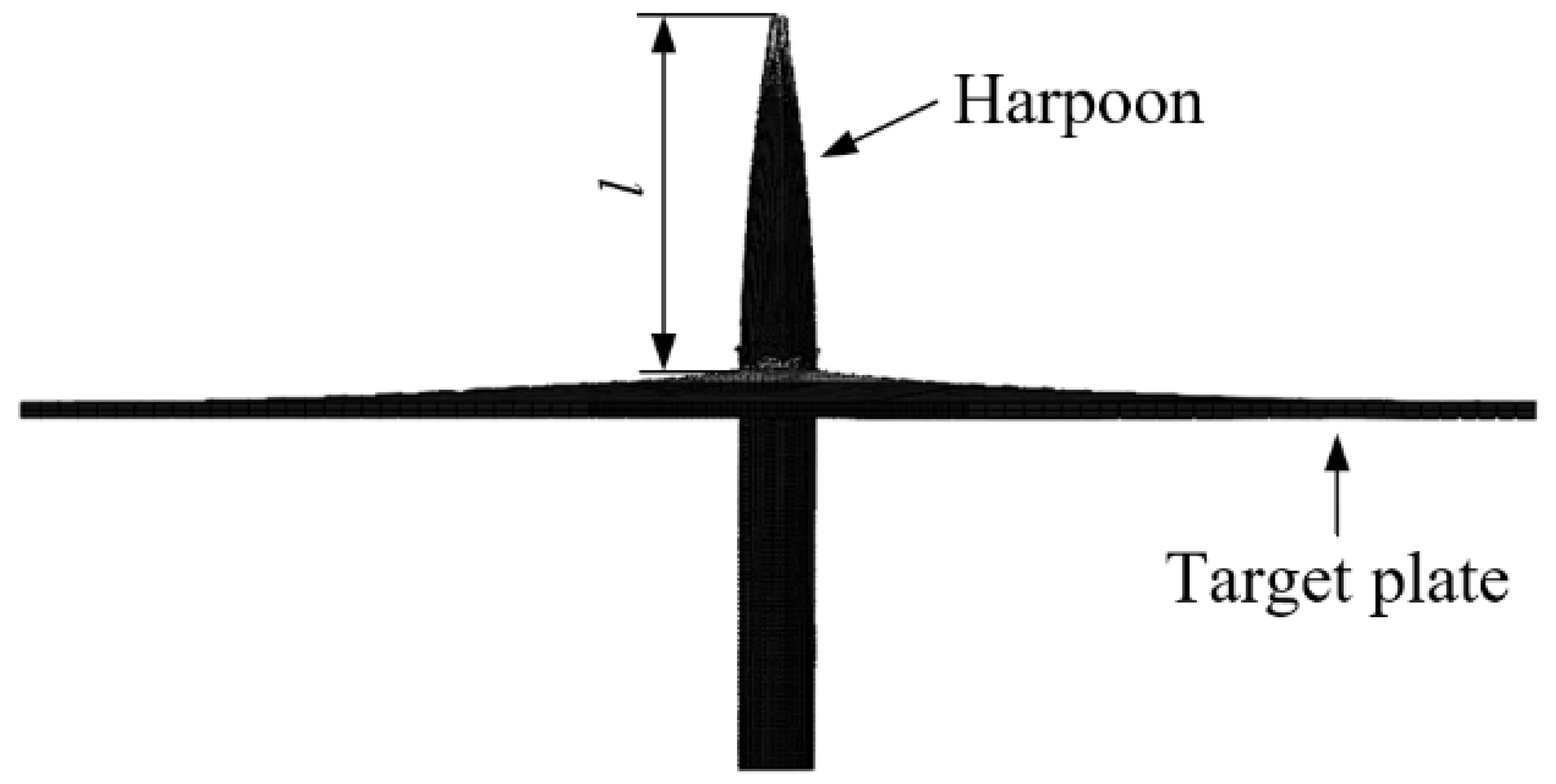
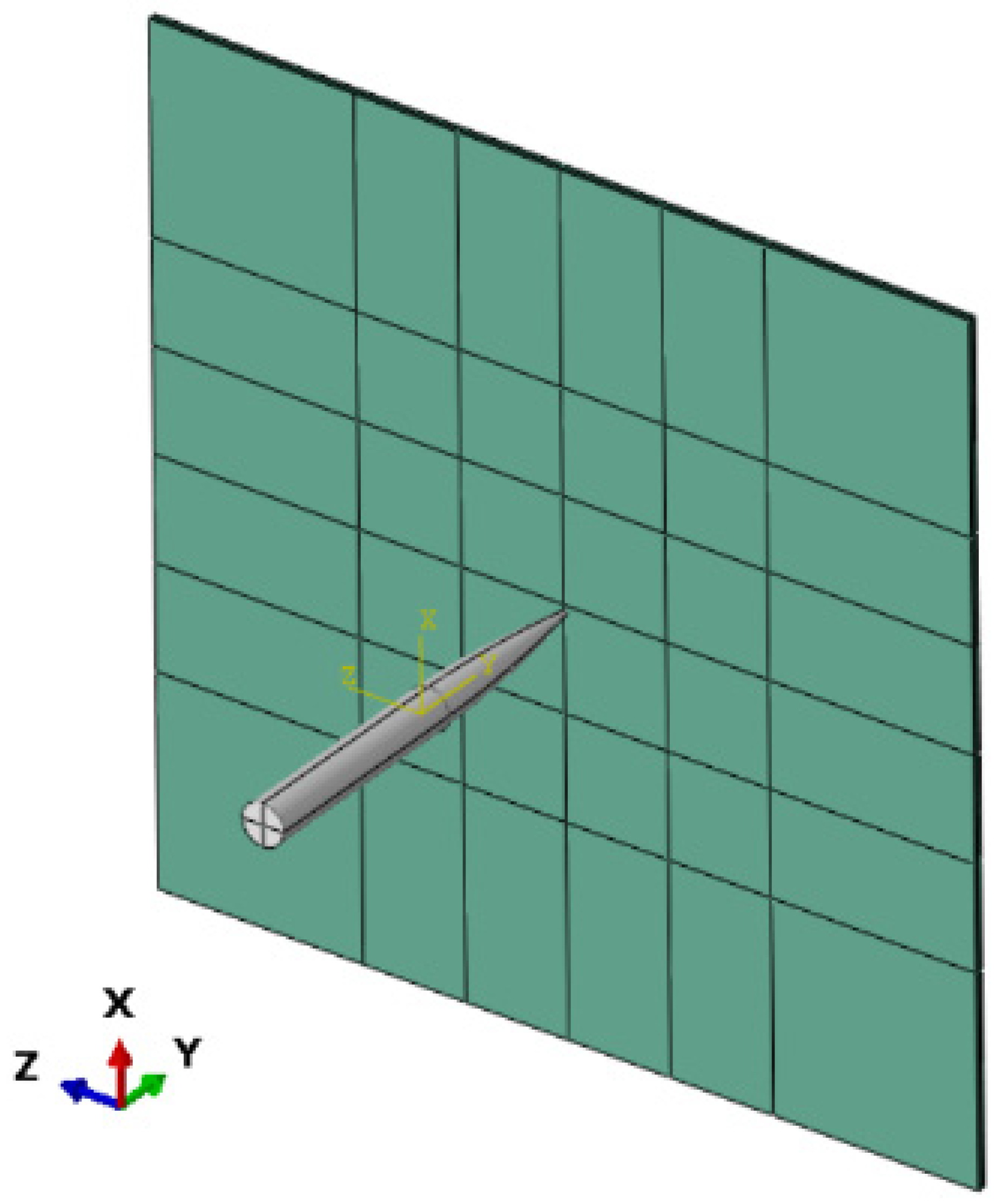
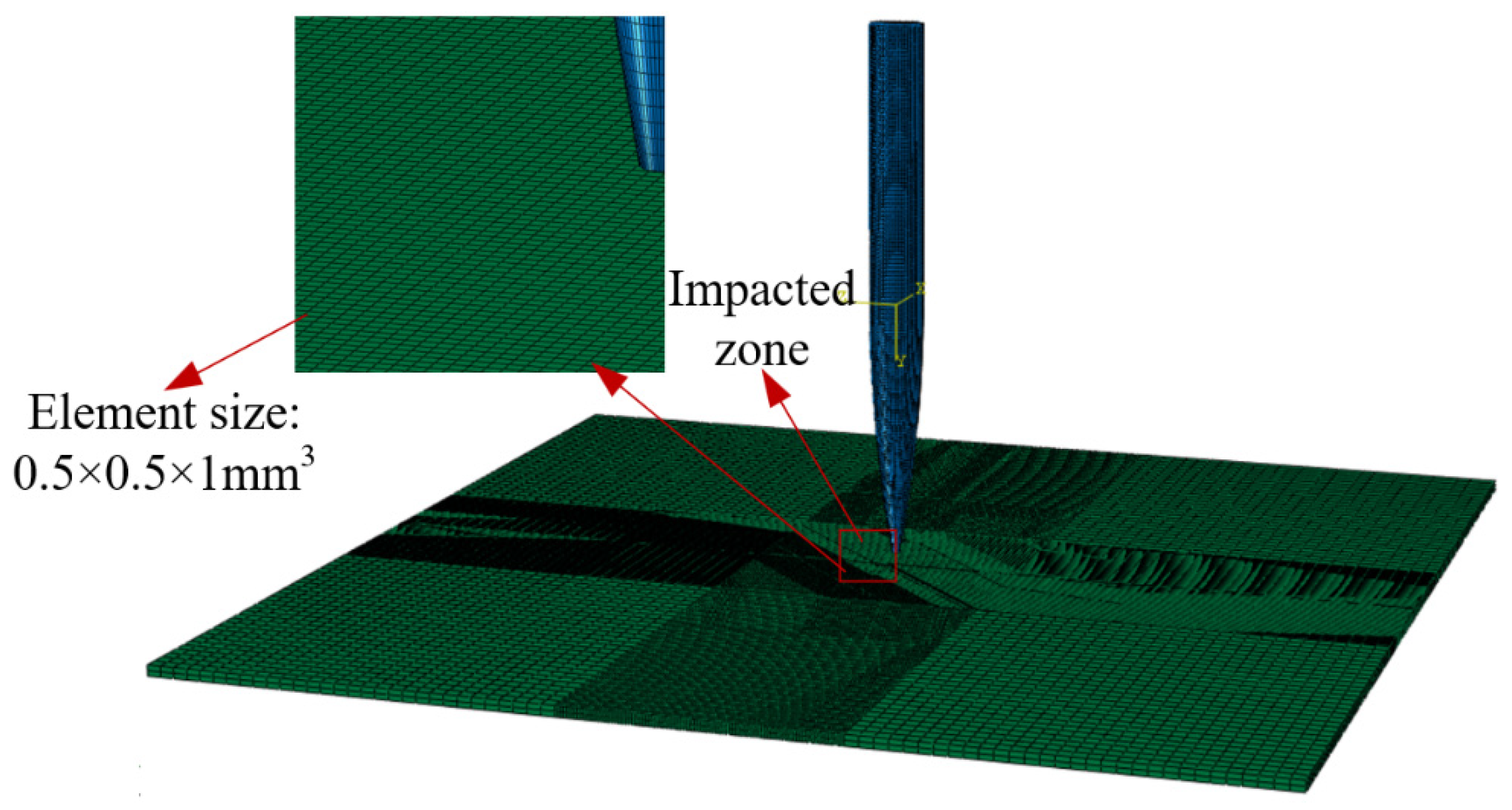
3.2. Harpoon–Target Plate Simulation Model
3.3. Comparison of Experimental and Simulation Conclusions
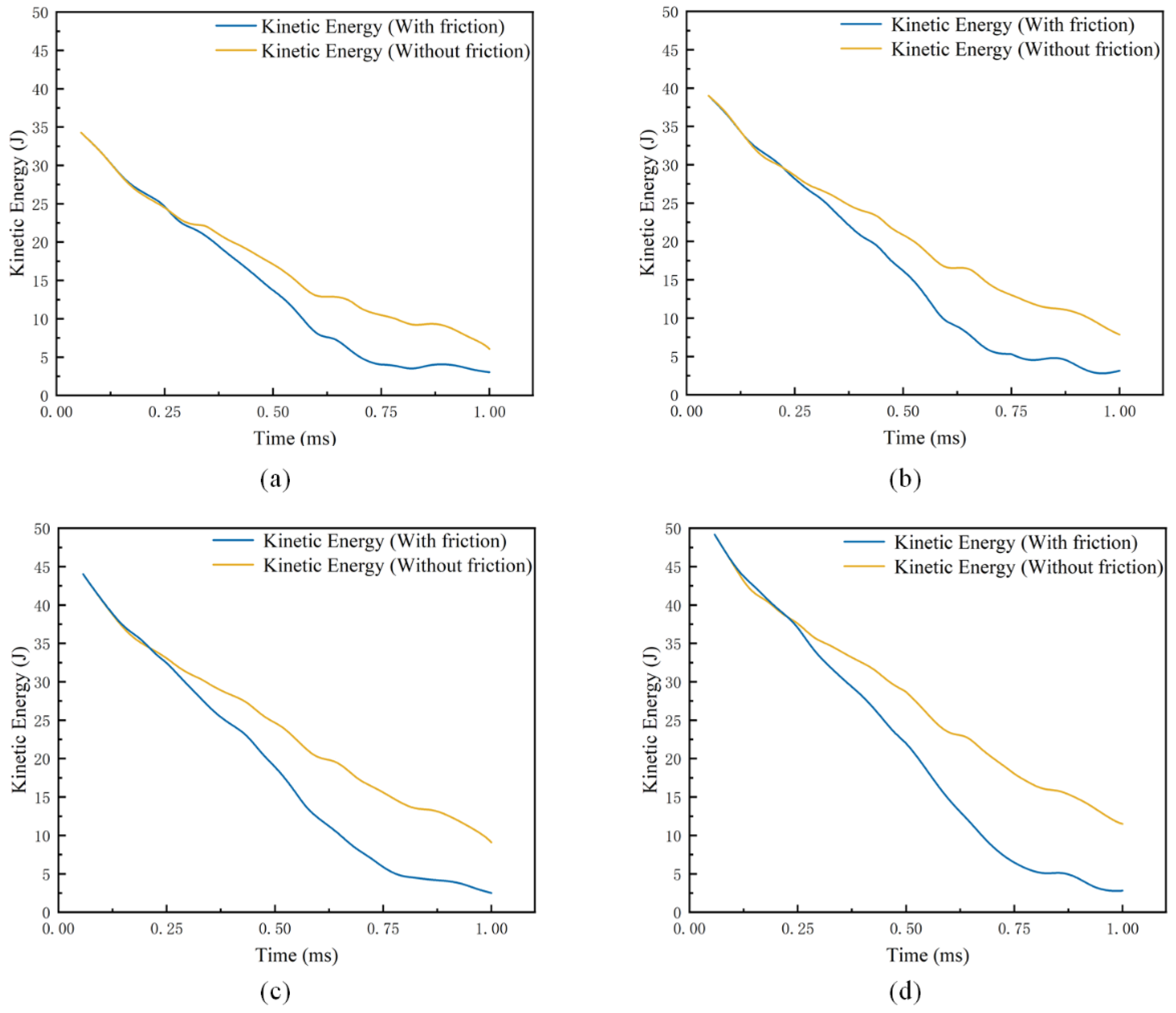
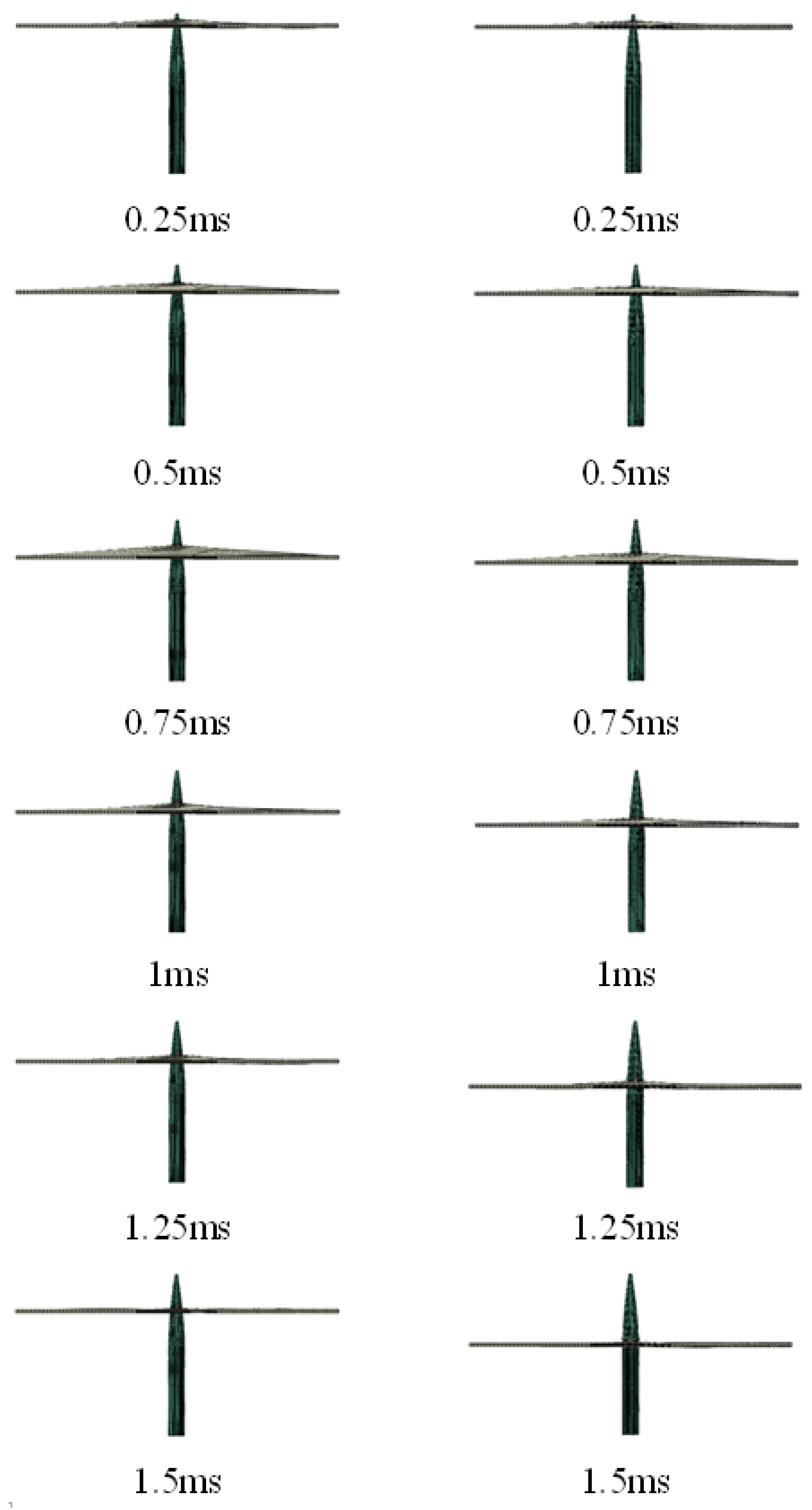
3.4. The Effect of Friction on Harpoon Head Embedding
3.5. The Effect of Friction on Harpoon Column Surface Embedding
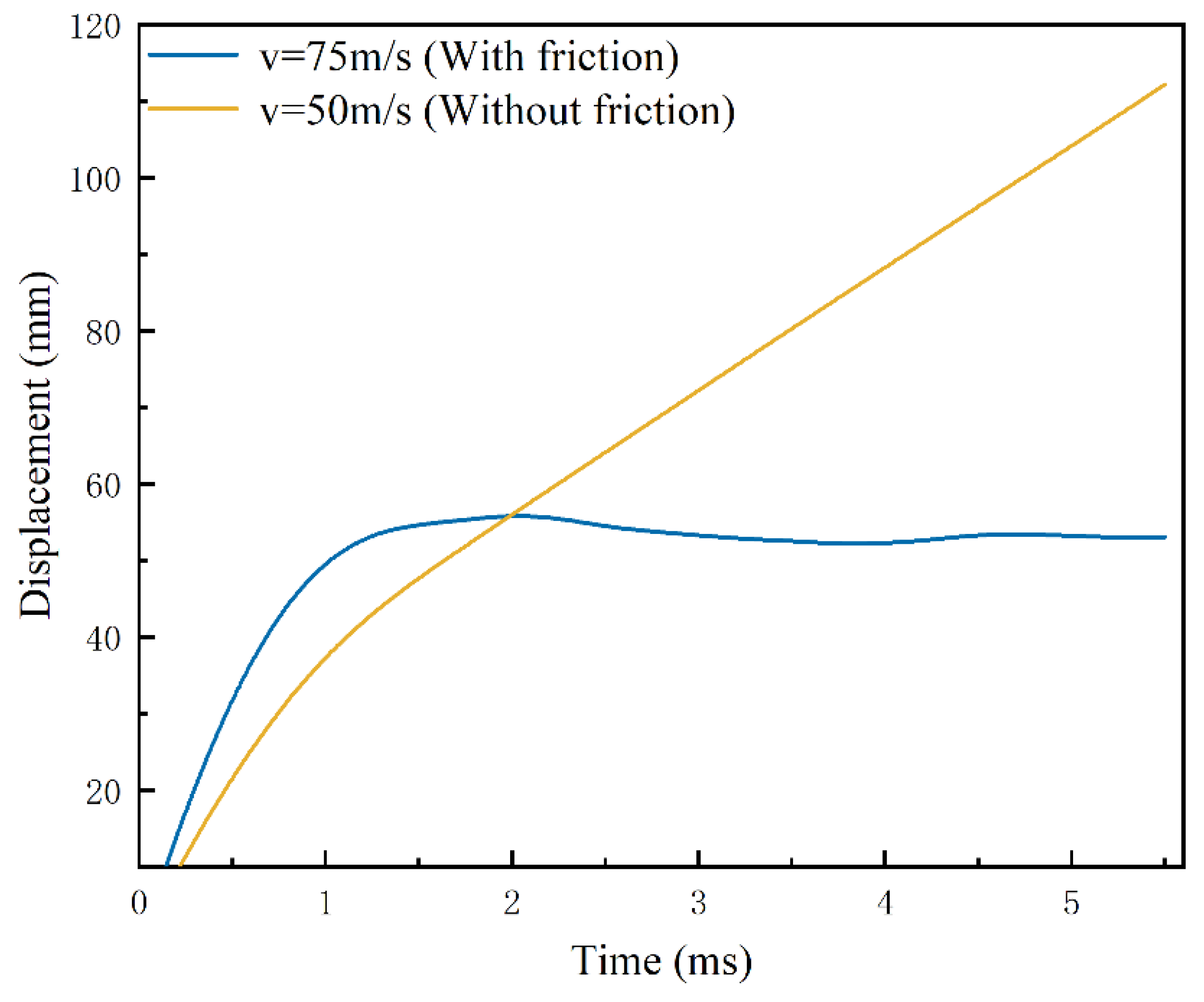
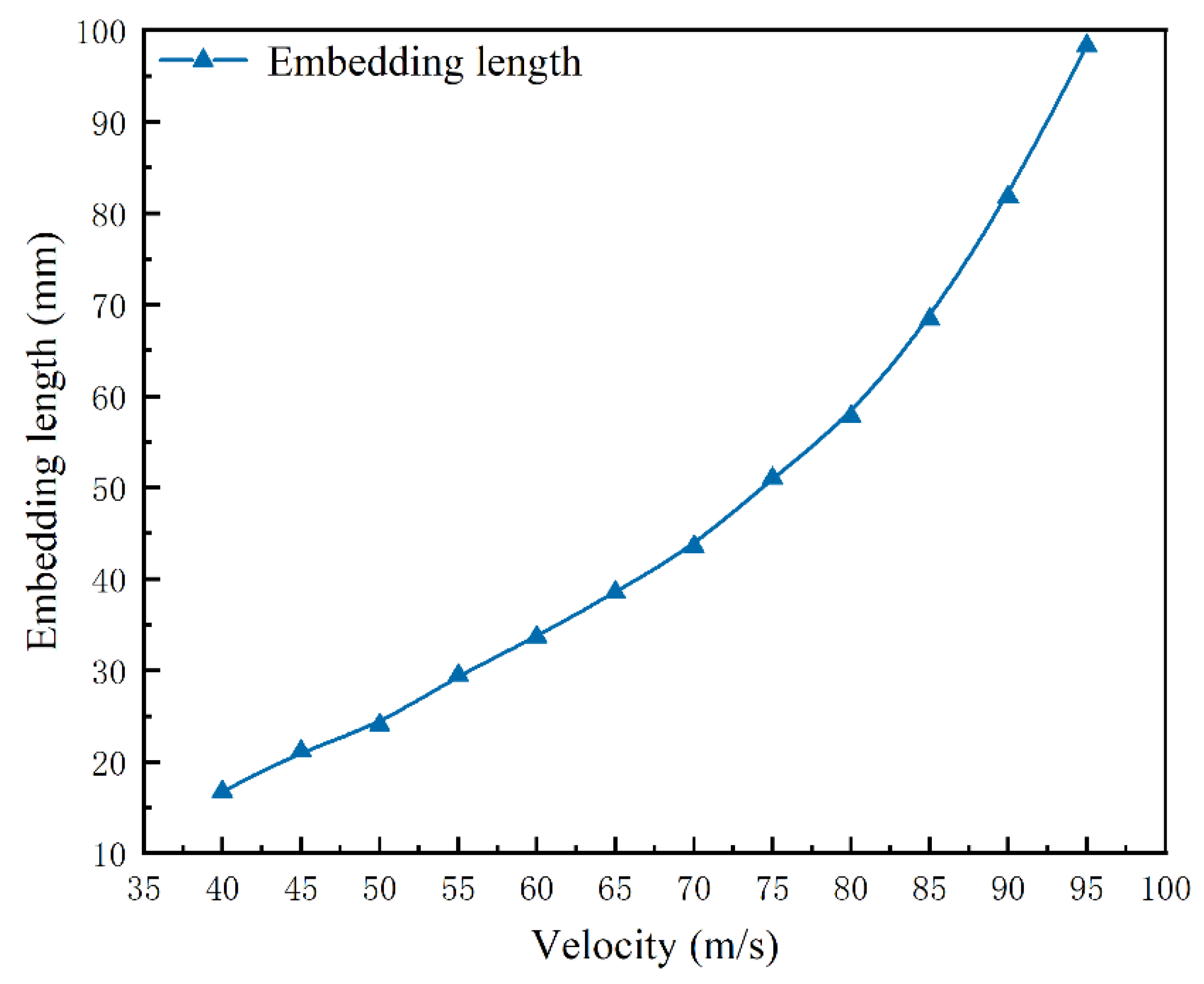
3.6. Velocity and Embedding Length
4. Conclusions
- In the problem of the harpoon impacting and embedding in the target plate at a velocity lower than the ballistic limit, the tangential friction effect is more obvious for the consumption of the kinetic energy of the harpoon itself, and it cannot be ignored;
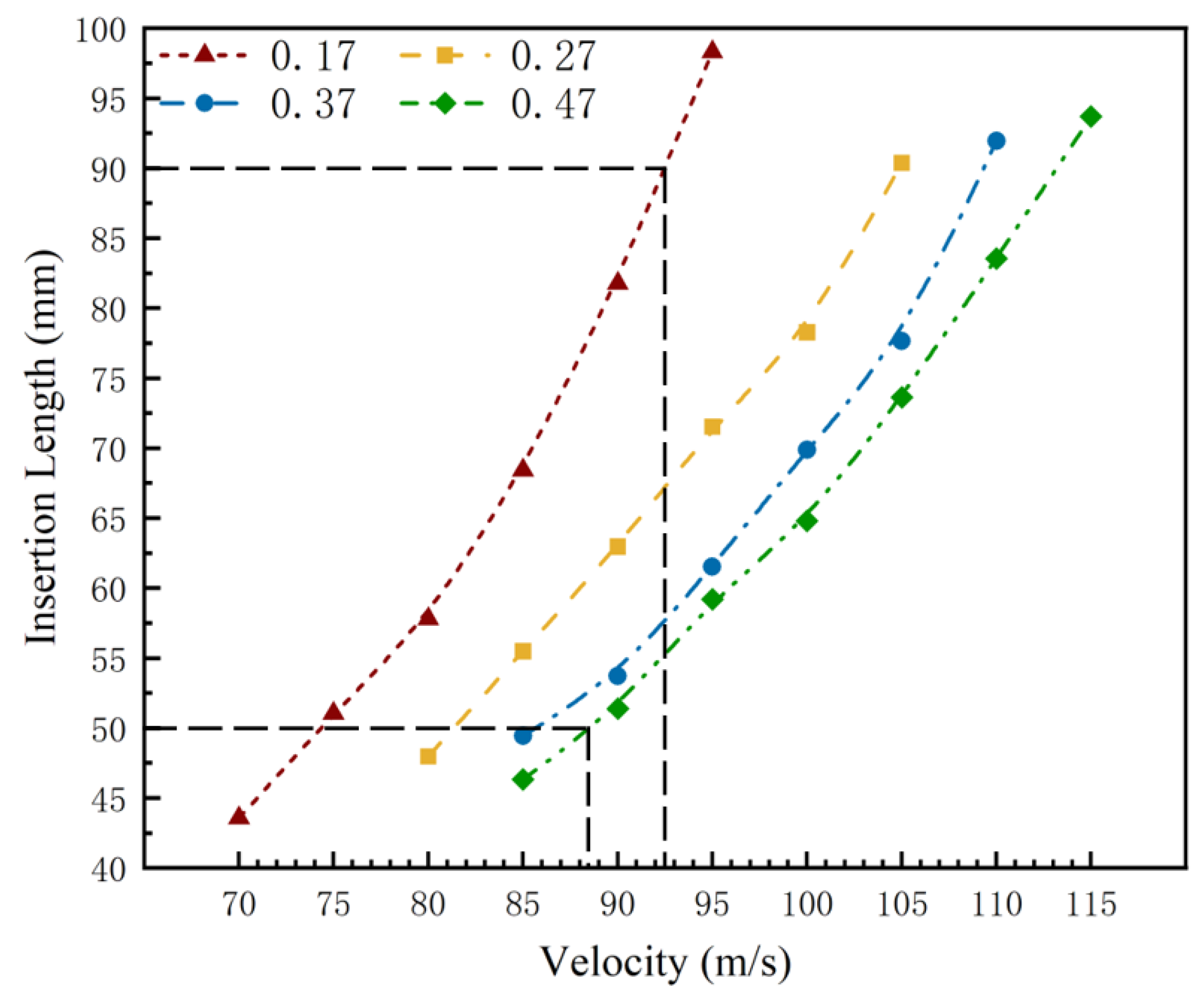
- When the head of the harpoon is embedded in the target plate, due to which the fluctuation of the target plate may rebound after the impact of the head of the harpoon, the embedding is not reliable. The effective embedding part of the harpoon is the bottom column surface position. Considering the influence of the target plate deformation on embedding, the effective embedding length range of the harpoon is 50~90 mm;
- Considering the effect of friction coefficient change, in order to adapt to the effective embedding length range of the harpoon under each friction coefficient condition to within 50~90 mm, the theoretical launch initial velocity of the harpoon should be between 88.4~92.5 m/s.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, Z.; Zhang, H.; Zhao, B.; Liu, X.; Ma, R. Impact Force Identification of the Variable Pressure Flexible Impact End-Effector in Space Debris Active Detumbling. Appl. Sci. 2020, 10, 3011. [Google Scholar] [CrossRef]
- Adushkin, V.V.; Aksenov OYu Veniaminov, S.S.; Kozlov, S.I.; Tyurenkova, V.V. The small orbital debris population and its impact on space activities and ecological safety. Acta Astronaut. 2020, 176, 591–597. [Google Scholar] [CrossRef]
- Ru, M.; Zhan, Y.; Cheng, B.; Zhang, Y. Capture Dynamics and Control of a Flexible Net for Space Debris Removal. Aerospace 2022, 9, 299. [Google Scholar] [CrossRef]
- Virgili, B.B.; Krag, H. Analyzing the criteria for a stable environment. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Girdwood, AK, USA, 31 July–4 August 2011; Volume 411. [Google Scholar]
- Liou, J.-C.; Johnson, N.; Hill, N. Controlling the growth of future LEO debris populations with active debris removal. Acta Astronaut. 2010, 66, 648–653. [Google Scholar] [CrossRef]
- Forshaw, J.L.; Aglietti, G.S.; Fellowes, S.; Salmon, T.; Retat, I.; Hall, A.; Chabot, T.; Pisseloup, A.; Tye, D.; Bernal, C.; et al. The active space debris removal mission RemoveDebris. Part 1: From concept to launch. Acta Astronaut. 2019, 168, 293–309. [Google Scholar] [CrossRef] [Green Version]
- Reed, J.; Barraclough, S. Development of Harpoon System for Capturing Space Debris. Eur. Conf. Space Debris 2013, 723, 174. [Google Scholar]
- Campbell, J.; Hughes, K.; Vignjevic, R.; Djordjevic, N.; Taylor, N.; Jardine, A. Development of modelling design tool for harpoon for active space debris removal. Int. J. Impact Eng. 2022, 166, 104236. [Google Scholar] [CrossRef]
- Dudziak, R.; Tuttle, S.; Barraclough, S. Harpoon technology development for the active removal of space debris. Adv. Space Res. 2015, 56, 509–527. [Google Scholar] [CrossRef]
- Aglietti, G.S.; Taylor, B.; Fellowes, S.; Salmon, T.; Retat, I.; Hall, A.; Chabot, T.; Pisseloup, A.; Cox, C.; Zarkesh, A.; et al. The active space debris removal mission RemoveDebris. Part 2: In orbit operations. Acta Astronaut. 2019, 168, 310–322. [Google Scholar] [CrossRef] [Green Version]
- Fras, T.; Roth, C.C.; Mohr, D. Dynamic perforation of ultra-hard high-strength armor steel: Impact experiments and modeling. Int. J. Impact Eng. 2019, 131, 256–271. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Xiao, X.; Vershinin, V.V.; Ge, R.; Li, D.-S. Effect of Lode angle incorporation into a fracture criterion in predicting the ballistic resistance of 2024-T351 aluminum alloy plates struck by cylindrical projectiles with different nose shapes. Int. J. Impact Eng. 2020, 139, 103498. [Google Scholar] [CrossRef]
- Kpenyigba, K.; Jankowiak, T.; Rusinek, A.; Pesci, R.; Wang, B. Effect of projectile nose shape on ballistic resistance of interstitial-free steel sheets. Int. J. Impact Eng. 2015, 79, 83–94. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Wu, H.; Zhang, Y.; Huang, X.; Xiao, X.; Lv, Y. Experimental and numerical study on the ballistic resistance of 6061-T651 aluminum alloy thin plates struck by different nose shapes of projectiles. Int. J. Impact Eng. 2022, 160, 104083. [Google Scholar] [CrossRef]
- Rusinek, A.; Rodríguez-Martínez, J.; Arias, A.; Klepaczko, J.; López-Puente, J. Influence of conical projectile diameter on perpendicular impact of thin steel plate. Eng. Fract. Mech. 2008, 75, 2946–2967. [Google Scholar] [CrossRef] [Green Version]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high tem-peratures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; Volume 21, pp. 541–548. [Google Scholar]
- Elek, P.M.; Jaramaz, S.S.; Micković, D.M.; Miloradović, N.M. Experimental and numerical investigation of perforation of thin steel plates by de-formable steel penetrators. Thin-Walled Struct. 2016, 102, 58–67. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Zhao, Z.; Liu, D.; Ou-Yang, X. Numerical study on penetration of a high-speed-rotating bullet into the moving sheet-metal plate. Impact Dyn. 2008, 28, 57–62. (In Chinese) [Google Scholar]
- Gang, W.; Wei, Z.; Yunfei, D. Identification and validation of constitutive parameters of 45 Steel based on J-C model. J. Vib. Shock 2019, 38, 173–178. (In Chinese) [Google Scholar]
- Chen, J.; Xu, W.; Xie, R.; Zhang, F.; Hu, W.; Huang, X.; Chen, G. Sample size effect on the dynamic torsional behaviour of the 2A12 aluminium alloy. Theor. Appl. Mech. Lett. 2017, 7, 317–324. [Google Scholar] [CrossRef]
- Rusinek, A.; Rodríguez-Martínez, J.; Zaera, R.; Klepaczko, J.; Arias, A.; Sauvelet, C. Experimental and numerical study on the perforation process of mild steel sheets subjected to perpendicular impact by hemispherical projectiles. Int. J. Impact Eng. 2009, 36, 565–587. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhang, X.; Liu, C.; Chen, H.; Wang, J.; Xiong, W. Study on mass erosion model of projectile penetrating concrete at high speed considering variation of friction coefficient. Explos. Shock. Waves 2021, 41, 114–124. (In Chinese) [Google Scholar]




| Model | Density/ g·cm−3 | Elastic Modulus/ Gpa | Poisson Ratio | Johnson-Cook Model Parameters | ||||
|---|---|---|---|---|---|---|---|---|
| A/MPa | B/Mpa | n | C | m | ||||
| Harpoon | 7.85 | 210 | 0.33 | 714 | 563 | 0.518 | 0.064 | 0.698 |
| Target plate | 2.77 | 71.7 | 0.33 | 375 | 592 | 0.42 | 0.001 | 1.426 |
| No. | Velocity/m·s−1 | Experimental Embedding Length/mm | Simulation Embedding Length/mm |
|---|---|---|---|
| 1 | 50.7 | 22 | 23.1 |
| 2 | 65 | 37 | 38.58 |
| 3 | 76.4 | 51.5 | 51.03 |
| No. | Friction Coefficient | Velocity/m·s−1 | Embedding Length—With Friction/mm | Embedding Length—Without Friction/mm |
|---|---|---|---|---|
| 1 | 0.17 | 37.5 | 15.48 | 25.71 |
| 2 | 0.17 | 40 | 16.74 | 29.41 |
| 3 | 0.17 | 42.5 | 19.37 | 33.99 |
| 4 | 0.17 | 45 | 21.18 | 36.63 |
| No. | Friction Coefficient | Velocity/m·s−1 | Embedding Length/mm |
|---|---|---|---|
| 1 | 0.17 | 40 | 16.74 |
| 2 | 0.17 | 45 | 21.18 |
| 3 | 0.17 | 50 | 24.05 |
| 4 | 0.17 | 55 | 29.49 |
| 5 | 0.17 | 60 | 33.67 |
| 6 | 0.17 | 65 | 38.58 |
| 7 | 0.17 | 70 | 43.57 |
| 8 | 0.17 | 75 | 51.03 |
| 9 | 0.17 | 80 | 57.80 |
| 10 | 0.17 | 85 | 68.42 |
| 11 | 0.17 | 90 | 81.78 |
| 12 | 0.17 | 95 | 98.32 |
| No. | Friction Coefficient | Velocity/m·s−1 | Embedding Length/mm |
|---|---|---|---|
| 1 | 0.17 | 70 | 43.57 |
| 75 | 51.03 | ||
| 80 | 57.80 | ||
| 85 | 68.42 | ||
| 90 | 81.78 | ||
| 95 | 98.32 | ||
| 2 | 0.27 | 80 | 47.96 |
| 85 | 55.48 | ||
| 90 | 62.96 | ||
| 95 | 71.52 | ||
| 100 | 78.27 | ||
| 105 | 90.37 | ||
| 3 | 0.37 | 85 | 49.42 |
| 90 | 53.72 | ||
| 95 | 61.51 | ||
| 100 | 69.88 | ||
| 105 | 77.65 | ||
| 110 | 91.94 | ||
| 4 | 0.47 | 85 | 46.31 |
| 90 | 51.37 | ||
| 95 | 59.19 | ||
| 100 | 64.78 | ||
| 105 | 73.61 | ||
| 110 | 83.54 | ||
| 115 | 93.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Pang, Z.; Zhao, Z.; Du, Z.; Zhu, W. A Simulation and an Experimental Study of Space Harpoon Low-Velocity Impact, Anchored Debris. Materials 2022, 15, 5041. https://doi.org/10.3390/ma15145041
Zhao W, Pang Z, Zhao Z, Du Z, Zhu W. A Simulation and an Experimental Study of Space Harpoon Low-Velocity Impact, Anchored Debris. Materials. 2022; 15(14):5041. https://doi.org/10.3390/ma15145041
Chicago/Turabian StyleZhao, Wei, Zhaojun Pang, Zhen Zhao, Zhonghua Du, and Weiliang Zhu. 2022. "A Simulation and an Experimental Study of Space Harpoon Low-Velocity Impact, Anchored Debris" Materials 15, no. 14: 5041. https://doi.org/10.3390/ma15145041
APA StyleZhao, W., Pang, Z., Zhao, Z., Du, Z., & Zhu, W. (2022). A Simulation and an Experimental Study of Space Harpoon Low-Velocity Impact, Anchored Debris. Materials, 15(14), 5041. https://doi.org/10.3390/ma15145041






