Nonsingular Stress Distribution of Edge Dislocations near Zero-Traction Boundary
Abstract
1. Introduction
2. Nonsingular Elastic Field in an Infinite Medium
3. Semi-Infinite Problem Solution
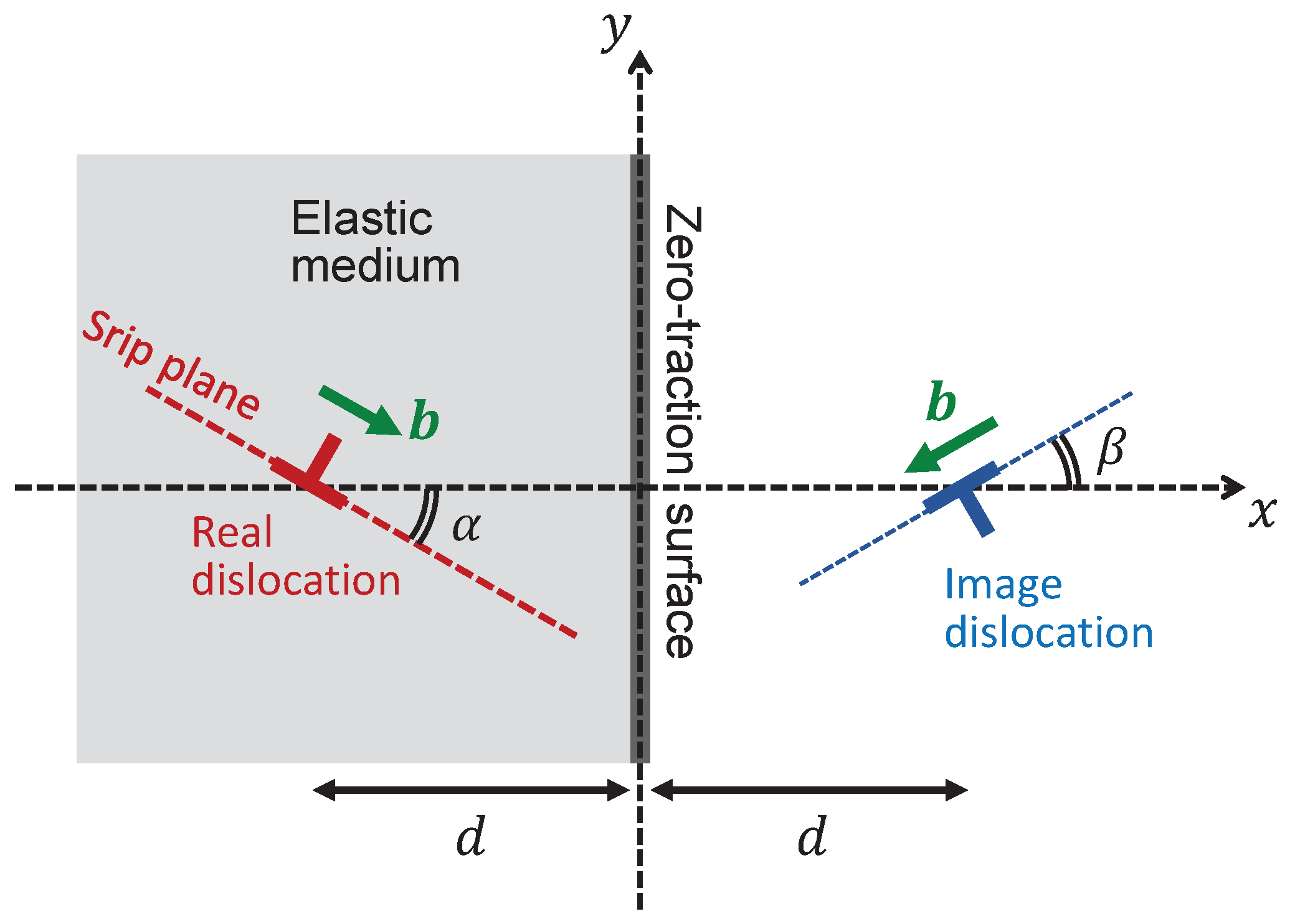
3.1. Outline of Strategy
3.2. Stress Due to the Real Dislocation at
3.3. Stress Due to the Image Dislocation at
3.4. Sum of the Shear Stress Components at a Free Surface
3.5. Stress from Excess Airy’s Function
4. Numerical Results
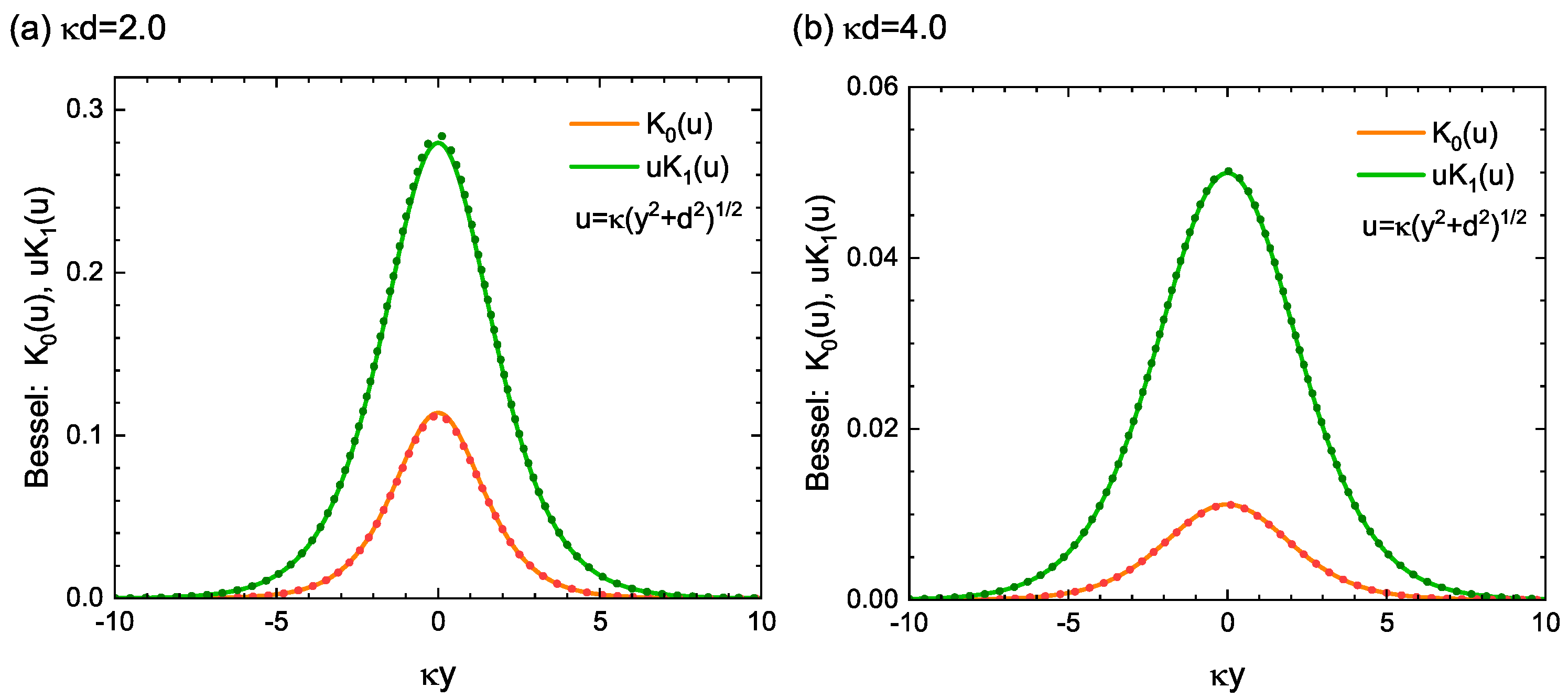
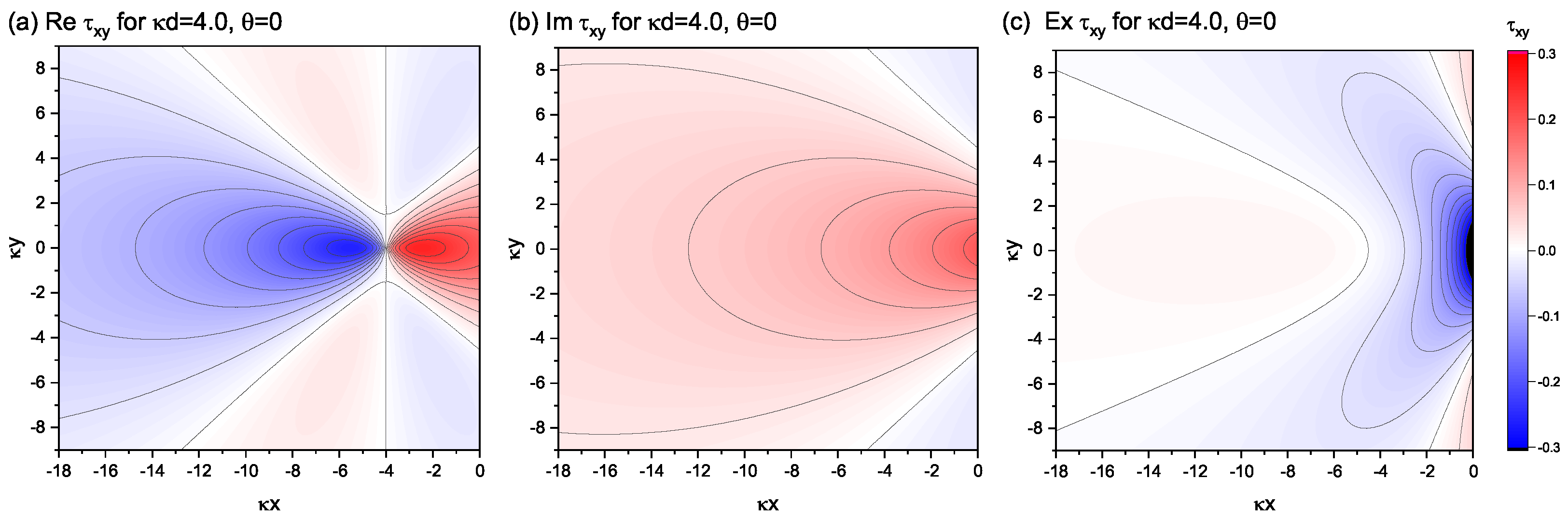
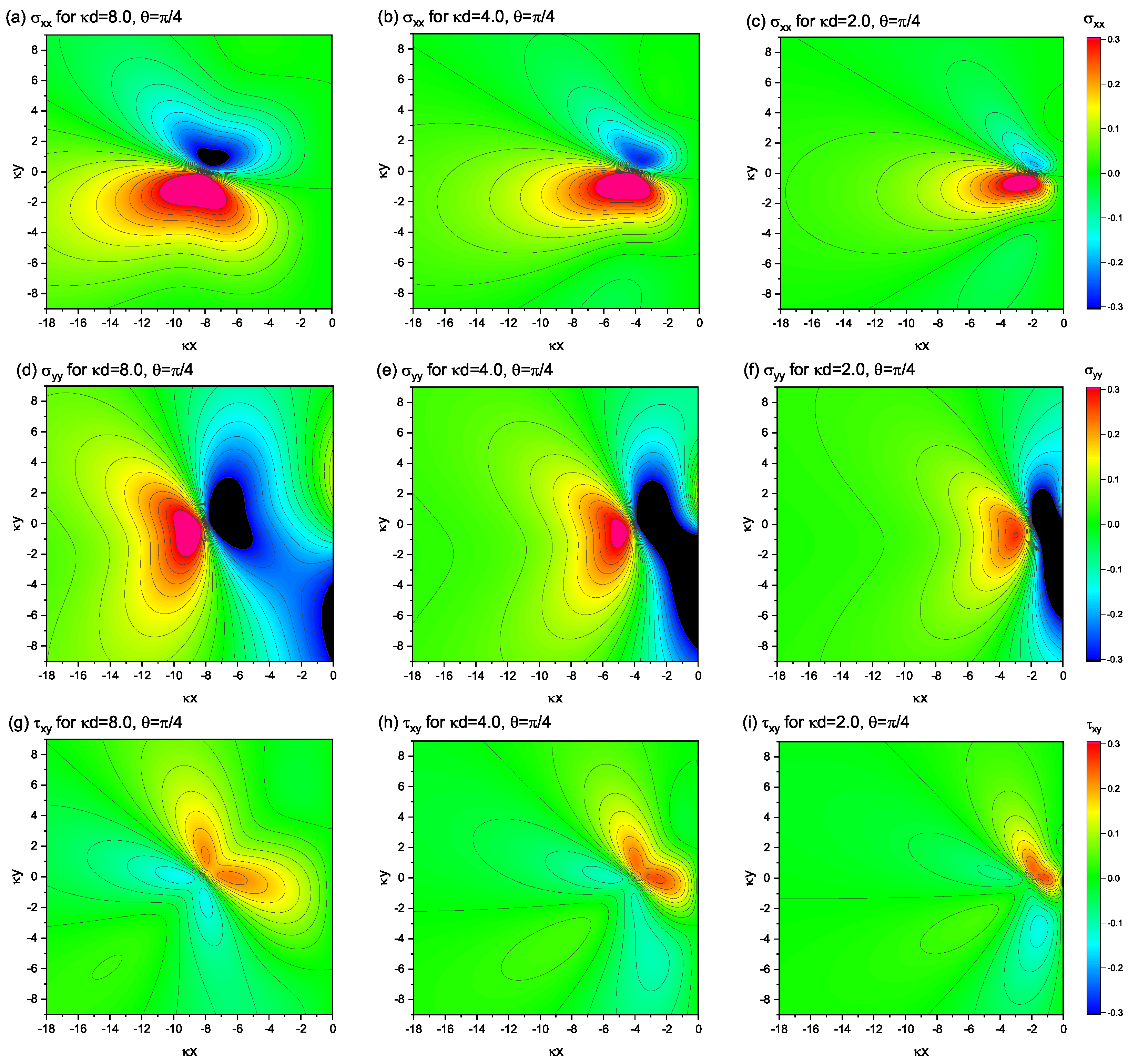
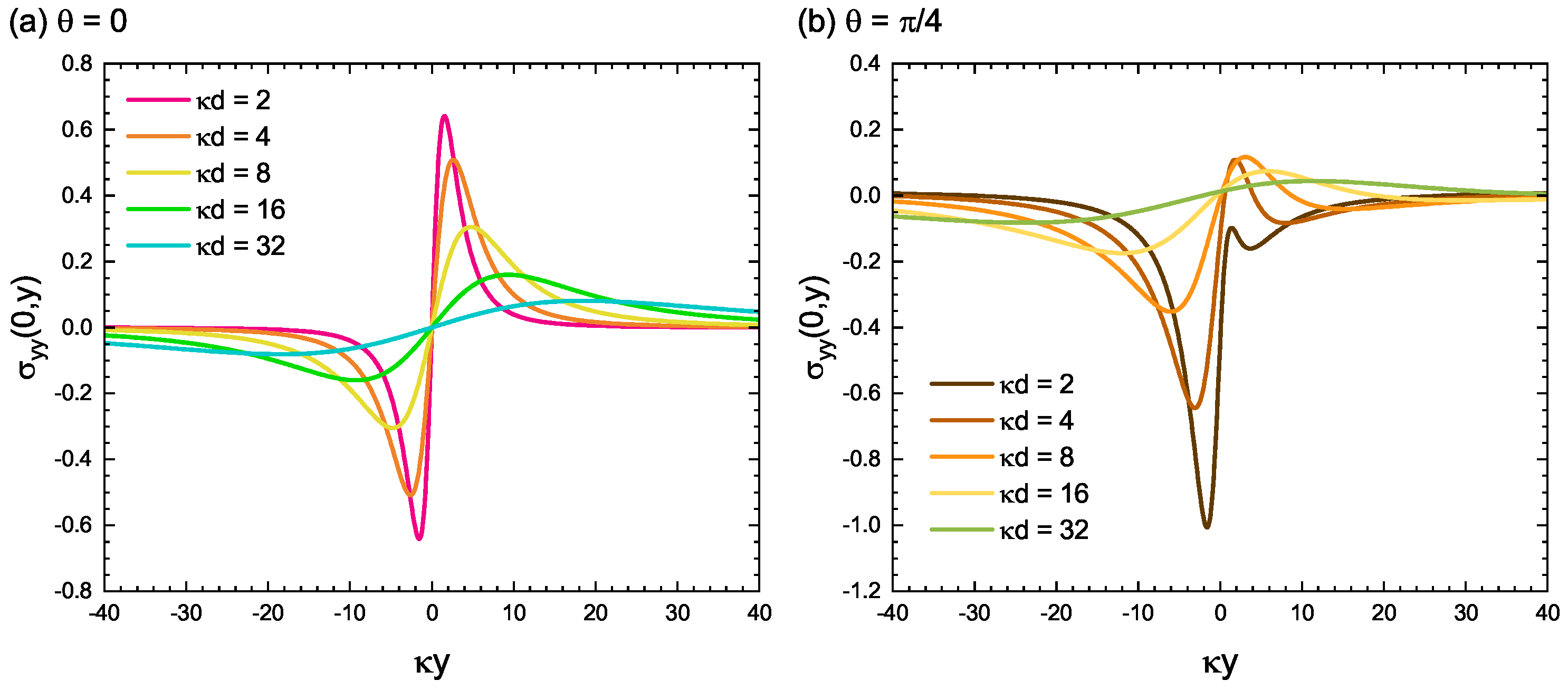
4.1. Nonsingular Stress Field of an Edge Dislocation
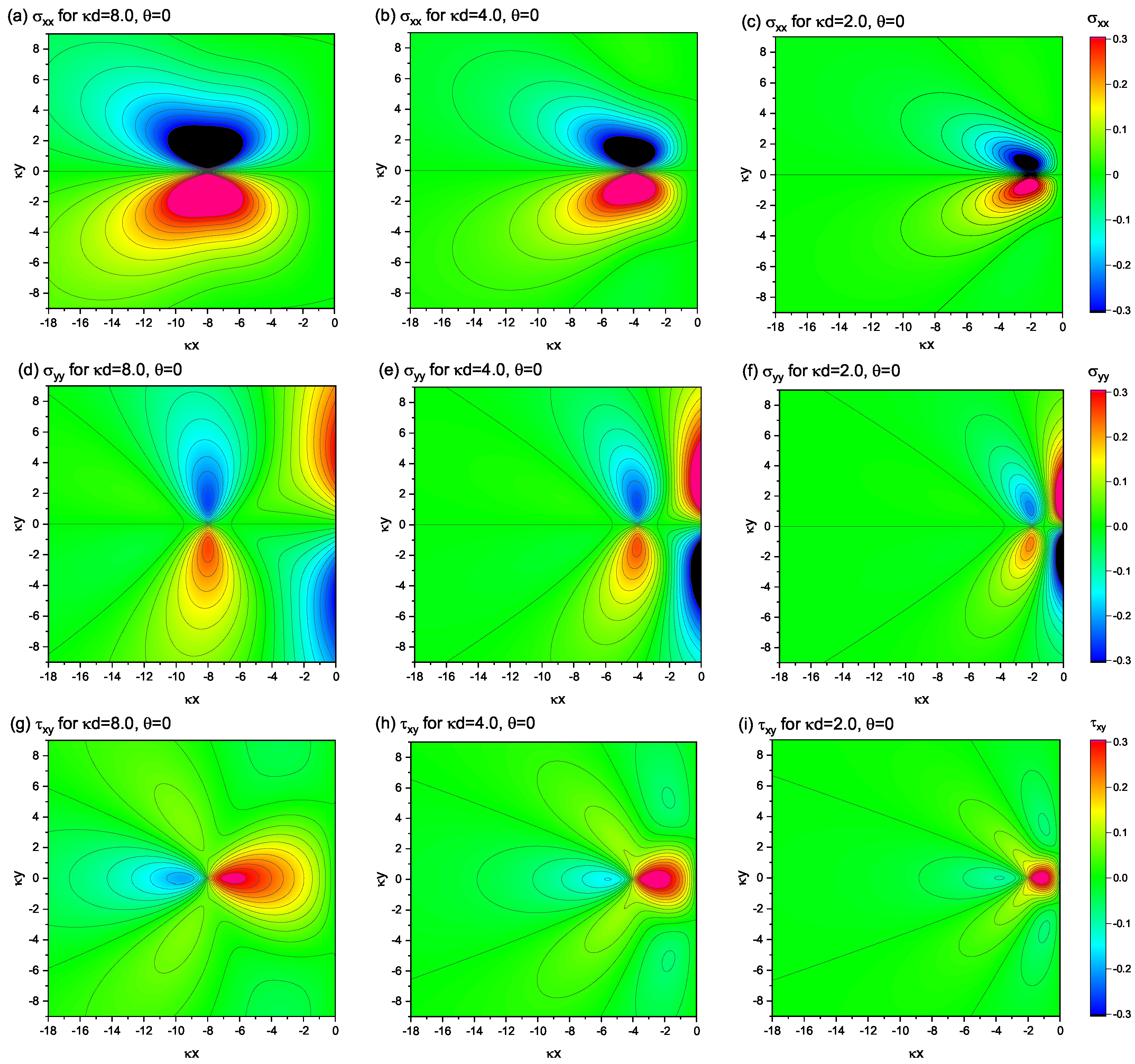
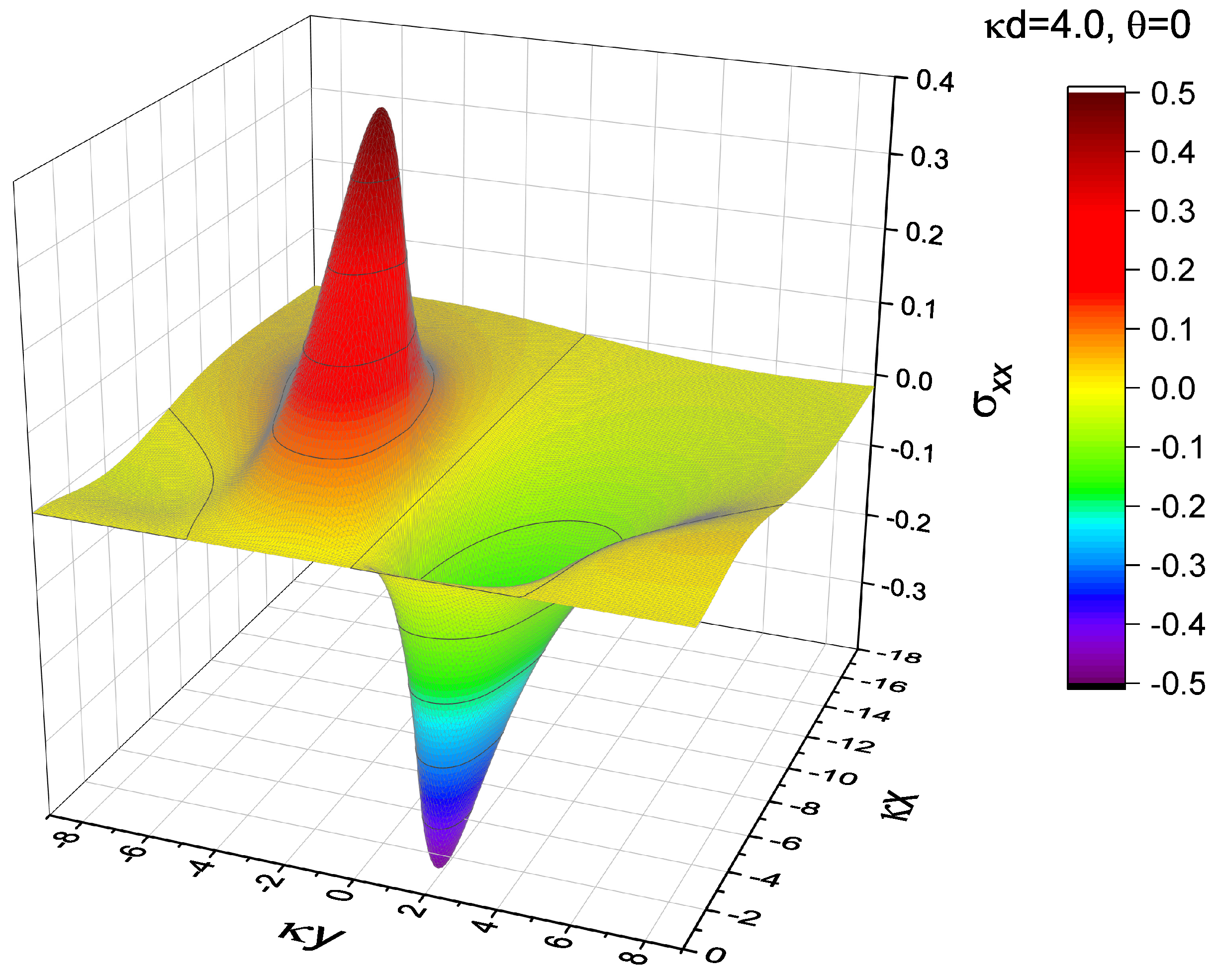
4.2. Spatial Field Modulation Induced by the Free Surface
5. Discussion
6. Concluding Remark
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Solution Method of Inhomogeneous Helmholtz Equation
Appendix B. Properties of the Modified Bessel Function
Appendix C. Method of the Variable Separation
References
- Berdichevsky, V.L. A continuum theory of edge dislocations. J. Mech. Phys. Solids 2017, 106, 95–132. [Google Scholar] [CrossRef]
- Epperly, E.N.; Sills, R.B. Comparison of continuum and cross-core theories of dynamic strain aging. J. Mech. Phys. Solids 2020, 141, 103944. [Google Scholar] [CrossRef]
- Anciaux, G.; Junge, T.; Hodapp, M.; Cho, T.; Molinari, J.F.; Curtin, W.A. The coupled atomistic/discrete-dislocation method in 3d part I: Concept and algorithms. J. Mech. Phys. Solids 2018, 118, 152–171. [Google Scholar] [CrossRef]
- Huang, K.; Sumigawa, T.; Kitamura, T. Experimental evaluation of loading mode effect on plasticity of microscale single-crystal copper. Mater. Sci. Eng. A 2021, 806, 140822. [Google Scholar] [CrossRef]
- Xu, Y.; Balint, D.S.; Dini, D. On the origin of plastic deformation and surface evolution in nano-fretting: A discrete dislocation plasticity analysis. Materials 2021, 14, 6511. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials; Cambridge University Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Weertman, J. Dislocation Based Fracture Mechanics; World Scientific Pub.: Singapore, 1996. [Google Scholar]
- Dai, M.; Schiavone, P.; Gao, C.F. Screw dislocation in a thin film with surface effects. Int. J. Solids Struct. 2017, 110, 89–93. [Google Scholar] [CrossRef]
- Pan, X.; Hu, W.; Wu, C.T. A generalized approach for solution to image stresses of dislocations. J. Mech. Phys. Solids 2017, 103, 3–21. [Google Scholar] [CrossRef]
- Shima, H.; Umeno, Y.; Sumigawa, T. Analytic formulation of elastic field around edge dislocation adjacent to slanted free surface. R. Soc. Open Sci. 2022, 9, 220151. [Google Scholar] [CrossRef]
- Amin, W.; Ali, M.A.; Vajragupta, N.; Hartmaier, A. Studying grain boundary strengthening by dislocation-based strain gradient crystal plasticity coupled with a multi-phase-field model. Materials 2019, 12, 2977. [Google Scholar] [CrossRef]
- Yuan, S.B.; Duchene, L.; Keller, C.; Hug, E.; Habraken, A.M. Tunable surface boundary conditions in strain gradient crystal plasticity model. Mech. Mater. 2020, 145, 103393. [Google Scholar] [CrossRef]
- Mianroodi, J.R.; Svendsen, B. Effect of twin boundary motion and dislocation-twin interaction on mechanical behavior in FCC metals. Materials 2020, 13, 2238. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; He, Y.; Zhang, X. Interactions between dislocations and boundaries during deformation. Materials 2021, 14, 1012. [Google Scholar] [CrossRef]
- Polizzotto, C. A micromorphic approach to stress gradient elasticity theory with an assessment of the boundary conditions and size effects. Zamm-Z. Angew. Math. Mech. 2018, 98, 1528–1553. [Google Scholar] [CrossRef]
- Zheng, H.; Cao, A.; Weinberger, C.R.; Huang, J.Y.; Du, K.; Wang, J.; Ma, Y.; Xia, Y.; Mao, S.X. Discrete plasticity in sub-10-nm-sized gold crystals. Nat. Commun. 2010, 1, 144. [Google Scholar] [CrossRef]
- Lu, Y.; Song, J.; Huang, J.Y.; Lou, J. Fracture of Sub-20nm Ultrathin Gold Nanowires. Adv. Funct. Mater. 2011, 21, 3982–3989. [Google Scholar] [CrossRef]
- Sumigawa, T.; Hikasa, K.; Kusunose, A.; Unno, H.; Masuda, K.; Shimada, T.; Kitamura, T. In situ TEM observation of nanodomain mechanics in barium titanate under external loads. Phys. Rev. Mater. 2020, 4, 054415. [Google Scholar] [CrossRef]
- Chen, X.W.; Yue, Z.Q. A unified mathematical treatment of interfacial edge dislocations in three-dimensional functionally graded materials. J. Mech. Phys. Solids 2021, 156, 104471. [Google Scholar] [CrossRef]
- Neding, B.; Pagan, D.C.; Hektor, J.; Hedstrom, P. Formation of dislocations and stacking faults in embedded individual grains during in situ tensile loading of an austenitic stainless steel. Materials 2021, 14, 5919. [Google Scholar] [CrossRef]
- Wang, R.Z.; Lin, F.; Niu, G.; Su, J.N.; Yan, X.L.; Wei, Q.; Wang, W.; Wang, K.Y.; Yu, C.; Wang, H.X. Reducing threading dislocations of single-crystal diamond via in situ tungsten incorporation. Materials 2022, 15, 444. [Google Scholar] [CrossRef]
- Kang, J.; Lee, J.H.; Lee, H.K.; Kim, K.T.; Kim, J.H.; Maeng, M.J.; Hong, J.A.; Park, Y.; Kim, K.H. Effect of threading dislocations on the electronic structure of La-doped BaSnO3 thin films. Materials 2022, 15, 2417. [Google Scholar] [CrossRef]
- Shi, T.T.; Liu, W.B.; Su, Z.X.; Yan, X.; Lu, C.Y.; Yun, D. Effect of carbon on dislocation loops formation during self-ion irradiation in Fe-Cr alloys at high temperatures. Materials 2022, 15, 2211. [Google Scholar] [CrossRef] [PubMed]
- Gurrutxaga-Lerma, B. A stochastic study of the collective effect of random distributions of dislocations. J. Mech. Phys. Solids 2019, 124, 10–34. [Google Scholar] [CrossRef]
- Salvalaglio, M.; Angheluta, L.; Huang, Z.F.; Voigt, A.; Elder, K.R.; Vinals, J. A coarse-grained phase-field crystal model of plastic motion. J. Mech. Phys. Solids 2020, 137, 103856. [Google Scholar] [CrossRef]
- Groma, I. Link between the microscopic and mesoscopic length-scale description of the collective behavior of dislocations. Phys. Rev. B 1997, 56, 5807–5813. [Google Scholar] [CrossRef]
- Acharya, A. A model of crystal plasticity based on the theory of continuously distributed dislocations. J. Mech. Phys. Solids 2001, 49, 761–784. [Google Scholar] [CrossRef]
- Hudson, T.; van Meurs, P.; Peletier, M. Atomistic origins of continuum dislocation dynamics. Math. Models Methods Appl. Sci. 2020, 30, 2557–2618. [Google Scholar] [CrossRef]
- Sumigawa, T.; Uegaki, S.; Yukishita, T.; Arai, S.; Takahashi, Y.; Kitamura, T. FE-SEM in situ observation of damage evolution in tension-compression fatigue of micro-sized single-crystal copper. Mater. Sci. Eng. A 2019, 764, 138218. [Google Scholar] [CrossRef]
- Lavenstein, S.; Gu, Y.; Madisetti, D.; El-Awady, J.A. The heterogeneity of persistent slip band nucleation and evolution in metals at the micrometer scale. Science 2020, 370, eabb2690. [Google Scholar] [CrossRef]
- Meng, F.; Ferrié, E.; Déprés, C.; Fivel, M. 3D discrete dislocation dynamic investigations of persistent slip band formation in FCC metals under cyclical deformation. Int. J. Fatig. 2021, 149, 106234. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lazar, M.; Agiasofitou, E.; Po, G. Three-dimensional nonlocal anisotropic elasticity: A generalized continuum theory of Angstrom-mechanics. Acta Mech. 2020, 231, 743–781. [Google Scholar] [CrossRef]
- Gutkin, M.Y.; Aifantis, E.C. Dislocations in the theory of gradient elasticity. Script. Mater. 1999, 40, 559–566. [Google Scholar] [CrossRef]
- Lazar, M.; Maugin, G.A. Nonsingular stress and strain fields of dislocations and disclinations in first strain gradient elasticity. Int. J. Eng. Sci. 2005, 43, 1157–1184. [Google Scholar] [CrossRef]
- Lazar, M. A nonsingular solution of the edge dislocation in the gauge theory of dislocations. J. Phys. A Math. Gen. 2003, 36, 1415–1437. [Google Scholar] [CrossRef]
- Lazar, M.; Anastassiadis, C. The gauge theory of dislocations: Static solutions of screw and edge dislocations. Phil. Mag. 2009, 89, 199–231. [Google Scholar] [CrossRef][Green Version]
- Zhou, X.D.; Reimuth, C.; Stein, P.; Xu, B.X. Driving forces on dislocations: Finite element analysis in the context of the non-singular dislocation theory. Arch. Appl. Mech. 2021, 91, 4499–4516. [Google Scholar] [CrossRef]
- Zhao, T.; Shen, Y.X. A nonlocal model for dislocations with embedded discontinuity peridynamics. Int. J. Mech. Sci. 2021, 197, 106301. [Google Scholar] [CrossRef]
- Taupin, V.; Gbemou, K.; Fressengeas, C.; Capolungo, L. Nonlocal elasticity tensors in dislocation and disclination cores. J. Mech. Phys. Solids 2017, 100, 62–84. [Google Scholar] [CrossRef]
- Po, G.; Lazar, M.; Seif, D.; Ghoniem, N. Singularity-free dislocation dynamics with strain gradient elasticity. J. Mech. Phys. Solids 2014, 68, 161–178. [Google Scholar] [CrossRef]
- Seif, D.; Po, G.; Mrovec, M.; Lazar, M.; Elsasser, C.; Gumbsch, P. Atomistically enabled nonsingular anisotropic elastic representation of near-core dislocation stress fields in alpha-iron. Phys. Rev. B 2015, 91, 184102. [Google Scholar] [CrossRef]
- Delfani, M.R.; Tavakol, E. Uniformly moving screw dislocation in strain gradient elasticity. Eur. J. Mech. A-Solids 2019, 73, 349–355. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Lazar, M. Distributed dislocation technique for cracks based on non-singular dislocations in nonlocal elasticity of Helmholtz type. Eng. Fract. Mech. 2015, 136, 79–95. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity; McGraw-Hill: London, UK, 1970. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Dover Publication: Mignola, NY, USA, 1965. [Google Scholar]
- Hull, D.; Bacon, D.J. Introduction to Dislocations; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Chen, X.L.; Richeton, T.; Motz, C.; Berbenni, S. Surface effects on image stresses and dislocation pile-ups in anisotropic bi-crystals. Int. J. Plast. 2021, 143, 102967. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics; Cambridge University Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Shima, H.; Nakayama, T. Higher Mathematics for Physics and Engineering; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Das, A.B.; Bhuiyan, M.I.H.; Alam, S.M.S. Classification of EEG signals using normal inverse Gaussian parameters in the dual-tree complex wavelet transform domain for seizure detection. Signal Image Video Process. 2016, 10, 259–266. [Google Scholar] [CrossRef]
- Hassan, A.R.; Bhuiyan, M.I.H. An automated method for sleep staging from EEG signals using normal inverse Gaussian parameters and adaptive boosting. Neurocomputing 2017, 219, 76–87. [Google Scholar] [CrossRef]
- O’Hagan, A.; Murphy, T.B.; Gormley, I.C.; McNicholas, P.D.; Karlis, D. Clustering with the multivariate normal inverse Gaussian distribution. Comput. Stat. Data Anal. 2016, 93, 18–30. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E. Normal inverse Gaussian distributions and stochastic volatility modelling. Scand. J. Stat. 1997, 24, 1–13. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shima, H.; Sumigawa, T.; Umeno, Y. Nonsingular Stress Distribution of Edge Dislocations near Zero-Traction Boundary. Materials 2022, 15, 4929. https://doi.org/10.3390/ma15144929
Shima H, Sumigawa T, Umeno Y. Nonsingular Stress Distribution of Edge Dislocations near Zero-Traction Boundary. Materials. 2022; 15(14):4929. https://doi.org/10.3390/ma15144929
Chicago/Turabian StyleShima, Hiroyuki, Takashi Sumigawa, and Yoshitaka Umeno. 2022. "Nonsingular Stress Distribution of Edge Dislocations near Zero-Traction Boundary" Materials 15, no. 14: 4929. https://doi.org/10.3390/ma15144929
APA StyleShima, H., Sumigawa, T., & Umeno, Y. (2022). Nonsingular Stress Distribution of Edge Dislocations near Zero-Traction Boundary. Materials, 15(14), 4929. https://doi.org/10.3390/ma15144929