Non-Iterative Optimal Design Method Based on LM Index for Steel Double-Beam Floor Systems Reinforced with Concrete Panels
Abstract
1. Introduction
2. Non-Iterative Optimal Design Method Using LM Index
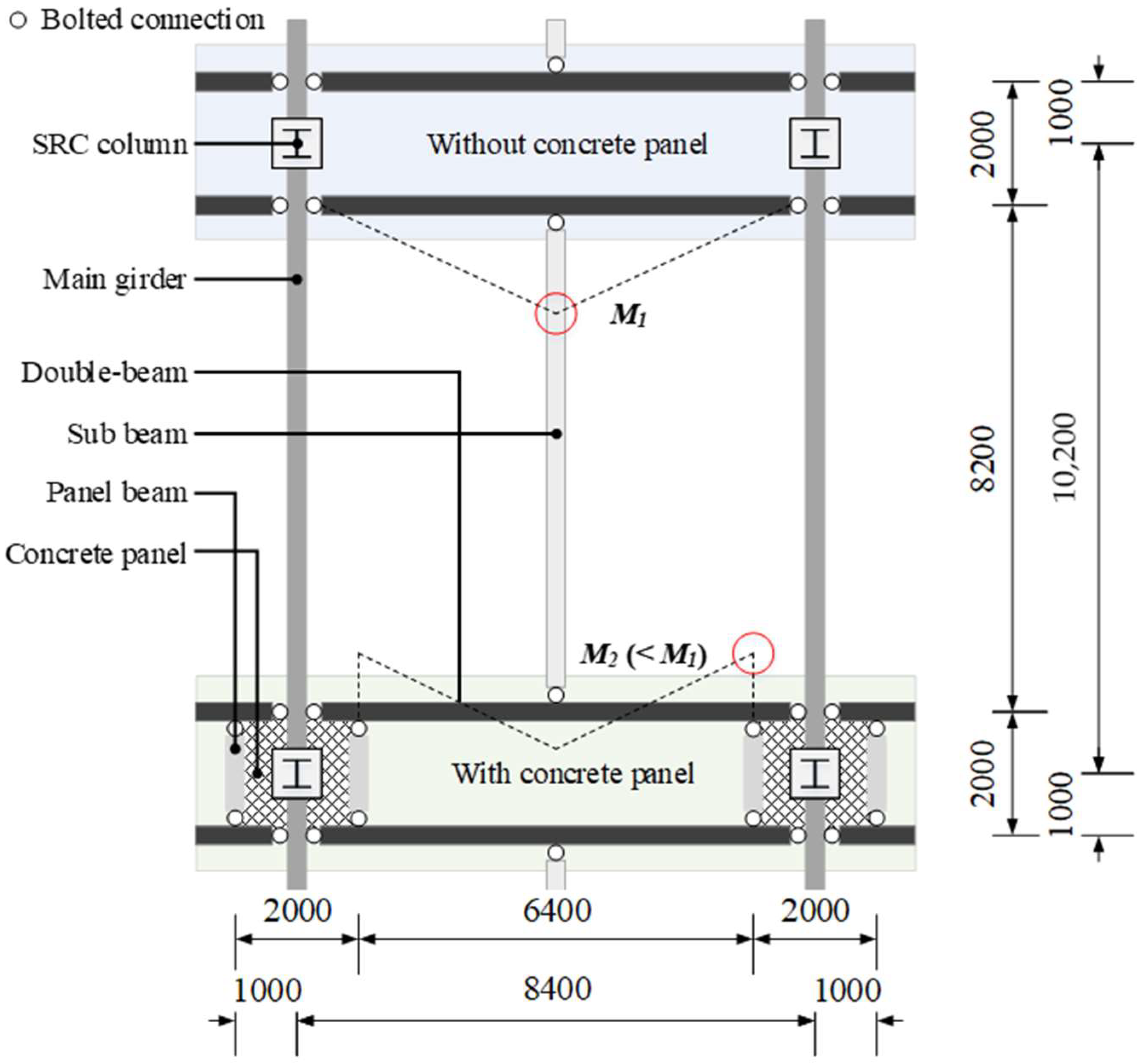
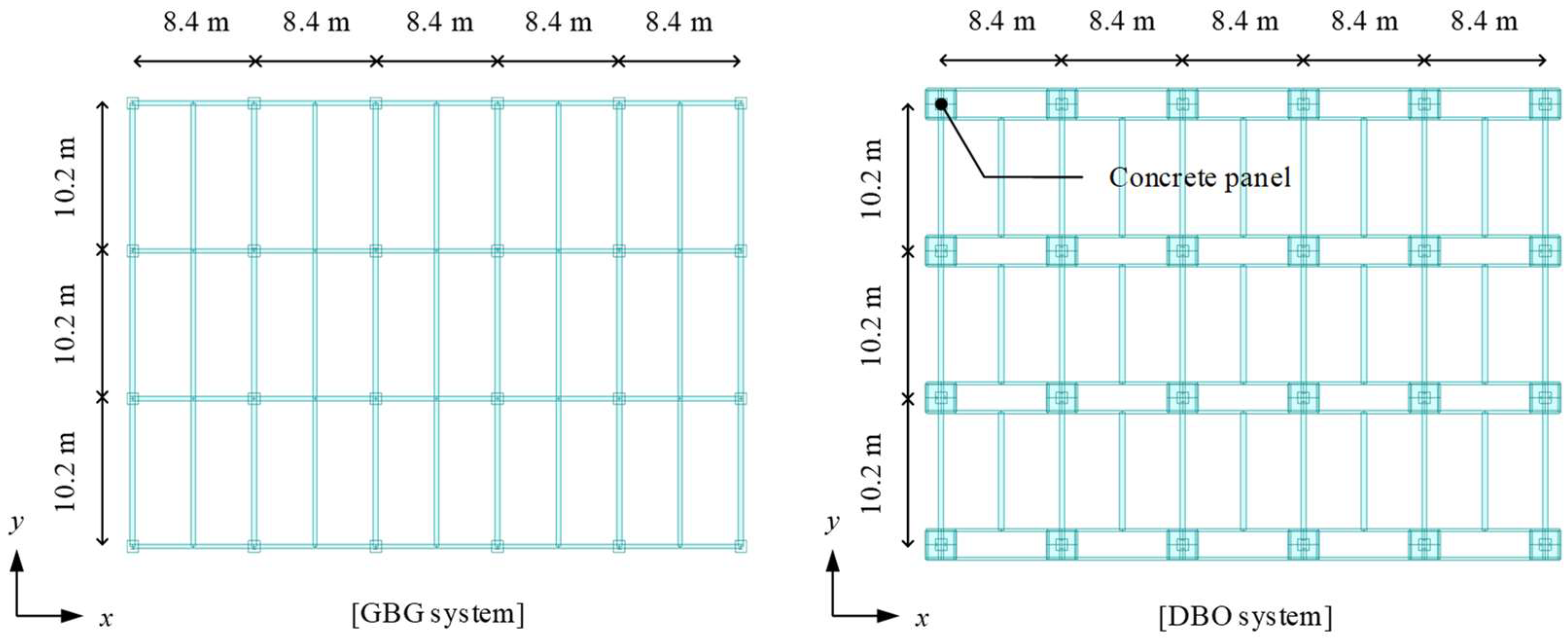
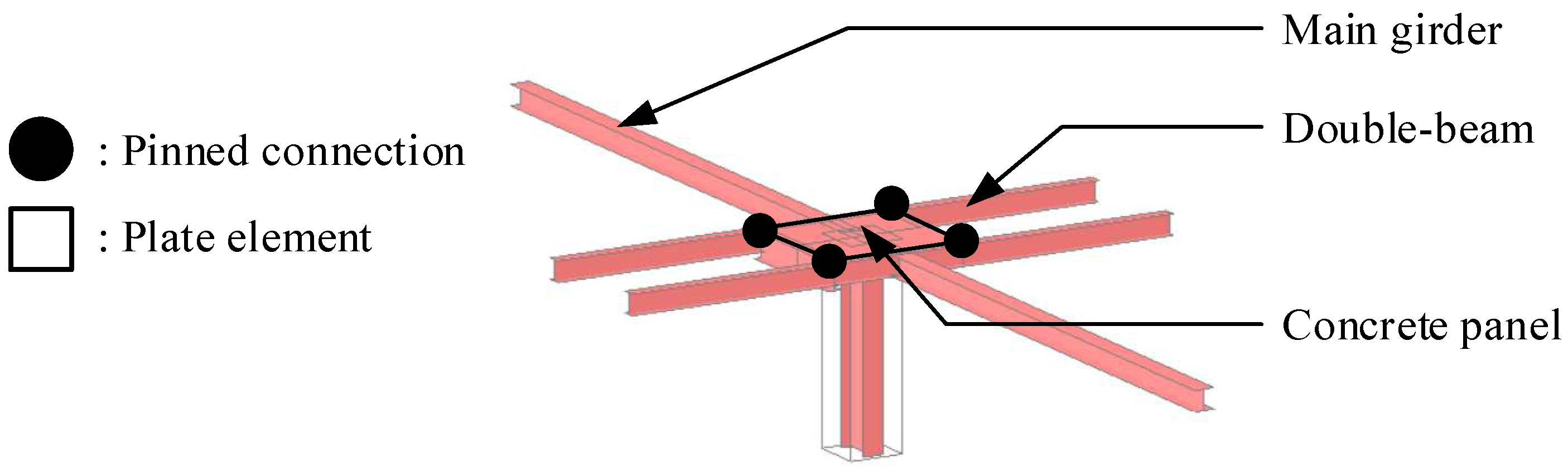
2.1. Description of Steel Double-Beam Floor Systems
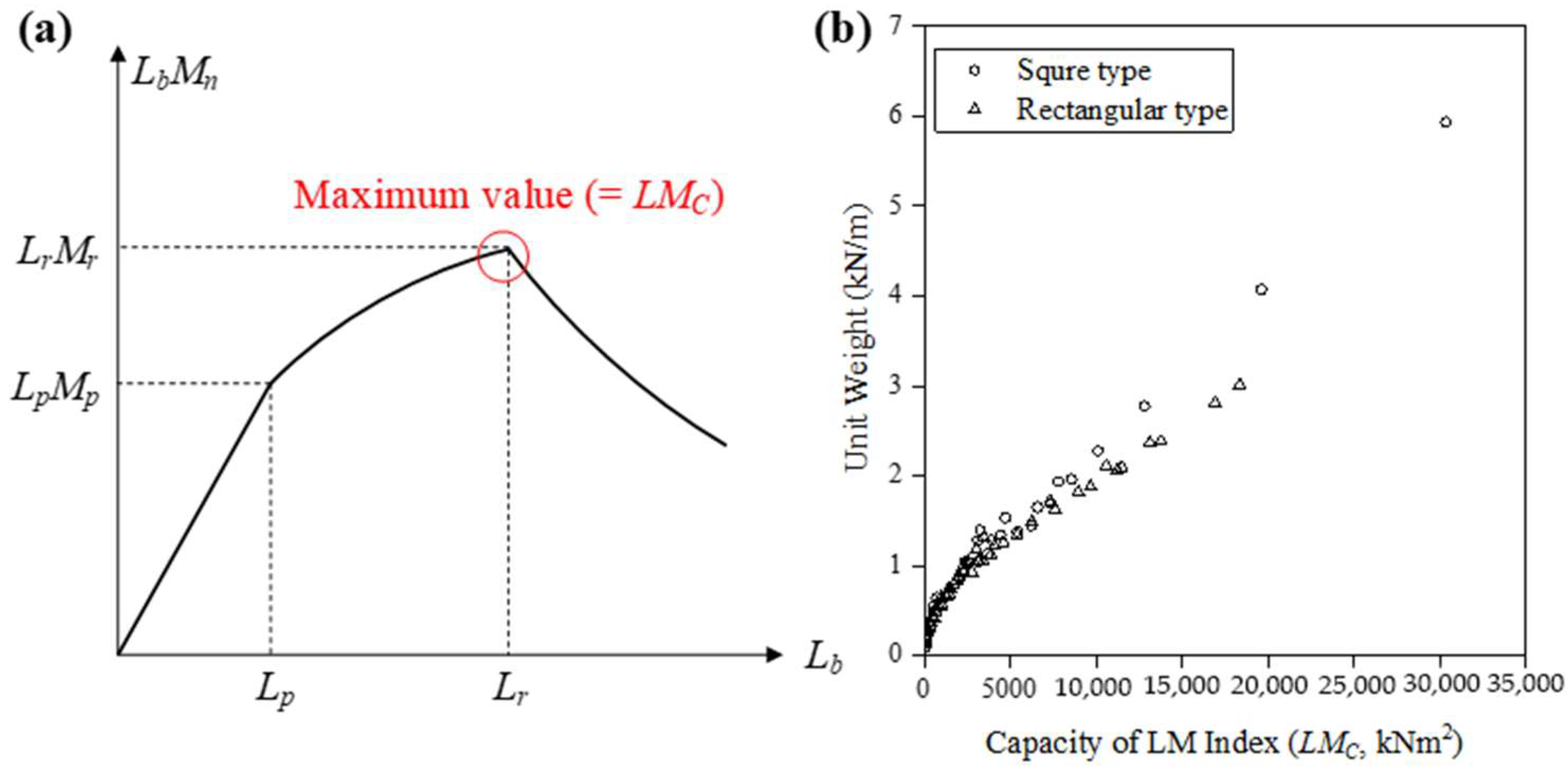
2.2. Formulation of Objective Function Using LM Index
2.3. Constraint Conditions Conforming Design Codes
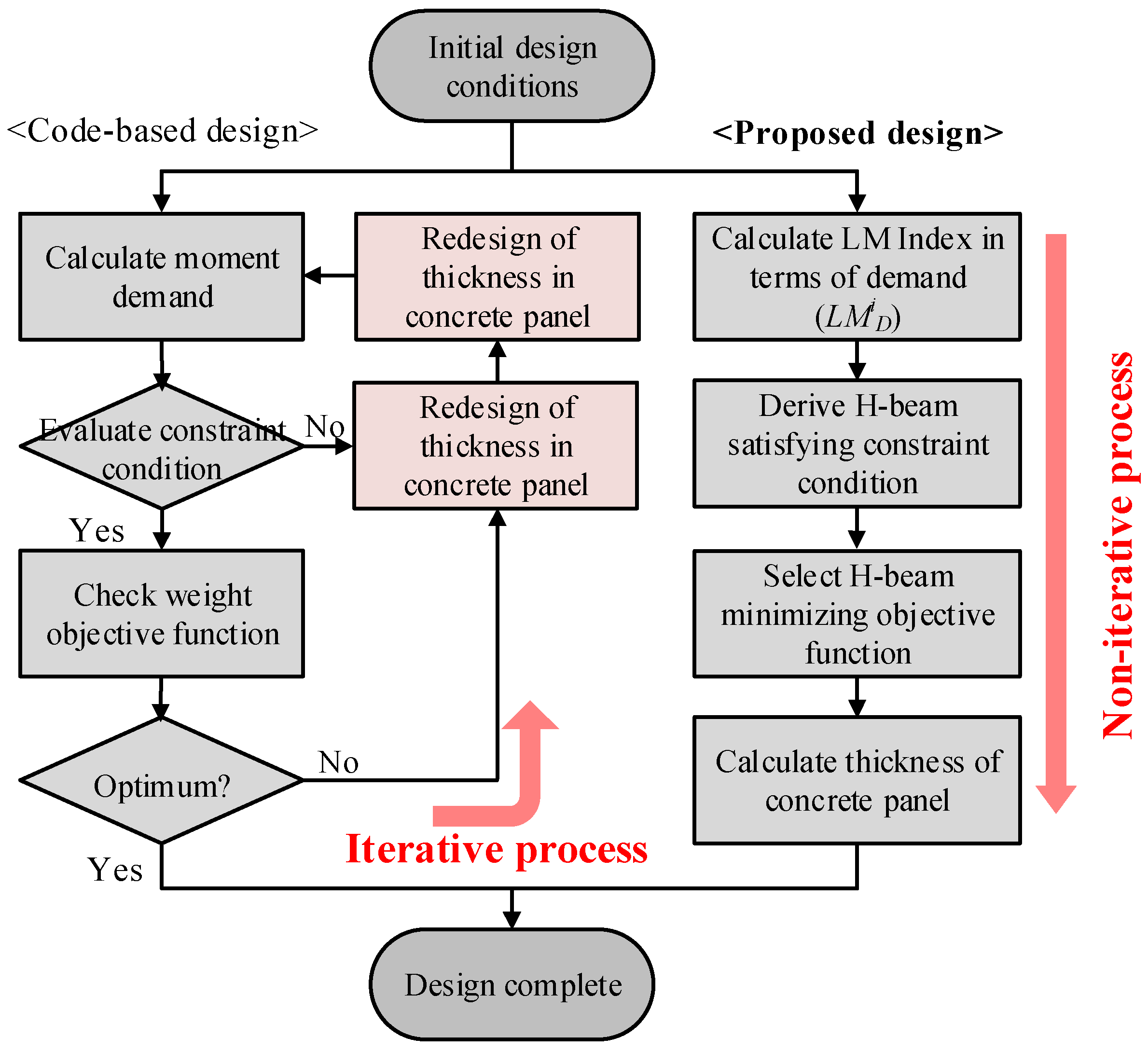
2.4. Non-Iterative Optimal Design Process
3. Validation of Proposed Optimal Design Method
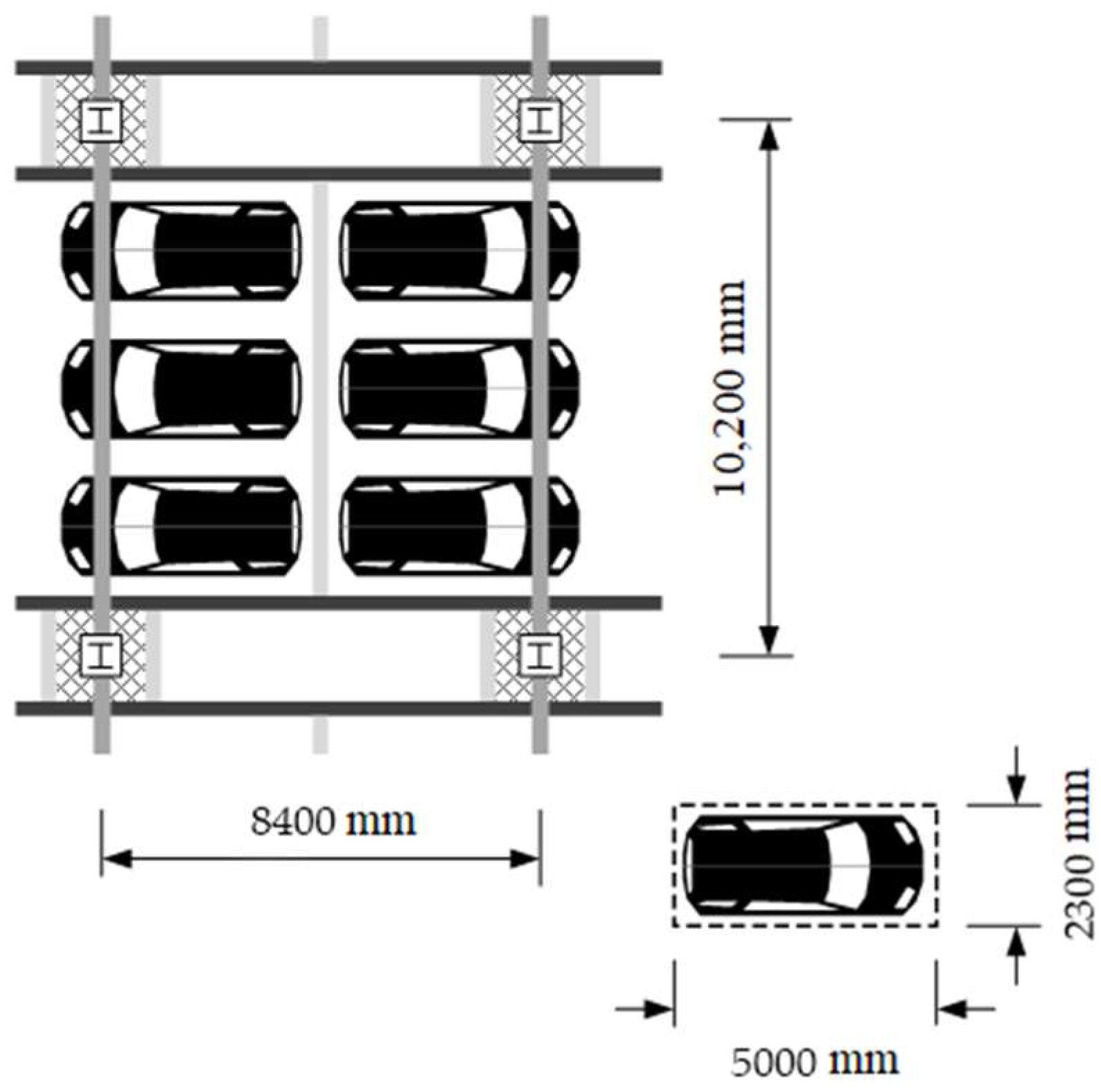
3.1. Typical Design Conditions of Underground Structures Used for Parking Lots
3.2. Structural Modeling for Steel Double-Beam Floor Systems
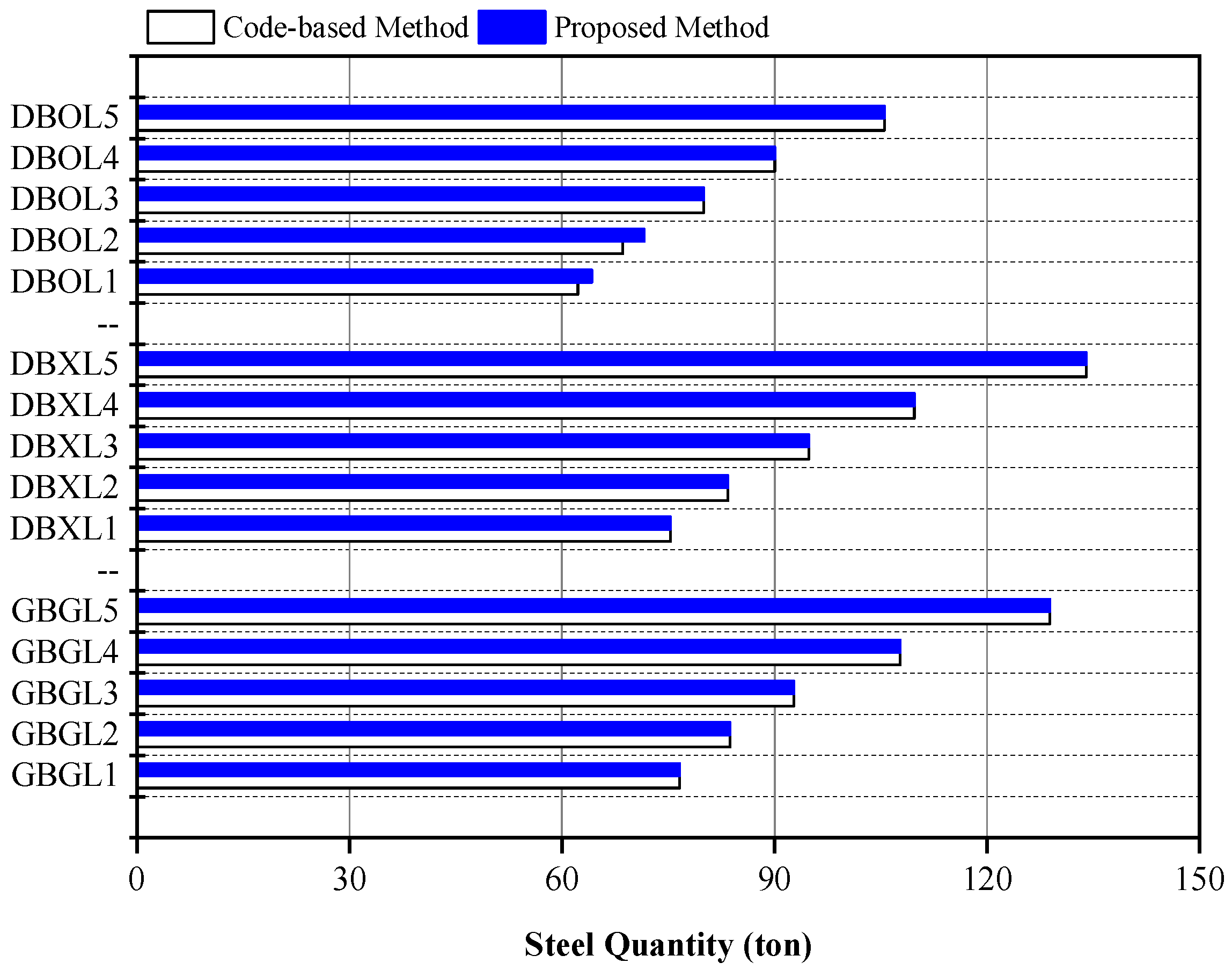
3.3. Design Feasibility of Proposed Optimal Design Method
3.4. Environmental Efficiency of Rotational Constraints
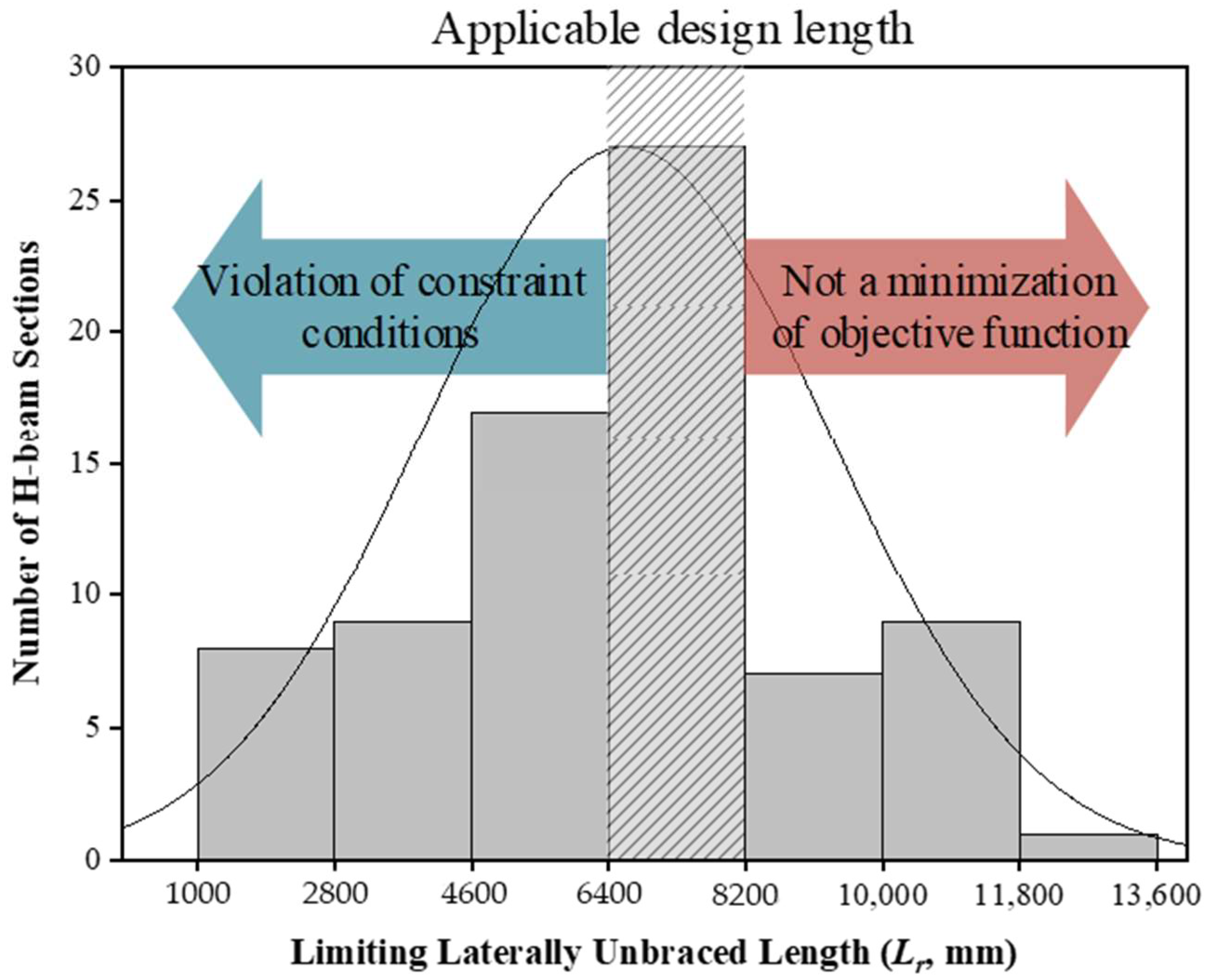
3.5. Applicable Design Conditions Using LM Index
4. Conclusions
- By introducing a new index named the LM index on the design parameters and formulating the objective function, the optimal cross-section of the steel beams can be selected by minimizing the material quantity related to the embodied CO2 emissions.
- As a result, considering five categories of live loads ranging from 2.5 to 12.0 kN/m2, the proposed optimal design method was superb at providing a quantity optimized design option under the high gravity loads with a live load of 6.0 kN/m2 or more.
- The structural rotational constraint induced by the concrete panel can improve the environmental performance of the steel double-beam floor systems by reducing the GWP compared to the steel beam–girder floor system.
- The applicable design length of steel beams for practical engineers to use the proposed optimal method is suggested from 6.4 m to 8.2 m based on the LM index and plan of the typical underground structure used for parking lots.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rhim, H.-C.; Kim, K.-M.; Kim, S.-W. Development of an Optimum Pre-Founded Column System for Top-down Construction. J. Civ. Eng. Manag. 2012, 18, 735–743. [Google Scholar] [CrossRef][Green Version]
- Kim, D.; Jeong, S.; Jung, G.; Park, J. Load-Sharing Ratio of Prebored and Precast Pile in Top-down Method Construction Process. Struct. Des. Tall Spec. Build. 2018, 27, e1472. [Google Scholar] [CrossRef]
- Fang, G.X.; Jin, Z.C. A Study of the Planning Methods in the Underground Work of Top-down Construction in High-Rise Buildings. In Proceedings of the Advanced Materials Research; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; Volume 1044–1045, pp. 561–565. [Google Scholar]
- Choi, I.; Kim, J.H.; Kim, H.-R. Composite Behavior of Insulated Concrete Sandwich Wall Panels Subjected to Wind Pressure and Suction. Materials 2015, 8, 1264–1282. [Google Scholar] [CrossRef]
- Choi, I.; Kim, J.H.; Kim, D.W.; Park, J.S. Effects of Grid-Type Shear Connector Arrangements Used for Insulated Concrete Sandwich Wall Panels with a Low Aspect Ratio. J. Build. Eng. 2022, 46, 103754. [Google Scholar] [CrossRef]
- Kim, J.H.; You, Y.-C. Composite Behavior of a Novel Insulated Concrete Sandwich Wall Panel Reinforced with GFRP Shear Grids: Effects of Insulation Types. Materials 2015, 8, 899–913. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, C.; Xiao, Y.; Dewancker, B. Investigation of Sustainability Embodied in Existing Buildings: A Case Study of Refurbishment Adopted in a Chinese Contemporary Building. Sci. Rep. 2021, 11, 17283. [Google Scholar] [CrossRef]
- IEA. CO2 Emissions from Fuel Combustion; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Wang, J.J.; Wang, Y.F.; Sun, Y.W.; Tingley, D.D.; Zhang, Y.R. Life Cycle Sustainability Assessment of Fly Ash Concrete Structures. Renew. Sustain. Energy Rev. 2017, 80, 1162–1174. [Google Scholar] [CrossRef]
- Marey, H.; Kozma, G.; Szabó, G. Effects of Using Green Concrete Materials on the CO2 Emissions of the Residential Building Sector in Egypt. Sustainability 2022, 14, 3592. [Google Scholar] [CrossRef]
- Dimoudi, A.; Tompa, C. Energy and Environmental Indicators Related to Construction of Office Buildings. Resour. Conserv. Recycl. 2008, 53, 86–95. [Google Scholar] [CrossRef]
- Lee, J.-M.; Kim, M.-J.; Lee, Y.-J.; Kim, S.-W.; Lee, J.-Y.; Kim, K.-H. Structural Performance of Composite Double Beam System. Adv. Struct. Eng. 2016, 19, 283–298. [Google Scholar] [CrossRef]
- Kinderis, T.; Daukšys, M.; Urat, E.; Mockien, J. Research on the Efficiency of Composite Beam Application in Multi-Storey Buildings. Sustainability 2020, 12, 8328. [Google Scholar] [CrossRef]
- Du, H.; Hu, X.; Shi, D.; Xue, W. Flexural Performance of Composite Beams Using High-Strength Steel and High-Strength Concrete. Int. J. Steel Struct. 2021, 22, 27–41. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, R.; Huo, X.; Zhou, X.; Roeder, C.W. Static Experiment on Mechanical Behavior of Innovative Flat Steel Plate-Concrete Composite Slabs. Int. J. Steel Struct. 2018, 18, 473–485. [Google Scholar] [CrossRef]
- Ju, Y.K.; Kim, J.-Y.; Kim, S.-D. Experimental Evaluation of New Concrete Encased Steel Composite Beam to Steel Column Joint. J. Struct. Eng. 2007, 133, 519–529. [Google Scholar] [CrossRef]
- Amadio, C.; Macorini, L.; Sorgon, S.; Suraci, G. A Novel Hybrid System with Rc-Encased Steel Joists. Eur. J. Environ. Civ. Eng. 2011, 15, 1433–1463. [Google Scholar] [CrossRef]
- Huang, P.; He, J.; Kong, F.; Mei, K.; Li, X. Experimental Study on the Bearing Capacity of PZ Shape Composite Dowel Shear Connectors with Elliptical Holes. Sci. Rep. 2022, 12, 2457. [Google Scholar] [CrossRef]
- Park, H.-G.; Hwang, H.-J.; Lee, C.-H.; Park, C.-H.; Lee, C.-N. Cyclic Loading Test for Concrete-Filled U-Shaped Steel Beam-RC Column Connections. Eng. Struct. 2012, 36, 325–336. [Google Scholar] [CrossRef]
- Choi, I.; Kim, J.H.; Jang, J.; Chang, H.; Kang, G. Composite Effects on Rotational Constraints of a Double-Beam System Reinforced with Beam-End Concrete. Eng. Struct. 2021, 228, 111585. [Google Scholar] [CrossRef]
- Choi, I.; Kim, J.; Kim, D. LCA-Based Investigation of Environmental Impacts for Novel Double-Beam Floor System Subjected to High Gravity Loads. Sustainability 2020, 12, 9193. [Google Scholar] [CrossRef]
- Szewczyk, P.; Szumigała, M. Optimal Design of Steel–Concrete Composite Beams Strengthened under Load. Materials 2021, 14, 4715. [Google Scholar] [CrossRef]
- Kaveh, A.; Izadifard, R.A.; Mottaghi, L. Optimal Design of Planar RC Frames Considering CO2 Emissions Using ECBO, EVPS and PSO Metaheuristic Algorithms. J. Build. Eng. 2020, 28, 101014. [Google Scholar] [CrossRef]
- Du, H.; Jiang, Q.; Xiong, W. Computer-Aided Optimal Design for Flexible Cable in Aerospace Products Based on Dynamic Analogy Modeling. Sci. Rep. 2022, 12, 5833. [Google Scholar] [CrossRef] [PubMed]
- Habashneh, M.; Rad, M.M. Reliability Based Geometrically Nonlinear Bi-Directional Evolutionary Structural Optimization of Elasto-Plastic Material. Sci. Rep. 2022, 12, 5989. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.G.; An, J.H.; Bae, S.G.; Oh, H.S.; Choi, J.; Yun, D.Y.; Hong, T.; Lee, D.-E.; Park, H.S. Multi-Objective Sustainable Design Model for Integrating CO 2 Emissions and Costs for Slabs in Office Buildings. Struct. Infrastruct. Eng. 2020, 16, 1096–1105. [Google Scholar] [CrossRef]
- Ahadzadeh Kolour, N.; Charkhtab Basim, M.; Chenaghlou, M. Multi-Objective Optimum Design of Nonlinear Viscous Dampers in Steel Structures Based on Life Cycle Cost. Structures 2021, 34, 3776–3788. [Google Scholar] [CrossRef]
- Negrin, I.A.; Chagoyén, E.L. Economic and Environmental Design Optimisation of Reinforced Concrete Frame Buildings: A Comparative Study. Structures 2022, 38, 64–75. [Google Scholar] [CrossRef]
- Hashemi, S.V.; Miri, M.; Rashki, M.; Etedali, S. Multi-Objective Optimal Design of SC-BRB for Structures Subjected to Different near-Fault Earthquake Pulses. Structures 2022, 36, 1021–1031. [Google Scholar] [CrossRef]
- Park, H.S.; Kwon, B.; Shin, Y.; Kim, Y.; Hong, T.; Choi, S.W. Cost and CO2 Emission Optimization of Steel Reinforced Concrete Columns in High-Rise Buildings. Energies 2013, 6, 5609–5624. [Google Scholar] [CrossRef]
- Breda, B.D.; Pietralonga, T.C.; Alves, É.C. Optimization of the Structural System with Composite Beam and Composite Slab Using Genetic Algorithm. Rev. IBRACON Estrut. Mater. 2020, 13, 2020. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Liu, A.; Pi, Y.-L.; Zhang, J.; Wang, Y.; Zhong, L. Experimental Study on Shear Behavior of High Strength Bolt Connection in Prefabricated Steel-Concrete Composite Beam. Compos. Part B Eng. 2019, 159, 481–489. [Google Scholar] [CrossRef]
- Yang, P.; Eatherton, M.R. A Phenomenological Component-Based Model to Simulate Seismic Behavior of Bolted Extended End-Plate Connections. Eng. Struct. 2014, 75, 11–26. [Google Scholar] [CrossRef]
- Lu, L.; Gao, M.; Yan, H.; Hao, H.; Ding, S.; Liu, Y. Determining the Effective Slab Width of Composite Joint with the Weak-Axis Connection for Ultimate Bearing Capacity. Structures 2022, 38, 553–571. [Google Scholar] [CrossRef]
- Kyprianou, C.; Kyvelou, P.; Gardner, L.; Nethercot, D.A. Characterisation of Material and Connection Behaviour in Sheathed Cold-Formed Steel Wall Systems—Part 2: Analytical Modelling. Structures 2021, 30, 1184–1199. [Google Scholar] [CrossRef]
- Kim, J.; Ghaboussi, J.; Elnashai, A.S. Mechanical and Informational Modeling of Steel Beam-to-Column Connections. Eng. Struct. 2010, 32, 449–458. [Google Scholar] [CrossRef]
- Kim, J.H.; Ghaboussi, J.; Elnashai, A.S. Hysteretic Mechanical–Informational Modeling of Bolted Steel Frame Connections. Eng. Struct. 2012, 45, 1–11. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, L.; Liu, X.; Yang, W.; Hao, X.; Tian, L. Design Optimization of a Passive Building with Green Roof through Machine Learning and Group Intelligent Algorithm. Buildings 2021, 11, 192. [Google Scholar] [CrossRef]
- Zhuang, X.; Zhou, S. The Prediction of Self-Healing Capacity of Bacteria-Based Concrete Using Machine Learning Approaches. Comput. Mater. Contin. 2019, 59, 57–77. [Google Scholar] [CrossRef]
- AISC Committee. Specification for Structural Steel Buildings (ANSI/AISC 360-16); AISC: Chicago, IL, USA, 2016. [Google Scholar]
- ACI Committee. Building Code Requirements for Structural Concrete and Commentary (ACI 318-19); ACI: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Camp, C.V.; Bichon, B.J.; Stovall, S.P. Design of Steel Frames Using Ant Colony Optimization. J. Struct. Eng. 2005, 131, 369–379. [Google Scholar] [CrossRef]
- KSD 3502:2021; Dimensions, Mass and Permissible Variations of Hot Rolled Steel Sections. Korean Standard Association: Seoul, Korea, 2021.
- ASCE/SEI 7-16; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2016.
- MOLIT. Korean Design Standard (in Korean); Ministry of Land, Infrastructure and Transport: Sejong, Korean, 2016. [Google Scholar]
- MIDAS IT. MIDAS/GEN V8.5.5 Users Manual; MIDAS IT: Seongnam-si, Korea, 2017. [Google Scholar]
- Chau, C.K.; Leung, T.M.; Ng, W.Y. A Review on Life Cycle Assessment, Life Cycle Energy Assessment and Life Cycle Carbon Emissions Assessment on Buildings. Appl. Energy 2015, 143, 395–413. [Google Scholar] [CrossRef]
- Myhre, G.; Shindell, D.; Bréon, F.M.; Collins, W.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.F.; Lee, D.; Mendoza, B. Anthropogenic and Natural Radiative Forcing, Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 659–740. [Google Scholar]
- Hammond, G.P.; Jones, C.I. Embodied Energy and Carbon in Construction Materials. In Proceedings of the Institution of Civil Engineers–Energy; Thomas Telford Ltd.: London, UK, 2008; Volume 161, pp. 87–98. [Google Scholar]
- Mavrokapnidis, D.; Mitropoulou, C.C.; Lagaros, N.D. Environmental Assessment of Cost Optimized Structural Systems in Tall Buildings. J. Build. Eng. 2019, 24, 100730. [Google Scholar] [CrossRef]
- Siverio Lima, M.S.; Buttgereit, A.; Queiroz, C.; Haritonovs, V.; Gschösser, F. Optimizing Financial Allocation for Maintenance and Rehabilitation of Munster’s Road Network Using the World Bank’s RONET Model. Infrastructures 2022, 7, 32. [Google Scholar] [CrossRef]

| Abbreviation | Usages | Live Load (kN/m2) |
|---|---|---|
| L1 | Offices | 2.50 |
| L2 | Passenger vehicles only | 4.00 |
| L3 | Storage warehouses | 6.00 |
| L4 | Knowledge industry center | 8.00 |
| L5 | Heavy vehicles | 12.00 |
| Live Load (kN/m2) | Model | Mu (kNm) | LMD (kNm2) |
|---|---|---|---|
| 2.5 | GBGL1 | 489.5 | 2055.9 |
| DBXL1 | 482.5 | 2026.5 | |
| DBOL1 | 181.2 | 579.8 | |
| 4 | GBGL2 | 600.5 | 2522.1 |
| DBXL2 | 594.3 | 2496.1 | |
| DBOL2 | 222.8 | 713.0 | |
| 6 | GBGL3 | 747.8 | 3140.8 |
| DBXL3 | 740.7 | 3110.9 | |
| DBOL3 | 278.6 | 891.5 | |
| 8 | GBGL4 | 896.5 | 3765.3 |
| DBXL4 | 891.3 | 3743.5 | |
| DBOL4 | 336.2 | 1075.8 | |
| 12 | GBGL5 | 1196.4 | 5024.9 |
| DBXL5 | 1188.7 | 4992.5 | |
| DBOL5 | 447.0 | 1430.4 |
| Model | Structural Member | Design Proposal | |
|---|---|---|---|
| Code-Based Method | Proposed Method | ||
| DBOL4 | Double-beam | H-400 × 200 × 8 × 13 | H-400 × 200 × 8 × 13 |
| Girder | H-482 × 300 × 11 × 15 | H-482 × 300 × 11 × 15 | |
| Sub-beam | H-394 × 398 × 11 × 18 | H-394 × 398 × 11 × 18 | |
| Concrete Panel | Tp = 0.250 m | Tp = 0.250 m | |
| DBOL5 | Double-beam | H-386 × 299 × 9 × 14 | H-386 × 299 × 9 × 14 |
| Girder | H-582 × 300 × 12 × 17 | H-582 × 300 × 12 × 17 | |
| Sub-beam | H-594 × 302 × 14 × 23 | H-594 × 302 × 14 × 23 | |
| Concrete Panel | Tp = 0.320 m | Tp = 0.320 m | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, I.; Kim, D.; Kim, J. Non-Iterative Optimal Design Method Based on LM Index for Steel Double-Beam Floor Systems Reinforced with Concrete Panels. Materials 2022, 15, 4538. https://doi.org/10.3390/ma15134538
Choi I, Kim D, Kim J. Non-Iterative Optimal Design Method Based on LM Index for Steel Double-Beam Floor Systems Reinforced with Concrete Panels. Materials. 2022; 15(13):4538. https://doi.org/10.3390/ma15134538
Chicago/Turabian StyleChoi, Insub, Dongwon Kim, and JunHee Kim. 2022. "Non-Iterative Optimal Design Method Based on LM Index for Steel Double-Beam Floor Systems Reinforced with Concrete Panels" Materials 15, no. 13: 4538. https://doi.org/10.3390/ma15134538
APA StyleChoi, I., Kim, D., & Kim, J. (2022). Non-Iterative Optimal Design Method Based on LM Index for Steel Double-Beam Floor Systems Reinforced with Concrete Panels. Materials, 15(13), 4538. https://doi.org/10.3390/ma15134538






