Accelerating Effects of Flow Behavior Index n on Breakup Dynamics for Droplet Evolution in Non-Newtonian Fluids
Abstract
:1. Introduction
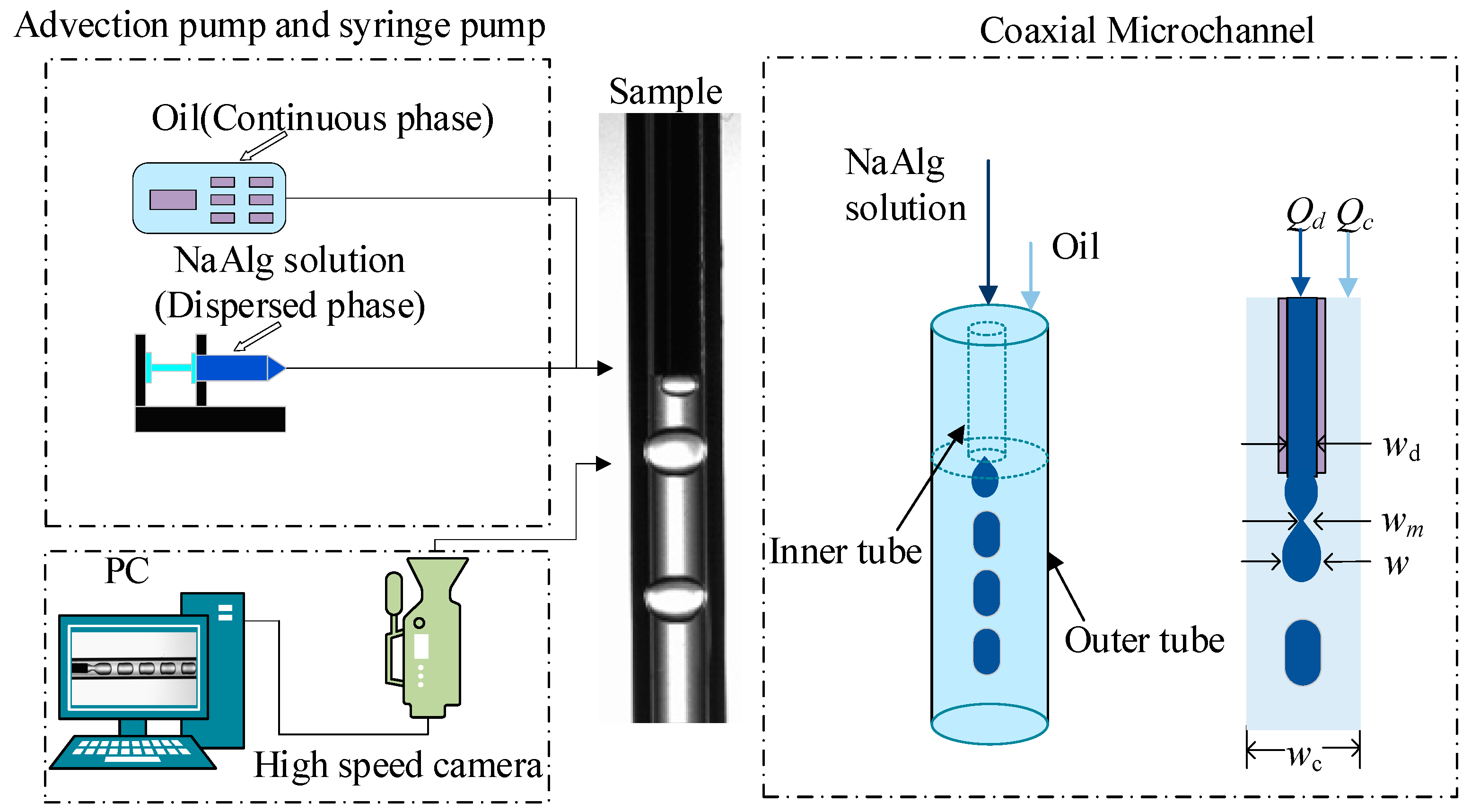
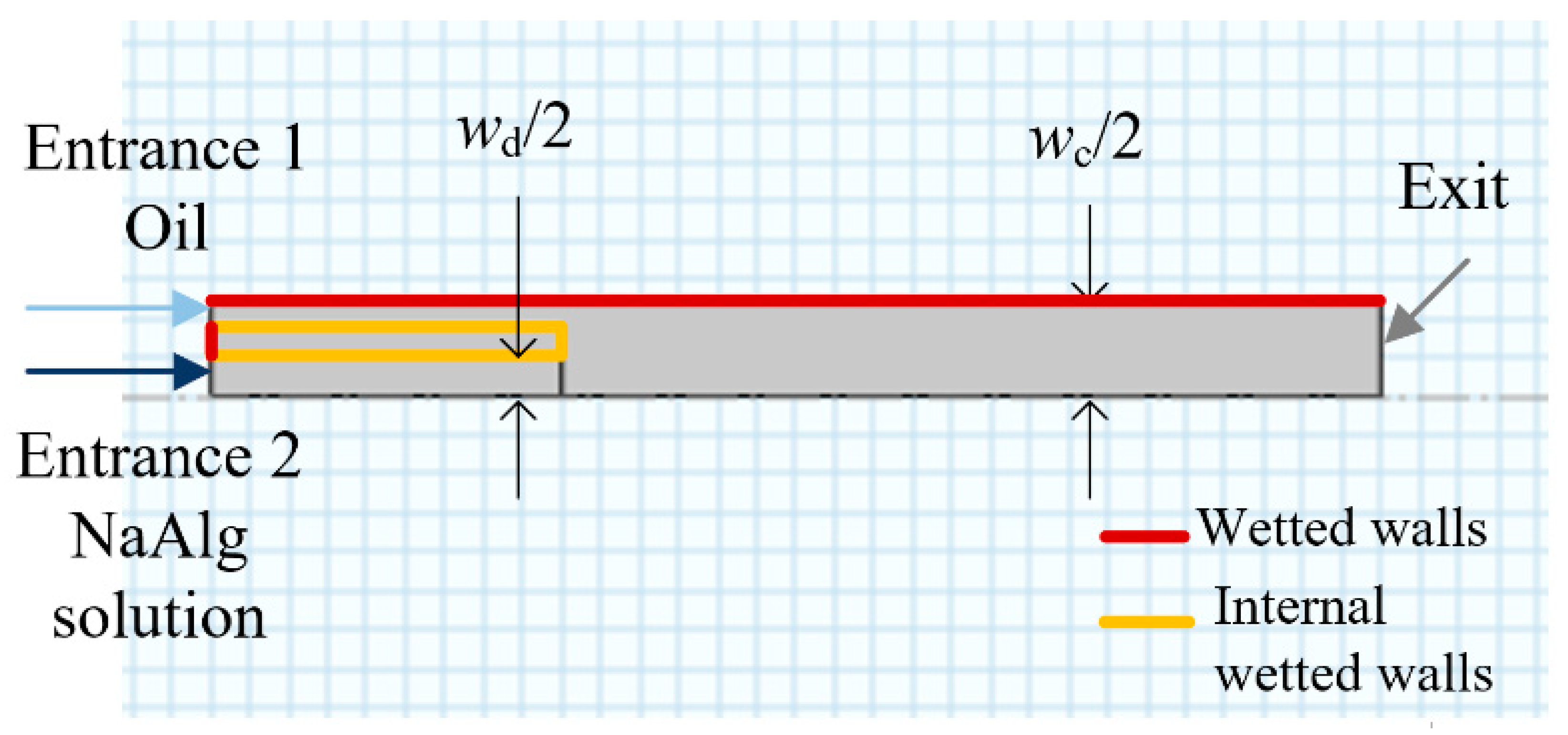
2. Experiments and Simulation
3. Results and Discussion
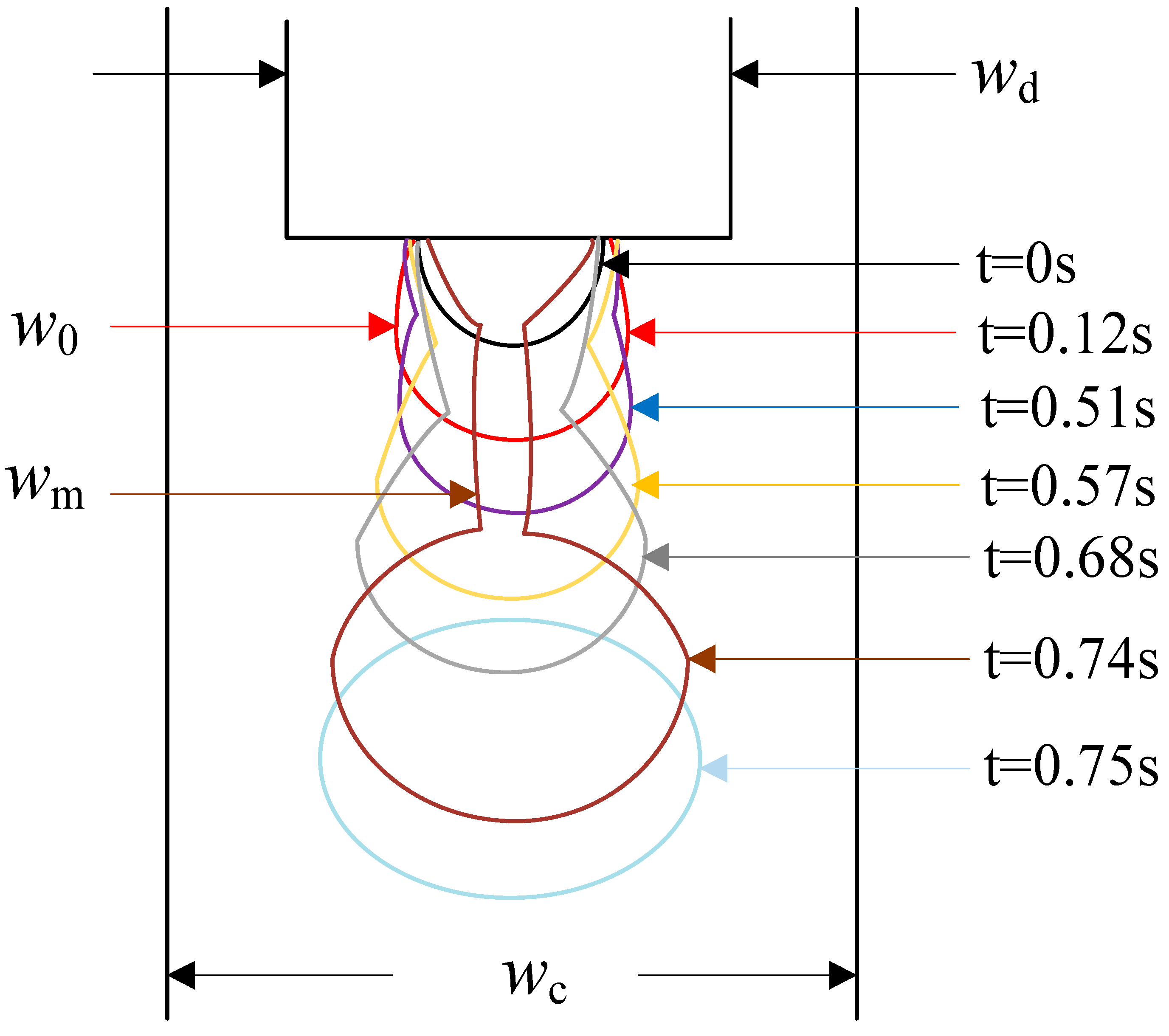
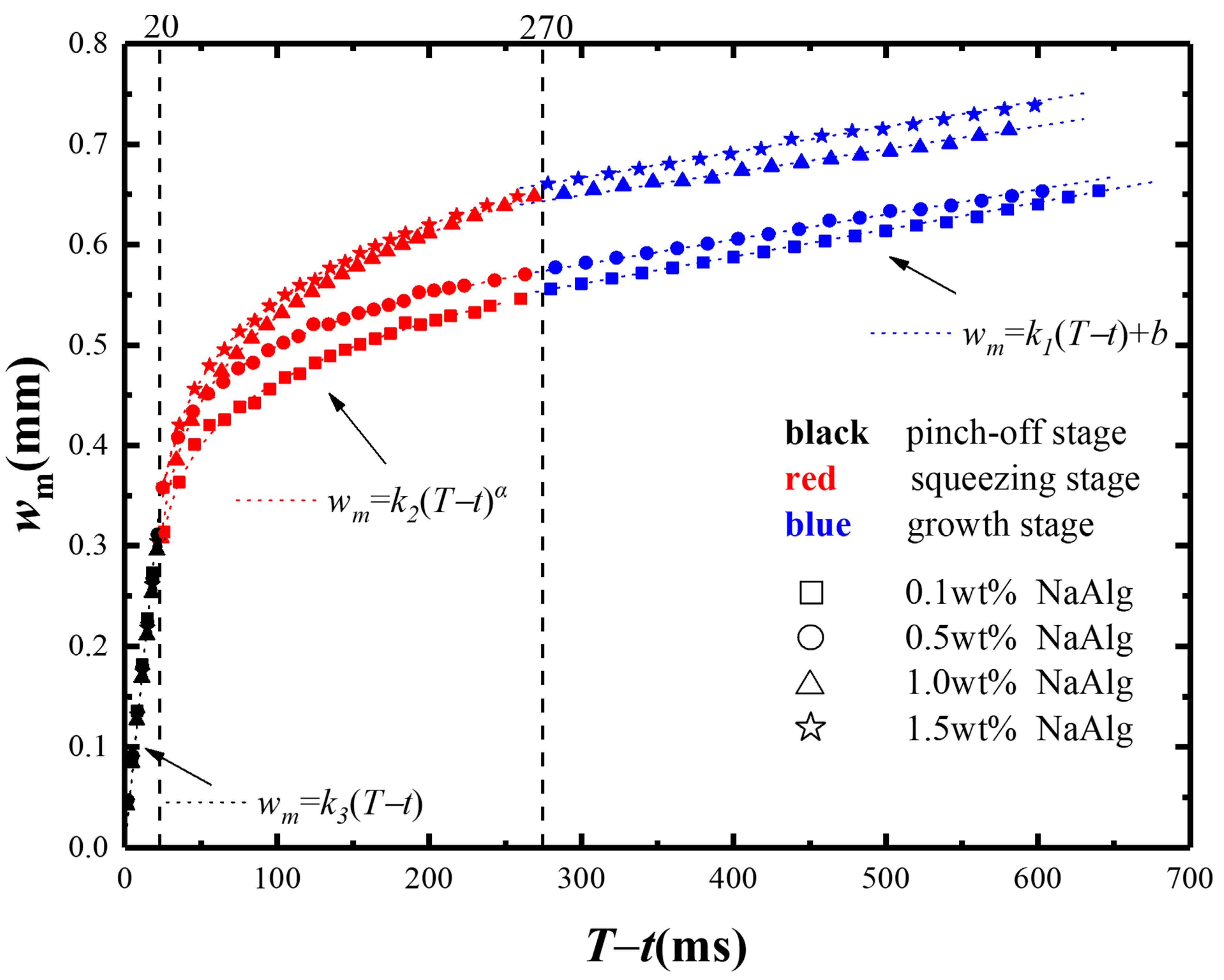
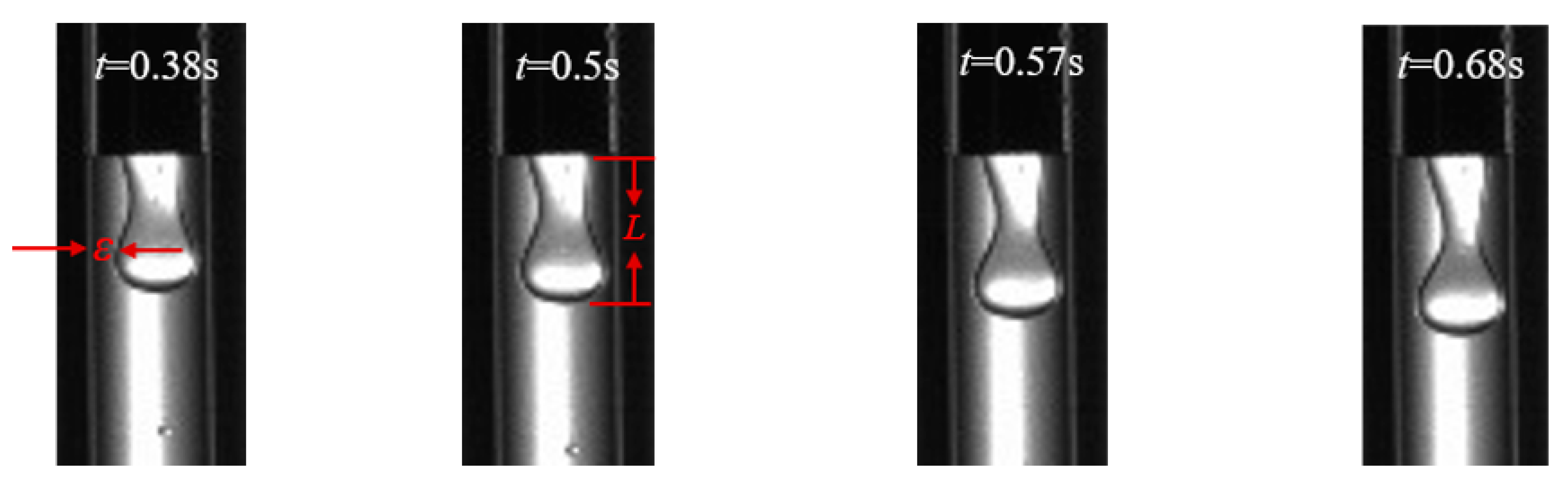
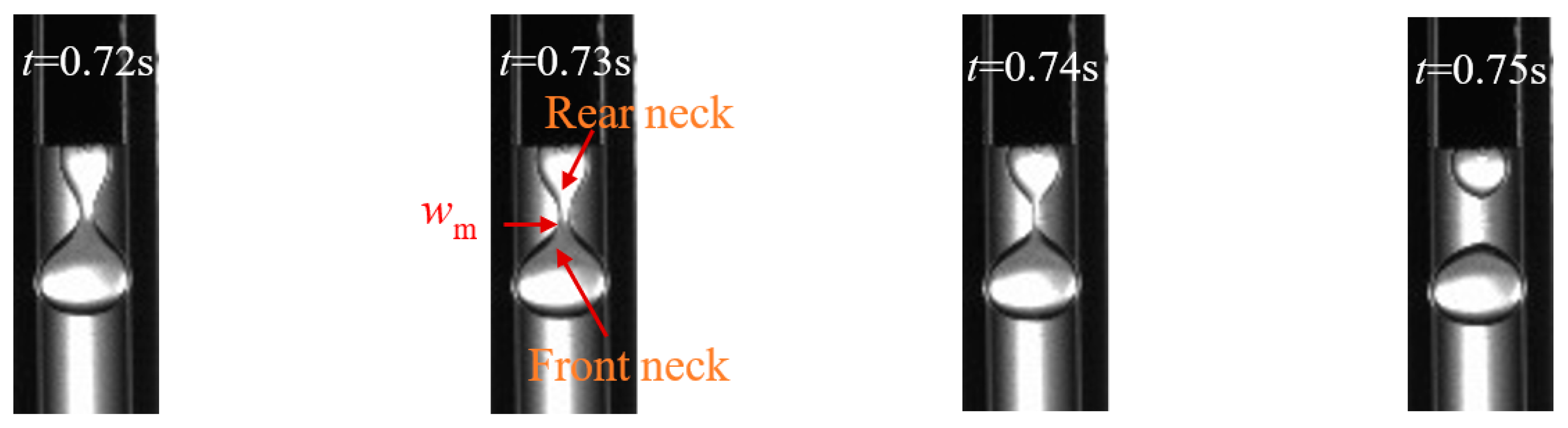
3.1. Formation and Breakup Mechanism of Micro-Droplet
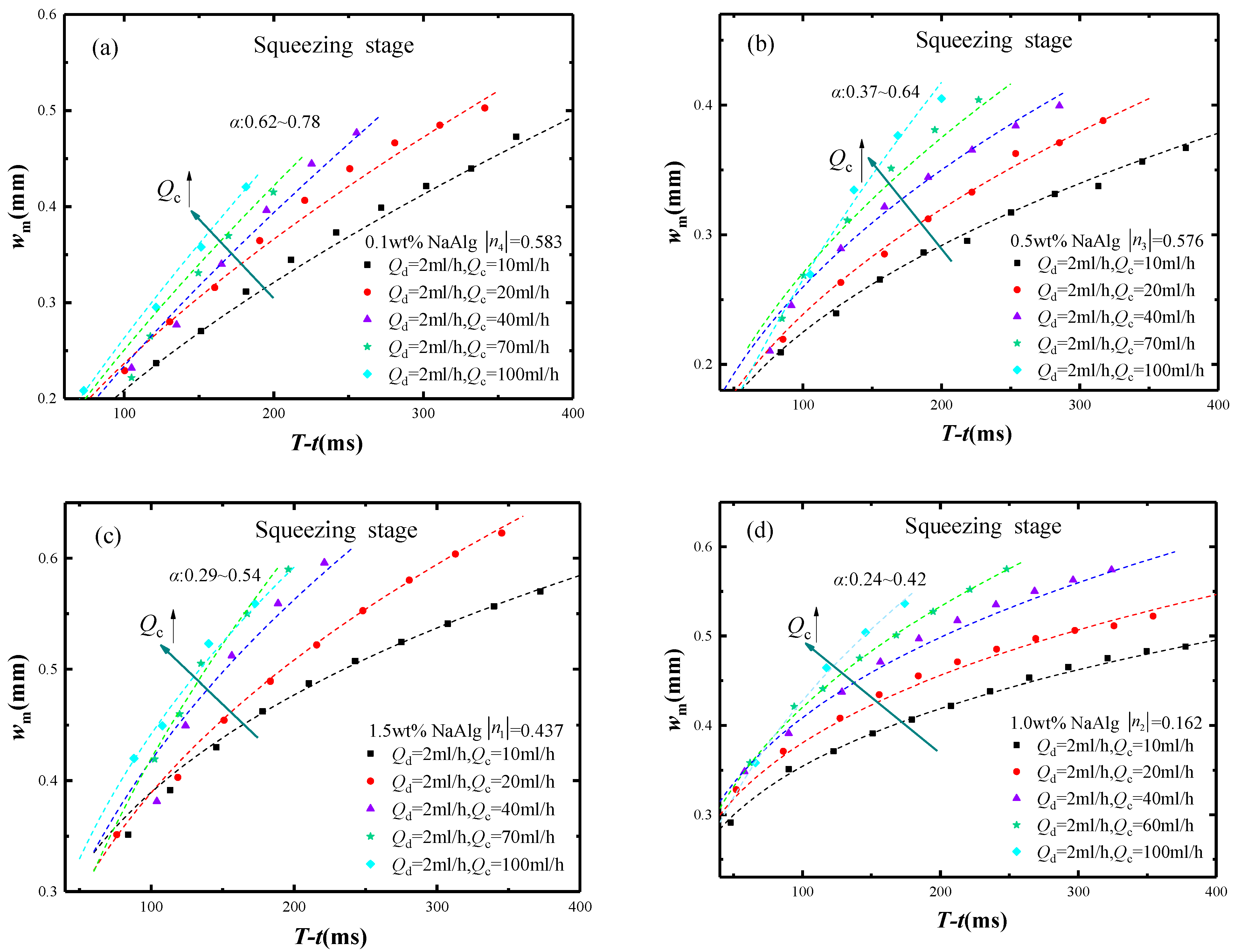
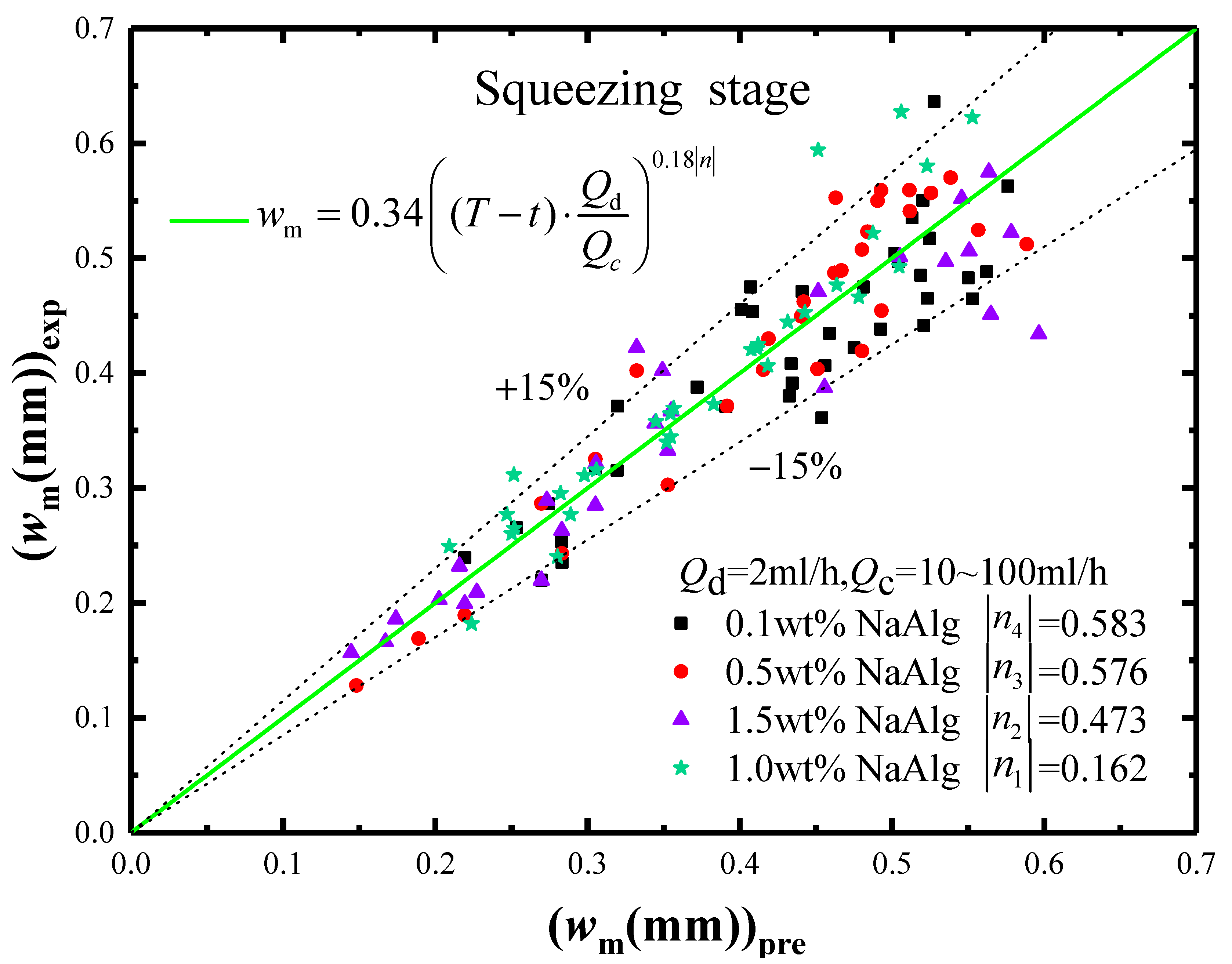
3.2. Squeezing Stage Dynamics
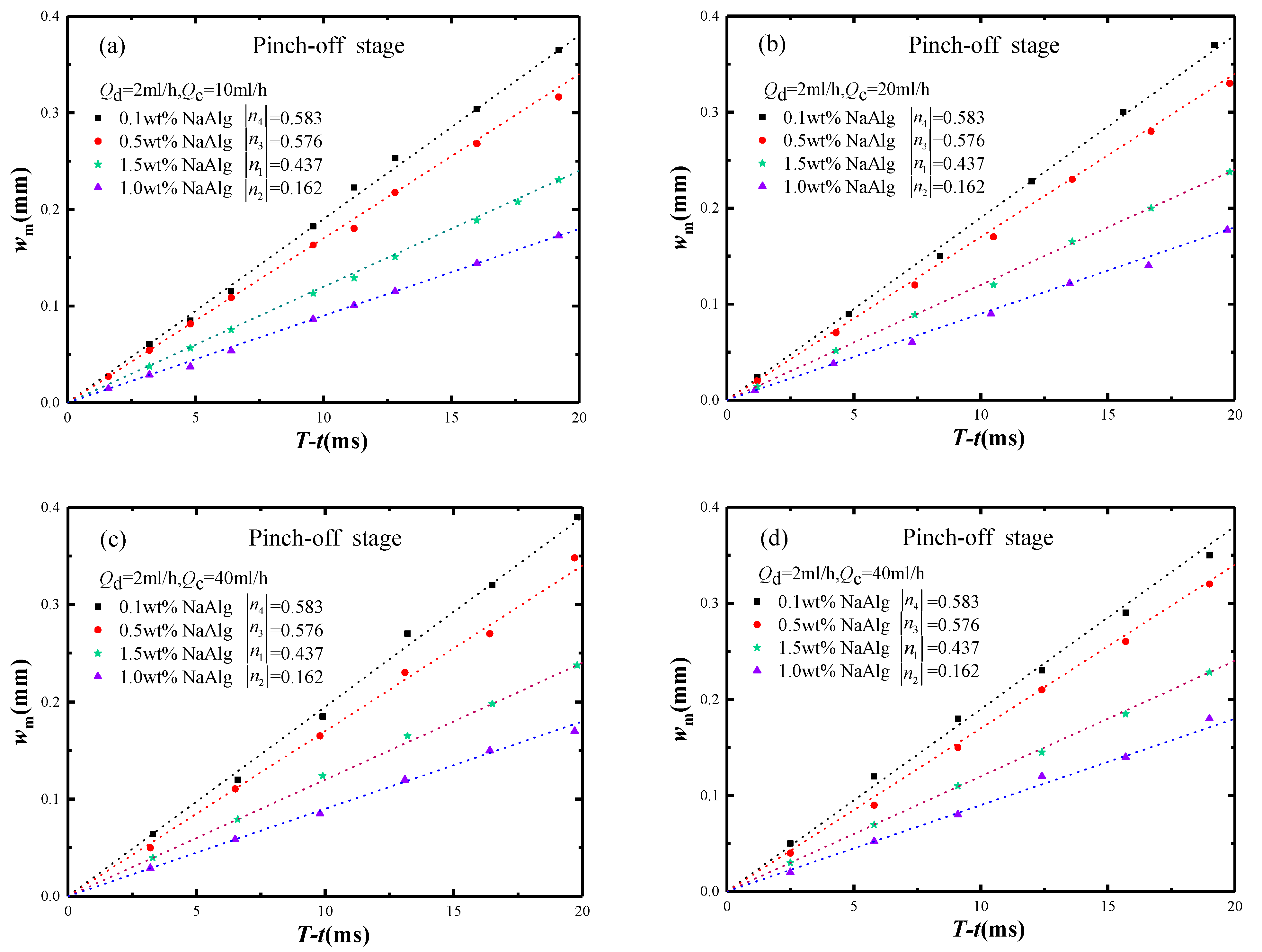
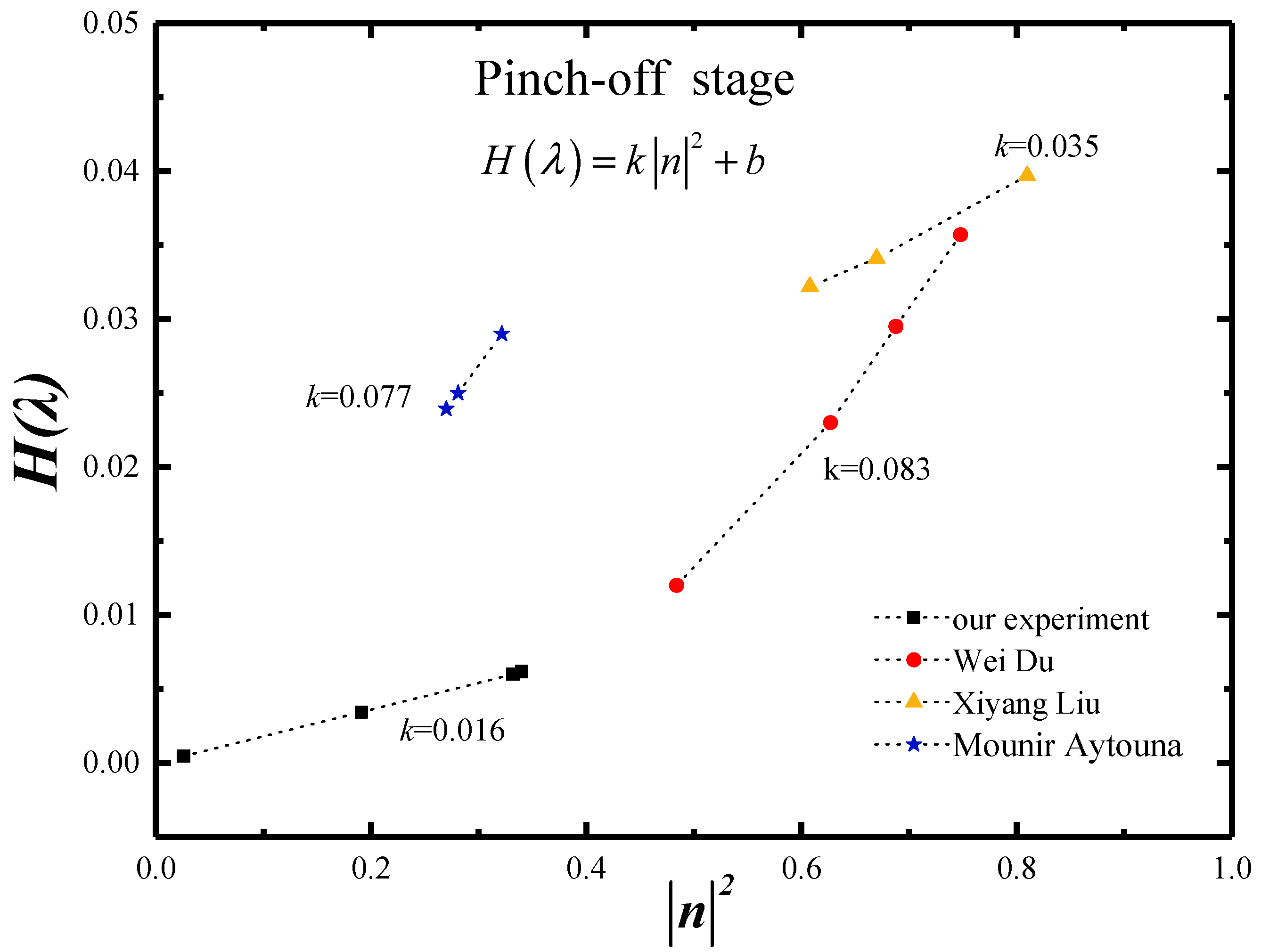
3.3. Pinch-Off Stage Dynamics
4. Conclusions
- (1)
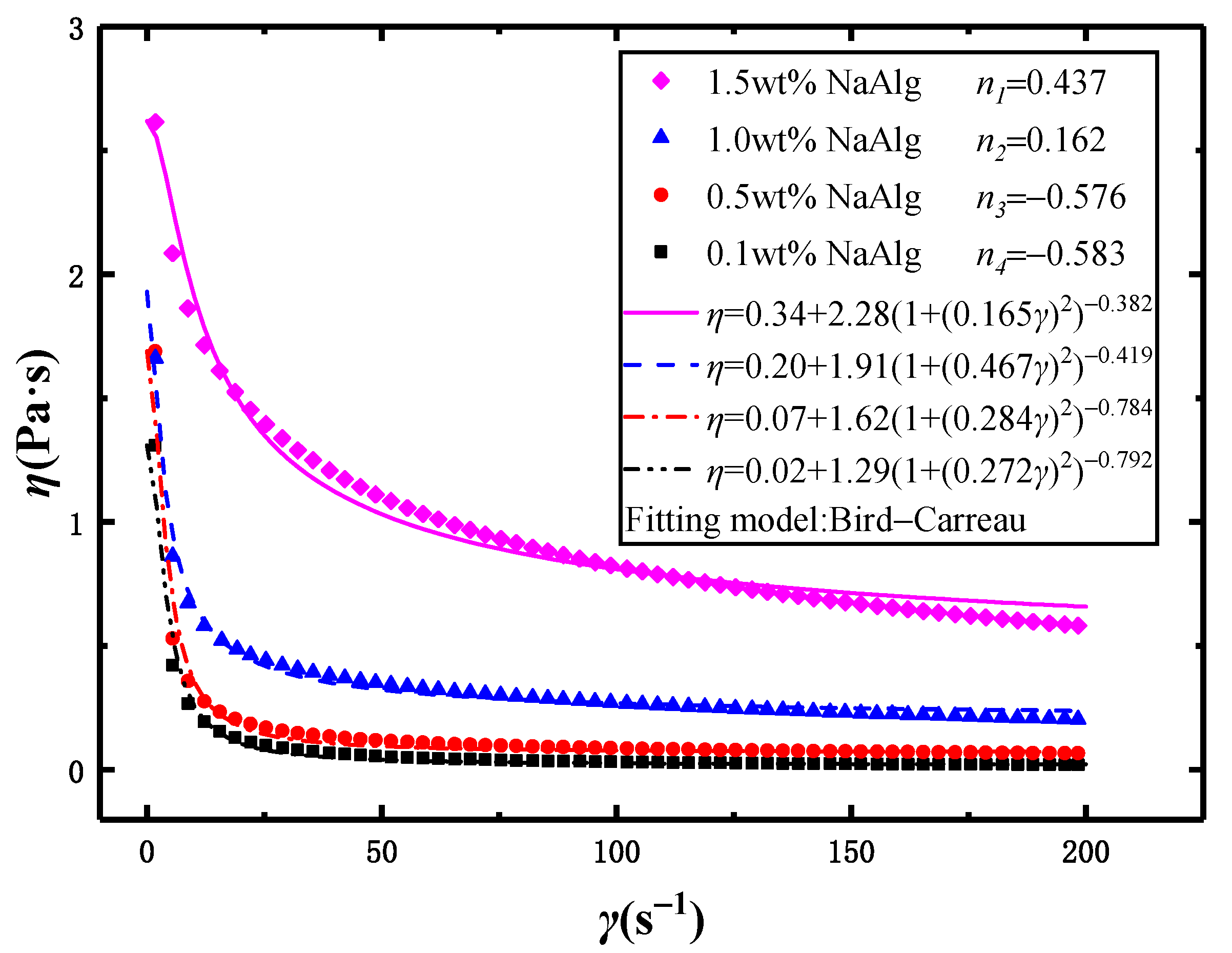
- It was found that as the mass fraction of NaAlg solution decreased, the n value changed from 1 > n > 0 to 0 > n > −1. Moreover, the smaller the n value was, the more significant the shear-thinning of fluid was;
- (2)
- In the growth stage, the minimum neck width wm of micro-droplet was linearly positively correlated to the remaining time T − t, and the influence of flow behavior index n was not significant;
- (3)
- In the squeezing stage, the new prediction model of minimum neck width wm was established with an error less than |15%| and it was suit for both the Newtonian and non-Newtonian fluids;
- (4)
- In the pinch-off stage, another new prediction model of minimum neck width wm by H(λ) function was established with an error less than |10%|. It matched Stokes scaling law and could be used in both the Newtonian and non-Newtonian fluids regardless the rheological models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| wc | the diameter of outer tube (μm) | ∆P | the squeezing force (Pa) |
| wd | the diameter of inner tube (μm) | Greek characters | |
| w | the width of neck (μm) | σ | the surface tension (N/m) |
| wm | the diameter of minimum droplet (μm) | ρ | the density (kg/m3) |
| w0 | the initial width of neck (μm) | η | the shear viscosity (Pa·s) |
| Q | the flow rate (mL/h) | α | the exponent |
| wt | the mass fraction (%) | λr | the relaxation time of material (s) |
| t | time (s) | λ | the viscosity ratio between dispersed and continuous phases |
| n | the flow behavior index | γ | the rate of shearing |
| T | the breakup period of droplet (s) | ε | the thickness of liquid film (μm) |
| T − t | the remaining time (s) | τa | the shear stress (Pa) |
| k | the coefficient | τr | the tensile stress (Pa) |
| h | the depth of microchannel (μm) | Subscripts | |
| L | the length of liquid film (μm) | c | the continuous phase |
| u | the velocity of liquid (m/s) | d | the dispersed phase |
References
- Eggers, J.; Villermaux, E. Physics of liquid jets. Rep. Prog. Phys. 2008, 71, 036601. [Google Scholar] [CrossRef]
- Thete, S.S.; Anthony, C.; Basaran, O.A.; Doshi, P. Self-similar rupture of thin free films of power-law fluids. Phys. Rev. E 2015, 92, 023014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, X.; Xu, E.; Meng, X.; Li, H.Z. The effect of viscosity ratio on drop pinch-off dynamics in two-fluid flow. J. Ind. Eng. Chem. 2020, 91, 347–354. [Google Scholar] [CrossRef]
- Yu, X.; Wu, Y.; Li, Y.; Yang, Z.; Ma, Y. The formation of satellite droplets in micro-devices due to the rupture of neck filament. Chem. Eng. Res. Des. 2019, 153, 435–442. [Google Scholar] [CrossRef]
- Rostami, B.; Morini, G.L. Experimental characterization of a micro cross-junction as generator of Newtonian and non-Newtonian droplets in silicone oil flow at low Capillary numbers. Exp. Therm. Fluid Sci. 2019, 103, 191–200. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Q.; Zhu, C.; Fu, T.; Ma, Y.; Li, H.Z. Formation of droplet and “string of sausages” for water-ionic liquid ([BMIM][PF6]) two-phase flow in a flow-focusing device. Chem. Eng. Process. 2018, 125, 8–17. [Google Scholar] [CrossRef]
- Nooranidoost, M.; Izbassarov, D.; Muradoglu, M. Droplet formation in a flow focusing configuration: Effects of viscoelasticity. Phys. Fluids 2016, 28, 123102. [Google Scholar] [CrossRef] [Green Version]
- Sahu, S.; Khair, A.S. Dynamics of a viscous drop under an oscillatory uniaxial extensional Stokes flow. Int. J. Multiph. Flow 2022, 146, 103844. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, S.; Zhu, C.; Ma, Y.; Fu, T. Bubble formation in T-junctions within parallelized microchannels: Effect of viscoelasticity. Chem. Eng. J. 2021, 426, 131783. [Google Scholar] [CrossRef]
- Luo, Z.Y.; Lu, X.; Zhao, H.Y.; Xu, F.G.; Bai, B.F. Negative synergistic effects of surfactant and fluid viscoelasticity on hydrodynamic resistance of single droplet in confined microchannel. Phys. Fluids 2021, 33, 122012. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, C.; Du, W.; Liu, C.; Fu, T.; Ma, Y.; Li, H.Z. Formation dynamics of elastic droplets in a microfluidic T-junction. Chem. Eng. Res. Des. 2018, 139, 188–196. [Google Scholar] [CrossRef]
- Maîtrejean, G.; Roux, D.C.D.; Xing, J.; Rosello, M.; Jay, P.; Barbet, B. Breakup length determination of continuous ink jets: Application to a shear-thinning industrial fluid. AIP Adv. 2021, 11, 115325. [Google Scholar] [CrossRef]
- Mehdaoui, H.; Abderrahmane, H.A.; Bouda, F.N.; Koulali, A.; Hamani, S. 2D numerical simulation of tear film dynamics: Effects of shear-thinning properties. Eur. J. Mech. B/Fluids 2021, 90, 128–136. [Google Scholar] [CrossRef]
- Salehi, M.S.; Esfidani, M.T.; Afshin, H.; Firoozabadi, B. Experimental investigation and comparison of Newtonian and non-Newtonian shear-thinning drop formation. Exp. Therm. Fluid Sci. 2018, 94, 148–158. [Google Scholar] [CrossRef]
- Rostami, B.; Morini, G.L. Generation of Newtonian and non-Newtonian droplets in silicone oil flow by means of a micro cross-junction. Int. J. Multiph. Flow 2018, 105, 202–216. [Google Scholar] [CrossRef]
- Chiarello, E.; Derzsi, L.; Pierno, M.; Mistura, G.; Piccin, E. Generation of Oil Droplets in a Non-Newtonian Liquid Using a Microfluidic T-Junction. Micromachines 2015, 6, 1825–1835. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Zhu, C.; Fu, T.; Ma, Y.; Li, H.Z. Dynamics of non-Newtonian droplet breakup with partial obstruction in microfluidic Y-junction. Chem. Eng. Sci. 2021, 240, 116696. [Google Scholar] [CrossRef]
- Chen, Q.; Li, J.; Song, Y.; Chen, B.; Christopher, D.M.; Li, X. Pressure-driven microfluidic droplet formation in Newtonian and shear-thinning fluids in glass flow-focusing microchannels. Int. J. Multiph. Flow 2021, 140, 103648. [Google Scholar] [CrossRef]
- Deng, K.; Liu, Z.; Luo, F.; Xie, R.; He, X.-H.; Jiang, M.-Y.; Ju, X.-J.; Wang, W.; Chu, L.-Y. Controllable fabrication of polyethersulfone hollow fiber membranes with a facile double co-axial microfluidic device. J. Membr. Sci. 2017, 526, 9–17. [Google Scholar] [CrossRef]
- Xiong, S.; Chen, Y.; Jia, W.; Yang, X.; Liu, K.; Li, C.; Ling, G. Optimization of the co-axial dispensing nozzle of a 3D bioprinter for the fabrication of tubular structures with micro-channel encapsulation. J. Micromech. Microeng. 2021, 31, 045009. [Google Scholar] [CrossRef]
- Du, W.; Fu, T.; Duan, Y.; Zhu, C.; Ma, Y.; Li, H.Z. Breakup dynamics for droplet formation in shear-thinning fluids in a flow-focusing device. Chem. Eng. Sci. 2018, 176, 66–76. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z.; Jiang, S.; Zhu, C.; Ma, Y.; Fu, T. Formation of droplets of shear-thinning non-Newtonian fluids in a step-emulsification microdevice. AIChE J. 2021, 68, e17395. [Google Scholar] [CrossRef]
- Chhabra, R.P. Bubbles, Drops, and Particles in Non-Newtonian Fluids; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Rodrigues, N.S.; Kulkarni, V.; Gao, J.; Chen, J.; Sojka, P.E. Spray formation and atomization characteristics of non-Newtonian impinging jets at high Carreau numbers. Int. J. Multiph. Flow 2018, 106, 280–295. [Google Scholar] [CrossRef]
- Duvarci, O.C.; Yazar, G.; Kokini, J.L. The SAOS, MAOS and LAOS behavior of a concentrated suspension of tomato paste and its prediction using the Bird-Carreau (SAOS) and Giesekus models (MAOS-LAOS). J. Food Eng. 2017, 208, 77–88. [Google Scholar] [CrossRef]
- Rodrigues, N.S. Impinging Jet Spray Formation Using Non-Newtonian Liquids; Purdue University: West Lafayette, IN, USA, 2014. [Google Scholar]
- Li, X.; Wu, Z.; Chen, X. Analysis on breakup dynamics of hydrogen taylor bubble formation in a cross-junction microchannel. Int. J. Hydrog. Energy 2021, 46, 33438–33452. [Google Scholar] [CrossRef]
- Li, X.; Huang, Y.; Chen, X.; Wu, Z. Breakup dynamics of low-density gas and liquid interface during Taylor bubble formation in a microchannel flow-focusing device. Chem. Eng. Sci. 2020, 215, 115473. [Google Scholar] [CrossRef]
- Zhu, P.; Wang, L. Droplet pinch-off with pressure fluctuations. Chem. Eng. Sci. 2018, 196, 333–343. [Google Scholar] [CrossRef]
- Fu, T.; Ma, Y. Bubble formation and breakup dynamics in microfluidic devices: A review. Chem. Eng. Sci. 2015, 135, 343–372. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, G.; Zhu, C.; Fu, T.; Ma, Y. Dynamics of droplet formation and mechanisms of satellite droplet formation in T-junction microchannel. Chem. Eng. Sci. 2021, 248, 117217. [Google Scholar] [CrossRef]
- Christopher, G.F.; Noharuddin, N.N.; Taylor, J.A.; Anna, S.L. Experimental observations of the squeezing-to-dripping transition in T-shaped microfluidic junctions. Phys. Rev. E 2008, 78, 036317. [Google Scholar] [CrossRef]
- Xu, J.H.; Li, S.W.; Tan, J.; Luo, G.S. Correlations of droplet formation in T-junction microfluidic devices: From squeezing to dripping. Microfluid. Nanofluidics 2008, 5, 711–717. [Google Scholar] [CrossRef]
- Arratia, P.E.; Gollub, J.P.; Durian, D.J. Polymeric filament thinning and breakup in microchannels. Phys. Rev. E 2008, 77, 036309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, D.; Liang, D.; Zhu, C.; Fu, T.; Ma, Y.; Yuan, X.; Li, H.Z. The breakup dynamics and mechanism of viscous droplets in Y-shaped microchannels. Chem. Eng. Sci. 2020, 231, 116300. [Google Scholar] [CrossRef]
- Xin, S.A.; Cz, A.; Tf, A.; Ym, A.; Hzl, B.J.C.E.S. Breakup dynamics of elastic droplet and stretching of polymeric filament in a T-junction. Chem. Eng. Sci. 2019, 206, 212–223. [Google Scholar]
- Sun, X.; Zhu, C.; Fu, T.; Ma, Y.; Li, H.Z. Dynamics of droplet breakup and formation of satellite droplets in a microfluidic T-junction. Chem. Eng. Sci. 2018, 188, 158–169. [Google Scholar] [CrossRef]
- Fu, T.; Ma, Y.; Li, H.Z. Breakup dynamics of slender droplet formation in shear-thinning fluids in flow-focusing devices. Chem. Eng. Sci. 2016, 144, 75–86. [Google Scholar] [CrossRef]
- Zhu, P.; Tang, X.; Tian, Y.; Wang, L. Pinch-off of microfluidic droplets with oscillatory velocity of inner phase flow. Sci. Rep. 2016, 6, 31436. [Google Scholar] [CrossRef] [Green Version]
- Lister, J.R.; Stone, H.A. Capillary breakup of a viscous thread surrounded by another viscous fluid. Phys. Fluids 1998, 10, 2758–2764. [Google Scholar] [CrossRef] [Green Version]
- Cohen, I.; Brenner, M.P.; Eggers, J.; Nagel, S.R. Two Fluid Drop Snap-Off Problem: Experiments and Theory. Phys. Rev. Lett. 1999, 83, 1147–1150. [Google Scholar] [CrossRef] [Green Version]
- Aytouna, M.; Paredes, J.; Shahidzadeh-Bonn, N.; Moulinet, S.; Wagner, C.; Amarouchene, Y.; Eggers, J.; Bonn, D. Drop Formation in Non-Newtonian Fluids. Phys. Rev. Lett. 2013, 110, 034501. [Google Scholar] [CrossRef] [Green Version]


| Phase | Material | n | ρ (kg/m3) | σ (mN/m) | η (Pa·s) | λr (s) | |
|---|---|---|---|---|---|---|---|
| η0 (Pa·s) | η∞ (Pa·s) | ||||||
| Dispersed Phase | 1.5 wt% NaAlg | 0.437 | 988 | 46.6 | 2.61 | 0.34 | 0.165 |
| 1.0 wt% NaAlg | 0.162 | 1004 | 51.3 | 1.93 | 0.21 | 0.467 | |
| 0.5 wt% NaAlg | −0.567 | 998 | 54.1 | 1.69 | 0.07 | 0.284 | |
| 0.1 wt% NaAlg | −0.583 | 1006 | 41.4 | 1.31 | 0.02 | 0.272 | |
| Continuous Phase | Oil | 1 | 896 | -- | 0.058 | -- | |
| Micro-Droplet | Scaling Law | Authors | |
|---|---|---|---|
| Newtonianian fluid | Glycerol solution | Ma [17] (2021) | |
| Silicone oil | Fu [39] (2016) | ||
| Glycerol solution | Sun [38] (2018) | ||
| Non-Newtonian fluid | PMMA | Xin [37] (2019) | |
| CMC solutions | Du [21] (2018) | ||
| NaAlg solution | This work |
| Micro-Droplets | Rheological Model | wt% | |n| | H(λ) | Our Model of wm | Authors | ||
|---|---|---|---|---|---|---|---|---|
| Scaling Law | k & b | |||||||
| CMC Solution | Power | 0.10 | 0.865 | 0.0357 | k = 0.083 b = −0.028 | Du [21] | ||
| 0.25 | 0.830 | 0.0295 | ||||||
| 0.50 | 0.792 | 0.0228 | ||||||
| 1.00 | 0.696 | 0.0160 | ||||||
| CMC Solution | Power | 0.1 | 0.90 | 0.0397 | k = 0.035 b = 0.011 | Liu [22] | ||
| 0.3 | 0.82 | 0.0341 | ||||||
| 0.5 | 0.78 | 0.0332 | ||||||
| Castor Oil | Herschel-Bulkley | 68 | 0.57 | 0.029 | k = 0.077 b = 0.004 | Aytouna [43] | ||
| 74 | 0.53 | 0.025 | ||||||
| 80 | 0.52 | 0.024 | ||||||
| NaAlg Solution | Bird-Carreau | 0.1 | 0.583 | 0.0062 | k = 0.016 b = 0.0008 | This work | ||
| 0.5 | 0.567 | 0.0059 | ||||||
| 1.0 | 0.162 | 0.0012 | ||||||
| 1.5 | 0.437 | 0.0039 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Han, Y.; Wang, Z. Accelerating Effects of Flow Behavior Index n on Breakup Dynamics for Droplet Evolution in Non-Newtonian Fluids. Materials 2022, 15, 4392. https://doi.org/10.3390/ma15134392
Zhang J, Han Y, Wang Z. Accelerating Effects of Flow Behavior Index n on Breakup Dynamics for Droplet Evolution in Non-Newtonian Fluids. Materials. 2022; 15(13):4392. https://doi.org/10.3390/ma15134392
Chicago/Turabian StyleZhang, Jinsong, Yufeng Han, and Zhiliang Wang. 2022. "Accelerating Effects of Flow Behavior Index n on Breakup Dynamics for Droplet Evolution in Non-Newtonian Fluids" Materials 15, no. 13: 4392. https://doi.org/10.3390/ma15134392
APA StyleZhang, J., Han, Y., & Wang, Z. (2022). Accelerating Effects of Flow Behavior Index n on Breakup Dynamics for Droplet Evolution in Non-Newtonian Fluids. Materials, 15(13), 4392. https://doi.org/10.3390/ma15134392






