Numerical Investigation of the Influence of Ultimate-Strength Heterogeneity on Crack Propagation and Fracture Toughness in Welded Joints
Abstract
:1. Introduction
2. Materials and Methods
3. Numerical Simulation Procedures
4. Results and Discussion
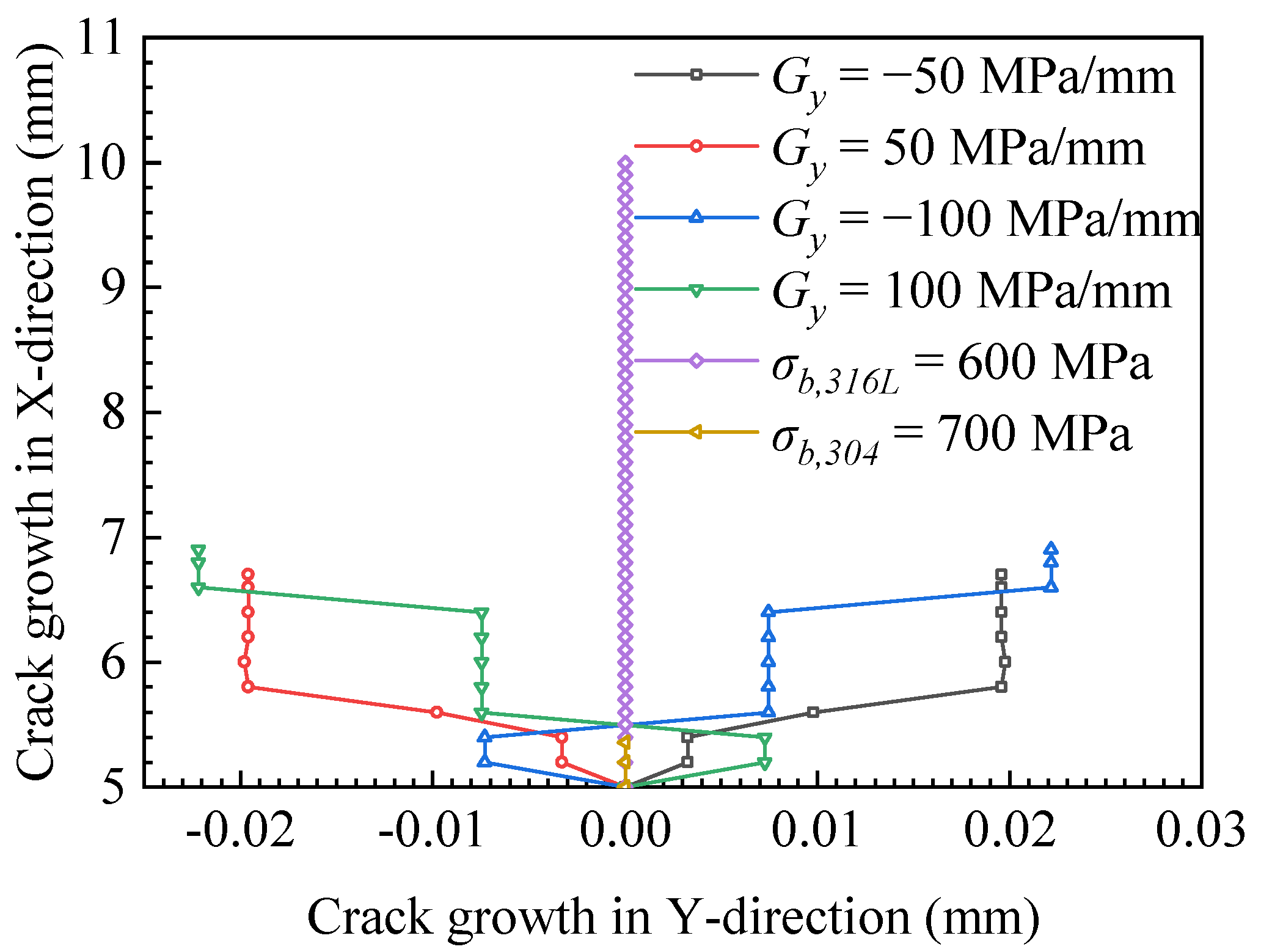
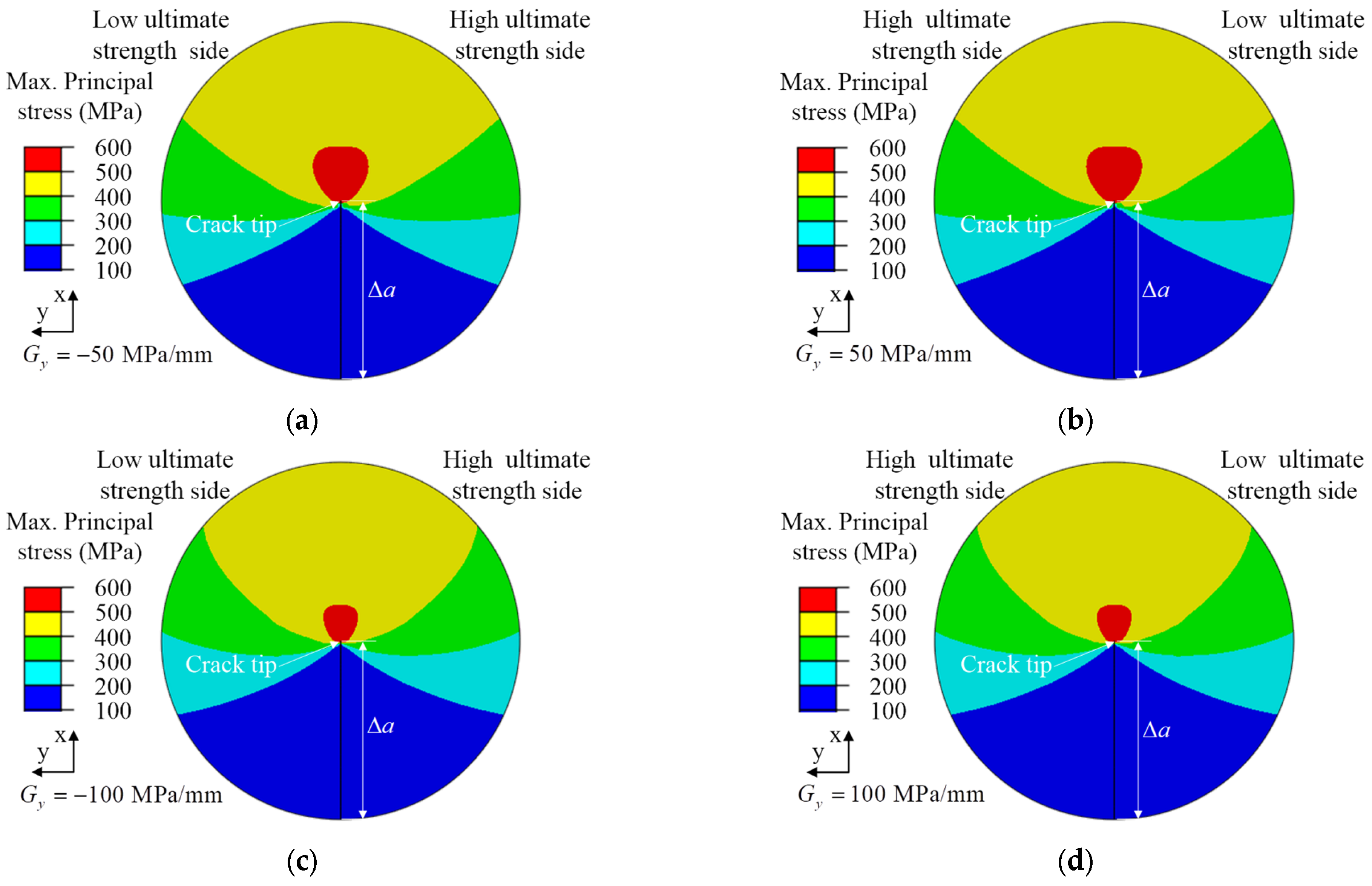
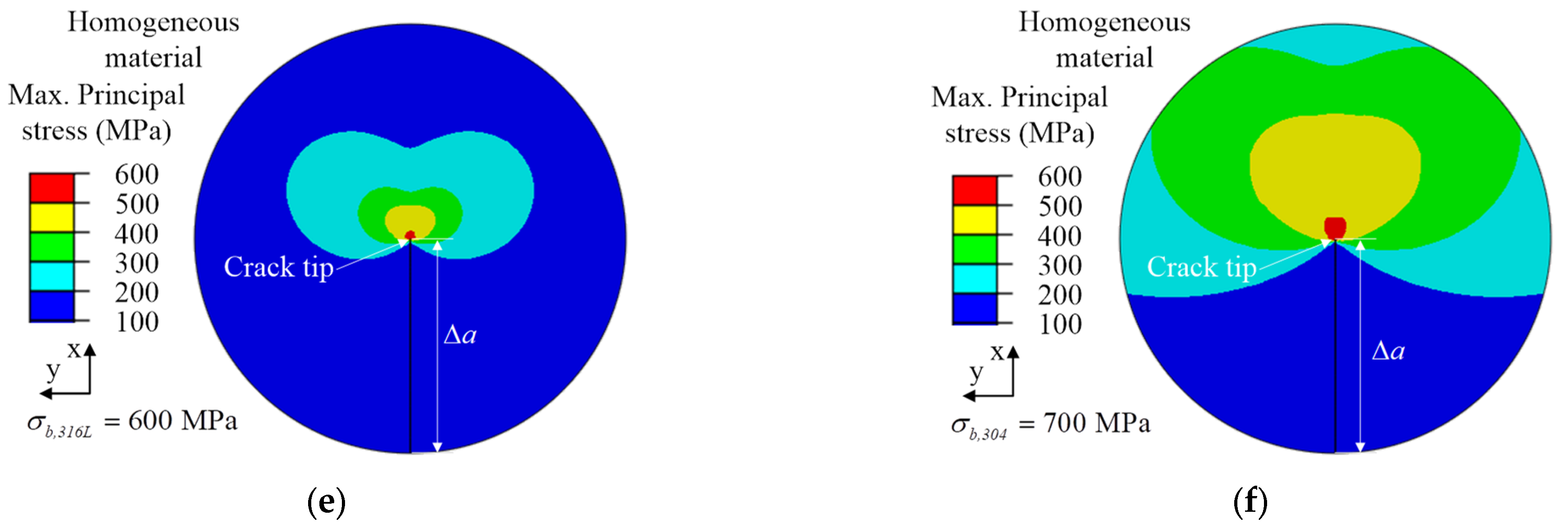
4.1. The Results of Ultimate Strength Change in y-Direction
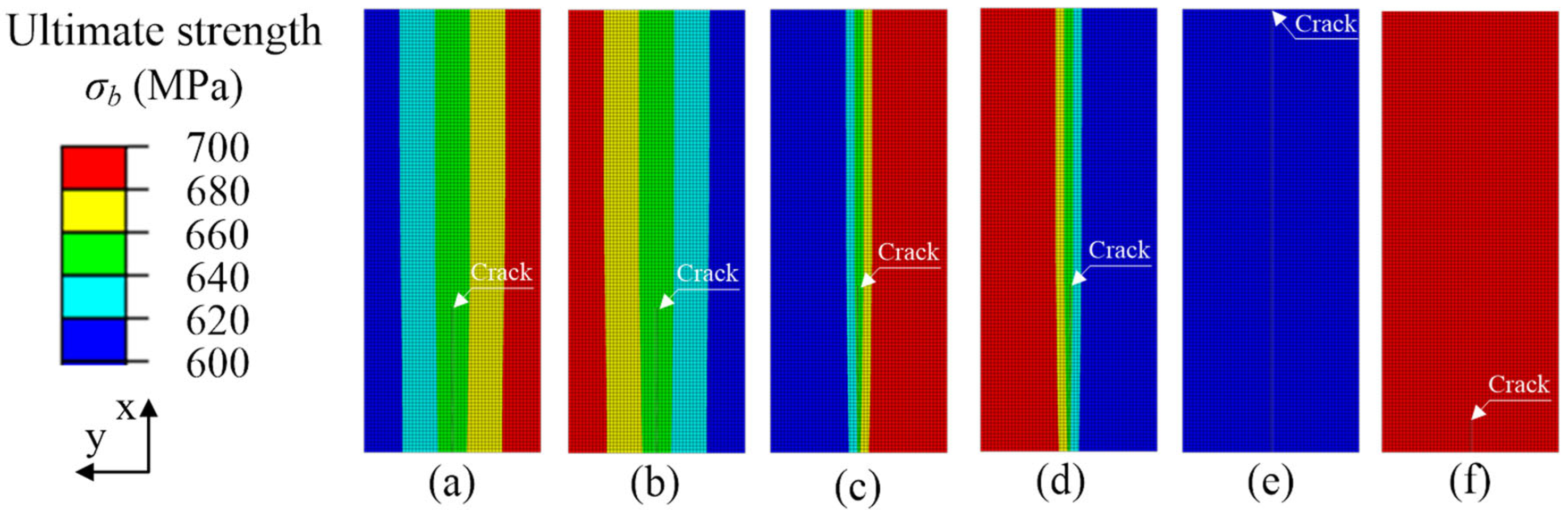
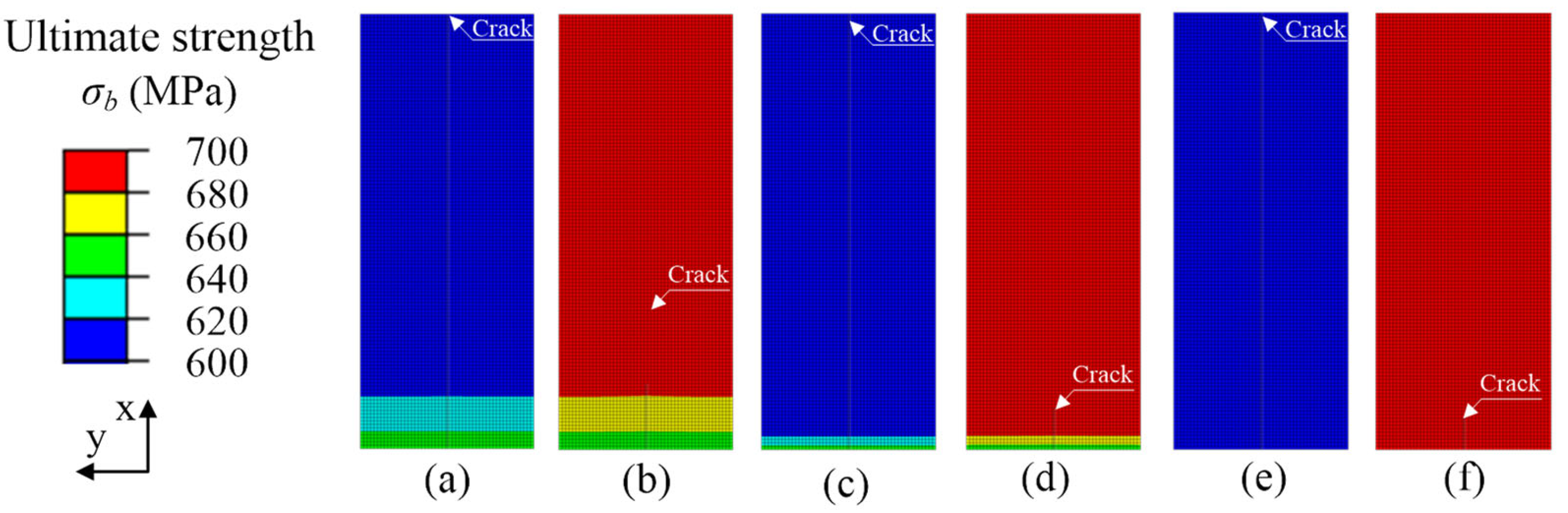
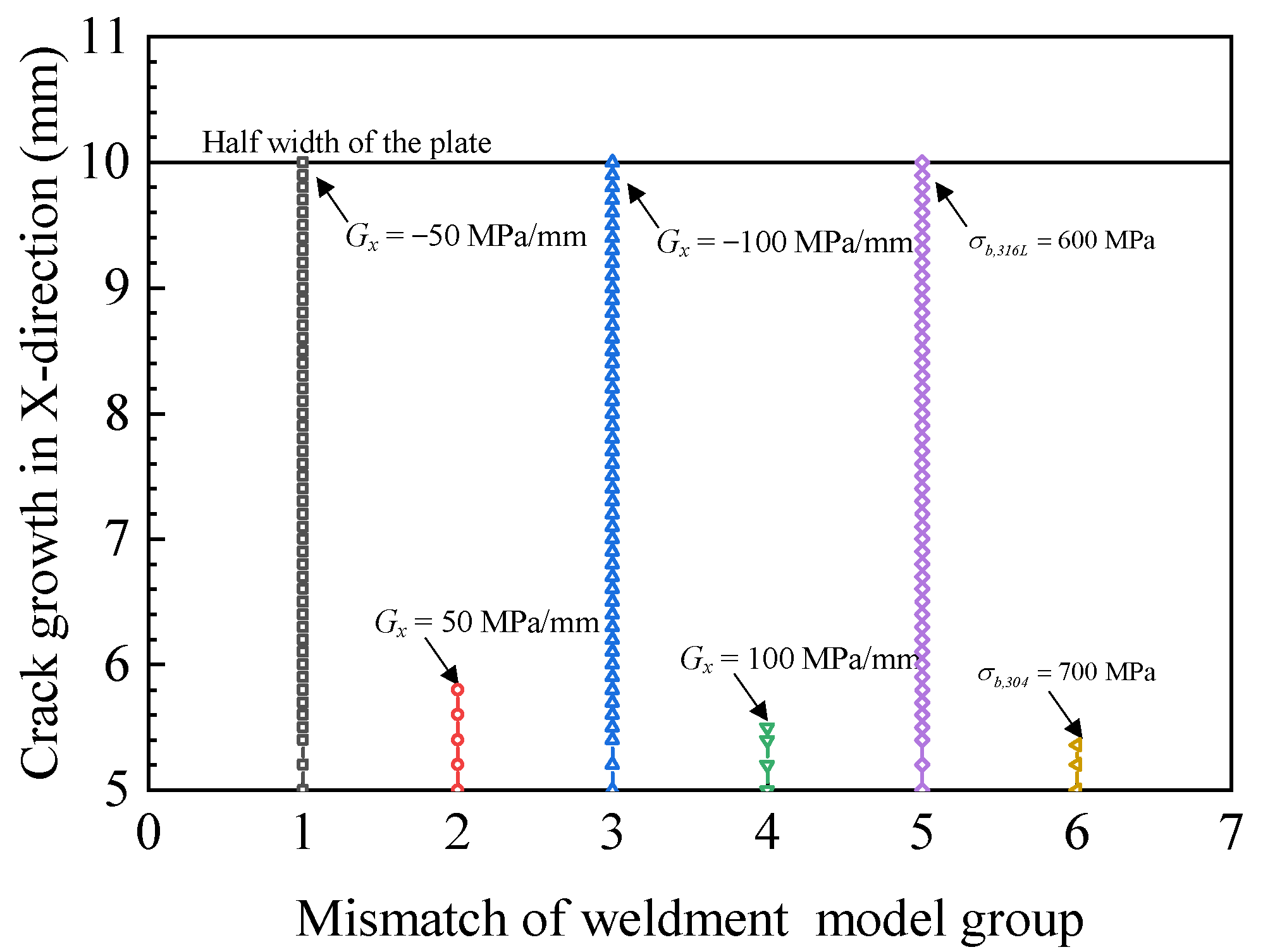
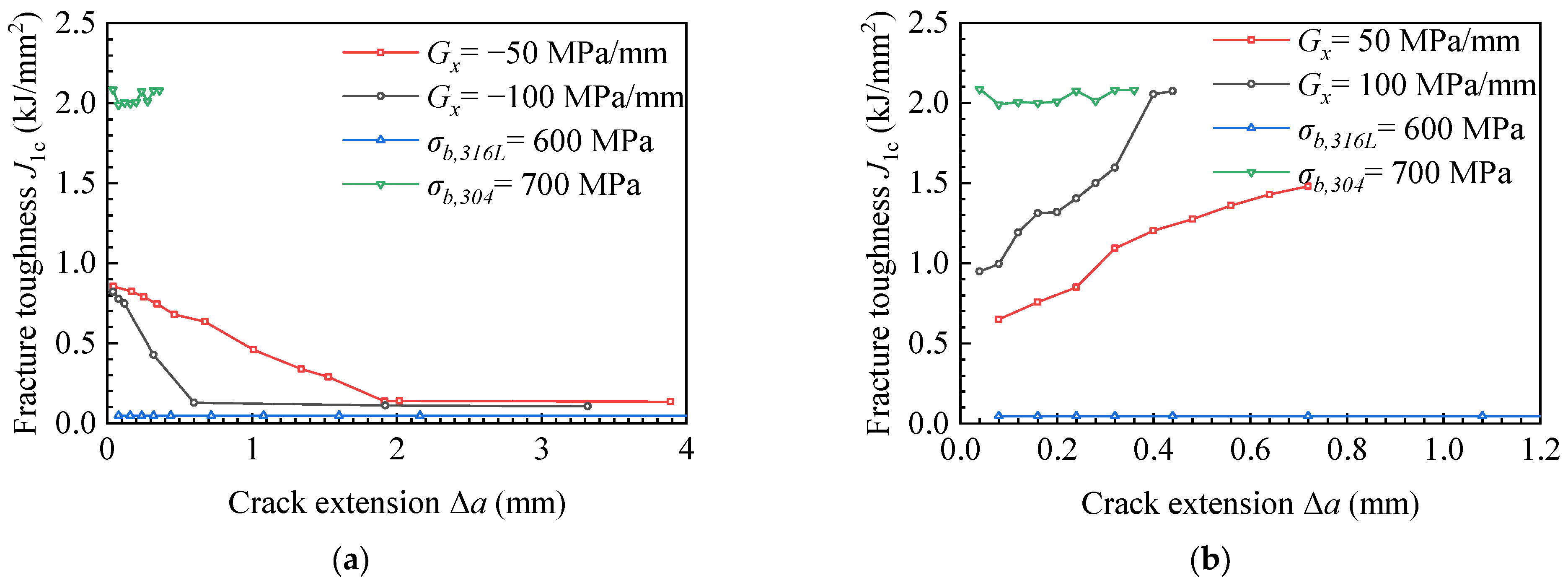
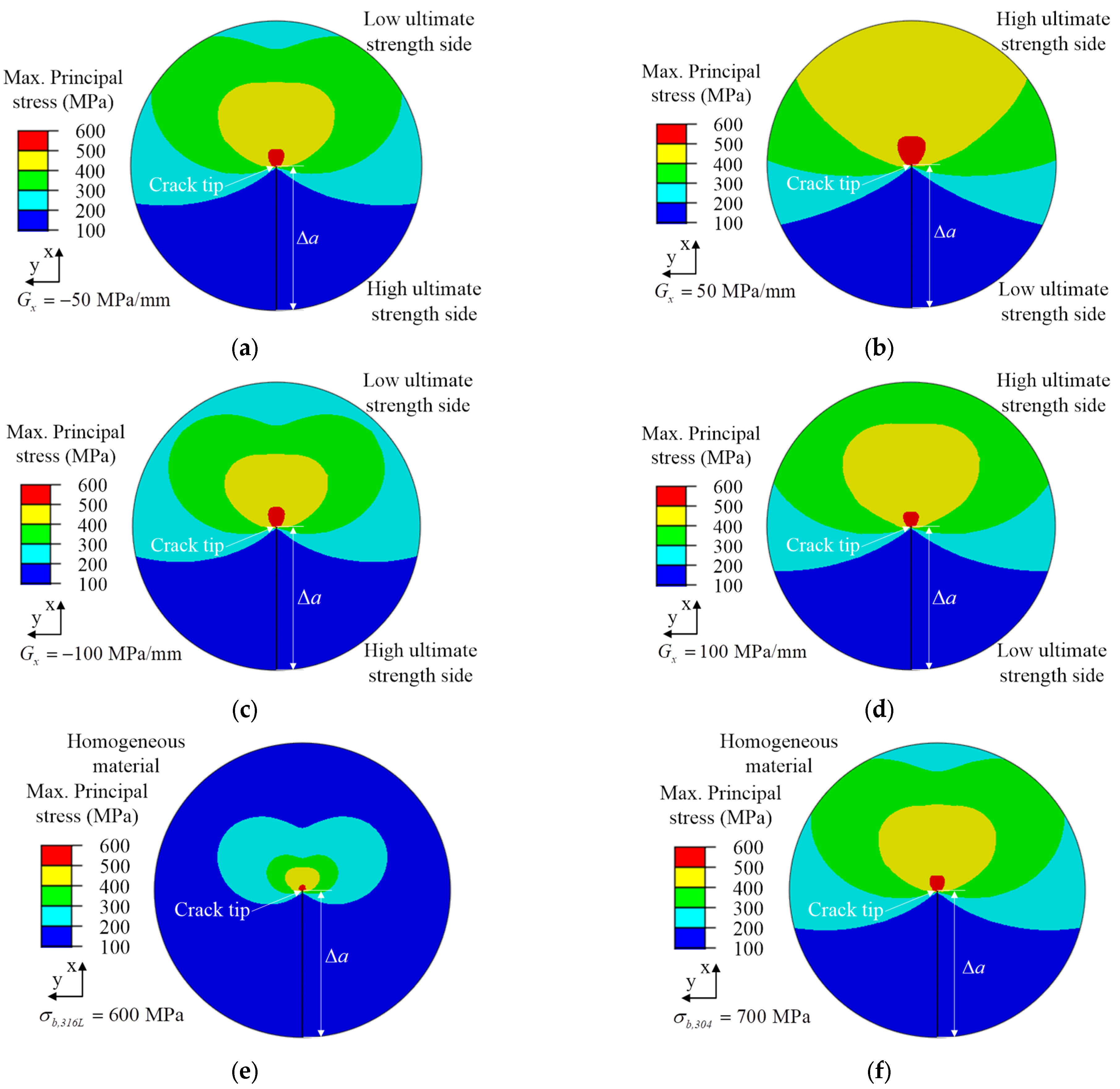
4.2. The Results of Ultimate Strength Change in x-Direction
5. Conclusions and Observations
- When the crack propagation direction was perpendicular to the change direction of ultimate strength, the crack path as well as the maximum principal stress field at the crack tip always deflected to the side of low ultimate strength. The fracture toughness decreased slightly during crack propagation.
- The crack length in the process of crack propagation to the low ultimate strength material side was greater than that to the high ultimate strength material, but the crack propagation resistance as well as the area of the maximum principal stress caused by material constraints were less than that to the low ultimate strength material, when the crack propagation direction was the same as the change direction of ultimate strength.
- When evaluating the structural safety of cracks in the connection area, where the ultimate strength of dissimilar metal-welded joints is between the ultimate strength of the base metal and the weld material, only considering the ultimate strength of the base metal or the weld material will inevitably lead to a conservative estimation or unsafe estimation results. Therefore, it is recommended to use the fracture toughness of local areas for evaluation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| strain tensor | ultimate strength | ||
| elastic strain tensor | critical damage variable | ||
| plastic strain tensor | field variable | ||
| stress tensor | field variable distribution function | ||
| isotropic damage variable | x coordinate value | ||
| elastic tensor | y coordinate value | ||
| stress rate | E | elasticity modulus | |
| damage variable rate | μ | Poisson’s ratio | |
| strain rate | a0 | initial crack length | |
| equivalent plastic strain rate | H | width of welded joint | |
| Von Mises yield condition | W | height of welded joint | |
| radius of yield surface | crack growth increment | ||
| partial stress tensor of damaged materials | σb,316L | ultimate strength of 316L stainless-steel | |
| back stress tensor of damaged materials | σb,304 | ultimate strength of 304 stainless-steel | |
| stress tensor | J1c | critical fracture toughness | |
| back stress tensor | dispmax | the max displacement load | |
| equivalent plastic strain rate | disp | displacement load | |
| unit direction tensor | Gx | gradient factor in x-direction | |
| maximum principal stress | Gy | gradient factor in y-direction |
References
- Jovanović, M.; Čamagić, I.; Sedmak, S.; Sedmak, A.; Burzić, Z. The Effect of Material Heterogeneity and Temperature on Impact Toughness and Fracture Resistance of SA-387 Gr. 91 Welded Joints. Materials 2022, 15, 1854. [Google Scholar] [CrossRef]
- Zhang, S.; Xue, H.; Wang, S.; Sun, Y.; Yang, F.; Zhang, Y. Effect of Mechanical Heterogeneity on Strain and Stress Fields at Crack Tips of SCC in Dissimilar Metal Welded Joints. Materials 2021, 14, 4450. [Google Scholar] [CrossRef]
- Tanguy, B.; Besson, J.; Piques, R.; Pineau, A. Ductile to brittle transition of an A508 steel characterized by Charpy impact test: Part I: Experimental results. Eng. Fract. Mech. 2005, 72, 49–72. [Google Scholar] [CrossRef] [Green Version]
- Eman, E.S.; Abla, E.; Aly, E.D.; Hassan, A.E. Residual stress effects on fatigue crack propagation in Butt-Welded joints for 304 stainless steel sheets. Manuf. Rev. 2021, 8, 19. [Google Scholar]
- Michał, B.; Mateusz, K.; Adam, N. Influence of the Elastoplastic Strain on Fatigue Durability Determined with the Use of the Spectral Method. Materials 2020, 13, 423. [Google Scholar]
- Konjatić, P.; Katinić, M.; Kozak, D.; Gubeljak, N. Yield Load Solutions for SE(B) Fracture Toughness Specimen with I-Shaped Heterogeneous Weld. Materials 2022, 15, 214. [Google Scholar] [CrossRef]
- Yang, J.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T.; Liu, C.J. Out-of-plane constraint effect on local fracture resistance of a dissimilar metal welded joint. Mater. Des. 2014, 55, 542–550. [Google Scholar] [CrossRef]
- Burstow, M.C.; Howard, I.C.; Ainsworth, R.A. The influence of constraint on crack tip stress fields in strength mismatched welded joints. J. Mech. Phys. Solids 1998, 46, 845–872. [Google Scholar] [CrossRef]
- Rakin, M.; Medjo, B.; Gubeljak, N.; Sedmak, A. Micromechanical assessment of mismatch effects on fracture of high-strength low alloyed steel welded joints. Eng. Fract. Mech. 2013, 109, 221–235. [Google Scholar] [CrossRef]
- Cetinel, H.; Aksoy, T. The effect of undermatching on crack tip constraint in a welded structure of nodular irons. J. Mater. Proc. Technol. 2008, 198, 183–190. [Google Scholar] [CrossRef]
- Cherepanov, G.P. The propagation of cracks in a continuous medium. J. Appl. Math. Mech. 1967, 3, 501–503. [Google Scholar]
- Rice, J. A path independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T.; Liu, C.J. An experimental investigation of in-plane constraint effect on local fracture resistance of a dissimilar metal welded joint. Mater. Des. 2014, 53, 611–619. [Google Scholar] [CrossRef]
- Wang, H.T.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T. An experimental investigation of local fracture resistance and crack growth paths in a dissimilar metal welded joint. Mater. Des. 2013, 44, 179–189. [Google Scholar] [CrossRef]
- Østby, E.; Zhang, Z.L.; Thaulow, C. Constraint effect on the near tip stress fields due to difference in plastic work hardening for bi-material interface cracks in small scale yielding. Int. J. Fract. 2001, 111, 87–103. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Sadowski, T.; Dimitrova, S. Three-dimensional free vibration analysis of thermally loaded FGM sandwich plates. Materials 2019, 12, 2377. [Google Scholar] [CrossRef] [Green Version]
- Szekrényes, A. Analytical solution of some delamination scenarios in thick structural sandwich plates. J. Sandw. Struct. Mater. 2019, 21, 1271–1315. [Google Scholar] [CrossRef] [Green Version]
- Geng, S.N.; Sun, J.S.; Guo, L.Y.; Wang, H.Q. Evolution of microstructure and corrosion behavior in 2205 duplex stainless steel GTA-welding joint. J. Manuf. Process. 2015, 19, 32–37. [Google Scholar] [CrossRef]
- Fan, K.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T. Local fracture resistance behavior of interface regions in a dissimilar metal welded joint. Eng. Fract. Mech. 2015, 136, 279–291. [Google Scholar] [CrossRef]
- Fan, K.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T. Local failure behavior of a dissimilar metal interface region with mechanical heterogeneity. Eng. Fail. Anal. 2016, 59, 419–433. [Google Scholar] [CrossRef]
- Fan, K.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T. Effects of work hardening mismatch on fracture resistance behavior of bi-material interface regions. Mater. Des. 2015, 68, 186–194. [Google Scholar] [CrossRef]
- Xue, H.; Ogawa, K.; Shoji, T. Effect of welded mechanical heterogeneity on local stress and strain ahead of stationary and growing crack tips. Nucl. Eng. Des. 2009, 239, 628–640. [Google Scholar] [CrossRef]
- Xue, H.; Wang, Z.W.; Zhao, L.Y.; Qiao, M.; Wang, W.B. Effect of Strength Matching of Welded Joint on Stress Corrosion Cracking in Nuclear Power Structures. Appl. Mech. Mater. 2013, 457–458, 593–596. [Google Scholar] [CrossRef]
- Zhao, L.Y.; Xue, H.; Tang, W.; Fang, X.R. Effect of welded mechanical heterogeneity on local stress and strain ahead of growing crack tips in the piping welds. Proc. ASME Press. Vessel. Pip. Conf. 2011, 3, 223–232. [Google Scholar]
- Zhao, L.Y.; Xue, H.; Wang, Z.W. Research on local plastic strain at crack tip of dissimilar weld joints in nuclear power plant. J. Chem. Pharm. Res. 2014, 6, 2346–2352. [Google Scholar]
- Lee, H.; Kim, Y.J. Interfacial crack-tip constraints and J-integral in plastically mismatched bi-materials. Eng. Fract. Mech. 2001, 68, 1013–1031. [Google Scholar] [CrossRef]
- Lee, H.; Kim, Y.J. Interfacial crack-tip constraints and J-integral for bi-materials with plastic hardening mismatch. Int. J. Fract. 2007, 143, 231–243. [Google Scholar] [CrossRef]
- Guo, R.; Xue, H.; Gong, X.Y. Influence of residual stress and heterogeneity on mechanical field at crack tips in safety end of nuclear power plant. Procedia Struct. Integr. 2018, 13, 2202–2209. [Google Scholar] [CrossRef]
- Xue, H.; Wang, Z.; Wang, S.; He, J.; Yang, H. Characterization of Mechanical Heterogeneity in Dissimilar Metal Welded Joints. Materials 2021, 14, 4145. [Google Scholar] [CrossRef]
- Bi, Y.; Yuan, X.; Lv, J.; Bashir, R.; Wang, S.; Xue, H. Effect of Yield Strength Distribution Welded Joint on Crack Propagation Path and Crack Mechanical Tip Field. Materials 2021, 14, 4947. [Google Scholar] [CrossRef]
- Dassault Systèmes Simulia Corp. ABAQUS 6.14 User Subroutines Reference Guide 6.14; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2014. [Google Scholar]
- Li, B.; Gong, Y.; Gao, Y.; Hou, M.; Li, L. Failure Analysis of Hat-Stringer-Stiffened Aircraft Composite Panels under Four-Point Bending Loading. Materials 2022, 15, 2430. [Google Scholar] [CrossRef]
- Wang, W.A.; Yi, Z.H.; Tian, B.; Zhang, Y.D.; Lu, S.J. Nonlinear finite element analysis of PBL shear connectors in hybrid structures. Structures 2021, 33, 4642–4654. [Google Scholar] [CrossRef]
- Patrick, J.M.; Pat, P. Comparison of ductile failure models using a simple elastic–plastic based degradation model. J. Mater. Process. Technol. 2004, 155–156, 1214–1219. [Google Scholar]
- Ebadi-Rajoli, J.; Akhavan-Safar, A.; Hosseini-Toudeshky, H.; da Silva, L.F.M. Progressive damage modeling of composite materials subjected to mixed mode cyclic loading using cohesive zone model. Mech. Mater. 2020, 143, 103322. [Google Scholar] [CrossRef]
- Lemaitre, J.; Desmorat, R. Engineering Damage Mechanics: Ductile, Creep, Fatigue and Brittle Failures; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Wang, S.; Wang, B.; Janin, Y.; Bourga, R.; Xue, H. Effects of the surface crack shape on J values along the front of an elliptical crack. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2944–2961. [Google Scholar] [CrossRef]


| Direction | Gradient Factor, G (MPa/mm) | Weldment Component | Distribution (mm) | |
|---|---|---|---|---|
| x-direction | Gx = −50 | Base metal (304) | 700 | −5 ≤ x < −1 |
| Fusion metal | −50x + 650 | −1 ≤ x ≤ 1 | ||
| Weld metal (316 L) | 600 | 1 < x ≤ 5 | ||
| Gx = 50 | Base metal (316 L) | 600 | −5 ≤ x < −1 | |
| Fusion metal | 50x + 650 | −1 ≤ x ≤ 1 | ||
| Weld metal (304) | 700 | 1 < x ≤ 5 | ||
| Gx = −100 | Base metal (304) | 700 | −5 ≤ x < −0.5 | |
| Fusion metal | 100x + 650 | −0.5 ≤ x ≤ 0.5 | ||
| Weld metal (316 L) | 600 | 0.5 < x ≤ 5 | ||
| Gx = 100 | Base metal (316 L) | 600 | −5 ≤ x < −0.5 | |
| Fusion metal | −100x + 650 | −0.5 ≤ x ≤ 0.5 | ||
| Weld metal (304) | 700 | 0.5 < x ≤ 5 | ||
| y-direction | Gy = −50 | Base metal (304) | 700 | −7.5 ≤ y < −1 |
| Fusion metal | −50y + 650 | −1 ≤ y ≤ 1 | ||
| Weld metal (316 L) | 600 | 1 < y ≤ 7.5 | ||
| Gy = 50 | Base metal (316 L) | 600 | −7.5 ≤ y < −1 | |
| Fusion metal | 50y + 650 | −1 ≤ y ≤ 1 | ||
| Weld metal (304) | 700 | 1 < y ≤ 7.5 | ||
| Gy = −100 | Base metal (304) | 700 | −7.5 ≤ y < −0.5 | |
| Fusion metal | −100y + 650 | −0.5 ≤ y ≤ 0.5 | ||
| Weld metal (316 L) | 600 | 0.5 < y ≤ 7.5 | ||
| Gy = 100 | Base metal (316 L) | 600 | −7.5 ≤ y < −0.5 | |
| Fusion metal | 100y + 650 | −0.5 ≤ y ≤ 0.5 | ||
| Weld metal (304) | 700 | 0.5 < y ≤ 7.5 | ||
| Homogeneous material | - | 316 L | 600 | - |
| - | 304 | 700 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, Y.; Yuan, X.; Hao, M.; Wang, S.; Xue, H. Numerical Investigation of the Influence of Ultimate-Strength Heterogeneity on Crack Propagation and Fracture Toughness in Welded Joints. Materials 2022, 15, 3814. https://doi.org/10.3390/ma15113814
Bi Y, Yuan X, Hao M, Wang S, Xue H. Numerical Investigation of the Influence of Ultimate-Strength Heterogeneity on Crack Propagation and Fracture Toughness in Welded Joints. Materials. 2022; 15(11):3814. https://doi.org/10.3390/ma15113814
Chicago/Turabian StyleBi, Yueqi, Xiaoming Yuan, Mingrui Hao, Shuai Wang, and He Xue. 2022. "Numerical Investigation of the Influence of Ultimate-Strength Heterogeneity on Crack Propagation and Fracture Toughness in Welded Joints" Materials 15, no. 11: 3814. https://doi.org/10.3390/ma15113814
APA StyleBi, Y., Yuan, X., Hao, M., Wang, S., & Xue, H. (2022). Numerical Investigation of the Influence of Ultimate-Strength Heterogeneity on Crack Propagation and Fracture Toughness in Welded Joints. Materials, 15(11), 3814. https://doi.org/10.3390/ma15113814






