Fractal Analysis of a Non-Newtonian Fluid Flow in a Rough-Walled Pipe
Abstract
:1. Introduction
2. Laminar Flow of a Non-Newtonian Fluid through a Pipe with a Smooth Surface
3. Laminar Flow of a Non-Newtonian Fluid through a Rough-Walled Pipe
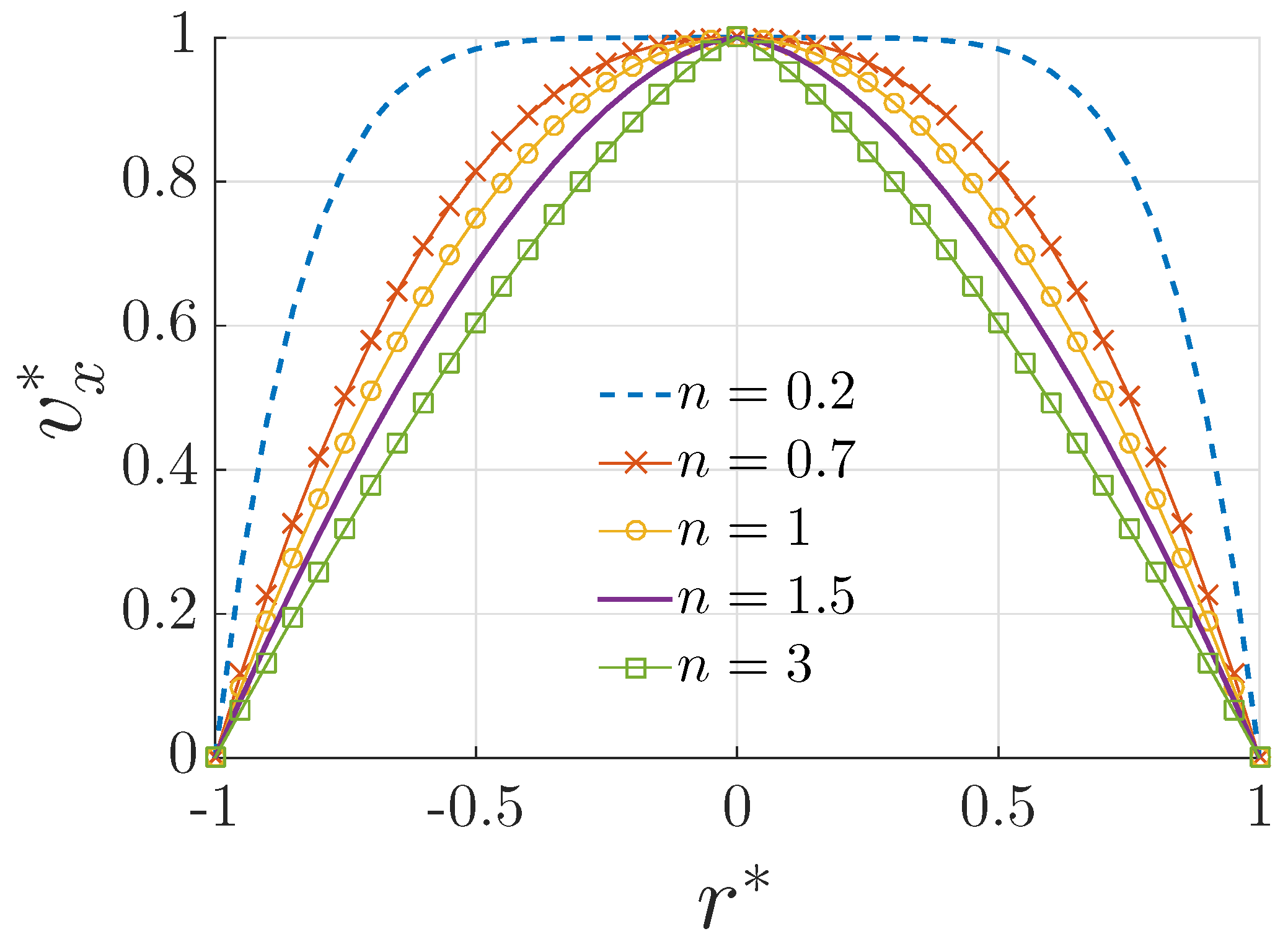
3.1. Velocity Profile
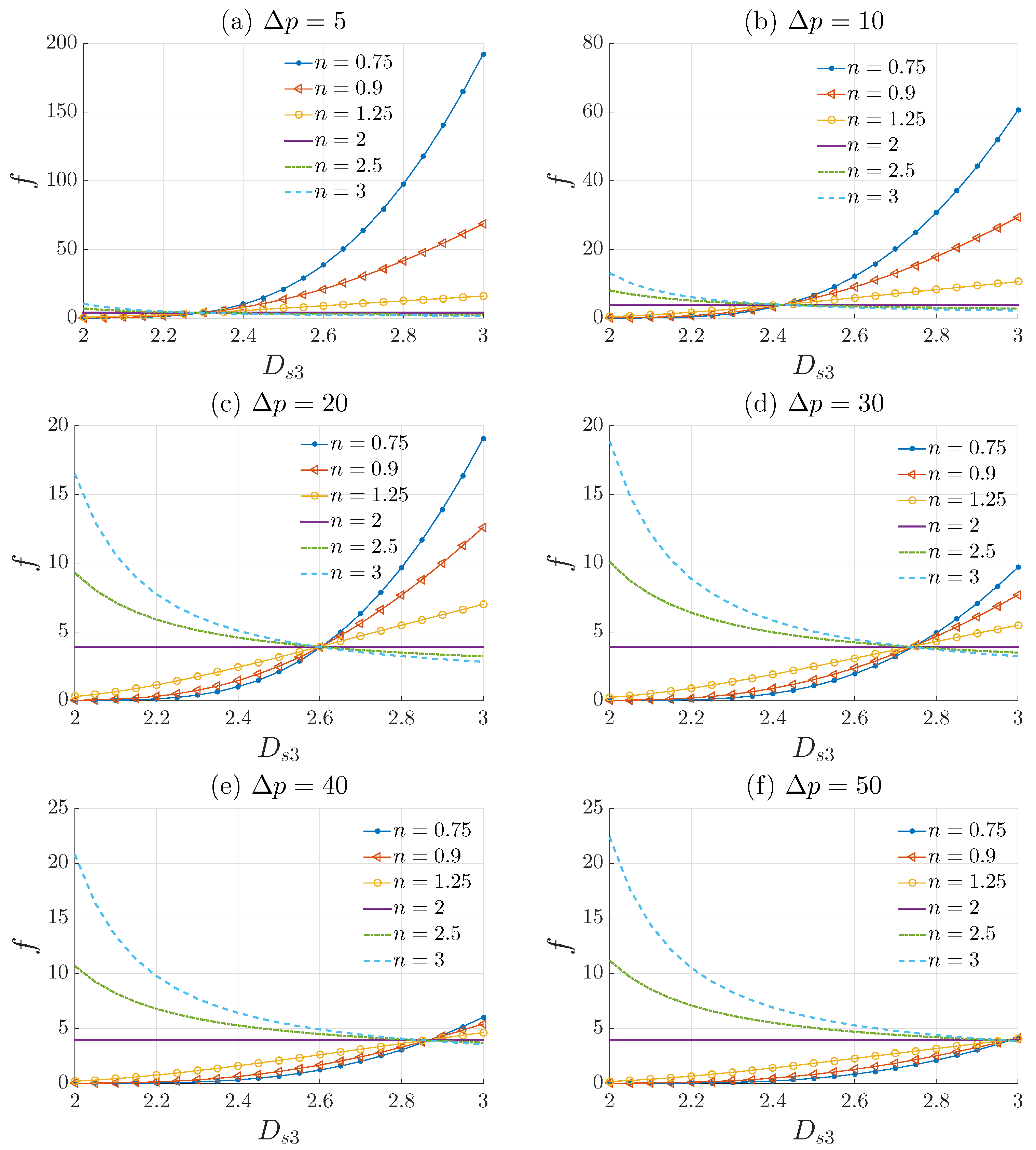
3.2. Darcy Friction Factor
4. Results and Discussion
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Addison, P.S. Fractals and Chaos: An Illustrated Course; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; p. 486. [Google Scholar]
- Tarasov, V.E. Poiseuille equation for steady flow of fractal fluid. Int. J. Mod. Phys. 2016, 30, 1650128. [Google Scholar] [CrossRef]
- Balankin, A.S.; Mena, B.; Susarrey, O.; Samayoa, S. Steady laminar flow of fractal fluids. Phys. Lett. 2017, 381, 623–628. [Google Scholar] [CrossRef]
- Akgül, A.; Siddique, I. Novel applications of the magnetohydrodynamics couple stress fluid flows between two plates with fractal-fractional derivatives. Numer. Methods Partial. Differ. Equ. 2021, 37, 2178–2189. [Google Scholar] [CrossRef]
- Xie, J.; Gao, M.; Zhang, R.; Liu, J.; Liu, Y.; Yang, B.; Wang, M.; Wang, F. Fluid flow characteristics of cross-fractures with two branch fractures of different roughness controlled by fractal dimension: An experimental study. J. Pet. Sci. Eng. 2021, 196, 107996. [Google Scholar] [CrossRef]
- Ortiz, C.H.; Cortes, E.S.; Bonilla, J.L.; Castañeda, H. Fractal di- mension and turbulence in giant hii regions. J. Phys. Conf. Ser. 2015, 582, 012049. [Google Scholar] [CrossRef] [Green Version]
- Gaite, J. The fractal geometry of the cosmic web and its formation. Adv. Astron. 2019, 2019, 6587138. [Google Scholar] [CrossRef]
- Lancaster, L.; Ostriker, E.C.; Kim, J.G.; Kim, C.G. Efficiently Cooled Stellar Wind Bubbles in Turbulent Clouds. I. Fractal Theory and Application to Star-forming Clouds. Astrophys. J. 2021, 914, 89. [Google Scholar] [CrossRef]
- Berbiche, A.; Fellah, M.; Fellah, Z.E.A.; Ogam, E.; Mitri, F.G.; Depollier, C. Transient acoustic wave in self-similar porous material having rigid frame: Low frequency domain. Wave Motion 2017, 68, 12–21. [Google Scholar] [CrossRef]
- Fellah, M.; Fellah, Z.E.A.; Berbiche, A.; Ogam, E.; Mitri, F.G.; Depollier, C. Transient ultrasonic wave propagation in porous material of non-integer space dimension. Wave Motion 2017, 72, 276–286. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Fellah, M.; Ogam, E.; Berbiche, A.; Depollier, C. Reflection and transmission of transient ultrasonic wave in fractal porous material: Application of fractional calculus. Wave Motion 2021, 106, 102804. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Fellah, M.; Ongwen, N.O.; Ogam, E.; Depollier, C. Acoustics of fractal porous material and fractional calculus. Mathematics 2021, 9, 1774. [Google Scholar] [CrossRef]
- Soille, P.; Rivest, J.F. On the validity of fractal dimension measurements in image analysis. J. Vis. Commun. Image Represent. 1996, 7, 217–229. [Google Scholar] [CrossRef]
- Guariglia, E. Primality, fractality, and image analysis. Entropy 2019, 21, 304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Av¸sar, E. Contribution of fractal dimension theory into the uniaxial compressive strength prediction of a volcanic welded bimrock. Bull. Eng. Geol. Environ. 2020, 79, 3605–3619. [Google Scholar] [CrossRef]
- Heping, X. Fractals in Rock Mechanics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2020; ISBN 9789054101338. [Google Scholar]
- Ildoromi, A. Separation of geological formations by comparing the density dimension of drainage network and fractal dimension of drainage network (Case study: Northern slopes of Hamedan). New Find. Appl. Geol. 2021. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Paudyal, H. Box Counting Fractal Dimension and Frequency Size Distributon of Earthquakes in the Central Himalaya Region. J. Inst. Sci. Technol. 2021, 26, 127–136. [Google Scholar] [CrossRef]
- Mambetsariev, I.; Mirzapoiazova, T.; Lennon, F.; Jolly, M.E.; Li, H.; Nasser, M.W.; Vora, L.; Kulkarni, P.; Batra, S.K.; Salgia, R. Small cell lung cancer therapeutic responses through fractal measurements: From radiology to mitochondrial biology. J. Clin. Med. 2019, 8, 1038. [Google Scholar] [CrossRef] [Green Version]
- Pham, D.T.; Musielak, Z.E. Spectra of Reduced Fractals and their Applications in Biology. arXiv 2021, arXiv:2111.01719. [Google Scholar]
- Szasz, A. Time-Fractal in Living Objects. Open J. Biophys. 2021, 12, 1–26. [Google Scholar] [CrossRef]
- Watanabe, H.; Hayano, K.; Ohira, G.; Imanishi, S.; Hanaoka, T.; Hirata, A.; Kano, M.; Matsubara, H. Quantification of structural heterogeneity using fractal analysis of contrast-enhanced CT image to predict survival in gastric cancer patients. Dig. Dis. Sci. 2021, 66, 2069–2074. [Google Scholar] [CrossRef]
- Soltani, P.; Sami, S.; Yaghini, J.; Golkar, E.; Riccitiello, F.; Spagnuolo, G. Application of Fractal Analysis in Detecting Trabecular Bone Changes in Periapical Radiograph of Patients with Periodontitis. Int. J. Dent. 2021, 2021, 3221448. [Google Scholar] [CrossRef] [PubMed]
- Elkington, L.; Adhikari, P.; Pradhan, P. Fractal Dimension Analysis to Detect the Progress of Cancer Using Transmission Optical Microscopy. Biophysica 2022, 2, 59–69. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Passoja, D.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Brown, S.R. Fluid flow through rock joints: The effect of surface roughness. J. Geophys. Res. Solid Earth 1987, 92, 1337–1347. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y.; Robert, L.J. An analysis of generated fractal and measured rough surfaces in regards to their multi-scale structure and fractal dimension. Tribol. Int. 2017, 108, 94–101. [Google Scholar] [CrossRef]
- Brown, S.R.; Stockman, H.W.; Reeves, S.J. Applicability of the reynolds equation for modeling fluid flow between rough surfaces. Geophys. Res. 1995, 22, 2537–2540. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, C.; Shi, M.; Peterson, G.P. Role of surface roughness characterized by fractal geometry on laminar flow in microchannels. Phys. Rev. E 2009, 80, 026301. [Google Scholar] [CrossRef]
- Wojciech, M.; Ricardo, B.; Mateusz, K.; Tadeusz, L. Fractal dimension for bending–torsion fatigue fracture characterisation. Measurement 2021, 184, 109910. [Google Scholar]
- Ghanbarian, B.; Hunt, A.G.; Daigle, H. Fluid flow in porous media with rough pore-solid interface. Water Resour. Res. 2016, 52, 2045–2058. [Google Scholar] [CrossRef] [Green Version]
- Gancarczyk, A.; Sindera, K.; Iwanisyzn, M.; Piątek, M.; Macek, W.; Jodlowski, P.J.; Wroński, S.; Sitarz, M.; Łojewska, J.; Kołodziej, A. Metal Foams as Novel Catalyst Support in Environmental Processes. Catalysts 2019, 9, 587. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Wang, Y. Fractal characterization of impact fracture surface of steel. Appl. Surf. Sci. 2012, 258, 4777–4781. [Google Scholar] [CrossRef]
- Hayat, T.; Yasmin, H.; Alhuthali, M.S.; Kutbi, M.A. Peristaltic Flow of a Non-Newtonian Fluid in an Asymmetric Channel with Convective Boundary Conditions. J. Mech. 2013, 29, 599–607. [Google Scholar] [CrossRef]
- Hayat, T.; Yasmin, H.; Alsaedi, A. Convective heat transfer analysis for peristaltic flow of power-law fluid in a channel. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 463–477. [Google Scholar] [CrossRef]
- Yasmin, H.; Iqbal, N.; Hussain, A. Convective heat/mass transfer analysis on Johnson-Segalman fluid in a symmetric curved channel with peristalsis: Engineering applications. Symmetry 2020, 12, 1475. [Google Scholar] [CrossRef]
- Vikash, P.; Sverre, H. Linking the fractional derivative and the Lomnitz creep law to non-Newtonian time-varying viscosity. Phys. Rev. E 2016, 94, 032606. [Google Scholar]
- Shapovalov, V.M. On the applicability of the Ostwald–de Waele model in solving applied problems. J. Eng. Phys. Thermophys. 2017, 90, 1213–1218. [Google Scholar] [CrossRef]
- Hussain, S.; Öztop, H.F. Impact of inclined magnetic field and power law fluid on double diffusive mixed convection in lid-driven curvilinear cavity. Int. Commun. Heat Mass Transf. 2021, 127, 105549. [Google Scholar] [CrossRef]
- Saeed Khan, M.W.; Ali, N. Thermal entry flow of power-law fluid through ducts with homogeneous slippery wall(s) in the presence of viscous dissipation. Int. Commun. Heat Mass Transf. 2021, 120, 105041. [Google Scholar] [CrossRef]
- Abu-Nab, A.K.; Selima, E.S.; Morad, A.M. Theoretical investigation of a single vapor bubble during Al2O3/H2O nanofluids in power-law fluid affected by a variable surface tension. Phys. Scr. 2021, 96, 035222. [Google Scholar] [CrossRef]
- Oyelami, F.H.; Ige, E.O.; Taiyese, N.O.; Saka-Balogun, O.Y. Magneto-radiative analysis of thermal effect in symmetrical stenotic arterial blood flow. J. Math. Comput. Sci. 2021, 11, 5213–5230. [Google Scholar]
- Haghighatkha, A.; Kahriz, M.A. Numerical simulation of intravenous blood flow. J. Multidiscip. Eng. Sci. Technol. 2021, 8, 13922–13926. [Google Scholar]
- Pakhomov, M.A.; Zhapbasbayev, U.K. RANS modeling of turbulent flow and heat transfer of non-Newtonian viscoplastic fluid in a pipe. Case Stud. Therm. Eng. 2021, 28, 101455. [Google Scholar] [CrossRef]
- Gabry’s, E.Z.; Rybaczuk, M.; K˛edzia, A. Blood flow simulation through fractal models of circulatory system. Chaos Solitons Fractals 2006, 27, 1–7. [Google Scholar] [CrossRef]
- G Jayalalitha, G.; Deviha, V.S.; Uthayakumar, R. Fractal model for blood flow in cardiovascular system. Comput. Biol. Med. 2008, 38, 684–693. [Google Scholar] [CrossRef]
- Deviha, V.S.; Rengarajan, P.; Hussain, R.J. Modeling blood flow in the blood vessels of the cardiovascular system using fractals. Appl. Math. Sci. 2013, 7, 527–537. [Google Scholar] [CrossRef]
- da Silva, J.L.; Rao, M.A. Rheology of Fluid and Semisolid Foods; Springer: Berlin/Heidelberg, Germany, 2007; Chapter 6; pp. 339–401. ISBN 978-0-387-70930-7. [Google Scholar]
- Schramm, L.L. Emulsions, Foams, and Suspensions Fundamentals and Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2005; ISBN 9783527606757. [Google Scholar]
- Wlczek, P.; Odgaard, A.; Sernetz, M. Fractal Geometry and Computer Graphics; Fractal 3d Analysis of Blood Vessels and Bones; Springer: Berlin/Heidelberg, Germany, 1992; pp. 240–248. ISBN 978-3-642-95678-2. [Google Scholar]
- Chen, C.; Zhang, X.; Ren, L.; Geng, Y.; Bai, G. Analysis of blood flow characteristics in fractal vascular network based on the time fractional order. Phys. Fluids 2021, 33, 041902. [Google Scholar] [CrossRef]
- Kundu, P.; Cohen, I.M.; Dowling, D.R. Fluid Mechanics; Academic Press: Cambridge, MA, USA, 2012; ISBN 978-0-12-382100-3. [Google Scholar]
- Richardson, S. On the no-slip boundary condition. J. Fluid Mech. 1973, 59, 707–719. [Google Scholar] [CrossRef]
- Dietrich, E.; Peter, P.; Mario, L. Boundary condition for fluid flow: Curved or rough surfaces. Phys. Rev. Lett. 1990, 64, 2269. [Google Scholar]
- Thompson, P.A.; Robbins, M.O. Shear flow near solids: Epitaxial order and flow boundary conditions. Phys. Rev. A 1990, 41, 6830. [Google Scholar] [CrossRef]
- Zhu, Y.; Granick, S. Limits of the hydrodynamic no-slip boundary condition. Phys. Rev. Lett. 2002, 88, 106102. [Google Scholar] [CrossRef] [Green Version]
- Koplik, J.; Banavar, J.R.; Willemsen, J.F. Molecular dynamics of fluid flow at solid surfaces. Phys. Fluids A Fluid Dyn. 1989, 1, 781–794. [Google Scholar] [CrossRef]
- Stieger, M. The rheology handbook-for users of rotational and oscillatory rheometers. Appl. Rheol. 2002, 12, 232. [Google Scholar] [CrossRef]
- Singh, R.P.; Heldman, D.R. Introduction to Food Engineering, 4th ed.; Sun, D.W., Ed.; Elsevier Academic Press: New York, NY, USA, 2001; ISBN 978-0-12-370900-4. [Google Scholar]
- Barnes, H.A.; Fletcher Hutton, J.F.; Walters, K. An Introduction to Rheology; Elsevier: Amsterdam, The Netherlands, 1989; ISBN 978-0-444-87469-6. [Google Scholar]
- Painter, P.C.; Coleman, M.M. Fundamentals of Polymer Science: An Introductory Text; Routledge: Boca Raton, FL, USA, 2019; ISBN 9780203755211. [Google Scholar]
- Hu, Y.; Werner, C.; Li, D. Influence of three-dimensional rough- ness on pressure-driven flow through microchannels. J. Fluids Eng. 2003, 125, 871–879. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y. Influence of three-dimensional wall roughness on the laminar flow in microtube. Int. J. Heat Fluid Flow 2007, 28, 220–228. [Google Scholar] [CrossRef]
- Lovejoy, S. Area-perimeter relation for rain and cloud areas. Science 1982, 216, 185–187. [Google Scholar] [CrossRef]
- Pachepsky, Y.; Yakovchenko, V.; Rabenhorst, M.C.; Pooley, C.; Sikora, L.J. Frac- tal parameters of pore surfaces as derived from micromorphological data: Effect of long-term management practices. Geoderma 1996, 74, 305–319. [Google Scholar] [CrossRef]
- Schlueter, E.M.; Zimmerman, R.W.; Witherspoon, P.A.; Cook, N.G.W. The fractal dimension of pores in sedimentary rocks and its influence on permeability. Eng. Geol. 1997, 48, 199–215. [Google Scholar] [CrossRef]
- Sahimi, M. Flow and Transport in Porous Media and Fractured Rock: From Classical Methods to Modern Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 9783527404858. [Google Scholar]
- Carr, J.R. Statistical self-affinity, fractal dimension, and geologic interpretation. Eng. Geol. 1997, 48, 269–282. [Google Scholar] [CrossRef]
- Brown, G.O. Environmental and Water Resources History; Chapter: The History of the Darcy-Weisbach Equation for Pipe Flow Resistance; Amer Society of Civil Engineers: Reston, VA, USA, 2003; pp. 34–43. ISBN 978-0784407387. [Google Scholar]

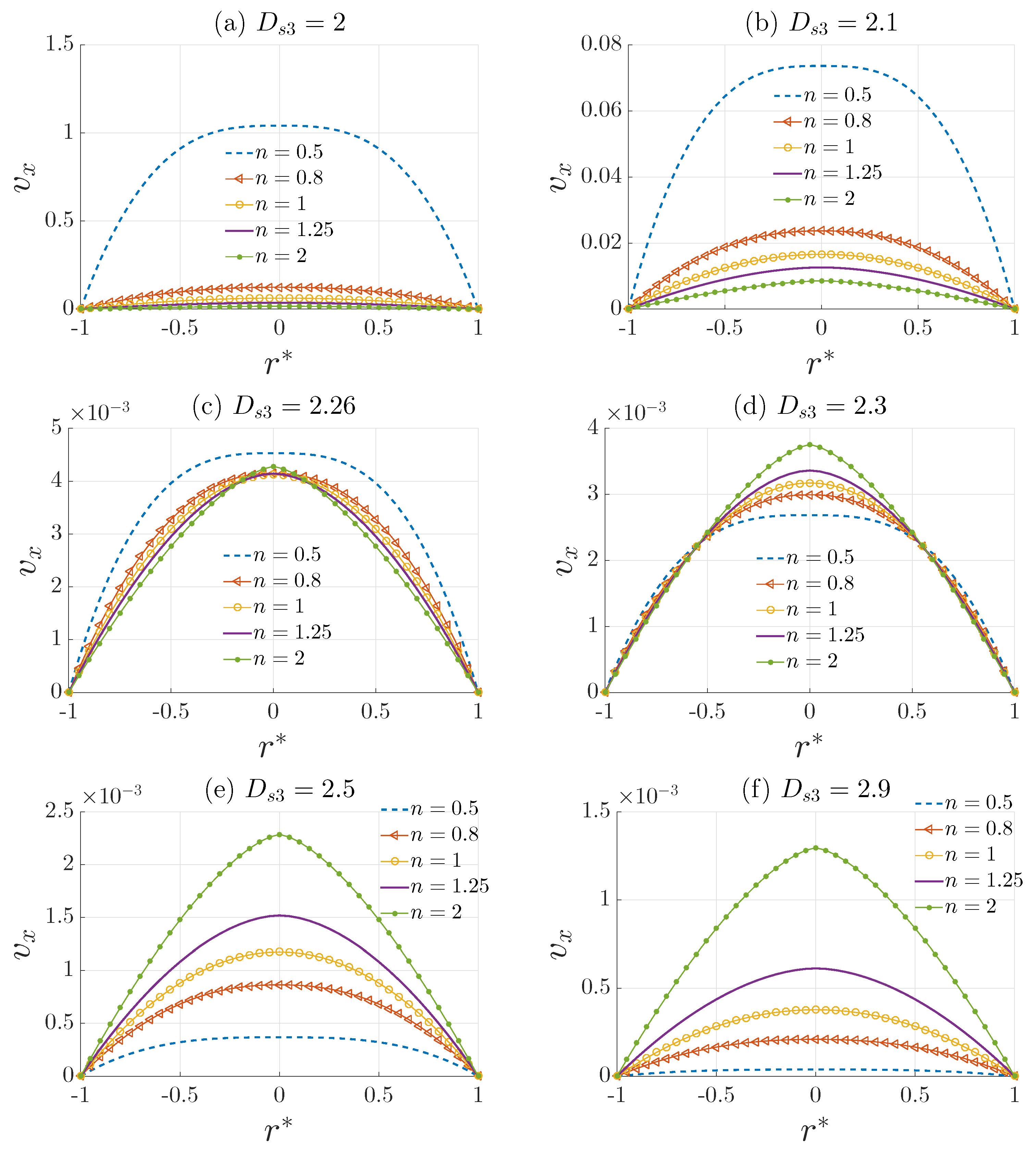
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouchendouka, A.; Fellah, Z.E.A.; Larbi, Z.; Louna, Z.; Ogam, E.; Fellah, M.; Depollier, C. Fractal Analysis of a Non-Newtonian Fluid Flow in a Rough-Walled Pipe. Materials 2022, 15, 3700. https://doi.org/10.3390/ma15103700
Bouchendouka A, Fellah ZEA, Larbi Z, Louna Z, Ogam E, Fellah M, Depollier C. Fractal Analysis of a Non-Newtonian Fluid Flow in a Rough-Walled Pipe. Materials. 2022; 15(10):3700. https://doi.org/10.3390/ma15103700
Chicago/Turabian StyleBouchendouka, Abdellah, Zine El Abiddine Fellah, Zakaria Larbi, Zineeddine Louna, Erick Ogam, Mohamed Fellah, and Claude Depollier. 2022. "Fractal Analysis of a Non-Newtonian Fluid Flow in a Rough-Walled Pipe" Materials 15, no. 10: 3700. https://doi.org/10.3390/ma15103700
APA StyleBouchendouka, A., Fellah, Z. E. A., Larbi, Z., Louna, Z., Ogam, E., Fellah, M., & Depollier, C. (2022). Fractal Analysis of a Non-Newtonian Fluid Flow in a Rough-Walled Pipe. Materials, 15(10), 3700. https://doi.org/10.3390/ma15103700








