Enhanced Cellular Materials through Multiscale, Variable-Section Inner Designs: Mechanical Attributes and Neural Network Modeling
Abstract
:1. Introduction
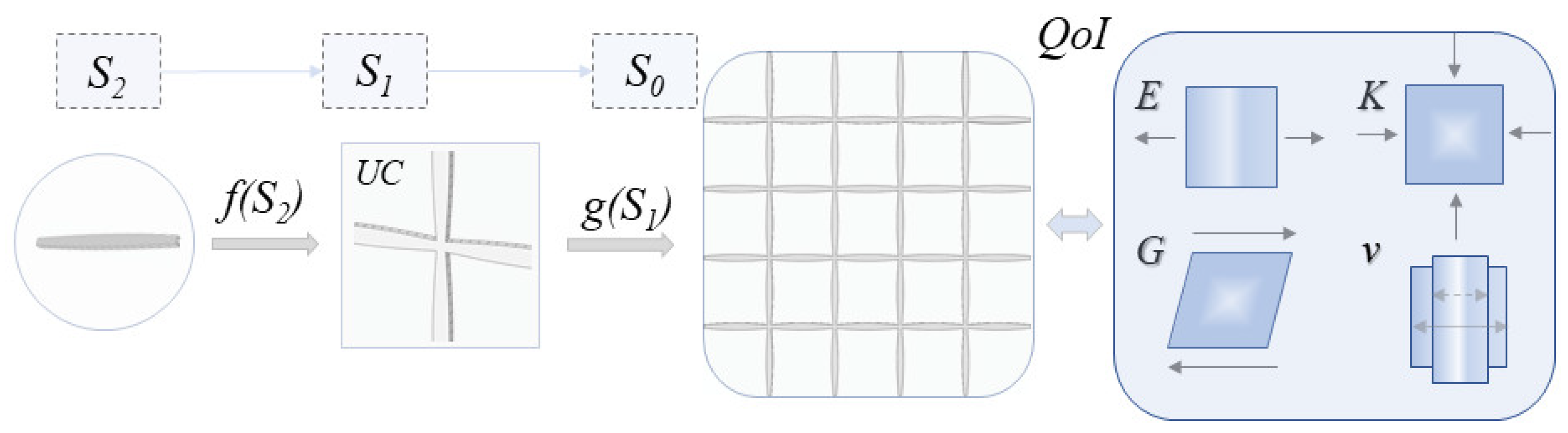
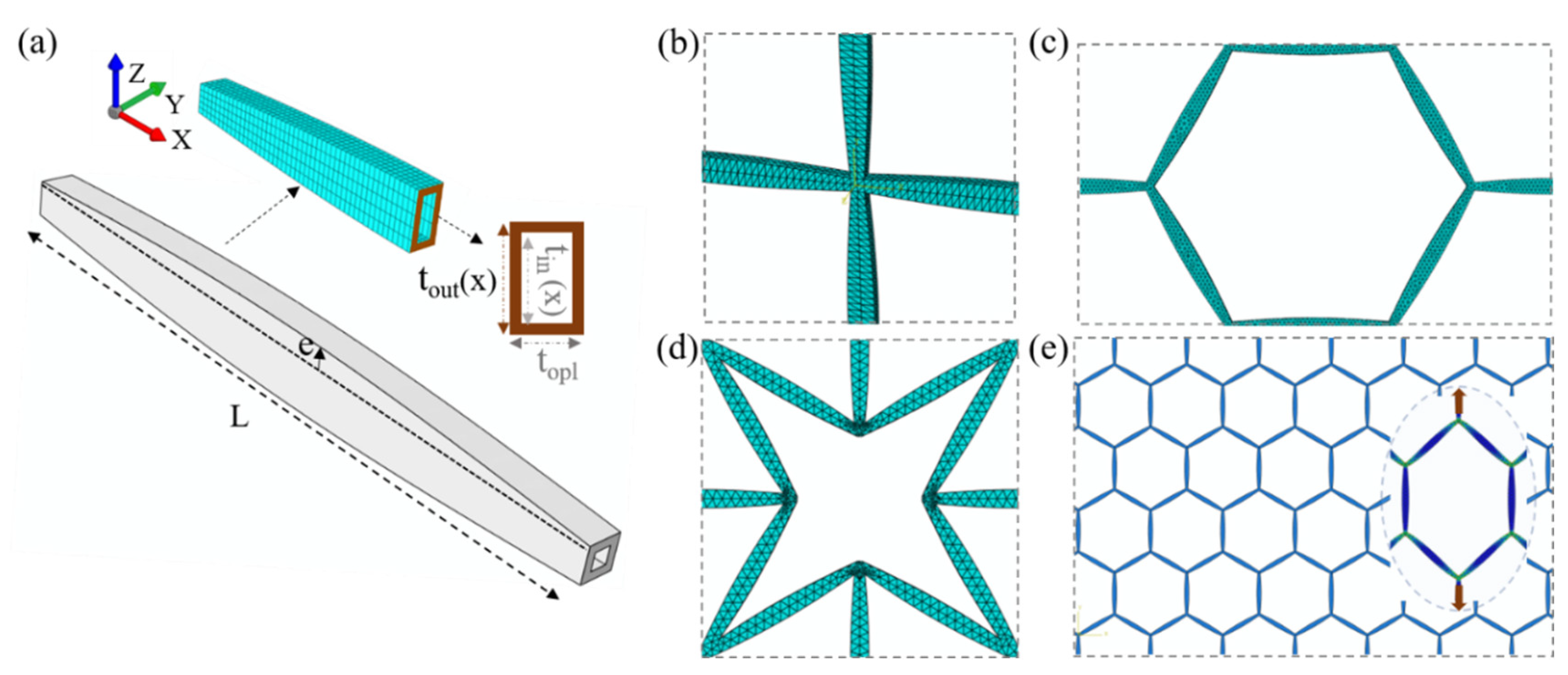
2. Multiscale Hollow and Variable Inner Cross-Section Cellular Material Designs
2.1. Analytical and Numerical Characterization
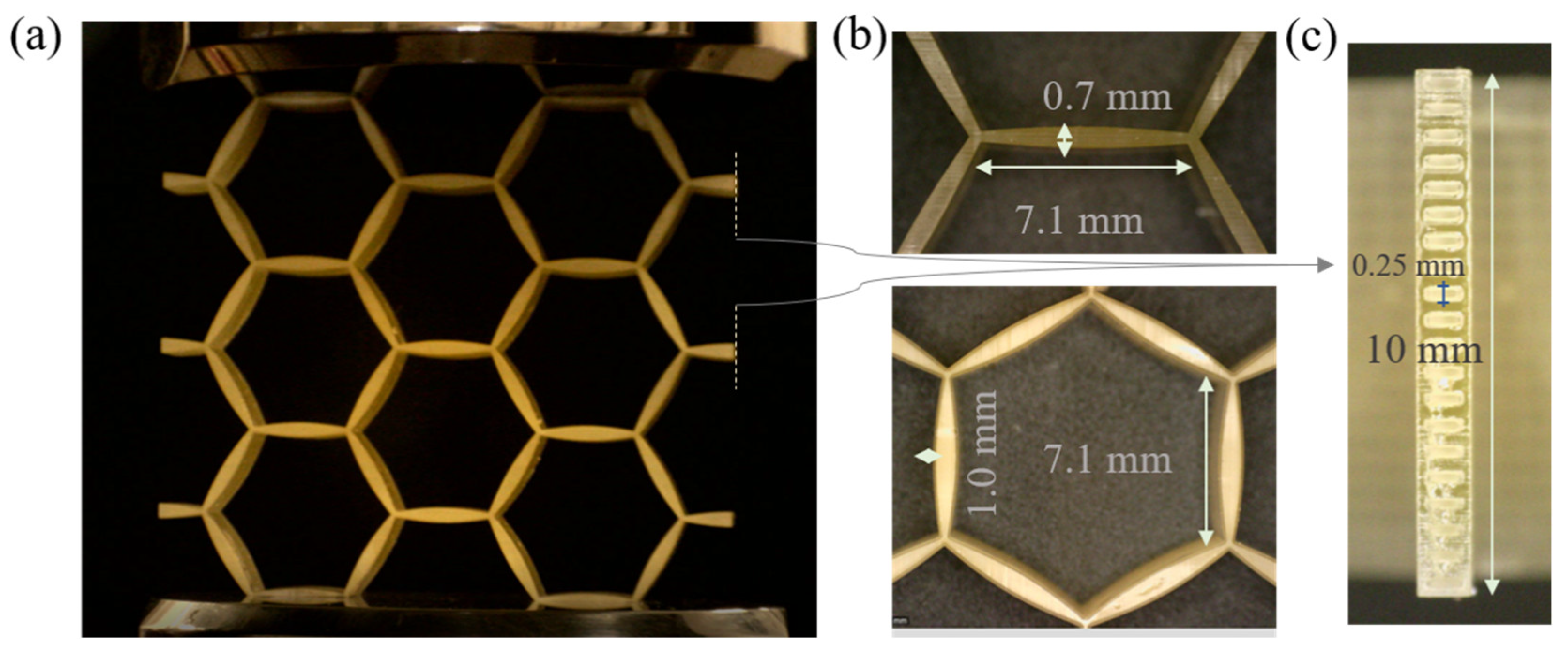
2.2. Additive Manufacturing and Experimental Characterization
3. Machine-Learning-Based Modeling and Design of Multiscale Metamaterial Architectures
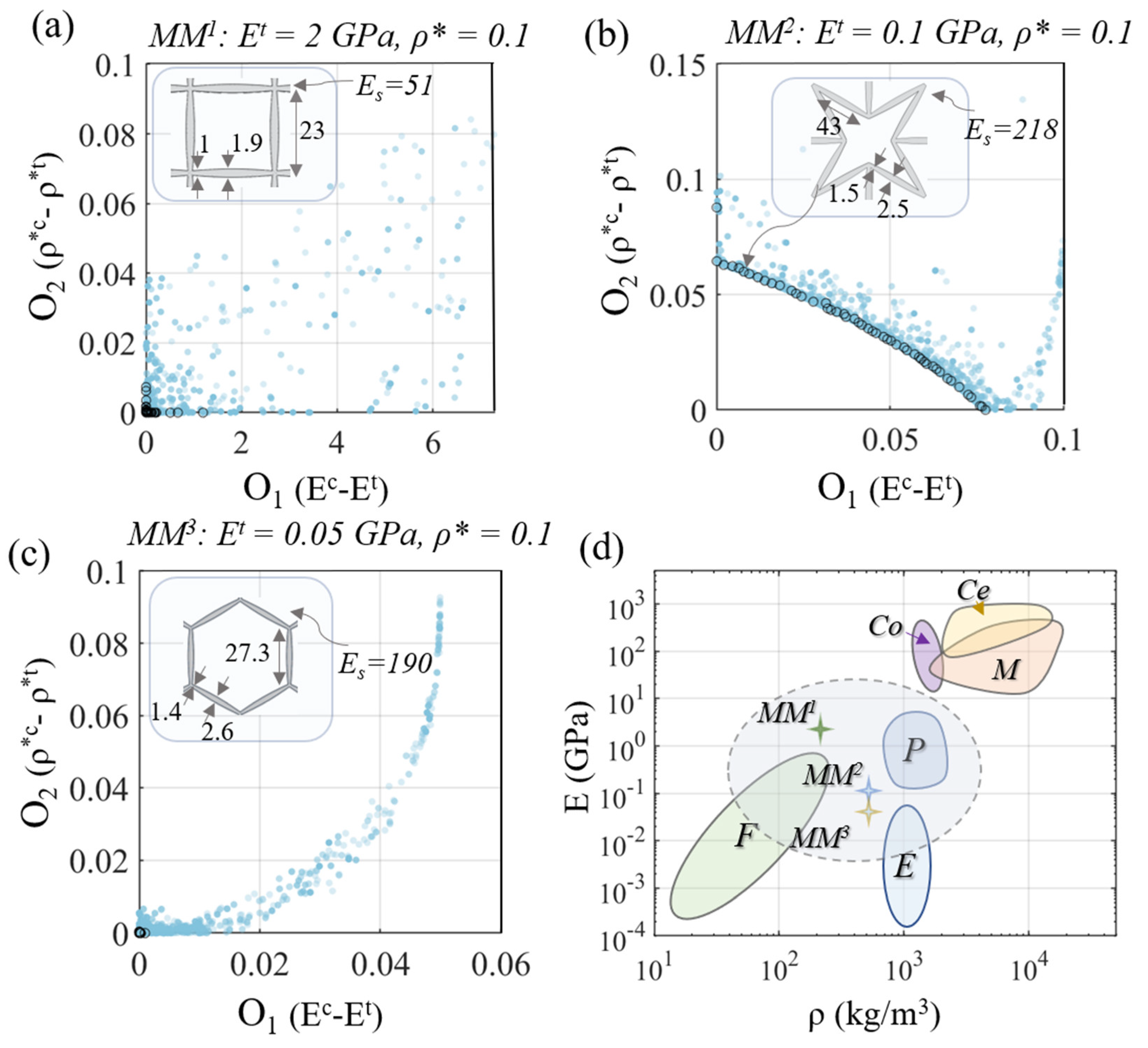
4. Effective Mechanical Attributes of Multiscale, Variable Inner Section Cellular Materials
5. Neural-Network-Based Multiscale Metamaterial Forward Modeling and Inverse Design
6. Discussion
7. Conclusions
- Hollow, variable-section inner structural designs allow for an enhanced, specific normal, shear and bulk metamaterial response, well beyond the range of single-scale metamaterial architectures.
- The insertion of a second inner scale affects the macroscale metamaterial performance in a non-unique manner, which depends on the uppermost-scale cellular pattern design.
- Multiscale designs can modify the stiffness-to-density scaling of cellular materials from a bending-dominated towards a stretching-dominated response.
- Low-numerical-cost neural network models can derive a robust link between the different inner scales and the complete set of effective elastic cellular material properties.
- Inverse multi-objective engineering tasks can, therefore, be performed, identifying the optimal multiscale cellular patterns that best satisfy the macroscale performance requests.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zhao, X.; Duan, G.; Li, A.; Chen, C.; Zhang, X. Integrating microsystems with metamaterials towards metadevices. Microsystems Nanoeng. 2019, 5, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, T.J.; Smith, D.R.; Liu, R.P. Metamaterials: Theory, Design and Applications; Springer: Cham, Switzerland, 2010; p. 367. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X. Metamaterials: A new frontier of science and technology. Chem. Soc. Rev. 2011, 40, 2494–2507. [Google Scholar] [CrossRef] [PubMed]
- Karathanasopoulos, N.; Reda, H.; Ganghoffer, J.-F. Designing two-dimensional metamaterials of controlled static and dynamic properties. Comput. Mater. Sci. 2017, 138, 323–332. [Google Scholar] [CrossRef]
- Fischer, S.C.L.; Hillen, L.; Eberl, C. Mechanical Metamaterials on the Way from Laboratory Scale to Industrial Applications: Challenges for Characterization and Scalability. Materials 2020, 13, 3605. [Google Scholar] [CrossRef] [PubMed]
- Karathanasopoulos, N.; Dos Reis, F.; Diamantopoulou, M.; Ganghoffer, J.-F. Mechanics of beams made from chiral metamaterials: Tuning deflections through normal-shear strain couplings. Mater. Des. 2020, 189, 108520. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gambarotta, L. Chiral two-dimensional periodic blocky materials with elastic interfaces: Auxetic and acoustic properties. Extreme Mech. Lett. 2020, 39, 100769. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gambarotta, L. Wave propagation in non-centrosymmetric beam-lattices with lumped masses: Discrete and micropolar modeling. Int. J. Solids Struct. 2017, 118–119, 128–145. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A.; et al. Ultralight, ultrastiff mechanical metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef] [Green Version]
- Tancogne-Dejean, T.; Karathanasopoulos, N.; Mohr, D. Stiffness and Strength of Hexachiral Honeycomb-Like Metamaterials. J. Appl. Mech. 2019, 86, 111010. [Google Scholar] [CrossRef]
- Lvov, V.A.; Senatov, F.S.; Veveris, A.A.; Skrybykina, V.A.; Lantada, A.D. Auxetic Metamaterials for Biomedical Devices: Current Situation, Main Challenges, and Research Trends. Materials 2022, 15, 1439. [Google Scholar] [CrossRef]
- Bilski, M.; Pigłowski, P.; Wojciechowski, K. Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs. Symmetry 2021, 13, 1127. [Google Scholar] [CrossRef]
- Barbarosie, C.; Toader, A.-M. Shape and topology optimization for periodic problems: Part II: Optimization algorithm and numerical examples. Struct. Multidiscip. Optim. 2010, 40, 393–408. [Google Scholar] [CrossRef]
- Peel, L.D. Exploration of high and negative Poisson’s ratio elastomer-matrix laminates. Phys. Status Solidi B 2007, 244, 988–1003. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Pasini, D. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extreme Mech. Lett. 2016, 9, 291–296. [Google Scholar] [CrossRef] [Green Version]
- Bilski, M.; Wojciechowski, K.W.; Stręk, T.; Kędziora, P.; Grima-Cornish, J.N.; Dudek, M.R. Extremely Non-Auxetic Behavior of a Typical Auxetic Microstructure Due to Its Material Properties. Materials 2021, 14, 7837. [Google Scholar] [CrossRef] [PubMed]
- Theocaris, P.S.; Stavroulakis, G.E.; Panagiotopoulos, P.D. Negative Poisson’s ratios in composites with star-shaped inclusions: A numerical homogenization approach. Arch. Appl. Mech. 1997, 67, 274–286. [Google Scholar] [CrossRef]
- Ai, L.; Gao, X.-L. An analytical model for star-shaped re-entrant lattice structures with the orthotropic symmetry and negative Poisson’s ratios. Int. J. Mech. Sci. 2018, 145, 158–170. [Google Scholar] [CrossRef]
- Gaspar, N.; Ren, J.; Smith, C.; Grima, J.; Evans, K. Novel honeycombs with auxetic behaviour. Acta Mater. 2005, 53, 2439–2445. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, X.; Fang, D. Mechanical Properties of two novel planar lattice structures. Int. J. Solids Struct. 2008, 45, 3751–3768. [Google Scholar] [CrossRef] [Green Version]
- Mahbod, M.; Asgari, M. Elastic and plastic characterization of a new developed additively manufactured functionally graded porous lattice structure: Analytical and numerical models. Int. J. Mech. Sci. 2019, 155, 248–266. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Zhang, Y.; Cui, S.; Yang, Z.; Lu, Z. Ultra-low density architectured metamaterial with superior mechanical properties and energy absorption capability. Compos. Part B Eng. 2020, 202, 108379. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Karathanasopoulos, N.; Dos Reis, F.; Reda, H.; Ganghoffer, J.-F. Computing the effective bulk and normal to shear properties of common two-dimensional architectured materials. Comput. Mater. Sci. 2018, 154, 284–294. [Google Scholar] [CrossRef]
- Zheng, X.; Smith, W.; Jackson, J.; Moran, B.; Cui, H.; Chen, D.; Ye, J.; Fang, N.; Rodriguez, N.; Weisgraber, T.; et al. Multiscale metallic metamaterials. Nat. Mater. 2016, 15, 1100–1106. [Google Scholar] [CrossRef] [PubMed]
- Al Nashar, M.; Sutradhar, A. Design of Hierarchical Architected Lattices for Enhanced Energy Absorption. Materials 2021, 14, 5384. [Google Scholar] [CrossRef] [PubMed]
- Karathanasopoulos, N.; Dos Reis, F. Extending the elastic and plastic design space of metamaterials through load-specific, multiscale inner material architectures. Int. J. Mech. Sci. 2020, 175, 105523. [Google Scholar] [CrossRef]
- Sha, Y.; Jiani, L.; Haoyu, C.; Ritchie, R.O.; Jun, X. Design and strengthening mechanisms in hierarchical architected materials processed using additive manufacturing. Int. J. Mech. Sci. 2018, 149, 150–163. [Google Scholar] [CrossRef]
- Queheillalt, D.T.; Wadley, H.N. Pyramidal lattice truss structures with hollow trusses. Mater. Sci. Eng. A 2005, 397, 132–137. [Google Scholar] [CrossRef]
- Wu, W.; Tao, Y.; Xia, Y.; Chen, J.; Lei, H.; Sun, L.; Fang, D. Mechanical properties of hierarchical anti-tetrachiral metastructures. Extreme Mech. Lett. 2017, 16, 18–32. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, L.; Liu, X.; Xu, J.; Hu, P.; Ma, Z.-D. Theoretical prediction of mechanical properties of 3D printed Kagome honeycombs and its experimental evaluation. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6559–6576. [Google Scholar] [CrossRef]
- Karathanasopoulos, N.; Dos Reis, F.; Hadjidoukas, P.; Ganghoffer, J. LatticeMech: A discrete mechanics code to compute the effective static properties of 2D metamaterial structures. SoftwareX 2020, 11, 100446. [Google Scholar] [CrossRef]
- Kaczmarczyk, Ł.; Pearce, C.J.; Bićanić, N. Studies of microstructural size effect and higher-order deformation in second-order computational homogenization. Comput. Struct. 2010, 88, 1383–1390. [Google Scholar] [CrossRef]
- Cadman, J.E.; Zhou, S.; Chen, Y.; Li, Q. On design of multi-functional microstructural materials. J. Mater. Sci. 2012, 48, 51–66. [Google Scholar] [CrossRef]
- Settgast, C.; Abendroth, M.; Kuna, M. Constitutive modeling of plastic deformation behavior of open-cell foam structures using neural networks. Mech. Mater. 2019, 131, 1–10. [Google Scholar] [CrossRef]
- Fleisch, M.; Thalhamer, A.; Meier, G.; Raguž, I.; Fuchs, P.; Pinter, G.; Schlögl, S.; Berer, M. Functional mechanical metamaterial with independently tunable stiffness in the three spatial directions. Mater. Today Adv. 2021, 11, 100155. [Google Scholar] [CrossRef]
- Kalinin, S.; Sumpter, B.; Archibald, R. Big–deep–smart data in imaging for guiding materials design. Nat. Mater. 2015, 14, 973–980. [Google Scholar] [CrossRef]
- Oses, C.; Toher, C.; Curtarolo, S. Data-driven design of inorganic materials with the Automatic Flow Framework for Materials Discovery. MRS Bull. 2018, 43, 670–675. [Google Scholar] [CrossRef] [Green Version]
- Draxl, C.; Scheffler, M. NOMAD: The FAIR concept for big data-driven materials science. MRS Bull. 2018, 43, 676–682. [Google Scholar] [CrossRef] [Green Version]
- Majid, A.; Khan, A.; Javed, G.; Mirza, A.M. Lattice constant prediction of cubic and monoclinic perovskites using neural networks and support vector regression. Comput. Mater. Sci. 2010, 50, 363–372. [Google Scholar] [CrossRef]
- Barrera, M.D.B.; Franco-Martínez, F.; Lantada, A.D. Artificial Intelligence Aided Design of Tissue Engineering Scaffolds Employing Virtual Tomography and 3D Convolutional Neural Networks. Materials 2021, 14, 5278. [Google Scholar] [CrossRef]
- Guo, K.; Yang, Z.; Yu, C.-H.; Buehler, M.J. Artificial intelligence and machine learning in design of mechanical materials. Mater. Horiz. 2021, 8, 1153–1172. [Google Scholar] [CrossRef]
- Yang, Z.; Yabansu, Y.C.; Al-Bahrani, R.; Liao, W.-K.; Choudhary, A.N.; Kalidindi, S.R.; Agrawal, A. Deep learning approaches for mining structure-property linkages in high contrast composites from simulation datasets. Comput. Mater. Sci. 2018, 151, 278–287. [Google Scholar] [CrossRef]
- Jose, K.V.J.; Artrith, N.; Behler, J. Construction of high-dimensional neural network potentials using environment-dependent atom pairs. J. Chem. Phys. 2012, 136, 194111. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.; Rajput, S.; Mehta, Y. Modeling of the hot deformation behavior of a high phosphorus steel using artificial neural networks. Mater. Discov. 2016, 6, 1–8. [Google Scholar] [CrossRef]
- Wang, K.; Sun, W. A multiscale multi-permeability poroplasticity model linked by recursive homogenizations and deep learning. Comput. Methods Appl. Mech. Eng. 2018, 334, 337–380. [Google Scholar] [CrossRef]
- Zheng, X.; Zheng, P.; Zhang, R.-Z. Machine learning material properties from the periodic table using convolutional neural networks. Chem. Sci. 2018, 9, 8426–8432. [Google Scholar] [CrossRef] [Green Version]
- Wei, H.; Zhao, S.; Rong, Q.; Bao, H. Predicting the effective thermal conductivities of composite materials and porous media by machine learning methods. Int. J. Heat Mass Transf. 2018, 127, 908–916. [Google Scholar] [CrossRef]
- Kollmann, H.T.; Abueidda, D.W.; Koric, S.; Guleryuz, E.; Sobh, N.A. Deep learning for topology optimization of 2D metamaterials. Mater. Des. 2020, 196, 109098. [Google Scholar] [CrossRef]
- Chen, P.Y.; Chen, C.H.; Wang, H.; Tsai, J.H.; Ni, W.X. Synthesis design of artificial magnetic metamaterials using a genetic algorithm. Opt. Express 2008, 16, 12806–12818. [Google Scholar] [CrossRef]
- Garland, A.P.; White, B.C.; Jensen, S.C.; Boyce, B.L. Pragmatic generative optimization of novel structural lattice metamaterials with machine learning. Mater. Des. 2021, 203, 109632. [Google Scholar] [CrossRef]
- Gao, J.; Li, H.; Gao, L.; Xiao, M. Topological shape optimization of 3D micro-structured materials using energy-based homogenization method. Adv. Eng. Softw. 2018, 116, 89–102. [Google Scholar] [CrossRef]
- Gao, J.; Xue, H.; Gao, L.; Luo, Z. Topology optimization for auxetic metamaterials based on isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2019, 352, 211–236. [Google Scholar] [CrossRef]
- Gao, J.; Luo, Z.; Xia, L.; Gao, L. Concurrent topology optimization of multiscale composite structures in Matlab. Struct. Multidiscip. Optim. 2019, 60, 2621–2651. [Google Scholar] [CrossRef]
- Zheng, L.; Kumar, S.; Kochmann, D.M. Data-driven topology optimization of spinodoid metamaterials with seamlessly tunable anisotropy. Comput. Methods Appl. Mech. Eng. 2021, 383, 113894. [Google Scholar] [CrossRef]
- Liu, F.; Jiang, X.; Wang, X.; Wang, L. Machine learning-based design and optimization of curved beams for multistable structures and metamaterials. Extreme Mech. Lett. 2020, 41, 101002. [Google Scholar] [CrossRef]
- Yang, Z.; Yabansu, Y.C.; Jha, D.; Liao, W.-K.; Choudhary, A.N.; Kalidindi, S.R.; Agrawal, A. Establishing structure-property localization linkages for elastic deformation of three-dimensional high contrast composites using deep learning approaches. Acta Mater. 2018, 166, 335–345. [Google Scholar] [CrossRef]
- Bessa, M.A.; Glowacki, P.; Houlder, M. Bayesian Machine Learning in Metamaterial Design: Fragile Becomes Supercompressible. Adv. Mater. 2019, 31, e1904845. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, C.; Zhang, Z.; Luce, B.; Pusateri, S.; Xie, B.; Rafiei, M.H.; Hu, N. Accelerated design and characterization of non-uniform cellular materials via a machine-learning based framework. NPJ Comput. Mater. 2020, 6, 40. [Google Scholar] [CrossRef]
- Noronha, J.; Qian, M.; Leary, M.; Kyriakou, E.; Brandt, M. Hollow-walled lattice materials by additive manufacturing: Design, manufacture, properties, applications and challenges. Curr. Opin. Solid State Mater. Sci. 2021, 25, 100940. [Google Scholar] [CrossRef]
- Shen, H.; Ren, H.; Ning, J. Structural Design and Dynamic Compressive Properties of Ti–6Al–4V Hollow Lattice Structures. Adv. Eng. Mater. 2021, 23, 2100173. [Google Scholar] [CrossRef]
- Wang, Z.-P.; Poh, L.H.; Dirrenberger, J.; Zhu, Y.; Forest, S. Isogeometric shape optimization of smoothed petal auxetic structures via computational periodic homogenization. Comput. Methods Appl. Mech. Eng. 2017, 323, 250–271. [Google Scholar] [CrossRef] [Green Version]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Demuth, H.B.; Beale, M.H.; De Jess, O.; Hagan, M.T. Neural Network Design, 2nd ed.; Martin Hagan: Stillwater, OK, USA, 2014. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Wepster, S. The Mathematics of the Heavens and the Earth: The Early History of Trigonometry—By Glen van Brummelen. Centaurus 2010, 52, 156–157. [Google Scholar] [CrossRef]
- Elsayed, M.S.; Pasini, D. Analysis of the elastostatic specific stiffness of 2D stretching-dominated lattice materials. Mech. Mater. 2010, 42, 709–725. [Google Scholar] [CrossRef] [Green Version]
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
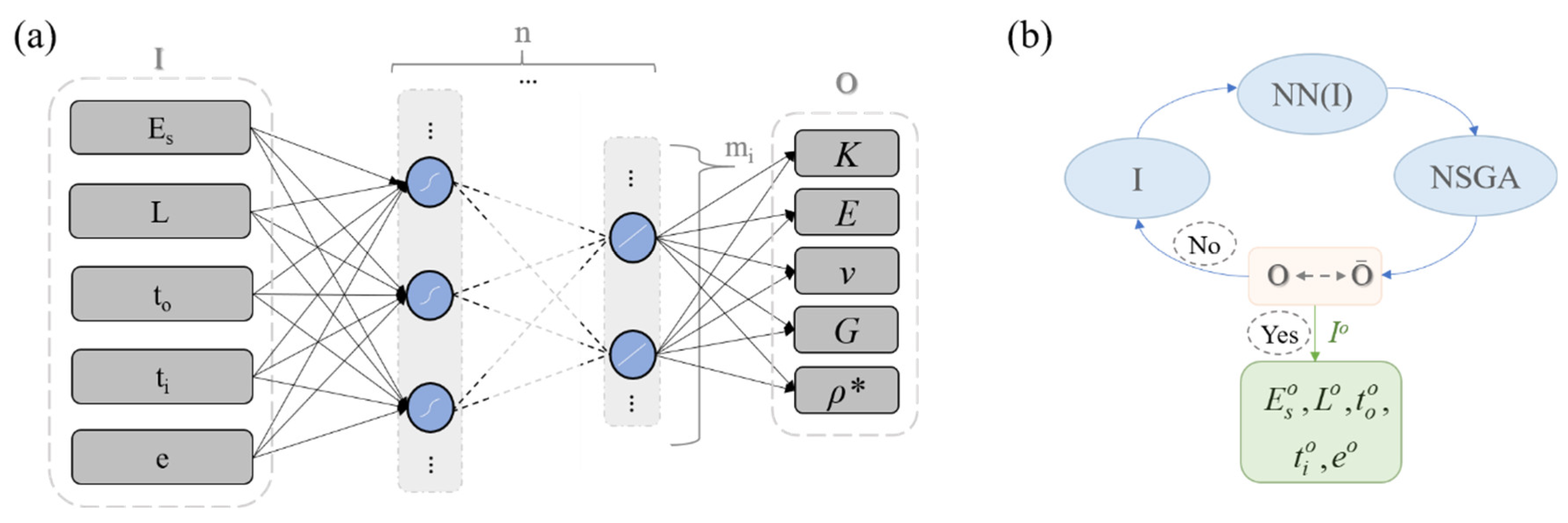
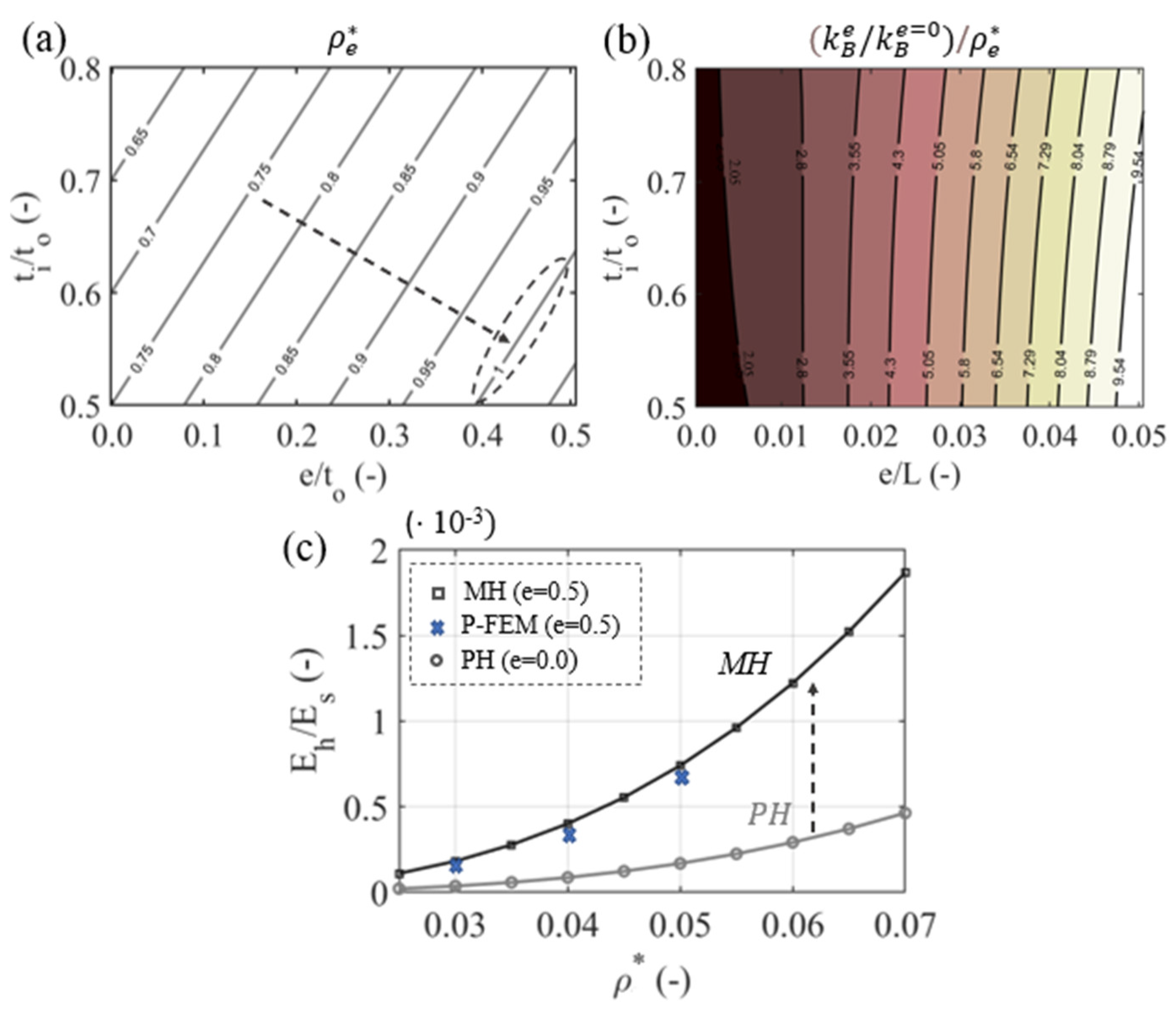
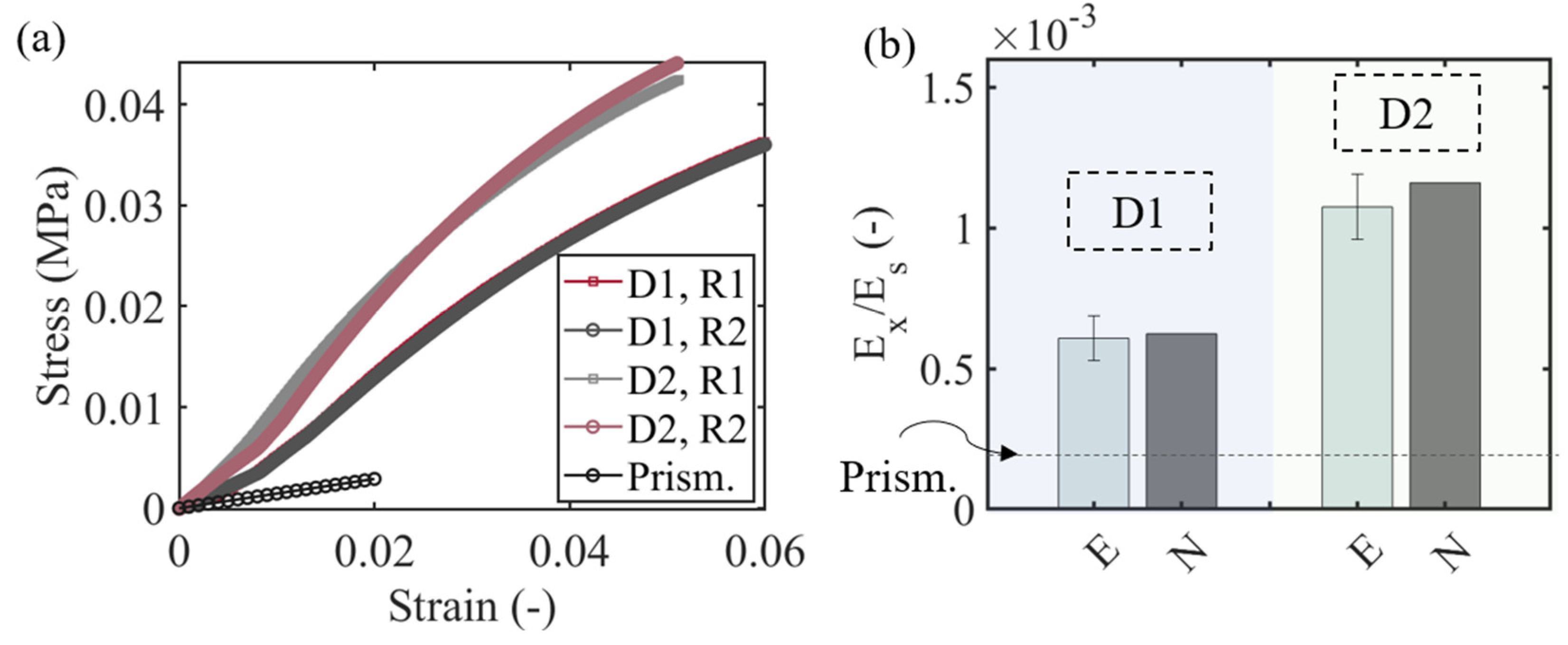
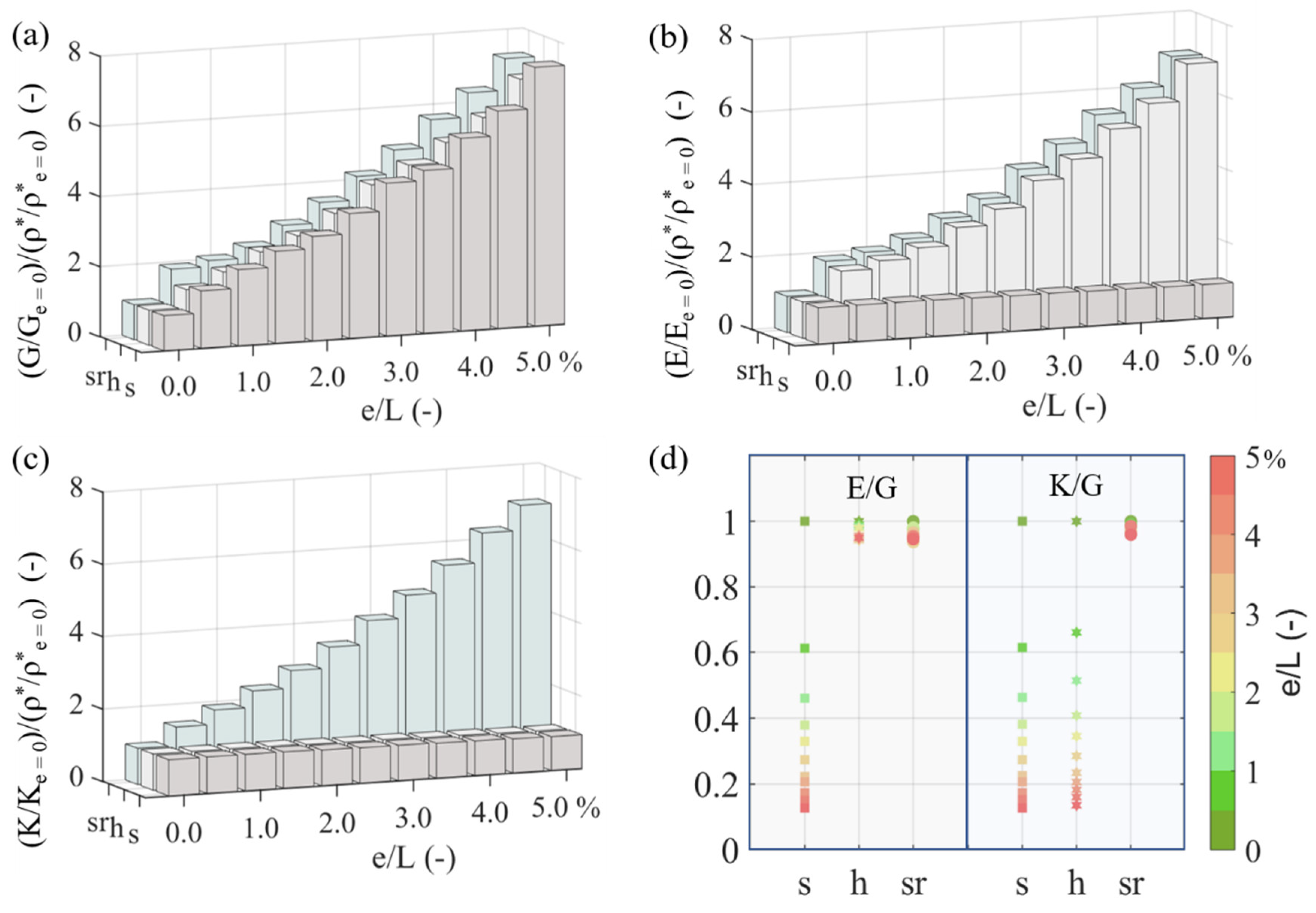
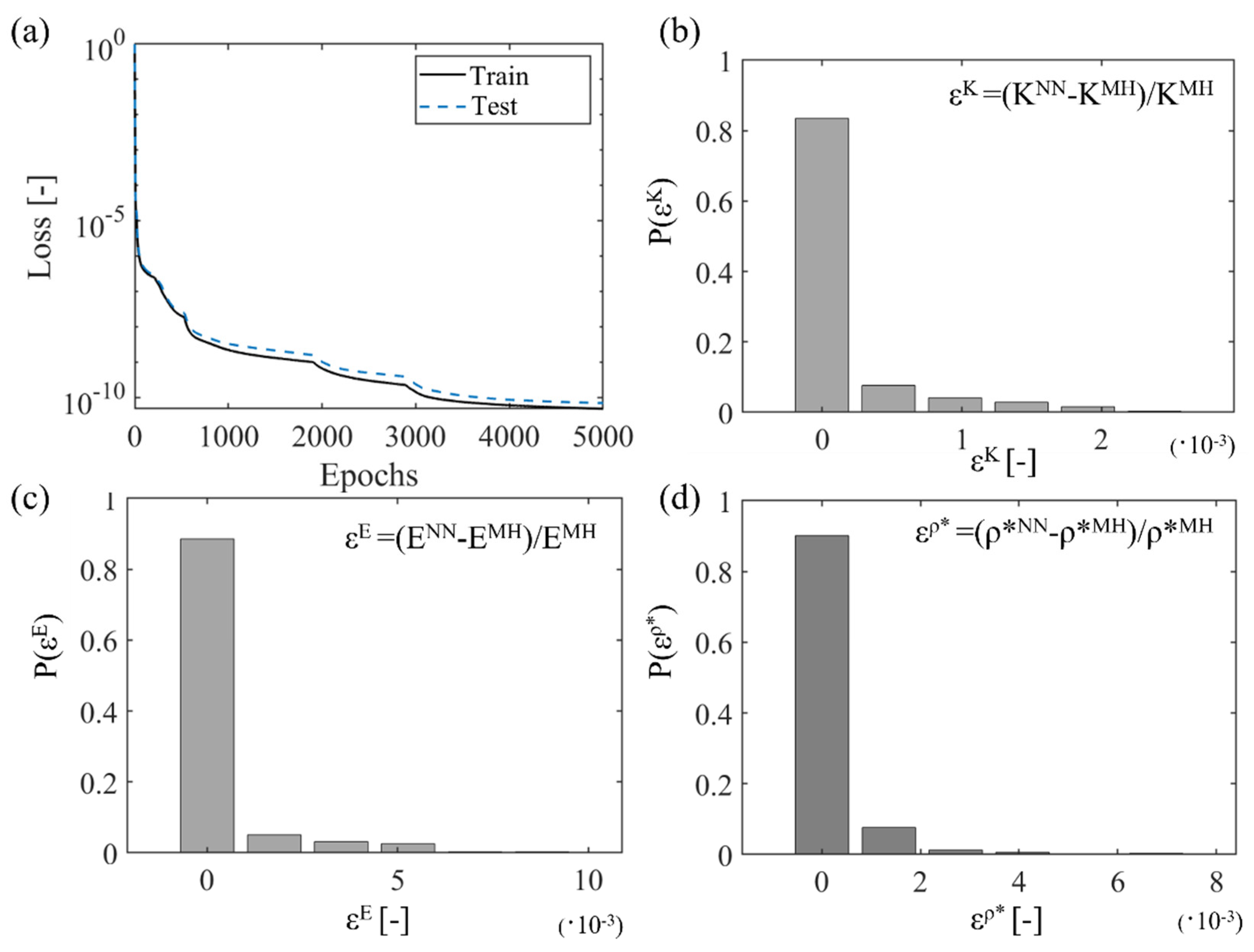
| Input Features | Range | Sampling Points |
|---|---|---|
| Es | 50–210 (GPa) | 9 |
| 0.5–1.5 (mm) | 11 | |
| 0.2–0.8 (-) | 7 | |
| 1/20–1/50 (0) | 7 | |
| 0–1 (-) | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karathanasopoulos, N.; Rodopoulos, D.C. Enhanced Cellular Materials through Multiscale, Variable-Section Inner Designs: Mechanical Attributes and Neural Network Modeling. Materials 2022, 15, 3581. https://doi.org/10.3390/ma15103581
Karathanasopoulos N, Rodopoulos DC. Enhanced Cellular Materials through Multiscale, Variable-Section Inner Designs: Mechanical Attributes and Neural Network Modeling. Materials. 2022; 15(10):3581. https://doi.org/10.3390/ma15103581
Chicago/Turabian StyleKarathanasopoulos, Nikolaos, and Dimitrios C. Rodopoulos. 2022. "Enhanced Cellular Materials through Multiscale, Variable-Section Inner Designs: Mechanical Attributes and Neural Network Modeling" Materials 15, no. 10: 3581. https://doi.org/10.3390/ma15103581
APA StyleKarathanasopoulos, N., & Rodopoulos, D. C. (2022). Enhanced Cellular Materials through Multiscale, Variable-Section Inner Designs: Mechanical Attributes and Neural Network Modeling. Materials, 15(10), 3581. https://doi.org/10.3390/ma15103581







