Spatial Dispersion in Hypercrystal Distributed Feedback Lasing
Abstract
1. Introduction
2. Theory
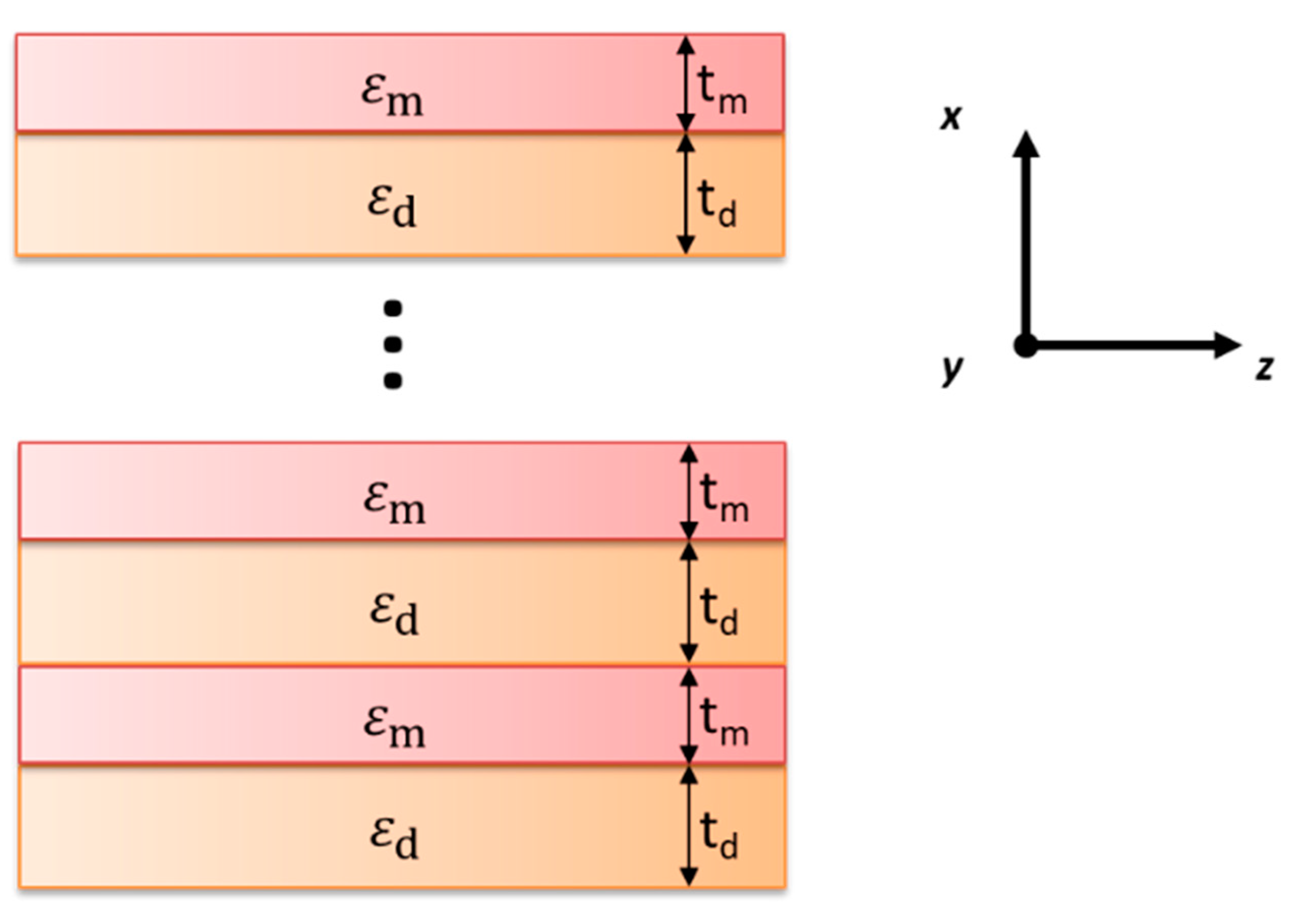
2.1. Local and Nonlocal Effective Medium Theory
2.2. Transfer Matrix Method Approach: Determination of Threshold Condition
3. Results
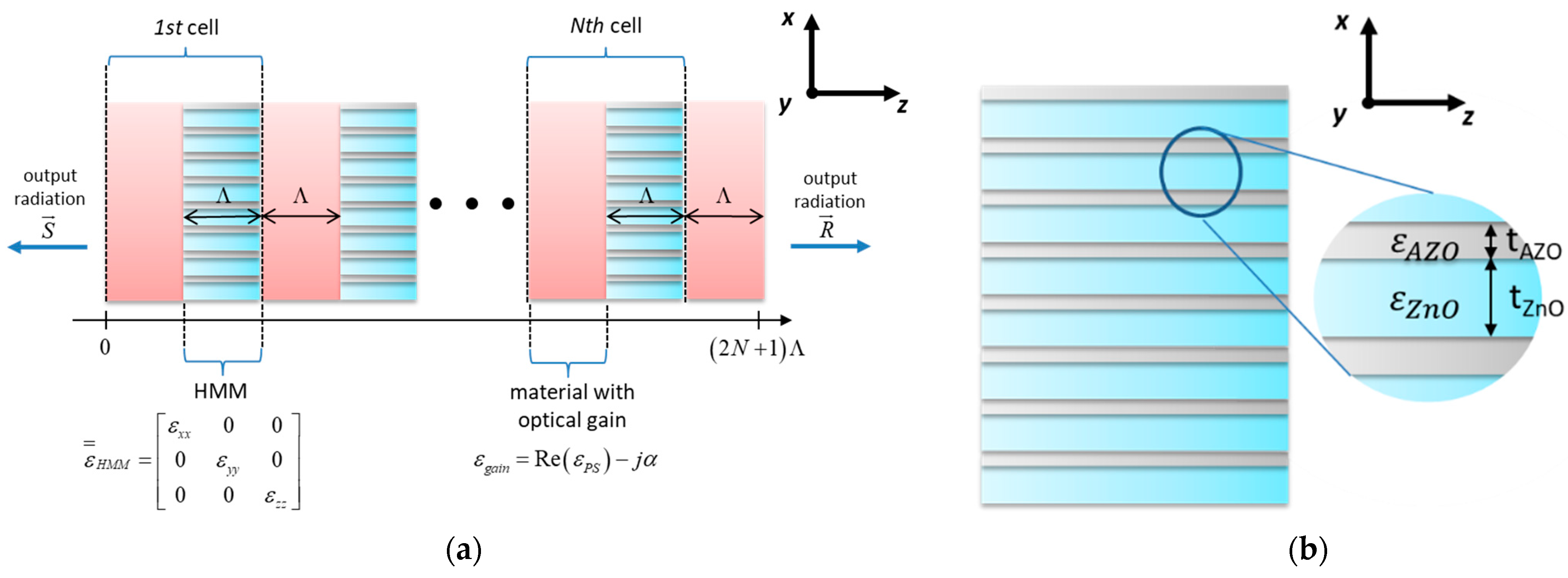
3.1. Distributed Feedback Laser Based on Hypercrystal
3.2. Modal Spectra
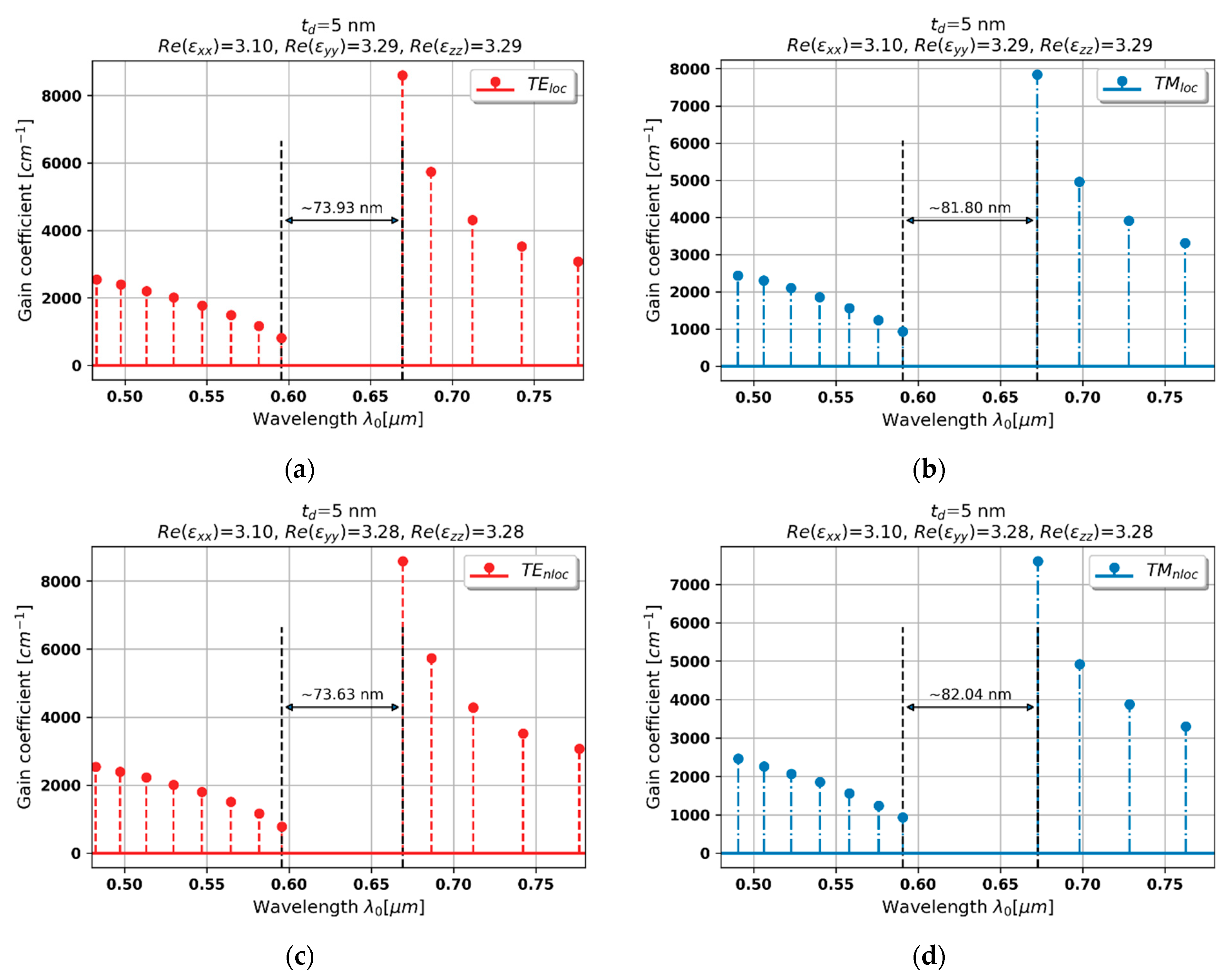
3.2.1. Case 1–5 nm Dielectric Layer
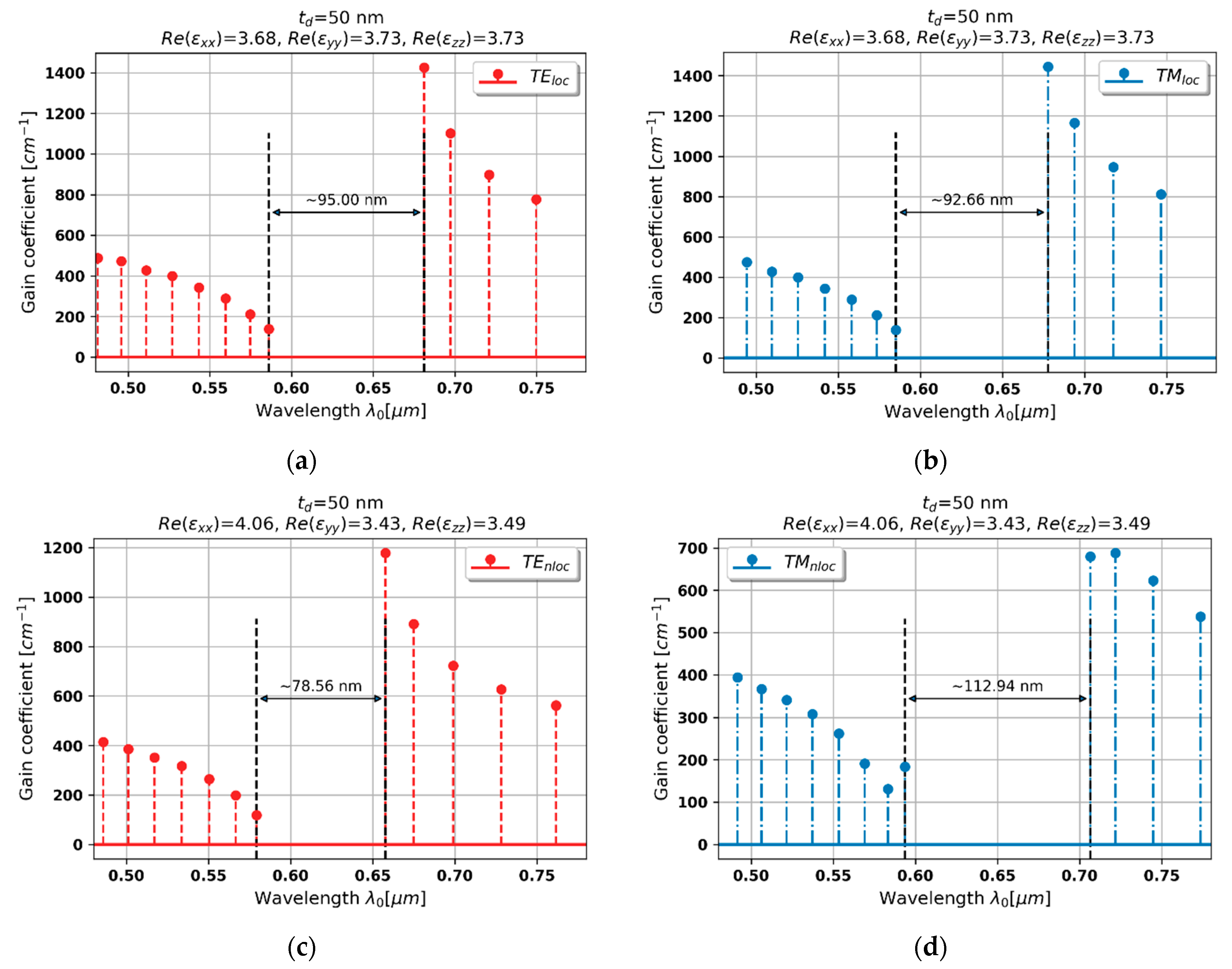
3.2.2. Case 2–50 nm Dielectric Layer
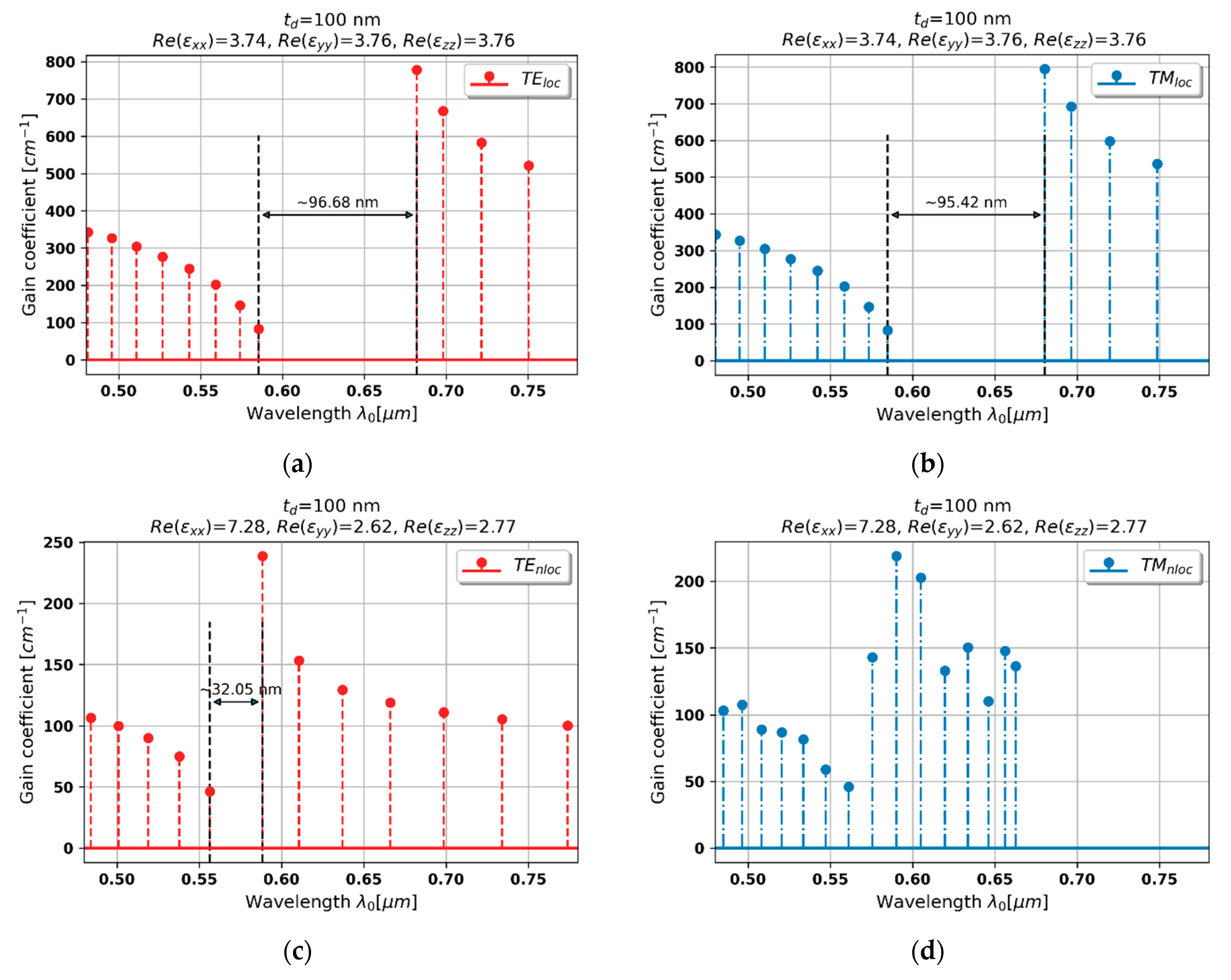
3.2.3. Case 3–100 nm Dielectric Layer
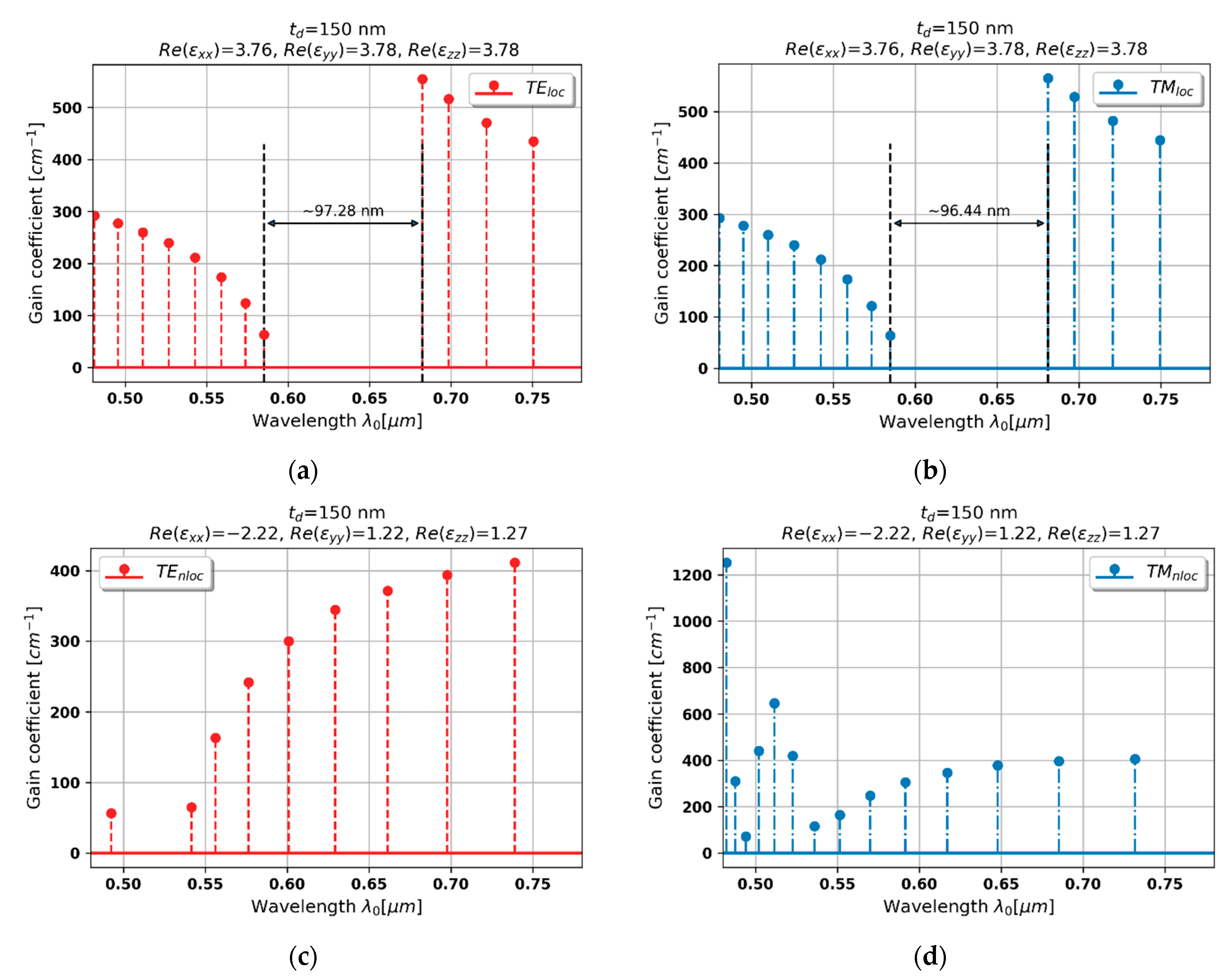
3.2.4. Case 4–150 nm Dielectric Layer
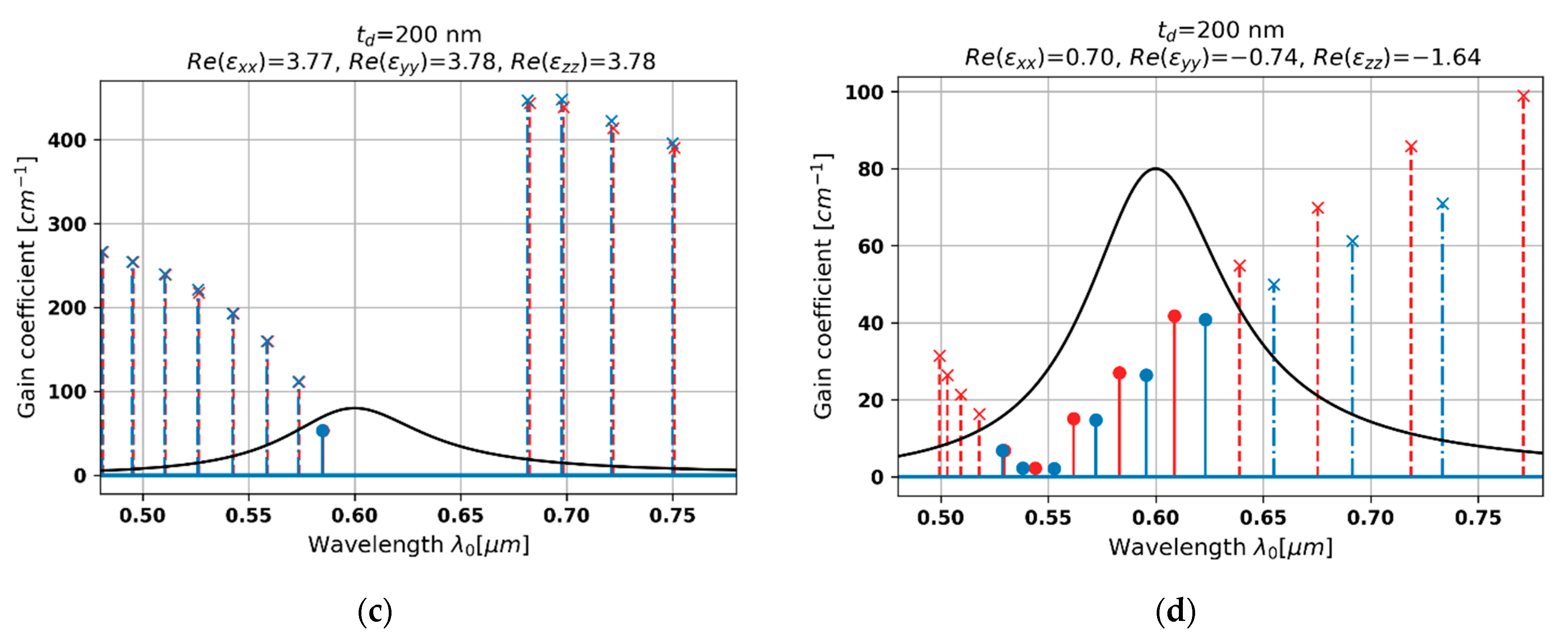
3.2.5. Case 5–200 nm Dielectric Layer
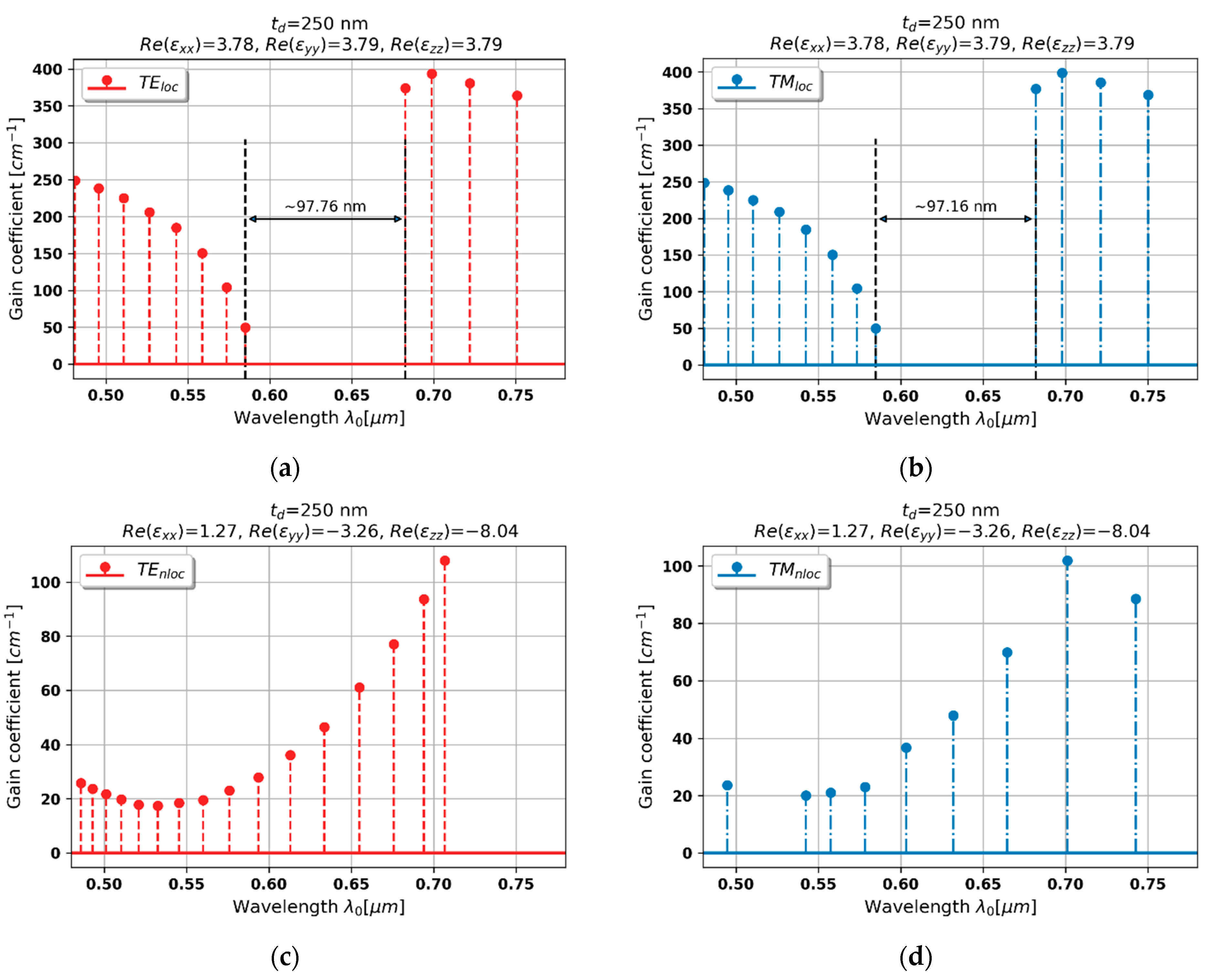
3.2.6. Case 6–250 nm Dielectric Layer
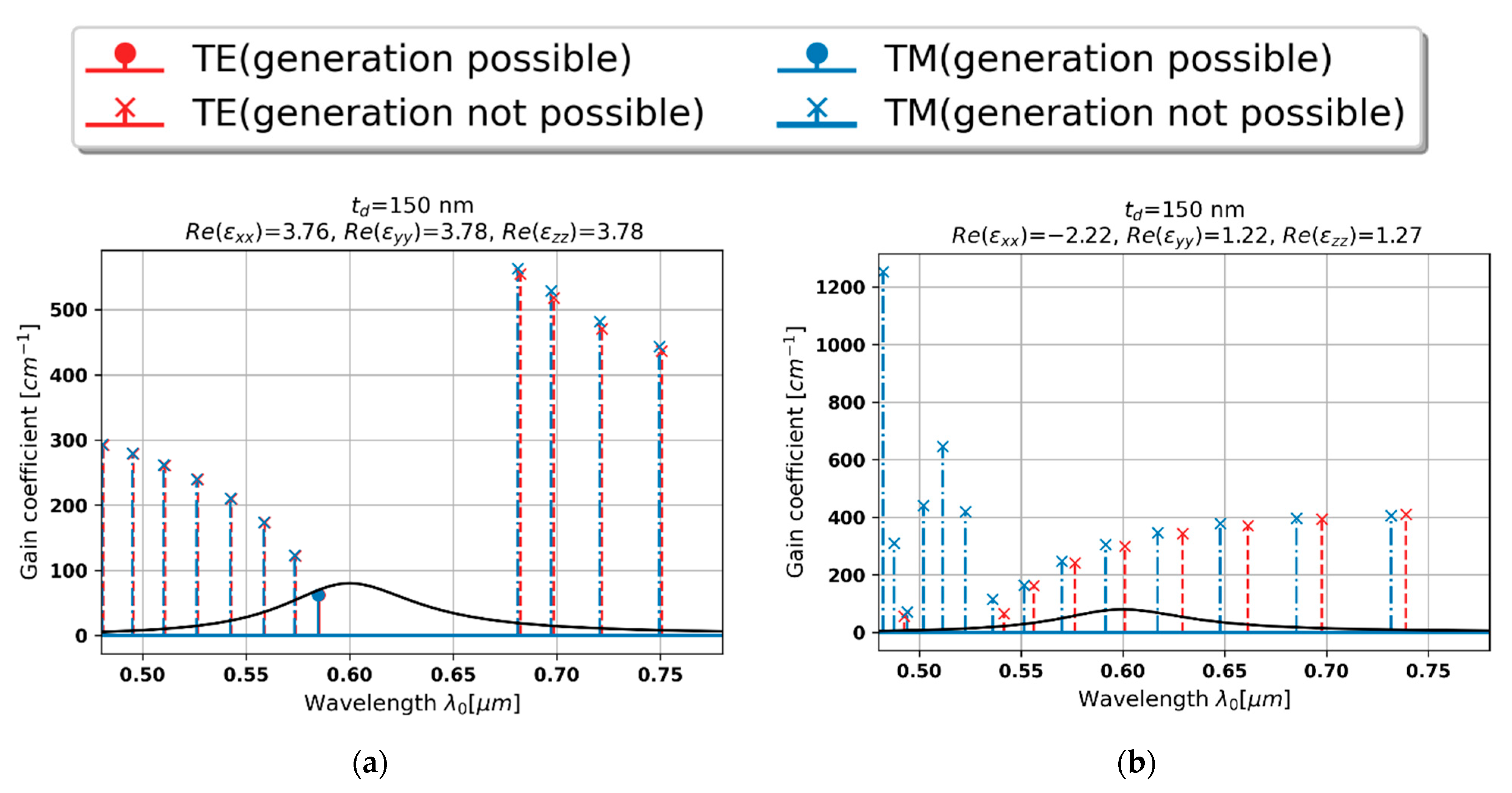
3.3. Local and Nonlocal Generation Spectra for a Realistic Gain Curve
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Belov, P.A.; Marqués, R.; Maslovski, S.I.; Nefedov, I.S.; Silveirinha, M.; Simovski, C.R.; Tretyakov, S.A. Strong Spatial Dispersion in Wire Media in the Very Large Wavelength Limit. Phys. Rev. B 2003, 67, 113103. [Google Scholar] [CrossRef]
- Raza, S.; Bozhevolnyi, S.I.; Wubs, M.; Asger Mortensen, N. Nonlocal Optical Response in Metallic Nanostructures. J. Phys. Condens. Matter 2015, 27, 183204. [Google Scholar] [CrossRef]
- Căbuz, A.I.; Felbacq, D.; Cassagne, D. Spatial Dispersion in Negative-Index Composite Metamaterials. Phys. Rev. A 2008, 77, 013807. [Google Scholar] [CrossRef]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Tymchenko, M.; Alù, A. Nonlocal Response of Hyperbolic Metasurfaces. Opt. Express 2015, 23, 29434. [Google Scholar] [CrossRef]
- Shalin, A.S.; Ginzburg, P.; Orlov, A.A.; Iorsh, I.; Belov, P.A.; Kivshar, Y.S.; Zayats, A.V. Scattering Suppression from Arbitrary Objects in Spatially Dispersive Layered Metamaterials. Phys. Rev. B 2015, 91, 125426. [Google Scholar] [CrossRef]
- Pollard, R.J.; Murphy, A.; Hendren, W.R.; Evans, P.R.; Atkinson, R.; Wurtz, G.A.; Zayats, A.V.; Podolskiy, V.A. Optical Nonlocalities and Additional Waves in Epsilon-Near-Zero Metamaterials. Phys. Rev. Lett. 2009, 102, 127405. [Google Scholar] [CrossRef]
- Wells, B.; Kudyshev, Z.A.; Litchinitser, N.; Podolskiy, V.A. Nonlocal Effects in Transition Hyperbolic Metamaterials. ACS Photonics 2017, 4, 2470–2478. [Google Scholar] [CrossRef]
- Janaszek, B.; Szczepański, P. Effect of Nonlocality in Spatially Uniform Anisotropic Metamaterials. Opt. Express 2020, 28, 15447. [Google Scholar] [CrossRef]
- Coppolaro, M.; Castaldi, G.; Galdi, V. Aperiodic Order Induced Enhancement of Weak Nonlocality in Multilayered Dielectric Metamaterials. Phys. Rev. B 2018, 98, 079904. [Google Scholar] [CrossRef]
- Savoia, S.; Castaldi, G.; Galdi, V. Optical Nonlocality in Multilayered Hyperbolic Metamaterials Based on Thue-Morse Superlattices. Phys. Rev. B 2013, 87, 235116. [Google Scholar] [CrossRef]
- Wurtz, G.A.; Pollard, R.; Hendren, W.; Wiederrecht, G.P.; Gosztola, D.J.; Podolskiy, V.A.; Zayats, A.V. Designed Ultrafast Optical Nonlinearity in a Plasmonic Nanorod Metamaterial Enhanced by Nonlocality. Nat. Nanotechnol. 2011, 6, 107–111. [Google Scholar] [CrossRef]
- Ginzburg, P.; Roth, D.J.; Nasir, M.E.; Segovia, P.; Krasavin, A.V.; Levitt, J.; Hirvonen, L.M.; Wells, B.; Suhling, K.; Richards, D.; et al. Spontaneous Emission in Non-Local Materials. Light Sci. Appl. 2017, 6, e16273. [Google Scholar] [CrossRef]
- Tarasenko, I.I.; Page, A.F.; Hamm, J.M.; Hess, O. Nonlocal Quantum Gain Facilitates Loss Compensation and Plasmon Amplification in Graphene Hyperbolic Metamaterials. Phys. Rev. B 2019, 99, 115430. [Google Scholar] [CrossRef]
- Lee, K.J.; Lee, Y.U.; Fages, F.; Ribierre, J.-C.; Wu, J.W.; D’Aléo, A. Blue-Shifting Intramolecular Charge Transfer Emission by Nonlocal Effect of Hyperbolic Metamaterials. Nano Lett. 2018, 18, 1476–1482. [Google Scholar] [CrossRef]
- Janaszek, B.; Kieliszczyk, M.; Tyszka-Zawadzka, A.; Szczepański, P. Influence of Nonlocality on Transmittance and Reflectance of Hyperbolic Metamaterials. Crystals 2020, 10, 577. [Google Scholar] [CrossRef]
- Janaszek, B.; Kieliszczyk, M.; Szczepański, P. Nonlocality-Enabled Magnetic Free Optical Isolation in Hyperbolic Metamaterials. Materials 2021, 14, 2865. [Google Scholar] [CrossRef]
- Xu, T.; Lezec, H.J. Visible-Frequency Asymmetric Transmission Devices Incorporating a Hyperbolic Metamaterial. Nat. Commun. 2014, 5, 4141. [Google Scholar] [CrossRef]
- Hu, H.; Gao, D.; Lin, X.; Hou, S.; Zhang, B.; Wang, Q.J.; Luo, Y. Directing Cherenkov Photons with Spatial Nonlocality. Nanophotonics 2020, 9, 3435–3442. [Google Scholar] [CrossRef]
- Hu, H.; Lin, X.; Zhang, J.; Liu, D.; Genevet, P.; Zhang, B.; Luo, Y. Nonlocality Induced Cherenkov Threshold. Laser Photonics Rev. 2020, 14, 2000149. [Google Scholar] [CrossRef]
- Narimanov, E.E. Photonic Hypercrystals. Phys. Rev. X 2014, 4, 041014. [Google Scholar] [CrossRef]
- Huang, Z.; Narimanov, E.E. Optical Imaging with Photonic Hyper-Crystals: Veselago Lens and Beyond. J. Opt. 2014, 16, 114009. [Google Scholar] [CrossRef]
- Ali, M.Z. Plasmon-Polariton Gap and Associated Phenomenon of Optical Bistability in Photonic Hypercrystals. Phys. Lett. A 2021, 387, 127026. [Google Scholar] [CrossRef]
- Wang, J.-R.; Chen, X.-D.; Zhao, F.-L.; Dong, J.-W. Full Polarization Conical Dispersion and Zero-Refractive-Index in Two-Dimensional Photonic Hypercrystals. Sci. Rep. 2016, 6, 22739. [Google Scholar] [CrossRef]
- Guo, S.; Hu, C.; Zhang, H. Unidirectional Ultrabroadband and Wide-Angle Absorption in Graphene-Embedded Photonic Crystals with the Cascading Structure Comprising the Octonacci Sequence. J. Opt. Soc. Am. B 2020, 37, 2678. [Google Scholar] [CrossRef]
- Janaszek, B.; Szczepański, P. Distributed Feedback Laser Based on Tunable Photonic Hypercrystal. Materials 2021, 14, 4065. [Google Scholar] [CrossRef]
- Janaszek, B.; Tyszka-Zawadzka, A.; Szczepański, P. Influence of Spatial Dispersion on Propagation Properties of Waveguides Based on Hyperbolic Metamaterial. Materials 2021, 14, 6885. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Liu, C.-H.; Liu, C.-H.; Zhang, S.; Marder, S.R.; Narimanov, E.E.; Zhong, Z.; Norris, T.B. Realization of Mid-Infrared Graphene Hyperbolic Metamaterials. Nat. Commun. 2016, 7, 10568. [Google Scholar] [CrossRef]
- Janaszek, B.; Kieliszczyk, M.; Tyszka-Zawadzka, A.; Szczepański, P. Multiresonance Response in Hyperbolic Metamaterials. Appl. Opt. 2018, 57, 2135. [Google Scholar] [CrossRef]
- Ferrari, L.; Wu, C.; Lepage, D.; Zhang, X.; Liu, Z. Hyperbolic Metamaterials and Their Applications. Prog. Quantum Electron. 2015, 40, 1–40. [Google Scholar] [CrossRef]
- Shekhar, P.; Atkinson, J.; Jacob, Z. Hyperbolic Metamaterials: Fundamentals and Applications. Nano Converg. 2014, 1, 14. [Google Scholar] [CrossRef]
- Pianelli, A.; Kowerdziej, R.; Dudek, M.; Sielezin, K.; Olifierczuk, M.; Parka, J. Graphene-Based Hyperbolic Metamaterial as a Switchable Reflection Modulator. Opt. Express 2020, 28, 6708. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y. Effective Medium Theory for Anisotropic Metamaterials. Sci Rep. 2015, 5, 7892. [Google Scholar] [CrossRef]
- Yan, W.; Asger Mortensen, N.; Wubs, M. Hyperbolic Metamaterial Lens with Hydrodynamic Nonlocal Response. Opt. Express 2013, 21, 15026. [Google Scholar] [CrossRef]
- Elser, J.; Podolskiy, V.A.; Salakhutdinov, I.; Avrutsky, I. Nonlocal Effects in Effective-Medium Response of Nanolayered Metamaterials. Appl. Phys. Lett. 2007, 90, 191109. [Google Scholar] [CrossRef]
- Chern, R.-L. Spatial Dispersion and Nonlocal Effective Permittivity for Periodic Layered Metamaterials. Opt. Express 2013, 21, 16514. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices, 2nd ed.; Dover Phoenix Editions with Corrections and Additions; Dover Publications: Mineola, NY, USA, 2003; ISBN 978-0-486-49556-9. [Google Scholar]
- Kang, X.-B.; Tan, W.; Wang, Z.-G. Validity of Effective Medium Theory for Metal-Dielectric Lamellar Gratings. Opt. Commun. 2011, 284, 4237–4242. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; ISBN 978-0-387-33150-8. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Cambridge University Press: Cambridge, MA, USA, 1999; ISBN 978-1-139-64418-1. [Google Scholar]
- Kogelnik, H.; Shank, C.V. Coupled-Wave Theory of Distributed Feedback Lasers. J. Appl. Phys. 1972, 43, 2327–2335. [Google Scholar] [CrossRef]
- Sultanova, N.; Kasarova, S.; Nikolov, I. Dispersion Properties of Optical Polymers. Acta Phys. Pol. A 2009, 116, 585–587. [Google Scholar] [CrossRef]
- Gozhyk, I.; Boudreau, M.; Haghighi, H.R.; Djellali, N.; Forget, S.; Chénais, S.; Ulysse, C.; Brosseau, A.; Pansu, R.; Audibert, J.-F.; et al. Gain Properties of Dye-Doped Polymer Thin Films. Phys. Rev. B 2015, 92, 214202. [Google Scholar] [CrossRef]
- Nedumpara, R.J.; Geetha, K.; Dann, V.J.; Vallabhan, C.P.G.; Nampoori, V.P.N.; Radhakrishnan, P. Light Amplification in Dye Doped Polymer Films. J. Opt. A Pure Appl. Opt. 2007, 9, 174–179. [Google Scholar] [CrossRef]
- Stelling, C.; Singh, C.R.; Karg, M.; König, T.A.F.; Thelakkat, M.; Retsch, M. Plasmonic Nanomeshes: Their Ambivalent Role as Transparent Electrodes in Organic Solar Cells. Sci. Rep. 2017, 7, 42530. [Google Scholar] [CrossRef]
- Shabani, A.; Nezhad, M.K.; Rahmani, N.; Mishra, Y.K.; Sanyal, B.; Adam, J. Revisiting the Optical Dispersion of Aluminum-Doped Zinc Oxide: New Perspectives for Plasmonics and Metamaterials. Adv. Photo Res. 2021, 2, 2000086. [Google Scholar] [CrossRef]
- Dimitrov, D.; Tsai, C.-L.; Petrov, S.; Marinova, V.; Petrova, D.; Napoleonov, B.; Blagoev, B.; Strijkova, V.; Hsu, K.Y.; Lin, S.H. Atomic Layer-Deposited Al-Doped ZnO Thin Films for Display Applications. Coatings 2020, 10, 539. [Google Scholar] [CrossRef]
- Mroczyński, R.; Iwanicki, D.; Fetliński, B.; Ożga, M.; Świniarski, M.; Gertych, A.; Zdrojek, M.; Godlewski, M. Optimization of Ultra-Thin Pulsed-DC Magnetron Sputtered Aluminum Films for the Technology of Hyperbolic Metamaterials. Crystals 2020, 10, 384. [Google Scholar] [CrossRef]
- DeRose, G.A.; Zhu, L.; Choi, J.M.; Poon, J.K.S.; Yariv, A.; Scherer, A. Two-Dimensional Bragg Grating Lasers Defined by Electron-Beam Lithography. J. Vac. Sci. Technol. B 2006, 24, 2926. [Google Scholar] [CrossRef][Green Version]
- Park, T.-H.; Kim, S.-M.; Oh, M.-C. Polymer-Waveguide Bragg-Grating Devices Fabricated Using Phase-Mask Lithography. Curr. Opt. Photonics 2019, 3, 401–407. [Google Scholar]
- Polman, A. Erbium Implanted Thin Film Photonic Materials. J. Appl. Phys. 1997, 82, 1–39. [Google Scholar] [CrossRef]
- Chinn, S. Effects of Mirror Reflectivity in a Distributed-Feedback Laser. IEEE J. Quantum Electron. 1973, 9, 574–580. [Google Scholar] [CrossRef]
- Zhang, S.; Holzapfel, W. Orthogonal Polarization in Lasers: Physical Phenomena and Engineering Applications; John Wiley & Sons, Inc.: Singapore, 2013; ISBN 978-1-118-34652-5. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janaszek, B.; Szczepański, P. Spatial Dispersion in Hypercrystal Distributed Feedback Lasing. Materials 2022, 15, 3482. https://doi.org/10.3390/ma15103482
Janaszek B, Szczepański P. Spatial Dispersion in Hypercrystal Distributed Feedback Lasing. Materials. 2022; 15(10):3482. https://doi.org/10.3390/ma15103482
Chicago/Turabian StyleJanaszek, Bartosz, and Paweł Szczepański. 2022. "Spatial Dispersion in Hypercrystal Distributed Feedback Lasing" Materials 15, no. 10: 3482. https://doi.org/10.3390/ma15103482
APA StyleJanaszek, B., & Szczepański, P. (2022). Spatial Dispersion in Hypercrystal Distributed Feedback Lasing. Materials, 15(10), 3482. https://doi.org/10.3390/ma15103482





