Burst Pressure Prediction of Subsea Supercritical CO2 Pipelines
Abstract
:1. Introduction
2. Unified Strength Theory
3. Mechanical Model of the Corroded Supercritical CO2 Pipeline
4. Equation for the Burst Pressure of the Corroded CO2 Pipeline
4.1. Stress Analysis
- q is an intermediate variable and ;
- k is an intermediate variable and .
4.2. Determination of Burst Pressure Equation Based on UST
4.3. Equations of Burst Pressure under Different Yield Criteria
4.3.1. The Burst Pressure Equation Based Tresca Criterion
4.3.2. The Burst Pressure Equation Based on the on Mises Criterion
4.3.3. The Burst Pressure Equation Based on the Zhu-Leis Flow Theory
4.3.4. The Burst Pressure Equation Based on the TS Criterion
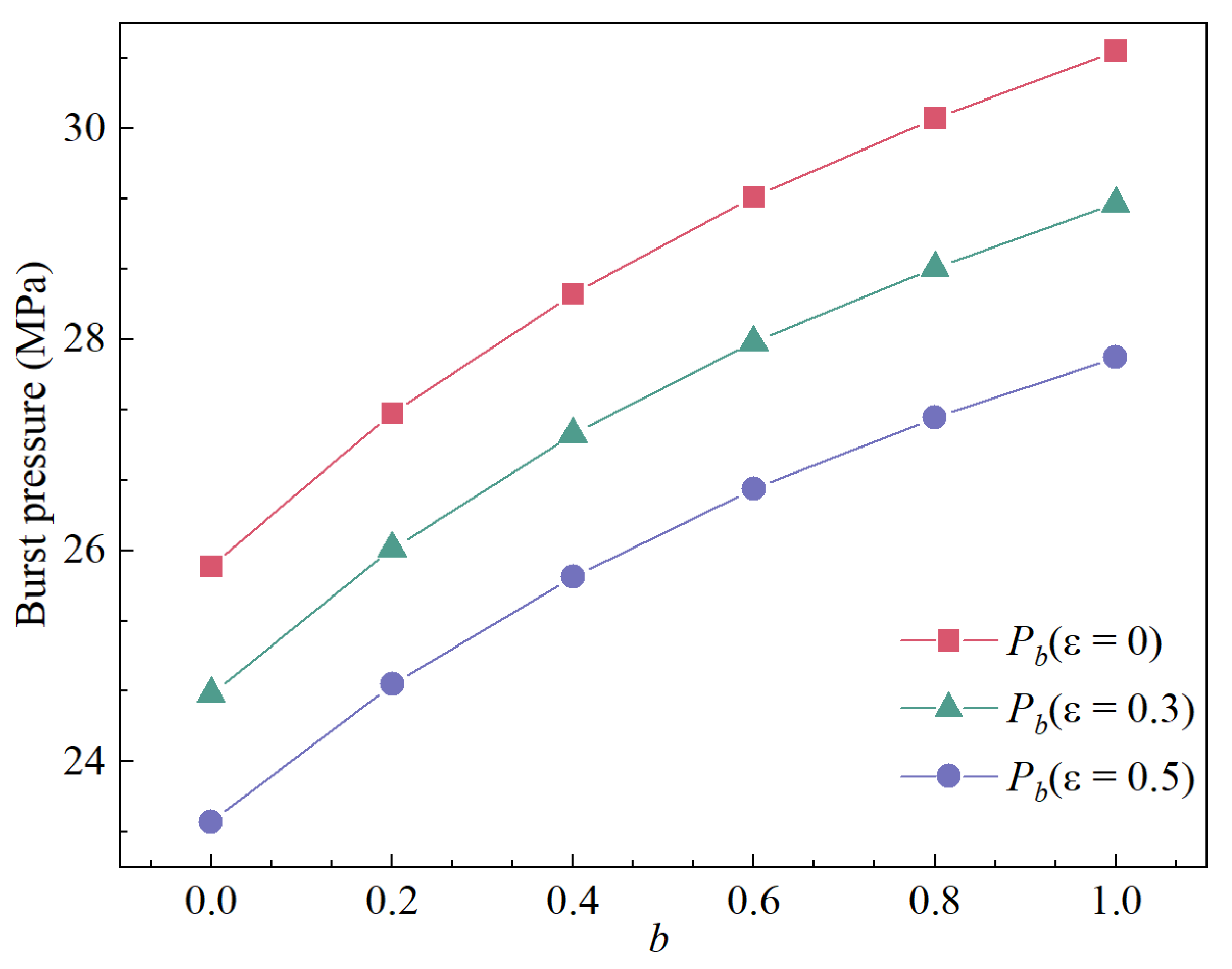
5. Influence of Parameter b on Burst Pressure
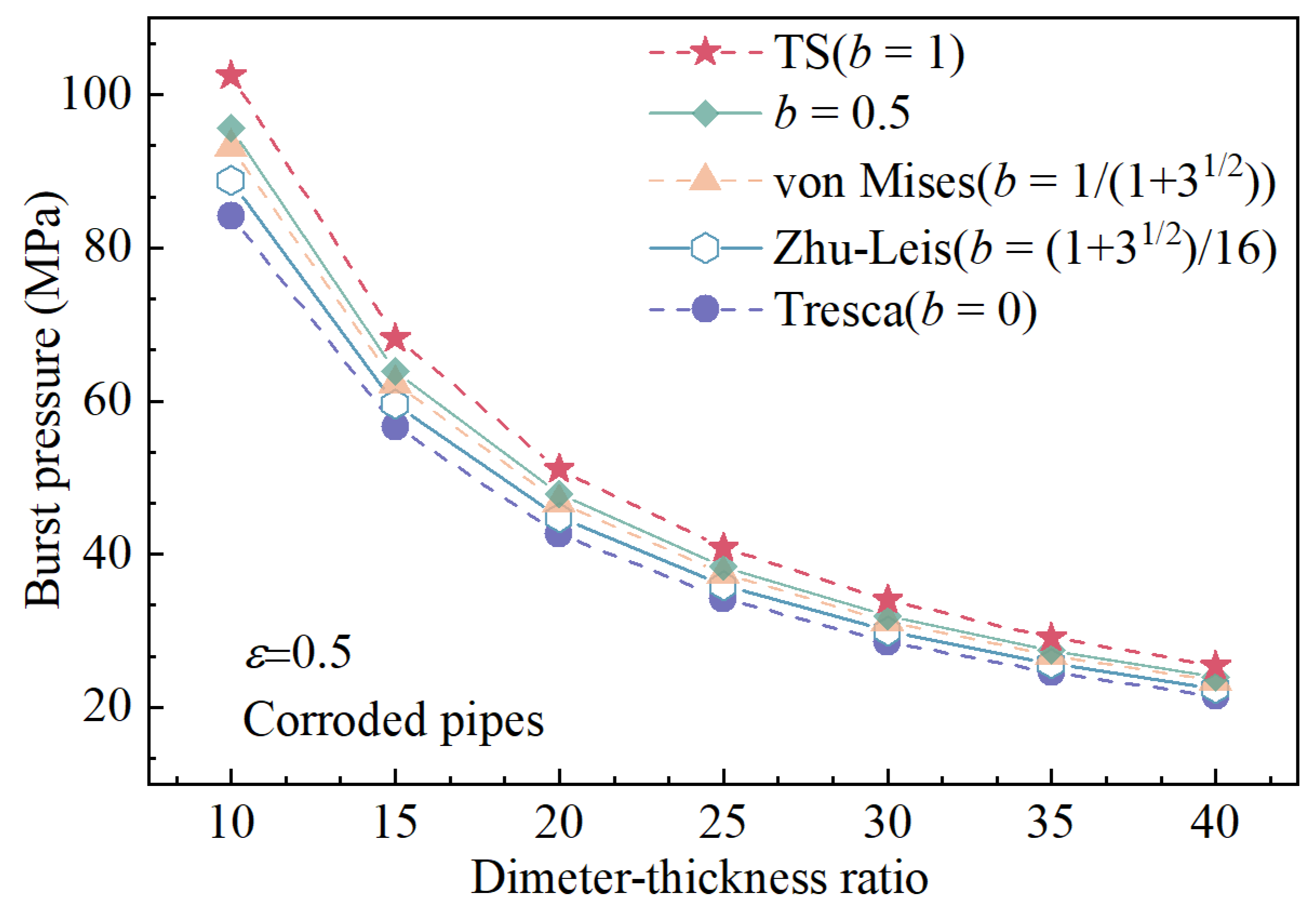
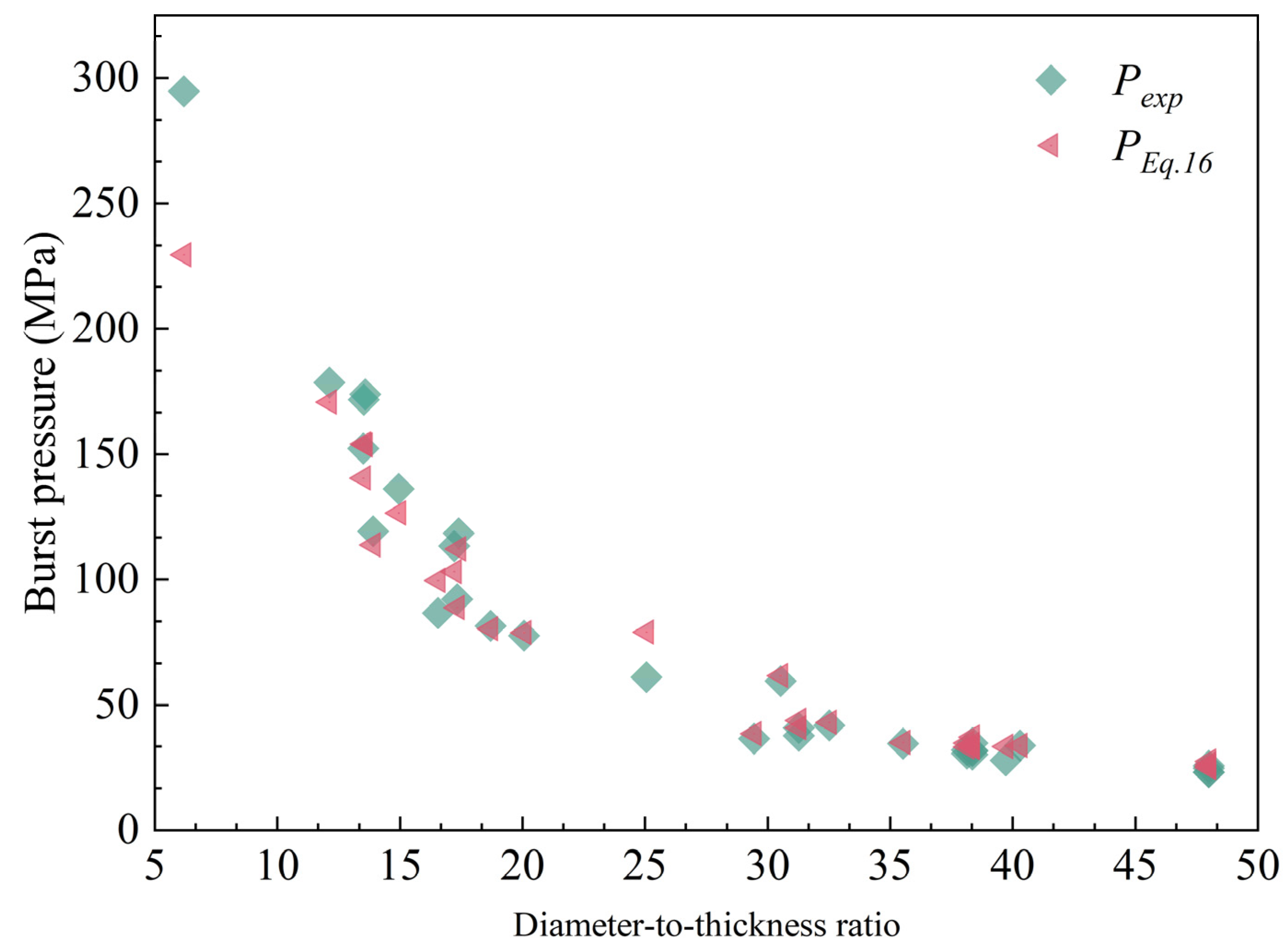
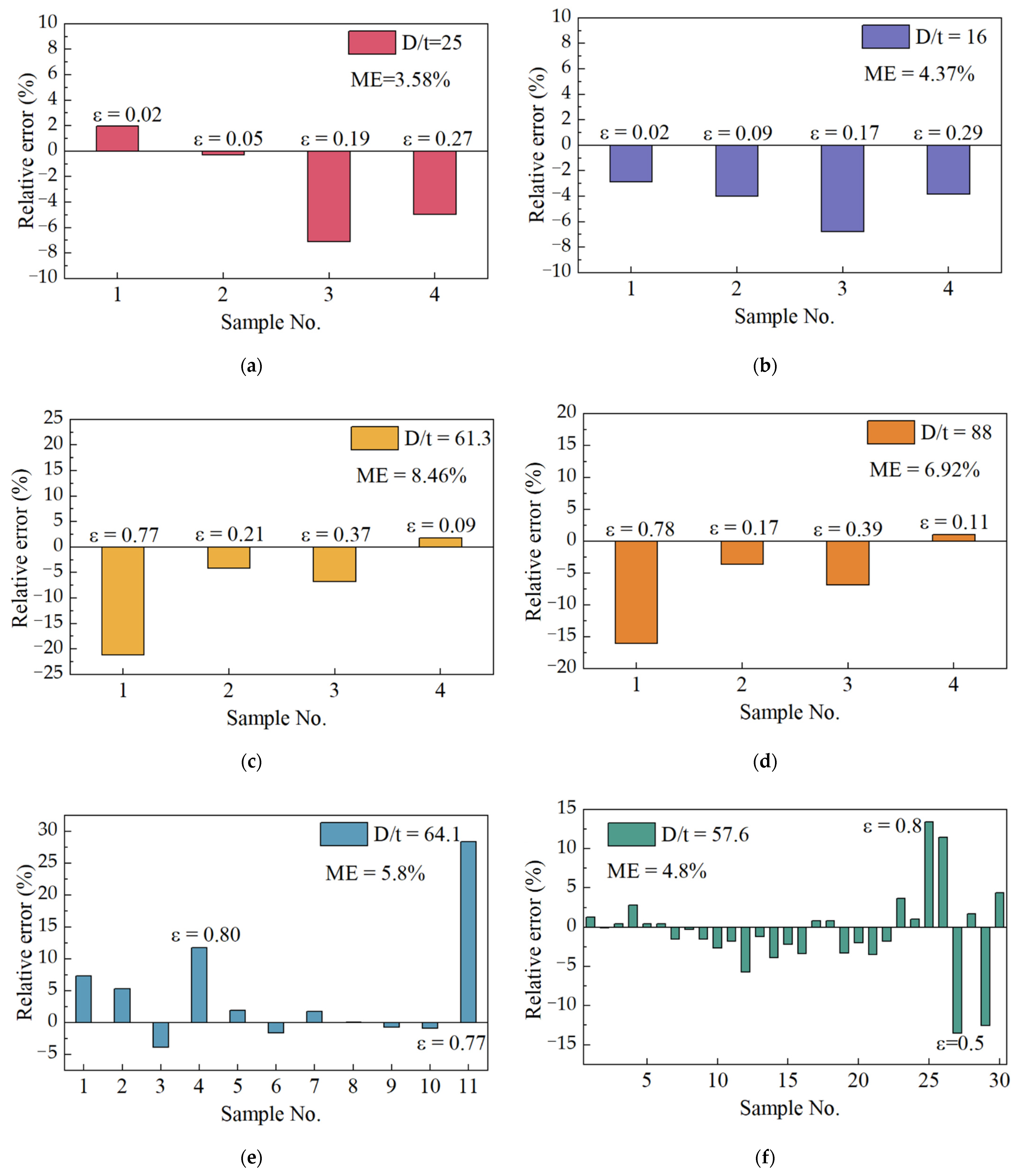
6. Validations and Discussions
6.1. Comparisons with Experimental Data for Unflawed Pipeline
6.2. Comparisons with Experimental Data for Corroded Pipelines
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Nomenclature
| First principal stress, second principal stress, third principal stress | |
| Radial stress, hoop stress, axial stress | |
| Coefficients in Equations (15) and (16) | |
| Coefficients in Equations (15) and (16) | |
| UST equivalent stress | |
| Shear strength and shear stress | |
| Yield-to-tensile strength ratio | |
| Influence coefficient of intermediate principal stress on material failure | |
| Thickness of an ideal pipeline | |
| Minimum wall thickness after corrosion | |
| Depth of corrosion defect | |
| Corrosion ratio | |
| Inner pressure, the burst pressure of the pipeline | |
| The ratio of thickness to diameter | |
| Poisson’s ratio | |
| Ultimate tensile strength, yield strength | |
| Variables in bipolar coordinate system | |
| Experimental bursting pressure | |
| q, k | Intermediate variable |
| Tensile strength | |
| The calculated burst pressure using Equation (15) in Table 2 and Appendix A | |
| The experimental data of burst pressure for the i-th sample | |
| N | The total number of experiments |
| Burst pressure calculated by Chen’s model. |
Appendix A
| No. | D (mm) | t (mm) | σy (MPa) | σu (MPa) | d (mm) | Pexp (MPa) | PEquation(15) (MPa) | Errors (PEquation (15)) | Errors (PChen) | Errors (PRAM) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 342 | 13.5 | 840 | 980 | 0.24 | 80.6 | 82.19 | 1.97% | 6.45% | 0.74% |
| 2 | 342 | 13.5 | 840 | 980 | 0.64 | 80.2 | 79.97 | −0.29% | 3.87% | −5.99% |
| 3 | 342 | 13.5 | 840 | 980 | 2.54 | 74.5 | 69.22 | −7.09% | −4.03% | −22.01% |
| 4 | 342 | 13.5 | 840 | 980 | 3.64 | 66.1 | 62.85 | −4.92% | −2.27% | −23.90% |
| 5 | 252 | 15.7 | 930 | 1070 | 0.33 | 143 | 138.9 | −2.87% | 5.94% | −2.66% |
| 6 | 252 | 15.7 | 930 | 1070 | 1.43 | 136 | 130.57 | −3.99% | 4.04% | −13.60% |
| 7 | 252 | 15.7 | 930 | 1070 | 2.63 | 130 | 121.23 | −6.75% | 0.31% | −22.08% |
| 8 | 252 | 15.7 | 930 | 1070 | 4.53 | 110 | 105.91 | −3.72% | 2.36% | −26.45% |
| 9 | 1219 | 19.9 | 585 | 715 | 15.41 | 7.6 | 5.99 | −21.18% | −25.00% | −40.79% |
| 10 | 1219 | 19.9 | 585 | 715 | 4.12 | 21.4 | 20.52 | −4.11% | −7.01% | −16.82% |
| 11 | 1219 | 19.9 | 592 | 723 | 7.44 | 17.7 | 16.51 | −6.72% | −9.60% | −23.73% |
| 12 | 1219 | 19.9 | 592 | 723 | 1.77 | 23.3 | 23.71 | 1.76% | −0.86% | −6.87% |
| 13 | 1219 | 13.8 | 568 | 705 | 10.78 | 4.7 | 3.94 | −16.17% | −21.28% | −34.04% |
| 14 | 1219 | 13.8 | 568 | 705 | 2.3 | 15.3 | 14.74 | −3.66% | −7.84% | −13.73% |
| 15 | 1219 | 13.8 | 589 | 731 | 5.45 | 12 | 11.17 | −6.92% | −10.83% | −21.67% |
| 16 | 1219 | 13.8 | 589 | 731 | 1.54 | 16.1 | 16.27 | 1.06% | −3.11% | −8.07% |
| 17 | 1320 | 22.9 | 782 | 803 | 2.52 | 27 | 27.35 | 1.30% | 7.04% | −8.52% |
| 18 | 1320 | 22.9 | 782 | 803 | 2.27 | 27.7 | 27.67 | −0.11% | 5.78% | −9.03% |
| 19 | 1320 | 22.9 | 782 | 803 | 2.31 | 27.5 | 27.62 | 0.44% | 6.18% | −8.73% |
| 20 | 1320 | 22.9 | 782 | 803 | 6.73 | 21.3 | 21.89 | 2.77% | 7.98% | −14.08% |
| 21 | 1320 | 22.9 | 782 | 803 | 6.73 | 21.8 | 21.89 | 0.41% | 5.50% | −16.06% |
| 22 | 1320 | 22.9 | 782 | 803 | 6.57 | 22 | 22.1 | 0.45% | 5.45% | −15.91% |
| 23 | 1320 | 22.9 | 782 | 803 | 11.45 | 15.9 | 15.66 | −1.51% | 3.14% | −22.64% |
| 24 | 1320 | 22.9 | 782 | 803 | 11.45 | 15.7 | 15.66 | −0.25% | 4.46% | −21.66% |
| 25 | 1320 | 22.9 | 782 | 803 | 11.45 | 15.9 | 15.66 | −1.51% | 3.14% | −22.64% |
| 26 | 1320 | 22.9 | 782 | 803 | 18.55 | 6.2 | 6.04 | −2.58% | 1.61% | −29.03% |
| 27 | 1320 | 22.9 | 782 | 803 | 19.01 | 5.5 | 5.41 | −1.64% | 1.82% | −27.27% |
| 28 | 1320 | 22.9 | 782 | 803 | 18.55 | 6.4 | 6.04 | −5.63% | −1.56% | −31.25% |
| 29 | 1320 | 20.6 | 782 | 803 | 2.06 | 23.2 | 24.89 | 7.28% | 13.36% | −2.16% |
| 30 | 1320 | 20.6 | 782 | 803 | 5.89 | 18.9 | 19.91 | 5.34% | 10.58% | −11.11% |
| 31 | 1320 | 20.6 | 782 | 803 | 11.33 | 13.2 | 12.69 | −3.86% | 0.00% | −24.24% |
| 32 | 1320 | 20.6 | 782 | 803 | 16.48 | 5.1 | 5.7 | 11.76% | 15.69% | −15.69% |
| 33 | 1320 | 22.9 | 782 | 803 | 4.58 | 25 | 24.69 | −1.24% | 4.00% | −14.40% |
| 34 | 1320 | 22.9 | 782 | 803 | 4.58 | 25.7 | 24.69 | −3.93% | 1.17% | −16.73% |
| 35 | 1320 | 22.9 | 782 | 803 | 11.45 | 16 | 15.66 | −2.13% | 2.50% | −23.13% |
| 36 | 1320 | 22.9 | 782 | 803 | 11.45 | 16.2 | 15.66 | −3.33% | 1.23% | −24.07% |
| 37 | 1320 | 22.9 | 782 | 803 | 18.32 | 6.3 | 6.36 | 0.95% | 4.76% | −25.40% |
| 38 | 1320 | 22.9 | 782 | 803 | 18.32 | 6.3 | 6.36 | 0.95% | 4.76% | −25.40% |
| 39 | 1320 | 20.6 | 782 | 803 | 4.12 | 21.8 | 22.22 | 1.93% | 7.34% | −11.01% |
| 40 | 1320 | 20.6 | 782 | 803 | 10.3 | 14.3 | 14.07 | −1.61% | 2.80% | −21.68% |
| 41 | 1320 | 20.6 | 782 | 803 | 16.85 | 5.1 | 5.19 | 1.76% | 5.88% | −23.53% |
| 42 | 1320 | 22.9 | 782 | 803 | 2.29 | 28.6 | 27.65 | −3.32% | 2.10% | −12.24% |
| 43 | 1320 | 22.9 | 782 | 803 | 2.29 | 28.2 | 27.65 | −1.95% | 3.55% | −10.99% |
| 44 | 1320 | 22.9 | 782 | 803 | 6.87 | 22.5 | 21.71 | −3.51% | 1.33% | −19.56% |
| 45 | 1320 | 22.9 | 782 | 803 | 6.87 | 22.1 | 22.71 | 2.76% | 3.17% | −18.10% |
| 46 | 1320 | 22.9 | 782 | 803 | 11.45 | 15.1 | 15.66 | 3.71% | 8.61% | −18.54% |
| 47 | 1320 | 22.9 | 782 | 803 | 11.45 | 15.5 | 15.66 | 1.03% | 5.81% | −20.65% |
| 48 | 1320 | 22.9 | 782 | 803 | 18.32 | 5.6 | 6.36 | 13.57% | 17.86% | −16.07% |
| 49 | 1320 | 22.9 | 782 | 803 | 18.32 | 5.7 | 6.36 | 11.58% | 15.79% | −17.54% |
| 50 | 1320 | 20.6 | 782 | 803 | 2.27 | 24.6 | 24.62 | 0.08% | 5.69% | −9.35% |
| 51 | 1320 | 20.6 | 782 | 803 | 6.39 | 19.4 | 19.25 | −0.77% | 4.12% | −16.49% |
| 52 | 1320 | 20.6 | 782 | 803 | 10.3 | 14.2 | 14.07 | −0.92% | 3.52% | −21.13% |
| 53 | 1320 | 20.6 | 782 | 803 | 15.86 | 5.1 | 6.55 | 28.43% | 33.33% | −3.92% |
| 54 | 1320 | 22.9 | 782 | 803 | 11.45 | 18.1 | 15.66 | −13.48% | −9.39% | −32.04% |
| 55 | 1320 | 22.9 | 782 | 803 | 11.45 | 15.4 | 15.66 | 1.69% | 6.49% | −20.13% |
| 56 | 1320 | 22.9 | 782 | 803 | 11.45 | 17.9 | 15.66 | −12.51% | −8.38% | −31.28% |
| 57 | 1320 | 22.9 | 782 | 803 | 11.45 | 15 | 15.66 | 4.40% | 9.33% | −18.00% |
References
- Vitali, M.; Zuliani, C.; Corvaro, F.; Marchetti, B.; Terenzi, A.; Tallone, F. Risks and Safety of CO2 Transport via Pipeline: A Review of Risk Analysis and Modeling Approaches for Accidental Releases. Energies 2021, 14, 4601. [Google Scholar] [CrossRef]
- Vitali, M.; Corvaro, F.; Marchetti, B.; Terenzi, A. Thermodynamic challenges for CO2 pipelines design: A critical review on the effects of impurities, water content, and low temperature. Int. J. Greenh. Gas Control 2022, 114, 103605. [Google Scholar] [CrossRef]
- Peletiri, S.; Rahmanian, N.; Mujtaba, I. CO2 Pipeline Design: A Review. Energies 2018, 11, 2184. [Google Scholar] [CrossRef] [Green Version]
- Onyebuchi, V.; Kolios, A.; Hanak, D.; Biliyok, C.; Manovic, V. A systematic review of key challenges of CO2 transport via pipelines. Renew. Sustain. Energy Rev. 2018, 81, 2563–2583. [Google Scholar] [CrossRef] [Green Version]
- Bilio, M.; Brown, S.; Fairweather, M.; Mahgerefteh, H. CO2 pipelines material and safety considerations. Hazards XXI: Process Safety and Environmental Protection in a Changing World. Inst. Chem. Eng. 2009, 155, 423–429. [Google Scholar]
- Gao, J.; Yang, P.; Li, X.; Zhou, J.; Liu, J. Analytical prediction of failure pressure for pipeline with long corrosion defect. Ocean Eng. 2019, 191, 106497. [Google Scholar] [CrossRef]
- Porter, R.T.; Fairweather, M.; Pourkashanian, M.; Woolley, R.M. The range and level of impurities in CO2 streams from different carbon capture sources. Int. J. Greenh. Gas Control 2015, 36, 161–174. [Google Scholar] [CrossRef]
- Provided by Global CCS Institute: Transport Overview. Available online: https://www.globalccsinstitute.com/resources/ccs-image-library/ (accessed on 13 December 2019).
- Shuai, Y.; Wang, X.-H.; Li, J.; Wang, J.-Q.; Wang, T.-T.; Han, J.-Y.; Cheng, Y.F. Assessment by finite element modelling of the mechano-electrochemical interaction at corrosion defect on elbows of oil/gas pipelines. Ocean Eng. 2021, 234, 109228. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Han, Y.; Xia, M.; Zheng, W. A semi-empirical model for peak strain prediction of buried X80 steel pipelines under compression and bending at strike-slip fault crossings. J. Nat. Gas Sci. Eng. 2016, 32, 465–475. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Wu, K.; Xia, M.; Chen, Y.; Li, M. Buckling failure mode analysis of buried X80 steel gas pipeline under reverse fault displacement. Eng. Fail. Anal. 2017, 77, 50–64. [Google Scholar] [CrossRef]
- ASME. B31G-2009 Manual for Determining the Remaining Strength of Corroded Pipelines. In Supplement to ASME B31G Code for Pressure Piping; The American Society of Mechanical Engineers: New York, NY, USA, 2009. [Google Scholar]
- Bjornoy, O.; Fu, B.; Sigurdsson, G.; Cramer, E.; Ritchie, D. Introduction and background to DNV RP-F101 Corroded Pipelines. In Proceedings of the International Offshore and Polar Engineering Conference, Brest, France, 30 May 1999. [Google Scholar]
- CSA Standard Z662–07; Oil and Gas Pipeline Systems. Canadian Standards Association: Mississauga, ON, USA, 2007.
- Stephens, B.N.L.D.R. An Alternative Approach to Assess the Integrity of Corroded Line Pipe—Part I: Current Status. In Proceedings of the Seventh International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 27 May 1997. [Google Scholar]
- Liu, X.; Xia, M.; Bolati, D.; Liu, J.; Zheng, Q.; Zhang, H. An ANN-based failure pressure prediction method for buried high-strength pipes with stray current corrosion defect. Energy Sci. Eng. 2019, 8, 248–259. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, Q.; Wu, K.; Yang, Y.; Zhao, Z.; Zhang, H. Development of a novel approach for strain demand prediction of pipes at fault crossings on the basis of multi-layer neural network driven by strain data. Eng. Struct. 2020, 214, 110685. [Google Scholar] [CrossRef]
- Klever, F.J.; Stewart, G.; Valk, C.A.C.v.d. New developments in burst strength predictions for locally corroded pipelines. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Copenhagen, Denmark, 18–22 June 1995; pp. 161–173. [Google Scholar]
- Klever, F.J. Burst Strength of Corroded Pipe: “Flow Stress” Revisited. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4 May 1992. [Google Scholar]
- Christopher, T.; Sarma, B.S.V.R.; Potti, P.K.G.; Rao, B.N.; Sankarnarayanasamy, K. A comparative study on failure pressure estimations of unflawed cylindrical vessels. Press. Vessel. Pip. 2002, 79, 53–66. [Google Scholar] [CrossRef]
- Zhu, X.-K.; Leis, B.N. Average shear stress yield criterion and its application to plastic collapse analysis of pipelines. Int. J. Press. Vessel. Pip. 2006, 83, 663–671. [Google Scholar] [CrossRef]
- Zhu, X.-K.; Leis, B.N. Analytic Prediction of Plastic Collapse Failure Pressure of Line Pipes. In Proceedings of the ASME 2005 Pressure Vessels and Piping Conference, Ann Arbor, MI, USA, 17–21 July 2005; pp. 109–118. [Google Scholar]
- Zhu, X.-K.; Leis, B.N. Evaluation of burst pressure prediction models for line pipes. Int. J. Press. Vessel. Pip. 2012, 89, 85–97. [Google Scholar] [CrossRef]
- Law, M.; Bowie, G. Prediction of failure strain and burst pressure in high yield-to-tensile strength ratio linepipe. Int. J. Press. Vessel. Pip. 2007, 84, 487–492. [Google Scholar] [CrossRef]
- Yu, M.H. Advances in strength theories for materials under complex stress state in the 20th century. Appl. Mech. Rev. 2002, 55, 169–218. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y. Plastic collapse analysis of thin-walled pipes based on unified yield criterion. Int. J. Mech. Sci. 2011, 53, 348–354. [Google Scholar] [CrossRef]
- Lin, Y.; Deng, K.; Sun, Y.; Zeng, D.; Xia, T. Through-wall yield collapse pressure of casing based on unified strength theory. Pet. Explor. Dev. 2016, 43, 506–513. [Google Scholar] [CrossRef]
- Kuanhai, D.; Yang, P.; Bing, L.; Yuanhua, L.; Jiandong, W. Through-wall yield ductile burst pressure of high-grade steel tube and casing with and without corroded defect. Mar. Struct. 2021, 76. [Google Scholar] [CrossRef]
- Kuanhai, D.; Yuanhua, L.; Bing, L.; Xiaohong, W. Investigation on the calculation model of burst pressure for tube and casing under practical service environment. Int. J. Hydrogen Energy 2019, 44, 23277–23288. [Google Scholar] [CrossRef]
- Zhang, S.H.; Liu, J.R.; Liu, X.Y. A weighted unification yield criterion and its application in analysis of burst pressure of pipe elbow. Int. J. Press. Vessel. Pip. 2021, 194, 104561. [Google Scholar] [CrossRef]
- Kuanhai, D.; Jialian, L.; Bin, L.; Lin, P.; Wanying, L.; Yuanhua, L. Study of internal pressure strength of the titanium-steel composite tube based on yield and shear failure mechanisms. Int. J. Hydrogen Energy 2019, 44, 2997–3012. [Google Scholar] [CrossRef]
- Chen, Z.-F.; Chu, W.-P.; Wang, H.-J.; Li, Y.; Wang, W.; Meng, W.-M.; Li, Y.-X. Structural integrity assessment of hydrogen-mixed natural gas pipelines based on a new multi-parameter failure criterion. Ocean Eng. 2022, 247, 110731. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, W.; Di, Q.; Wang, W. Prediction of Burst Pressure of Pipes With Geometric Eccentricity. J. Press. Vessel Technol. 2015, 137. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zhu, W.; Di, Q.; Li, S. Numerical and theoretical analysis of burst pressures for casings with eccentric wear. J. Pet. Sci. Eng. 2016, 145, 585–591. [Google Scholar] [CrossRef] [Green Version]
- Lyons, C.J.; Race, J.M.; Wetenhall, B.; Chang, E.; Hopkins, H.F.; Barnett, J. Assessment of the Applicability of Failure Frequency Models for Dense Phase Carbon Dioxide Pipelines. Int. J. Greenh. Gas Control 2019, 87, 112–120. [Google Scholar] [CrossRef]
- Yu, M.H.; He, L.N. A new model and theory on yield and failure of materials under the complex stress state. In Proceedings of the Mechanical Behaviour of Materials VI Proceedings of the Sixth International Conference, Kyoto, Japan, 29 July–August 1991; Volume 4, pp. 841–846. [Google Scholar]
- Netto, T.A.; Ferraz, U.S.; Estefen, S.F. The effect of corrosion defects on the burst pressure of pipelines. J. Constr. Steel Res. 2005, 61, 1185–1204. [Google Scholar] [CrossRef]
- Fekete, G.; Varga, L. The effect of the width to length ratios of corrosion defects on the burst pressures of transmission pipelines. Eng. Fail. Anal. 2012, 21, 21–30. [Google Scholar] [CrossRef]
- Qian, G.; Niffenegger, M.; Zhou, W.; Li, S. Effect of correlated input parameters on the failure probability of pipelines with corrosion defects by using FITNET FFS procedure. Int. J. Press. Vessel. Pip. 2013, 105–106, 19–27. [Google Scholar] [CrossRef]
- Al-Owaisi, S.; Becker, A.A.; Sun, W.; Al-Shabibi, A.; Al-Maharbi, M.; Pervez, T.; Al-Salmi, H. An experimental investigation of the effect of defect shape and orientation on the burst pressure of pressurised pipes. Eng. Fail. Anal. 2018, 93, 200–213. [Google Scholar] [CrossRef]
- Shuai, Y.; Wang, X.-H.; Feng, C.; Zhu, Y.; Wang, C.-L.; Sun, T.; Han, J.; Cheng, Y.F. A novel strain-based assessment method of compressive buckling of X80 corroded pipelines subjected to bending moment load. Thin-Walled Struct. 2021, 167, 108172. [Google Scholar] [CrossRef]
- Yu, M.-H. Unified Strength Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Bilio, S.B.M.; Fairweather, M.; Mahgerefteh, H. CO2 pipelines material and safety considerations. In Proceedings of the 2009 IChemE, London, UK, 9–12 November 2009. [Google Scholar]
- Abdalla Filho, J.E.; Machado, R.D.; Bertin, R.J.; Valentini, M.D. On the failure pressure of pipelines containing wall reduction and isolated pit corrosion defects. Comput. Struct. 2014, 132, 22–33. [Google Scholar] [CrossRef]
- Huang, X.; Chen, Y.; Lin, K.; Mihsein, M.; Kibble, K.; Hall, R. Burst Strength Analysis of Casing With Geometrical Imperfections. J. Press. Vessel Technol. 2006, 129, 763–770. [Google Scholar] [CrossRef]
- Bhardwaj, U.; Teixeira, A.P.; Guedes Soares, C.; Azad, M.S.; Punurai, W.; Asavadorndeja, P. Reliability assessment of thick high strength pipelines with corrosion defects. Int. J. Press. Vessel. Pip. 2019, 177, 103982. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, S.; Ye, H.; Shen, X.; Jin, Z. Effect of the Y/T on the burst pressure for corroded pipelines with high strength. J. Pet. Sci. Eng. 2017, 157, 760–766. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Steel grade | X65 |
| Yield strength (/MPa) | 467 |
| Ultimate tensile strength (/MPa) | 576 |
| Diameter (mm) | 762 |
| Wall-thickness (mm) | 17.5 |
| No. | D (mm) | t (mm) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 912 | 19 | 457.8 | 546.0 | 23.11 | 24.90 | 1.08 |
| 2 | 912 | 19 | 426.7 | 578.0 | 23.17 | 26.36 | 1.14 |
| 3 | 912 | 19 | 517.1 | 559.0 | 24.85 | 25.49 | 1.03 |
| 4 | 912 | 19 | 508.8 | 604.0 | 25.80 | 27.55 | 1.07 |
| 5 | 893.7 | 22.5 | 526.0 | 608.0 | 27.93 | 33.40 | 1.20 |
| 6 | 609.6 | 15.9 | 501.2 | 581.0 | 30.20 | 33.05 | 1.09 |
| 7 | 762.4 | 20 | 531.5 | 608.0 | 30.63 | 34.78 | 1.14 |
| 8 | 609.6 | 15.9 | 511.5 | 600.0 | 31.72 | 34.13 | 1.08 |
| 9 | 609.6 | 15.9 | 440.5 | 585.0 | 31.76 | 33.27 | 1.05 |
| 10 | 762.4 | 20 | 555.0 | 580.0 | 31.95 | 33.18 | 1.04 |
| 11 | 544.05 | 13.5 | 623.9 | 624.0 | 33.84 | 33.80 | 1.00 |
| 12 | 507.93 | 14.3 | 508.8 | 571.0 | 34.50 | 35.00 | 1.01 |
| 13 | 609.6 | 15.9 | 534.3 | 653.0 | 34.79 | 37.14 | 1.07 |
| 14 | 397.6 | 13.5 | 364.0 | 523.0 | 36.50 | 38.50 | 1.05 |
| 15 | 591.2 | 18.9 | 563.0 | 589.0 | 37.68 | 40.88 | 1.08 |
| 16 | 591.2 | 18.9 | 607.0 | 630.0 | 40.79 | 43.73 | 1.07 |
| 17 | 591.8 | 18.2 | 636.0 | 645.0 | 41.76 | 43.11 | 1.03 |
| 18 | 390.8 | 12.8 | 807.0 | 869.0 | 59.60 | 61.76 | 1.04 |
| 19 | 247.1 | 9.86 | 641.1 | 916.9 | 61.08 | 78.96 | 1.29 |
| 20 | 179.4 | 8.94 | 468.8 | 737.7 | 77.70 | 78.73 | 1.01 |
| 21 | 252.4 | 13.5 | 606.7 | 703.2 | 81.56 | 80.32 | 0.98 |
| 22 | 162.2 | 9.8 | 602.0 | 776.0 | 86.60 | 99.57 | 1.15 |
| 23 | 180.3 | 10.4 | 613.6 | 723.8 | 92.17 | 88.86 | 0.96 |
| 24 | 67.3 | 3.91 | 689.4 | 834.2 | 113.34 | 103.12 | 0.91 |
| 25 | 179.1 | 10.3 | 848.0 | 916.9 | 118.51 | 112.24 | 0.95 |
| 26 | 90.35 | 6.5 | 696.3 | 751.4 | 119.27 | 113.74 | 0.95 |
| 27 | 179.6 | 12.01 | 779.0 | 896.2 | 136.09 | 126.61 | 0.93 |
| 28 | 179.5 | 13.3 | 834.2 | 903.1 | 152.29 | 140.54 | 0.92 |
| 29 | 198.9 | 14.7 | 903.1 | 992.7 | 171.66 | 154.11 | 0.90 |
| 30 | 198.2 | 14.6 | 903.1 | 992.7 | 173.80 | 153.64 | 0.88 |
| 31 | 180.6 | 14.9 | 903.1 | 992.7 | 178.55 | 170.82 | 0.96 |
| 32 | 89 | 14.4 | 606.7 | 730.8 | 294.65 | 229.47 | 0.78 |
| Mean | 1.03 |
| Comparison Results | PEquation(15) | PChen | PRAM |
|---|---|---|---|
| ME | 4.57% | 6.7% | 18.1% |
| SD | 0.055 | 0.062 | 0.084 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, W.; Chen, Z.; Chu, W.; Wang, H.; Yang, H.; Wang, C.; Li, Y. Burst Pressure Prediction of Subsea Supercritical CO2 Pipelines. Materials 2022, 15, 3465. https://doi.org/10.3390/ma15103465
Li Y, Wang W, Chen Z, Chu W, Wang H, Yang H, Wang C, Li Y. Burst Pressure Prediction of Subsea Supercritical CO2 Pipelines. Materials. 2022; 15(10):3465. https://doi.org/10.3390/ma15103465
Chicago/Turabian StyleLi, Yan, Wen Wang, Zhanfeng Chen, Weipeng Chu, Huijie Wang, He Yang, Chuanyong Wang, and Yuxing Li. 2022. "Burst Pressure Prediction of Subsea Supercritical CO2 Pipelines" Materials 15, no. 10: 3465. https://doi.org/10.3390/ma15103465
APA StyleLi, Y., Wang, W., Chen, Z., Chu, W., Wang, H., Yang, H., Wang, C., & Li, Y. (2022). Burst Pressure Prediction of Subsea Supercritical CO2 Pipelines. Materials, 15(10), 3465. https://doi.org/10.3390/ma15103465







