Influence of Temperature on Void Collapse in Single Crystal Nickel under Hydrostatic Compression
Abstract
1. Introduction
2. Simulation Method
3. Results and Discussion
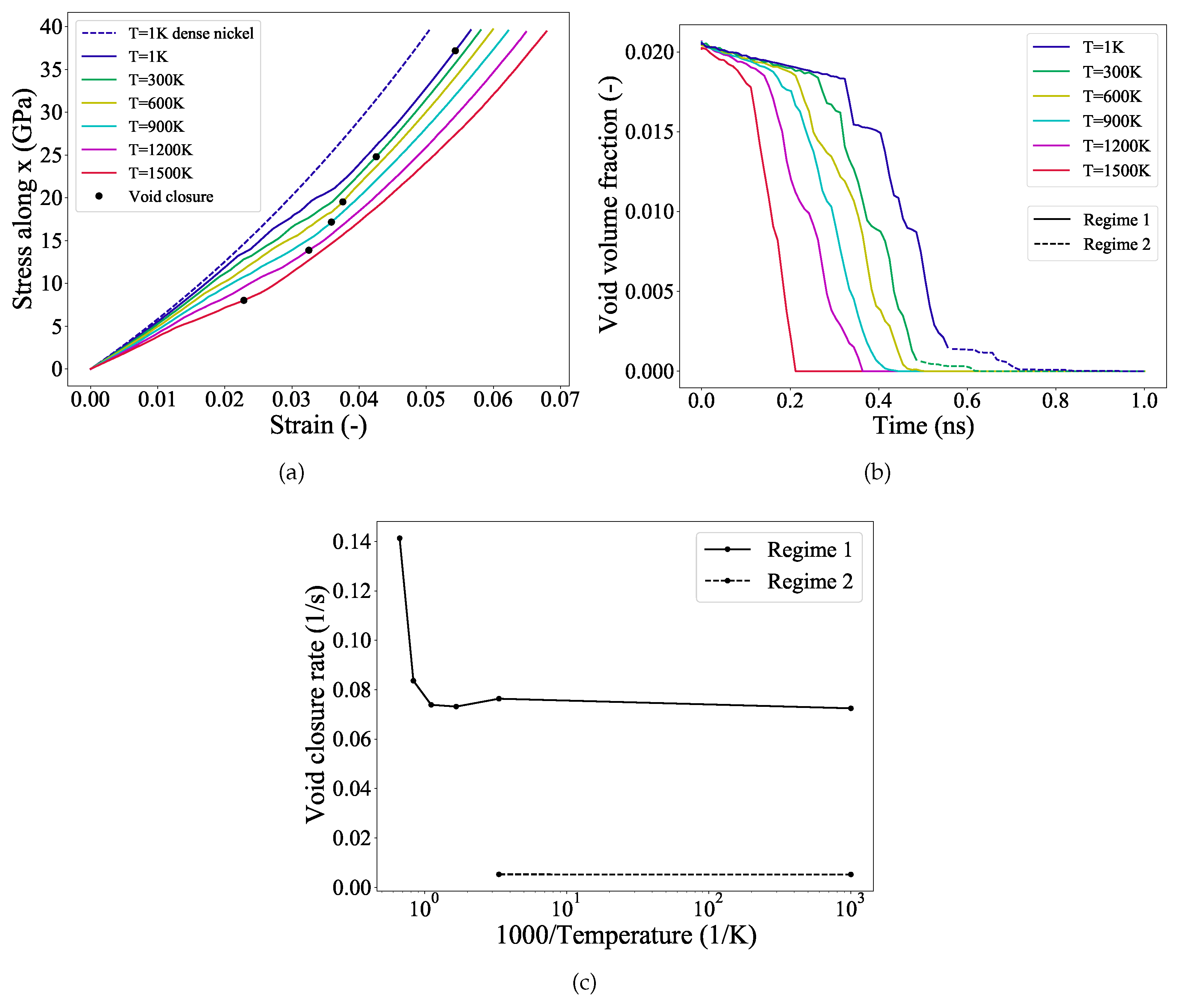
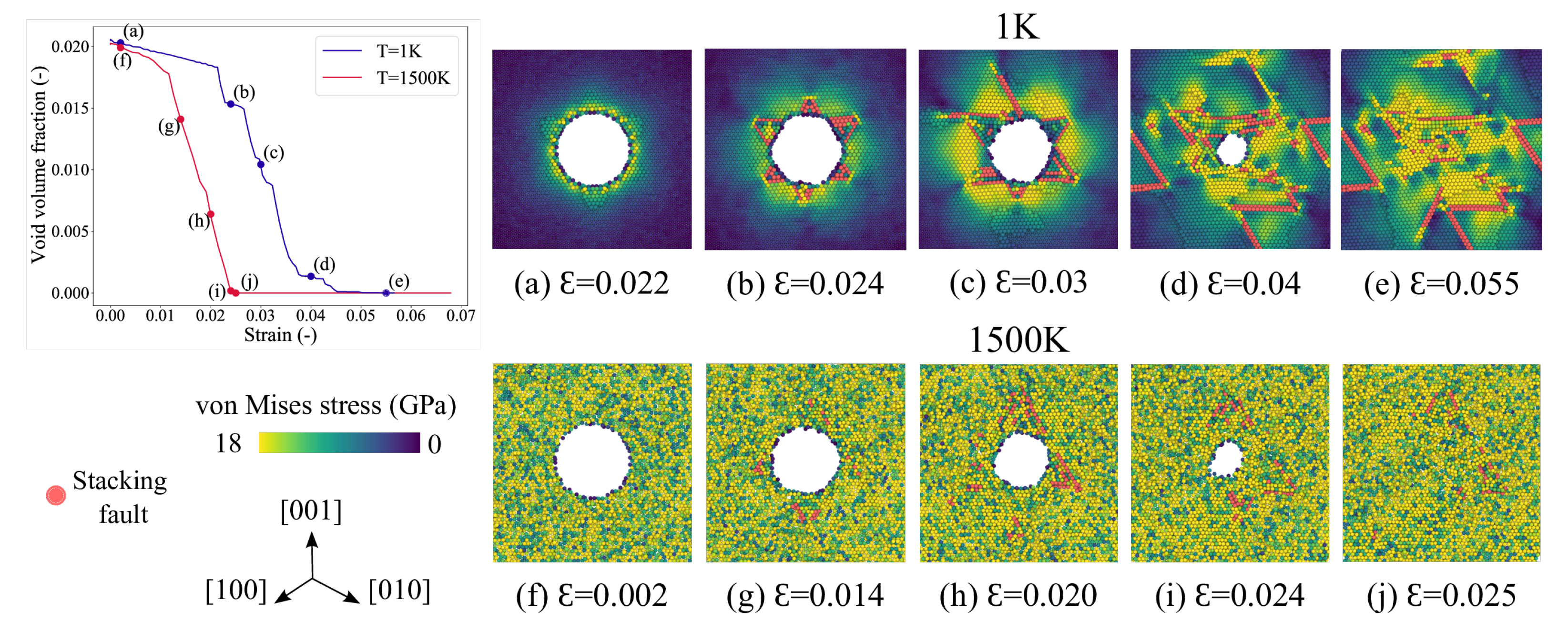
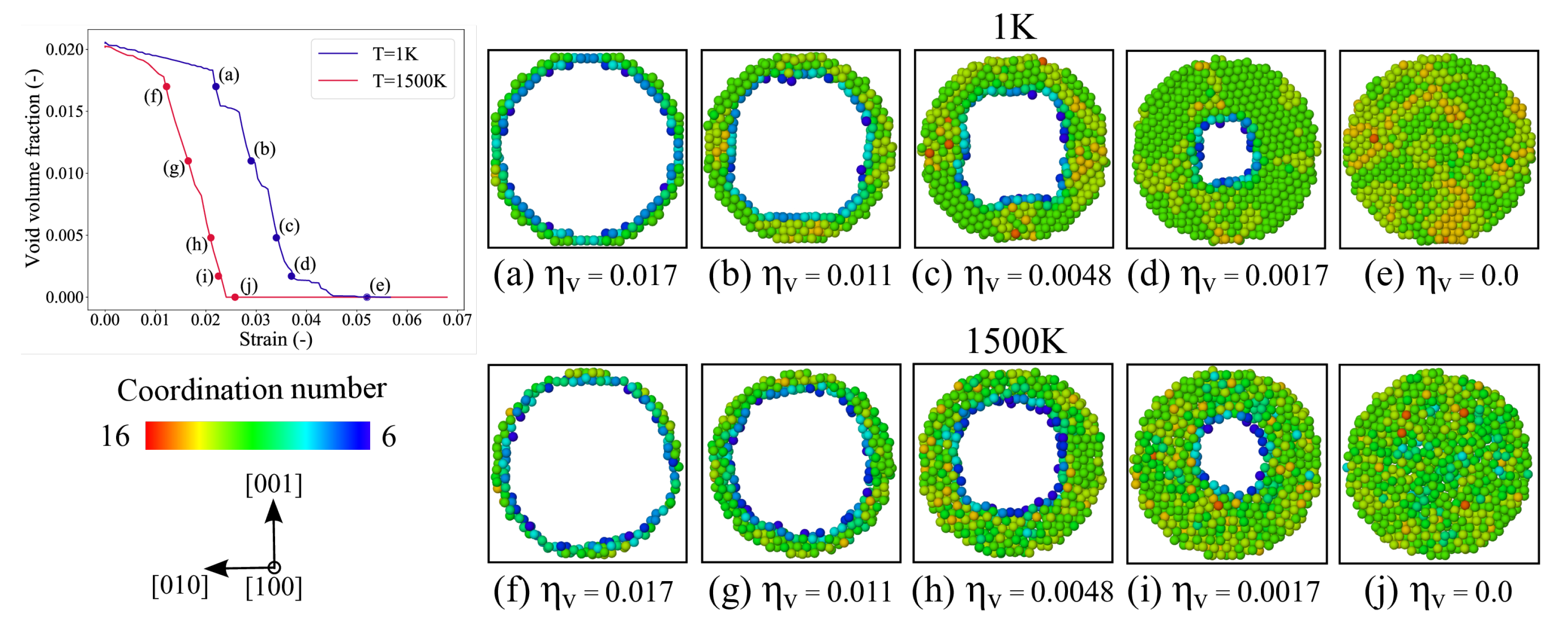
3.1. Void Closure Strains
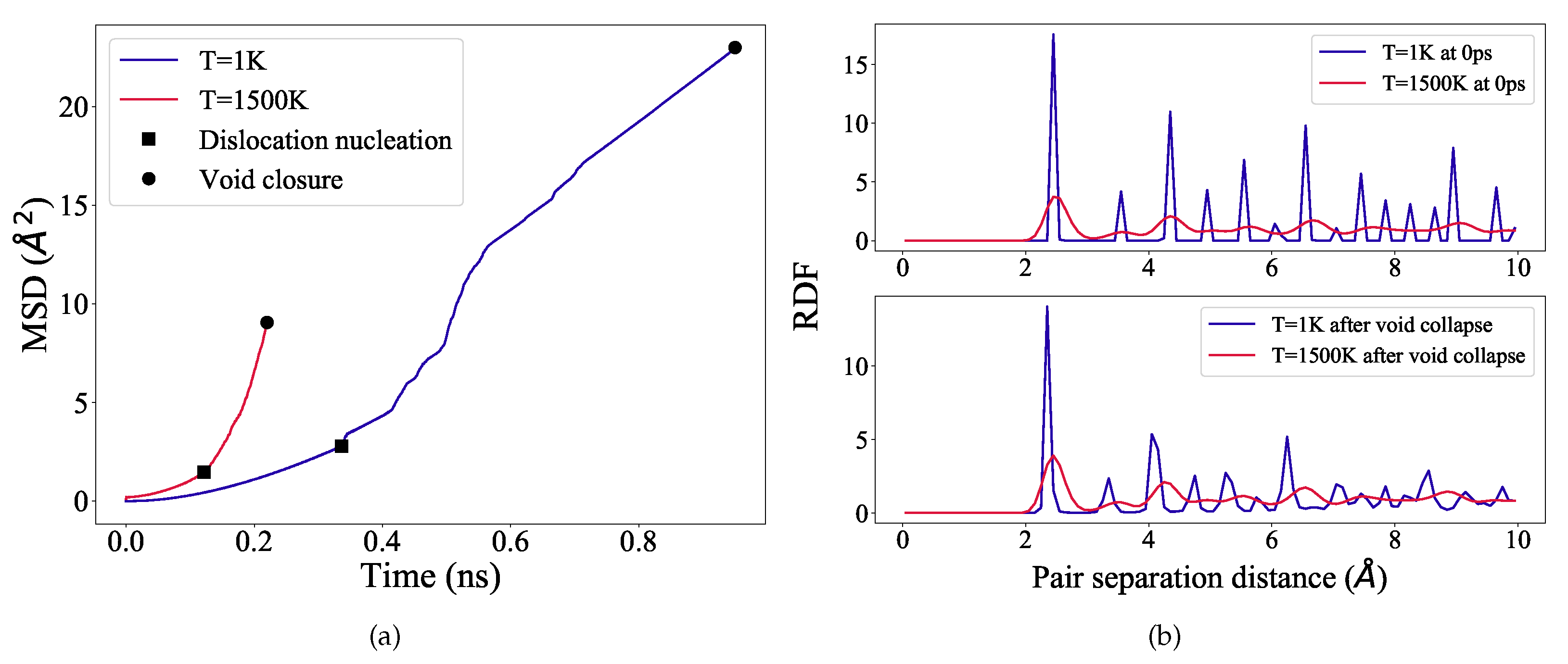
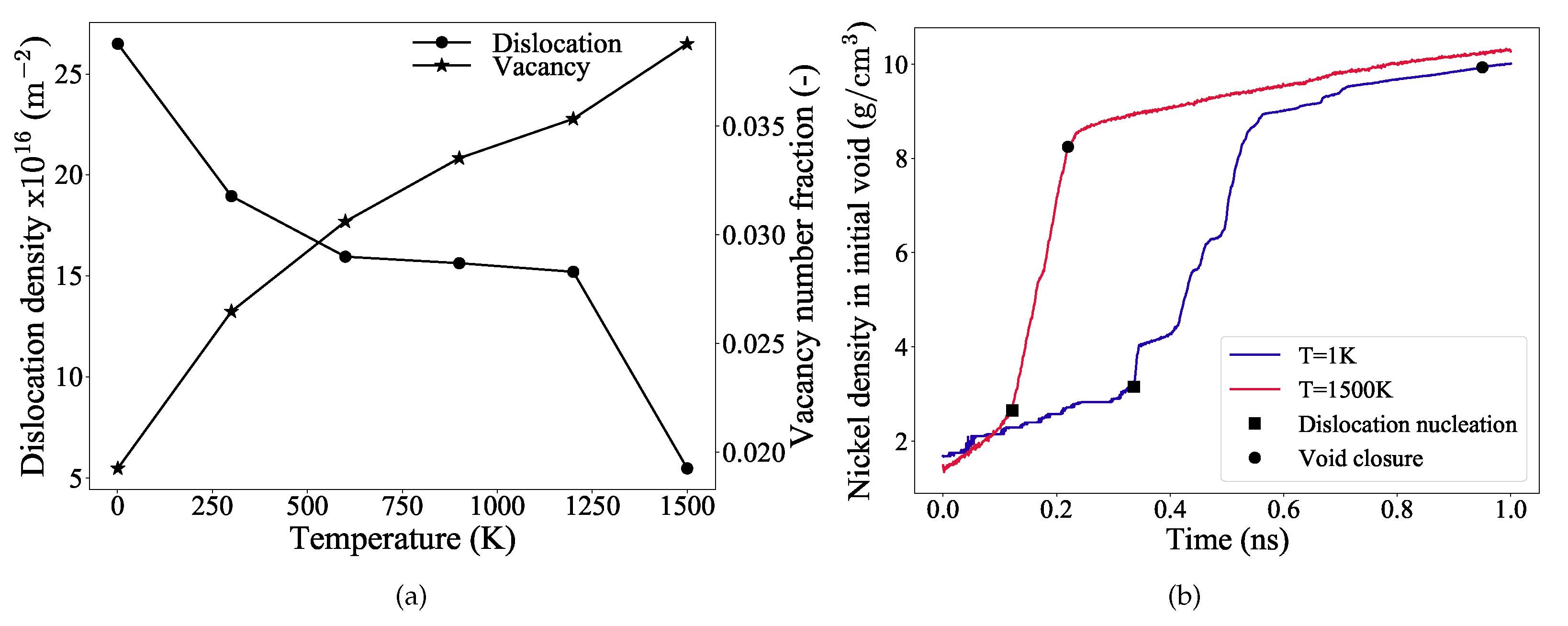
3.2. Diffusion of Nickel
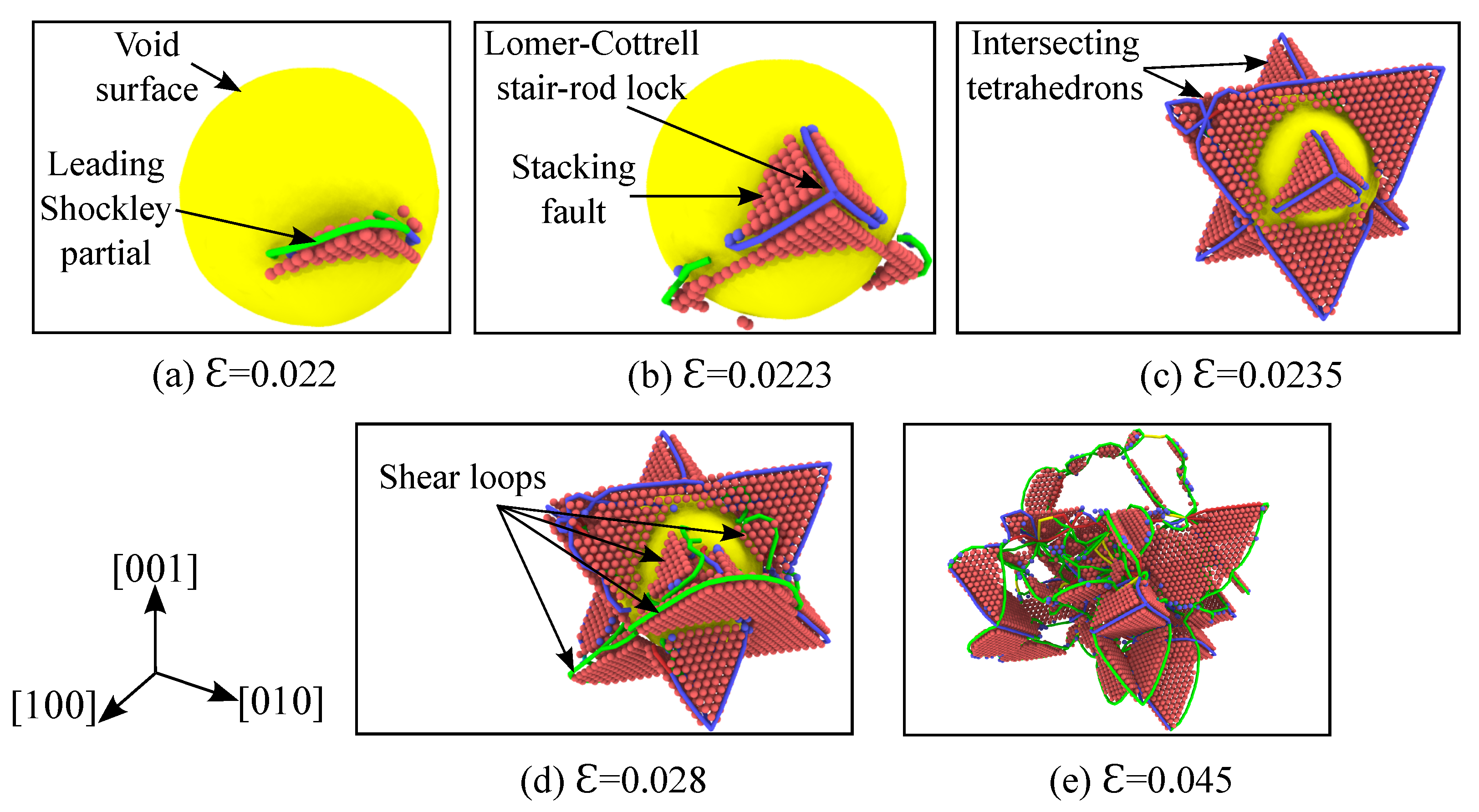
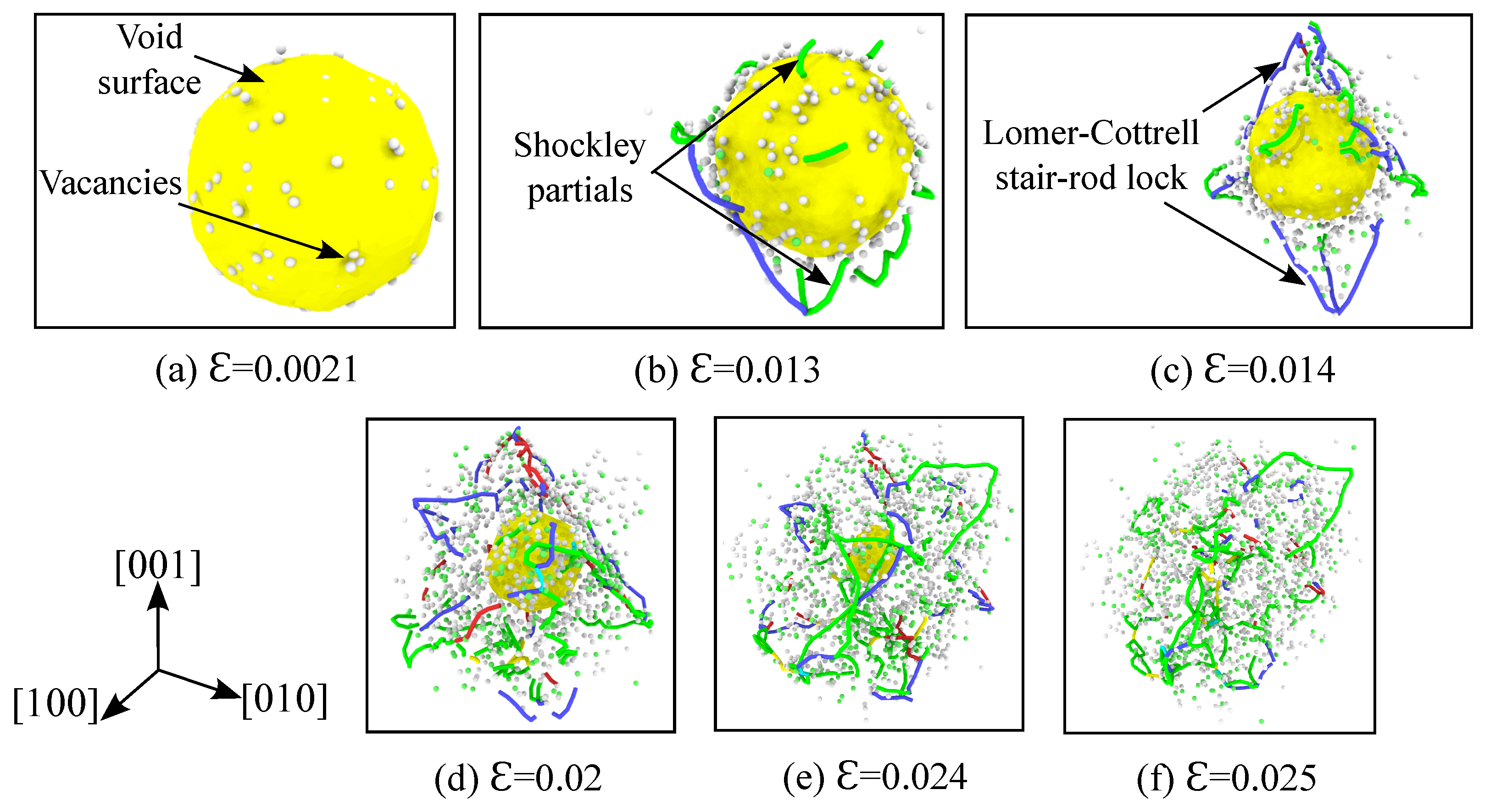
3.3. Evolution of Defects
3.4. Analysis of Void Collapse at 1 K
3.5. Analysis of Void Collapse at 1500 K
3.6. Void Closure Mechanisms
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Traiviratana, S.; Bringa, E.M.; Benson, D.J.; Meyers, M.A. Void growth in metals: Atomistic calculations. Acta Mater. 2008, 56, 3874–3886. [Google Scholar] [CrossRef]
- Bringa, E.M.; Traiviratana, S.; Meyers, M.A. Void initiation in fcc metals: Effect of loading orientation and nanocrystalline effects. Acta Mater. 2010, 58, 4458–4477. [Google Scholar] [CrossRef]
- Tvergaard, V. Material failure by void growth to coalescence. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1989; Volume 27, pp. 83–151. [Google Scholar]
- Cuitino, A.; Ortiz, M. Ductile fracture by vacancy condensation in fcc single crystals. Acta Mater. 1996, 44, 427–436. [Google Scholar] [CrossRef]
- Faleskog, J.; Shih, C.F. Micromechanics of coalescence—I. Synergistic effects of elasticity, plastic yielding and multi-size-scale voids. J. Mech. Phys. Solids 1997, 45, 21–50. [Google Scholar] [CrossRef]
- Kellett, B.; Lange, F.F. Experiments on pore closure during hot isostatic pressing and forging. J. Am. Ceram. Soc. 1988, 71, 7–12. [Google Scholar] [CrossRef]
- Saby, M.; Bouchard, P.O.; Bernacki, M. A geometry-dependent model for void closure in hot metal forming. Finite Elem. Anal. Des. 2015, 105, 63–78. [Google Scholar] [CrossRef]
- Tammas-Williams, S.; Withers, P.J.; Todd, I.; Prangnell, P.B. The effectiveness of hot isostatic pressing for closing porosity in titanium parts manufactured by selective electron beam melting. Metall. Mater. Trans. A 2016, 47, 1939–1946. [Google Scholar] [CrossRef]
- Epishin, A.; Fedelich, B.; Link, T.; Feldmann, T.; Svetlov, I.L. Pore annihilation in a single-crystal nickel-base superalloy during hot isostatic pressing: Experiment and modelling. Mater. Sci. Eng. A 2013, 586, 342–349. [Google Scholar] [CrossRef]
- Epishin, A.I.; Link, T.; Fedelich, B.; Svetlov, I.L.; Golubovskiy, E.R. Hot isostatic pressing of single-crystal nickel-base superalloys: Mechanism of pore closure and effect on Mechanical properties. MATEC Web Conf. 2014, 14, 08003. [Google Scholar] [CrossRef]
- Epishin, A.I.; Bokstein, B.S.; Svetlov, I.L.; Fedelich, B.; Feldmann, T.; Le Bouar, Y.; Ruffini, A.; Finel, A.; Viguier, B.; Poquillon, D. A Vacancy Model of Pore Annihilation During Hot Isostatic Pressing of Single Crystals of Nickel-Base Superalloys. Inorg. Mater. Appl. Res. 2018, 9, 57–65. [Google Scholar] [CrossRef]
- Prasad, M.R.; Gao, S.; Vajragupta, N.; Hartmaier, A. Influence of Trapped Gas on Pore Healing under Hot Isostatic Pressing in Nickel-Base Superalloys. Crystals 2020, 10, 1147. [Google Scholar] [CrossRef]
- McClintock, F.A. A criterion for ductile fracture by the growth of holes. J. Appl. Mech. 1968, 35, 363–371. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Koplik, J.; Needleman, A. Void growth and coalescence in porous plastic solids. Int. J. Solids Struct. 1988, 24, 835–853. [Google Scholar] [CrossRef]
- Pardoen, T.; Hutchinson, J. An extended model for void growth and coalescence. J. Mech. Phys. Solids 2000, 48, 2467–2512. [Google Scholar] [CrossRef]
- Potirniche, G.; Hearndon, J.; Horstemeyer, M.; Ling, X. Lattice orientation effects on void growth and coalescence in fcc single crystals. Int. J. Plast. 2006, 22, 921–942. [Google Scholar] [CrossRef]
- Le Roy, G.; Embury, J.; Edwards, G.; Ashby, M. A model of ductile fracture based on the nucleation and growth of voids. Acta Metall. 1981, 29, 1509–1522. [Google Scholar] [CrossRef]
- Lubarda, V.; Schneider, M.; Kalantar, D.; Remington, B.; Meyers, M. Void growth by dislocation emission. Acta Mater. 2004, 52, 1397–1408. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Z. Material transport via the emission of shear loops during void growth: A molecular dynamics study. J. Appl. Phys. 2016, 119, 225102. [Google Scholar] [CrossRef]
- Rudd, R.E.; Belak, J.F. Void nucleation and associated plasticity in dynamic fracture of polycrystalline copper: An atomistic simulation. Comput. Mater. Sci. 2002, 24, 148–153. [Google Scholar] [CrossRef]
- Ashby, M.F.; Gelles, S.; Tanner, L.E. The stress at which dislocations are generated at a particle-matrix interface. Philos. Mag. 1969, 19, 757–771. [Google Scholar] [CrossRef]
- Ashby, M. The deformation of plastically non-homogeneous materials. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Bringa, E.M.; Cazamias, J.U.; Erhart, P.; Stölken, J.; Tanushev, N.; Wirth, B.D.; Rudd, R.E.; Caturla, M.J. Atomistic shock Hugoniot simulation of single-crystal copper. J. Appl. Phys. 2004, 96, 3793–3799. [Google Scholar] [CrossRef]
- Erhart, P.; Bringa, E.M.; Kumar, M.; Albe, K. Atomistic mechanism of shock-induced void collapse in nanoporous metals. Phys. Rev. B 2005, 72, 052104. [Google Scholar] [CrossRef]
- Davila, L.; Erhart, P.; Bringa, E.; Meyers, M.; Lubarda, V.; Schneider, M.; Becker, R.; Kumar, M. Atomistic modeling of shock-induced void collapse in copper. Appl. Phys. Lett. 2005, 86, 161902. [Google Scholar] [CrossRef]
- Cao, B.; Bringa, E.M.; Meyers, M.A. Shock compression of monocrystalline copper: Atomistic simulations. Metall. Mater. Trans. A 2007, 38, 2681–2688. [Google Scholar] [CrossRef]
- Neogi, A.; Mitra, N. On shock response of nano-void closed/open cell copper material: Non-equilibrium molecular dynamic simulations. J. Appl. Phys. 2014, 115, 013504. [Google Scholar] [CrossRef]
- Neogi, A.; He, L.; Abdolrahim, N. Atomistic simulations of shock compression of single crystal and core-shell Cu@Ni nanoporous metals. J. Appl. Phys. 2019, 126, 015901. [Google Scholar] [CrossRef]
- Potirniche, G.; Horstemeyer, M.; Wagner, G.; Gullett, P. A molecular dynamics study of void growth and coalescence in single crystal nickel. Int. J. Plast. 2006, 22, 257–278. [Google Scholar] [CrossRef]
- Zhao, K.; Chen, C.; Shen, Y.; Lu, T. Molecular dynamics study on the nano-void growth in face-centered cubic single crystal copper. Comput. Mater. Sci. 2009, 46, 749–754. [Google Scholar] [CrossRef]
- Tang, T.; Kim, S.; Horstemeyer, M. Molecular dynamics simulations of void growth and coalescence in single crystal magnesium. Acta Mater. 2010, 58, 4742–4759. [Google Scholar] [CrossRef]
- Mi, C.; Buttry, D.A.; Sharma, P.; Kouris, D.A. Atomistic insights into dislocation-based mechanisms of void growth and coalescence. J. Mech. Phys. Solids 2011, 59, 1858–1871. [Google Scholar] [CrossRef]
- Xu, S.; Hao, Z.; Su, Y.; Yu, Y.; Wan, Q.; Hu, W. An analysis on nanovoid growth in body-centered cubic single crystalline vanadium. Comput. Mater. Sci. 2011, 50, 2411–2421. [Google Scholar] [CrossRef]
- Tang, F.L.; Cai, H.M.; Bao, H.W.; Xue, H.T.; Lu, W.J.; Zhu, L.; Rui, Z.Y. Molecular dynamics simulations of void growth in γ-TiAl single crystal. Comput. Mater. Sci. 2014, 84, 232–237. [Google Scholar] [CrossRef]
- Tanguy, D.; Mareschal, M.; Lomdahl, P.S.; Germann, T.C.; Holian, B.L.; Ravelo, R. Dislocation nucleation induced by a shock wave in a perfect crystal: Molecular dynamics simulations and elastic calculations. Phys. Rev. B 2003, 68, 144111. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Bringa, E.M.; Stukowski, A.; Nieva, J.R.; Bertolino, G.; Tang, Y.; Meyers, M. Atomistic simulation of the mechanical response of a nanoporous body-centered cubic metal. Scr. Mater. 2013, 68, 817–820. [Google Scholar] [CrossRef]
- Xu, X.T.; Tang, F.L.; Xue, H.T.; Yu, W.Y.; Zhu, L.; Rui, Z.Y. Molecular dynamics simulations of void shrinkage in γ-TiAl single crystal. Comput. Mater. Sci. 2015, 107, 58–65. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, S.; Zhu, X.; Zhao, Y. Influence of void density on dislocation mechanisms of void shrinkage in nickel single crystal based on molecular dynamics simulation. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 90, 90–97. [Google Scholar] [CrossRef]
- Tang, Y.; Bringa, E.M.; Remington, B.A.; Meyers, M.A. Growth and collapse of nanovoids in tantalum monocrystals. Acta Mater. 2011, 59, 1354–1372. [Google Scholar] [CrossRef]
- Guan, Y.L.; Shao, J.L.; Song, W. Molecular dynamics study on nanoscale void collapse in single crystal aluminum under 1D and 3D compressions. Comput. Mater. Sci. 2019, 161, 385–393. [Google Scholar] [CrossRef]
- Xu, Q.; Li, W.; Zhou, J.; Yin, Y.; Nan, H.; Feng, X. Molecular dynamics study on void collapse in single crystal hcp-Ti under hydrostatic compression. Comput. Mater. Sci. 2020, 171, 109280. [Google Scholar] [CrossRef]
- Epishin, A.I.; Svetlov, I.L. Evolution of pore morphology in single-crystals of nickel-base superalloys. Inorg. Mater. Appl. Res. 2016, 7, 45–52. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mishin, Y. Atomistic modeling of the γ and γ-phases of the Ni–Al system. Acta Mater. 2004, 52, 1451–1467. [Google Scholar] [CrossRef]
- Suzuki, A.; Mishin, Y. Atomic mechanisms of grain boundary diffusion: Low versus high temperatures. J. Mater. Sci. 2005, 40, 3155–3161. [Google Scholar] [CrossRef]
- Gornostyrev, Y.N.; Kontsevoi, O.Y.; Khromov, K.Y.; Katsnelson, M.; Freeman, A.J. The role of thermal expansion and composition changes in the temperature dependence of the lattice misfit in two-phase γ/γ superalloys. Scr. Mater. 2007, 56, 81–84. [Google Scholar] [CrossRef]
- Faken, D.; Jónsson, H. Systematic analysis of local atomic structure combined with 3D computer graphics. Comput. Mater. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Neogi, A.; Mitra, N. A metastable phase of shocked bulk single crystal copper: An atomistic simulation study. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Neogi, A.; Alam, M.; Hartmaier, A.; Janisch, R. Anisotropic failure behavior of ordered intermetallic TiAl alloys under pure mode-I loading. Model. Simul. Mater. Sci. Eng. 2020, 28, 065016. [Google Scholar] [CrossRef]
- Neogi, A.; Mitra, N. Shock induced deformation response of single crystal copper: Effect of crystallographic orientation. Comput. Mater. Sci. 2017, 135, 141–151. [Google Scholar] [CrossRef]
- Stukowski, A. Computational analysis methods in atomistic modeling of crystals. Jom 2014, 66, 399–407. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J.; Mura, T. Theory of Dislocations. J. Appl. Mech. 1983, 50, 476. [Google Scholar] [CrossRef]
- Schäublin, R.; Yao, Z.; Baluc, N.; Victoria, M. Irradiation-induced stacking fault tetrahedra in fcc metals. Philos. Mag. 2005, 85, 769–777. [Google Scholar] [CrossRef]
- Neogi, A.; Mitra, N. Evolution of dislocation mechanisms in single-crystal Cu under shock loading in different directions. Model. Simul. Mater. Sci. Eng. 2017, 25, 025013. [Google Scholar] [CrossRef]
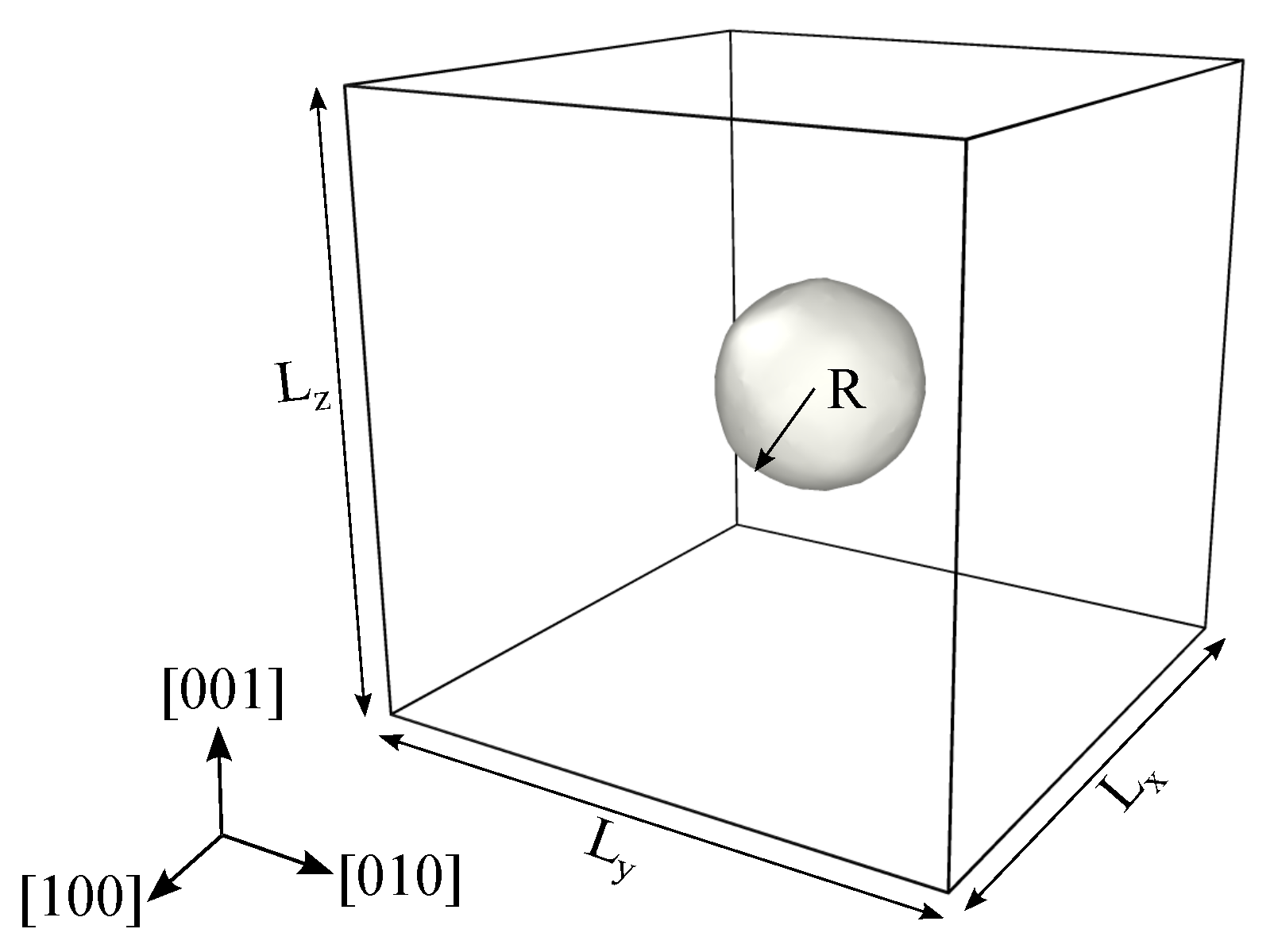
| Parameters | Values |
|---|---|
| Temperature (K) | 1, 300, 600, 900, 1200, 1500 |
| Specimen size, (Å) | 141 |
| Void radius, R (Å) | 23 |
| Void volume fraction, | 0.02 |
| Number of atoms | 251,079 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prasad, M.R.G.; Neogi, A.; Vajragupta, N.; Janisch, R.; Hartmaier, A. Influence of Temperature on Void Collapse in Single Crystal Nickel under Hydrostatic Compression. Materials 2021, 14, 2369. https://doi.org/10.3390/ma14092369
Prasad MRG, Neogi A, Vajragupta N, Janisch R, Hartmaier A. Influence of Temperature on Void Collapse in Single Crystal Nickel under Hydrostatic Compression. Materials. 2021; 14(9):2369. https://doi.org/10.3390/ma14092369
Chicago/Turabian StylePrasad, Mahesh R. G., Anupam Neogi, Napat Vajragupta, Rebecca Janisch, and Alexander Hartmaier. 2021. "Influence of Temperature on Void Collapse in Single Crystal Nickel under Hydrostatic Compression" Materials 14, no. 9: 2369. https://doi.org/10.3390/ma14092369
APA StylePrasad, M. R. G., Neogi, A., Vajragupta, N., Janisch, R., & Hartmaier, A. (2021). Influence of Temperature on Void Collapse in Single Crystal Nickel under Hydrostatic Compression. Materials, 14(9), 2369. https://doi.org/10.3390/ma14092369







