High-Performance Face Milling of 42CrMo4 Steel: Influence of Entering Angle on the Measured Surface Roughness, Cutting Force and Vibration Amplitude
Abstract
1. Introduction
2. Materials and Methods
- universal face cutter MFA145-063R04A22-SE13 (ENGRAM)—entering angle κr = 45°,
- High-Feed face cutter MKB113-063R04A22-SD12 (ENGRAM)—entering angle κr = 21.3°.
3. Results and Discussion
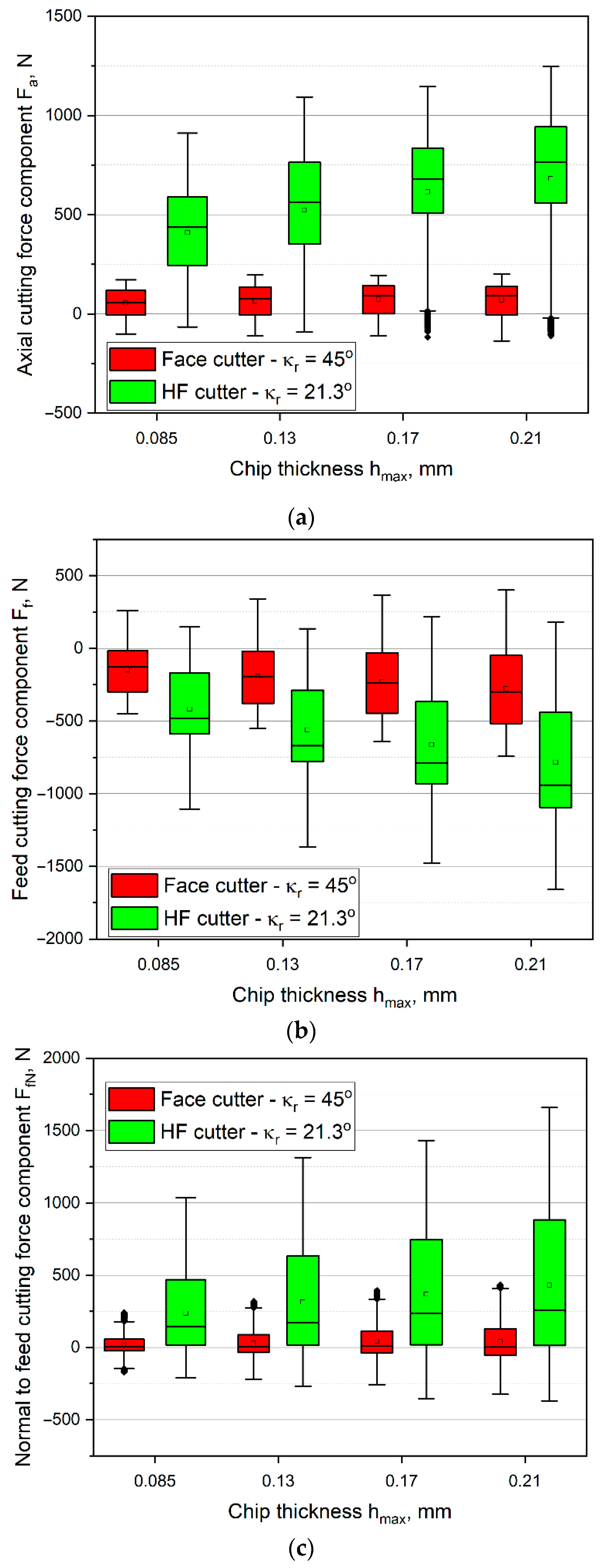
3.1. The Analysis of Cutting Force Components in HF and Conventional Face Milling
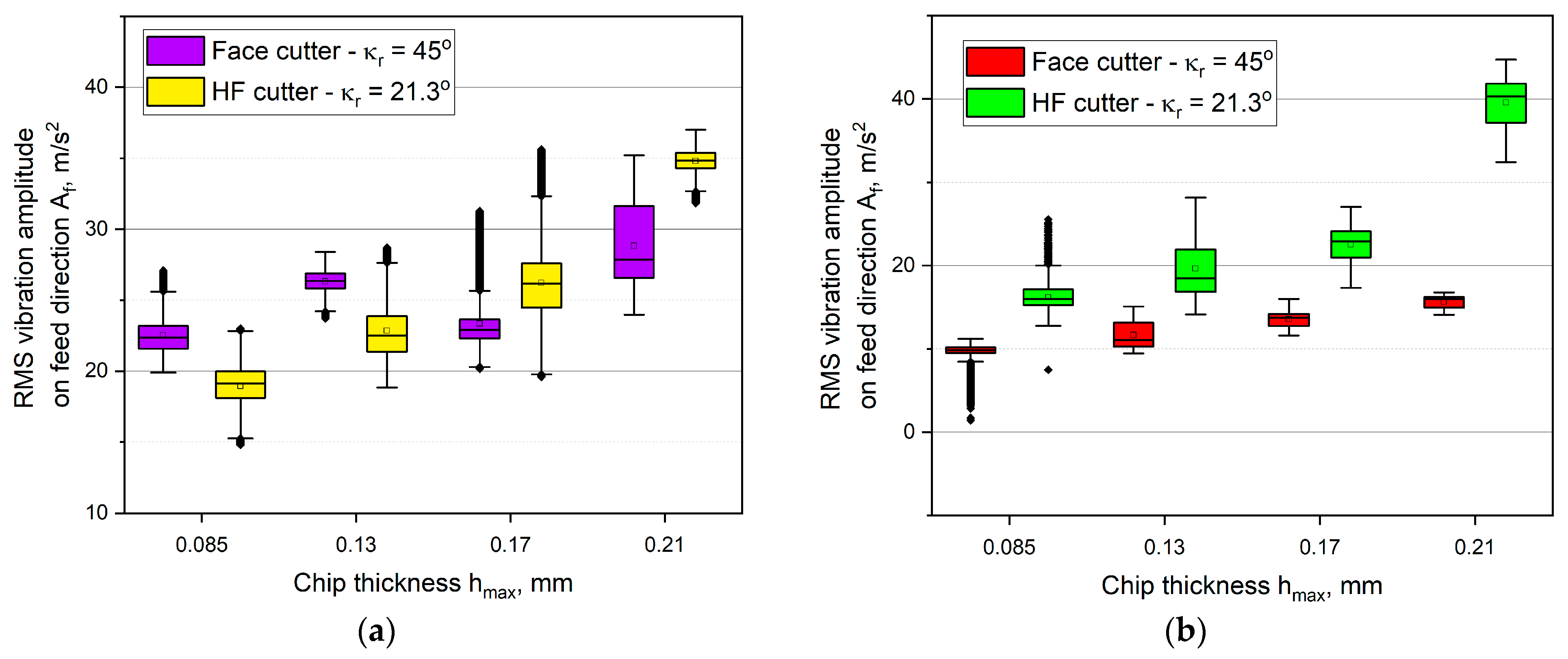
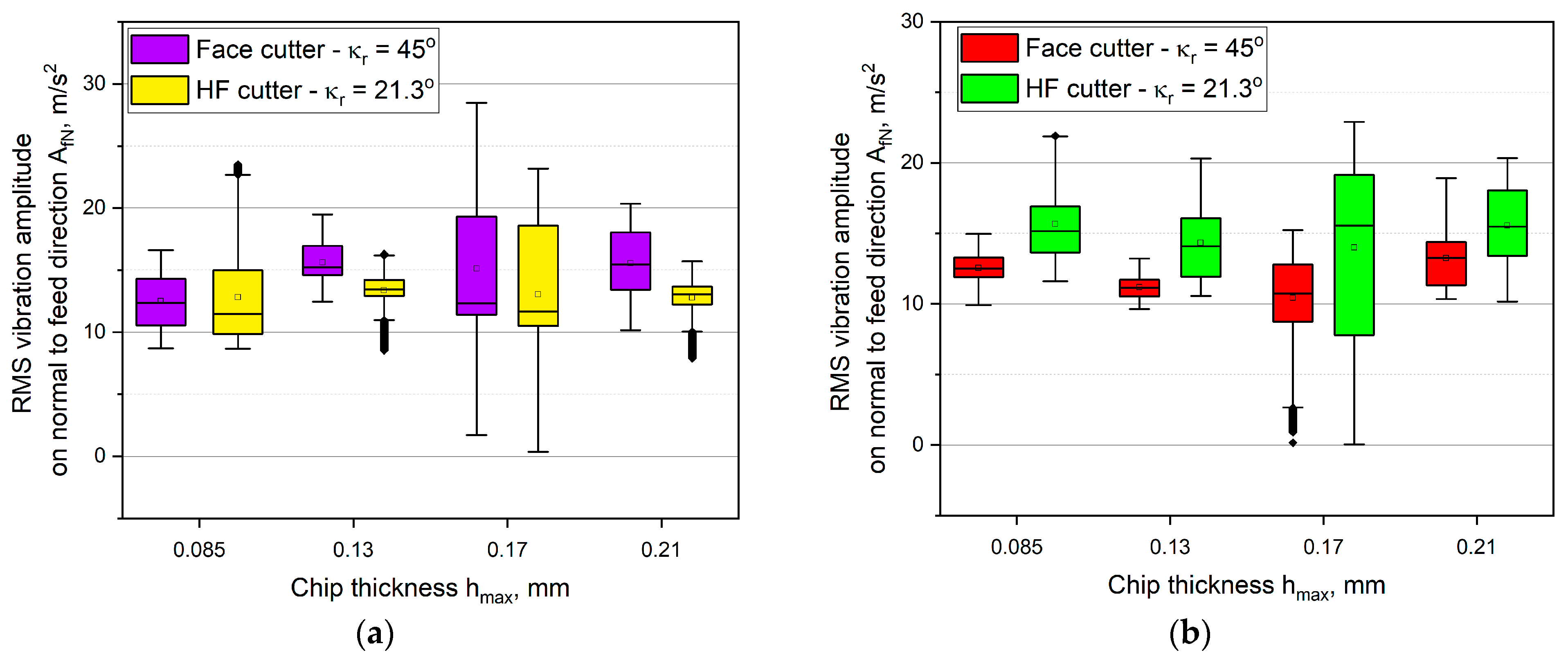
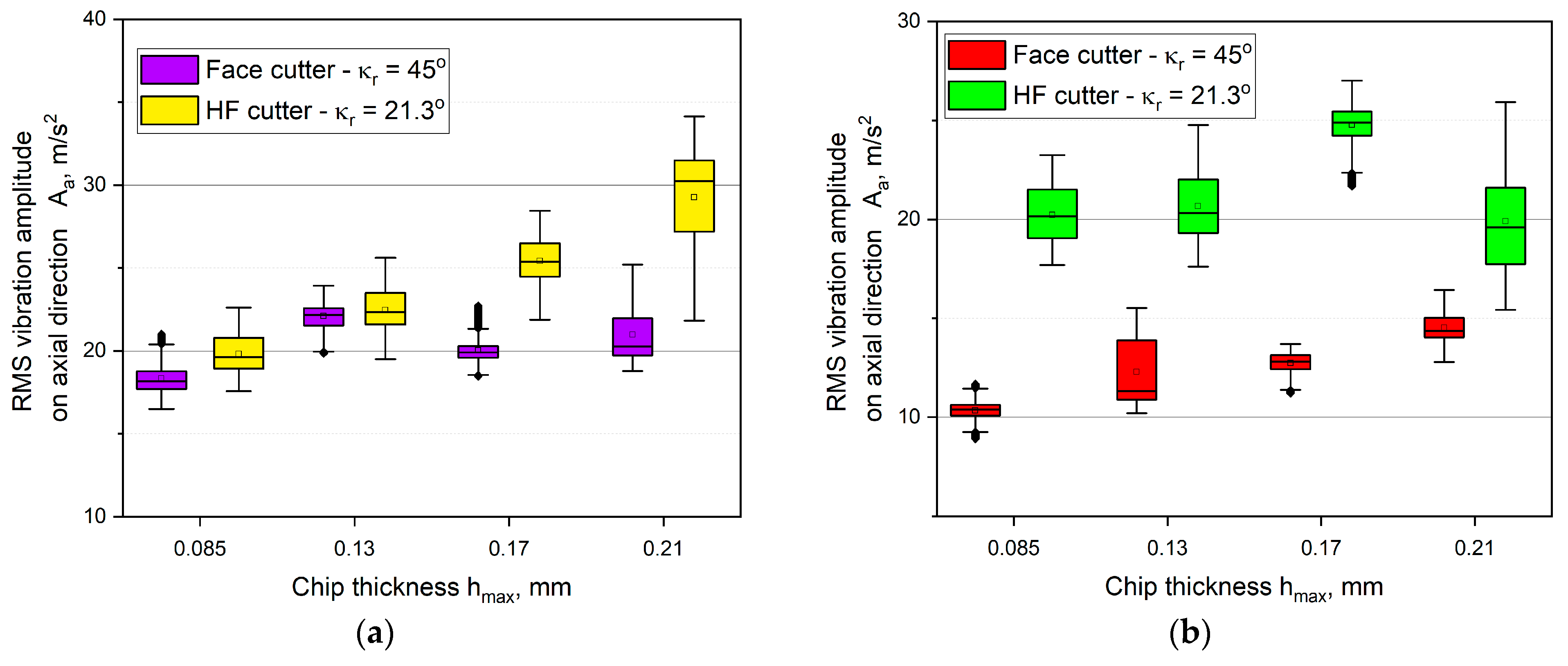
3.2. Analysis of the Vibration Amplitude Components during HF and Conventional Face Milling
3.3. Analysis of the Surface Roughness after HF and Conventional Face Milling
4. Conclusions
- using the HF cutter, it is possible to achieve over twice the cutting volumes obtained during milling with the use of a conventional face cutter with the entering angle of κr = 45°, with constant cut layer thickness hmax;
- during milling with the HF cutter, higher values of the cutting force components occur, eight times the increase in the value of the axial cutting force component Fa, four times the increase in the feed cutting force component Ff, and two times the increase in the normal to feed component FfN were recorded;
- despite the different shape of the cut layer cross-section during milling with the HF cutter, specific values of the cutting force in relation to the cut layer cross-section are similar for both tool;
- taking into consideration the distribution and values of the cutting force components (mainly high values of the axial component, exerting load on spindle’s bearings) as well as vibration amplitude values, it can be concluded, that the HF milling process should take place on stiff machine tools, of which the design enables transferring high loads in the direction of a spindle’s axis;
- milling with the use of the HF cutter in most cases contributes to occurring higher vibration amplitudes, compared with milling with the face cutter with the entering angle of κr = 45°, which results from different values of cut layer thickness in cross-sectional area;
- the reason for the higher level of vibrations is the chip forming process as well as the shape and size of a cut layer during milling with the HF cutter, where cut layer thickness h varies with the depth of cut and where there is an area below hmin, where elastic-plastic deformation of the material is increased and the tool is deflected;
- the average vibration RMS values in the feed and normal-to-feed directions for up milling with the HF cutter are equal to or even lower than for the conventional cutter. It means that in some machining conditions, milling with the HF cutter presents an alternative for the conventional cutter, with significantly higher machining efficiency and similar machining loads;
- the use of the HF cutter causes significantly higher surface roughness, in comparison with the conventional face cutter with the entering angle of κr = 45°, due to the variation in cut layer cross-sectional thickness and increase in plastic deformation of the material;
- the increase in cut layer thickness during HF milling results in reducing the surface roughness, which can be explained by the reduction of the elastic-plastic area in the cut layer below the value of the minimal cut layer hmin.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tsai, M.Y.; Chang, C.T.; Ho, J.K. The Machining of Hard Mold Steel by Ultrasonic Assisted End Milling. Appl. Sci. 2016, 6, 373. [Google Scholar] [CrossRef]
- Habrat, W.; Markopoulos, A.P.; Motyka, M.; Sieniawski, J. Chapter 11—Machinability. In Micro and Nano Technologies, Nanocrystalline Titanium; Garbacz, H., Semenova, I.P., Zherebtsov, S., Motyka, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 209–236. [Google Scholar]
- Karaguzel, U.; Budak, E. Investigating effects of milling conditions on cutting temperatures through analytical and experimental methods. J. Mater. Process. Technol. 2018, 262, 532–540. [Google Scholar] [CrossRef]
- Abbas, A.T.; Anwar, S.; Abdelnasser, E.; Luqman, M.; Qudeiri, J.E.A.; Elkaseer, A. Effect of Different Cooling Strategies on Surface Quality and Power Consumption in Finishing End Milling of Stainless Steel 316. Materials 2021, 14, 903. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, D.; Altintas, Y. Mechanism of cutting force and surface generation in dynamic milling. J. Eng. Ind. 1991, 113, 160–168. [Google Scholar] [CrossRef]
- Zhang, Z.; Qi, Y.; Cheng, Q.; Liu, Z.; Tao, Z.; Cai, L. Machining accuracy reliability during the peripheral milling process of thin-walled components. Robot. Comput. Integr. Manuf. 2019, 59, 222–234. [Google Scholar] [CrossRef]
- Wu, T.-Y.; Lin, C.-C. Optimization of Machining Parameters in Milling Process of Inconel 718 under Surface Roughness Constraints. Appl. Sci. 2021, 11, 2137. [Google Scholar] [CrossRef]
- Hussain, A.; Lazoglu, I. Distortion in milling of structural parts. Cirp Ann. 2019, 68, 105–108. [Google Scholar] [CrossRef]
- Ren, S.; Long, X.; Meng, G. Dynamics and stability of milling thin walled pocket structure. J. Sound Vib. 2018, 429, 325–347. [Google Scholar] [CrossRef]
- Li, D.; Cao, H.; Zhang, X.; Chen, X.; Yan, R. Model predictive control based active chatter control in milling process. Mech. Syst. Signal Process. 2019, 128, 266–281. [Google Scholar] [CrossRef]
- Lajmert, P.; Rusinek, R.; Kruszyński, B. Chatter identification in milling of Inconel 625 based on recurrence plot technique and Hilbert vibration decomposition, International Conference on Engineering Vibration. In Proceedings of the MATEC Web of Conferences, International Conference on Engineering Vibration (ICoEV 2017), Sofia, Bulgaria, 4–7 September 2017; Volume 148. [Google Scholar]
- Karpuschewski, B.; Kundrák, J.; Felhő, C.; Varga, G.; Sztankovics, I.; Makkai, T.; Borysenko, D. Preliminary Investigations for the Effect of Cutting Tool Edge Geometry in High-Feed Face Milling. In Vehicle and Automotive Engineering 2. VAE 2018. Lecture Notes in Mechanical Engineering; Jármai, K., Bolló, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 241–254. [Google Scholar]
- Burek, J.; Zylka, L.; Plodzien, M.; Gdula, M.; Sulkowicz, P. The influence of the cutting edge shape on high performance cutting. Aircr. Eng. Aerosp. Technol. 2018, 90, 134–145. [Google Scholar] [CrossRef]
- Niesłony, P.; Grzesik, W.; Chudy, R.; Habrat, W. Meshing strategies in FEM simulation of the machining process. Arch. Civ. Mech. Eng. 2015, 15, 62–70. [Google Scholar] [CrossRef]
- Pelayo, G.U. Modelling of static and dynamic milling forces in inclined operations with circle-segment end mills. Precis. Eng. 2019, 56, 123–135. [Google Scholar] [CrossRef]
- Totis, G.; Insperger, T.; Sortino, M.; Gábor, S. Symmetry breaking in milling dynamics. Int. J. Mach. Tools Manuf. 2019, 139, 37–59. [Google Scholar] [CrossRef]
- Li, X.P.; Zheng, H.Q.; Wong, Y.S.; Nee, A.Y.C. An approach to theoretical modelling and simulation of face milling forces. J. Manuf. Process. 2000, 2, 225–240. [Google Scholar] [CrossRef]
- Korkut, I.; Donertas, M.A. The influence of feed rate and cutting speed on the cutting forces, surface roughness and tool–chip contact length during face milling. Mater. Des. 2007, 28, 308–312. [Google Scholar] [CrossRef]
- Sheth, S.; George, P.M. Experimental investigation and prediction of flatness and surface roughness during face milling operation of WCB material. Procedia Technol. 2016, 23, 344–351. [Google Scholar] [CrossRef]
- Fulemova, J.; Janda, Z. Influence of the cutting edge radius and the cutting edge preparation on tool life and cutting forces at inserts with Wiper geometry. Procedia Eng. 2014, 69, 565–573. [Google Scholar] [CrossRef]
- Tapoglou, N.; Antoniadis, A. 3-Dimensional kinematics simulation of face milling. Measurement 2012, 45, 1396–1405. [Google Scholar] [CrossRef]
- Muñoz-Escalona, P.; Maropoulos, P.G. A geometrical model for surface roughness prediction when face milling Al 7075-T7351 with square insert tools. J. Manuf. Syst. 2015, 36, 216–223. [Google Scholar] [CrossRef]
- Karpuschewski, B.; Batt, S. Improvement of dynamic properties in milling by integrated stepped cutting. Cirp Ann. 2007, 56, 85–88. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M. A review of methods of random surface topography modeling. Tribol. Int. 2020, 152, 106530. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M.; Krolczyk, G. Material ratio curve as information on the state of surface topography—A review. Precis. Eng. 2020, 65, 240–258. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Guzeev, V.I.; Krolczyk, G.M.; Mia, M.; Wojciechowski, S. Modeling flatness deviation in face milling considering angular movement of the machine tool system components and tool flank wear. Precis. Eng. 2018, 54, 327–337. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Hassui, A.; Wojciechowski, S.; Mia, M.; Magri, A.; Suyama, D.I.; Bustillo, A.; Krolczyk, G.M.; Gupta, M.K. Effect of the Relative Position of the Face Milling Tool towards the Workpiece on Machined Surface Roughness and Milling Dynamics. Appl. Sci. 2019, 9, 842. [Google Scholar] [CrossRef]
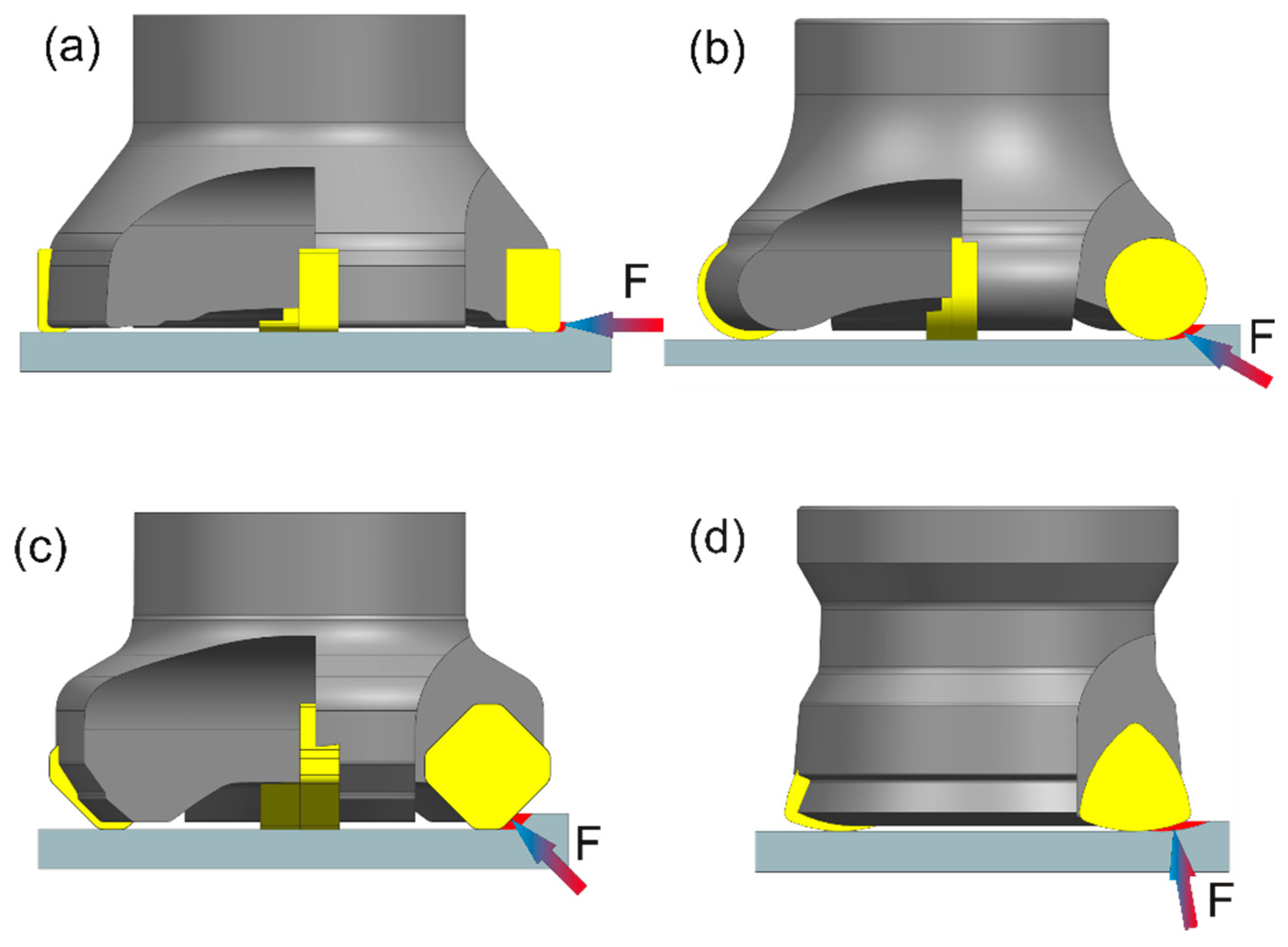
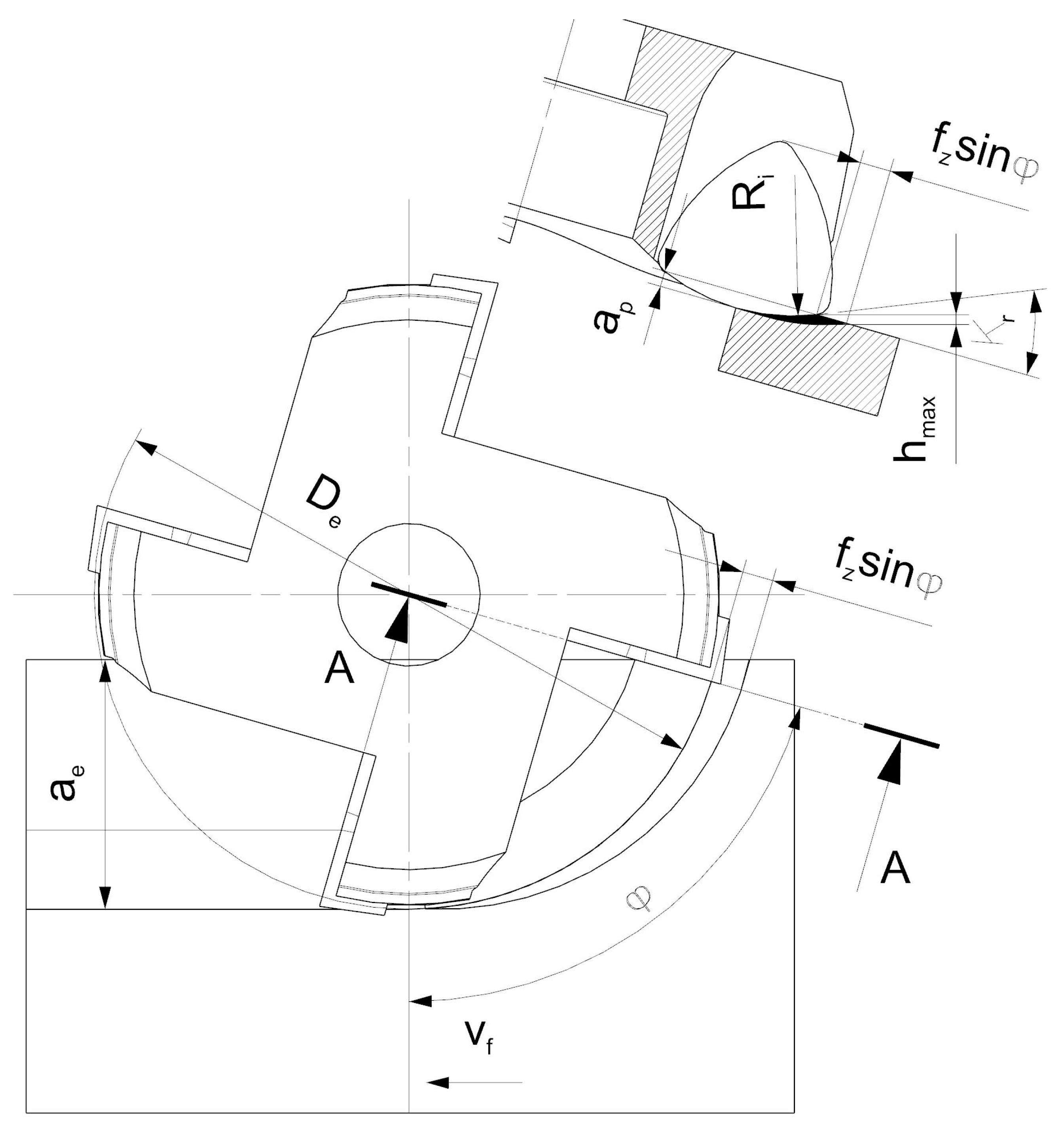


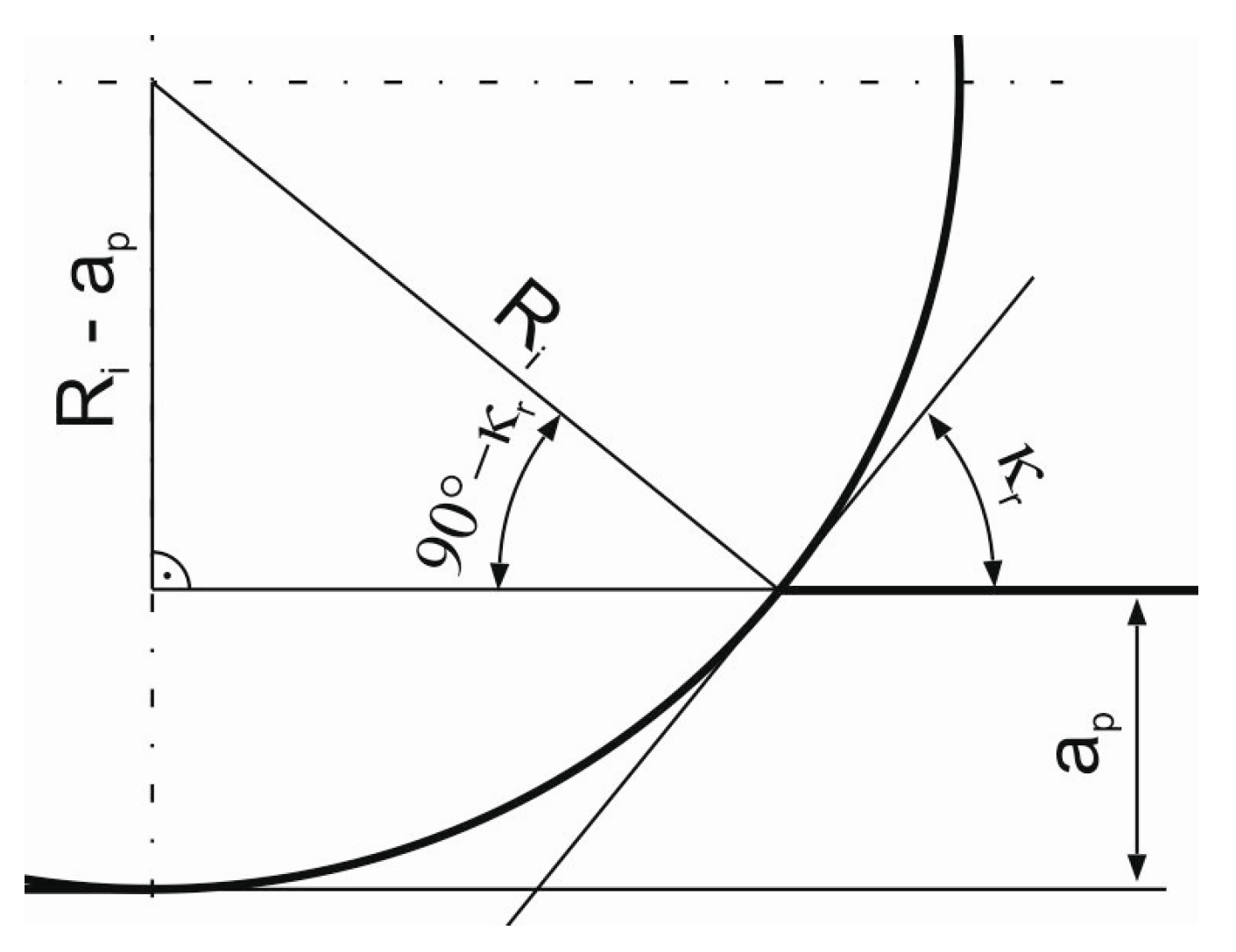





| Chip thickness hmax, mm | 0.085 | 0.13 | 0.17 | 0.21 | Type of mill cutter |
| Cross section area Scmax, mm2 | 0.12 | 0.18 | 0.24 | 0.3 | Face mill |
| 0.24 | 0.35 | 0.45 | 0.55 | HF face mill | |
| Feed per tooth fz, mm/tooth | 0.14 | 0.21 | 0.28 | 0.35 | Face mill |
| 0.28 | 0.42 | 0.55 | 0.68 | HF face mill | |
| Cutting efficiency Qw, mm3/min | 6417 | 9815 | 12835 | 15855 | Face mill |
| 12,472 | 19,106 | 24,958 | 30,854 | HF face mill |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Płodzień, M.; Żyłka, Ł.; Sułkowicz, P.; Żak, K.; Wojciechowski, S. High-Performance Face Milling of 42CrMo4 Steel: Influence of Entering Angle on the Measured Surface Roughness, Cutting Force and Vibration Amplitude. Materials 2021, 14, 2196. https://doi.org/10.3390/ma14092196
Płodzień M, Żyłka Ł, Sułkowicz P, Żak K, Wojciechowski S. High-Performance Face Milling of 42CrMo4 Steel: Influence of Entering Angle on the Measured Surface Roughness, Cutting Force and Vibration Amplitude. Materials. 2021; 14(9):2196. https://doi.org/10.3390/ma14092196
Chicago/Turabian StylePłodzień, Marcin, Łukasz Żyłka, Paweł Sułkowicz, Krzysztof Żak, and Szymon Wojciechowski. 2021. "High-Performance Face Milling of 42CrMo4 Steel: Influence of Entering Angle on the Measured Surface Roughness, Cutting Force and Vibration Amplitude" Materials 14, no. 9: 2196. https://doi.org/10.3390/ma14092196
APA StylePłodzień, M., Żyłka, Ł., Sułkowicz, P., Żak, K., & Wojciechowski, S. (2021). High-Performance Face Milling of 42CrMo4 Steel: Influence of Entering Angle on the Measured Surface Roughness, Cutting Force and Vibration Amplitude. Materials, 14(9), 2196. https://doi.org/10.3390/ma14092196









