Research Status of High-Purity Metals Prepared by Zone Refining
Abstract
1. Introduction
| Metal | Application |
|---|---|
| In [8] | ITO targets, CIGS solar cells, liquid crystal displays, etc. |
| Sn [9] | Packaging materials, integrated circuits, refractory materials, etc. |
| Ni [10] | Stainless steel, alloy steel, high-temperature structural materials, etc. |
| Cu [11] | Audio products, integrated circuits, fatigue-resistant cables, etc. |
| Co [12] | Magnetic materials, super alloys, electronic component targets, etc. |
| Ti [13] | Large-scale integrated circuits, decorative materials, etc. |
| Ga [14] | Semiconductor materials, solar cells, catalytic materials, etc. |
| Ge [15] | Integrated circuits, photovoltaic cells, infrared optical materials, etc. |
| Te [16] | Aerospace, atomic energy, electronics industry, etc. |
| Al [17] | Target materials, integrated circuit wiring, optoelectronic storage media, etc. |
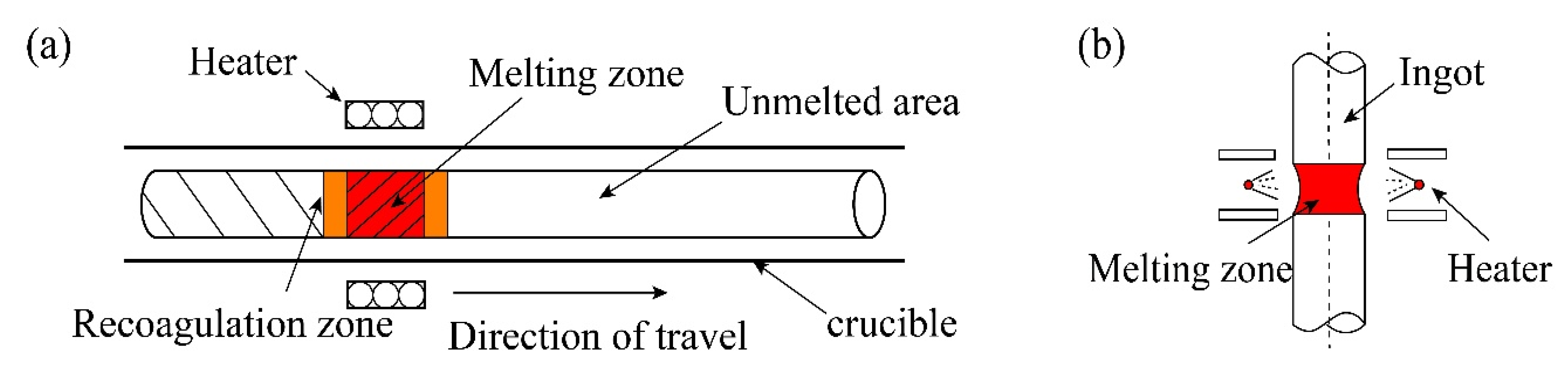
2. Zone Refining Mechanism
2.1. Basic Principles
2.2. Analysis of Changes in Impurities during Zone Refining
3. Influencing Factors and Optimization of Zone Refining
3.1. Balanced Distribution Coefficient
3.2. Zone Refining Rate
3.3. Length of Melting Zone
3.4. Zone Refining Scans
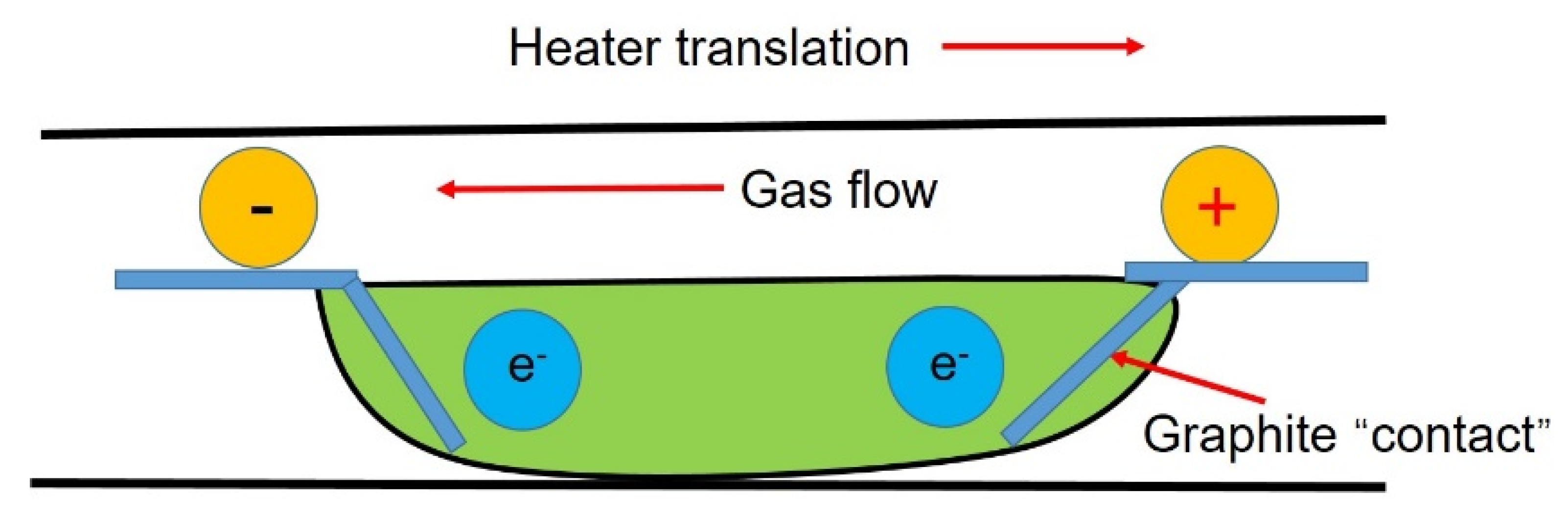
3.5. Application of Current in Impurity Transmission
3.6. Inclination
4. Types of Zone Refining
5. High-Purity Metal Analysis Method
- (1)
- In terms of the number of measured elements, it will develop from single elements to multiple elements simultaneously or continuously.
- (2)
- In the analysis method, it will develop from offline/manual operation to online/automatic mode.
- (3)
- In terms of data collection and processing, the application of mathematical methods such as chemo-metrics, pattern recognition, expert systems, artificial intelligence, and neural networks will help to improve the integrity and accuracy of test data.
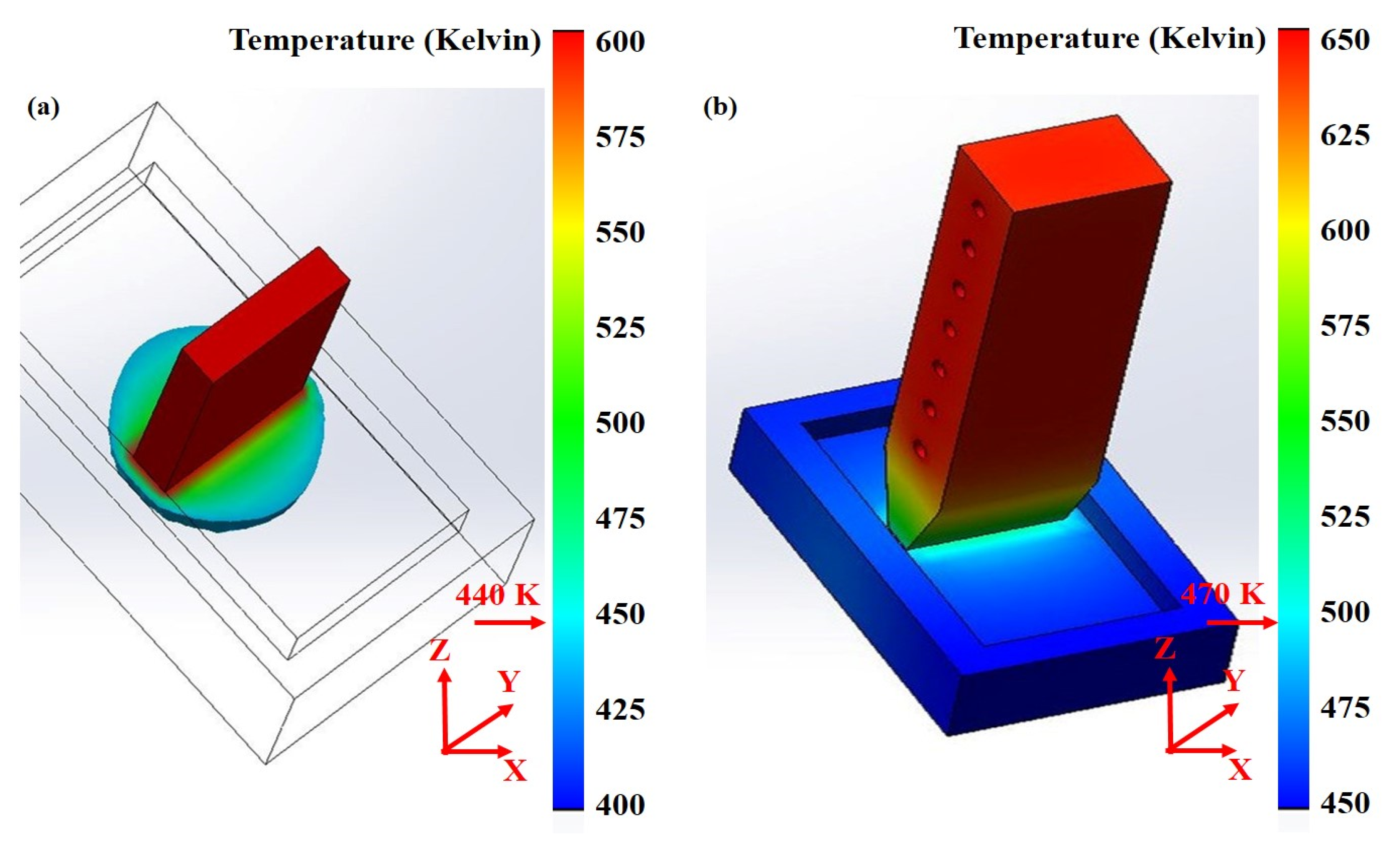
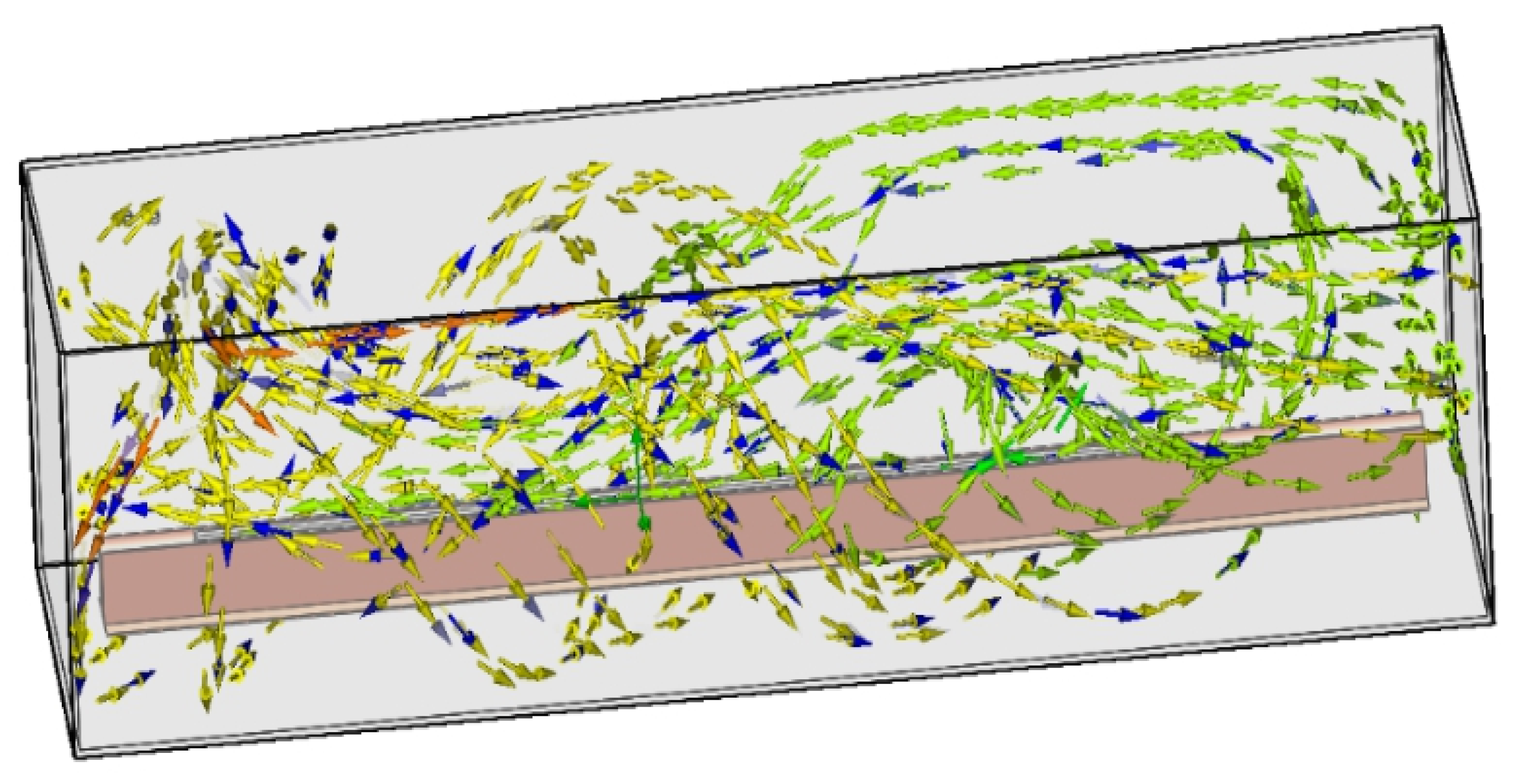
6. Numerical Simulation
6.1. Iterative Modeling of Constant K
6.2. Iterative Modeling of Variable K
6.3. Iterative Modeling Considering Diffusion Area
6.4. Evaluation Modeling and Experiment
7. Existing Problems and Prospects
- (1)
- The requirements for raw materials are high. The purity of the raw material rod must meet certain requirements, and the gap impurities C, H, O, etc. contained in it must be controlled within a certain range, so as to avoid the power and temperature fluctuations caused by gas impurities in the zone refining process, which affects the quality of the material.
- (2)
- For impurities with a balanced distribution coefficient close to 1, the content of the raw material rods must be strictly controlled so as not to affect the final performance of the materials: for example, magnesium, calcium, iron, and antimony in bismuth; lead, magnesium, silicon, and aluminum in indium.
- (3)
- The influence of side effects. Side effects include the evaporation of high vapor pressure impurities in the melting zone caused by agitation, temperature increase, or low pressure inert gas flow through the melting zone, due to chemical reactions between impurities (such as between carbon and sulfur, hydrogen, or oxygen), and the slagging process often brings complex problems that are difficult to predict. Sometimes, in order to remove an impurity, it is necessary to add a second reaction element to complete, and the latter is selected to generate a compound with the former. During zone refining, it is easier than removing certain impurities alone.
- (4)
- The bar size is limited. The emergence of refining in the suspension zone solves the crucible pollution existing in the conventional zone refining, making the zone refining technology develop rapidly. However, due to gravity, the technique requires that the size of the raw material rod must be controlled within a certain range to obtain a stable refining zone.
- (5)
- Low production efficiency and high cost. The low speed and multiple refining required by the zone refining greatly extend the production time and reduce the production efficiency; after each zone refining, the first and last ends of the bar need to be removed, which reduces the utilization rate of raw materials and increases the production cost.
- (6)
- The development speed of product testing and analysis technology lags behind. With the improvement of purification technology, a variety of highly sensitive impurity analysis methods came into being, but these methods have certain limitations, which restrict the development of zone refining technology.
- (7)
- The large-scale application of advanced zone refining technology is limited. The research on zone refining technology has made great progress, and it has been used in industrial production in certain fields, but some of the deficiencies have hindered its large-scale application: the suspension zone refining technology equipment investment is expensive, and raw material storage container selection is more difficult. Moreover, it is susceptible to secondary pollution during operation, and the optimal production process parameters are easily changed with the material.
- (1)
- Combining zone refining technology with other purification technologies, developing an ideal purification method combining multiple technologies, such as electromigration/zone refining, vacuum degassing-zone refining, to effectively remove gas impurities and ensure the stability of subsequent zone refining proceed to obtain higher purity materials.
- (2)
- Upgrade the zone refining equipment, increase the degree of automation and improve the zone refining technology to obtain a stable and simple operation process, improve production efficiency, and reduce production costs.
- (3)
- Improve trace element analysis technology to make simultaneous or continuous determination of trace and ultra-trace multi-elements. In addition, the industrialization of zone refining technology is also the main development direction in the future. With the deepening of research, zone refining technology will definitely develop toward the industrialization of low cost, practicality, high efficiency, high reliability, and high complexity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, X.Y.; Tian, Q.H. High Purity Metal. Materials; Metallurgical Industry Press: Beijing, China, 2010. [Google Scholar]
- Guo, X.; Zhou, Y.; Zha, G. A novel method for extracting metal Ag and Cu from high value-added secondary resources by vacuum distillation. Sep. Purif. Technol. 2020, 242, 116787. [Google Scholar] [CrossRef]
- Virolainen, S.; Suppula, I.; Sainio, T. Continuous ion exchange for hydrometallurgy: Purification of Ag(I)–NaCl from divalent metals with aminomethylphosphonic resin using counter-current and cross-current operation. Hydrometallurgy 2014, 142, 84–93. [Google Scholar] [CrossRef]
- Itam, Z.; Beddu, S.; Mohammad, D. Extraction of metal oxides from coal bottom ash by carbon reduction and chemical leaching. Mater. Today Proc. 2019, 17, 727–735. [Google Scholar] [CrossRef]
- Lu, X.W.; Peng, J.B. Preparation of high purity indium by electrolytic refining method. Min. Metall. 2018, 27, 54–57. [Google Scholar]
- Zhao, Q.S.; Niu, X.D. Purification of high purity germanium by zone refining. Guangzhou Chem. Ind. 2019, 47, 88–90. [Google Scholar]
- Pfann, W.G.; Olsen, K.M. Purification and prevention of segregation in single crystals of germanium. Phys. Rev. 1953, 89, 322–323. [Google Scholar] [CrossRef]
- Ho, C.D.; Yeh, H.M.; Yeh, T.L. Optimal zone lengths in multi-pass zone-refining processes. Sep. Technol. 1996, 6, 227–233. [Google Scholar] [CrossRef]
- Liu, Y.B.; Yang, H.A. Determination on 15 trace impurity elements in high purity tin by glow-discharge mass spectrometry. Yunnan Metall. 2018, 47, 72–77. [Google Scholar]
- Reeks, W.; Davies, H.; Marchisio, S. A review: Interlayer Joining of Nickel Base Alloys. J. Adv. Join. Process. 2020. [Google Scholar] [CrossRef]
- Ledford, C.; Rock, C.; Tung, M. Evaluation of electron beam powder bed fusion additive manufacturing of high purity copper for overhang structures using in-situ real time backscatter electron monitoring. Procedia Manuf. 2020, 48, 828–838. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Z.; Cao, Y. Overview of cobalt resources and comprehensive analysis of cobalt recovery from zinc plant purification residue-a review. Hydrometallurgy 2020, 193, 105327. [Google Scholar] [CrossRef]
- Jiao, H.; Song, W.L.; Chen, H. Sustainable recycling of titanium scraps and purity titanium production via molten salt electrolysis. J. Clean. Prod. 2020, 261, 121314. [Google Scholar] [CrossRef]
- Xie, H.; Zhao, H.; Wang, J. High-performance bismuth-gallium positive electrode for liquid metal battery. J. Power Sources 2020, 472, 228634. [Google Scholar] [CrossRef]
- Li, X.Y.; Lin, Z.L.; Mi, J.R. Research on preparation technology of ultra-high purity germanium polycrystalline material. Yunnan Metall. 2020, 49, 56–60. [Google Scholar]
- Xu, S.L.; Liu, Z.Q.; Chang, Y.C. Summary of the preparation method of high purity to tellurium and their oxides. Mar. Electr. 2019, 39, 46–50. [Google Scholar]
- Mahinroosta, M.; Allahverdi, A. Production of high purity α-alumina and γ-alumina from aluminum dross. Encycl. Renew. Sustain. Mater. 2020. [Google Scholar] [CrossRef]
- Li, W.L.; Luo, Y.H. The review of high purity metal produced by zone refining. Min. Metall. 2010, 19, 57–62. [Google Scholar]
- Zhou, Z.H.; Mo, H.B. Preparation of high purity indium by electrolytic refining-zone melting. Chin. J. Rare Met. 2004, 28, 807–810. [Google Scholar]
- Hong, W.; Hong, Y.; Dan, W. Making the metal in high solidification by the way of zone refining. Chem. Eng. 2001, 3, 16–17. [Google Scholar]
- Pfann, W.G. Techniques of zone melting and crystal growing. Solid State Phys. 1957, 4, 423–521. [Google Scholar]
- Pfann, W.G. Principles of zone-melting. J. Miner. Met. Mater. Soc. 1952, 4, 747–753. [Google Scholar] [CrossRef]
- Yang, G.; Govani, J.; Mei, H. Investigation of influential factors on the purification of zone-refined germanium ingot. Cryst. Res. Technol. 2014, 49, 269–275. [Google Scholar] [CrossRef]
- Zhai, X.J.; Fu, Y.; Zhang, X.M. The calculation and determination on distribution coefficient of impurities Fe and Si in aluminum. Light Met. 2000, 12, 37–39. [Google Scholar]
- Hu, G.X.; Cai, X. Materials Science; Shanghai Jiao Tong University Press: Shanghai, China, 2006. [Google Scholar]
- Burton, J.A.; Prim, R.C.; Slichter, W.P. The distribution of solute in crystals grown from the melt. Part, I. Theoretical. J. Chem. Phys. 1953, 21, 1987–1991. [Google Scholar] [CrossRef]
- Liu, W.S.; Liu, S.H.; Ma, Y.Z. The latest development of zone melting technology. Rare Met. Cem. Carbides 2013, 41, 66–71. [Google Scholar]
- Prasad, D.S.; Munirathnam, N.R.; Rao, J.V. Effect of multi-pass, zone length and translation rate on impurity segregation during zone refining of tellurium. Mater. Lett. 2006, 60, 1875–1879. [Google Scholar] [CrossRef]
- Ho, C.D.; Yeh, H.M.; Yeh, T.L. The optimal variation of zone lengths in multi-pass zone refining processes. Sep. Purif. Technol. 1999, 15, 69–78. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, J.; Xu, J. Preparation of high-purity tin by zone melting. Russ. J. Non Ferr. Met. 2020, 61, 9–20. [Google Scholar] [CrossRef]
- Wan, H.; Xu, B.; Yang, B. The impurities distribution and purification efficiency of high-purity aluminum preparation by zone melting in vacuum. Vacuum 2020, 171, 108839. [Google Scholar] [CrossRef]
- Liu, J.; Zee, R.H. Growth of molybdenum-based alloy single crystals using electron beam zone melting. J. Cryst. Growth 1996, 163, 259–265. [Google Scholar] [CrossRef]
- Su, H.; Shen, Z.; Ren, Q. Evolutions of rod diameter, molten zone and temperature gradient of oxide eutectic ceramics during laser floating zone melting. Ceram. Int. 2020, 46, 18750–18757. [Google Scholar] [CrossRef]
- Hu, J.; Ruo, Q.B. Application of a genetic algorithm to optimize redistribution process in zone refining of cerium. Rare Metal. Mater. Eng. 2017, 46, 3633–3638. [Google Scholar]
- Li, H.G. Principles of Metallurgy; Science Press: Beijing, China, 2005. [Google Scholar]
- Ho, C.D.; Yeh, H.M.; Yeh, T.L. Numerical analysis on optimal zone lengths for each pass in multi-pass zone-refining processes. Can. J. Chem. Eng. 1998, 76, 113–119. [Google Scholar] [CrossRef]
- Ghosh, K.; Mani, V.N.; Dhar, S. Numerical study and experimental investigation of zone refining in ultra-high purification of gallium and its use in the growth of GaAs epitaxial layers. J. Cryst. Growth 2009, 311, 1521–1528. [Google Scholar] [CrossRef]
- Ghosh, K.; Mani, V.N.; Dhar, S.A. Computational study and experimental validation of zone refining process for ultra-purification of gallium for opto-electronic applications. Trans. Indian Inst. Met. 2008, 61, 201–206. [Google Scholar] [CrossRef]
- Bachmann, K.J.; Clark, L.; Buehler, E. Zone melting of indium phosphide. J. Electron. Mater. 1975, 4, 741–756. [Google Scholar] [CrossRef]
- Dost, S.; Liu, Y.C.; Haas, J. Effect of applied electric current on impurity transport in zone refining. J. Cryst. Growth 2007, 307, 211–218. [Google Scholar] [CrossRef]
- Yuan, G.; Shiming, Z. Preparation of ultra-pure indium. Non Ferr. Met. Extr. Metall. 2013, 7, 61–64. [Google Scholar]
- Zhou, Z.H.; Mo, H.B. Preparation of high purity indium. Min. Metall. Eng. 2003, 23, 40–43. [Google Scholar]
- Yin, W.H. New development of high purity and ultra high purity refractory metals. Rare Metal. Mater. Eng. 1991, 3, 1–9. [Google Scholar]
- Zhang, X.; Friedrich, S.; Friedrich, B. Production of high purity metals: A review on zone refining process. J. Cryst. Process. Technol. 2018, 8, 23. [Google Scholar] [CrossRef]
- Liang, J.; Li, Y.C.; Lin, X.H. Application of high purity metal detection technology. China Molybdenum Ind. 2019, 43, 5–8. [Google Scholar]
- Reiss, H. Mathematical methods for zone-melting processes. J. Miner. Met. Mater. Soc. 1954, 6, 1053–1059. [Google Scholar] [CrossRef]
- Lee, H.Y.; Oh, J.K.; Lee, D.H. Purification of tin by zone refining with development of a new model. Metall. Trans. 1990, 21, 455–461. [Google Scholar] [CrossRef]
- Cheung, T.; Cheung, N.; Tobar, C.M. Application of a genetic algorithm to optimize purification in the zone refining process. Mater. Manuf. Process. 2011, 26, 493–500. [Google Scholar] [CrossRef]
- Tan, Y. Contact Heating Metal. Indium Zone-Refining Device and the Analysis of Temperature Field Simulation; Guilin University of Technology: Guilin, China, 2017. [Google Scholar]
- Chen, L.N. Research on Purification of Indium by Oxidation Refining-Zone Refining Combined Method; Guilin University of Technology: Guilin, China, 2021. [Google Scholar]
- Bochegov, V.I.; Parakhin, A.S. Lmiting impurity distribution during zone refining. Tech. Phys. Lett. 2014, 40, 460–461. [Google Scholar] [CrossRef]
- Spim, J.A.; Bernadou, M.J.S.; Garcia, A. Numerical modeling and optimization of zone refining. J. Alloy. Compd. 2000, 298, 299–305. [Google Scholar] [CrossRef]
- Cheung, N.; Bertazzoli, R.; Garcia, A. Numerical and experimental analysis of an approach based on variable solute distribution coefficients during purification by zone refining. Sep. Purif. Technol. 2007, 52, 504–511. [Google Scholar] [CrossRef]
- Zhang, X.; Friedrich, S.; Liu, B. Computation-assisted analyzing and forecasting on impurities removal behavior during zone refining of antimony. J. Mater. Res. Technol. 2020, 9, 1221–1230. [Google Scholar] [CrossRef]
- Nakamura, M.; Watanabe, M.; Tanaka, K. Zone refining of aluminum and its simulation. Mater. Trans. 2014, 55, 664–670. [Google Scholar] [CrossRef]
- Li, Q. Purification of Indium by Zone Refining Method and Its Simulation; Guilin University of Technology: Guilin, China, 2018. [Google Scholar]
- Li, Y.C.; Liu, Y.; Zhang, C.S.; Le, W.H.; Yu, L.; Luo, K. Research on the preparation of high-purity indium by zone refining. Min. Metall. Eng. 2014, 34, 104–107. [Google Scholar]

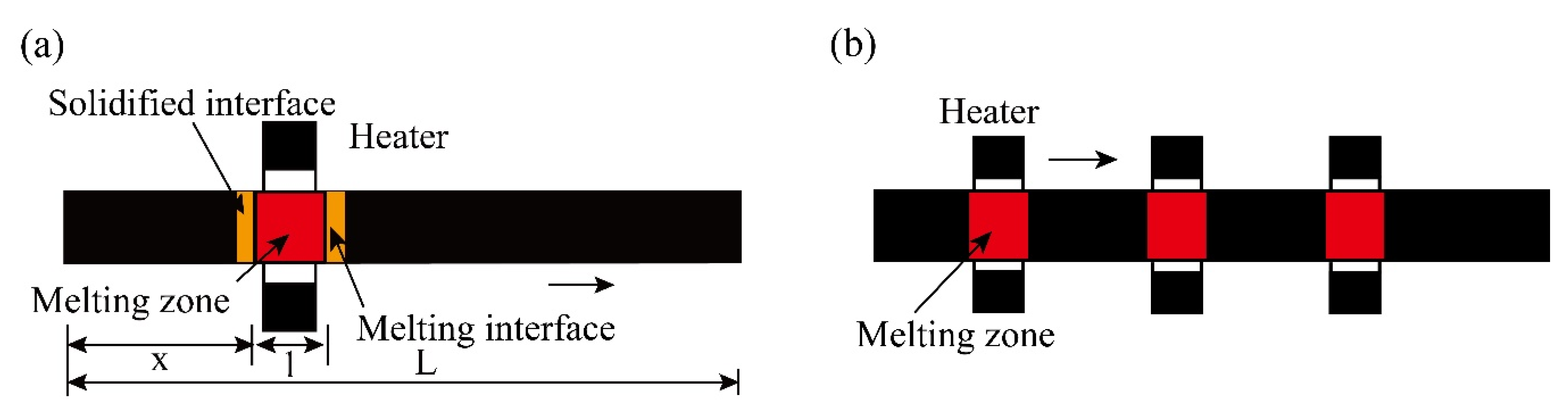

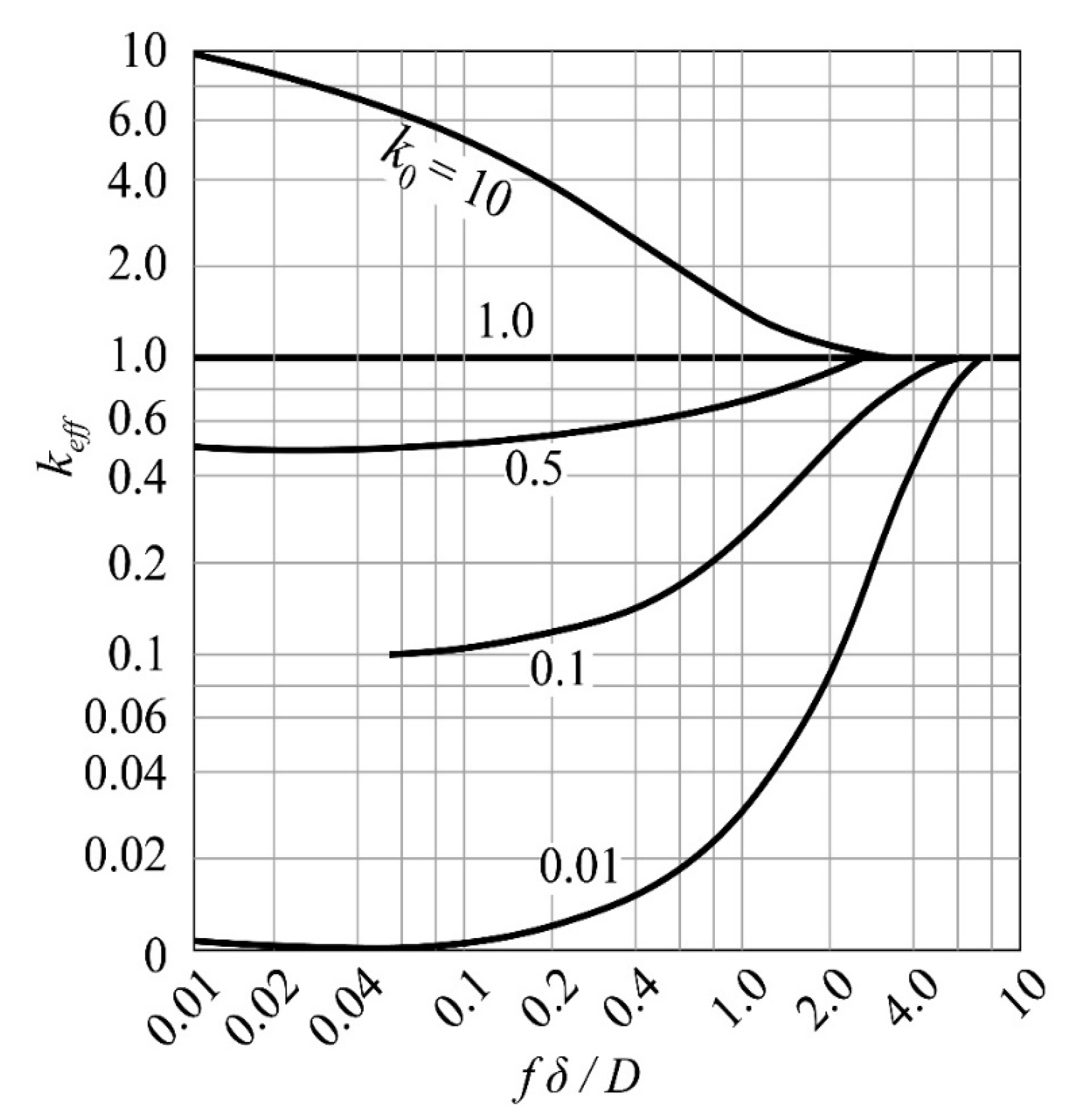
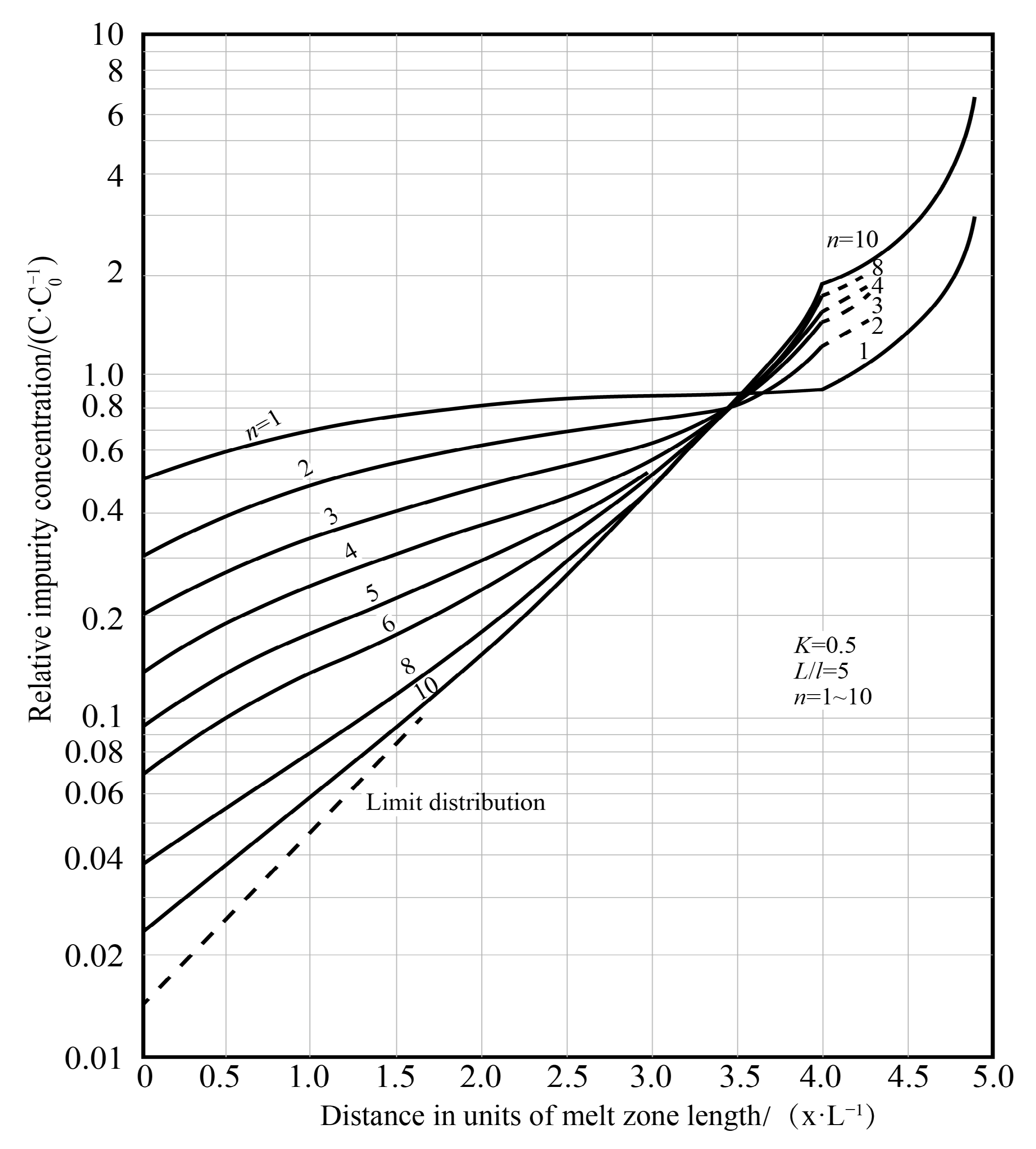
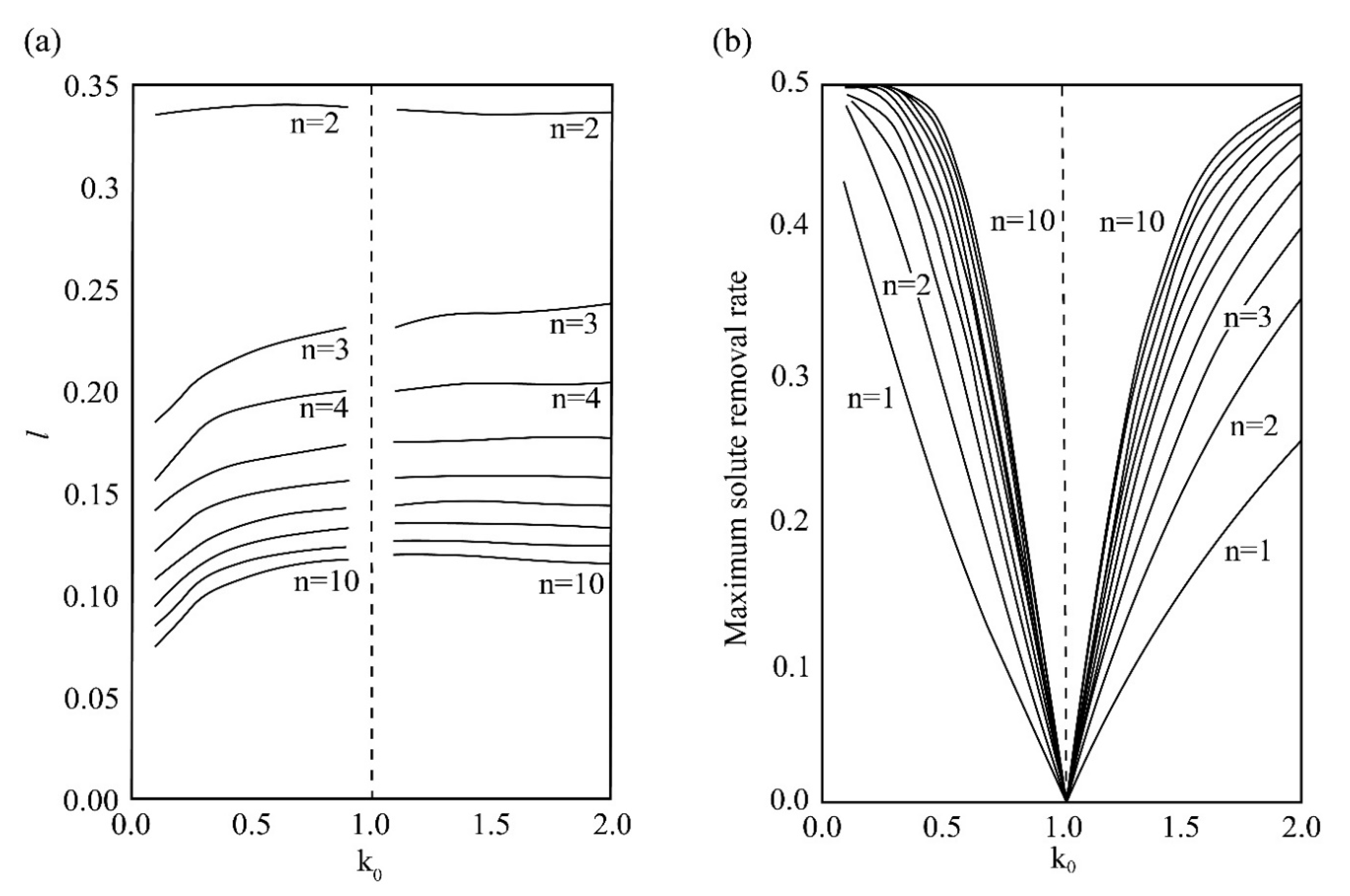
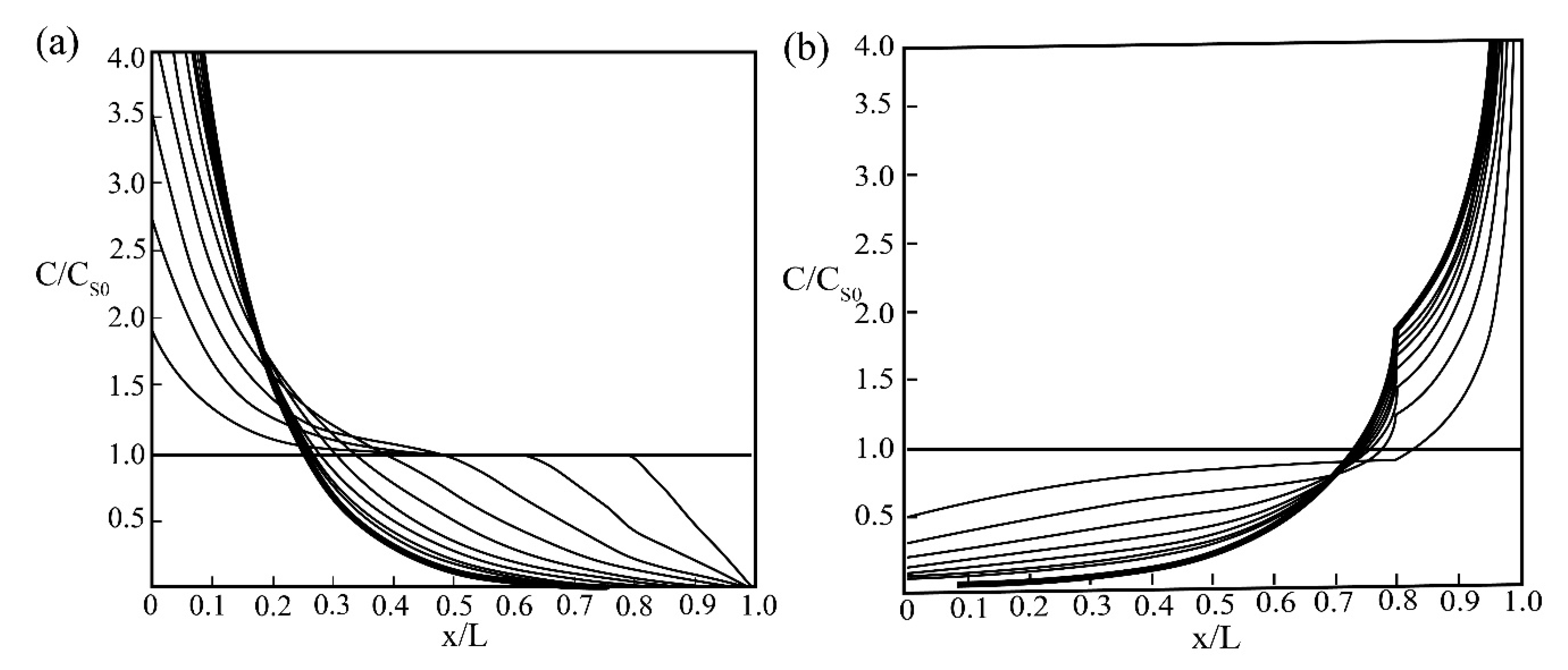

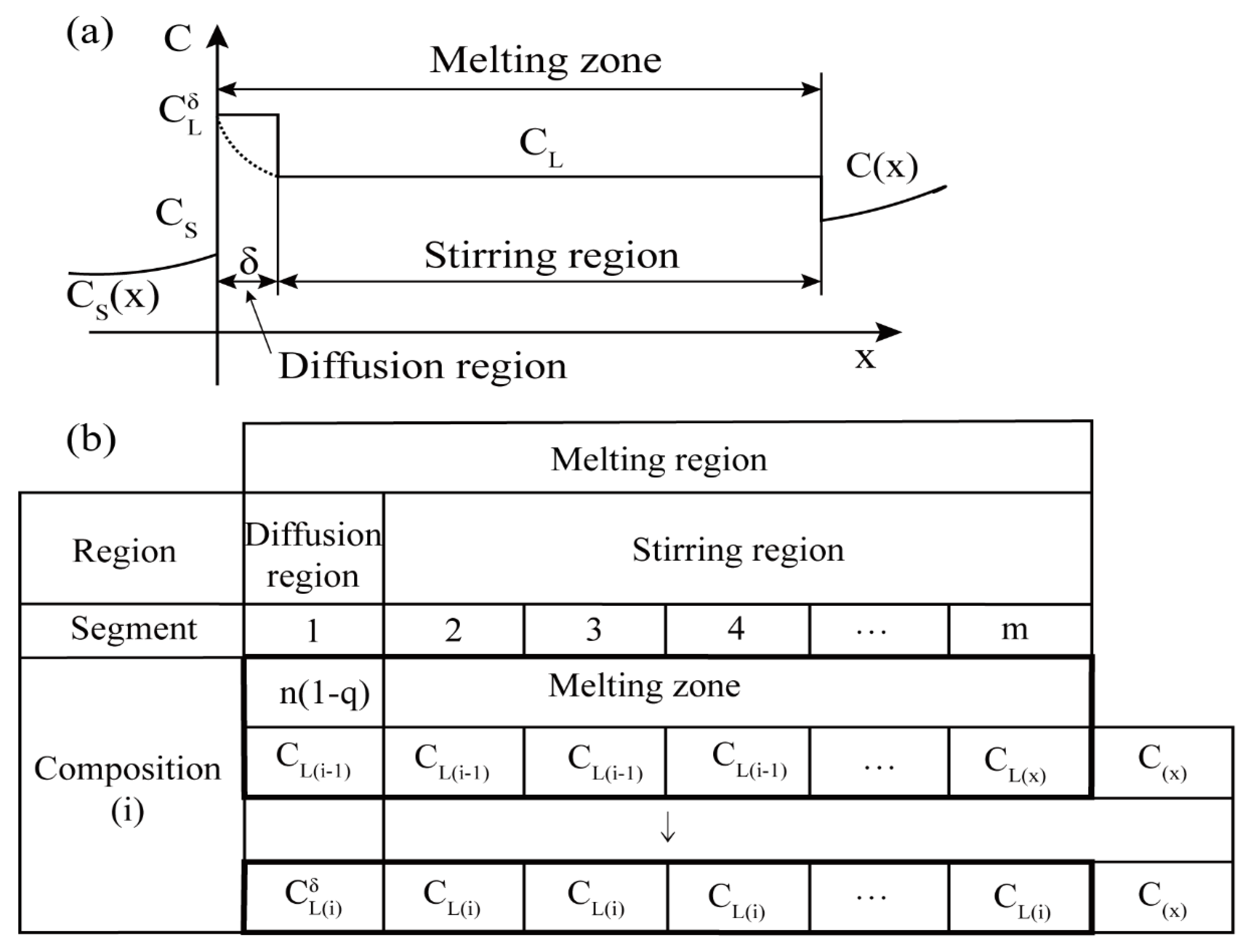
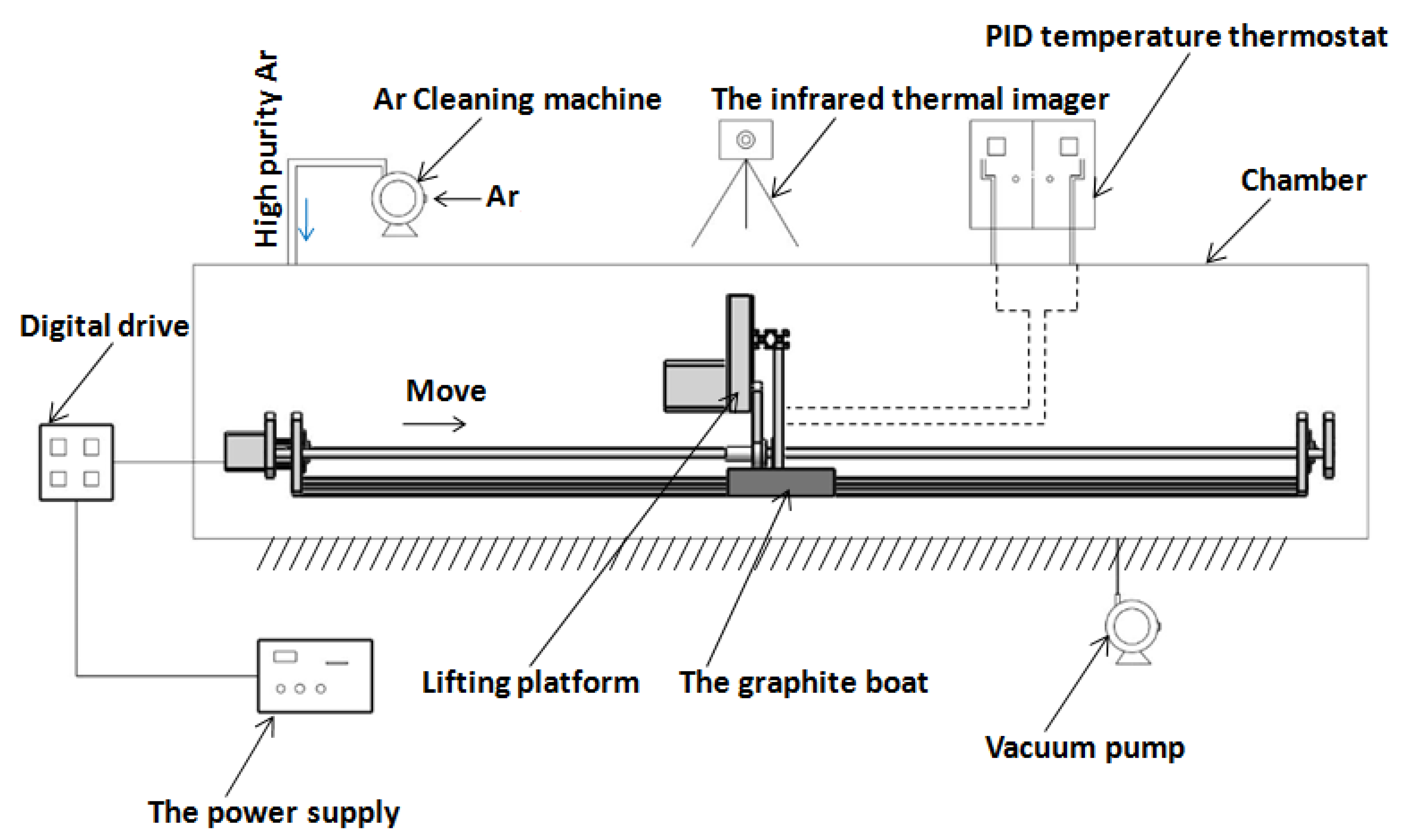

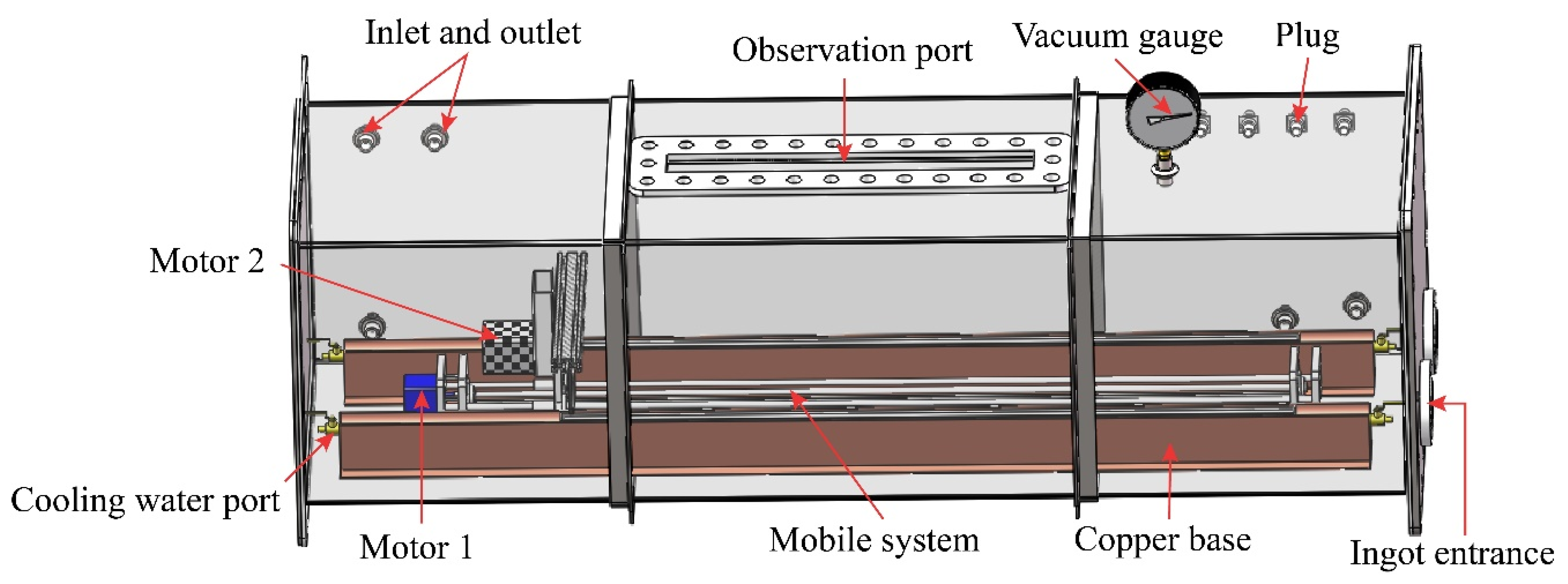
| Zone Refining Times | 1 | 2 | 3 | 4 | 5–8 | 9–19 | ≥20 | |
|---|---|---|---|---|---|---|---|---|
| Normalized melting zone length | 1 | 0.35 | 0.25 | 0.2 | 0.15 | 0.1 | 0.05 |
| Elements | Al | As | Cd | Cu | Fe | Mg | Ni | Pb | Ga | Si | Sn | Te | Zn | Ag |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Purity grade | 9N | 9N | 7N | 10N | 9N | 8N | 7N | 7N | 7N | 9N | 7N | 7N | 7N | 8N |
| Elements | Ge | In | Ce | |||||||||||
| Purity grade | 10N | 7N | 7N |
| Category | Heating Method | Advantage | Disadvantage | Scale |
|---|---|---|---|---|
| Floating zone refining | Electron beam heating, induction heating, plasma heating, light heating | The ingot does not touch the container, so the product purity is high, and the equipment occupies a small space. | The melting zone is supported by surface tension, so controlling the shape and stability of the melting zone is the key, and the output is low. | Small batch |
| Horizontal zone refining | Induction heating, resistance heating | Simple equipment, continuous purification of multiple melting zones, easy loading and unloading of materials, easy identification of interfaces, and the total length of ingots can be increased or decreased as needed | Large footprint | Batch |
| Analytical Method | Sampling Method | Measuring Range (g/g) | Explanation |
|---|---|---|---|
| GDMS [44] | Solid | Constant~10−12 | The matrix effect is small, the sample processing is simple, it can avoid pretreatment pollution and loss, it is fast and efficient, the detection limit is low, and standard samples can be used, but the price is expensive. The discharge is stable, and the analysis sample can be peeled layer by layer for surface and depth analysis. The self-absorption effect is small. Multiple elements can be determined simultaneously. |
| ICP-MS | Liquid | 10−6~10−12 | High resolution and sensitivity, a wide measurement range, a need to try to eliminate the matrix effect and isotope interference, and the sample processing process is longer. |
| GF-AAS | Solid | 10−6~10−9 | The number of single analysis is small, the analysis range is narrow, and it is not suitable for high melting point metals. |
| ICP-AES [45] | Liquid | Constant~10−6 | Fast speed, high sensitivity, small matrix effect, low detection limit, and serious spectrum interference and matrix interference. Multi-element simultaneous analysis method with the widest range of analysis elements and the largest content span. |
| TXRF | Solid | Constant~10−12 | Fast, simple, and economical non-destructive testing, which can perform multi-element analysis at the same time, but it can only perform surface analysis, and the detection limit is low. |
| NAA | Solid, liquid | 10−6~10−13 | High sensitivity, high accuracy and precision, and sensitivity varies from element to element. It can only measure the content of elements. It requires a small nuclear reactor and has the risk of nuclear radiation. Less sampling, non-destructive analysis. The detection equipment is expensive. |
| NTIMS | Liquid | 10−10~10−14 | It has a lower detection limit than ICP-MS, can be used for isotope age studies, and can accurately measure Re and Os. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Kang, X.; Chen, L.; Luo, K.; Jiang, Y.; Cao, X. Research Status of High-Purity Metals Prepared by Zone Refining. Materials 2021, 14, 2064. https://doi.org/10.3390/ma14082064
Yu L, Kang X, Chen L, Luo K, Jiang Y, Cao X. Research Status of High-Purity Metals Prepared by Zone Refining. Materials. 2021; 14(8):2064. https://doi.org/10.3390/ma14082064
Chicago/Turabian StyleYu, Liang, Xiaoan Kang, Luona Chen, Kun Luo, Yanli Jiang, and Xiuling Cao. 2021. "Research Status of High-Purity Metals Prepared by Zone Refining" Materials 14, no. 8: 2064. https://doi.org/10.3390/ma14082064
APA StyleYu, L., Kang, X., Chen, L., Luo, K., Jiang, Y., & Cao, X. (2021). Research Status of High-Purity Metals Prepared by Zone Refining. Materials, 14(8), 2064. https://doi.org/10.3390/ma14082064






