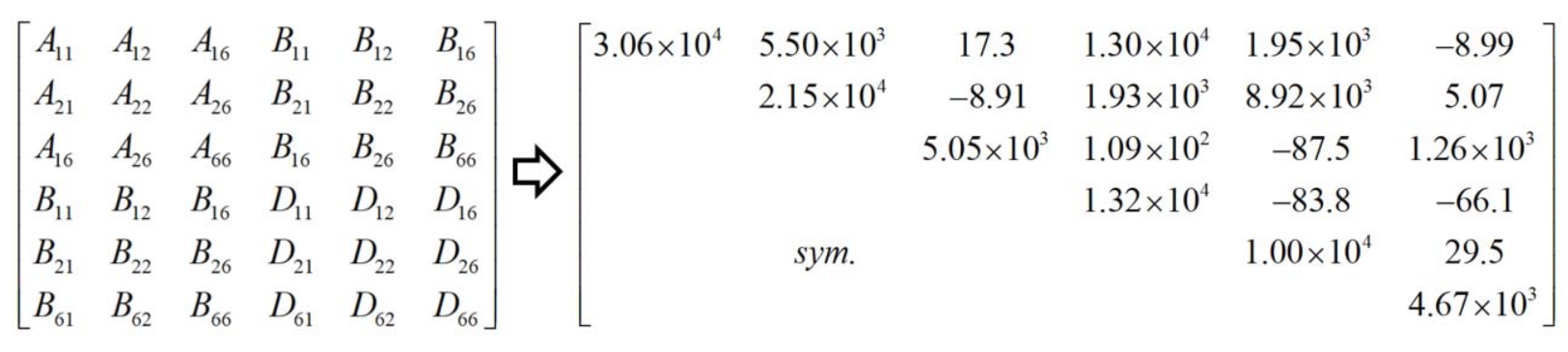1. Introduction
With the development of modern science and technology, thin plate theory cannot meet the requirement of industrial production. The main disadvantage is that the increase in stiffness can only be achieved by changing the thickness of thin plate, but the thin plate theory is no longer applicable when the thickness of thin plate reaches a certain value, and the shear effect needs to be considered. In addition, the increase in stiffness can also be achieved by bonding laminated plates and sandwich plates, which is not suitable for industrial production and cannot meet engineering requirements [
1,
2]. Moreover, subsequent studies have found that the production process of laminated plates and sandwich plates is relatively complex and prone to degumming or dislocation, which is not conducive to the use in industrial production [
3,
4,
5].
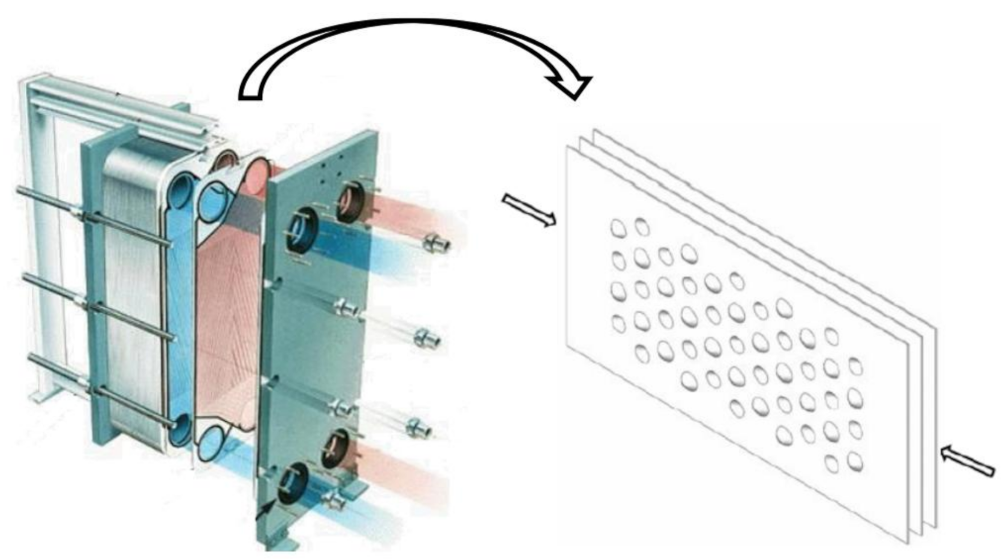
As a new type of lightweight structure, the convex-concave plate, made by stamping and rolling can avoid the shortcomings of the degumming, dislocation, and complicated process, resulting in high industrial application value and reliability. Although its thickness is very small, it has light weight, high strength, and high stiffness. This is because the convexities of the plate changes the plate structure after stamping or rolling, and the stiffness is greatly enhanced. Furthermore, the convexities can absorb a lot of energy in the process of impact vibration, and the loss of the plate can be greatly reduced [
6]. This kind of plate also has high heat dissipation efficiency and excellent sound insulation and heat insulation performance, which cannot be achieved by the sandwich plate and laminated plate. In fact, it has been used as the plate heat exchanger as shown in
Figure 1.
Due to the existence of the convexities, the energy absorption capacity is obviously improved and the service life is greatly enhanced [
7,
8,
9]. Haldar et al. [
10] focused on studying the influence of the thickness of convexities on the energy absorption and obtained the optimal energy absorption properties of the convex-concave plate by comparing the experimental and finite element simulation results. Sashikumar [
11] tested the energy absorption capacity of an aluminum egg-box plate in commercial vehicles and proposed that the natural constraints within the geometric structure of egg-box plates have a positive impact on their energy absorption capacity. Akisanya and Fleck [
12] discussed the dependence of strength and energy absorption of egg-box material on the geometric shape by using the finite element prediction method and determined the variation of the stiffness and strength of egg-box material with relative density. Ma et al. [
13] concluded that the periodic origami structure has better energy absorption capacity by comparing the dynamic analysis and experimental and numerical results.
In addition to the traditional single-layer convex-concave plate, the laminated convex-concave plate has also been widely investigated. Chang et al. [
14,
15,
16] adopted the experimental method to study the energy absorbing ability and deformation process of two kinds of sinusoidal convex-concave plate reinforced by fiber materials during quasi-static compression. Zhang et al. [
17] tested the performance of egg-box panel stuffed whipple shield from impact area, cell size and the axial offset etc. At present, experiments and finite element simulation are mostly used to investigate the energy absorption capacity, failure, and heat transfer performance of concave-convex plates.
The laminated composite plate by nature has two dimensions larger than the thickness dimension by an order of magnitude. In recent years, the variational asymptotic method (VAM) has been used to strictly split the plate/shell problem into the through-the-thickness linear analysis (1-D analysis) and 2D nonlinear plate analysis by using the small parameter of width-to-thickness ratio. This method combines advantages of both asymptotic and variational methods, and considers all possible deformations during problem formulations while avoiding any kinematic assumptions. Atilgan and Hodges [
18,
19] developed VAM for laminated plates in which each lamina exhibits monoclinic symmetry about its own midplane. Sutyrin and Hodges [
20] extended VAM to laminated plate, the material properties of which varied through the thickness and for which each lamina was orthotropic. Later, Sutyrin [
21] developed linear, asymptotically correct theories for inhomogeneous orthotropic plates, for example, laminated plates with orthotropic laminae. Yu et al. [
22] developed an accurate stress/strain recovery procedure for laminated plates that can be implemented in standard finite element programs. Kamineni and Burela [
23] developed constraint method for laminated composite flat stiffened panel using VAM. Further, Zhong and Yu [
24,
25,
26,
27,
28] successfully constructed the equivalent model of various composite structures by using this method.
The composite conical convex-concave plate (CCCP) studied in this article is a new type of convex-concave plate. Most of the research at this stage is limited to the manufacturing process, and its equivalent mechanical properties have not been investigated, especially the natural vibration and stability characteristics. Therefore, it is necessary to study the equivalent stiffness of the orthotropic convex-concave plate, which lays a foundation for studying the deformation of convex-concave plates under applied load and provides a theoretical basis for the reasonable design of its geometric parameters.
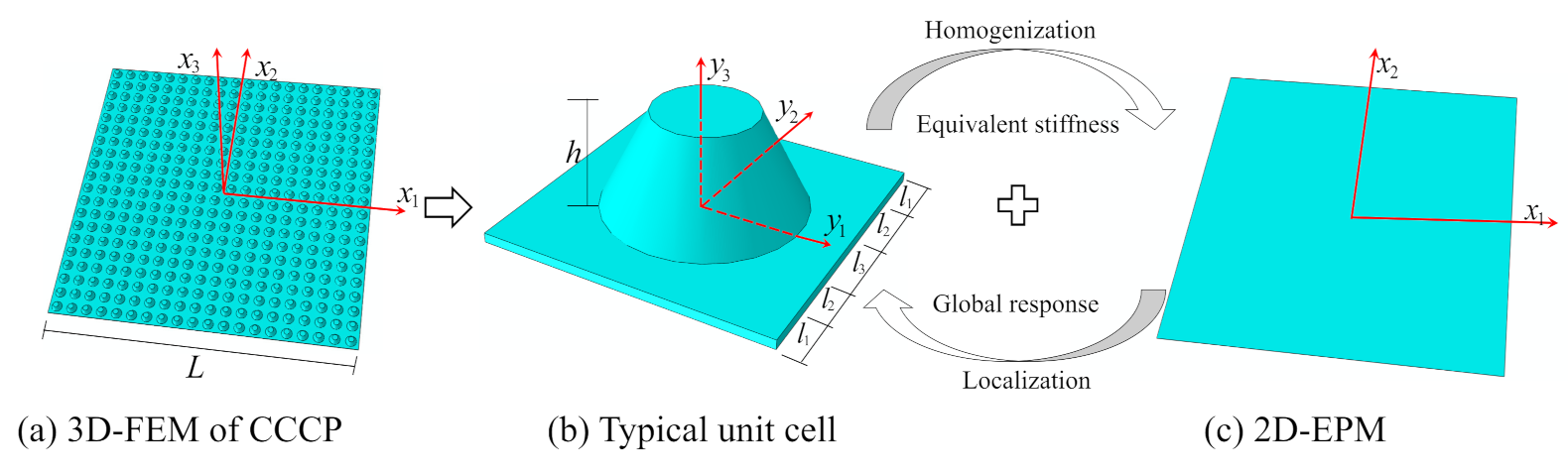
In this work, a VAM-based equivalent plate model is developed to predict the effective performance of CCCP. The organization of this paper is as follows. The theoretical formulation for the VAM-based 2D equivalent plate model (2D-EPM) is deduced in
Section 2. Numerical examples of static displacement, global buckling, and free-vibration analysis of CCCP are used in
Section 3 to verify the accuracy and effectiveness of 2D-EPM.
Section 4 investigates the influences of layup configurations and geometric parameters on the effective performances of CCCP by using the 2D-EPM. In
Section 5, the effective performance of bidirectional CCCP and CCCP is compared. Finally, some conclusions are drawn in
Section 6.
3. Model Validation
In this section, the accuracy and effectiveness of the equivalent model are verified by comparing with the results of static displacement, free-vibration, and global buckling analysis of the three-dimensional finite element model (3D-FEM).
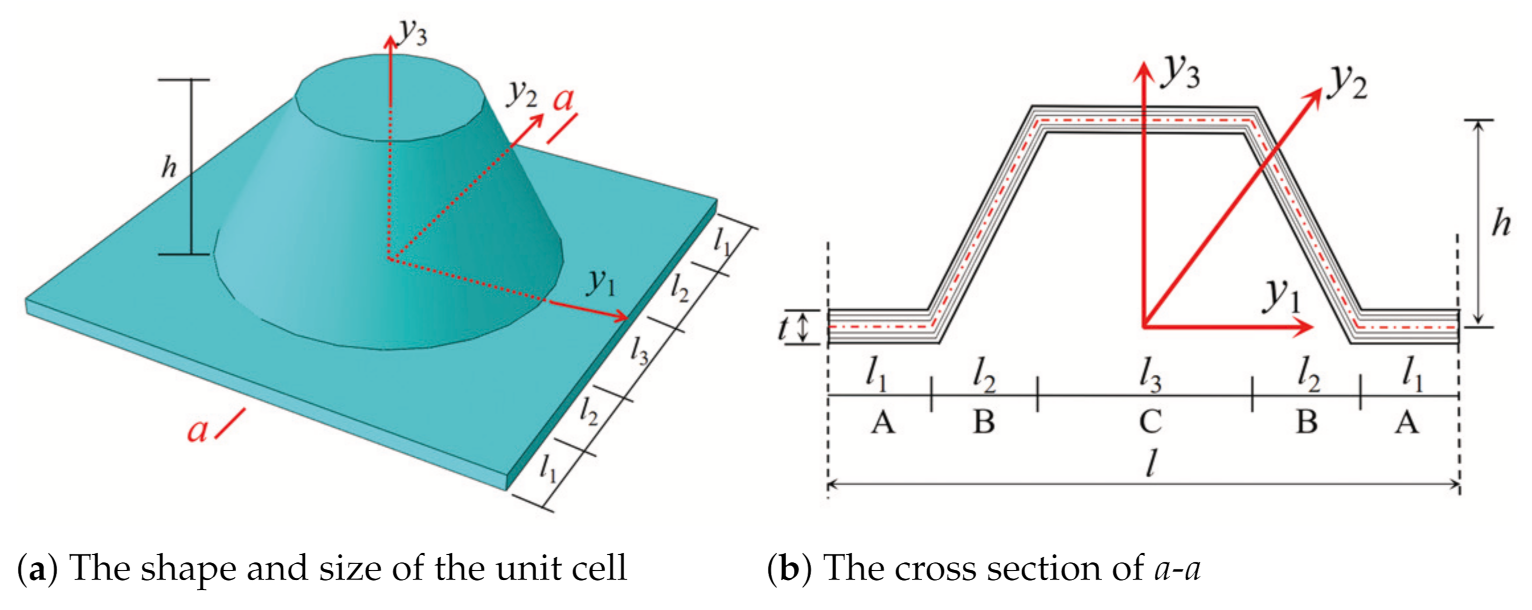
The dimensions of unit cell are
mm,
mm,
mm,
mm,
mm, and
mm. The whole model of CCCP is the repetition of the unit cell in
Figure 2b 20 times along
and
directions. The layup configuration of laminate is
, and each ply thickness equals 0.1 mm. The material used is a unidirectional carbon fiber/epoxy resin composite (T300/7901), and the lamina properties are
= 48.36 GPa,
= 12.74 GPa,
= 11.37 GPa,
=
= 4.59 GPa,
= 0.078,
=
= 0.397,
= 1670
. The effective plate properties of CCCP obtained by present model is shown in
Figure 4.
3.1. Static Deformation Analysis
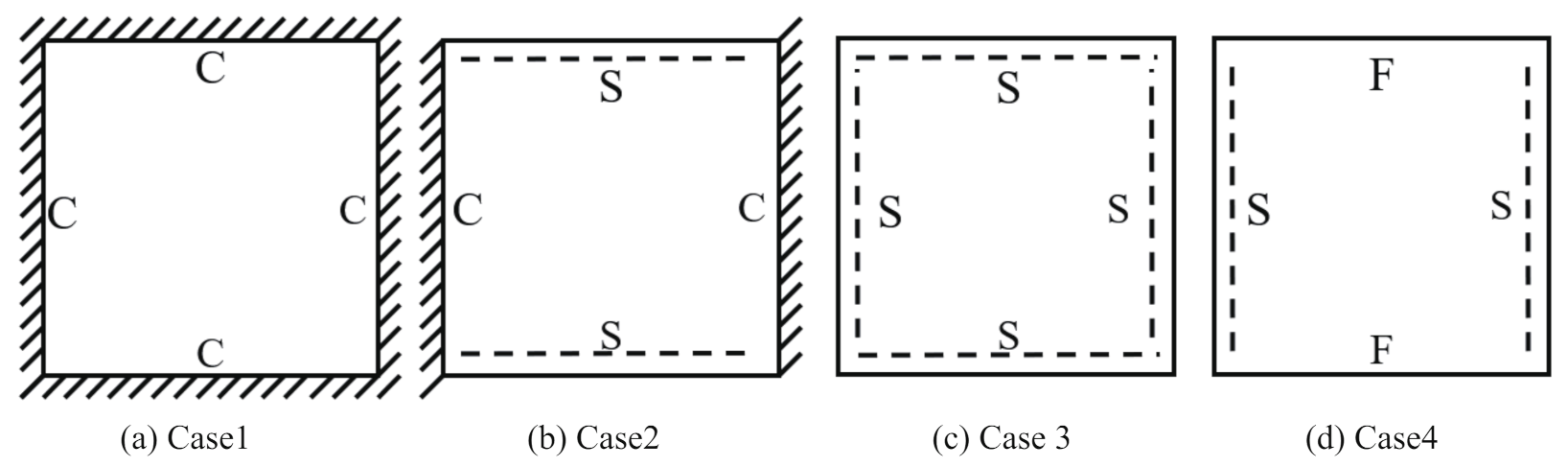
To investigate the static deformation of CCCP under different boundary conditions, the four cases shown in
Figure 5 are considered.
Table 1 lists the static displacements of 2D-EPM and 3D-FEM when a concentrated load of 100 N is applied to the center of the plate. It can be seen that the displacement distribution of 2D-EPM agrees with that of 3D-FEM under different boundary conditions. The boundary condition has a great influence on the relative errors. The smaller the boundary constraint is, the larger the displacement error is. However, the maximum error is less than 6% in Case 4, indicating the equivalent stiffness obtained by VAM is accurate, and the present 2D-EPM can well reflect the static displacement of CCCP under different boundary conditions.
3.2. Recovery 3D Field
As shown in Equations (
36)–(
38), the global displacements and strains of 2D-EPM should be imputed into the corresponding unit cell to recover the local field distribution. Note that most of the simplified models cannot predict the accurate local field distribution.
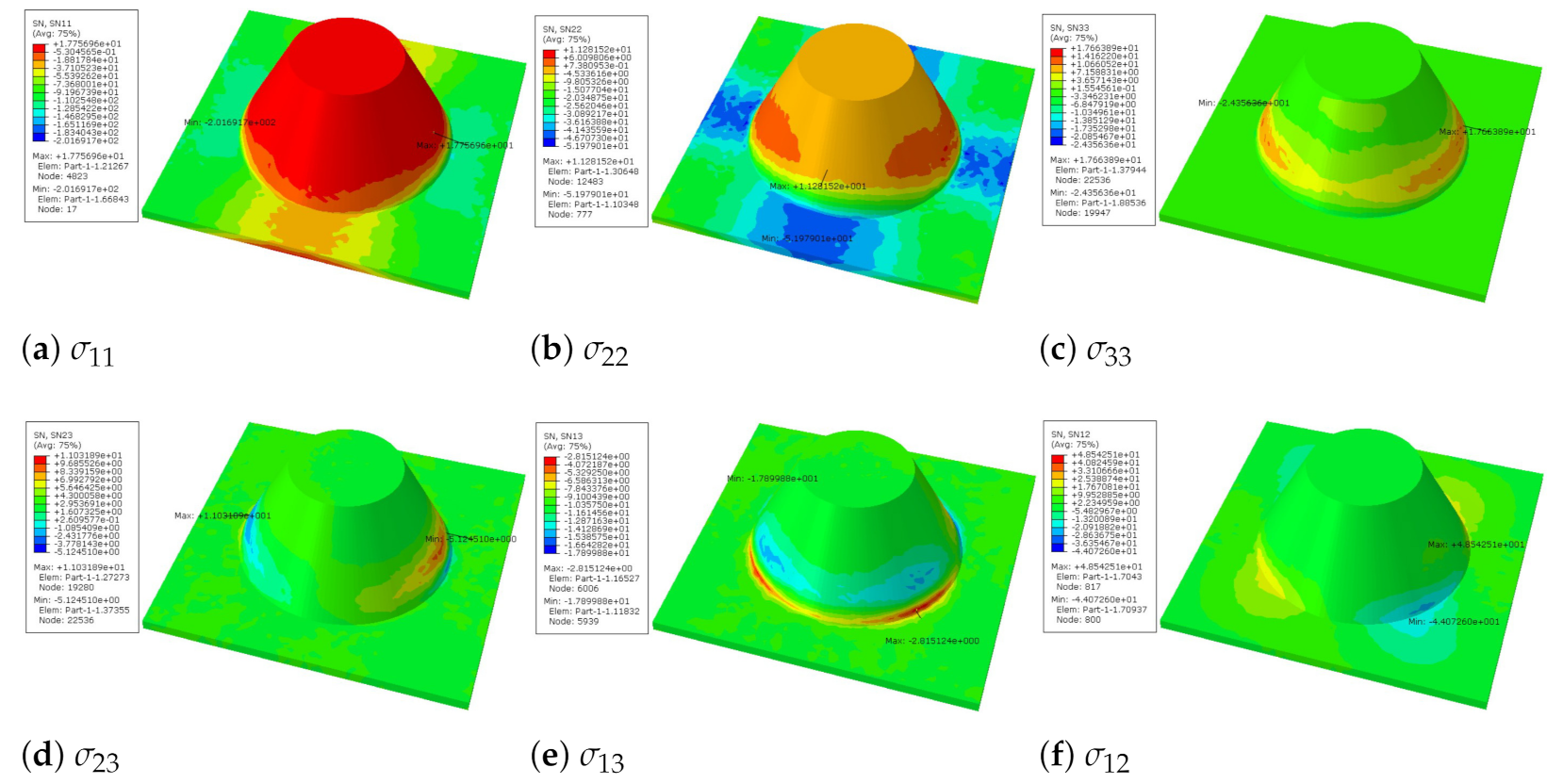
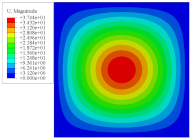
It can be seen from
Figure 6 that the distribution of local stress within the unit cell is not uniform. The values of
and
are larger on the conical convexity, while other stresses are mainly concentrated at the intersection between the flat plate and the conical convexity. That is, these stresses on the conical convexity are very small, and the conical convexity cannot completely resist the load. It can be reasonably explained that the plate fails at the intersection of the flat plate and the conical convexity.
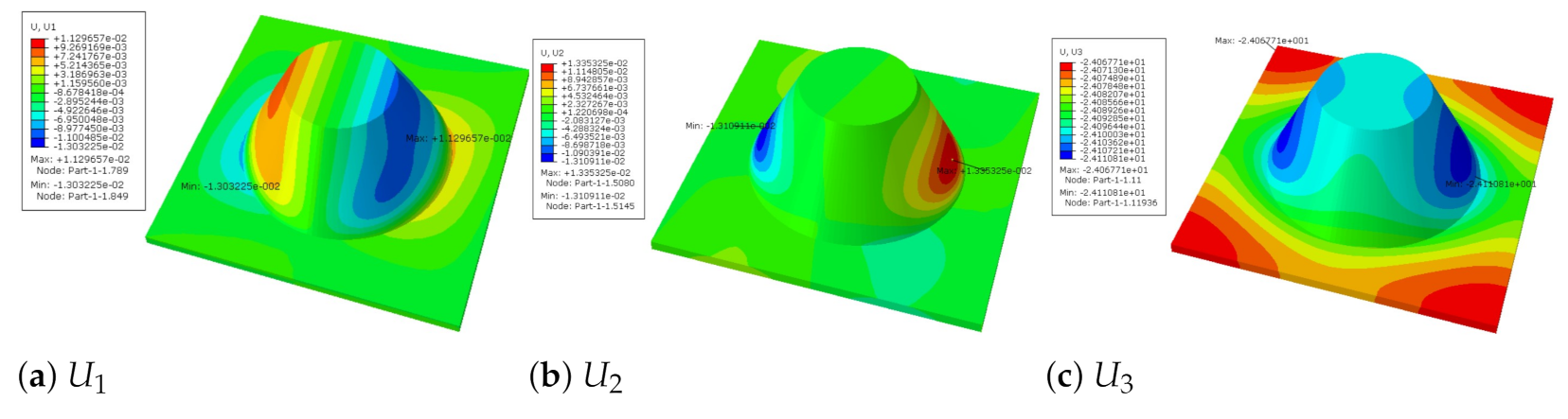
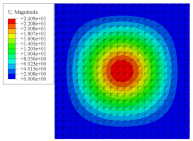
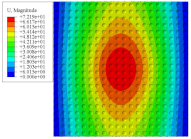
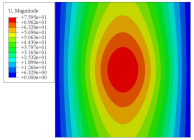
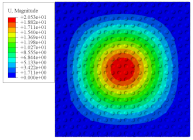
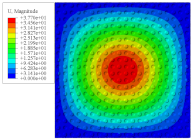
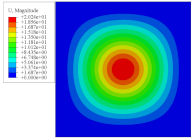
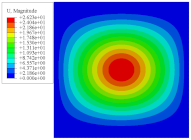
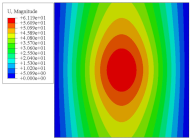
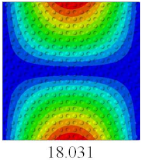
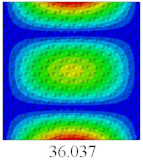
Figure 7 shows the distribution of the local fields within the unit cell closest to the midpoint of the plate in Case 1 (CCCC). It is seen that the displacement within the unit cell is symmetrically distributed, and the minimum displacement is located at the edge of the flat plate, while the maximum displacement is located at the intersection of the flat plate and the conical convexity. The changes of
and
are opposite on both sides of the conical convexity, and the maximum and minimum values of
and
are also located close to the intersection of the flat plate and the conical convexity.
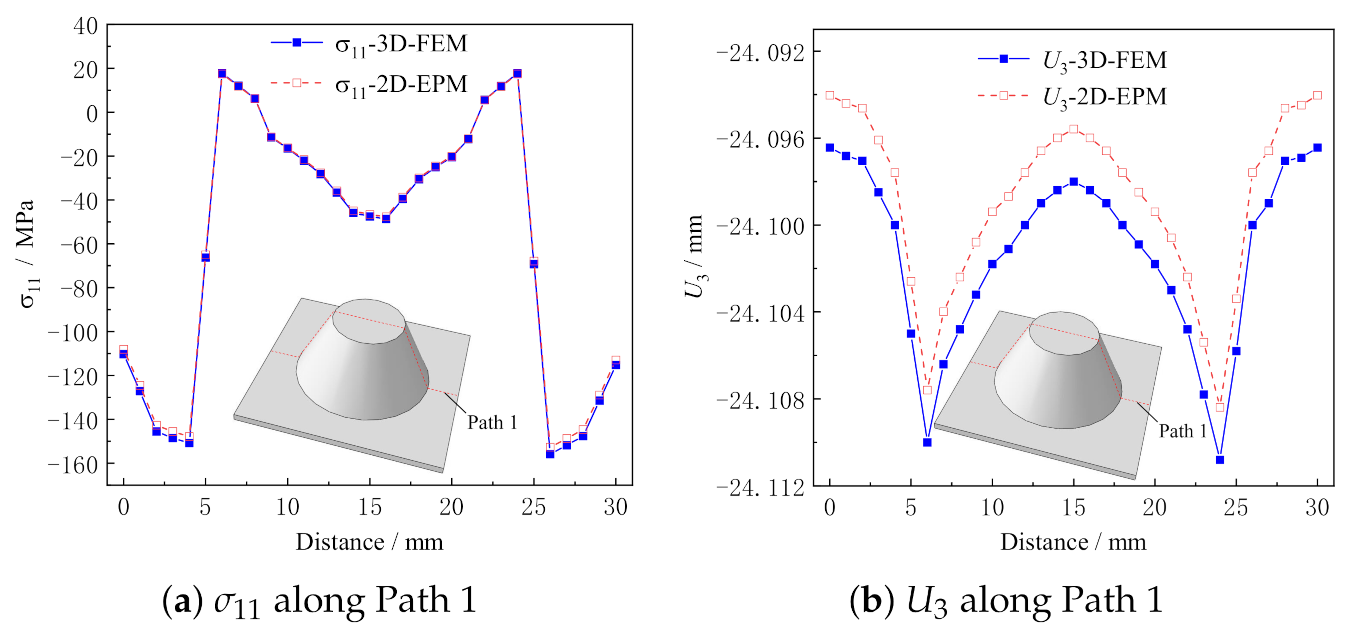
Figure 8 shows the local stress and displacement distributions along Path 1 predicted by 2D-EPM and 3D-FEM. It can be seen that the local stress and displacement distributions predicted by the two models are in good agreement, and the maximum error is less than 2%. The location of stress concentration and the change trend can be obtained directly according to the local field distribution, which provides a reference for the damage analysis of the structure.
3.3. Global Buckling Analysis
In this section, the linear buckling behavior of CCCP is predicted by 2D-EPM and 3D-FEM under the assumption of small displacements. Four sides of CCCP are simple-supported and two opposite sides are pressed.
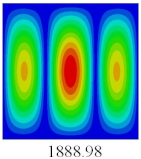
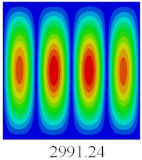
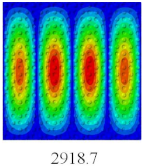
Table 2 shows that the global buckling modes of 2D-EPM are consistent with those of 3D-FEM. For example, there are one, two, three, and four half-wave along the horizontal direction in the first, second, third, and fourth mode shape of 2D-EPM and 3D-FEM, respectively. The maximum error of critical buckling load is 2.08% in the first order buckling mode, indicating the equivalent model based on VAM has high accuracy in buckling analysis of CCCP.
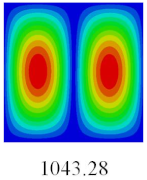
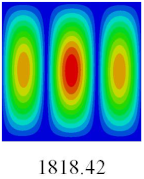
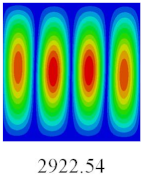
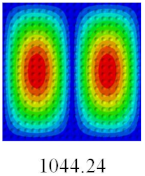
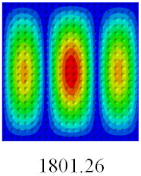
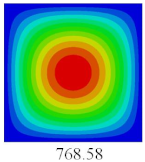
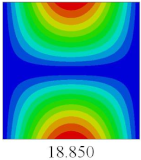
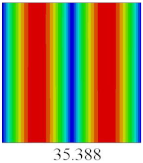
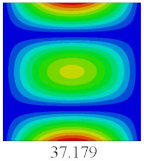
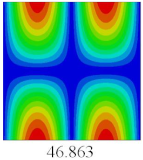
3.4. Free-Vibration Analysis
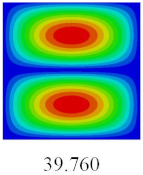
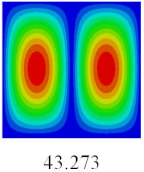
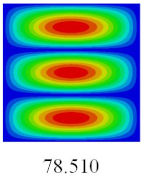
In this section, the natural frequencies and vibration mode shapes of CCCP are predicted by 2D-EPM and 3D-FEM. The geometry and boundary conditions are the same as those in
Section 3.3.
Table 3 shows that the vibration modes predicted by 2D-EPM are consistent with those predicted by 3D-FEM, and the maximum error of natural frequency is within 5%. The accuracy of 2D-EPM based on VAM is verified from the aspect of vibration characteristics.
3.5. Comparison of Calculation Efficiency
To further demonstrate the advantages of the model, the computational efficiencies of the three-dimensional FE model and two-dimensional equivalent model are compared as shown in
Table 4. It can be observed that the present model is more time-efficient and cost-efficient than 3D-FEM in performing static, global buckling, and free-vibration analysis of CCCP. Note that the geometry of CCCP studied in this article is relatively simple, and the advantages of 2D-EPM can be reflected in more complex composite structures.
5. Bidirectional CCCP
The structure introduced in this section is a bidirectional CCCP, and the convex direction along each row and column of the structure is alternately arranged up and down periodically as shown in
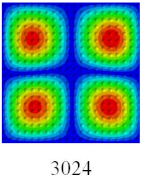
Figure 15, which can be used to improve heat transfer effect and reduce pressure drop. Each convexity and its periphery is regarded as a small element, and only four adjacent elements (2 × 2) need to be studied due to the periodicity of bidirectional CCCP.
The geometrical sizes of unit cell are:
h = 10 mm,
t = 1.0 mm,
= 5 mm,
= 5 mm,
= 10 mm, periodic length
l = 60 mm. The material properties and boundary conditions are the same as those in
Section 3.1. The equivalent stiffness matrix of the bidirectional CCCP obtained by the present model is shown in
Figure 16 for reference.
Table 5 shows the displacements of bidirectional CCCP predicted by 3D-FEM and 2D-EPM when the concentrated load of 100 N is applied at the center of the plate. It can be seen that the displacements of bidirectional CCCP predicted by 2D-EPM and 3D-FEM under four different boundary conditions are basically the same, and the maximum displacement deviation is only 3.10%. Therefore, the VAM-based equivalent model can be used to evaluate the static behavior of bidirectional CCCP with confidence.
Based on the obtained equivalent stiffness, the buckling critical eigenvalues of the equivalent model obtained by linear buckling analysis are compared with those of 3D-FEM.
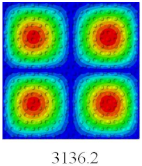
Table 6 shows that the global buckling modes of 2D-EPM are consistent with those of 3D-FEM, and the buckling critical load error of each mode is less than 4%. Therefore, the VAM-based equivalent model has high accuracy in global buckling analysis of complex convex-concave plates.
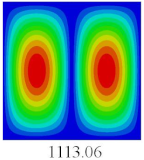
To fully verify the correctness of the equivalent model of the bidirectional CCCP, the vibration modes and natural frequencies of 2D-EPM are analyzed by using the SFSF boundary conditions.
Table 7 shows the comparison results of the first five vibration modes and natural frequencies between 3D-FEM and 2D-EPM of bidirectional CCCP. It can be seen that the vibration modes of 2D-EPM are consistent with those of 3D-FEM, and the natural frequency error of each mode is less than 2.6%, indicating the VAM-based equivalent model can be confidently used to predict the free vibration of complex convex-concave plates.
It can be concluded from the comparative analysis of
Table 1,
Table 2,
Table 5 and
Table 6 that compared with CCCP, the static displacement of bidirectional CCCP decreases and the buckling load increases under the same loading and boundary conditions, indicating the stiffness and stability of the bidirectional CCCP are greatly improved, which is consistent with the results of the previous equivalent stiffness analysis.
6. Conclusions
In this work, a VAM-based equivalent model (2D-EPM) is established to predict the effective performance of CCCP. As the approximate energy of 2D-EPM is as close as possible to that of the original 3D plate, it can be used to replace the original CCCP for the global analysis. The following conclusions can be obtained.
(1) The global displacements, buckling modes, and vibration modes of 2D-EPM under different boundary conditions are coincident with those of 3D-FEM, verifying the accuracy of the VAM-based 2D-EPM. Furthermore, the details of local field distribution within unit cell of CCCP are well captured. Compared with CCCP, the static displacement of bidirectional CCCP decreases and the buckling load are significantly increased, indicating the stiffness and stability of the bidirectional CCCP are greatly improved.
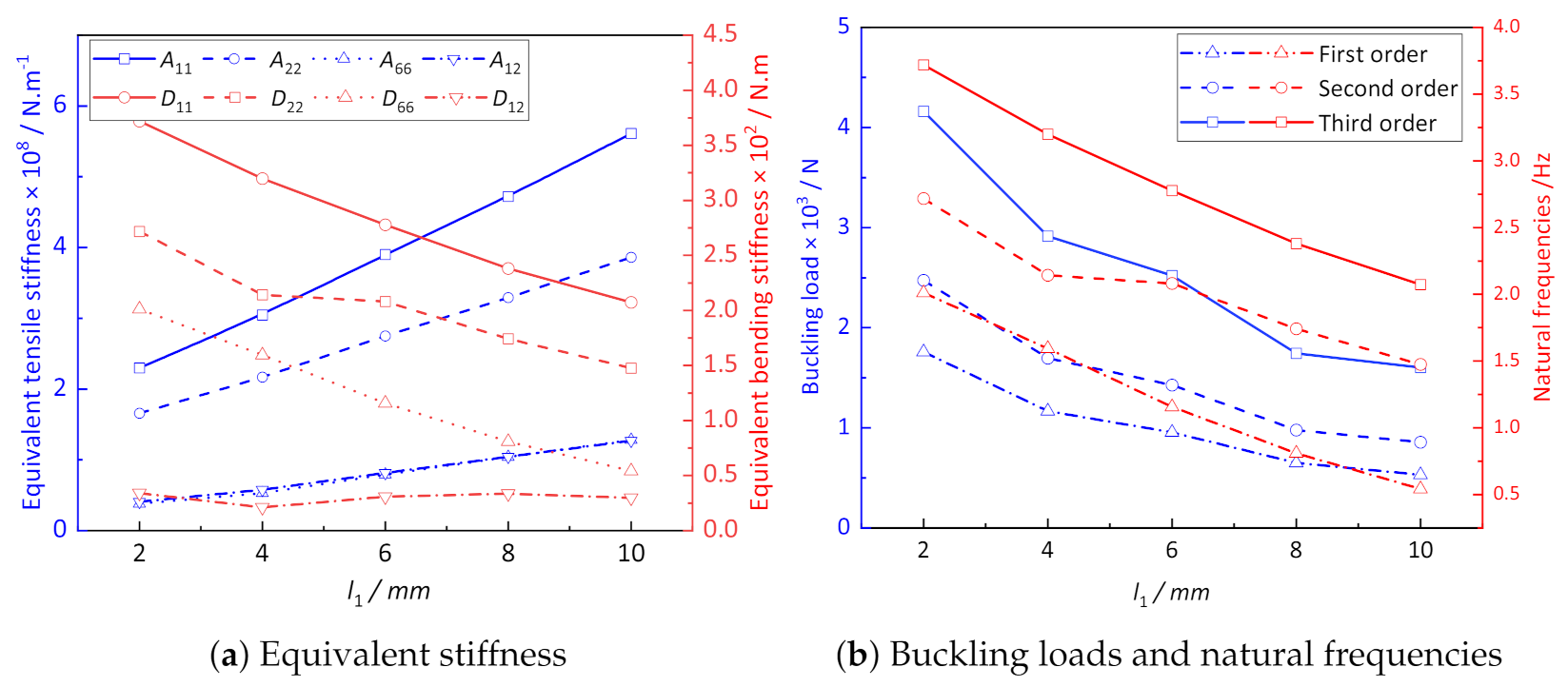
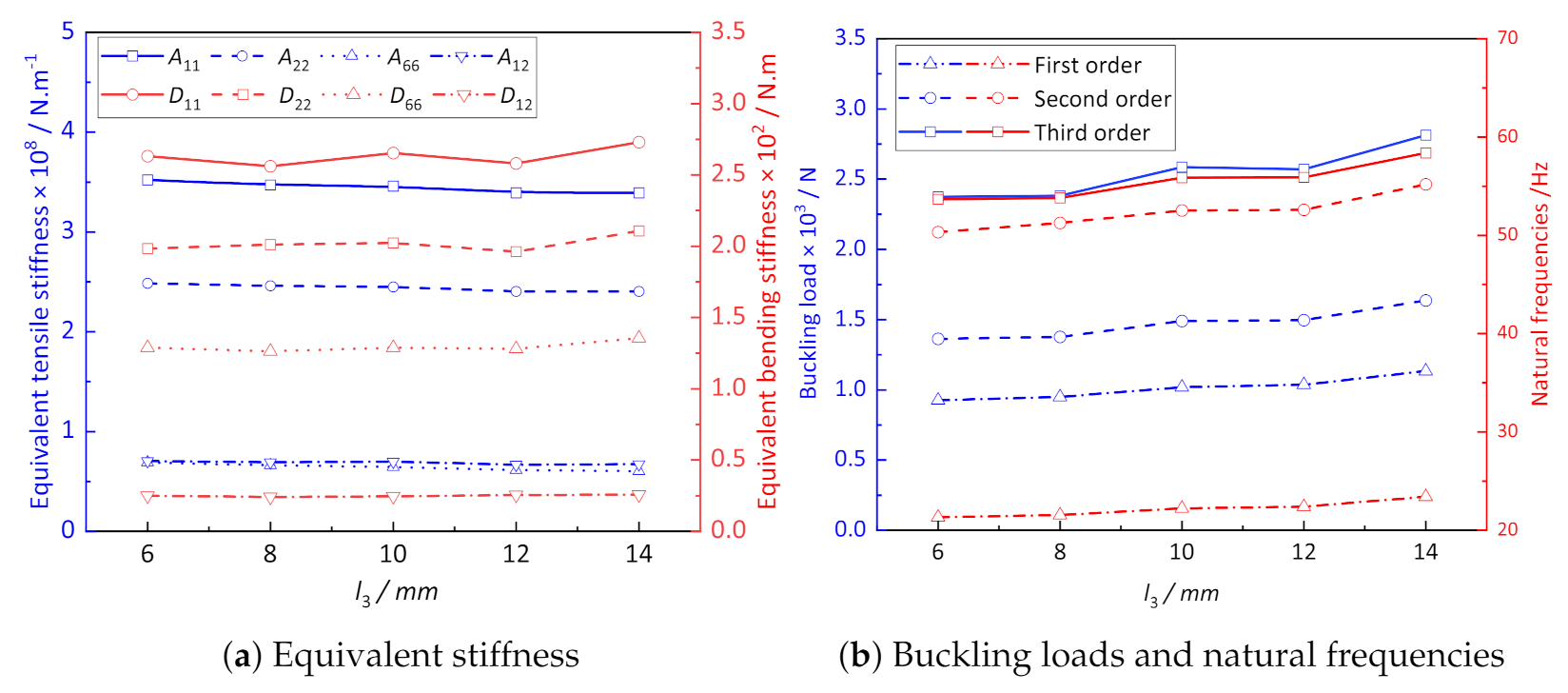
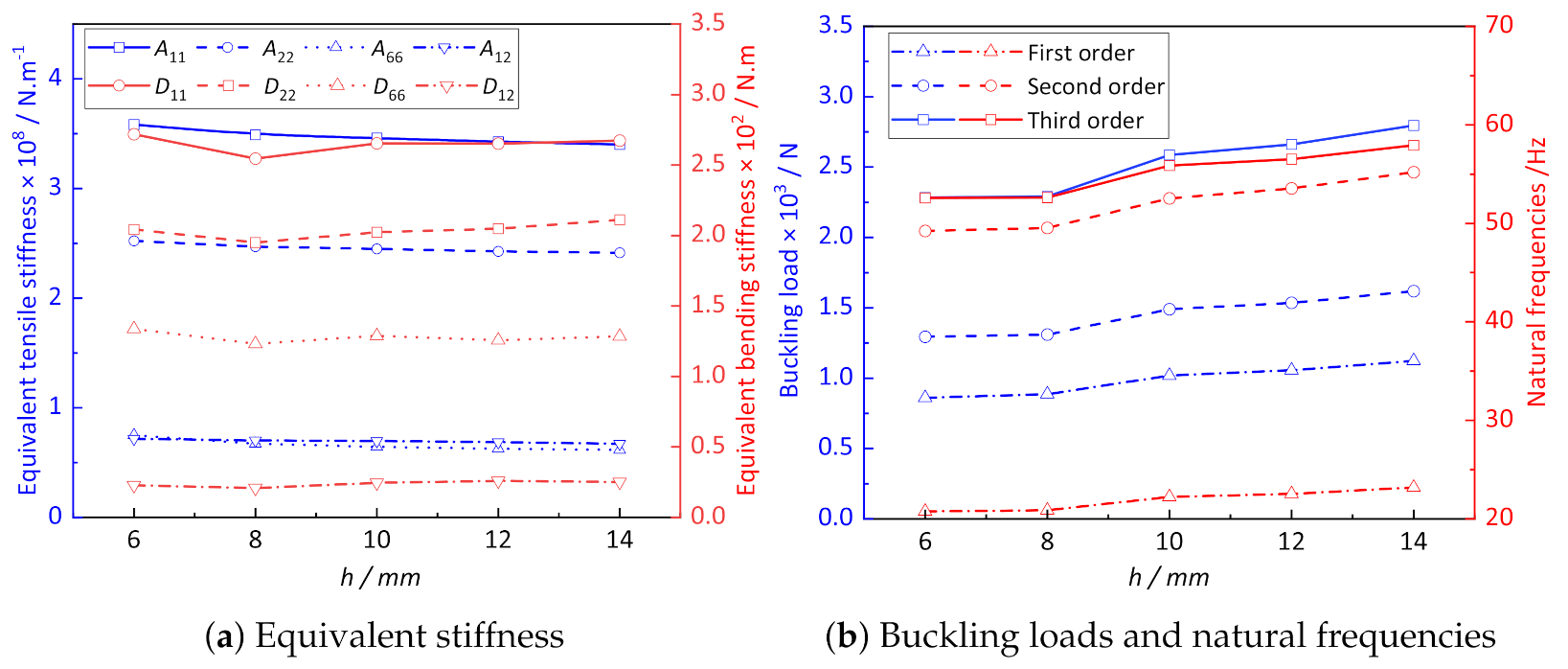
(2) The parameter analysis shows that the structural anisotropy of CCCP is more obvious with increasing of the convex height h, and the equivalent tensile stiffness decreases gradually, while the change of the equivalent bending stiffness is the opposite of the trend. The equivalent tensile stiffness increases gradually, and the equivalent bending stiffness decreases nonlinearly with increasing of the spacing between adjacent convexities, which may be because the anisotropy of CCCP is not obvious when the spacing between adjacent convexities increases.
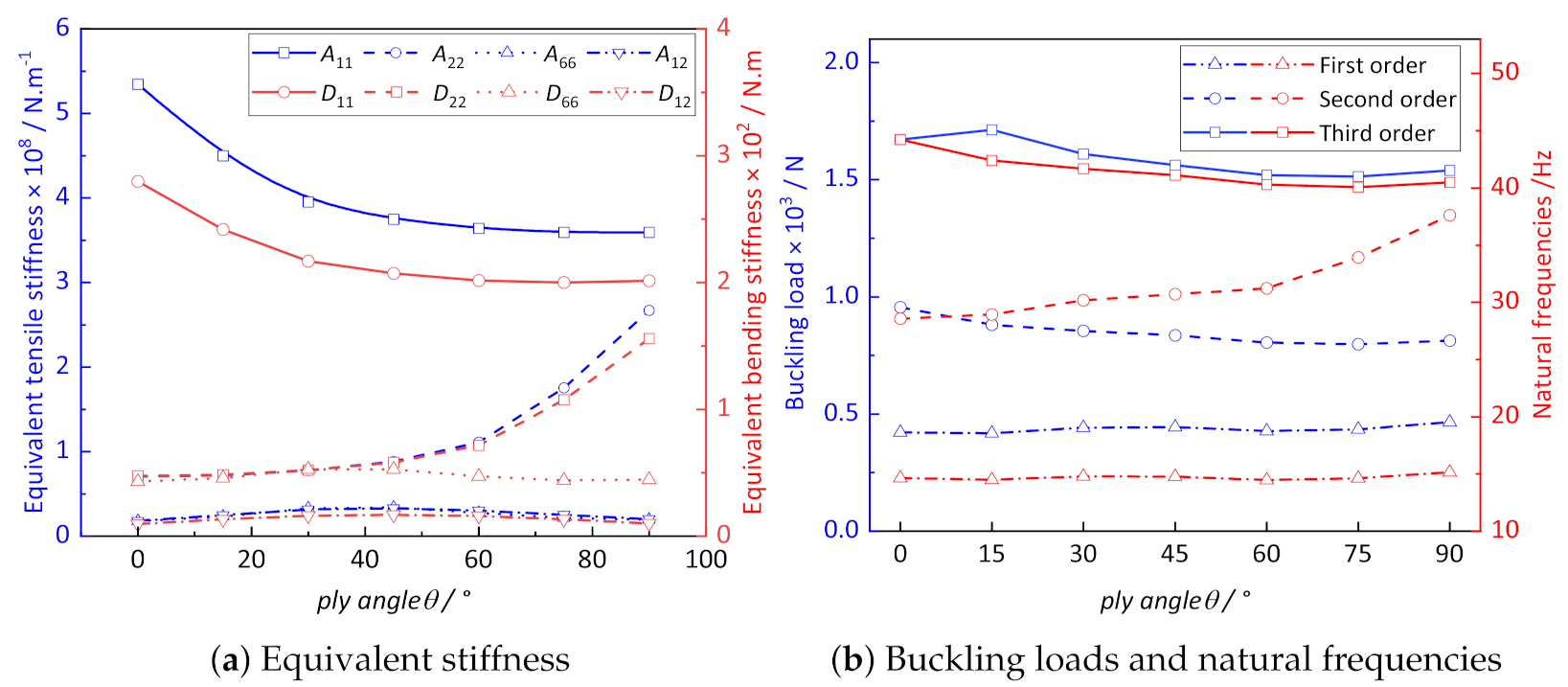
(3) The ply angle of composite laminate has a great influence on the equivalent stiffness of CCCP. With increasing of the ply angle, the equivalent tensile and bending stiffness along the direction present a nonlinear decrease, while the equivalent tensile and bending stiffness along the direction gradually increases, but it has no significant influence on the buckling critical load and natural frequency of CCCP. With the increase in proportion of ply, the change of tensile and bending stiffness show a trend of linear increase, and the buckling critical load is also increased to a certain extent.
In short, compared with 3D-FEM, the present model has high accuracy for static, buckling, and free vibration analysis of CCCP. At the same time, the DOFs of the 2D-EPM is greatly reduced, resulting in a great improvement in computational efficiency. The present model is particularly useful in the early design stage of composite convex-concave structures where many design trade-offs need to be made over a vast design space in terms of material selection, ply angles, and geometric parameters.