Dynamics of Space-Fractional Euler–Bernoulli and Timoshenko Beams
Abstract
1. Introduction
- formulation of the general governing equations describing the dynamic behavior of the s-FEBB and s-FTB models;
- elaboration of the numerical algorithms for both fractional beams for the case of free vibrations;
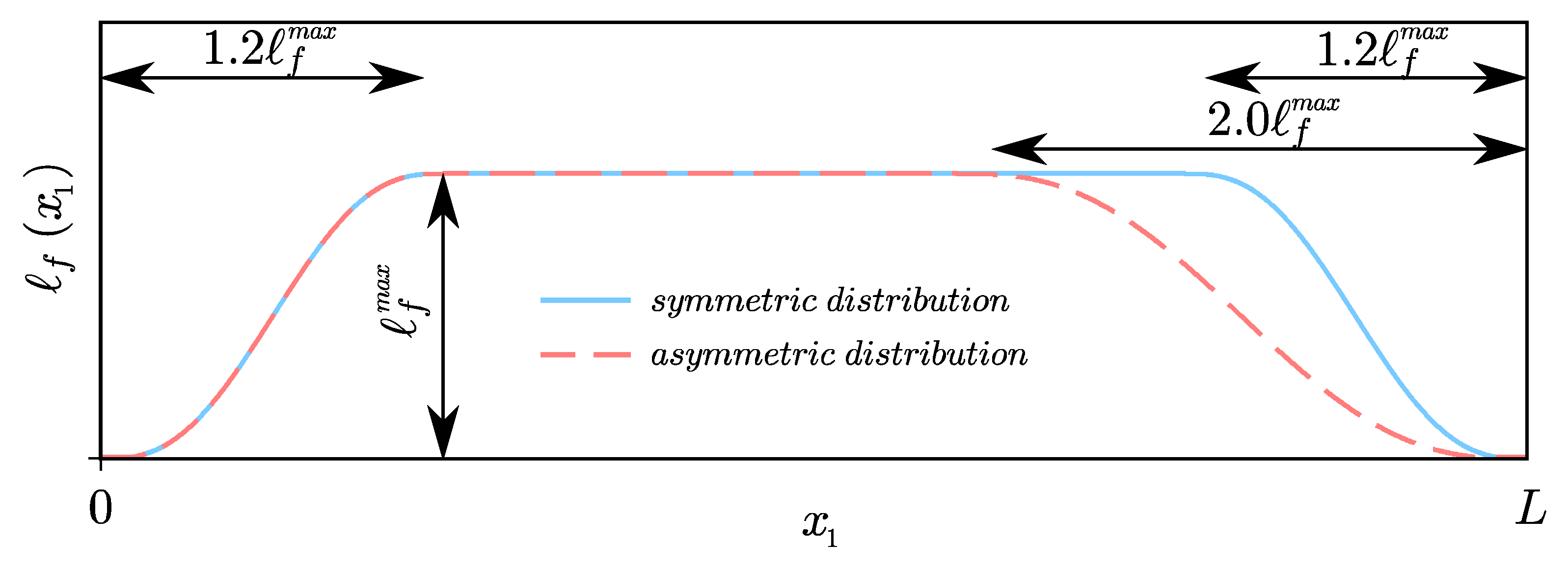
- in-depth study of the influence of non-locality parameters on the eigenfrequencies and the shape of modes;
- determination of the geometric criterion (which is more restrictive than in the statics) according to which s-FEBB can be reasonably applied, in both fractional and classical approaches; and
2. Governing Equations
3. Numerical Study
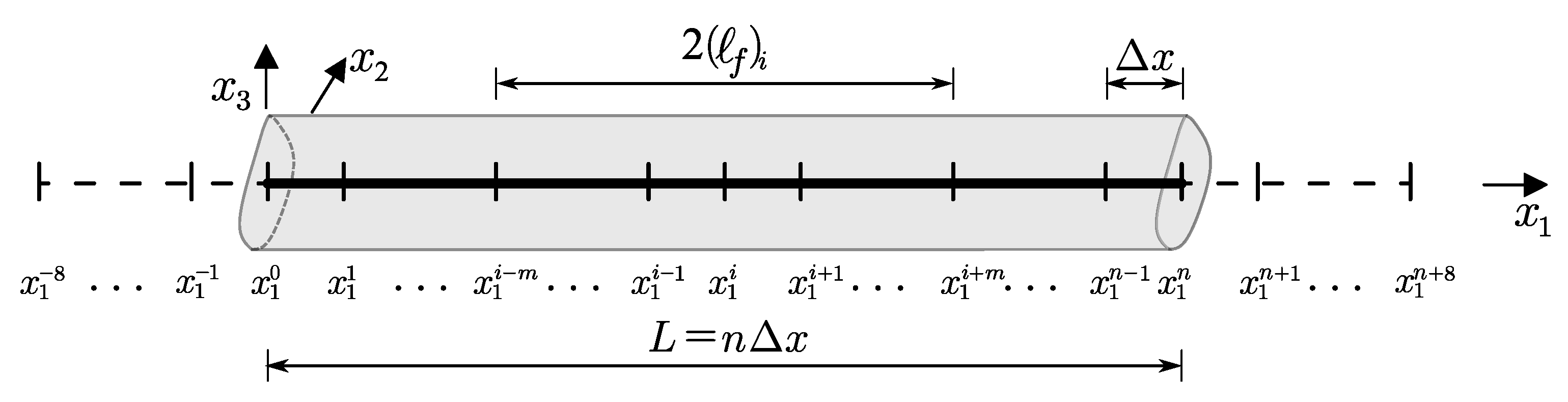
- By equating of the central and forward finite difference schemes at points and the central and backward finite difference schemes at points for the fourth-order derivative of displacement,
- additionally for s-FTB model, by equating the central and forward finite difference schemes at points and the central and backward finite difference schemes at points for the third order derivative of strain,
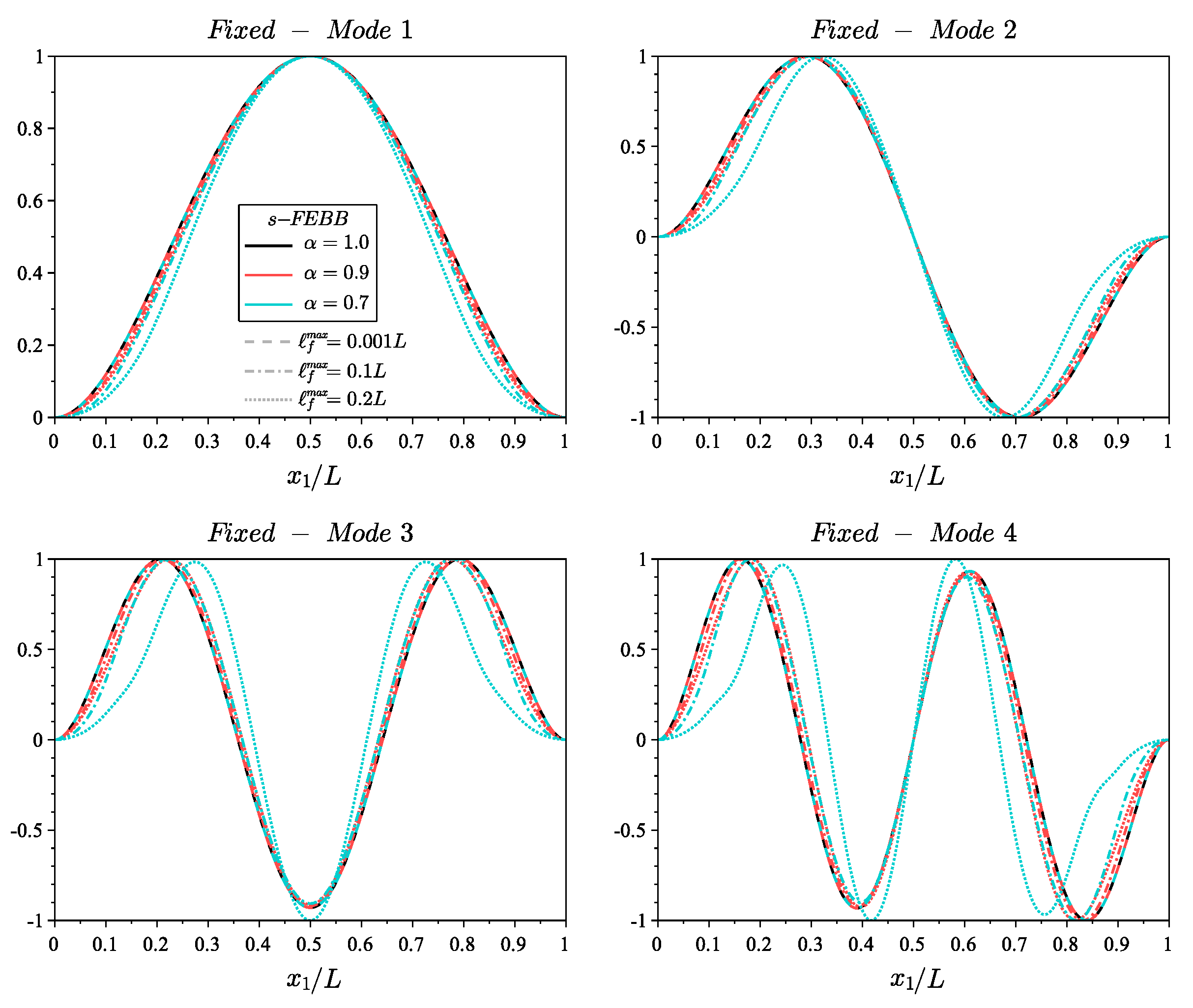
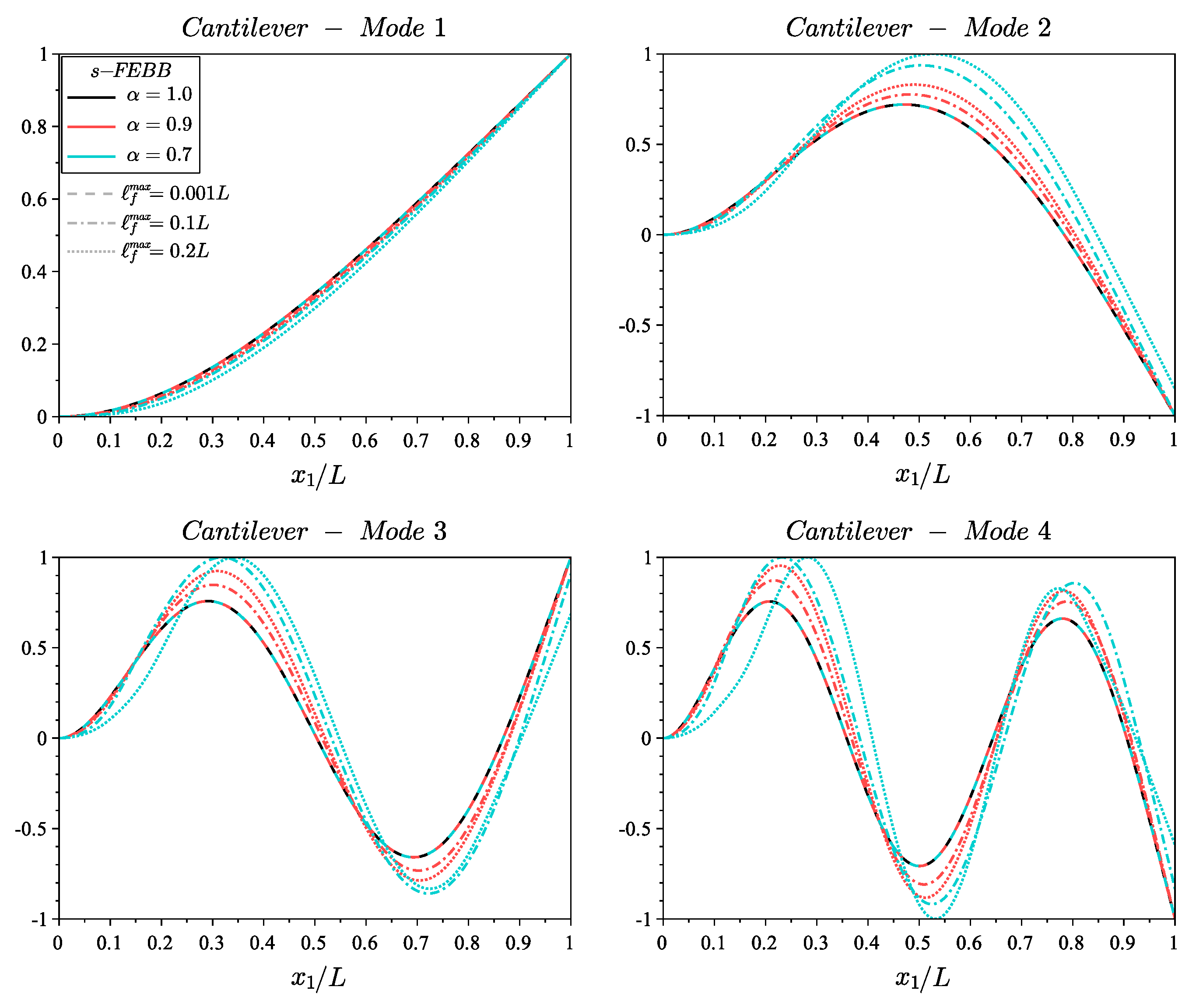
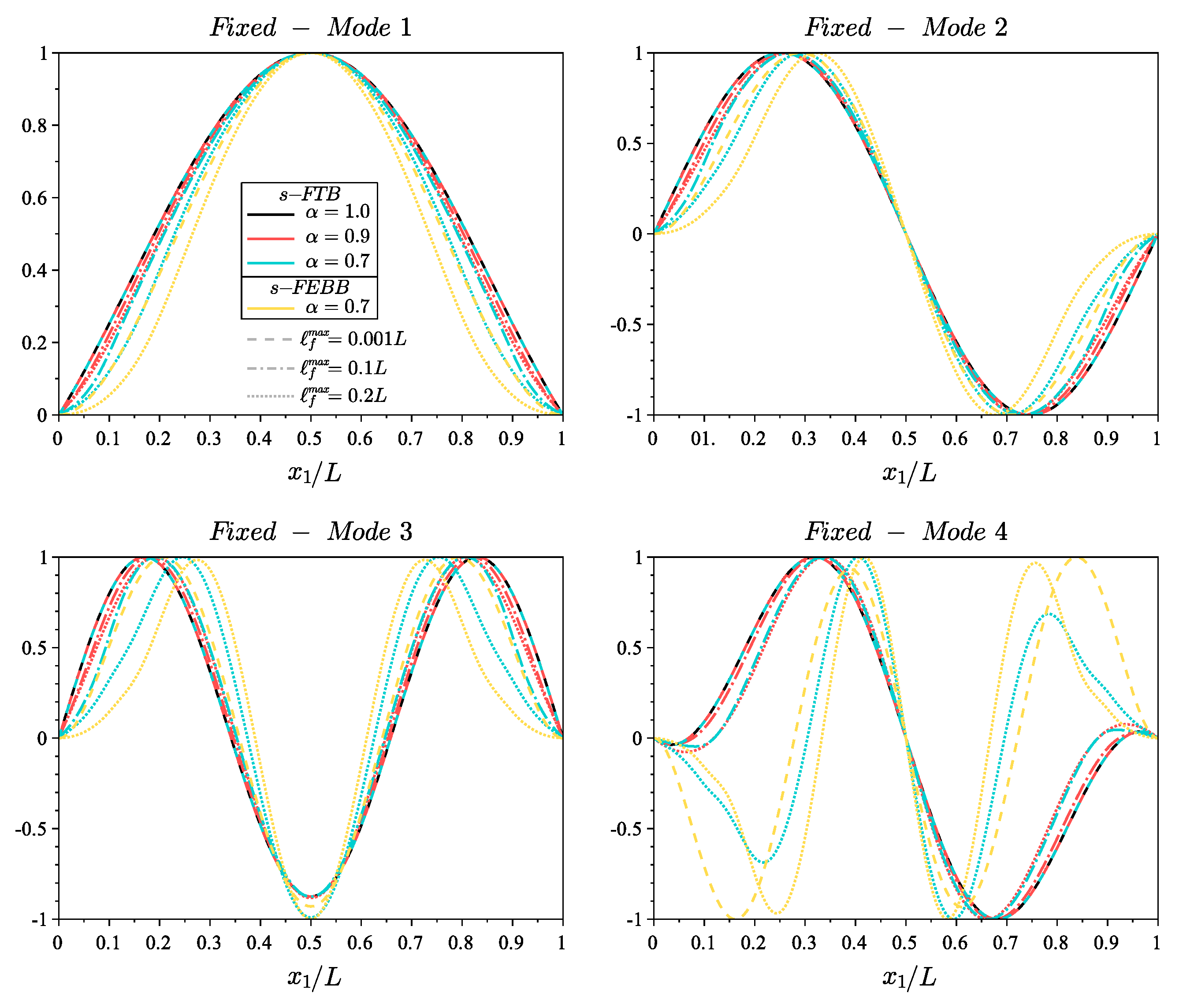
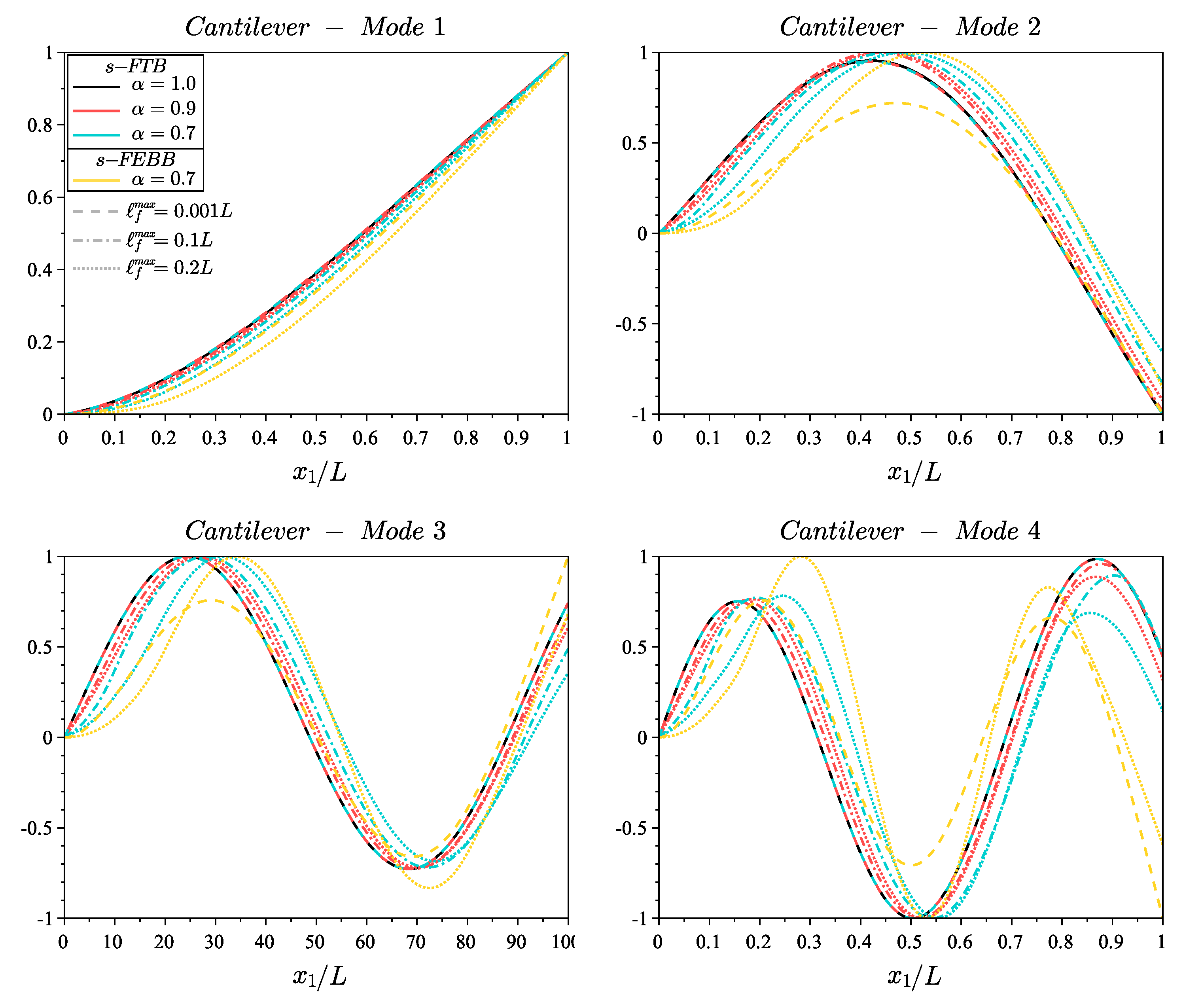
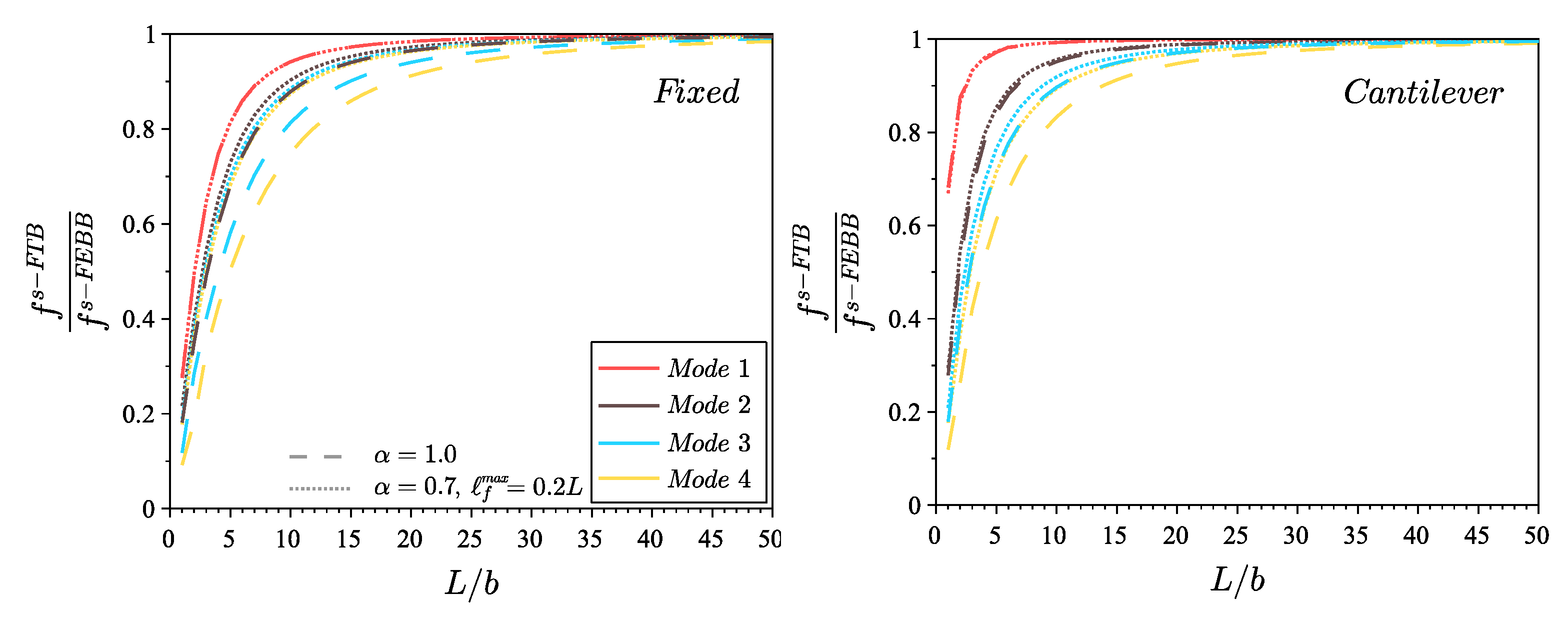
4. Parametric Study
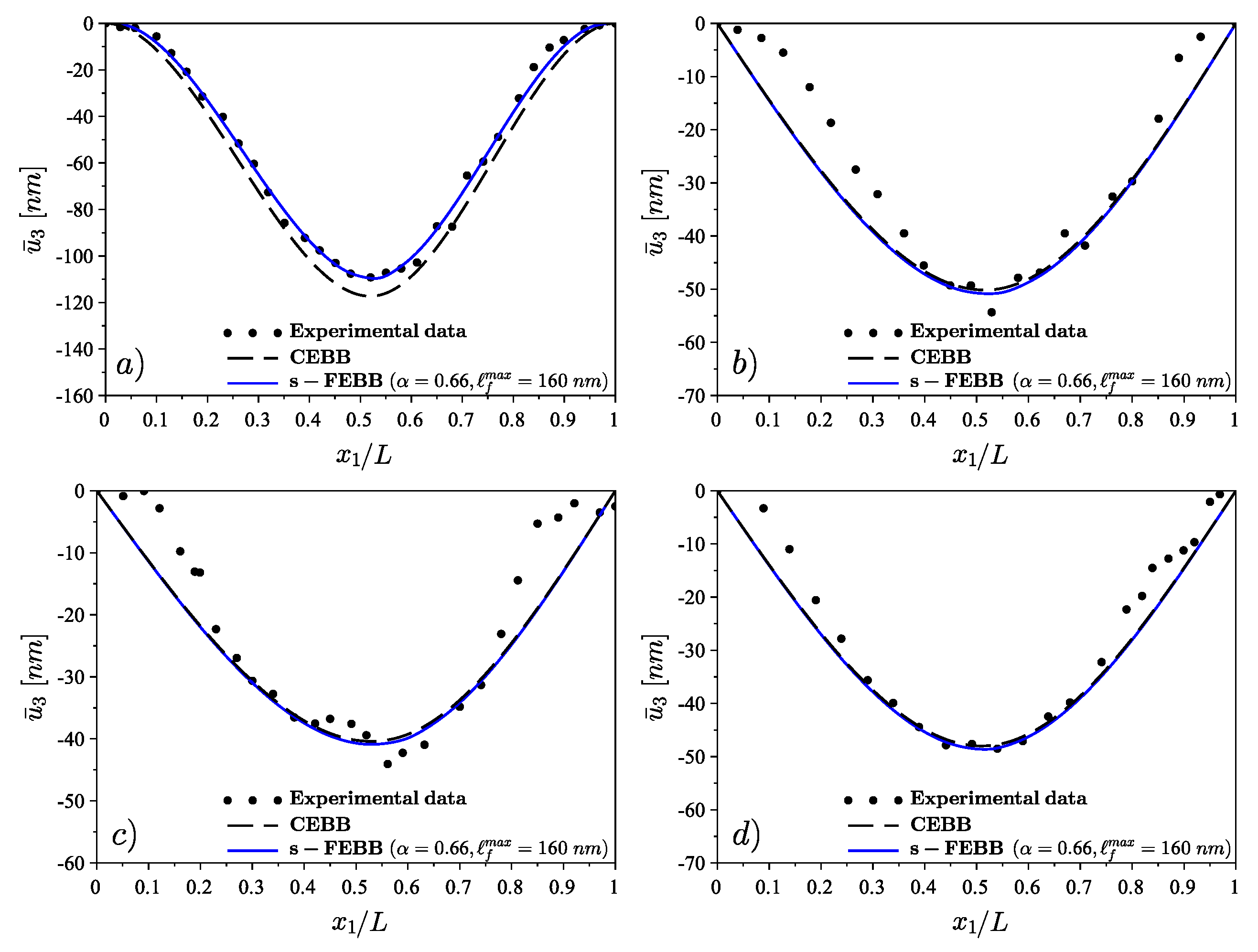
5. Experimental Validation
| Cross- Section | Diameter d [nm] | Length L [nm] | Load P [nN] | L1 [−] | Elastic Modulus E [GPa] | α [−] | [nm] | |
|---|---|---|---|---|---|---|---|---|
| (a) | circle | 57.0 | 3054 | 122.7 | 0.54 | 295 | 0.66 | 160 |
| (b) | haxagon | 89.3 | 2398 | 112.3 | 0.55 | |||
| (c) | 97.8 | 2465 | 127.7 | 0.60 | ||||
| (d) | 109.7 | 2558 | 200.0 | 0.53 |
6. Conclusions
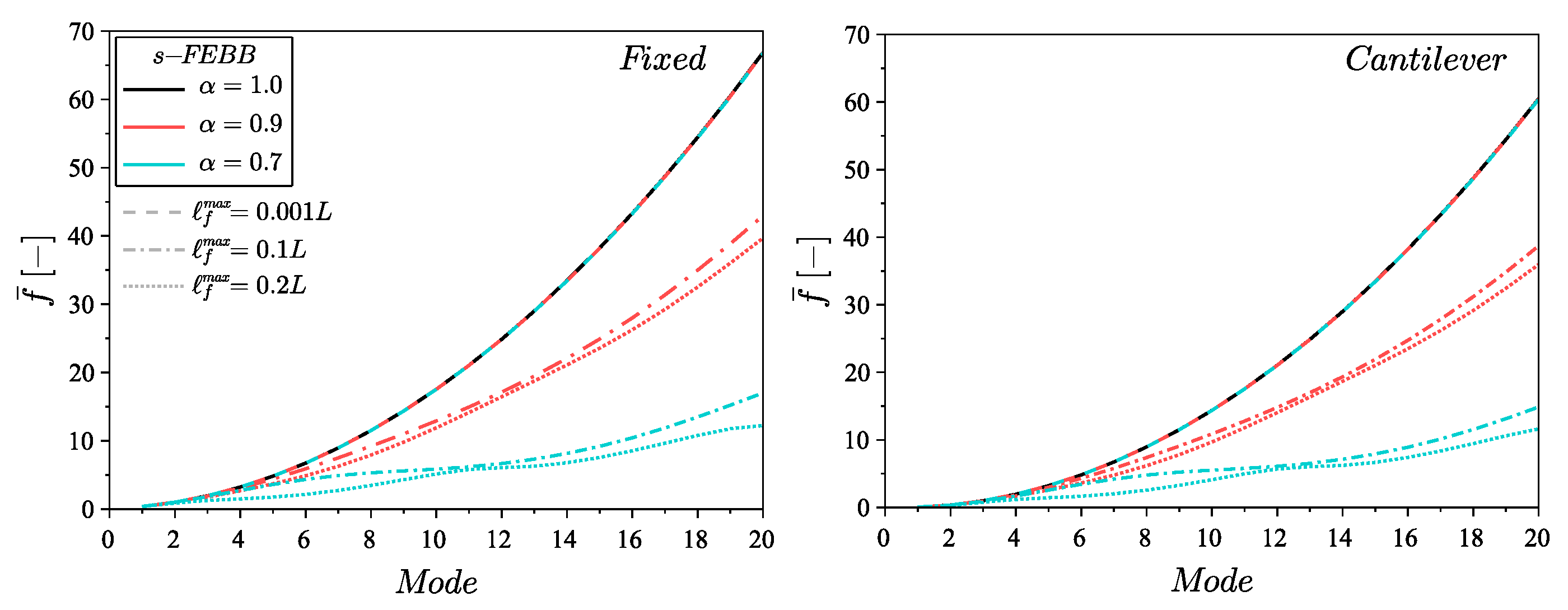
- the non-local parameters and control the frequency value and the shape of a specific mode of the fractional beam;
- taking into account the small-scale effect results in lower frequency values compared to the classical beam theories (except for the first two frequencies of the fixed beam);
- the higher mode number, the more significant the non-locality effect;
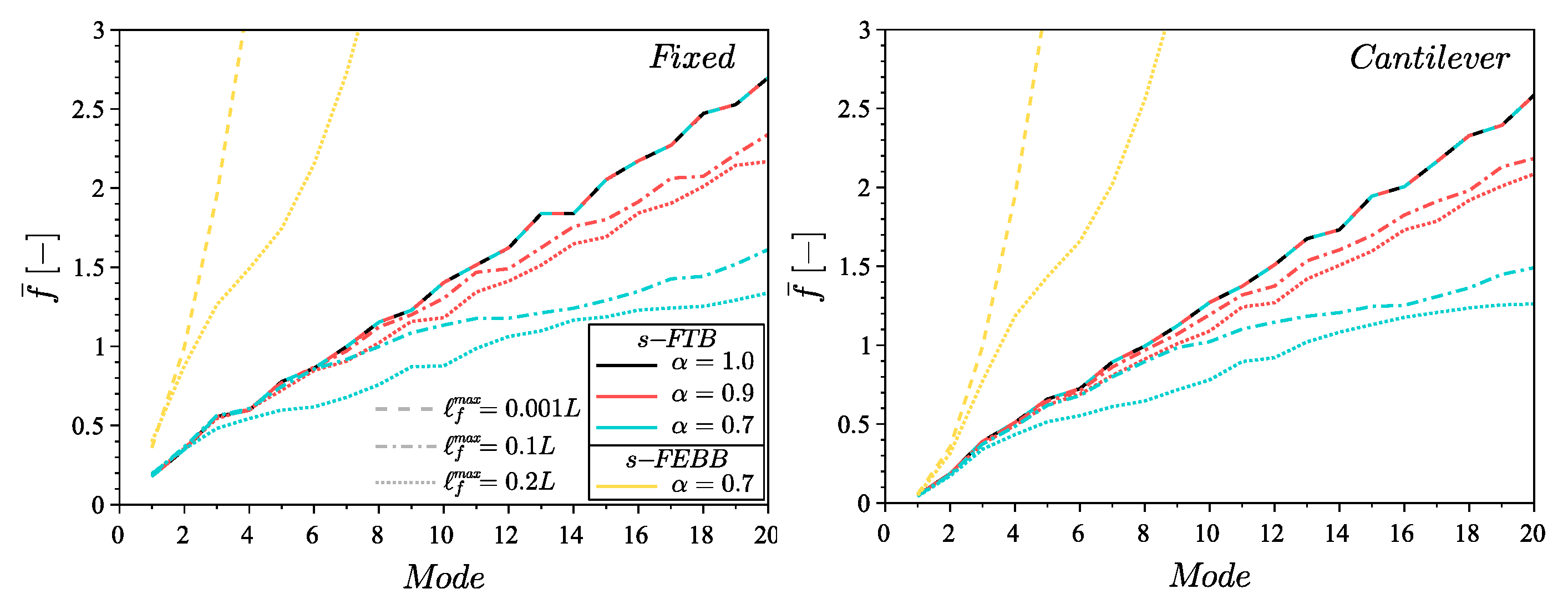
- taking into account the shear effect and rotational inertia in the s-FTB results in lower frequency values compared to the s-FEBB;
- in the case of dynamics, the Timoshenko beam model should be considered even for significantly slender beams, which is in contrast to the case of static analysis, especially for the higher mode numbers;
- including the non-locality means that the shear effect and the rotational inertia can be neglected for beams with a smaller length to height ratio compared to the local approach;
- the higher mode number, the more significant is the difference in frequencies received in Timoshenko and Euler–Bernoulli theory, both in the fractional and in the classical approach;
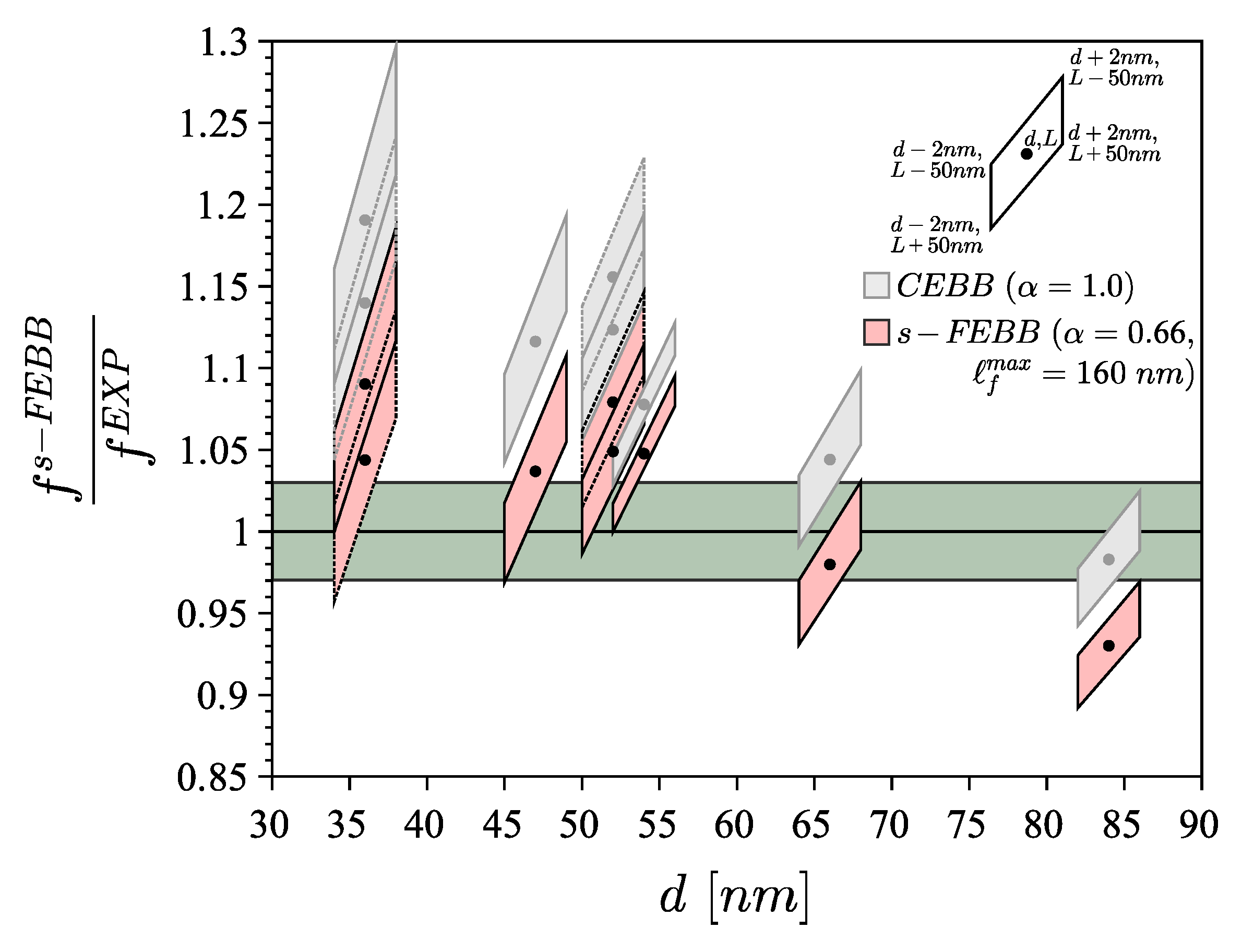
- validation has confirmed that the fractional beam model exhibits very good agreement with the experimental results for both the static and the dynamic cases; and
- it has been proven that for the fractional beams it is possible to establish constant parameters and related to the material and its microstructure, independent of the beam geometry, the boundary conditions, and the type of analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Morris, W. American Heritage Dictionary of the English Language; Houghton Mifflin Harcourt Publishing Company: Boston, MA, USA, 2011. [Google Scholar]
- Marsden, J.; Hughes, T. Mathematical Foundations of Elasticity; Prentice-Hall: Hoboken, NJ, USA, 1983. [Google Scholar]
- Haupt, P. Continuum Mechanics and Theory of Materials, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Toupin, R. Elastic materials with couple-stress. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Mindlin, R.; Eshel, N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Aifantis, E. On the Microstructural Origin of Certain Inelastic Models. J. Eng. Mater. Technol. ASME 1984, 106, 326–330. [Google Scholar] [CrossRef]
- Li, J.; Wang, B. Fracture mechanics analysis of an anti-plane crack in gradient elastic sandwich composite structures. Int. J. Mech. Mater. Des. 2019, 15, 507–519. [Google Scholar] [CrossRef]
- Lazopoulos, A.K. On fractional peridynamic deformations. Arch. Appl. Mech. 2016, 86, 1987–1994. [Google Scholar] [CrossRef]
- Postek, E.; Pecherski, R.; Nowak, Z. Peridynamic Simulation of Crushing Processes in Copper Open-Cell Foam. Arch. Metall. Mater. 2019, 64, 1603–1610. [Google Scholar]
- Cosserat, E.; Cosserat, F. Theorie des Corps Deformables; Librairie Scientifique A. Hermann et Fils: Paris, France, 1909. [Google Scholar]
- Eringen, A. Linear Theory of Micropolar Elasticity. J. Math. Mech. 1966, 15, 909–923. [Google Scholar]
- Nowacki, W. Theory of Micropolar Elasticity; CISM: Udine, Italy, 1972. [Google Scholar]
- Eringen, A. On differential equations of nonlocal elasticity and solutions of screw dislocations and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Peddieson, J.; Buchanan, G.; McNitt, R. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Eringen, A. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2010. [Google Scholar]
- Gurtin, M.E.; Murdoch, A.I. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Atanackovic, T.; Stankovic, B. Generalized wave equation in nonlocal elasticity. Acta Mech. 2009, 208, 1–10. [Google Scholar] [CrossRef]
- Sumelka, W. Thermoelasticity in the Framework of the Fractional Continuum Mechanics. J. Therm. Stress. 2014, 37, 678–706. [Google Scholar] [CrossRef]
- Drapaca, C.; Sivaloganathan, S. Brief Review of Continuum Mechanics Theories. Fields Inst. Monogr. 2019, 37, 5–37. [Google Scholar]
- Reddy, J. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Lewinski, T.; Sokoł, T.; Graczykowski, C. Michell Structures; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–569. [Google Scholar]
- Magnucki, K.; Lewiński, J.; Magnucka-Blandzi, E. A Shear Deformation Theory of Beams with Bisymmetrical Cross-Sections Based on the Zhuravsky Shear Stress Formula. Eng. Trans. 2020, 68, 353–370. [Google Scholar]
- Stachiv, I. Impact of surface and residual stresses and electro-/magnetostatic axial loading on the suspended nanomechanical based mass sensors: A theoretical study. J. Appl. Phys. 2014, 115, 214310. [Google Scholar] [CrossRef]
- Stachiv, I.; Fang, T.H.; Chen, T.H. Micro-/nanosized cantilever beams and mass sensors under applied axial tensile/compressive force vibrating in vacuum and viscous fluid. AIP Adv. 2015, 5, 117140. [Google Scholar] [CrossRef]
- Ghaffari, I.; Yaghoobi, M.; Ghannad, M. Complete mechanical behavior analysis of FG Nano Beam under non-uniform loading using non-local theory. Mater. Res. Express 2018, 5, 015016. [Google Scholar] [CrossRef]
- Sumelka, W.; Blaszczyk, T.; Liebold, C. Fractional Euler–Bernoulli beams: Theory, numerical study and experimental validation. Eur. J. Mech. A/Solids 2015, 54, 243–251. [Google Scholar] [CrossRef]
- Challamel, N. Static and dynamic behaviour of nonlocal elastic bar using integral strain-based and peridynamic models. C. R. Mec. 2018, 346, 320–335. [Google Scholar] [CrossRef]
- Huang, F.Y.; Yan, B.H.; Yan, J.L.; Yang, D.U. Bending analysis of micropolar elastic beam using a 3-D finite element method. Int. J. Eng. Sci. 2000, 38, 275–286. [Google Scholar] [CrossRef]
- Ramezani, S.; Naghdabadi, R.; Sohrabpour, S. Analysis of micropolar elastic beams. Eur. J. Mech. A/Solids 2009, 28, 202–208. [Google Scholar] [CrossRef]
- Hassanpour, S.; Heppler, G. Comprehensive and easy-to-use torsion and bending theories for micropolar beams. Int. J. Mech. Sci. 2016, 114, 71–87. [Google Scholar] [CrossRef]
- Zhang, N.; Yan, J.; Li, C.; Zhou, J. Combined bending-tension/compression deformation of micro-bars accounting for strain-driven long-range interactions. Arch. Mech. 2019, 71, 3–21. [Google Scholar]
- Sidhardh, S.; Patnaik, S.; Semperlotti, F. Geometrically nonlinear response of a fractional-order nonlocal model of elasticity. Int. J. Non-Linear Mech. 2020, 125, 103529. [Google Scholar] [CrossRef]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. A Ritz-based finite element method for a fractional-order boundary value problem of nonlocal elasticity. Int. J. Solids Struct. 2020, 202, 398–417. [Google Scholar] [CrossRef]
- Stempin, P.; Sumelka, W. Space-fractional Euler-Bernoulli beam model—Theory and identification for silver nanobeam bending. Int. J. Mech. Sci. 2020, 186, 105902. [Google Scholar] [CrossRef]
- Stempin, P.; Sumelka, W. Formulation and experimental validation of space-fractional Timoshenko beam model with functionally graded materials effects. Comput. Mech. 2021. [Google Scholar] [CrossRef]
- Sumelka, W.; Blaszczyk, T. Fractional continua for linear elasticity. Arch. Mech. 2014, 66, 147–172. [Google Scholar]
- Chen, Y.; Stevenson, I.; Pouy, R.; Wang, L.; McIlroy, D.N.; Pounds, T.; Norton, M.G.; Aston, D.E. Mechanical elasticity of vapour–liquid–solid grown GaN nanowires. Nanotechnology 2007, 18, 135708. [Google Scholar] [CrossRef]
- Nam, C.Y.; Jaroenapibal, P.; Tham, D.; Luzzi, D.E.; Evoy, S.; Fischer, J.E. Diameter-Dependent Electromechanical Properties of GaN Nanowires. Nano Lett. 2006, 6, 153–158. [Google Scholar] [CrossRef] [PubMed]
- Sumelka, W. On fractional non-local bodies with variable length scale. Mech. Res. Commun. 2017, 86, 5–10. [Google Scholar] [CrossRef]
- Szajek, K.; Sumelka, W. Discrete mass-spring structure identification in nonlocal continuum space-fractional model. Eur. Phys. J. Plus 2019, 134, 448. [Google Scholar] [CrossRef]
- Szajek, K.; Sumelka, W.; Blaszczyk, T.; Bekus, K. On selected aspects of space-fractional continuum mechanics model approximation. Int. J. Mech. Sci. 2020, 167, 105287. [Google Scholar] [CrossRef]
- Leszczyński, J. An Introduction to Fractional Mechanics; Monographs No 198; The Publishing Office of Czestochowa University of Technology: Częstochowa, Poland, 2011. [Google Scholar]
- Odibat, Z. Approximations of fractional integrals and Caputo fractional derivatives. Appl. Math. Comput. 2006, 178, 527–533. [Google Scholar] [CrossRef]
- Khorshidi, M.A. The material length scale parameter used in couple stress theories is not a material constant. Int. J. Eng. Sci. 2018, 133, 15–25. [Google Scholar] [CrossRef]
- Liang, Y.; Han, Q. Prediction of the nonlocal scaling parameter for graphene sheet. Eur. J. Mech. A/Solids 2014, 45, 153–160. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Challamel, N.; Elishakoff, I. Obtaining Eringen’s length scale coefficient for vibrating nonlocal beams via continualization method. J. Sound Vib. 2014, 333, 4977–4990. [Google Scholar] [CrossRef]
- Wang, C.M.; Zhang, Z.; Challamel, N.; Duan, W.H. Calibration of Eringen’s small length scale coefficient for initially stressed vibrating nonlocal Euler beams based on microstructured beam model. J. Phys. D Appl. Phys. 2013, 46, 345501. [Google Scholar] [CrossRef]
- Odzijewicz, T.; Malinowska, A.B.; Torres, D.F. Fractional variational calculus with classical and combined Caputo derivatives. Nonlinear Anal. Theory Methods Appl. 2012, 75, 1507–1515. [Google Scholar] [CrossRef]
- Malinowska, A.; Torres, D. Fractional calculus of variations for a combined Caputo derivative. Fract. Calc. Appl. Anal. 2011, 14. [Google Scholar] [CrossRef]

| Forward | Backward | Central | Central | |
|---|---|---|---|---|
| Beam Type | Conditions for s-FEBB | |
|---|---|---|
| Simply supported | , , | , |
| , | ||
| Fixed | , , | , |
| , | ||
| Propped cantilever | , , | , |
| , | ||
| Cantilever | , , | , |
| , | ||
| Beam Type | Conditions for s-FTB | |
|---|---|---|
| Simply supported | , | , |
| , | ||
| , | ||
| Fixed | , | , |
| , | ||
| , | ||
| Propped cantilever | , | , |
| , | ||
| , | ||
| Cantilever | , | , |
| , | ||
| , | ||
| Beam Type | |||||
|---|---|---|---|---|---|
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | ||
| Fixed | Classical () | 11 | 17 | 22 | 28 |
| , | 11 | 15 | 16 | 17 | |
| Cantilever | Classical () | 4 | 10 | 15 | 21 |
| , | 4 | 9 | 13 | 16 | |
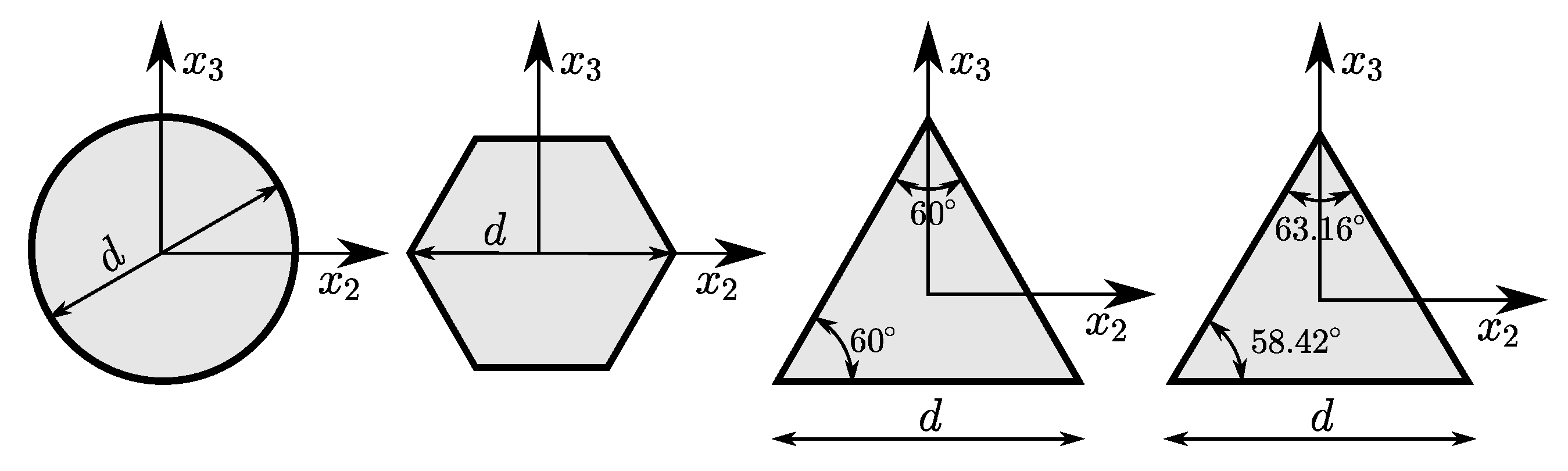
| No. | Cross-Section | Diameter | Length | Frequency [MHz] | Frequency [MHz] | Elastic Modulus E [GPa] | Density | α [−] | [nm] |
|---|---|---|---|---|---|---|---|---|---|
| 1 | isosceles triangle | 36 | 3200 | 2.194 | 2.440 | 295 | 6150 | 0.66 | 160 |
| 2 | equilateral triangle | 47 | 3950 | 2.135 | 2.135 | ||||
| 3 | isosceles triangle | 52 | 4300 | 1.860 | 1.925 | ||||
| 4 | equilateral triangle | 66 | 4700 | 2.264 | 2.264 | ||||
| 5 | equilateral triangle | 54 | 11,200 | 0.316 | 0.316 | ||||
| 6 | equilateral triangle | 84 | 5500 | 2.223 | 2.235 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stempin, P.; Sumelka, W. Dynamics of Space-Fractional Euler–Bernoulli and Timoshenko Beams. Materials 2021, 14, 1817. https://doi.org/10.3390/ma14081817
Stempin P, Sumelka W. Dynamics of Space-Fractional Euler–Bernoulli and Timoshenko Beams. Materials. 2021; 14(8):1817. https://doi.org/10.3390/ma14081817
Chicago/Turabian StyleStempin, Paulina, and Wojciech Sumelka. 2021. "Dynamics of Space-Fractional Euler–Bernoulli and Timoshenko Beams" Materials 14, no. 8: 1817. https://doi.org/10.3390/ma14081817
APA StyleStempin, P., & Sumelka, W. (2021). Dynamics of Space-Fractional Euler–Bernoulli and Timoshenko Beams. Materials, 14(8), 1817. https://doi.org/10.3390/ma14081817







