In-Silico Monte Carlo Simulation Trials for Investigation of V2O5 Reinforcement Effect on Ternary Zinc Borate Glasses: Nuclear Radiation Shielding Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. Behavioral Changes in ZnO-B2O3-V2O5 Glasses
2.2. MCNPX Monte Carlo Simulations
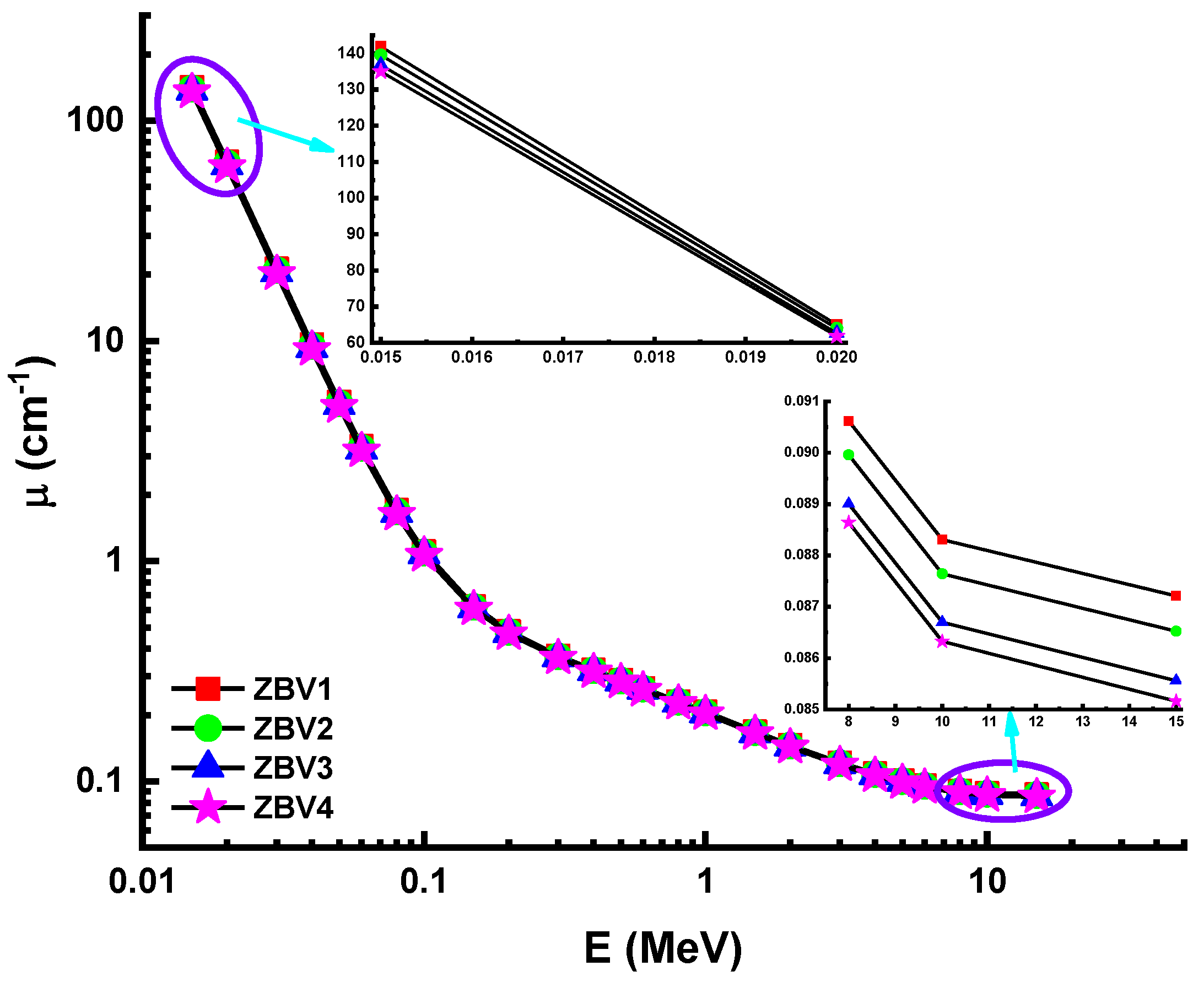
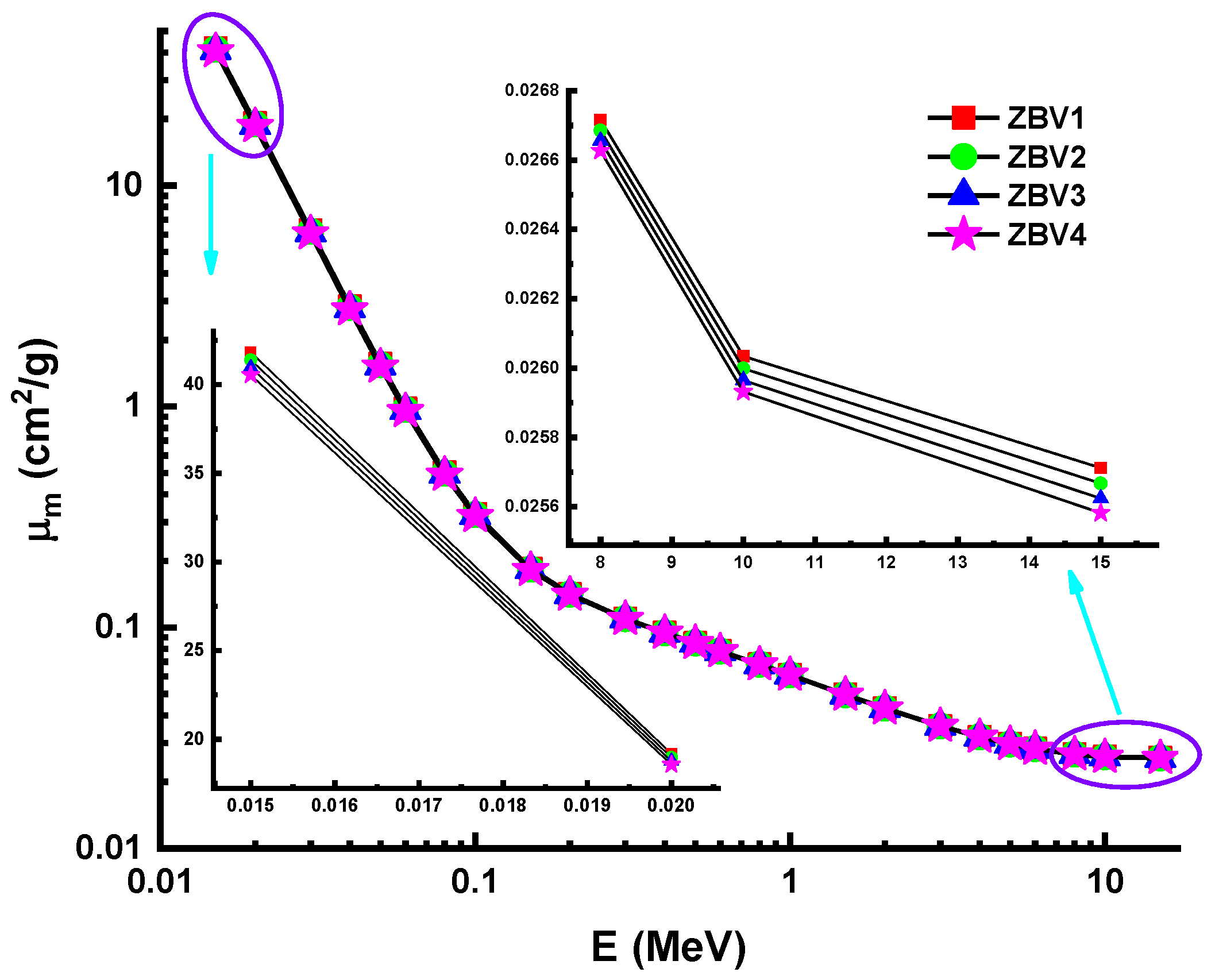
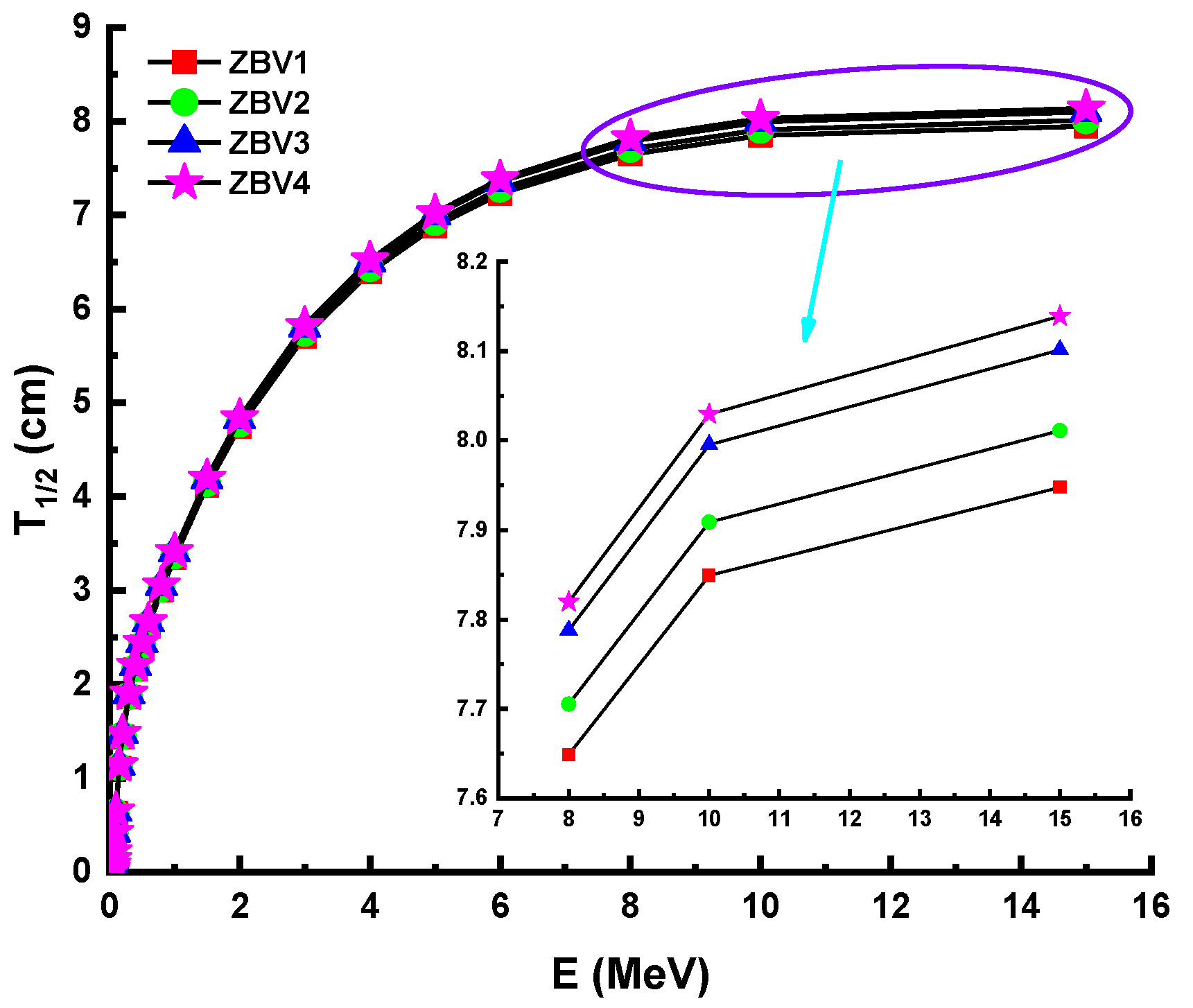
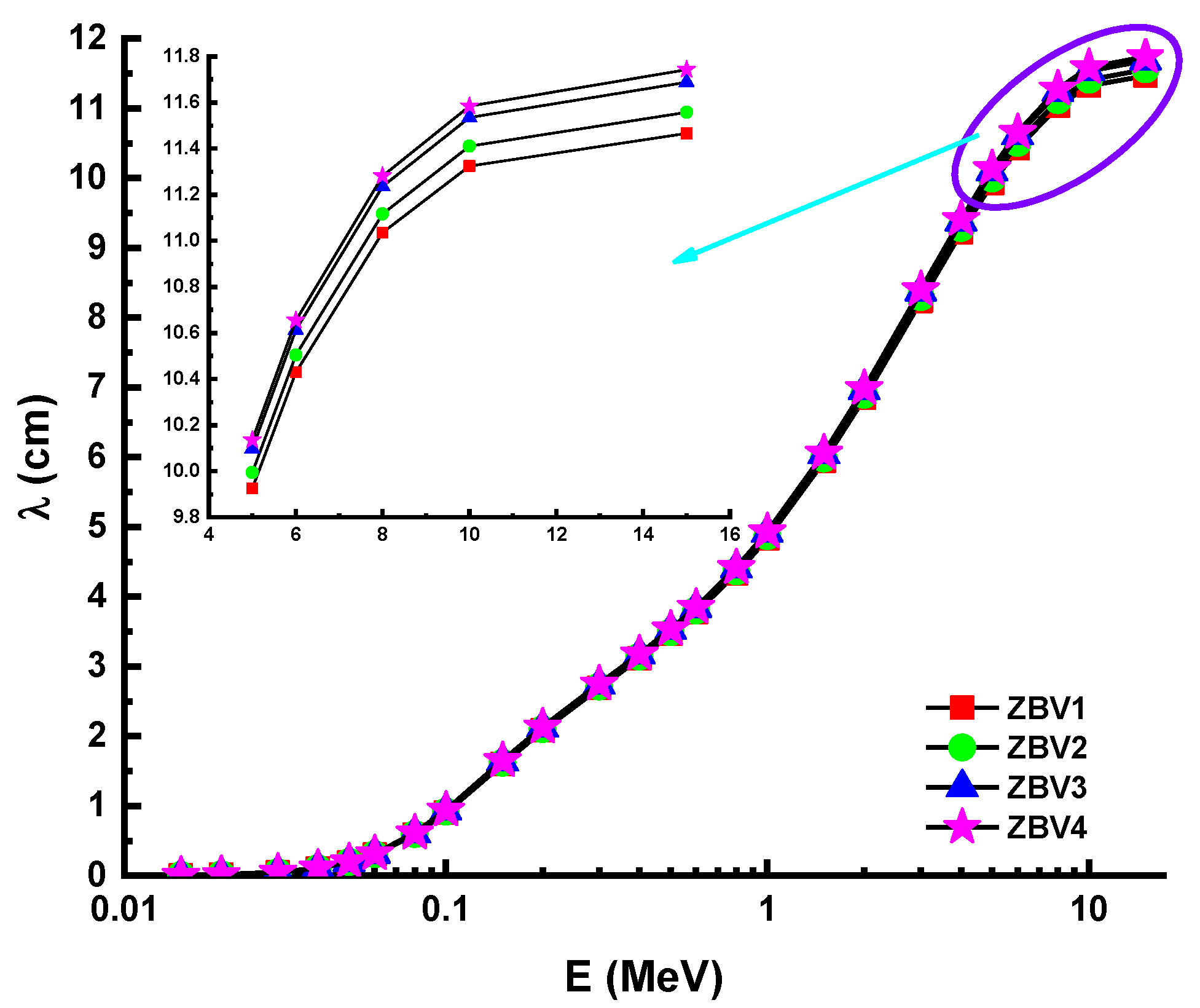
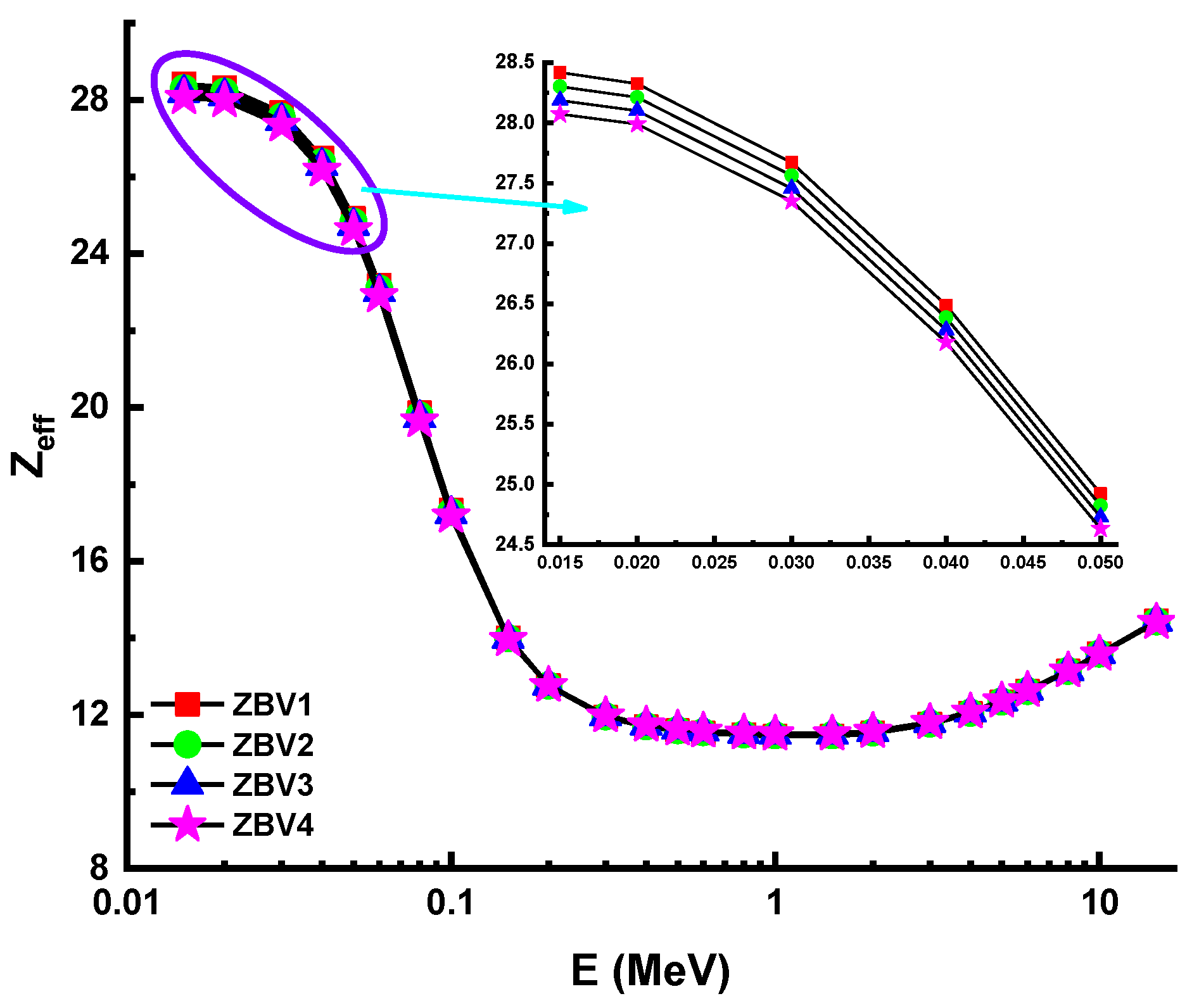
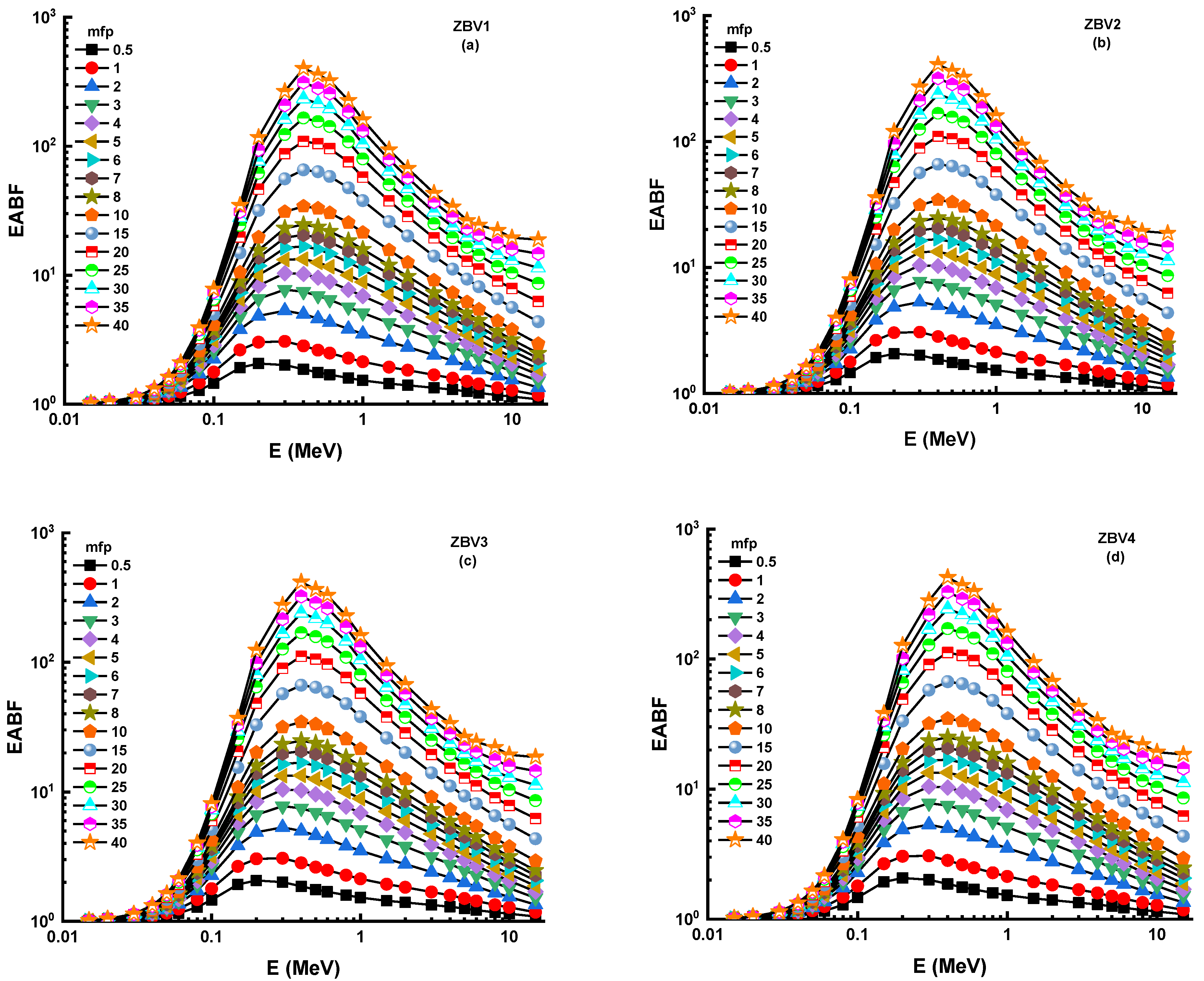
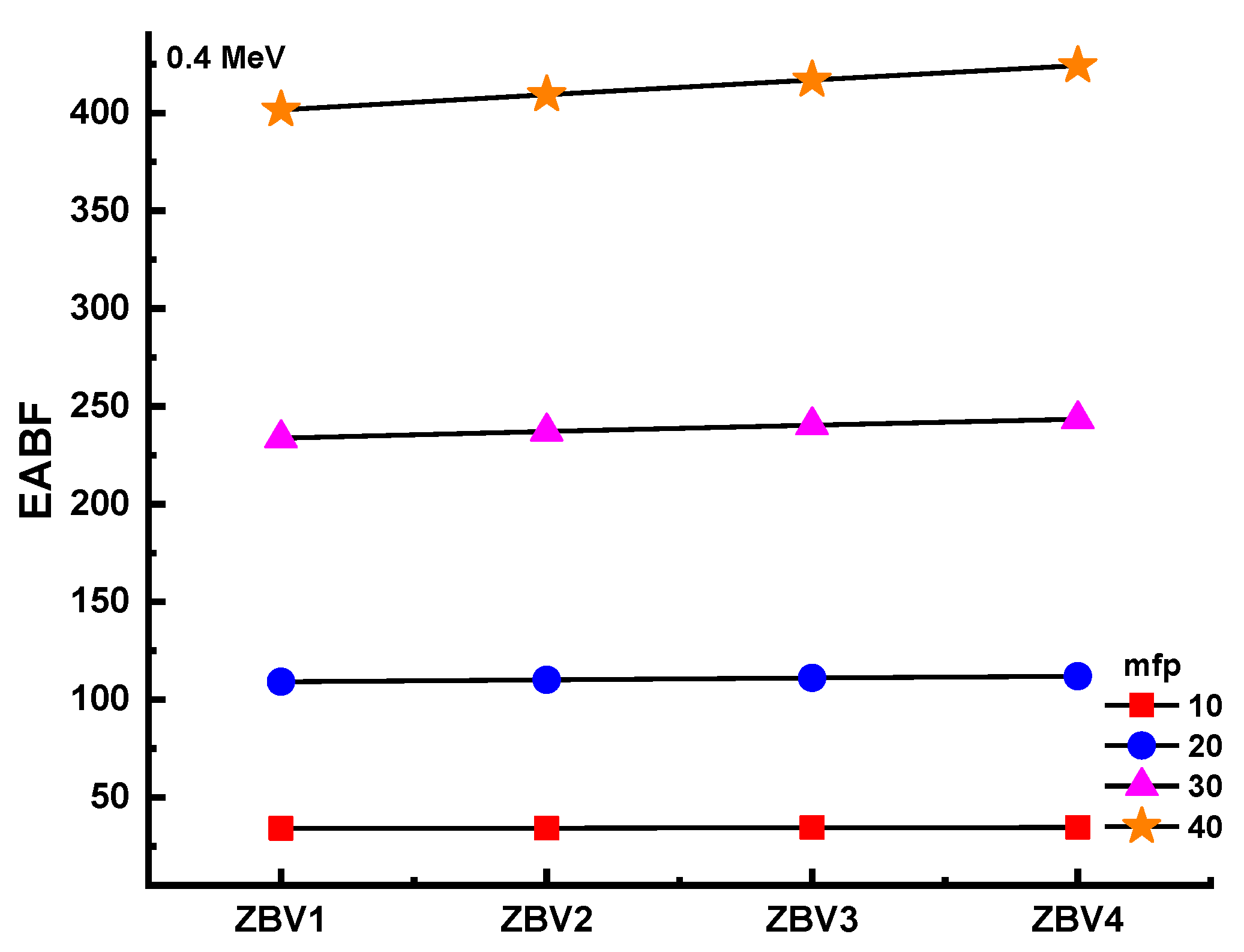
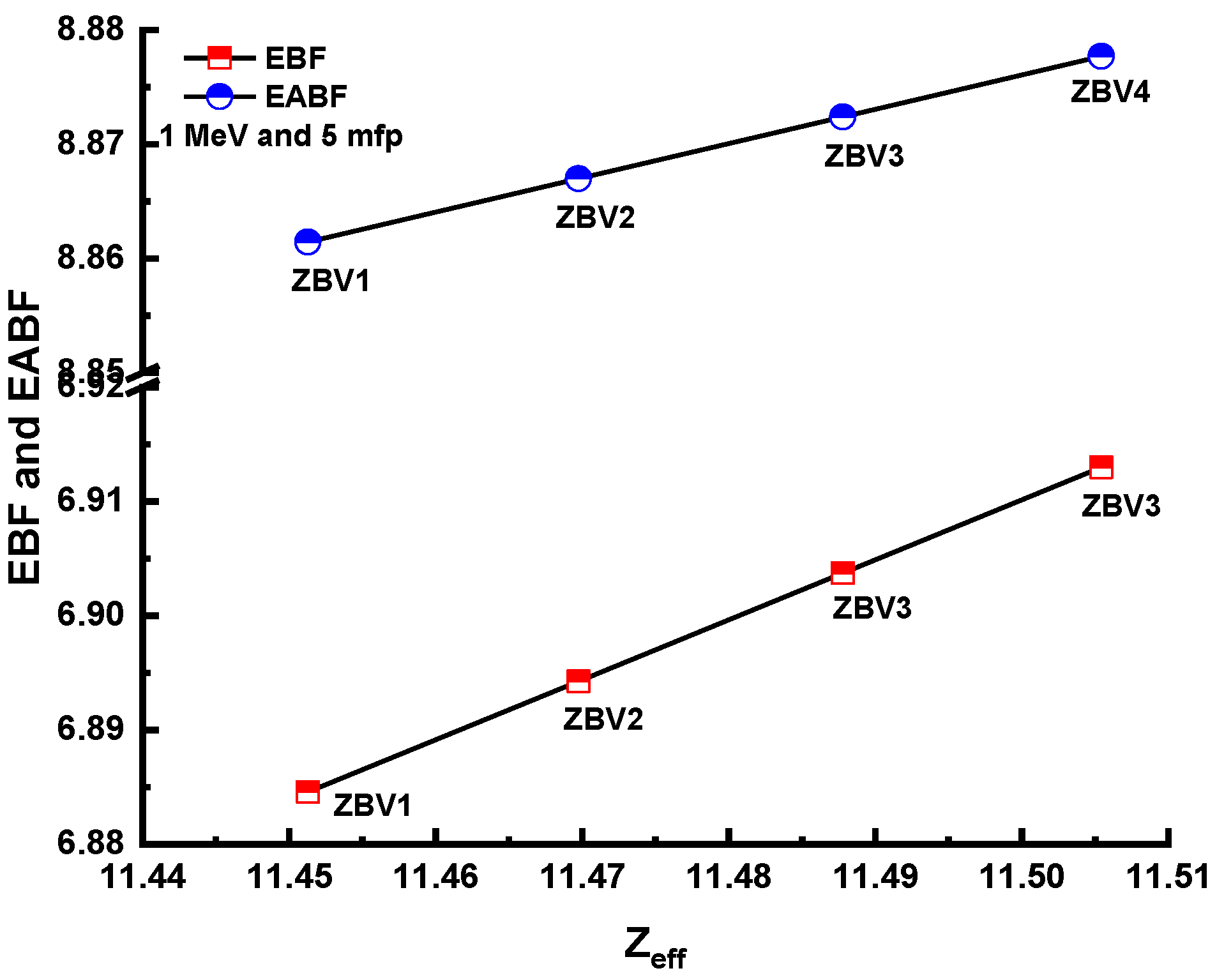
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kilic, G.I.U. Synthesis of Nb5+ Doped Zinc Borate Glasses for Optoelectronic Applications and Determination of Optical, Thermal and Structural Properties. J. Adv. Res. Nat. Appl. Sci. 2020, 6, 66–80. [Google Scholar]
- El-Falaky, G.; Gaafar, M.; El-Aal, N.A. Ultrasonic relaxation in Zinc–Borate glasses. Curr. Appl. Phys. 2012, 12, 589–596. [Google Scholar] [CrossRef]
- Wu, J.; Xie, C.; Hu, J.; Zeng, D.; Wang, A. Microstructure and electrical characteristics of ZnO–B2O3–PbO–V2O5–MnO2 ceramics prepared from ZnO nanopowders. J. Eur. Ceram. Soc. 2004, 24, 3635–3641. [Google Scholar] [CrossRef]
- Kilic, G.; Ilik, E.; Issever, U.G.; Peker, M. The effect of B2O3/CdO substitution on structural, thermal, and optical properties of new black PVB/Cd semiconducting oxide glasses. Appl. Phys. A 2020, 126, 1–12. [Google Scholar] [CrossRef]
- Kiliç, G.; Aral, E. Determination of optical band gaps and structural properties of Cu2+ Doped B2O3-Na2O-Al2O3-V2O5 Glasses. Gazi Univ. J. Sci. 2009, 22, 129–139. [Google Scholar]
- Rao, R.B.; Veeraiah, N.; Nalluri, V. Study on some physical properties of Li2O–MO–B2O3: V2O5 glasses. Phys. B Condens. Matter 2004, 348, 256–271. [Google Scholar] [CrossRef]
- Ilik, E.; Kilic, G.; Issever, U.G. Synthesis of novel AgO-doped vanadium–borophosphate semiconducting glasses and investigation of their optical, structural, and thermal properties. J. Mater. Sci. Mater. Electron. 2020, 31, 8986–8995. [Google Scholar] [CrossRef]
- El-Batal, H.A.R.; Ezz-El-Din, F.M. Interaction of gamma-rays with Some Alkali-Alkaline-Earth Borate Glasses Containing Chromium. J. Am. Ceram. Soc. 1993, 76, 523–529. [Google Scholar] [CrossRef]
- Marltan, W.; Rao, P.V.; Tekin, H.; Sayyed, M.; Klement, R.; Galusek, D.; Lakshminarayana, G.; Prasad, P.S.; Veeraiah, N. Analysis of red mud doped Bi2O3-B2O3-BaO glasses for application as glass solder in radiation shield repair using MCNPX simulation. Ceram. Int. 2019, 45, 7619–7626. [Google Scholar] [CrossRef]
- Kilic, G.; Ilik, E.; Mahmoud, K.; El-Mallawany, R.; El-Agawany, F.; Rammah, Y. Novel zinc vanadyl boro-phosphate glasses: ZnO–V2O5–P2O5–B2O3: Physical, thermal, and nuclear radiation shielding properties. Ceram. Int. 2020, 46, 19318–19327. [Google Scholar] [CrossRef]
- He, F.; Wang, J.; Deng, D. Effect of Bi2O3 on structure and wetting studies of Bi2O3–ZnO–B2O3 glasses. J. Alloys Compd. 2011, 509, 6332–6336. [Google Scholar] [CrossRef]
- Li, S.; Chen, P.; Li, Y. Structural and physical properties in the system ZnO–B2O3–P2O5–RnOm. Phys. B Condens. Matter 2010, 405, 4845–4850. [Google Scholar] [CrossRef]
- Aleksandrov, L.A.; Komatsu, T.; Iordanova, R.; Dimitriev, Y. Structure study of MoO3–ZnO–B2O3 glasses by Raman spectroscopy and formation of α-ZnMoO4 nanocrystals. Opt. Mater. 2011, 33, 839–845. [Google Scholar] [CrossRef]
- Bale, S.; Rahman, S. Electrical conductivity studies of Bi2O3–Li2O–ZnO–B2O3 glasses. Mater. Res. Bull. 2012, 47, 1153–1157. [Google Scholar] [CrossRef]
- Ozturk, S.; Ilik, E.; Kilic, G.; Issever, U.G. Ta2O5-doped zinc-borate glasses: Physical, structural, optical, thermal, and radiation shielding properties. Appl. Phys. A 2020, 126, 1–16. [Google Scholar] [CrossRef]
- Tekin, H.O.; Kassab, L.R.P.; Issa, S.A.M.; Dias da Silva Bordon, C.; Al-Buriahi, M.S.; de Oliviera Pereira Delboni, F.; Kilic, G.; Magalhaes, E.S. Structural and physical characterization study on synthesized tellurite (TeO2) and germanate (GeO2) glass shields using XRD, Raman spectroscopy, FLUKA and PHITS. Opt. Mater. 2020, 110. [Google Scholar] [CrossRef]
- Kilic, G.; Issa, S.; Ilik, E.; Kilicoglu, O.; Tekin, H. A journey for exploration of Eu2O3 reinforcement effect on zinc-borate glasses: Synthesis, optical, physical and nuclear radiation shielding properties. Ceram. Int. 2021, 47, 2572–2583. [Google Scholar] [CrossRef]
- Işsever, U.G.; Kilic, G.; Peker, M.; Ünaldi, T.; Aybek, A. Şenol Effect of low ratio V5+ doping on structural and optical properties of borotellurite semiconducting oxide glasses. J. Mater. Sci. Mater. Electron. 2019, 30, 15156–15167. [Google Scholar] [CrossRef]
- Dimitrov, V.; Dimitriev, Y.; Montenero, A. IR spectra and structure of V2O5GeO2Bi2O3 glasses. J. Non. Cryst. Solids 1994, 180, 51–57. [Google Scholar] [CrossRef]
- Ravikumar, R.; Reddy, V.R.; Chandrasekhar, A.; Reddy, B.; Reddy, Y.; Rao, P. Tetragonal site of transition metal ions doped sodium phosphate glasses. J. Alloys Compd. 2002, 337, 272–276. [Google Scholar] [CrossRef]
- Hirashima, H.; Arai, D.; Yoshida, T. Electrical Conductivity of PbO-P2O5-V2O5 Glasses. J. Am. Ceram. Soc. 1985, 68, 486–489. [Google Scholar] [CrossRef]
- Srinivas, B.; Hameed, A.; Shareefuddin, M.; Chary, M.N. EPR and optical studies of BaO-TeO2-TiO2-B2O3 glasses containing V4+ and Cu2+ transitional metal ion. In Proceedings of the Materials Today: Proceedings; Elsevier Ltd: Amsterdam, the Netherlands, 2015; Volume 2, pp. 1915–1922. [Google Scholar]
- Nagaraja, N.; Sankarappa, T.; Kumar, M.P. Electrical conductivity studies in single and mixed alkali doped cobalt–borate glasses. J. Non-Crystalline Solids 2008, 354, 1503–1508. [Google Scholar] [CrossRef]
- Hemeda, O.; Eid, M.; Sharshar, T.; Ellabany, H.; Henaish, A. Synthesis of nanometer-sized PbZr Ti1-O3 for gamma-ray attenuation. J. Phys. Chem. Solids 2021, 148, 109688. [Google Scholar] [CrossRef]
- Sallam, O.; Madbouly, A.; Elalaily, N.; Ezz-Eldin, F. Physical properties and radiation shielding parameters of bismuth borate glasses doped transition metals. J. Alloys Compd. 2020, 843, 156056. [Google Scholar] [CrossRef]
- Henaish, A.M.A.; Mostafa, M.; Salem, B.I.; Zakaly, H.M.H.; Issa, S.A.M.; Weinstein, I.A.; Hemeda, O.M. Spectral, electrical, magnetic and radiation shielding studies of Mg-doped Ni–Cu–Zn nanoferrites. J. Mater. Sci. Mater. Electron. 2020, 1–13. [Google Scholar] [CrossRef]
- Abouhaswa, A.; Zakaly, H.M.; Issa, S.A.; Rashad, M.; Pyshkina, M.; Tekin, H.; El-Mallawany, R.; Mostafa, M.Y. Synthesis, physical, optical, mechanical, and radiation attenuation properties of TiO2–Na2O–Bi2O3–B2O3 glasses. Ceram. Int. 2021, 47, 185–204. [Google Scholar] [CrossRef]
- Elazaka, A.; Zakaly, H.M.; Issa, S.A.; Rashad, M.; Tekin, H.; Saudi, H.; Gillette, V.; Erguzel, T.; Mostafa, A. New approach to removal of hazardous Bypass Cement Dust (BCD) from the environment: 20Na2O-20BaCl2-(60−x)B2O3-(x)BCD glass system and Optical, mechanical, structural and nuclear radiation shielding competences. J. Hazard. Mater. 2021, 403, 123738. [Google Scholar] [CrossRef]
- Zakaly, H.M.; Saudi, H.; Issa, S.A.; Rashad, M.; Elazaka, A.; Tekin, H.; Saddeek, Y. Alteration of optical, structural, mechanical durability and nuclear radiation attenuation properties of barium borosilicate glasses through BaO reinforcement: Experimental and numerical analyses. Ceram. Int. 2021, 47, 5587–5596. [Google Scholar] [CrossRef]
- Zakaly, H.M.; Abouhaswa, A.; Issa, S.A.M.; Mostafa, M.Y.A.; Pyshkina, M.; El-Mallawany, R. Optical and nuclear radiation shielding properties of zinc borate glasses doped with lanthanum oxide. J. Non-Crystalline Solids 2020, 543, 120151. [Google Scholar] [CrossRef]
- Mostafa, A.; Zakaly, H.M.; Pyshkina, M.; Issa, S.A.; Tekin, H.; Sidek, H.; Matori, K.; Zaid, M. Multi-objective optimization strategies for radiation shielding performance of BZBB glasses using Bi2O3: A FLUKA Monte Carlo code calculations. J. Mater. Res. Technol. 2020, 9, 12335–12345. [Google Scholar] [CrossRef]
- Saudi, H.A.; El Kameesy, S.U. Effect of barium addition and plasma nitriding treatment on chemical and physical properties of Al, Pb borate glass system as a developed radiation shield. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Luxor, Egypt, 2019; Volume 1253, p. 012033. [Google Scholar]
- Singh, K.; Singh, H.; Sharma, G.; Gerward, L.; Khanna, A.; Kumar, R.; Nathuram, R.; Sahota, H.S. Gamma-ray shielding properties of CaO–SrO–B2O3 glasses. Radiat. Phys. Chem. 2005, 72, 225–228. [Google Scholar] [CrossRef]
- Kaplan, M.F. Concrete Radiation Shielding; John Wiley & Sons, Inc: New York, NY, USA, 1989. [Google Scholar]
- Kiliç, G. Synthesis and Optical, Thermal, Structural Investigation of Zinc-Borate Glasses Containing V2O5. Adıyaman Univ. J. Sci. 2020, 10, 307–325. [Google Scholar] [CrossRef]
- Issa, S.A. Effective atomic number and mass attenuation coefficient of PbO–BaO–B2O3 glass system. Radiat. Phys. Chem. 2016, 120, 33–37. [Google Scholar] [CrossRef]
- Yasmin, S.; Barua, B.S.; Khandaker, M.U.; Chowdhury, F.-U.-Z.; Rashid, A.; Bradley, D.A.; Olatunji, M.A.; Kamal, M. Studies of ionizing radiation shielding effectiveness of silica-based commercial glasses used in Bangladeshi dwellings. Results Phys. 2018, 9, 541–549. [Google Scholar] [CrossRef]
- Tunes, M.; De Oliveira, C.; Schön, C. Multi-objective optimization of a compact pressurized water nuclear reactor computational model for biological shielding design using innovative materials. Nucl. Eng. Des. 2017, 313, 20–28. [Google Scholar] [CrossRef]
- Kaewkhao, J.; Pokaipisit, A.; Limsuwan, P. Study on borate glass system containing with Bi2O3 and BaO for gamma-rays shielding materials: Comparison with PbO. J. Nucl. Mater. 2010, 399, 38–40. [Google Scholar] [CrossRef]
- Limkitjaroenporn, P.; Kaewkhao, J.; Limsuwan, P.; Chewpraditkul, W. Physical, optical, structural and gamma-ray shielding properties of lead sodium borate glasses. J. Phys. Chem. Solids 2011, 72, 245–251. [Google Scholar] [CrossRef]
- Kirdsiri, K.; Kaewkhao, J.; Chanthima, N.; Limsuwan, P. Comparative study of silicate glasses containing Bi2O3, PbO and BaO: Radiation shielding and optical properties. Ann. Nucl. Energy 2011, 38, 1438–1441. [Google Scholar] [CrossRef]
- Kaewjang, S.; Maghanemi, U.; Kothan, S.; Kim, H.; Limkitjaroenporn, P.; Kaewkhao, J. New gadolinium based glasses for gamma-rays shielding materials. Nucl. Eng. Des. 2014, 280, 21–26. [Google Scholar] [CrossRef]
- Chanthima, N.; Kaewkhao, J.; Limkitjaroenporn, P.; Tuscharoen, S.; Kothan, S.; Tungjai, M.; Kaewjaeng, S.; Sarachai, S.; Limsuwan, P. Development of BaO–ZnO–B2O3 glasses as a radiation shielding material. Radiat. Phys. Chem. 2017, 137, 72–77. [Google Scholar] [CrossRef]
- Boonin, K.; Yasaka, P.; Limkitjaroenporn, P.; Rajaramakrishna, R.; Askin, A.; Sayyed, M.; Kothan, S.; Kaewkhao, J. Effect of BaO on lead free zinc barium tellurite glass for radiation shielding materials in nuclear application. J. Non-Crystalline Solids 2020, 550, 120386. [Google Scholar] [CrossRef]
- Cheewasukhanont, W.; Limkitjaroenporn, P.; Kothan, S.; Kedkaew, C.; Kaewkhao, J. The effect of particle size on radiation shielding properties for bismuth borosilicate glass. Radiat. Phys. Chem. 2020, 172, 108791. [Google Scholar] [CrossRef]
- Kaewjaeng, S.; Kothan, S.; Chaiphaksa, W.; Chanthima, N.; Rajaramakrishna, R.; Kim, H.; Kaewkhao, J. High transparency La2O3-CaO-B2O3-SiO2 glass for diagnosis x-rays shielding material application. Radiat. Phys. Chem. 2019, 160, 41–47. [Google Scholar] [CrossRef]
- ElBatal, F.; Ibrahim, S.; Abdelghany, A. Optical and FTIR spectra of NdF3-doped borophosphate glasses and effect of gamma irradiation. J. Mol. Struct. 2012, 1030, 107–112. [Google Scholar] [CrossRef]
- Elbatal, H.; Abdelghany, A.; Elbatal, F.; Elbadry, K.; Moustaffa, F. UV–visible and infrared absorption spectra of gamma irradiated CuO-doped lithium phosphate, lead phosphate and zinc phosphate glasses: A comparative study. Phys. B Condens. Matter 2011, 406, 3694–3703. [Google Scholar] [CrossRef]
- Gerward, L.; Guilbert, N.; Jensen, K.; Levring, H. WinXCom—a program for calculating X-ray attenuation coefficients. Radiat. Phys. Chem. 2004, 71, 653–654. [Google Scholar] [CrossRef]
- Tekin, H.O. MCNP-X Monte Carlo Code Application for Mass Attenuation Coefficients of Concrete at Different Energies by Modeling 3 × 3 Inch NaI(Tl) Detector and Comparison with XCOM and Monte Carlo Data. Sci. Technol. Nucl. Install. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Tekin, H.O.; Singh, V.P.; Manici, T.; Altunsoy, E.E. Validation of MCNPX with Experimental Results of Mass Attenuation Coefficients for Cement, Gypsum and Mixture. J. Radiat. Prot. Res. 2017, 42, 154–157. [Google Scholar] [CrossRef]
- RSICC Computer Code Collection, MCNPX User’s Manual Version 2.4.0. Monte Carlo N-Particle Transport Code System for Multiple and High Energy Application. 2002. Available online: https://rsicc.ornl.gov/codes/ccc/ccc8/ccc-810.html (accessed on 15 January 2021).
- Şakar, E.; Özpolat, Ö.F.; Alım, B.; Sayyed, M.; Kurudirek, M. Phy-X/PSD: Development of a user friendly online software for calculation of parameters relevant to radiation shielding and dosimetry. Radiat. Phys. Chem. 2020, 166, 108496. [Google Scholar] [CrossRef]
- Bashter, I. Calculation of radiation attenuation coefficients for shielding concretes. Ann. Nucl. Energy 1997, 24, 1389–1401. [Google Scholar] [CrossRef]
- Issa, S.A.; Saddeek, Y.B.; Tekin, H.; Sayyed, M.; Shaaban, K.S. Investigations of radiation shielding using Monte Carlo method and elastic properties of PbO-SiO2-B2O3-Na2O glasses. Curr. Appl. Phys. 2018, 18, 717–727. [Google Scholar] [CrossRef]

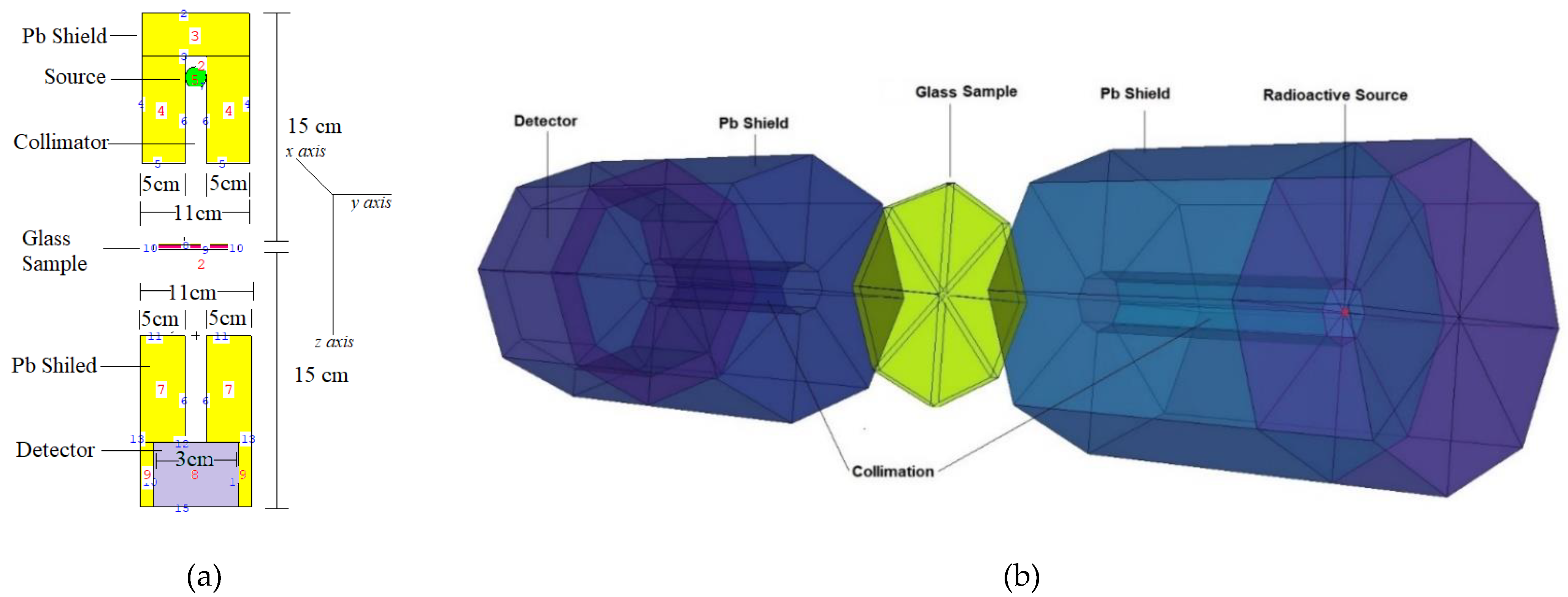



| Glass Code | mol% | wt% | Density (g/cm3) | |||||
|---|---|---|---|---|---|---|---|---|
| ZnO | B2O3 | V2O5 | B | O | V | Zn | ||
| ZBV1 | 59.4 | 39.6 | 1 | 0.110149663 | 0.377094852 | 0.013108056 | 0.499647429 | 3.392 |
| ZBV2 | 58.8 | 39.2 | 2 | 0.1075809 | 0.378557769 | 0.025866008 | 0.487995323 | 3.371 |
| ZBV3 | 58.2 | 38.8 | 3 | 0.105079843 | 0.379982128 | 0.038287697 | 0.476650332 | 3.339 |
| ZBV4 | 57.6 | 38.4 | 4 | 0.102643849 | 0.381369433 | 0.050386245 | 0.465600473 | 3.329 |
| Energy (MeV) | ZBV1 | ZBV2 | ZBV3 | ZBV4 | ||||
|---|---|---|---|---|---|---|---|---|
| Phy-X PSD | MCNPX | Phy-X PSD | MCNPX | Phy-X PSD | MCNPX | Phy-X PSD | MCNPX | |
| 0.015 | 41.8266 | 43.2654 | 41.3902 | 42.8624 | 40.9654 | 41.2416 | 40.5516 | 41.0625 |
| 0.02 | 19.1754 | 19.6521 | 18.9681 | 19.5124 | 18.7662 | 18.8126 | 18.5695 | 18.7250 |
| 0.03 | 6.2674 | 6.3124 | 6.1978 | 6.3004 | 6.1300 | 6.1526 | 6.0640 | 6.1236 |
| 0.04 | 2.8399 | 2.8524 | 2.8087 | 2.8324 | 2.7782 | 2.7816 | 2.7485 | 2.7628 |
| 0.05 | 1.5617 | 1.5721 | 1.5451 | 1.5629 | 1.5289 | 1.523 | 1.5131 | 1.5321 |
| 0.06 | 0.9800 | 0.9936 | 0.9701 | 0.9824 | 0.9605 | 0.972 | 0.9512 | 0.9626 |
| 0.08 | 0.5032 | 0.5092 | 0.4989 | 0.5054 | 0.4947 | 0.5023 | 0.4906 | 0.4926 |
| 0.1 | 0.3261 | 0.3295 | 0.3238 | 0.3286 | 0.3217 | 0.3251 | 0.3195 | 0.3198 |
| 0.15 | 0.1842 | 0.1901 | 0.1835 | 0.1882 | 0.1828 | 0.1862 | 0.1821 | 0.1832 |
| 0.2 | 0.1417 | 0.1421 | 0.1414 | 0.141 | 0.1411 | 0.1406 | 0.1408 | 0.1409 |
| 0.3 | 0.1096 | 0.111 | 0.1095 | 0.1101 | 0.1094 | 0.1091 | 0.1093 | 0.1089 |
| 0.4 | 0.0946 | 0.0952 | 0.0946 | 0.095 | 0.0945 | 0.0947 | 0.0945 | 0.0946 |
| 0.5 | 0.0851 | 0.086 | 0.085 | 0.0856 | 0.085 | 0.0854 | 0.085 | 0.0852 |
| 0.6 | 0.0781 | 0.0792 | 0.078 | 0.079 | 0.078 | 0.0782 | 0.078 | 0.0781 |
| 0.8 | 0.068 | 0.0695 | 0.068 | 0.0692 | 0.068 | 0.0688 | 0.068 | 0.0684 |
| 1 | 0.061 | 0.0624 | 0.0609 | 0.0621 | 0.0609 | 0.0619 | 0.0609 | 0.0612 |
| 1.5 | 0.0496 | 0.0501 | 0.0496 | 0.0499 | 0.0496 | 0.0495 | 0.0496 | 0.0494 |
| 2 | 0.043 | 0.0446 | 0.043 | 0.0439 | 0.043 | 0.0436 | 0.043 | 0.0434 |
| 3 | 0.0358 | 0.0363 | 0.0358 | 0.036 | 0.0358 | 0.0359 | 0.0358 | 0.0356 |
| 4 | 0.032 | 0.0334 | 0.032 | 0.0333 | 0.0319 | 0.0331 | 0.0319 | 0.0325 |
| 5 | 0.0297 | 0.0309 | 0.0297 | 0.0305 | 0.0297 | 0.0302 | 0.0296 | 0.0301 |
| 6 | 0.0283 | 0.0286 | 0.0282 | 0.0284 | 0.0282 | 0.0283 | 0.0282 | 0.0282 |
| 8 | 0.0267 | 0.0271 | 0.0267 | 0.027 | 0.0267 | 0.0268 | 0.0266 | 0.0267 |
| 10 | 0.026 | 0.0263 | 0.026 | 0.0261 | 0.026 | 0.026 | 0.0259 | 0.0259 |
| 15 | 0.0257 | 0.0262 | 0.0257 | 0.026 | 0.0256 | 0.0259 | 0.0256 | 0.0257 |
| Energy (MeV) | Zeq | G–P Fitting Parameters for EBF | G–P Fitting Parameters for EABF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | Xk | a | b | c | d | Xk | ||
| 0.015 | 22.43 | 0.230 | 1.006 | 1.018 | 0.227 | 0.223 | 1.006 | 1.011 | 0.217 | 7.920 | −0.223 |
| 0.020 | 22.78 | 0.398 | 1.014 | 0.287 | −0.348 | 0.283 | 1.014 | 0.314 | −0.236 | 14.711 | 0.283 |
| 0.030 | 23.21 | 0.206 | 1.041 | 0.373 | −0.231 | 0.246 | 1.040 | 0.337 | −0.172 | 16.253 | 0.246 |
| 0.040 | 23.47 | 0.243 | 1.086 | 0.347 | −0.125 | 0.238 | 1.085 | 0.350 | −0.127 | 13.895 | 0.238 |
| 0.050 | 23.65 | 0.225 | 1.145 | 0.380 | −0.129 | 0.237 | 1.154 | 0.360 | −0.134 | 14.335 | 0.237 |
| 0.060 | 23.80 | 0.203 | 1.211 | 0.422 | −0.113 | 0.216 | 1.240 | 0.398 | −0.126 | 14.724 | 0.216 |
| 0.080 | 24.00 | 0.168 | 1.358 | 0.502 | −0.092 | 0.174 | 1.463 | 0.482 | −0.098 | 15.336 | 0.174 |
| 0.100 | 24.13 | 0.129 | 1.495 | 0.600 | −0.073 | 0.156 | 1.772 | 0.541 | −0.094 | 15.276 | 0.156 |
| 0.150 | 24.32 | 0.065 | 1.763 | 0.796 | −0.043 | 0.125 | 2.632 | 0.657 | −0.101 | 14.589 | 0.125 |
| 0.200 | 24.43 | 0.023 | 1.919 | 0.960 | −0.030 | 0.061 | 3.026 | 0.856 | −0.062 | 13.065 | 0.061 |
| 0.300 | 24.55 | −0.016 | 2.024 | 1.131 | −0.017 | −0.001 | 3.065 | 1.086 | −0.030 | 11.983 | −0.001 |
| 0.400 | 24.61 | −0.031 | 2.030 | 1.210 | −0.013 | −0.029 | 2.828 | 1.204 | −0.013 | 14.934 | −0.029 |
| 0.500 | 24.65 | −0.041 | 2.000 | 1.253 | −0.008 | −0.041 | 2.624 | 1.256 | −0.008 | 11.683 | −0.041 |
| 0.600 | 24.67 | −0.044 | 1.969 | 1.264 | −0.005 | −0.043 | 2.484 | 1.266 | −0.006 | 12.436 | −0.043 |
| 0.800 | 24.70 | −0.042 | 1.917 | 1.250 | −0.006 | −0.044 | 2.273 | 1.262 | −0.007 | 9.857 | −0.044 |
| 1.000 | 24.70 | −0.050 | 1.853 | 1.258 | 0.014 | −0.051 | 2.130 | 1.265 | 0.013 | 17.995 | −0.051 |
| 1.500 | 22.35 | −0.042 | 1.777 | 1.205 | 0.012 | −0.043 | 1.937 | 1.210 | 0.013 | 15.494 | −0.043 |
| 2.000 | 19.86 | −0.030 | 1.738 | 1.147 | 0.008 | −0.029 | 1.834 | 1.144 | 0.007 | 17.096 | −0.029 |
| 3.000 | 18.94 | −0.004 | 1.658 | 1.047 | −0.011 | −0.008 | 1.685 | 1.057 | −0.006 | 12.383 | −0.008 |
| 4.000 | 18.68 | 0.008 | 1.579 | 1.003 | −0.017 | 0.014 | 1.590 | 0.984 | −0.023 | 12.087 | 0.014 |
| 5.000 | 18.56 | 0.014 | 1.510 | 0.982 | −0.021 | 0.021 | 1.501 | 0.962 | −0.033 | 14.147 | 0.021 |
| 6.000 | 18.48 | 0.021 | 1.462 | 0.962 | −0.026 | 0.027 | 1.435 | 0.944 | −0.034 | 12.913 | 0.027 |
| 8.000 | 18.40 | 0.032 | 1.381 | 0.935 | −0.036 | 0.034 | 1.339 | 0.928 | −0.034 | 12.212 | 0.034 |
| 10.000 | 18.35 | 0.039 | 1.319 | 0.922 | −0.042 | 0.044 | 1.281 | 0.903 | −0.047 | 13.903 | 0.044 |
| 15.000 | 18.31 | 0.064 | 1.236 | 0.866 | −0.065 | 0.035 | 1.176 | 0.944 | −0.039 | 14.486 | 0.035 |
| Energy (MeV) | Zeq | G–P Fitting Parameters for EBF | G–P Fitting Parameters for EABF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | Xk | a | b | c | d | Xk | ||
| 0.015 | 22.35 | 0.222 | 1.006 | 1.004 | 0.223 | 6.425 | 0.215 | 1.006 | 0.998 | 0.213 | 7.978 |
| 0.020 | 22.70 | 0.392 | 1.014 | 0.291 | −0.341 | 11.131 | 0.282 | 1.014 | 0.316 | −0.234 | 14.615 |
| 0.030 | 23.13 | 0.206 | 1.041 | 0.373 | −0.228 | 21.387 | 0.245 | 1.040 | 0.338 | −0.171 | 16.167 |
| 0.040 | 23.39 | 0.242 | 1.087 | 0.347 | −0.126 | 12.627 | 0.238 | 1.086 | 0.351 | −0.127 | 13.894 |
| 0.050 | 23.57 | 0.225 | 1.147 | 0.381 | −0.129 | 14.059 | 0.236 | 1.156 | 0.361 | −0.134 | 14.333 |
| 0.060 | 23.71 | 0.202 | 1.214 | 0.423 | −0.113 | 14.198 | 0.215 | 1.243 | 0.399 | −0.126 | 14.725 |
| 0.080 | 23.91 | 0.168 | 1.362 | 0.503 | −0.092 | 14.438 | 0.173 | 1.468 | 0.484 | −0.097 | 15.347 |
| 0.100 | 24.04 | 0.129 | 1.500 | 0.602 | −0.073 | 14.167 | 0.154 | 1.780 | 0.544 | −0.094 | 15.290 |
| 0.150 | 24.23 | 0.064 | 1.768 | 0.798 | −0.042 | 14.004 | 0.124 | 2.644 | 0.661 | −0.100 | 14.567 |
| 0.200 | 24.34 | 0.022 | 1.924 | 0.963 | −0.030 | 13.066 | 0.060 | 3.034 | 0.860 | −0.062 | 13.062 |
| 0.300 | 24.46 | −0.016 | 2.027 | 1.133 | −0.017 | 11.487 | −0.002 | 3.067 | 1.090 | −0.030 | 11.952 |
| 0.400 | 24.52 | −0.031 | 2.032 | 1.212 | −0.013 | 10.506 | −0.029 | 2.829 | 1.207 | −0.012 | 15.154 |
| 0.500 | 24.56 | −0.041 | 2.002 | 1.254 | −0.008 | 8.420 | −0.041 | 2.624 | 1.259 | −0.008 | 11.778 |
| 0.600 | 24.58 | −0.044 | 1.971 | 1.265 | −0.004 | 11.502 | −0.044 | 2.484 | 1.267 | −0.005 | 12.591 |
| 0.800 | 24.61 | −0.043 | 1.918 | 1.252 | −0.005 | 10.254 | −0.044 | 2.273 | 1.263 | −0.007 | 9.970 |
| 1.000 | 24.61 | −0.050 | 1.854 | 1.258 | 0.014 | 18.992 | −0.051 | 2.130 | 1.266 | 0.013 | 17.965 |
| 1.500 | 22.26 | −0.042 | 1.777 | 1.205 | 0.012 | 15.823 | −0.043 | 1.937 | 1.210 | 0.013 | 15.498 |
| 2.000 | 19.78 | −0.030 | 1.738 | 1.147 | 0.008 | 17.345 | −0.029 | 1.834 | 1.145 | 0.007 | 17.043 |
| 3.000 | 18.88 | −0.004 | 1.658 | 1.048 | −0.011 | 11.312 | −0.008 | 1.686 | 1.056 | −0.006 | 12.417 |
| 4.000 | 18.62 | 0.008 | 1.579 | 1.003 | −0.017 | 11.339 | 0.014 | 1.590 | 0.984 | −0.022 | 12.128 |
| 5.000 | 18.50 | 0.014 | 1.510 | 0.982 | −0.021 | 13.395 | 0.021 | 1.501 | 0.963 | −0.032 | 14.300 |
| 6.000 | 18.42 | 0.021 | 1.462 | 0.963 | −0.026 | 13.579 | 0.027 | 1.435 | 0.944 | −0.034 | 12.928 |
| 8.000 | 18.34 | 0.031 | 1.381 | 0.936 | −0.035 | 13.418 | 0.034 | 1.339 | 0.927 | −0.034 | 12.221 |
| 10.000 | 18.30 | 0.039 | 1.319 | 0.921 | −0.042 | 13.453 | 0.044 | 1.281 | 0.905 | −0.046 | 13.904 |
| 15.000 | 18.25 | 0.066 | 1.237 | 0.862 | −0.066 | 13.770 | 0.035 | 1.176 | 0.944 | −0.038 | 14.494 |
| Energy (MeV) | Zeq | G–P Fitting Parameters for EBF | G–P Fitting Parameters for EABF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | Xk | a | b | c | d | Xk | ||
| 0.015 | 22.27 | 0.214 | 1.006 | 0.991 | 0.220 | 6.445 | 0.207 | 1.006 | 0.984 | 0.210 | 8.035 |
| 0.020 | 22.62 | 0.386 | 1.014 | 0.295 | −0.334 | 11.124 | 0.281 | 1.014 | 0.318 | −0.232 | 14.520 |
| 0.030 | 23.04 | 0.207 | 1.041 | 0.373 | −0.225 | 21.137 | 0.245 | 1.040 | 0.339 | −0.170 | 16.081 |
| 0.040 | 23.30 | 0.242 | 1.088 | 0.348 | −0.126 | 12.661 | 0.237 | 1.087 | 0.351 | −0.127 | 13.892 |
| 0.050 | 23.48 | 0.225 | 1.148 | 0.381 | −0.128 | 14.061 | 0.236 | 1.157 | 0.361 | −0.134 | 14.330 |
| 0.060 | 23.62 | 0.202 | 1.216 | 0.424 | −0.113 | 14.199 | 0.215 | 1.246 | 0.401 | −0.125 | 14.726 |
| 0.080 | 23.82 | 0.167 | 1.366 | 0.505 | −0.092 | 14.437 | 0.173 | 1.474 | 0.486 | −0.097 | 15.357 |
| 0.100 | 23.95 | 0.128 | 1.505 | 0.604 | −0.072 | 14.169 | 0.153 | 1.789 | 0.547 | −0.093 | 15.303 |
| 0.150 | 24.14 | 0.063 | 1.774 | 0.801 | −0.042 | 13.998 | 0.123 | 2.655 | 0.665 | −0.099 | 14.546 |
| 0.200 | 24.25 | 0.022 | 1.928 | 0.966 | −0.030 | 13.057 | 0.059 | 3.042 | 0.863 | −0.061 | 13.059 |
| 0.300 | 24.37 | −0.016 | 2.030 | 1.135 | −0.017 | 11.464 | −0.003 | 3.069 | 1.093 | −0.030 | 11.921 |
| 0.400 | 24.43 | −0.032 | 2.035 | 1.214 | −0.013 | 10.492 | −0.030 | 2.829 | 1.210 | −0.012 | 15.370 |
| 0.500 | 24.47 | −0.041 | 2.004 | 1.255 | −0.008 | 8.425 | −0.042 | 2.623 | 1.261 | −0.007 | 11.871 |
| 0.600 | 24.49 | −0.044 | 1.972 | 1.267 | −0.004 | 11.717 | −0.044 | 2.484 | 1.269 | −0.005 | 12.743 |
| 0.800 | 24.52 | −0.043 | 1.919 | 1.253 | −0.005 | 10.408 | −0.045 | 2.273 | 1.265 | −0.006 | 10.080 |
| 1.000 | 24.52 | −0.050 | 1.855 | 1.259 | 0.014 | 18.959 | −0.051 | 2.130 | 1.267 | 0.013 | 17.936 |
| 1.500 | 22.17 | −0.042 | 1.778 | 1.205 | 0.012 | 15.821 | −0.043 | 1.937 | 1.211 | 0.013 | 15.502 |
| 2.000 | 19.71 | −0.030 | 1.739 | 1.147 | 0.007 | 17.271 | −0.029 | 1.834 | 1.145 | 0.007 | 16.991 |
| 3.000 | 18.82 | −0.004 | 1.658 | 1.048 | −0.010 | 11.333 | −0.008 | 1.686 | 1.056 | −0.006 | 12.451 |
| 4.000 | 18.56 | 0.008 | 1.579 | 1.003 | −0.017 | 11.305 | 0.014 | 1.590 | 0.984 | −0.022 | 12.169 |
| 5.000 | 18.44 | 0.014 | 1.511 | 0.982 | −0.021 | 13.393 | 0.020 | 1.501 | 0.964 | −0.032 | 14.450 |
| 6.000 | 18.37 | 0.020 | 1.462 | 0.963 | −0.025 | 13.595 | 0.027 | 1.435 | 0.944 | −0.034 | 12.943 |
| 8.000 | 18.29 | 0.031 | 1.381 | 0.936 | −0.035 | 13.413 | 0.034 | 1.340 | 0.927 | −0.034 | 12.231 |
| 10.000 | 18.24 | 0.039 | 1.320 | 0.921 | −0.042 | 13.447 | 0.043 | 1.281 | 0.906 | −0.046 | 13.905 |
| 15.000 | 18.20 | 0.067 | 1.239 | 0.858 | −0.067 | 13.791 | 0.034 | 1.176 | 0.945 | −0.038 | 14.502 |
| Energy (MeV) | Zeq | G–P Fitting Parameters for EBF | G–P Fitting Parameters for EABF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | Xk | a | b | c | d | Xk | ||
| 0.015 | 22.19 | 0.206 | 1.006 | 0.978 | 0.217 | 6.465 | 0.198 | 1.006 | 0.971 | 0.207 | 8.091 |
| 0.020 | 22.54 | 0.380 | 1.014 | 0.300 | −0.326 | 11.117 | 0.280 | 1.014 | 0.319 | −0.231 | 14.426 |
| 0.030 | 22.96 | 0.207 | 1.042 | 0.373 | −0.223 | 20.895 | 0.245 | 1.041 | 0.339 | −0.170 | 15.999 |
| 0.040 | 23.22 | 0.242 | 1.089 | 0.348 | −0.126 | 12.695 | 0.237 | 1.088 | 0.352 | −0.127 | 13.891 |
| 0.050 | 23.40 | 0.224 | 1.150 | 0.382 | −0.128 | 14.062 | 0.236 | 1.159 | 0.362 | −0.134 | 14.328 |
| 0.060 | 23.54 | 0.202 | 1.219 | 0.424 | −0.113 | 14.200 | 0.214 | 1.249 | 0.402 | −0.125 | 14.727 |
| 0.080 | 23.73 | 0.167 | 1.370 | 0.506 | −0.091 | 14.435 | 0.172 | 1.479 | 0.488 | −0.096 | 15.367 |
| 0.100 | 23.86 | 0.127 | 1.510 | 0.606 | −0.072 | 14.172 | 0.152 | 1.797 | 0.550 | −0.093 | 15.317 |
| 0.150 | 24.05 | 0.063 | 1.779 | 0.804 | −0.042 | 13.993 | 0.121 | 2.666 | 0.669 | −0.098 | 14.525 |
| 0.200 | 24.16 | 0.021 | 1.933 | 0.969 | −0.029 | 13.049 | 0.058 | 3.050 | 0.867 | −0.061 | 13.056 |
| 0.300 | 24.28 | −0.017 | 2.033 | 1.137 | −0.016 | 11.443 | −0.004 | 3.071 | 1.096 | −0.029 | 11.891 |
| 0.400 | 24.35 | −0.032 | 2.037 | 1.215 | −0.013 | 10.479 | −0.030 | 2.829 | 1.212 | −0.011 | 15.580 |
| 0.500 | 24.38 | −0.041 | 2.006 | 1.256 | −0.008 | 8.430 | −0.042 | 2.623 | 1.263 | −0.007 | 11.961 |
| 0.600 | 24.40 | −0.045 | 1.974 | 1.268 | −0.004 | 11.927 | −0.045 | 2.484 | 1.271 | −0.004 | 12.891 |
| 0.800 | 24.43 | −0.043 | 1.920 | 1.254 | −0.004 | 10.559 | −0.045 | 2.272 | 1.266 | −0.006 | 10.188 |
| 1.000 | 24.43 | −0.050 | 1.856 | 1.259 | 0.014 | 18.927 | −0.051 | 2.130 | 1.267 | 0.013 | 17.908 |
| 1.500 | 22.08 | −0.042 | 1.779 | 1.205 | 0.012 | 15.819 | −0.043 | 1.937 | 1.211 | 0.013 | 15.506 |
| 2.000 | 19.64 | −0.030 | 1.739 | 1.147 | 0.007 | 17.198 | −0.029 | 1.834 | 1.145 | 0.007 | 16.941 |
| 3.000 | 18.76 | −0.004 | 1.658 | 1.048 | −0.010 | 11.354 | −0.008 | 1.687 | 1.056 | −0.006 | 12.484 |
| 4.000 | 18.50 | 0.008 | 1.579 | 1.003 | −0.016 | 11.271 | 0.014 | 1.590 | 0.984 | −0.022 | 12.208 |
| 5.000 | 18.39 | 0.014 | 1.511 | 0.981 | −0.021 | 13.392 | 0.020 | 1.501 | 0.965 | −0.032 | 14.597 |
| 6.000 | 18.31 | 0.020 | 1.462 | 0.963 | −0.025 | 13.610 | 0.027 | 1.435 | 0.944 | −0.034 | 12.957 |
| 8.000 | 18.23 | 0.031 | 1.380 | 0.936 | −0.035 | 13.409 | 0.035 | 1.340 | 0.926 | −0.034 | 12.240 |
| 10.000 | 18.19 | 0.039 | 1.320 | 0.921 | −0.042 | 13.441 | 0.043 | 1.281 | 0.907 | −0.045 | 13.906 |
| 15.000 | 18.15 | 0.068 | 1.240 | 0.854 | −0.068 | 13.812 | 0.034 | 1.176 | 0.946 | −0.037 | 14.509 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tekin, H.O.; Issa, S.A.M.; Kilic, G.; Zakaly, H.M.H.; Abuzaid, M.M.; Tarhan, N.; Alshammari, K.; Sidek, H.A.A.; Matori, K.A.; Zaid, M.H.M. In-Silico Monte Carlo Simulation Trials for Investigation of V2O5 Reinforcement Effect on Ternary Zinc Borate Glasses: Nuclear Radiation Shielding Dynamics. Materials 2021, 14, 1158. https://doi.org/10.3390/ma14051158
Tekin HO, Issa SAM, Kilic G, Zakaly HMH, Abuzaid MM, Tarhan N, Alshammari K, Sidek HAA, Matori KA, Zaid MHM. In-Silico Monte Carlo Simulation Trials for Investigation of V2O5 Reinforcement Effect on Ternary Zinc Borate Glasses: Nuclear Radiation Shielding Dynamics. Materials. 2021; 14(5):1158. https://doi.org/10.3390/ma14051158
Chicago/Turabian StyleTekin, Huseyin O., Shams A. M. Issa, Gokhan Kilic, Hesham M. H. Zakaly, Mohamed M. Abuzaid, Nevzat Tarhan, Khatar Alshammari, Hj Ab Aziz Sidek, Khamirul A. Matori, and Mohd H. M. Zaid. 2021. "In-Silico Monte Carlo Simulation Trials for Investigation of V2O5 Reinforcement Effect on Ternary Zinc Borate Glasses: Nuclear Radiation Shielding Dynamics" Materials 14, no. 5: 1158. https://doi.org/10.3390/ma14051158
APA StyleTekin, H. O., Issa, S. A. M., Kilic, G., Zakaly, H. M. H., Abuzaid, M. M., Tarhan, N., Alshammari, K., Sidek, H. A. A., Matori, K. A., & Zaid, M. H. M. (2021). In-Silico Monte Carlo Simulation Trials for Investigation of V2O5 Reinforcement Effect on Ternary Zinc Borate Glasses: Nuclear Radiation Shielding Dynamics. Materials, 14(5), 1158. https://doi.org/10.3390/ma14051158










