Lagrangian Differencing Dynamics for Time-Independent Non-Newtonian Materials
Abstract
:1. Introduction
2. Governing Equations
2.1. Bingham Model
2.2. Casson Model
2.3. Power Law Model
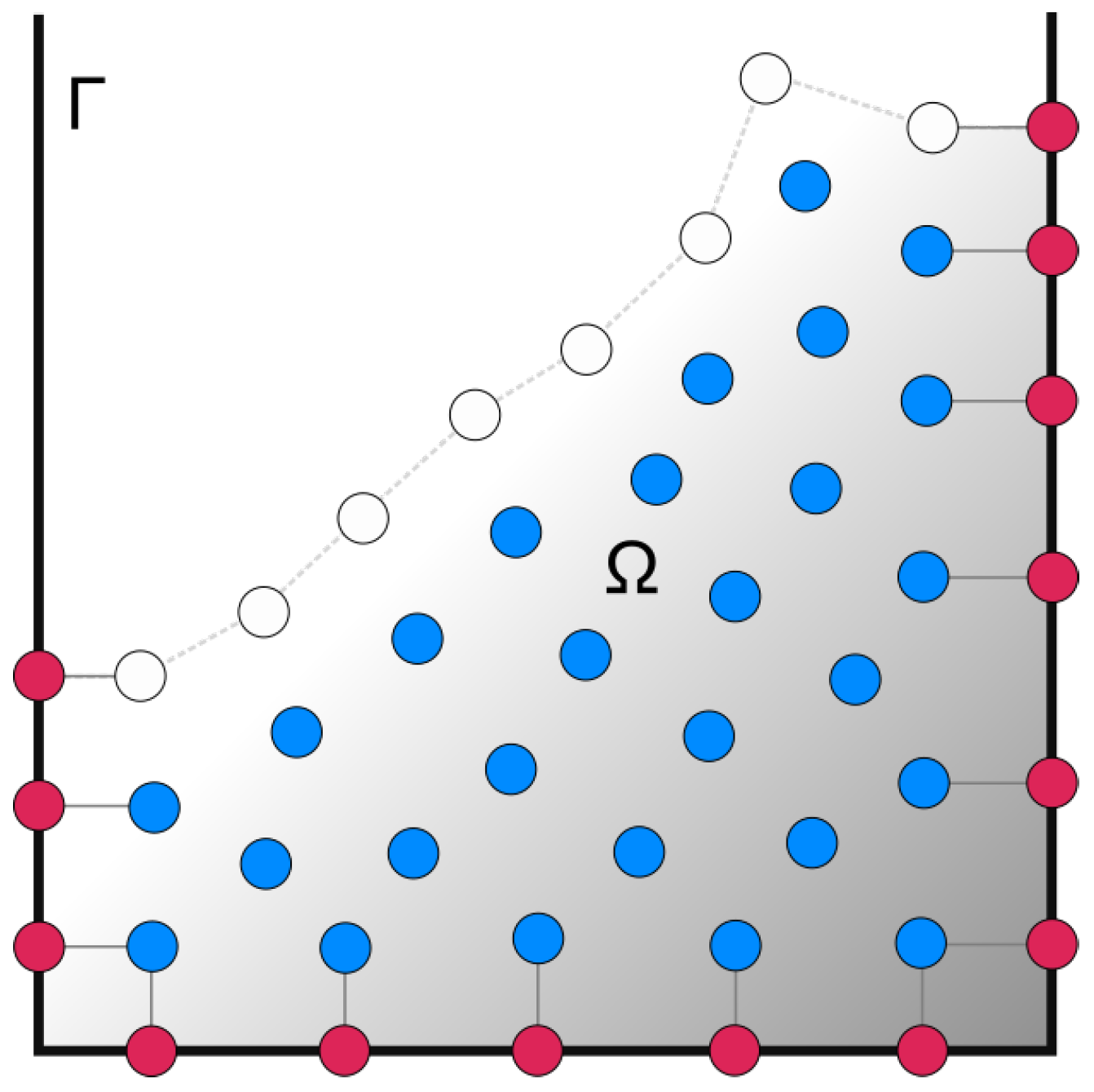
3. Numerical Procedure
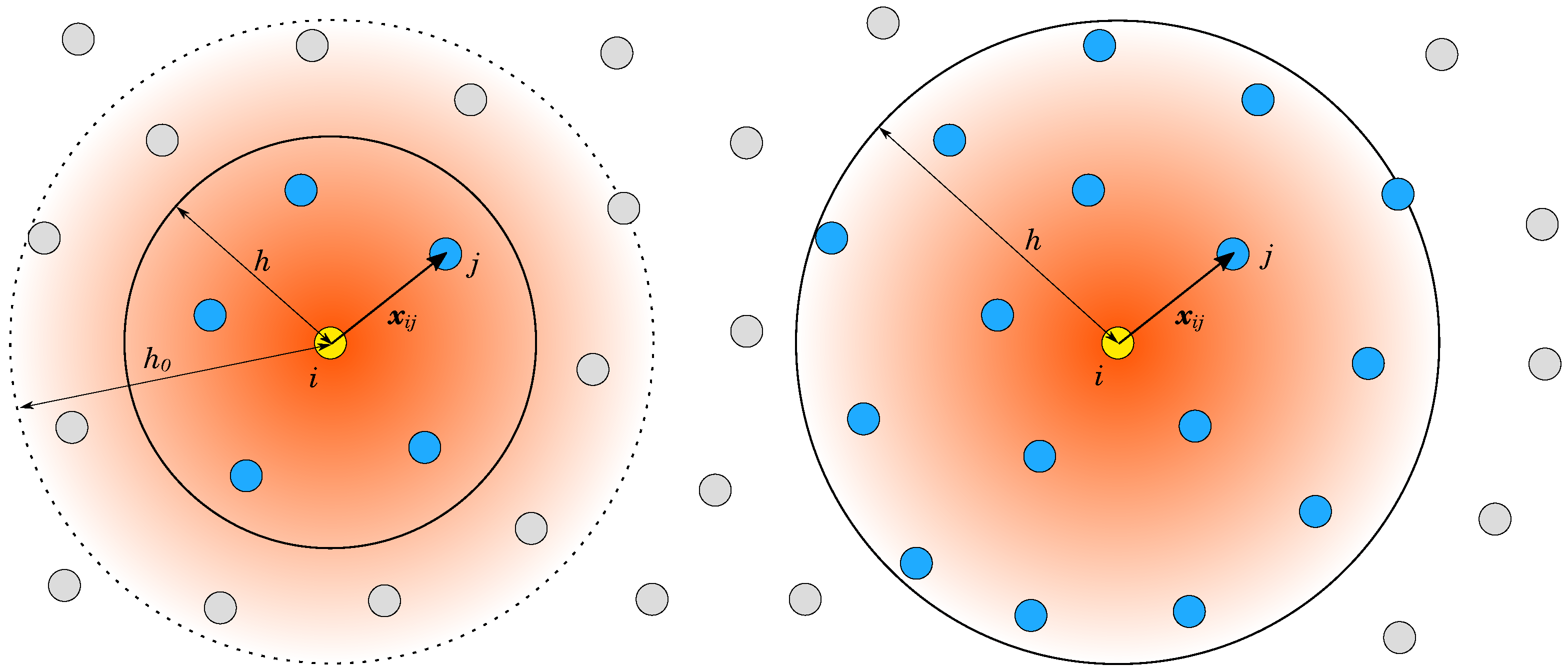
3.1. Lagrangian Differencing
3.2. Numerical Solver
4. Results and Discussion
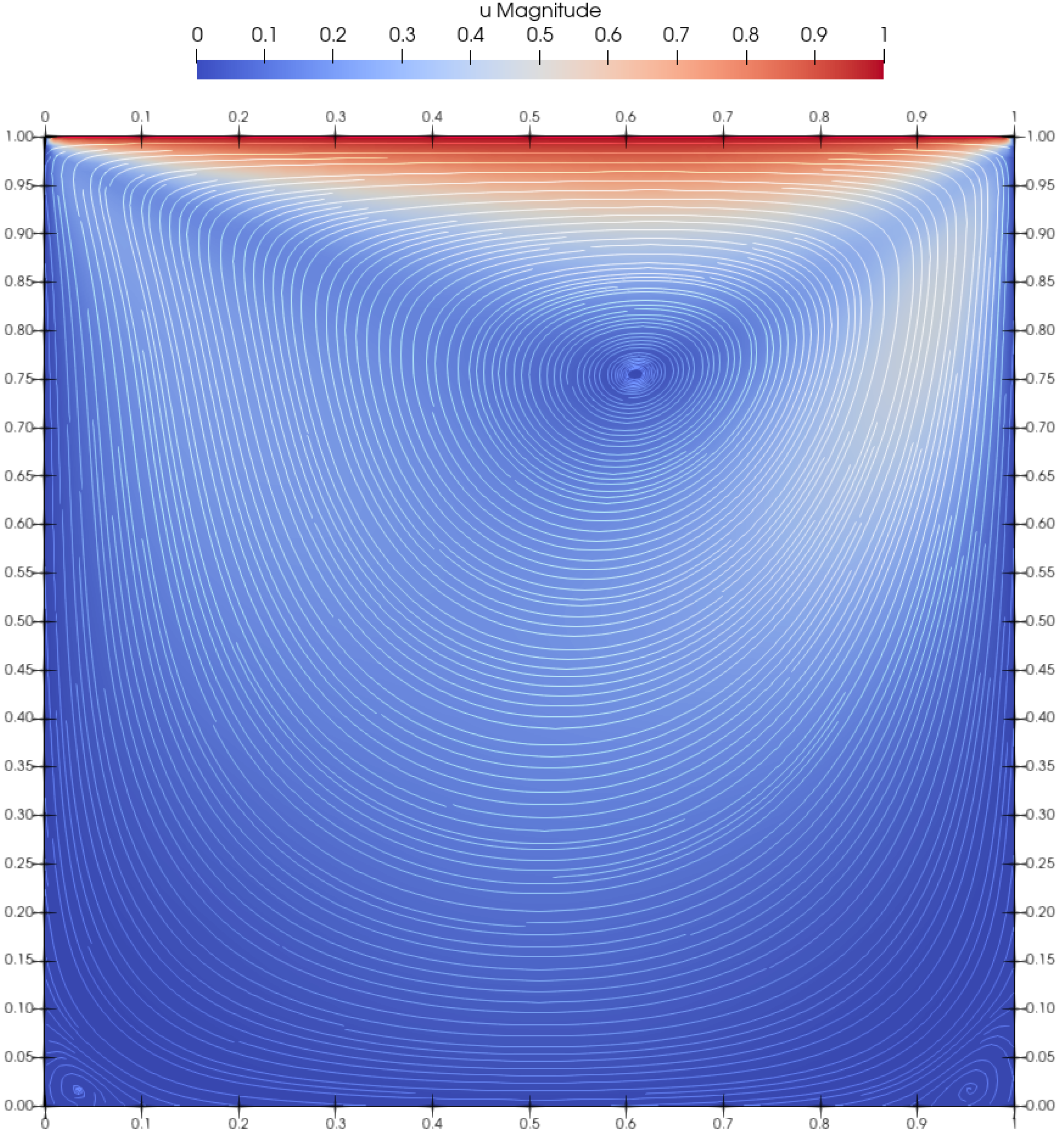
4.1. Square Lid-Driven Cavity Flow
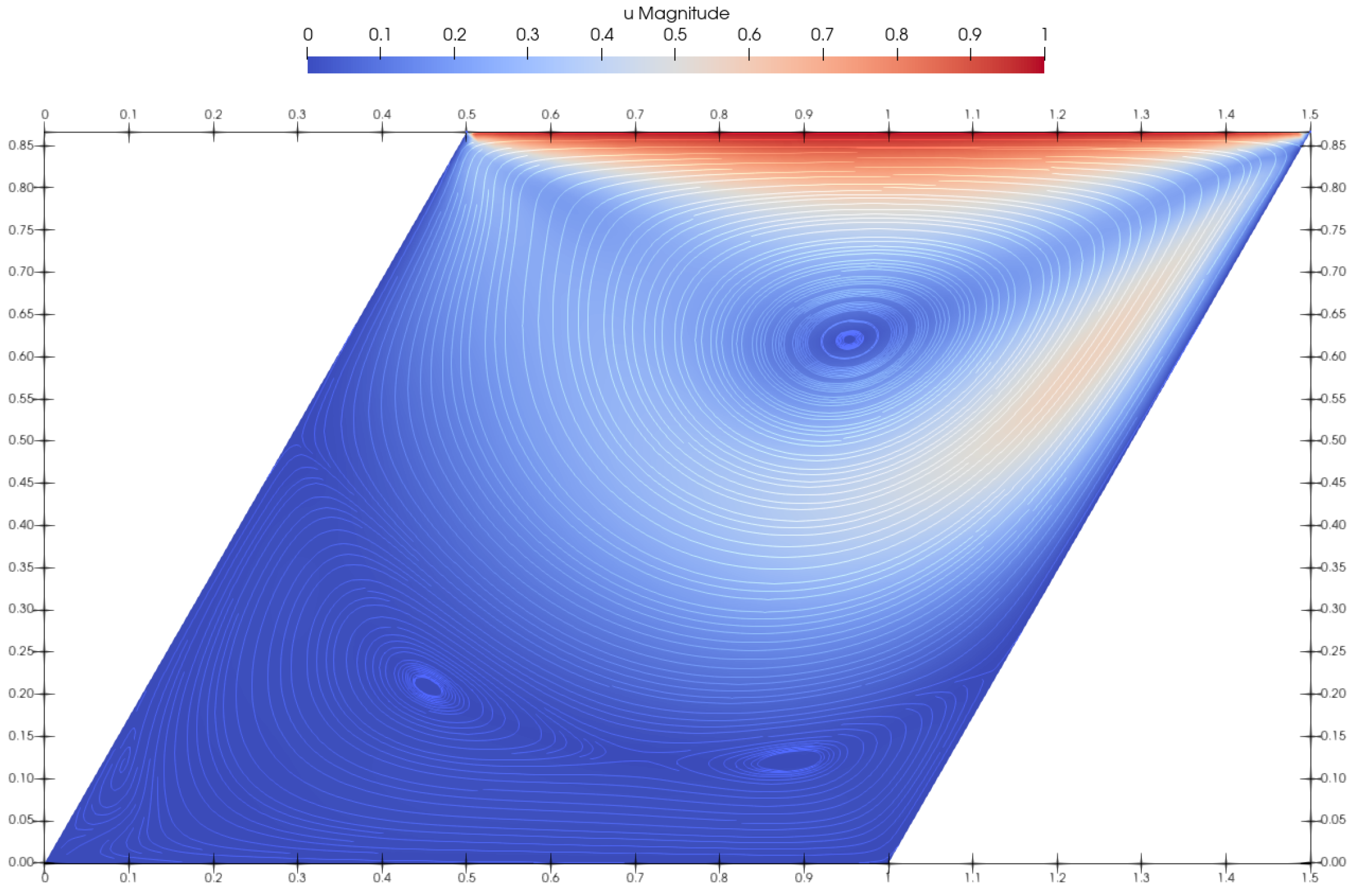
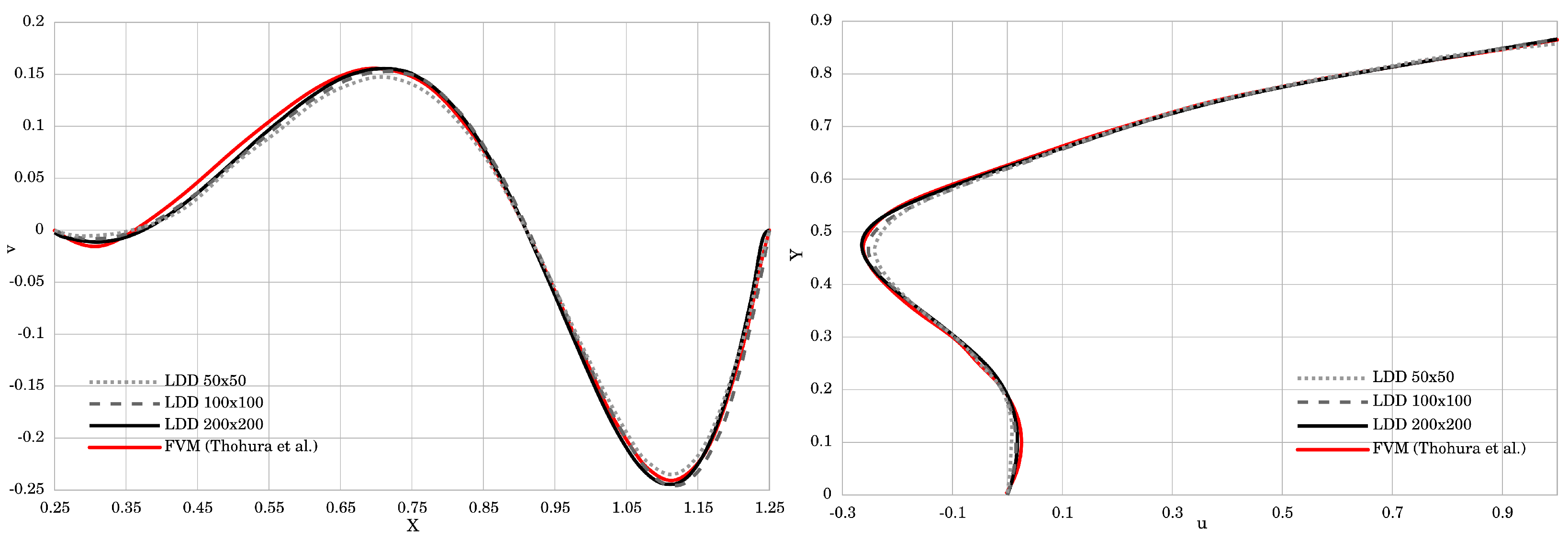
4.2. Skewed Lid-Driven Cavity Flow
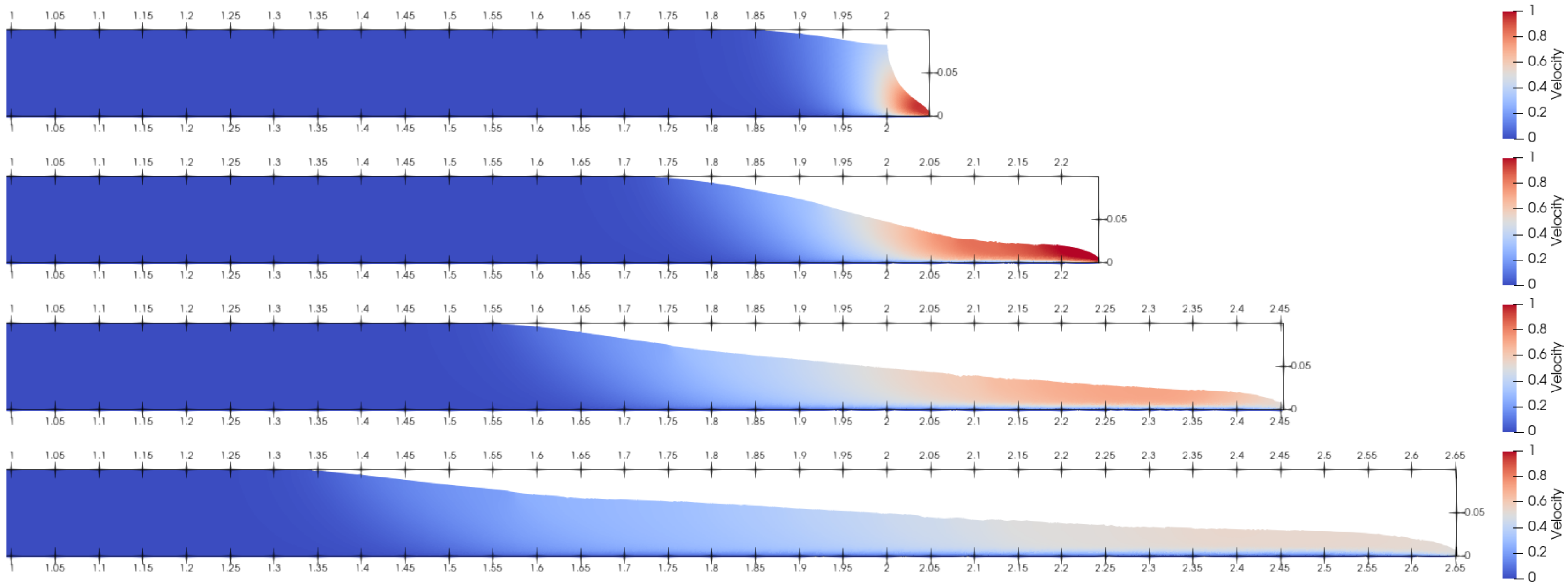
4.3. Dam Break of a Bingham Fluid
4.4. Fresh Concrete Slump Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Casson, N. A Flow Equation for Pigment-Oil Suspensions of the Printing Ink Type. In Rheology of Disperse Systems; Mill, C.C., Ed.; Rheology of Disperse System; Pergamon Press: Oxford, UK, 1959; pp. 84–104. [Google Scholar]
- Reiner, M.; Schoenfeld-Reiner, R. Viskosimetrische Untersuchungen an Lösungen hochmolekularer Naturstoffe. I. Mitteilung. Kautschuk in Toluol. Kolloid-Zeitschrift 1933, 65, 44–62. [Google Scholar] [CrossRef]
- Bingham, E.C. Fluidity and Plasticity. In McGraw-Hill Book; Company, Inc.: New York, NY, USA, 1922. [Google Scholar]
- Ancey, C. Plasticity and geophysical flows: A review. J. Non-Newton. Fluid Mech. 2007, 142, 4–35. [Google Scholar] [CrossRef]
- Fortin, M.; Fortin, A. A new approach for the FEM simulation of viscoelastic flows. J. Non-Newton. Fluid Mech. 1989, 32, 295–310. [Google Scholar] [CrossRef]
- Szady, M.J.; Salamon, T.R.; Liu, A.W.; Bornside, D.E.; Armstrong, R.C.; Brown, R.A. A new mixed finite element method for viscoelastic flows governed by differential constitutive equations. J. Non-Newton. Fluid Mech. 1995, 59, 215–243. [Google Scholar] [CrossRef]
- Grillet, A.M.; Yang, B.; Khomami, B.; Shaqfeh, E.S. Modeling of viscoelastic lid driven cavity flow using finite element simulations. J. Non-Newton. Fluid Mech. 1999, 88, 99–131. [Google Scholar] [CrossRef]
- Křen, J.; Hynčík, L. Modelling of non-Newtonian fluids. Math. Comput. Simul. 2007, 76, 116–123. [Google Scholar] [CrossRef]
- Huilgol, R.R.; Kefayati, G.H. Natural convection problem in a Bingham fluid using the operator-splitting method. J. Non-Newton. Fluid Mech. 2015, 220, 22–32. [Google Scholar] [CrossRef]
- Celigueta, M.A.; Deshpande, K.M.; Latorre, S.; Oñate, E. A FEM-DEM technique for studying the motion of particles in non-Newtonian fluids. Application to the transport of drill cuttings in wellbores. Comput. Part. Mech. 2016, 3, 263–276. [Google Scholar] [CrossRef] [Green Version]
- Neofytou, P. A 3rd order upwind finite volume method for generalised Newtonian fluid flows. Adv. Eng. Softw. 2005, 36, 664–680. [Google Scholar] [CrossRef]
- Zou, S.; Yuan, X.F.; Yang, X.; Yi, W.; Xu, X. An integrated lattice Boltzmann and finite volume method for the simulation of viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2014, 211, 99–113. [Google Scholar] [CrossRef]
- De, S.; Das, S.; Kuipers, J.A.; Peters, E.A.; Padding, J.T. A coupled finite volume immersed boundary method for simulating 3D viscoelastic flows in complex geometries. J. Non-Newton. Fluid Mech. 2016, 232, 67–76. [Google Scholar] [CrossRef] [Green Version]
- De, S.; Kuipers, J.A.; Peters, E.A.; Padding, J.T. Viscoelastic flow simulations in random porous media. J. Non-Newton. Fluid Mech. 2017, 248, 50–61. [Google Scholar] [CrossRef]
- Salazar, F.; Irazábal, J.; Larese, A.; Oñate, E. Numerical modelling of landslide-generated waves with the particle finite element method (PFEM) and a non-Newtonian flow model. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 809–826. [Google Scholar] [CrossRef] [Green Version]
- Cremonesi, M.; Meduri, S.; Perego, U.; Frangi, A. An explicit Lagrangian finite element method for free-surface weakly compressible flows. Comput. Part. Mech. 2017, 4, 357–369. [Google Scholar] [CrossRef] [Green Version]
- Larese, A. A Lagrangian PFEM approach for non-Newtonian viscoplastic materials. Rev. Int. Metod. Numer. Para Calc. Diseno Ing. 2017, 33, 307–317. [Google Scholar] [CrossRef] [Green Version]
- Franci, A.; Zhang, X. 3D numerical simulation of free-surface Bingham fluids interacting with structures using the PFEM. J. Non-Newton. Fluid Mech. 2018, 259, 1–15. [Google Scholar] [CrossRef]
- Della Vecchia, G.; Cremonesi, M.; Pisanò, F. On the rheological characterisation of liquefied sands through the dam-breaking test. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1410–1425. [Google Scholar] [CrossRef] [Green Version]
- Marchi, C.H.; Suero, R.; Araki, L.K. The lid-driven square cavity flow: Numerical solution with a 1024 × 1024 grid. J. Braz. Soc. Mech. Sci. Eng. 2009, 31. [Google Scholar] [CrossRef]
- Bognár, G.; Csáti, Z. Spectral method for time dependent Navier-Stokes equations. Miskolc Math. Notes 2016, 17, 43. [Google Scholar] [CrossRef]
- Bruneau, C.H.; Saad, M. The 2D lid-driven cavity problem revisited. Comput. Fluids 2006, 35, 326–348. [Google Scholar] [CrossRef]
- Coclite, A.; Coclite, G.; De Tommasi, D. Capsules Rheology in Carreau—Yasuda Fluids. Nanomaterials 2020, 10, 2190. [Google Scholar] [CrossRef]
- Coclite, A. Vascular journey and adhesion mechanics of micro-sized carriers in narrow capillaries. Microvasc. Res. 2020, 132, 104069. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics and its diverse applications. Annu. Rev. Fluid Mech. 2011, 44, 323–346. [Google Scholar] [CrossRef]
- Xenakis, A.; Lind, S.; Stansby, P.; Rogers, B. An incompressible SPH scheme with improved pressure predictions for free-surface generalised Newtonian flows. J. Non-Newton. Fluid Mech. 2015, 218, 1–15. [Google Scholar] [CrossRef]
- Fang, J.; Owens, R.G.; Tacher, L.; Parriaux, A. A numerical study of the SPH method for simulating transient viscoelastic free surface flows. J. Non-Newton. Fluid Mech. 2006, 139, 64–84. [Google Scholar] [CrossRef] [Green Version]
- Shao, S.; Lo, E.Y. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Resour. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Manzari, M.T.; Hannani, S.K. A fully explicit three-step SPH algorithm for simulation of non-Newtonian fluid flow. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 715–735. [Google Scholar] [CrossRef]
- Fan, X.J.; Tanner, R.I.; Zheng, R. Smoothed particle hydrodynamics simulation of non-Newtonian moulding flow. J. Non-Newton. Fluid Mech. 2010, 165, 219–226. [Google Scholar] [CrossRef]
- Zhu, H.; Martys, N.S.; Ferraris, C.; Kee, D.D. A numerical study of the flow of Bingham-like fluids in two-dimensional vane and cylinder rheometers using a smoothed particle hydrodynamics (SPH) based method. J. Non-Newton. Fluid Mech. 2010, 165, 362–375. [Google Scholar] [CrossRef]
- Papanastasiou, T.C. Flows of Materials with Yield. J. Rheol. 1987, 31, 385–404. [Google Scholar] [CrossRef]
- Xu, X.; Ouyang, J.; Yang, B.; Liu, Z. SPH simulations of three-dimensional non-Newtonian free surface flows. Comput. Methods Appl. Mech. Eng. 2013, 256, 101–116. [Google Scholar] [CrossRef]
- Peng, C.; Bašić, M.; Blagojević, B.; Bašić, J.; Wu, W. A Lagrangian differencing dynamics method for granular flow modeling. Comput. Geotech. 2021, 137, 104297. [Google Scholar] [CrossRef]
- Basic, J.; Degiuli, N.; Ban, D. A class of renormalised meshless Laplacians for boundary value problems. J. Comput. Phys. 2018, 354, 269–287. [Google Scholar] [CrossRef]
- Bašić, J.; Degiuli, N.; Malenica, Š.; Ban, D. Lagrangian finite-difference method for predicting green water loadings. Ocean Eng. 2020, 209, 107533. [Google Scholar] [CrossRef]
- Thohura, S.; Molla, M.M.; Sarker, M.M.A. Numerical Simulation of Non-Newtonian Power-Law Fluid Flow in a Lid-Driven Skewed Cavity. Int. J. Appl. Comput. Math. 2019, 5, 14. [Google Scholar] [CrossRef]
- Vila, J.P. On particle weighted methods and smooth particle hydrodynamics. Math. Model. Methods Appl. Sci. 1999, 9, 161–209. [Google Scholar] [CrossRef]
- Macklin, M.; Müller, M. Position based fluids. ACM Trans. Graph. 2013, 32, 1–12. [Google Scholar] [CrossRef]
- Burggraf, O.R. Analytical and numerical studies of the structure of steady separated flows. J. Fluid Mech. 1966, 24, 113–151. [Google Scholar] [CrossRef]
- Demirdžić, I.; Lilek, Z.; Perić, M. Fluid flow and heat transfer test problems for non-orthogonal grids: Bench-mark solutions. Int. J. Numer. Methods Fluids 1992, 15, 329–354. [Google Scholar] [CrossRef]
- Komatina, D.; Jovanovíc, M. Experimental study of steady and unsteady free surface flows with water-clay mixtures. J. Hydraul. Res. 1997, 354, 579–590. [Google Scholar] [CrossRef]
- Roussel, N.; Coussot, P. “Fifty-cent rheometer” for yield stress measurements: From slump to spreading flow. J. Rheol. 2005, 49, 705–718. [Google Scholar] [CrossRef]

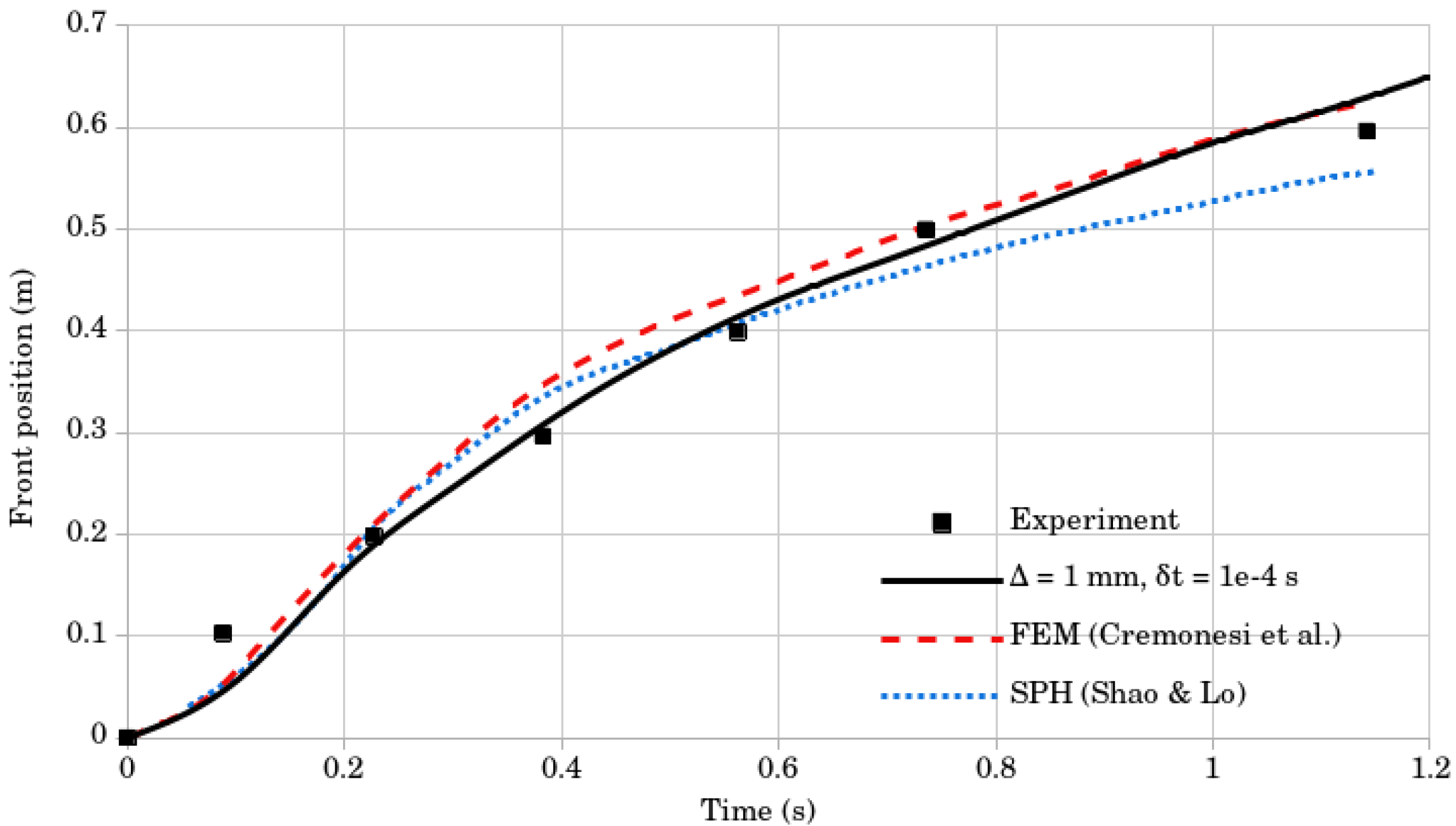
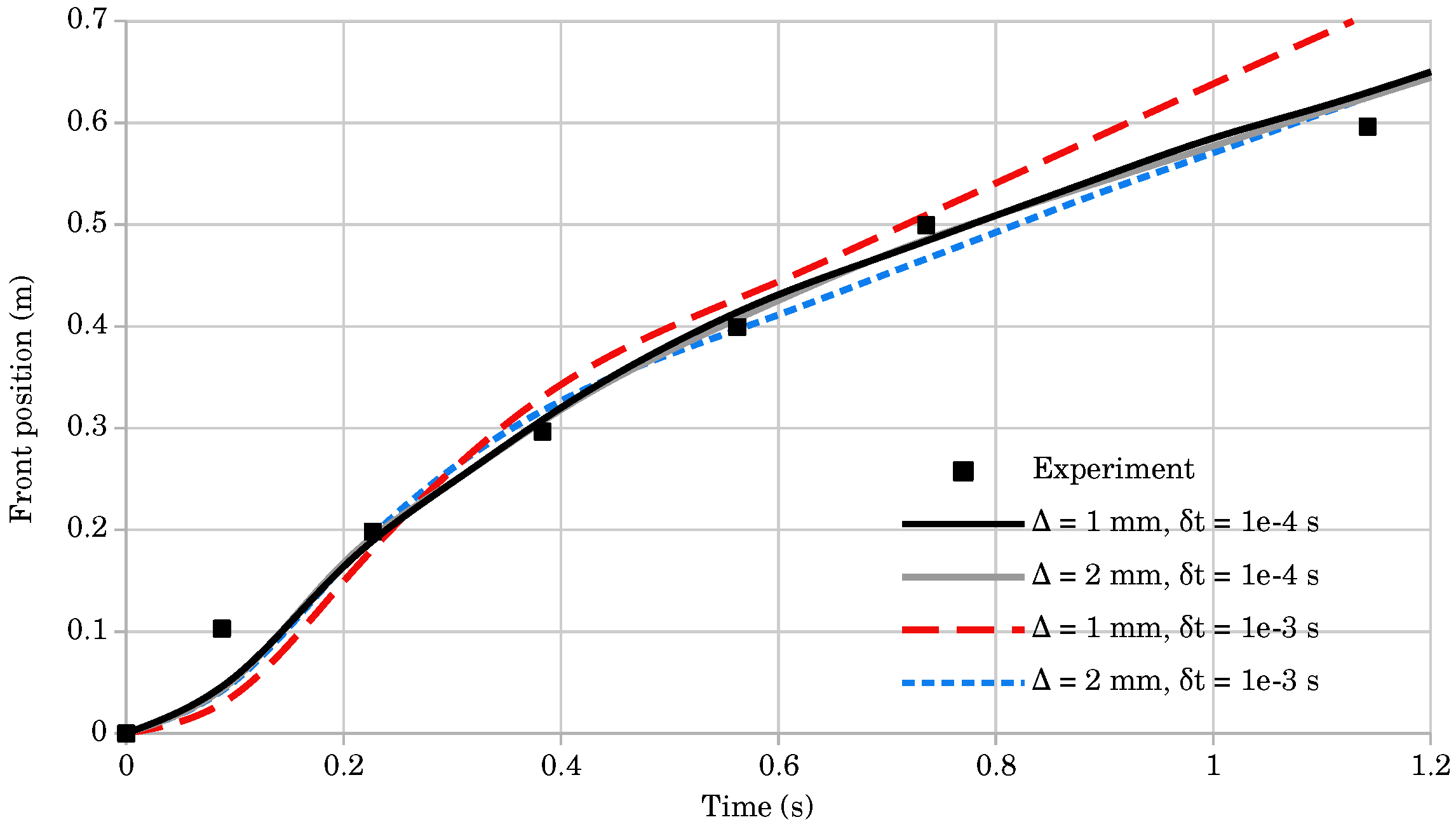
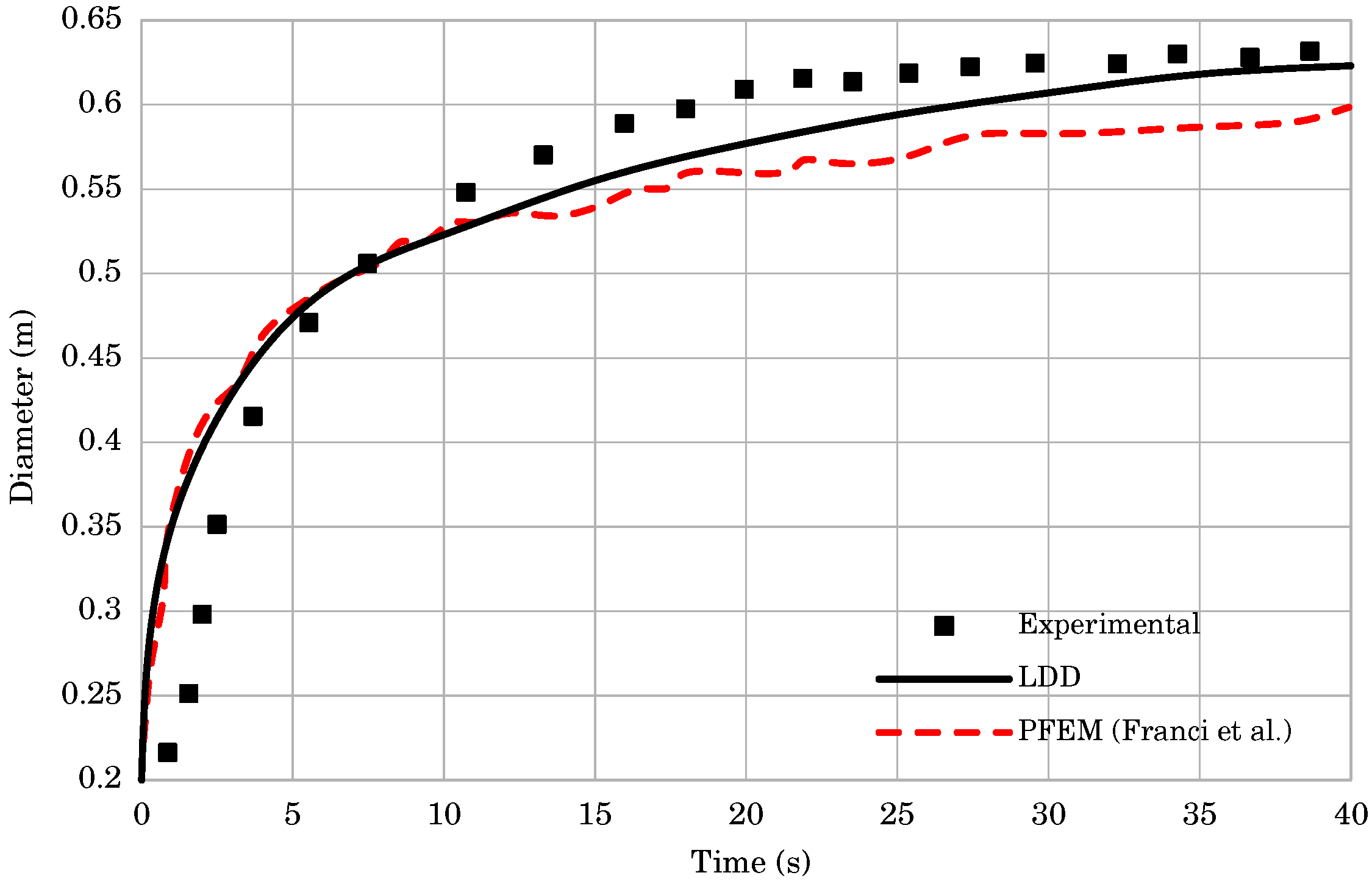
| Time (s) | Exp. Data | Mass Front (m), mm | Mass Front (m), mm | ||
|---|---|---|---|---|---|
| s | s | s | s | ||
| 0.09 | 0.103 | 0.030 | 0.048 | 0.043 | 0.044 |
| 0.23 | 0.198 | 0.185 | 0.190 | 0.195 | 0.191 |
| 0.38 | 0.297 | 0.328 | 0.304 | 0.314 | 0.308 |
| 0.56 | 0.399 | 0.427 | 0.414 | 0.396 | 0.407 |
| 0.74 | 0.499 | 0.508 | 0.484 | 0.467 | 0.486 |
| 1.14 | 0.596 | 0.705 | 0.628 | 0.621 | 0.625 |
| , m | , m | , m | , kg/m | , Pa·s | , Pa |
|---|---|---|---|---|---|
| 0.3 | 0.2 | 0.1 | 2200 | 255 | 32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bašić, M.; Blagojević, B.; Peng, C.; Bašić, J. Lagrangian Differencing Dynamics for Time-Independent Non-Newtonian Materials. Materials 2021, 14, 6210. https://doi.org/10.3390/ma14206210
Bašić M, Blagojević B, Peng C, Bašić J. Lagrangian Differencing Dynamics for Time-Independent Non-Newtonian Materials. Materials. 2021; 14(20):6210. https://doi.org/10.3390/ma14206210
Chicago/Turabian StyleBašić, Martina, Branko Blagojević, Chong Peng, and Josip Bašić. 2021. "Lagrangian Differencing Dynamics for Time-Independent Non-Newtonian Materials" Materials 14, no. 20: 6210. https://doi.org/10.3390/ma14206210
APA StyleBašić, M., Blagojević, B., Peng, C., & Bašić, J. (2021). Lagrangian Differencing Dynamics for Time-Independent Non-Newtonian Materials. Materials, 14(20), 6210. https://doi.org/10.3390/ma14206210






