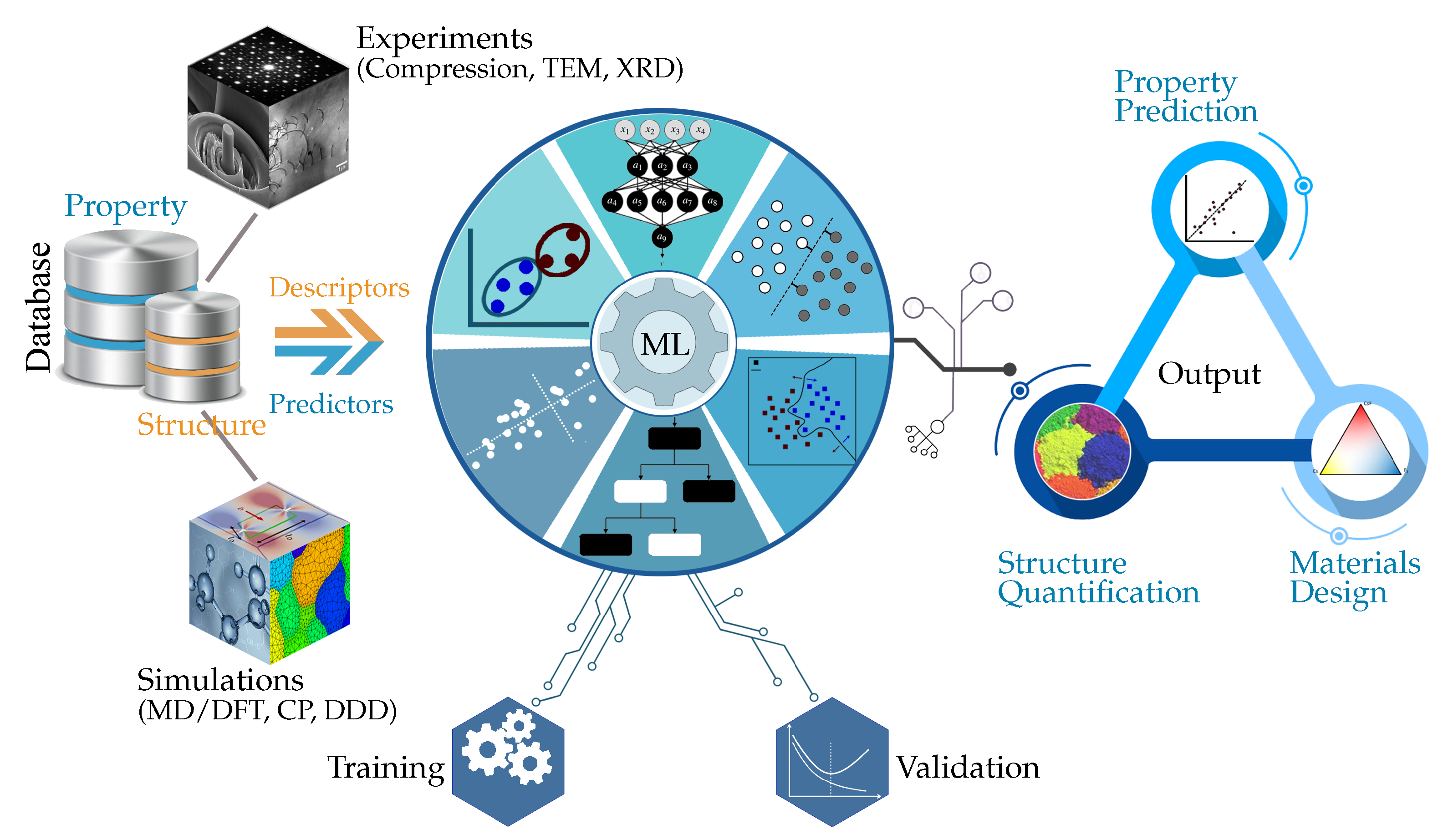
Materials Informatics for Mechanical Deformation: A Review of Applications and Challenges
Abstract
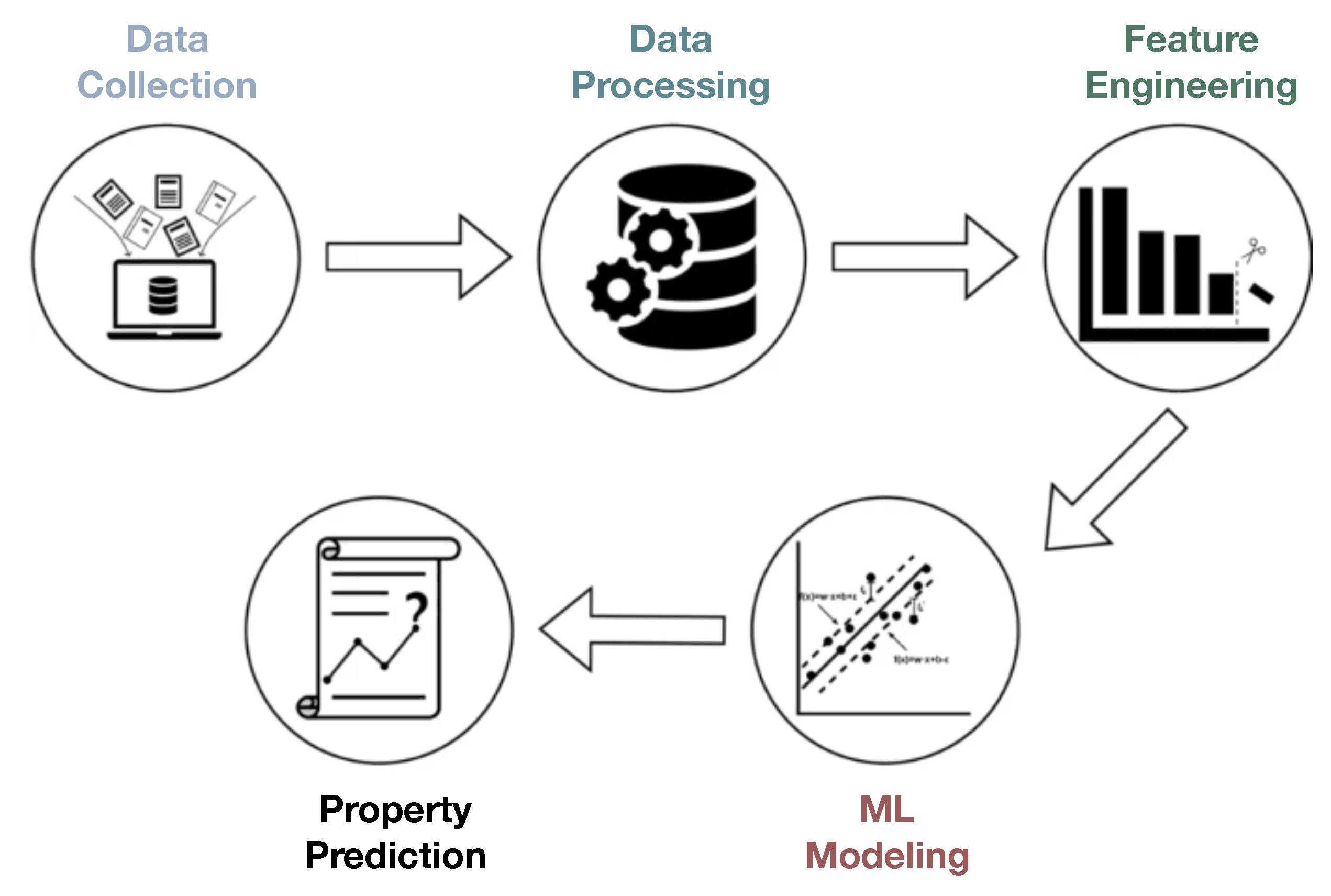
:1. Introduction
2. Materials Informatics in Microstructural Image Classification
3. Informatics in Deformation Experiments and Simulations
3.1. Searching for Microstructural Features and Machine Learning
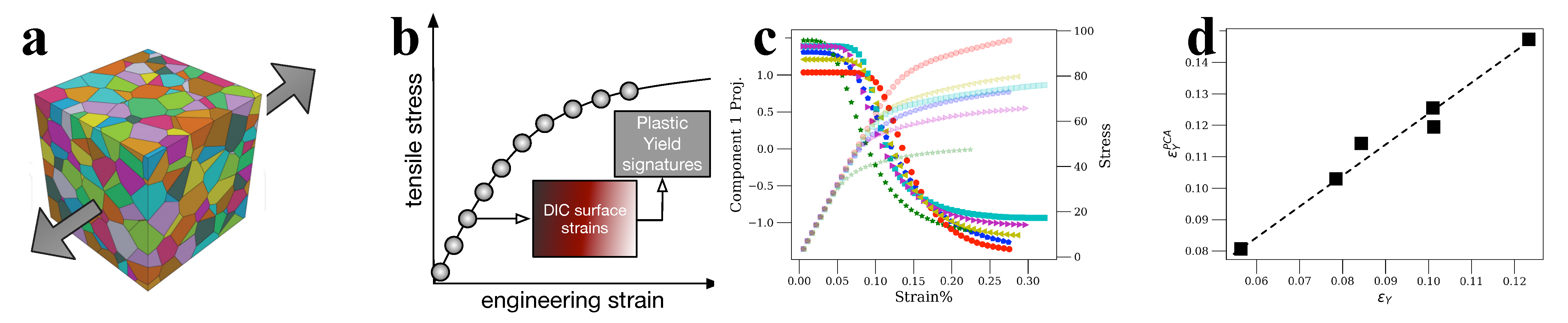
3.2. Materials Informatics and In Situ Loading: DIC and Surrogate Models Based on Plasticity
4. Learning from Crystal Defects: Dislocation Ensembles
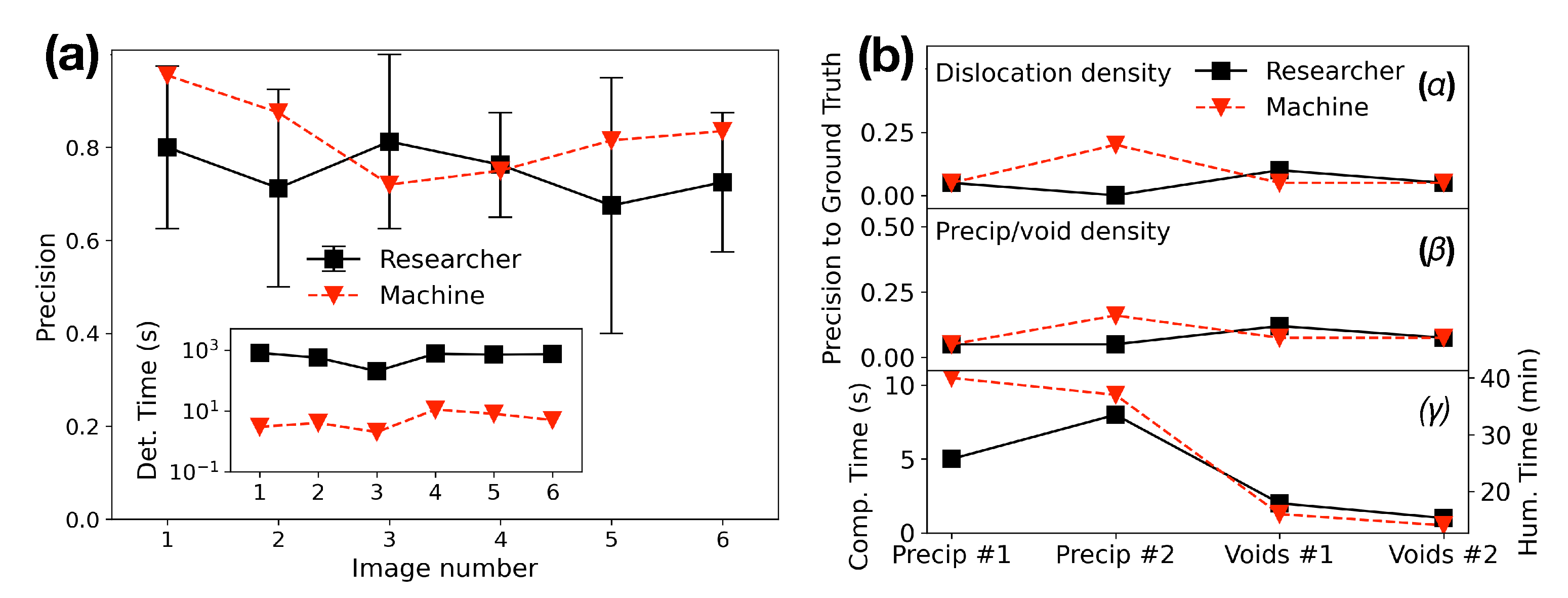
5. Learning Dislocation Features from Nanomechanics In Situ Experiments
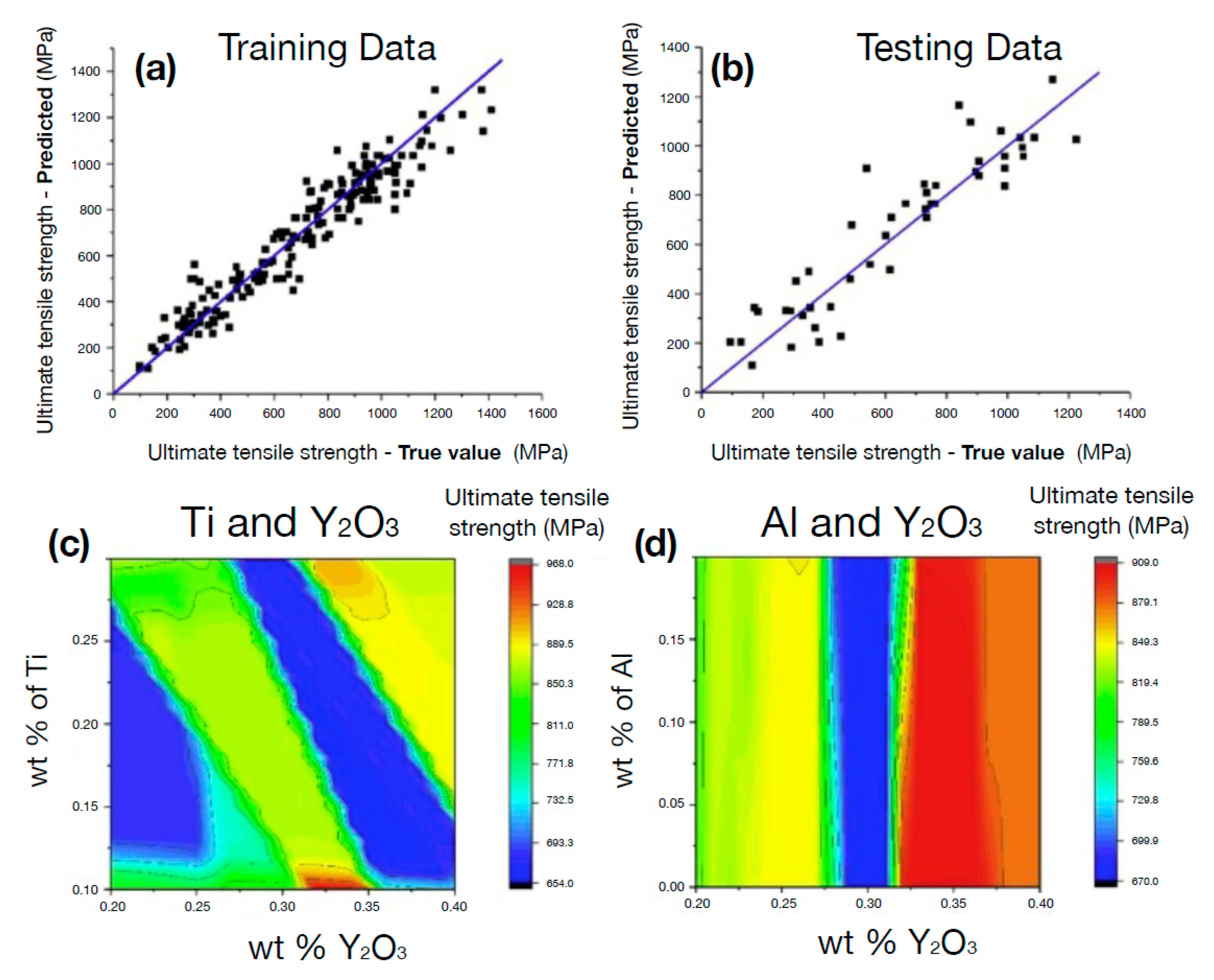
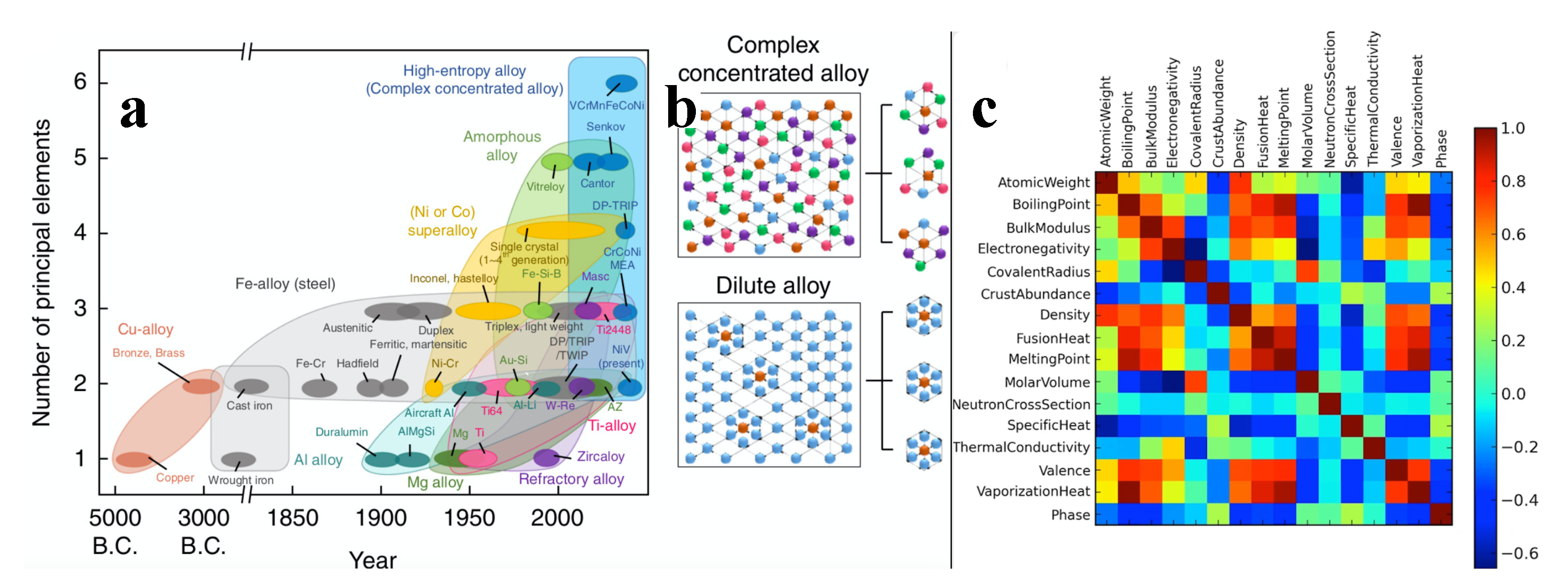
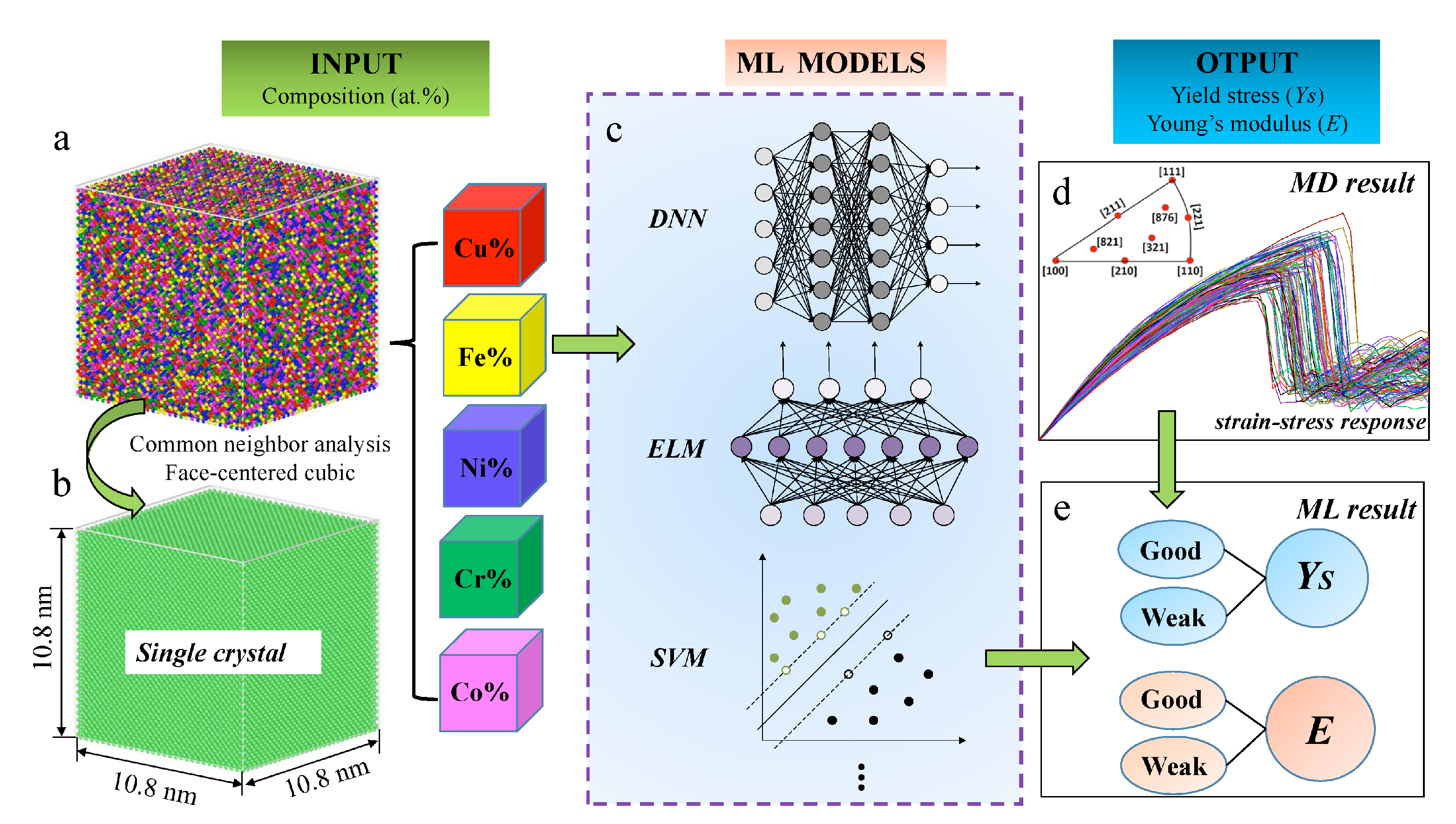
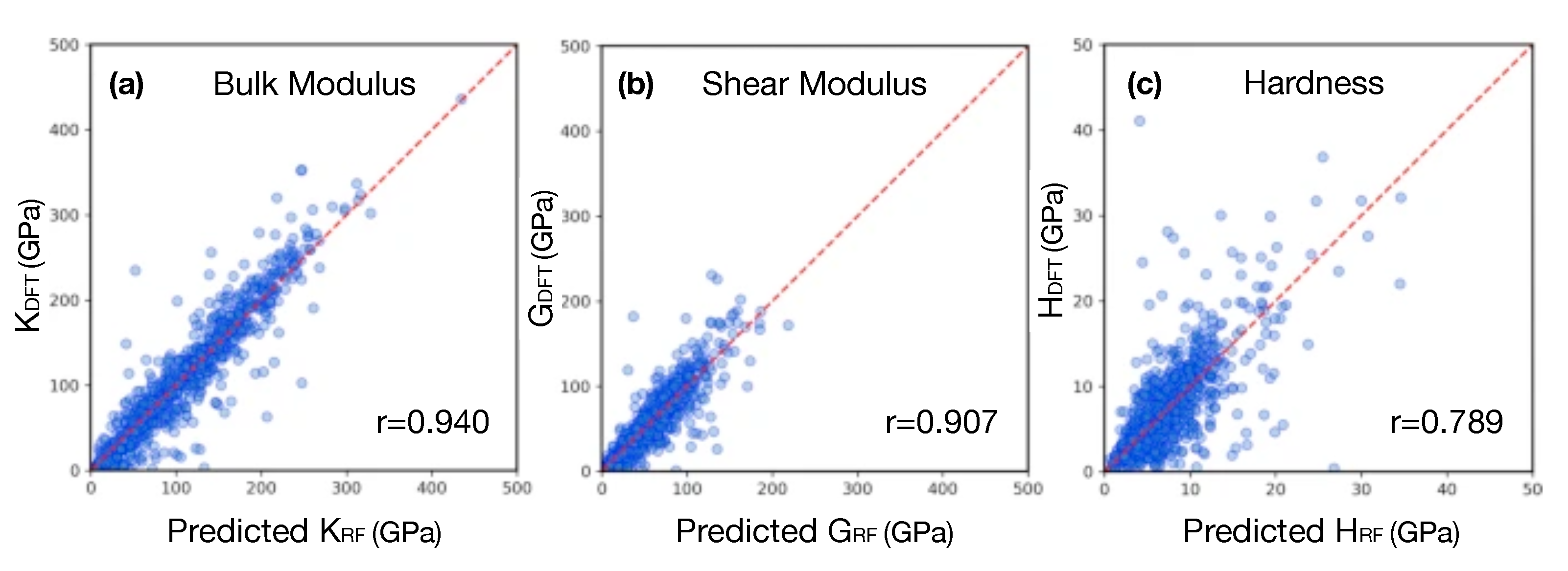
6. Beyond Mechanical Property Empirical Rules: Learning How to Design Metal Alloys
7. Materials Deformation Informatics: Challenges, Prospects and Ontology
7.1. Interoperability
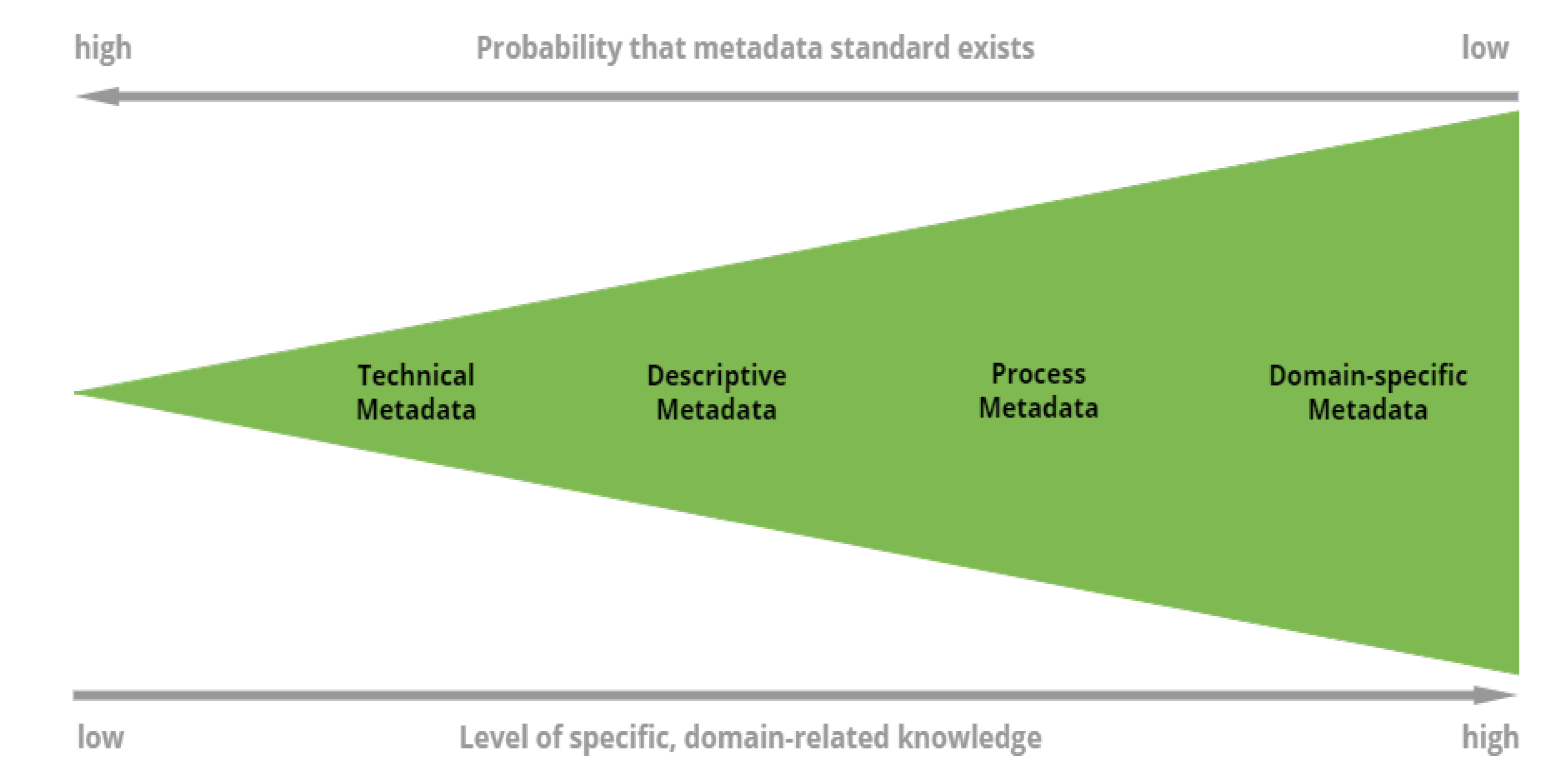
7.2. Metadata
- Technical metadata: Technical aspect of the research asset, mostly the file attributes on a file system level and similar syntactic information (file sizes, checksum information, storage location, access dates, file formats),
- Descriptive metadata: General information about the research asset (authors, keywords, title),
- Process metadata: Information on the generation process of the research asset (for example the computational environment and software used to generate or process the data). It may consist of several consecutive steps,
- Domain-specific metadata: Domain-specific description of the research objects. For example in computational engineering, this includes details about the simulated system, methods of simulation, resolution, etc.
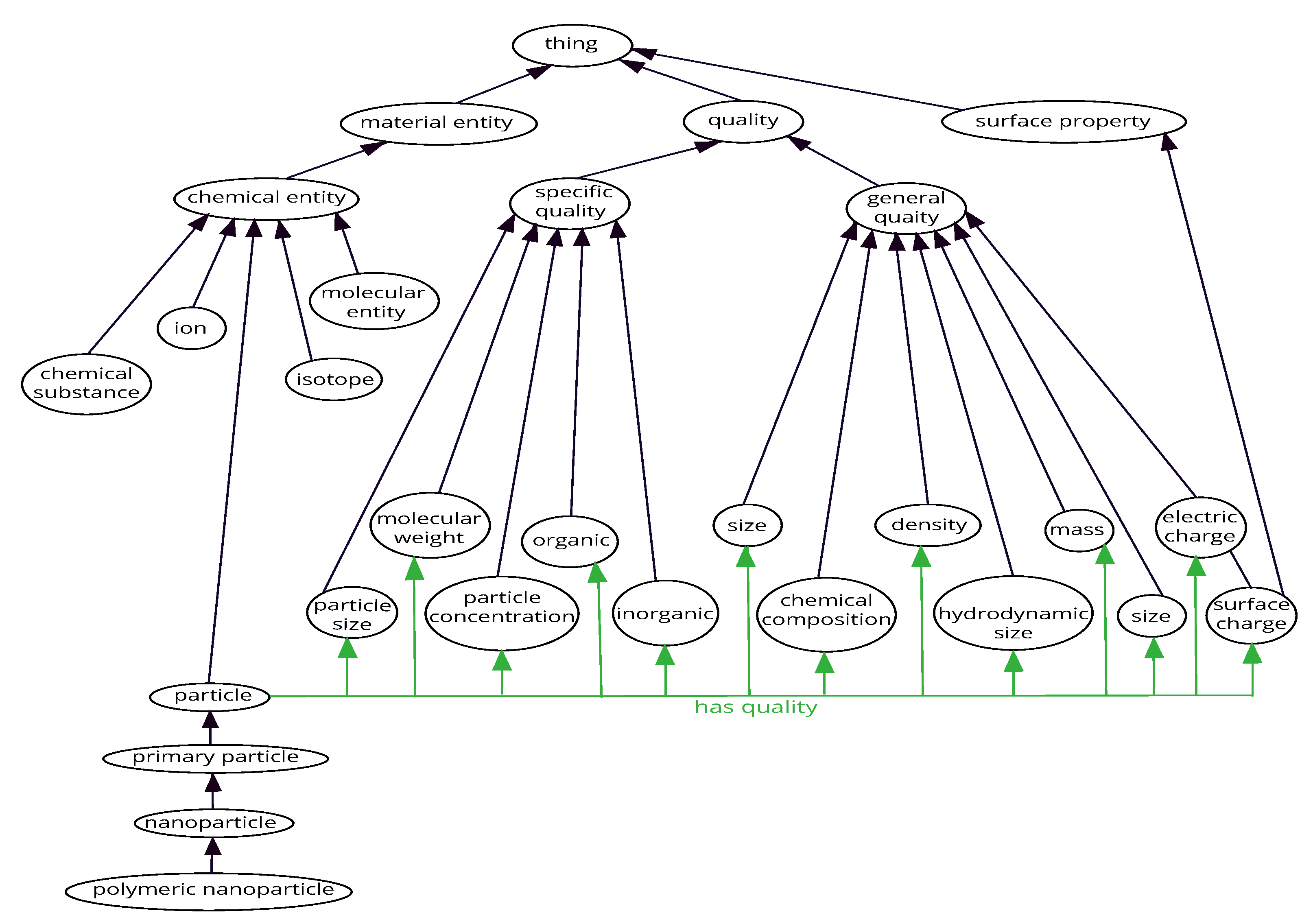
7.3. Ontologies
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kalidindi, S.R. Hierarchical Materials Informatics: Novel Analytics for Materials Data; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Lookman, T.; Alexander, F.J.; Rajan, K. Information Science for Materials Discovery and Design; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Isayev, O.; Tropsha, A.; Curtarolo, S. (Eds.) Materials Informatics: Methods, Tools, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Rajan, K. Materials informatics. Mater. Today 2005, 8, 38–45. [Google Scholar] [CrossRef]
- Rickman, J.M.; Lookman, T.; Kalinin, S.V. Materials informatics: From the atomic-level to the continuum. Acta Mater. 2019, 168, 473–510. [Google Scholar] [CrossRef]
- Ramakrishna, S.; Zhang, T.Y.; Lu, W.C.; Qian, Q.; Low, J.S.C.; Yune, J.H.R.; Tan, D.Z.L.; Bressan, S.; Sanvito, S.; Kalidindi, S.R. Materials informatics. J. Intell. Manuf. 2019, 30, 2307–2326. [Google Scholar] [CrossRef]
- Rodgers, J.R.; Cebon, D. Materials informatics. MRS Bull. 2006, 31, 975–980. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, I.; Rajan, K.; Wolverton, C. Data-centric science for materials innovation. MRS Bull. 2018, 43, 659–663. [Google Scholar] [CrossRef] [Green Version]
- Reyes, K.G.; Maruyama, B. The machine learning revolution in materials? MRS Bull. 2019, 44, 530–537. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.R.; Allen, P.; Lampman, S.; Zorc, T.B.; Henry, S.D.; Daquila, J.L.; Ronke, A.W. Metals Handbook: Properties and Selection: Nonferrous Alloys and Special-Purpose Materials; ASM international: Almere, The Netherlands, 1990. [Google Scholar]
- DeCost, B.L.; Francis, T.; Holm, E.A. Exploring the microstructure manifold: Image texture representations applied to ultrahigh carbon steel microstructures. Acta Mater. 2017, 133, 30–40. [Google Scholar] [CrossRef] [Green Version]
- DeCost, B.L.; Lei, B.; Francis, T.; Holm, E.A. High throughput quantitative metallography for complex microstructures using deep learning: A case study in ultrahigh carbon steel. Microsc. Microanal. 2019, 25, 21–29. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Jia, L.; Kong, B.; Feng, S.; Zhang, H.; Zhang, H. Artificial neural network application to microstructure design of Nb-Si alloy to improve ultimate tensile strength. Mater. Sci. Eng. A 2017, 707, 452–458. [Google Scholar] [CrossRef]
- Hart, G.L.; Mueller, T.; Toher, C.; Curtarolo, S. Machine learning for alloys. Nat. Rev. Mater. 2021, 6, 730–755. [Google Scholar] [CrossRef]
- Kim, G.; Diao, H.; Lee, C.; Samaei, A.; Phan, T.; de Jong, M.; An, K.; Ma, D.; Liaw, P.K.; Chen, W. First-principles and machine learning predictions of elasticity in severely lattice-distorted high-entropy alloys with experimental validation. Acta Mater. 2019, 181, 124–138. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, Y.; Wang, C.; Xue, D.; Bai, Y.; Antonov, S.; Dai, L.; Lookman, T.; Su, Y. Machine learning assisted design of high entropy alloys with desired property. Acta Mater. 2019, 170, 109–117. [Google Scholar] [CrossRef] [Green Version]
- Ward, L.; O’Keeffe, S.C.; Stevick, J.; Jelbert, G.R.; Aykol, M.; Wolverton, C. A machine learning approach for engineering bulk metallic glass alloys. Acta Mater. 2018, 159, 102–111. [Google Scholar] [CrossRef]
- Islam, N.; Huang, W.; Zhuang, H.L. Machine learning for phase selection in multi-principal element alloys. Comput. Mater. Sci. 2018, 150, 230–235. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, Y.; He, Q.; Ding, Z.; Li, F.; Yang, Y. Machine learning guided appraisal and exploration of phase design for high entropy alloys. NPJ Comput. Mater. 2019, 5, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wen, C.; Wang, C.; Antonov, S.; Xue, D.; Bai, Y.; Su, Y. Phase prediction in high entropy alloys with a rational selection of materials descriptors and machine learning models. Acta Mater. 2020, 185, 528–539. [Google Scholar] [CrossRef]
- Wang, C.; Fu, H.; Jiang, L.; Xue, D.; Xie, J. A property-oriented design strategy for high performance copper alloys via machine learning. NPJ Comput. Mater. 2019, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Xue, D.; Balachandran, P.V.; Hogden, J.; Theiler, J.; Xue, D.; Lookman, T. Accelerated search for materials with targeted properties by adaptive design. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Botu, V.; Ramprasad, R. Adaptive machine learning framework to accelerate ab initio molecular dynamics. Int. J. Quantum Chem. 2015, 115, 1074–1083. [Google Scholar] [CrossRef]
- Bartók, A.P.; De, S.; Poelking, C.; Bernstein, N.; Kermode, J.R.; Csányi, G.; Ceriotti, M. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 2017, 3, e1701816. [Google Scholar] [CrossRef] [Green Version]
- Morgan, D.; Jacobs, R. Opportunities and challenges for machine learning in materials science. Annu. Rev. Mater. Res. 2020, 50, 71–103. [Google Scholar] [CrossRef]
- Friederich, P.; Häse, F.; Proppe, J.; Aspuru-Guzik, A. Machine-learned potentials for next-generation matter simulations. Nat. Mater. 2021, 20, 750–761. [Google Scholar] [CrossRef]
- Furrer, D.U.; Dimiduk, D.M.; Cotton, J.D.; Ward, C.H. Making the case for a model-based definition of engineering materials. Integr. Mater. Manuf. Innov. 2017, 6, 249–263. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics New York; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Schmidt, J.; Marques, M.R.; Botti, S.; Marques, M.A. Recent advances and applications of machine learning in solid-state materials science. NPJ Comput. Mater. 2019, 5, 1–36. [Google Scholar] [CrossRef]
- Shang, Y.; Brechtl, J.; Psitidda, C.; Liaw, P.K. Mechanical behavior of high-entropy alloys: A review. arXiv 2021, arXiv:2102.09055. [Google Scholar]
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef] [Green Version]
- Villars, P.; Cenzual, K. Pearson’s Crystal Data®: Crystal Structure Database for Inorganic Compounds; ASM International: Materials Park, OH, USA, 2007. [Google Scholar]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Salvador, C.A.; Zornio, B.F.; Miranda, C.R. Discovery of Low-Modulus Ti-Nb-Zr Alloys Based on Machine Learning and First-Principles Calculations. ACS Appl. Mater. Interfaces 2020, 12, 56850–56861. [Google Scholar] [CrossRef]
- Furmanchuk, A.; Agrawal, A.; Choudhary, A. Predictive analytics for crystalline materials: Bulk modulus. RSC Adv. 2016, 6, 95246–95251. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, T.Y.; Shi, S.Q. Machine learning prediction of elastic properties and glass-forming ability of bulk metallic glasses. MRS Commun. 2019, 9, 576–585. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.J.; Jui, C.Y.; Lee, W.J.; Yeh, A.C. Prediction of the composition and hardness of high-entropy alloys by machine learning. JOM 2019, 71, 3433–3442. [Google Scholar] [CrossRef]
- Mansouri Tehrani, A.; Oliynyk, A.O.; Parry, M.; Rizvi, Z.; Couper, S.; Lin, F.; Miyagi, L.; Sparks, T.D.; Brgoch, J. Machine learning directed search for ultraincompressible, superhard materials. J. Am. Chem. Soc. 2018, 140, 9844–9853. [Google Scholar] [CrossRef]
- Fan, Z.; Ding, J.; Ma, E. Machine learning bridges local static structure with multiple properties in metallic glasses. Mater. Today 2020, 40, 48–62. [Google Scholar] [CrossRef]
- Jafary-Zadeh, M.; Khoo, K.H.; Laskowski, R.; Branicio, P.S.; Shapeev, A.V. Applying a machine learning interatomic potential to unravel the effects of local lattice distortion on the elastic properties of multi-principal element alloys. J. Alloy. Compd. 2019, 803, 1054–1062. [Google Scholar] [CrossRef]
- Sharp, T.A.; Thomas, S.L.; Cubuk, E.D.; Schoenholz, S.S.; Srolovitz, D.J.; Liu, A.J. Machine learning determination of atomic dynamics at grain boundaries. Proc. Natl. Acad. Sci. USA 2018, 115, 10943–10947. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.C.; Schmidt, J.N.; Yan, D.; Vohra, Y.K.; Chen, C.C. Machine learning and evolutionary prediction of superhard BCN compounds. NPJ Comput. Mater. 2021, 7, 1–8. [Google Scholar] [CrossRef]
- Avery, P.; Wang, X.; Oses, C.; Gossett, E.; Proserpio, D.M.; Toher, C.; Curtarolo, S.; Zurek, E. Predicting superhard materials via a machine learning informed evolutionary structure search. NPJ Comput. Mater. 2019, 5, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Papanikolaou, S. Microstructural inelastic fingerprints and data-rich predictions of plasticity and damage in solids. Comput. Mech. 2020, 66, 141–154. [Google Scholar] [CrossRef]
- Fernandez-Lozano, C. Statistical Inference from High Dimensional Data; MDPI: Basel, Switzerland, 2021. [Google Scholar]
- Hu, M.; Tan, Q.; Knibbe, R.; Wang, S.; Li, X.; Wu, T.; Jarin, S.; Zhang, M.X. Prediction of Mechanical Properties of Wrought Aluminium Alloys Using Feature Engineering Assisted Machine Learning Approach. Metall. Mater. Trans. A 2021, 1–12. [Google Scholar]
- Guo, K.; Yang, Z.; Yu, C.H.; Buehler, M.J. Artificial intelligence and machine learning in design of mechanical materials. Mater. Horizons 2021, 8, 1153–1172. [Google Scholar] [CrossRef]
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A review of the application of machine learning and data mining approaches in continuum materials mechanics. Front. Mater. 2019, 6, 110. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Fu, Z.; Yang, K.; Xu, X.; Bauchy, M. Machine learning for glass science and engineering: A review. J. Non-Cryst. Solids 2021, 557, 119419. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. NPJ Comput. Mater. 2017, 3, 1–13. [Google Scholar] [CrossRef]
- Papanikolaou, S. Learning local, quenched disorder in plasticity and other crackling noise phenomena. NPJ Comput. Mater. 2018, 4, 1–7. [Google Scholar] [CrossRef]
- Bulgarevich, D.S.; Tsukamoto, S.; Kasuya, T.; Demura, M.; Watanabe, M. Pattern recognition with machine learning on optical microscopy images of typical metallurgical microstructures. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Bulgarevich, D.S.; Tsukamoto, S.; Kasuya, T.; Demura, M.; Watanabe, M. Automatic steel labeling on certain microstructural constituents with image processing and machine learning tools. Sci. Technol. Adv. Mater. 2019, 20, 532–542. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Inoue, J.; Kasuya, T. Unsupervised microstructure segmentation by mimicking metallurgists’ approach to pattern recognition. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Boukhtache, S.; Abdelouahab, K.; Berry, F.; Blaysat, B.; Grediac, M.; Sur, F. When Deep Learning Meets Digital Image Correlation. Opt. Lasers Eng. 2021, 136, 106308. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Tzimas, M.; Reid, A.C.; Langer, S.A. Spatial strain correlations, machine learning, and deformation history in crystal plasticity. Phys. Rev. E 2019, 99, 053003. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Tzimas, M. Effects of rate, size, and prior deformation in microcrystal plasticity. In Mechanics and Physics of Solids at Micro- and Nano-Scales; ISTE, Ltd.: London, UK, 2019; pp. 25–54. [Google Scholar]
- Papanikolaou, S.; Alava, M.J. Direct detection of plasticity onset through total-strain profile evolution. Phys. Rev. Mater. 2021, 5, 083602. [Google Scholar] [CrossRef]
- Cidade, R.A.; Castro, D.S.; Castrodeza, E.M.; Kuhn, P.; Catalanotti, G.; Xavier, J.; Camanho, P.P. Determination of mode I dynamic fracture toughness of IM7-8552 composites by digital image correlation and machine learning. Compos. Struct. 2019, 210, 707–714. [Google Scholar] [CrossRef] [Green Version]
- Rezaie, A.; Achanta, R.; Godio, M.; Beyer, K. Comparison of crack segmentation using digital image correlation measurements and deep learning. Constr. Build. Mater. 2020, 261, 120474. [Google Scholar] [CrossRef]
- Gehri, N.; Mata-Falcón, J.; Kaufmann, W. Automated crack detection and measurement based on digital image correlation. Constr. Build. Mater. 2020, 256, 119383. [Google Scholar] [CrossRef]
- Strohmann, T.; Starostin-Penner, D.; Breitbarth, E.; Requena, G. Automatic detection of fatigue crack paths using digital image correlation and convolutional neural networks. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 1336–1348. [Google Scholar] [CrossRef]
- Azimi, S.M.; Britz, D.; Engstler, M.; Fritz, M.; Mücklich, F. Advanced steel microstructural classification by deep learning methods. Sci. Rep. 2018, 8, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Mulewicz, B.; Korpala, G.; Kusiak, J.; Prahl, U. Autonomous interpretation of the microstructure of steels and special alloys. In Materials Science Forum; Trans Tech Publications Ltd.: Pfaffikon, Switzerland, 2019; Volume 949, pp. 24–31. [Google Scholar]
- Gola, J.; Webel, J.; Britz, D.; Guitar, A.; Staudt, T.; Winter, M.; Mücklich, F. Objective microstructure classification by support vector machine (SVM) using a combination of morphological parameters and textural features for low carbon steels. Comput. Mater. Sci. 2019, 160, 186–196. [Google Scholar] [CrossRef]
- Wu, Z.H.; Bai, J.J.; Zhang, D.D.; Huang, G.; Zhu, T.B.; Chang, X.J.; Liu, R.D.; Lin, J.; Sun, J.A. Statistical analysis of helium bubbles in transmission electron microscopy images based on machine learning method. Nucl. Sci. Tech. 2021, 32, 1–11. [Google Scholar] [CrossRef]
- Chen, Z.; Daly, S. Deformation twin identification in magnesium through clustering and computer vision. Mater. Sci. Eng. A 2018, 736, 61–75. [Google Scholar] [CrossRef]
- Chen, Z.; Daly, S. Automated identification of deformation twin systems in Mg WE43 from SEM DIC. Mater. Charact. 2020, 169, 110628. [Google Scholar] [CrossRef]
- Ding, Z.; Pascal, E.; De Graef, M. Indexing of electron back-scatter diffraction patterns using a convolutional neural network. Acta Mater. 2020, 199, 370–382. [Google Scholar] [CrossRef]
- Kaufmann, K.; Zhu, C.; Rosengarten, A.S.; Vecchio, K.S. Deep neural network enabled space group identification in EBSD. Microsc. Microanal. 2020, 26, 447–457. [Google Scholar] [CrossRef]
- Kaufmann, K.; Zhu, C.; Rosengarten, A.S.; Maryanovsky, D.; Wang, H.; Vecchio, K.S. Phase Mapping in EBSD using convolutional neural networks. Microsc. Microanal. 2020, 26, 458–468. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, K.; Lane, H.; Liu, X.; Vecchio, K.S. Efficient few-shot machine learning for classification of EBSD patterns. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef]
- Orme, A.D.; Chelladurai, I.; Rampton, T.M.; Fullwood, D.T.; Khosravani, A.; Miles, M.P.; Mishra, R.K. Insights into twinning in Mg AZ31: A combined EBSD and machine learning study. Comput. Mater. Sci. 2016, 124, 353–363. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ngan, A.H. Extracting dislocation microstructures by deep learning. Int. J. Plast. 2019, 115, 18–28. [Google Scholar] [CrossRef]
- Madsen, J.; Liu, P.; Kling, J.; Wagner, J.B.; Hansen, T.W.; Winther, O.; Schiøtz, J. A deep learning approach to identify local structures in atomic-resolution transmission electron microscopy images. Adv. Theory Simulations 2018, 1, 1800037. [Google Scholar] [CrossRef] [Green Version]
- Lee, B.; Yoon, S.; Lee, J.W.; Kim, Y.; Chang, J.; Yun, J.; Ro, J.C.; Lee, J.S.; Lee, J.H. Statistical characterization of the morphologies of nanoparticles through machine learning based electron microscopy image analysis. ACS Nano 2020, 14, 17125–17133. [Google Scholar] [CrossRef] [PubMed]
- Horwath, J.P.; Zakharov, D.N.; Mégret, R.; Stach, E.A. Understanding important features of deep learning models for segmentation of high-resolution transmission electron microscopy images. NPJ Comput. Mater. 2020, 6, 1–9. [Google Scholar] [CrossRef]
- Ziatdinov, M.; Dyck, O.; Maksov, A.; Li, X.; Sang, X.; Xiao, K.; Unocic, R.R.; Vasudevan, R.; Jesse, S.; Kalinin, S.V. Deep learning of atomically resolved scanning transmission electron microscopy images: Chemical identification and tracking local transformations. ACS Nano 2017, 11, 12742–12752. [Google Scholar] [CrossRef] [Green Version]
- Cho, P.; Wood, A.; Mahalingam, K.; Eyink, K. Defect Detection in Atomic Resolution Transmission Electron Microscopy Images Using Machine Learning. Mathematics 2021, 9, 1209. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Cui, Y.; Ghoniem, N. Avalanches and plastic flow in crystal plasticity: An overview. Model. Simul. Mater. Sci. Eng. 2017, 26, 013001. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, Y.; Hattori, M.; Ohyama, J.; Satsuma, A.; Tanaka, N.; Muto, S. Twinned/untwinned catalytic gold nanoparticles identified by applying a convolutional neural network to their Hough transformed Z-contrast images. Microscopy 2018, 67, 321–330. [Google Scholar] [CrossRef]
- Dan, J.; Zhao, X.; Pennycook, S.J. A machine perspective of atomic defects in scanning transmission electron microscopy. InfoMat 2019, 1, 359–375. [Google Scholar] [CrossRef] [Green Version]
- Kalinin, S.V.; Lupini, A.R.; Dyck, O.; Jesse, S.; Ziatdinov, M.; Vasudevan, R.K. Lab on a beam—Big data and artificial intelligence in scanning transmission electron microscopy. MRS Bull. 2019, 44, 565–575. [Google Scholar] [CrossRef]
- Was, G.S. Fundamentals of Radiation Materials Science: Metals and Alloys; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Li, W.; Field, K.G.; Morgan, D. Automated defect analysis in electron microscopic images. NPJ Comput. Mater. 2018, 4, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Shen, M.; Li, G.; Wu, D.; Yaguchi, Y.; Haley, J.C.; Field, K.G.; Morgan, D. A deep learning based automatic defect analysis framework for In-situ TEM ion irradiations. Comput. Mater. Sci. 2021, 197, 110560. [Google Scholar] [CrossRef]
- Bai, B.; Han, X.; Zheng, Q.; Jia, L.; Zhang, C.; Yang, W. Composition optimization of high strength and ductility ODS alloy based on machine learning. Fusion Eng. Des. 2020, 161, 111939. [Google Scholar] [CrossRef]
- Revi, V.; Kasodariya, S.; Talapatra, A.; Pilania, G.; Alankar, A. Machine learning elastic constants of multi-component alloys. Comput. Mater. Sci. 2021, 198, 110671. [Google Scholar] [CrossRef]
- Chun, M.; Biglou, J.; Lenard, J.; Kim, J. Using neural networks to predict parameters in the hot working of aluminum alloys. J. Mater. Process. Technol. 1999, 86, 245–251. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Khalesian, A.; Abedi, H. Artificial neural network modeling to predict the hot deformation behavior of an A356 aluminum alloy. Mater. Des. 2013, 49, 386–391. [Google Scholar] [CrossRef]
- Ji, G.; Li, F.; Li, Q.; Li, H.; Li, Z. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behaviour in Aermet100 steel. Mater. Sci. Eng. A 2011, 528, 4774–4782. [Google Scholar] [CrossRef]
- Mandal, S.; Sivaprasad, P.; Venugopal, S.; Murthy, K. Artificial neural network modeling to evaluate and predict the deformation behavior of stainless steel type AISI 304L during hot torsion. Appl. Soft Comput. 2009, 9, 237–244. [Google Scholar] [CrossRef]
- Sun, Y.; Zeng, W.; Zhao, Y.; Qi, Y.; Ma, X.; Han, Y. Development of constitutive relationship model of Ti600 alloy using artificial neural network. Comput. Mater. Sci. 2010, 48, 686–691. [Google Scholar] [CrossRef]
- Ozerdem, M.S.; Kolukisa, S. Artificial Neural Network approach to predict mechanical properties of hot rolled, nonresulfurized, AISI 10xx series carbon steel bars. J. Mater. Process. Technol. 2008, 199, 437–439. [Google Scholar] [CrossRef]
- Ozerdem, M.S.; Kolukisa, S. Artificial neural network approach to predict the mechanical properties of Cu–Sn–Pb–Zn–Ni cast alloys. Mater. Des. 2009, 30, 764–769. [Google Scholar] [CrossRef]
- Guo, Z.; Sha, W. Modelling the correlation between processing parameters and properties of maraging steels using artificial neural network. Comput. Mater. Sci. 2004, 29, 12–28. [Google Scholar] [CrossRef] [Green Version]
- Malinov, S.; Sha, W.; McKeown, J. Modelling the correlation between processing parameters and properties in titanium alloys using artificial neural network. Comput. Mater. Sci. 2001, 21, 375–394. [Google Scholar] [CrossRef] [Green Version]
- Thankachan, T.; Prakash, K.S.; Pleass, C.D.; Rammasamy, D.; Prabakaran, B.; Jothi, S. Artificial neural network to predict the degraded mechanical properties of metallic materials due to the presence of hydrogen. Int. J. Hydrog. Energy 2017, 42, 28612–28621. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, S.; Murugananth, M.; Bhadeshia, H. δ TRIP steel. Mater. Sci. Technol. 2007, 23, 819–827. [Google Scholar] [CrossRef]
- Mahfouf, M.; Jamei, M.; Linkens, D. Optimal design of alloy steels using multiobjective genetic algorithms. Mater. Manuf. Process. 2005, 20, 553–567. [Google Scholar] [CrossRef]
- Arceri, F.; Landes, F.P.; Berthier, L.; Biroli, G. Glasses and aging: A statistical mechanics perspective. arXiv 2020, arXiv:2006.09725. [Google Scholar]
- Cubuk, E.D.; Schoenholz, S.S.; Kaxiras, E.; Liu, A.J. Structural properties of defects in glassy liquids. J. Phys. Chem. B 2016, 120, 6139–6146. [Google Scholar] [CrossRef]
- Royall, C.P.; Kob, W. Locally favoured structures and dynamic length scales in a simple glass-former. J. Stat. Mech. Theory Exp. 2017, 2017, 024001. [Google Scholar] [CrossRef] [Green Version]
- Boattini, E.; Marín-Aguilar, S.; Mitra, S.; Foffi, G.; Smallenburg, F.; Filion, L. Autonomously revealing hidden local structures in supercooled liquids. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Schoenholz, S.S.; Cubuk, E.D.; Kaxiras, E.; Liu, A.J. Relationship between local structure and relaxation in out-of-equilibrium glassy systems. Proc. Natl. Acad. Sci. USA 2017, 114, 263–267. [Google Scholar] [CrossRef] [Green Version]
- Hufnagel, T.C.; Schuh, C.A.; Falk, M.L. Deformation of metallic glasses: Recent developments in theory, simulations, and experiments. Acta Mater. 2016, 109, 375–393. [Google Scholar] [CrossRef] [Green Version]
- Ding, J.; Cheng, Y.; Ma, E. Correlating local structure with inhomogeneous elastic deformation in a metallic glass. Appl. Phys. Lett. 2012, 101, 121917. [Google Scholar] [CrossRef]
- Fan, Y.; Iwashita, T.; Egami, T. Evolution of elastic heterogeneity during aging in metallic glasses. Phys. Rev. E 2014, 89, 062313. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Cheng, Y.Q.; Ma, E. Full icosahedra dominate local order in Cu64Zr34 metallic glass and supercooled liquid. Acta Mater. 2014, 69, 343–354. [Google Scholar] [CrossRef]
- Ding, J.; Patinet, S.; Falk, M.L.; Cheng, Y.; Ma, E. Soft spots and their structural signature in a metallic glass. Proc. Natl. Acad. Sci. USA 2014, 111, 14052–14056. [Google Scholar] [CrossRef] [Green Version]
- Ma, E.; Ding, J. Tailoring structural inhomogeneities in metallic glasses to enable tensile ductility at room temperature. Mater. Today 2016, 19, 568–579. [Google Scholar] [CrossRef]
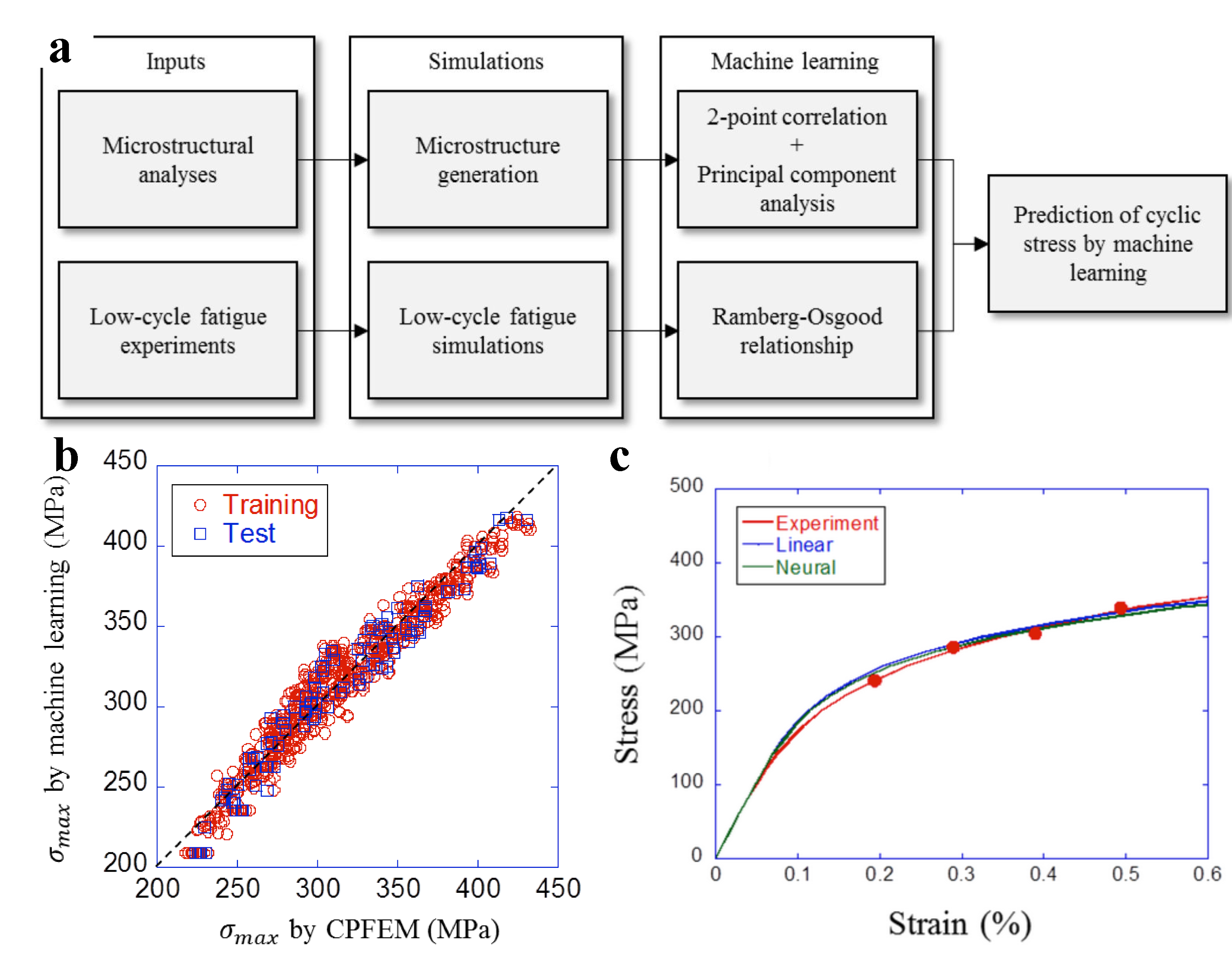
- Miyazawa, Y.; Briffod, F.; Shiraiwa, T.; Enoki, M. Prediction of cyclic stress–strain property of steels by crystal plasticity simulations and machine learning. Materials 2019, 12, 3668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schoenholz, S.S. Combining machine learning and physics to understand glassy systems. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2018; Volume 1036, p. 012021. [Google Scholar]
- Xiong, J.; Shi, S.Q.; Zhang, T.Y. A machine-learning approach to predicting and understanding the properties of amorphous metallic alloys. Mater. Des. 2020, 187, 108378. [Google Scholar] [CrossRef]
- Peng, J.; Yamamoto, Y.; Hawk, J.A.; Lara-Curzio, E.; Shin, D. Coupling physics in machine learning to predict properties of high-temperatures alloys. NPJ Comput. Mater. 2020, 6, 1–7. [Google Scholar] [CrossRef]
- Schoenholz, S.S.; Cubuk, E.D.; Sussman, D.M.; Kaxiras, E.; Liu, A.J. A structural approach to relaxation in glassy liquids. Nat. Phys. 2016, 12, 469–471. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Liu, A.J.; Kaxiras, E.; Schoenholz, S.S. Unifying framework for strong and fragile liquids via machine learning: A study of liquid silica. arXiv 2020, arXiv:2008.09681. [Google Scholar]
- Cubuk, E.D.; Schoenholz, S.S.; Rieser, J.M.; Malone, B.D.; Rottler, J.; Durian, D.J.; Kaxiras, E.; Liu, A.J. Identifying structural flow defects in disordered solids using machine-learning methods. Phys. Rev. Lett. 2015, 114, 108001. [Google Scholar] [CrossRef] [Green Version]
- Cubuk, E.D.; Ivancic, R.; Schoenholz, S.S.; Strickland, D.; Basu, A.; Davidson, Z.; Fontaine, J.; Hor, J.L.; Huang, Y.R.; Jiang, Y.; et al. Structure-property relationships from universal signatures of plasticity in disordered solids. Science 2017, 358, 1033–1037. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rocks, J.W.; Ridout, S.A.; Liu, A.J. Learning-based approach to plasticity in athermal sheared amorphous packings: Improving softness. APL Mater. 2021, 9, 021107. [Google Scholar] [CrossRef]
- Tainio, O.; Viitanen, L.; Mac Intyre, J.R.; Aydin, M.; Koivisto, J.; Puisto, A.; Alava, M. Predicting and following T1 events in dry foams from geometric features. Phys. Rev. Mater. 2021, 5, 075601. [Google Scholar] [CrossRef]
- Lim, H.; Carroll, J.; Battaile, C.C.; Buchheit, T.; Boyce, B.; Weinberger, C. Grain-scale experimental validation of crystal plasticity finite element simulations of tantalum oligocrystals. Int. J. Plast. 2014, 60, 1–18. [Google Scholar] [CrossRef]
- Guan, Y.; Chen, B.; Zou, J.; Britton, T.B.; Jiang, J.; Dunne, F.P. Crystal plasticity modelling and HR-DIC measurement of slip activation and strain localization in single and oligo-crystal Ni alloys under fatigue. Int. J. Plast. 2017, 88, 70–88. [Google Scholar] [CrossRef] [Green Version]
- Kapoor, K.; Sangid, M.D. Initializing type-2 residual stresses in crystal plasticity finite element simulations utilizing high-energy diffraction microscopy data. Mater. Sci. Eng. A 2018, 729, 53–63. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Mello, A.W.; Kapoor, K.; Reinhold, M.P.; Broderick, T.F.; Sangid, M.D. On the crack initiation and heterogeneous deformation of Ti-6Al-4V during high cycle fatigue at high R ratios. J. Mech. Phys. Solids 2019, 129, 61–82. [Google Scholar] [CrossRef]
- Zhang, T.; Collins, D.M.; Dunne, F.P.; Shollock, B.A. Crystal plasticity and high-resolution electron backscatter diffraction analysis of full-field polycrystal Ni superalloy strains and rotations under thermal loading. Acta Mater. 2014, 80, 25–38. [Google Scholar] [CrossRef]
- Kartal, M.; Kiwanuka, R.; Dunne, F. Determination of sub-surface stresses at inclusions in single crystal superalloy using HR-EBSD, crystal plasticity and inverse eigenstrain analysis. Int. J. Solids Struct. 2015, 67, 27–39. [Google Scholar] [CrossRef]
- Rovinelli, A.; Guilhem, Y.; Proudhon, H.; Lebensohn, R.A.; Ludwig, W.; Sangid, M.D. Assessing reliability of fatigue indicator parameters for small crack growth via a probabilistic framework. Model. Simul. Mater. Sci. Eng. 2017, 25, 045010. [Google Scholar] [CrossRef]
- Rovinelli, A.; Sangid, M.D.; Proudhon, H.; Guilhem, Y.; Lebensohn, R.A.; Ludwig, W. Predicting the 3D fatigue crack growth rate of small cracks using multimodal data via Bayesian networks: In-situ experiments and crystal plasticity simulations. J. Mech. Phys. Solids 2018, 115, 208–229. [Google Scholar] [CrossRef] [Green Version]
- Ali, U.; Muhammad, W.; Brahme, A.; Skiba, O.; Inal, K. Application of artificial neural networks in micromechanics for polycrystalline metals. Int. J. Plast. 2019, 120, 205–219. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Niezgoda, S.R.; Landi, G.; Vachhani, S.; Fast, T. A Novel Framework for Building Materials Knowledge Systems. Comput. Mater. Contin. 2010, 17, 103–126. [Google Scholar]
- Brough, D.B.; Wheeler, D.; Kalidindi, S.R. Materials knowledge systems in python—A data science framework for accelerated development of hierarchical materials. Integr. Mater. Manuf. Innov. 2017, 6, 36. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Medford, A.J.; Mcdowell, D.L. Vision for data and informatics in the future materials innovation ecosystem. JOM 2016, 68, 2126–2137. [Google Scholar] [CrossRef]
- Paulson, N.H.; Priddy, M.W.; McDowell, D.L.; Kalidindi, S.R. Reduced-order structure-property linkages for polycrystalline microstructures based on 2-point statistics. Acta Mat. 2017, 129, 428–438. [Google Scholar] [CrossRef] [Green Version]
- Priddy, M.W.; Paulson, N.H.; Kalidindi, S.R.; McDowell, D.L. Strategies for rapid parametric assessment of microstructure-sensitive fatigue for HCP polycrystals. Int. J. Fatigue 2017, 104, 231–242. [Google Scholar] [CrossRef]
- Paulson, N.H.; Priddy, M.W.; McDowell, D.L.; Kalidindi, S.R. Data-driven reduced-order models for rank-ordering the high cycle fatigue performance of polycrystalline microstructures. Mater. Des. 2018, 154, 170–183. [Google Scholar] [CrossRef]
- Paulson, N.H.; Priddy, M.W.; McDowell, D.L.; Kalidindi, S.R. Reduced-order microstructure-sensitive protocols to rank-order the transition fatigue resistance of polycrystalline microstructures. Int. J. Fatigue 2019, 119, 1–10. [Google Scholar] [CrossRef]
- Kubin, L.; Canova, G. The modelling of dislocation patterns. Scr. Metall. Mater. 1992, 27, 957–962. [Google Scholar] [CrossRef]
- Devincre, B.; Kubin, L. Mesoscopic simulations of dislocations and plasticity. Mater. Sci. Eng. A 1997, 234–236, 8–14. [Google Scholar] [CrossRef]
- Hirth, J.; Lothe, J. Theory of Dislocations; Krieger Publishing Company: Malabar, FL, USA, 1982. [Google Scholar]
- Ananthakrishna, G. Statistical and Dynamical Approaches to Collective Behavior of Dislocations. In Dislocations in Solids; Nabarro, F., Hirth, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Chapter 73; Volume 13, pp. 81–223. [Google Scholar] [CrossRef]
- Fivel, M.C. Discrete dislocation dynamics: An important recent break-through in the modelling of dislocation collective behaviour. Comptes Rendus Phys. 2008, 9, 427–436. [Google Scholar] [CrossRef]
- Lefebvre, S.; Devincre, B.; Hoc, T. Yield stress strengthening in ultrafine-grained metals: A two-dimensional simulation of dislocation dynamics. J. Mech. Phys. Solids 2007, 55, 788–802. [Google Scholar] [CrossRef]
- Kumar, R.; Nicola, L.; Van der Giessen, E. Density of grain boundaries and plasticity size effects: A discrete dislocation dynamics study. Mater. Sci. Eng. A 2009, 527, 7–15. [Google Scholar] [CrossRef]
- Zhou, C.; Biner, S.B.; LeSar, R. Discrete dislocation dynamics simulations of plasticity at small scales. Acta Mater. 2010, 58, 1565–1577. [Google Scholar] [CrossRef]
- Han, C.S.; Hartmaier, A.; Gao, H.; Huang, Y. Discrete dislocation dynamics simulations of surface induced size effects in plasticity. Mater. Sci. Eng. A 2006, 415, 225–233. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Dimiduk, D.M.; Choi, W.; Sethna, J.P.; Uchic, M.D.; Woodward, C.F.; Zapperi, S. Quasi-periodic events in crystal plasticity and the self-organized avalanche oscillator. Nature 2012, 490, 517–521. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Papanikolaou, S. From statistical correlations to stochasticity and size effects in sub-micron crystal plasticity. Metals 2019, 9, 835. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Dimiduk, D.; Papanikolaou, S. Universality class of nanocrystal plasticity: Localization and self-organization in discrete dislocation dynamics. Phys. Rev. Lett. 2019, 122, 178001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Madec, R.; Devincre, B.; Kubin, L.; Hoc, T.; Rodney, D. The role of collinear interaction in dislocation-induced hardening. Science 2003, 301, 1879–1882. [Google Scholar] [CrossRef] [PubMed]
- Bulatov, V.; Abraham, F.F.; Kubin, L.; Devincre, B.; Yip, S. Connecting atomistic and mesoscale simulations of crystal plasticity. Nature 1998, 391, 669–672. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Po, G. Λ-Invariant and Topological Pathways to Influence the Strength of Submicron Crystals. Phys. Rev. Lett. 2020, 124, 205502. [Google Scholar] [CrossRef]
- Akhondzadeh, S.; Sills, R.; Papanikolaou, S.; Van der Giessen, E.; Cai, W. Geometrically projected discrete dislocation dynamics. Model. Simul. Mater. Sci. Eng. 2018, 26, 065011. [Google Scholar] [CrossRef] [Green Version]
- Csikor, F.F.; Motz, C.; Weygand, D.; Zaiser, M.; Zapperi, S. Dislocation avalanches, strain bursts, and the problem of plastic forming at the micrometer scale. Science 2007, 318, 251–254. [Google Scholar] [CrossRef] [Green Version]
- Devincre, B.; Hoc, T.; Kubin, L. Dislocation Mean Free Paths and Strain Hardening of Crystals. Science 2008, 320, 1745–1748. [Google Scholar] [CrossRef]
- Chen, Y.J.; Papanikolaou, S.; Sethna, J.P.; Zapperi, S.; Durin, G. Avalanche spatial structure and multivariable scaling functions: Sizes, heights, widths, and views through windows. Phys. Rev. E 2011, 84, 061103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bolin, R.; Yavas, H.; Song, H.; Hemker, K.J.; Papanikolaou, S. Bending nanoindentation and plasticity noise in FCC single and polycrystals. Crystals 2019, 9, 652. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Yavas, H.; Van der Giessen, E.; Papanikolaou, S. Discrete dislocation dynamics simulations of nanoindentation with pre-stress: Hardness and statistics of abrupt plastic events. J. Mech. Phys. Solids 2019, 123, 332–347. [Google Scholar] [CrossRef] [Green Version]
- Ni, X.; Papanikolaou, S.; Vajente, G.; Adhikari, R.X.; Greer, J.R. Probing microplasticity in small-scale fcc crystals via dynamic mechanical analysis. Phys. Rev. Lett. 2017, 118, 155501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bertin, N.; Sills, R.B.; Cai, W. Frontiers in the Simulation of Dislocations. Annu. Rev. Mater. Res. 2020, 50, 437–464. [Google Scholar] [CrossRef]
- Prakash, A.; Sandfeld, S. Chances and Challenges in Fusing Data Science with Materials Science. Pract. Metallogr. 2018, 55, 493–514. [Google Scholar] [CrossRef]
- Sarvilahti, M.; Skaugen, A.; Laurson, L. Machine learning depinning of dislocation pileups. APL Mater. 2020, 8, 101109. [Google Scholar] [CrossRef]
- Biswas, S.; Castellanos, D.F.; Zaiser, M. Prediction of creep failure time using machine learning. Sci. Rep. 2020, 10, 1. [Google Scholar] [CrossRef]
- Hiemer, S.; Zapperi, S. From mechanism-based to data-driven approaches in materials science. Mater. Theory 2021, 5, 1–9. [Google Scholar] [CrossRef]
- Salmenjoki, H.; Alava, M.J.; Laurson, L. Machine learning plastic deformation of crystals. Nat. Commun. 2018, 9, 5307. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.S.; Choi, W.; Papanikolaou, S.; Sethna, J.P. Bending crystals: Emergence of fractal dislocation structures. Phys. Rev. Lett. 2010, 105, 105501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.S.; Choi, W.; Papanikolaou, S.; Bierbaum, M.; Sethna, J.P. Scaling theory of continuum dislocation dynamics in three dimensions: Self-organized fractal pattern formation. Int. J. Plast. 2013, 46, 94–129. [Google Scholar] [CrossRef] [Green Version]
- Salmenjoki, H.; Laurson, L.; Alava, M.J. Probing the transition from dislocation jamming to pinning by machine learning. Mater. Theory 2020, 4, 1–16. [Google Scholar] [CrossRef]
- Yang, Z.; Papanikolaou, S.; Reid, A.C.; keng Liao, W.; Choudhary, A.N.; Campbell, C.; Agrawal, A. Learning to Predict Crystal Plasticity at the Nanoscale: Deep Residual Networks and Size Effects in Uniaxial Compression Discrete Dislocation Simulations. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Steinberger, D.; Song, H.; Sandfeld, S. Machine Learning-Based Classification of Dislocation Microstructures. Front. Mater. 2019, 6, 141. [Google Scholar] [CrossRef]
- Messner, M.C.; Rhee, M.; Arsenlis, A.; Barton, N.R. A crystal plasticity model for slip in hexagonal close packed metals based on discrete dislocation simulations. Model. Simul. Mater. Sci. Eng. 2017, 25, 044001. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Panico, M.; Berbenni, S.; Schwarz, K.W. Discrete dislocation dynamics simulations to interpret plasticity size and surface effects in freestanding FCC thin films. Int. J. Plast. 2006, 22, 2091–2117. [Google Scholar] [CrossRef]
- Wang, Z.; McCabe, R.J.; Ghoniem, N.M.; LeSar, R.; Misra, A.; Mitchell, T.E. Dislocation motion in thin Cu foils: A comparison between computer simulations and experiment. Acta Mater. 2004, 52, 1535–1542. [Google Scholar] [CrossRef]
- Weygand, D.; Poignant, M.; Gumbsch, P.; Kraft, O. Three-dimensional dislocation dynamics simulation of the influence of sample size on the stress-strain behavior of fcc single-crystalline pillars. Mater. Sci. Eng. A 2008, 483–484, 188–190. [Google Scholar] [CrossRef]
- Senger, J.; Weygand, D.; Gumbsch, P.; Kraft, O. Discrete dislocation simulations of the plasticity of micro-pillars under uniaxial loading. Scr. Mater. 2008, 58, 587–590. [Google Scholar] [CrossRef]
- Akarapu, S.; Zbib, H.M.; Bahr, D.F. Analysis of heterogeneous deformation and dislocation dynamics in single crystal micropillars under compression. Int. J. Plast. 2010, 26, 239–257. [Google Scholar] [CrossRef]
- Zhang, J.L.; Zaefferer, S.; Raabe, D. A study on the geometry of dislocation patterns in the surrounding of nanoindents in a TWIP steel using electron channeling contrast imaging and discrete dislocation dynamics simulations. Mater. Sci. Eng. A 2015, 636, 231–242. [Google Scholar] [CrossRef]
- Sangid, M.D. Coupling in situ experiments and modeling–Opportunities for data fusion, machine learning, and discovery of emergent behavior. Curr. Opin. Solid State Mater. Sci. 2020, 24, 100797. [Google Scholar] [CrossRef]
- Vishnubhotla, S.B.; Chen, R.; Khanal, S.R.; Hu, X.; Martini, A.; Jacobs, T.D.B. Matching Atomistic Simulations and In Situ Experiments to Investigate the Mechanics of Nanoscale Contact. Tribol. Lett. 2019, 67, 97. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Cao, G.; Zhang, Z.; Sansoz, F. Size-dependent dislocation-twin interactions. Nanoscale 2019, 11, 12672–12679. [Google Scholar] [CrossRef]
- Hata, S.; Honda, T.; Saito, H.; Mitsuhara, M.; Petersen, T.; Murayama, M. Electron tomography: An imaging method for materials deformation dynamics. Curr. Opin. Solid State Mater. Sci. 2020, 24, 100850. [Google Scholar] [CrossRef]
- Chowdhury, A.; Kautz, E.; Yener, B.; Lewis, D. Image driven machine learning methods for microstructure recognition. Comput. Mater. Sci. 2016, 123, 176–187. [Google Scholar] [CrossRef] [Green Version]
- Roberts, G.; Haile, S.Y.; Sainju, R.; Edwards, D.J.; Hutchinson, B.; Zhu, Y. Deep Learning for Semantic Segmentation of Defects in Advanced STEM Images of Steels. Sci. Rep. 2019, 9, 12744. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cantor, B.; Chang, I.; Knight, P.; Vincent, A. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Flory, P.J. Phase equilibria in solutions of rod-like particles. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 234, 73–89. [Google Scholar]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Bernal, J.D. A geometrical approach to the structure of liquids. Nature 1959, 183, 141–147. [Google Scholar] [CrossRef]
- Seko, A. Machine learning potentials for multicomponent systems: The Ti-Al binary system. Phys. Rev. B 2020, 102, 174104. [Google Scholar] [CrossRef]
- Singh, R.; Sharma, A.; Singh, P.; Balasubramanian, G.; Johnson, D.D. Accelerating computational modeling and design of high-entropy alloys. Nat. Comput. Sci. 2021, 1, 54–61. [Google Scholar] [CrossRef]
- Kaufmann, K.; Vecchio, K.S. Searching for high entropy alloys: A machine learning approach. Acta Mater. 2020, 198, 178–222. [Google Scholar] [CrossRef]
- Tsuzuki, H.; Branicio, P.S.; Rino, J.P. Structural characterization of deformed crystals by analysis of common atomic neighborhood. Comput. Phys. Commun. 2007, 177, 518–523. [Google Scholar] [CrossRef]
- Honeycutt, J.D.; Andersen, H.C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
- Blaisten-Barojas, E.; Andersen, H.C. Effects of three-body interactions on the structure of clusters. Surf. Sci. 1985, 156, 548–555. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.; Hamilton, J. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085. [Google Scholar] [CrossRef]
- Li, J. AtomEye: An efficient atomistic configuration viewer. Model. Simul. Mater. Sci. Eng. 2003, 11, 173. [Google Scholar] [CrossRef]
- Posada-Amarillas, A.; Garzón, I.L. Microstructural analysis of simulated liquid and amorphous Ni. Phys. Rev. B 1996, 53, 8363. [Google Scholar] [CrossRef]
- Schiötz, J.; Di Tolla, F.D.; Jacobsen, K.W. Softening of nanocrystalline metals at very small grain sizes. Nature 1998, 391, 561–563. [Google Scholar] [CrossRef]
- Schiötz, J.; Vegge, T.; Di Tolla, F.; Jacobsen, K.W. Atomic-scale simulations of the mechanical deformation of nanocrystalline metals. Phys. Rev. B 1999, 60, 11971. [Google Scholar] [CrossRef] [Green Version]
- Yavari, A.R. A new order for metallic glasses. Nature 2006, 439, 405–406. [Google Scholar] [CrossRef]
- Van Swygenhoven, H.; Weertman, J.R. Deformation in nanocrystalline metals. Mater. Today 2006, 9, 24–31. [Google Scholar] [CrossRef]
- Monk, J.; Farkas, D. Strain-induced grain growth and rotation in nickel nanowires. Phys. Rev. B 2007, 75, 045414. [Google Scholar] [CrossRef] [Green Version]
- Bringa, E.; Rosolankova, K.; Rudd, R.; Remington, B.; Wark, J.; Duchaineau, M.; Kalantar, D.; Hawreliak, J.; Belak, J. Shock deformation of face-centred-cubic metals on subnanosecond timescales. Nat. Mater. 2006, 5, 805–809. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramétres continus á la théorie des formes quadratiques. Deuxiéme mémoire. Recherches sur les parallélloédres primitifs. J. Die Reine Angew. Math. (Crelles J.) 1908, 1908, 198–287. [Google Scholar] [CrossRef]
- Stukowski, A. Structure identification methods for atomistic simulations of crystalline materials. Model. Simul. Mater. Sci. Eng. 2012, 20, 045021. [Google Scholar] [CrossRef]
- Lazar, E.A. VoroTop: Voronoi cell topology visualization and analysis toolkit. Model. Simul. Mater. Sci. Eng. 2017, 26, 015011. [Google Scholar] [CrossRef] [Green Version]
- Lazar, E.A.; Han, J.; Srolovitz, D.J. Topological framework for local structure analysis in condensed matter. Proc. Natl. Acad. Sci. USA 2015, 112, E5769–E5776. [Google Scholar] [CrossRef] [Green Version]
- Trybula, M.E. Structure and transport properties of the liquid Al80Cu20 alloy–a molecular dynamics study. Comput. Mater. Sci. 2016, 122, 341–352. [Google Scholar] [CrossRef]
- Trybula, M.E.; Szafrański, P.W.; Korzhavyi, P.A. Structure and chemistry of liquid Al–Cu alloys: Molecular dynamics study versus thermodynamics-based modelling. J. Mater. Sci. 2018, 53, 8285–8301. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Han, J.; Fang, H.; Wang, J.; Liang, Y.; Shang, S.; Wang, Y.; Liu, X.; Kecskes, L.; Mathaudhu, S.; et al. Anomalous structural dynamics in liquid Al80Cu20: An ab initio molecular dynamics study. Acta Mater. 2015, 97, 75–85. [Google Scholar] [CrossRef]
- Du, Q.; Liu, X.; Fan, H.; Zeng, Q.; Wu, Y.; Wang, H.; Chatterjee, D.; Ren, Y.; Ke, Y.; Voyles, P.M.; et al. Reentrant glass transition leading to ultrastable metallic glass. Mater. Today 2020, 34, 66–77. [Google Scholar] [CrossRef]
- Nagamanasa, K.H.; Gokhale, S.; Ganapathy, R.; Sood, A. Confined glassy dynamics at grain boundaries in colloidal crystals. Proc. Natl. Acad. Sci. USA 2011, 108, 11323–11326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LaViolette, R.A.; Stillinger, F.H. Enumeration of random packings for atomic substances. Phys. Rev. B 1987, 35, 5446. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Weber, T.A. Hidden structure in liquids. Phys. Rev. A 1982, 25, 978. [Google Scholar] [CrossRef]
- Oh, H.S.; Kim, S.J.; Odbadrakh, K.; Ryu, W.H.; Yoon, K.N.; Mu, S.; Körmann, F.; Ikeda, Y.; Tasan, C.C.; Raabe, D.; et al. Engineering atomic-level complexity in high-entropy and complex concentrated alloys. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Pei, Z.; Yin, J.; Hawk, J.A.; Alman, D.E.; Gao, M.C. Machine-learning informed prediction of high-entropy solid solution formation: Beyond the Hume-Rothery rules. NPJ Comput. Mater. 2020, 6, 1–8. [Google Scholar] [CrossRef]
- Zhang, L.; Qian, K.; Schuller, B.W.; Shibuta, Y. Prediction on Mechanical Properties of Non-Equiatomic High-Entropy Alloy by Atomistic Simulation and Machine Learning. Metals 2021, 11, 922. [Google Scholar] [CrossRef]
- Artrith, N.; Morawietz, T.; Behler, J. High-dimensional neural-network potentials for multicomponent systems: Applications to zinc oxide. Phys. Rev. B 2011, 83, 153101. [Google Scholar] [CrossRef] [Green Version]
- Artrith, N.; Urban, A.; Ceder, G. Efficient and accurate machine-learning interpolation of atomic energies in compositions with many species. Phys. Rev. B 2017, 96, 014112. [Google Scholar] [CrossRef] [Green Version]
- Hume-Rothery, W.; Powell, H.M. On the theory of super-lattice structures in alloys. Z. Krist.-Cryst. Mater. 1935, 91, 23–47. [Google Scholar] [CrossRef]
- Hume-Rothery, W.; Raynor, G.V. The Structure of Metals and Alloys; Institute of Metals: London, UK, 1954. [Google Scholar]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Troparevsky, M.C.; Morris, J.R.; Kent, P.R.; Lupini, A.R.; Stocks, G.M. Criteria for predicting the formation of single-phase high-entropy alloys. Phys. Rev. X 2015, 5, 011041. [Google Scholar] [CrossRef] [Green Version]
- George, E.P.; Raabe, D.; Ritchie, R.O. High-entropy alloys. Nat. Rev. Mater. 2019, 4, 515–534. [Google Scholar] [CrossRef]
- Inoue, A. Stabilization of metallic supercooled liquid and bulk amorphous alloys. Act. Mater. 2000, 48, 279–306. [Google Scholar] [CrossRef]
- Xiong, J.; Shi, S.; Zhang, T. Machine learning prediction of glass-forming ability in bulk metallic glasses. Comput. Mater. Sci. 2021, 192, 110362. [Google Scholar] [CrossRef]
- Ren, R.; Hung, T.; Tan, K.C. A generic deep-learning-based approach for automated surface inspection. IEEE Trans. Cybern. 2017, 48, 929–940. [Google Scholar] [CrossRef] [PubMed]
- Pei, Z.; Yin, J. Machine learning as a contributor to physics: Understanding Mg alloys. Mater. Des. 2019, 172, 107759. [Google Scholar] [CrossRef]
- Kostiuchenko, T.; Körmann, F.; Neugebauer, J.; Shapeev, A. Impact of lattice relaxations on phase transitions in a high-entropy alloy studied by machine-learning potentials. NPJ Comput. Mater. 2019, 5, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Abu-Odeh, A.; Galvan, E.; Kirk, T.; Mao, H.; Chen, Q.; Mason, P.; Malak, R.; Arróyave, R. Efficient exploration of the High Entropy Alloy composition-phase space. Acta Mater. 2018, 152, 41–57. [Google Scholar] [CrossRef]
- Huang, W.; Martin, P.; Zhuang, H.L. Machine-learning phase prediction of high-entropy alloys. Acta Mater. 2019, 169, 225–236. [Google Scholar] [CrossRef]
- Jha, D.; Gupta, V.; Ward, L.; Yang, Z.; Wolverton, C.; Foster, I.; Liao, W.K.; Choudhary, A.; Agrawal, A. Enabling deeper learning on big data for materials informatics applications. Sci. Rep. 2021, 11, 1–2. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data-driven computing. In Advances in Computational Plasticity; Springer: Berlin/Heidelberg, Germany, 2018; pp. 165–183. [Google Scholar]
- Kalidindi, S.R.; De Graef, M. Materials data science: Current status and future outlook. Annu. Rev. Mater. Res. 2015, 45, 171–193. [Google Scholar] [CrossRef]
- Moreno Torres, B.; Volker, C.; Nagel, S.M.; Hanke, T.; Kruschwitz, S. An Ontology-based approach to enable data-driven research in the field of NDT in Civil Engineering. Remote Sens. 2021, 13, 2426. [Google Scholar] [CrossRef]
- Horsch, M.T.; Chiacchiera, S.; Cavalcanti, W.L.; Schembera, B. Data Technology in Materials Modelling; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Forte, E.; Jirasek, F.; Bortz, M.; Burger, J.; Vrabec, J.; Hasse, H. Digitalization in thermodynamics. Chem. Ing. Tech 2019, 91, 201–214. [Google Scholar] [CrossRef] [Green Version]
- Tchipev, N.; Seckler, S.; Heinen, M.; Vrabec, J.; Gratl, F.; Horsch, M.; Bernreuther, M.; Glass, C.; Niethammer, C.; Hammer, N.; et al. TweTriS: Twenty trillion-atom simulation. Int. J. High Perform. Comput. Appl. 2019, 33, 838–854. [Google Scholar] [CrossRef] [Green Version]
- Stephan, S.; Horsch, M.; Vrabec, J.; Hasse, H. MolMod–An open access database of force fields for molecular simulations of fluids. Mol. Simul. 2019, 45, 806–814. [Google Scholar] [CrossRef] [Green Version]
- Schmitz, G. Microstructure modeling in integrated computational materials engineering (ICME) settings: Can HDF5 provide the basis for an emerging standard for describing microstructures? JOM 2016, 68, 77–83. [Google Scholar] [CrossRef]
- Morbach, J.; Wiesner, A.; Marquardt, W. OntoCAPE 2.0: A (re-)usable ontology for computeraided process engineering. Comput. Aided Chem. Eng. 2008, 25, 991–996. [Google Scholar]
- Morbach, J.; Wiesner, A.; Marquardt, W. Shedding light on the dark data in the long tail of science. Libr. Trends 2008, 57, 280–299. [Google Scholar]
- Schembera, B.; Durán, J. Dark data as the new challenge for big data science and the introduction of the scientific data officer. Philos. Technol. 2020, 33, 93–115. [Google Scholar] [CrossRef] [Green Version]
- Bicarregui, J. Building and Sustaining Data Infrastructures: Putting Policy into Practice. Policy Document. 2016. Available online: https://wellcome.org/sites/default/files/building-and-sustaining-data-infrastructures-oct16.pdf (accessed on 1 October 2012).
- Ribes, A.; Caremoli, C. Salomé platform component model for numerical simulation. In Proceedings of the 31st Annual International Computer Software and Applications Conference (COMPSAC 2007), Beijing, China, 24–27 July 2007; Chang, C.K., Ed.; IEEE: Los Alamitos, CA, USA, 2007; Volume 2, pp. 553–564. [Google Scholar]
- Schneider, T.; Simkus, M. Ontologies and data management: A brief survey. Kunstl. Intell. 2020, 34, 329–353. [Google Scholar] [CrossRef]
- Mons, B. Data Stewardship for Open Science; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Schoop, M.; Moor, A.D.; Dietz, J.L. The pragmatic web: A manifesto. Commun. ACM 2006, 49, 75–76. [Google Scholar] [CrossRef]
- Neiva, F.W.; David, J.; Braga, R.; Borges, M.; Campos, F. SM2PIA: A model to support the development of pragmatic interoperability requirements. In Proceedings of ICGSE 2016; Redmiles, D., Gerosa, M.A., Hildenbrand, T., Eds.; IEEE: New York, NY, USA, 2016; pp. 119–128. [Google Scholar]
- Neiva, F.W.; David, J.; Braga, R.; Campos, F. Towards pragmatic interoperability to support collaboration: A systematic review and mapping of the literature. Inf. Softw. Technol. 2016, 72, 137–150. [Google Scholar] [CrossRef]
- Hey, A.; Trefethen, A. The data deluge: An e-science perspective. In Grid Computing: Making the Global Infrastructure a Reality; Berman, F., Fox, G.C., Hey, A.J.G., Eds.; Wiley: Hoboken, NJ, USA, 2003; Volume 72, pp. 809–824. [Google Scholar]
- Edwards, P.; Mayernik, M.; Batcheller, A.; Bowker, G.; Borgman, C. Science friction: Data, metadata, and collaboration. Soc. Stud. Sci. 2011, 41, 667–690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Greenberg, J. Metadata and the world wide web. Encycl. Libr. Inf. Sci. 2003, 3, 1876–1888. [Google Scholar]
- Neumann, J.; Brase, J. DataCite. Names for research data. J. Comput.-Aided Mol. Des. 2014, 28, 1035–1041. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.; Boettiger, C.; Mayes, A.C.; Smith, A.; Slaughter, P.; Niemeyer, K.; Gil, Y.; Fenner, M.; Nowak, K.; Hahnel, M.; et al. CodeMeta: An Exchange Schema for Software Metadata, Version 2.0; Technical Report; KNB Data Repository: Santa Barbara, CA, USA, 2017. [Google Scholar]
- Druskat, S.; Hong, N.; Haines, R.; Baker, J. Ation File Format (CFF): Specifications; Technical Report; Zenodo: Genève, Switzerland, 2018. [Google Scholar]
- Li, H.; Armiento, R.; Lambrix, P. A Method for Extending Ontologies with Application to the Materials Science Domain. Data Sci. J. 2019, 18, 1–21. [Google Scholar] [CrossRef]
- Thomas, D.G.; Pappu, R.V.; Baker, N.A. NanoParticle Ontology for cancer nanotechnology research. J. Biomed. Inform. 2011, 44, 59–74. [Google Scholar] [CrossRef] [Green Version]
- Staab, S. Wissensmanagement mit Ontologien und Metadaten. Informatik-Spektrum 2002, 25, 194–209. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frydrych, K.; Karimi, K.; Pecelerowicz, M.; Alvarez, R.; Dominguez-Gutiérrez, F.J.; Rovaris, F.; Papanikolaou, S. Materials Informatics for Mechanical Deformation: A Review of Applications and Challenges. Materials 2021, 14, 5764. https://doi.org/10.3390/ma14195764
Frydrych K, Karimi K, Pecelerowicz M, Alvarez R, Dominguez-Gutiérrez FJ, Rovaris F, Papanikolaou S. Materials Informatics for Mechanical Deformation: A Review of Applications and Challenges. Materials. 2021; 14(19):5764. https://doi.org/10.3390/ma14195764
Chicago/Turabian StyleFrydrych, Karol, Kamran Karimi, Michal Pecelerowicz, Rene Alvarez, Francesco Javier Dominguez-Gutiérrez, Fabrizio Rovaris, and Stefanos Papanikolaou. 2021. "Materials Informatics for Mechanical Deformation: A Review of Applications and Challenges" Materials 14, no. 19: 5764. https://doi.org/10.3390/ma14195764
APA StyleFrydrych, K., Karimi, K., Pecelerowicz, M., Alvarez, R., Dominguez-Gutiérrez, F. J., Rovaris, F., & Papanikolaou, S. (2021). Materials Informatics for Mechanical Deformation: A Review of Applications and Challenges. Materials, 14(19), 5764. https://doi.org/10.3390/ma14195764





