Abstract
Nowadays, fused deposition modeling additive technology is becoming more and more popular in parts manufacturing due to its ability to reproduce complex geometries with many different thermoplastic materials, such as the TPU. On the other hand, objects obtained through this technology are mainly used for prototyping activities. For this reason, analyzing the functional behavior of FDM parts is still a topic of great interest. Many studies are conducted to broaden the spectrum of materials used to ensure an ever-increasing use of FDM in various production scenarios. In this study, the effects of several phenomena that influence the mechanical properties of printed lattice structures additively obtained by FDM are evaluated. Three different configurations of lattice structures with designs developed from unit cells were analyzed both experimentally and numerically. As the main result of the study, several parameters of the FDM process and their correlation were identified as possible detrimental factors of the mechanical properties by about 50% of the same parts used as isotropic cell solids. The best parameter configurations in terms of mechanical response were then highlighted by numerical analysis.
1. Introduction
As opposed to traditional production, which is mainly subtractive in nature, additive manufacturing represents the idea of future production, thanks to its considerable savings in materials and the extended possibilities in producing complex geometries. The major advantage of the fused deposition modeling (FDM) additive process lies in the customized production of printed objects. At the same time, various limitations prevent their dominance in the production of fully functional mechanical components, for example, the limited size of produced parts, but the cost should not be underestimated as well [1]. Furthermore, many printing process parameters have an influence on the resulting microstructure of printed objects, as observed by Ziemian et al. and Durgun et al. and discussed below [2,3].
FDM additive process is based on the extrusion of material and on the principle of stacking layer by layer, in order to create parts that can have sophisticated 3D geometries. Due to this principle of deposition of the material, this technology presents some pitfalls. In fact, by building FDM parts from bottom to top, the material in the current layer solidifies before the next one is placed on it [4], causing incomplete interlayer adhesion and often leaving voids in solidified structure, resulting in a decrease in mechanical performance [5]. In addition to this, a combination of several parameters such as raster orientation, air gap, bead width, color, model temperature, infill, etc. causes a decrease in the compressive strength of FDM products [6,7]. The layering effect represents the main challenge in additive manufacturing with fused deposition technology and will be analyzed in depth in the discussion below.
In this study, the printed parts under examination were lattice structures made of the repetition of three different unit cells with the same relative density—namely, open cell, closed thin-walled cell, and closed thick-walled cell. The unit cells repeated with the principle of tessellation along the three principal directions constitute the resulting lattice structures [8] (Figure 1). Fabrication of these structures by conventional manufacturing is not trivial, but Kumar et al. have found that with additive technologies, it is possible to produce them without any support structure [9]. An undoubted advantage of lattice structures, which are basically metamaterials since they are specifically designed to impart special physical properties normally absent in the constituent materials [10], is lightness, often a valuable attribute in engineering applications [11]. The material here used for printing is the thermoplastic polyurethane (TPU) 90A, which has hyperelastic and viscoelastic properties [12]. Three specimens of each configuration were additively realized and were tested under compression loads. Comparative analysis among the three configurations was carried out based on the mechanical property of stiffness. At present, the mechanical properties of most 3D-FDM printed polymeric parts often do not meet the requirements of industrial applications [13].
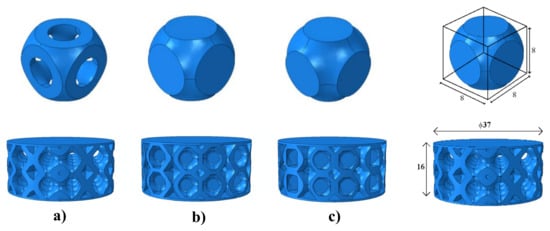
Figure 1.
Unit cells and, respectively, lattice structures with their appropriate geometries and sizes [mm]: (a) open cell; (b) closed thin-walled cell; (c) closed thick-walled cell.
Hence, this paper aimed at evaluating the stiffness of produced lattice structures under compression, both numerically and experimentally, to make a comparison between the consistency assumed by finite element software and layering effects of experimental samples.
2. Fused Deposition Modeling on Lattice Structures
2.1. Design
Lattice structures were made by means of tessellation of a unit cell repeating it along the three main directions, essentially creating a honeycomb structure; see Figure 1. As known, honeycomb structures offer great advantages, especially in terms of minimum weight and great resistance to high stresses [14].
Three configurations of lattice structures were designed and analyzed, starting from three different unit cells with the same relative density, respectively, open cell, closed thin-walled cell, and closed thick-walled cell. These configurations of cells were designed based on the design for additive manufacturing. In detail, in accordance with the printing parameters used in the laboratory shown in Table 1, in particular the minimum thickness, the unit cells were produced, as illustrated in Figure 2.

Table 1.
Printing process parameters.
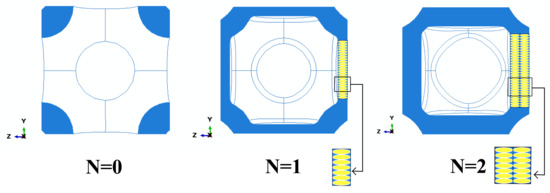
Figure 2.
Section of unit cells: wall’s contours.
It is immediately evident that the number of adjacent contours, , in the walls of cells varies from for open cell, is equal to for thin-walled type, and is equal to for thick-walled type. This choice of wall sizes will be the determining feature of the best geometry in terms of specific stiffness since layer thickness is one of the various parameters influencing the 3D-FDM printed objects [15,16].
The building orientation for all the configurations of lattice structures was the horizontal building direction, shown in Figure 3. This is another important printing process parameter in the mechanical response of the printed samples since it is found that building orientation plays an important role in the compressive strength of FDM printed parts [17,18].
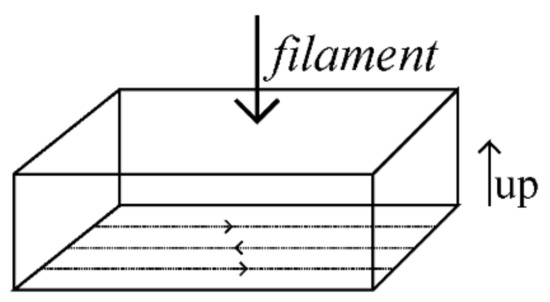
Figure 3.
Building orientation of lattice structures.
The greatest advantage of these designed lattice structures, in addition to lightness, is that no support structures are required during the printing phase. This is due to the maximum overhang angle of 50 degrees of the used MEX 3D printer machine (Figure 4) (High speed 3D printing research center, National Taiwan University of Science and Technology, Taipei, Taiwan). In fact, 3D printers use a barely appreciable horizontal offset between consecutive layers. In this way, the upper layer does not perfectly overlap the underlying layer but stacks with this small offset, allowing to print overhangs with respect to the vertical of an overhang angle that varies from machine to machine, in a range from 20 to 70 degrees. In any 3D printer, the test for identifying the maximum overhang angle that allows printing without support is called the “massive overhang test”.
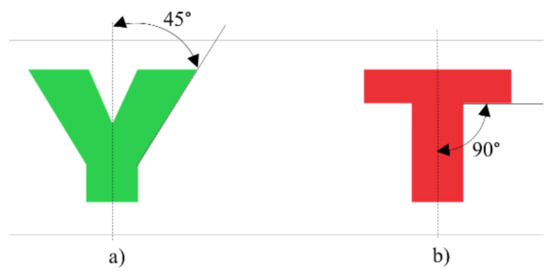
Figure 4.
Overhang angle: (a) does not need support structures; (b) needs support structure.
Hence, the 3D printing of self-supported structures is definitely convenient for saving material, printing time, and post-printing processing. There is also no risk of damaging the printed object when removing the support structure.
2.2. Experimental Tests
Three specimens of each configuration of lattice structure were printed by MEX 3D printer Flashforge dreamer© with TPU 90A filament. Monotonic compression tests were then performed on lattice structures under displacement control of 5 mm/min for three deformation levels, respectively, 10, 20, and 30% of the specimens’ height. For each configuration, load-displacement data were plotted in one graph to understand the geometry effect on compression behavior, in particular the number of contours with specific stiffness.
This was performed while bearing in mind that geometry in FDM parts is an important factor that influences the stress distribution and mechanical properties of samples. Preliminary tests were carried out on cubic and cylindrical TPU 90A FDM samples for different deformation levels at the same strain rate. In order to highlight differences in the mechanical behavior of the two geometric configurations, the nominal stress-strain curves corresponding to 36% of deformation, shown in Figure 5, were obtained using the classical Equations (1) and (2) as follows:
where is the compression applied load, is the cross-sectional area of the samples, is the displacement, and is the initial height of the samples.
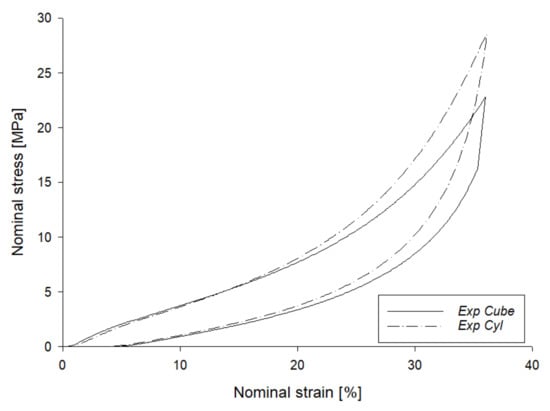
Figure 5.
Compression-release tests on cubic and cylindrical TPU FDM samples.
The geometric configuration’s significant effect on the mechanical behavior of FDM printed parts became suddenly clear. In particular, at the beginning of the test, the cubic sample shows a higher Young’s modulus with a consequently lower plateau regime than the cylindric one. Experimental tests were performed by a servo-hydraulic MTS 810 with a 100 kN load cell. The load was applied perpendicularly to the building orientation of lattice structures so that the layers tend to crush each other, not stressing the weaker adhesion layer. In fact, in FDM printing, an anisotropic layering effect occurs, i.e., the printed parts are stronger in one direction than in the other [19].
A compression test is useful for unveiling the isotropic or anisotropic behavior of printed objects [20]. Given its layer-by-layer nature, the FDM process and many other 3D printing technologies, by definition, give rise to anisotropic parts in their structure [21,22]. This is due to the printing technique: when placing one layer on top of another, the underlying layer begins to partially solidify, causing incorrect and incomplete adhesion between the layers. This tends to create voids between the two adjacent layers, giving the printed object a consequent stiffness depending on the load application direction and also leads to its anisotropic behavior [23]. Obviously, this is one of the main difficulties in using and studying objects obtained by additive processes. Furthermore, the anisotropy present in FDM printed parts have different properties depending on the process parameters used in the printing phase [24]. This can have major consequences on the mechanical and functional properties of the printed parts in industrial applications.
2.3. FDM Process in Conjunction with TPU
As previously mentioned, the FDM additive process does not ensure mechanical properties equal to those of traditionally manufactured objects. This is certainly due to the considerable variability of the numerous process parameters of this type of 3D printing. Each of these parameters, as well as their combination, has different impacts on the mechanical properties of printed parts [25,26,27]. Through an extensive literature review, many FDM process parameters, such as layer thickness, air gap, bed temperature, raster orientation, model temperature, building orientation, etc. [28], have been found to influence the compressive strength of the samples obtained with the same technology. It must be noted that in all these works, the material used for printing is mostly ABS, while TPU has never been studied. This is of interest in our research, as TPU is increasingly used in conjunction with 3D printing in the manufacturing of thermoplastic printed parts since it offers a wide range of applications. This is due to the capability of TPU to combine mechanical performance characteristics of rubber with the possibility of being processed as a thermoplastic material.
At the same time, TPU is also a very complex material due to its hyperelastic and viscoelastic properties, hygroscopic nature of its filament, and wide range of values that its Young’s modulus can assume (from 10 to 2000 MPa).
3. Finite Element Method on Lattice Structures
3.1. Material: Models
To simulate the behavior of lattice structures in TPU, an advanced model of hyperelastic material with hysteretic capability was defined in the Abaqus/CAE software (2020, Simulia Dassault Systèmes, Vélizy-Villacoublay, France). Uniaxial tensile test data from a TPU 90A dog bone sample were included in the Abaqus material model to identify the best match between experimental behavior and the different strain energy potential models available in the software, in the strain range of interest. It was found that in the strain energy potential model, described by means of Equation (3), the best approximate value of the experimental nominal stress-strain trend is the second-order Ogden model (Figure 6).
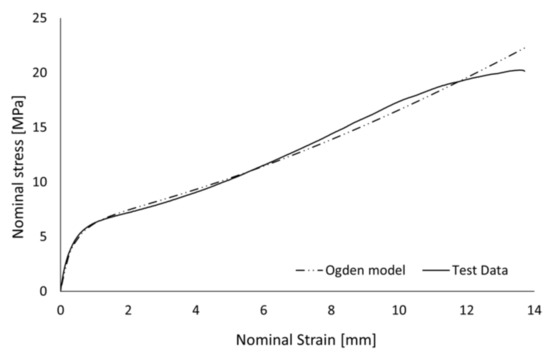
Figure 6.
The test data for the second-order Ogden model vs. dog bone sample.
The strain energy potential of Ogden form is expressed through the parameters , , , , which represent, respectively, the elastic volume ratio, the deviatoric principal stretches, and the temperature-dependent material parameters, illustrated in Table 2. Using the second-order Ogden model and a compression-release test performed on a cubic FDM TPU sample, the best hysteresis loop was reproduced by modifying the Abaqus hysteresis parameters until the loop that best approximates the real behavior was reached (Figure 7). Numerically, in fact, the hysteretic behavior is governed by the following formulation:
where the effective creep strain rate, and also the mechanical response, is described by means of two networks, A and B—network A identifies the equilibrium-relaxation part and network B, the non-linear one. In particular, for the term definitions of network B, represents the nominal creep strain, and σB is the effective stress. Table 3 shows the editable parameters in the Abaqus formulation for Equation (4), identified in the literature [29,30], and after an optimization procedure on cubic and cylindrical numerical models, S is the stress scaling factor, is an exponent usually bigger than , is an exponent that can assume values from to , and and are constants.

Table 2.
The parameters of the second-order Ogden model.
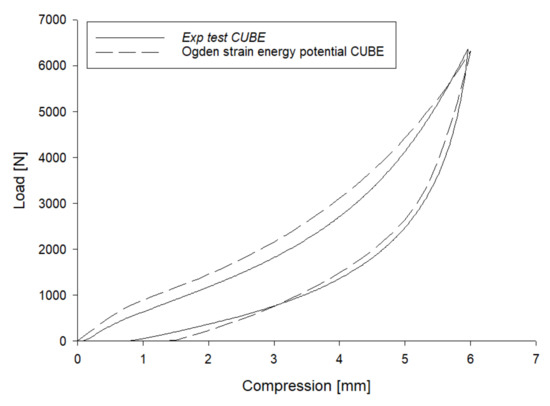
Figure 7.
Determination of the hysteresis cycle.

Table 3.
Abaqus hysteresis parameters.
Voids left in the structure by additive technique and layering effects also need to be considered and analyzed in depth in FE analysis. FDM, as previously mentioned, generates an anisotropic, layered structure. This was considered by defining a local orientation of the lattice structure. Material structure orientation was used in conjunction with a new material model, i.e., an anisotropic elastic material model with an “engineering constants” option, to compare the isotropic and anisotropic behaviors.
By means of the second-order Ogden model, the isotropic behavior was analyzed since the FE software considers structures as isotropic solid. Simulations were also performed for a linear elastic material, both for anisotropic and isotropic materials, to show the possible effects of anisotropy on the mechanical response of the samples.
A linear elastic anisotropic material model was then adopted, in order to tune and reproduce the experimental results. The engineering constants that define this model—namely, elastic modulus, Poisson ratio, and shear modulus, in three principal directions (Table 4) were arbitrarily chosen on the basis of literature data [31,32], imposing a level of anisotropy of 50%. Here, the direction of the applied load was set as the second direction, while the first and third directions were the axes that defined the layer plane. In this way, the intra-filament elasticity was halved, simulating the FDM layer deposition effect.

Table 4.
Engineering constants: Young’s modulus, Poisson ratio, and shear modulus in the three principal directions.
3.2. Simulations and Overviews
To simulate these tests in the Abaqus/CAE environment, the lattice structures were placed between two rigid analytical plates. The load was applied to the reference point of the upper plate by means of an imposed displacement (Figure 8). Three deformation levels were simulated for each geometrical configuration, which were, respectively, 10, 20, and 30% of specimens’ height, at the same strain rate of 5 mm/min.
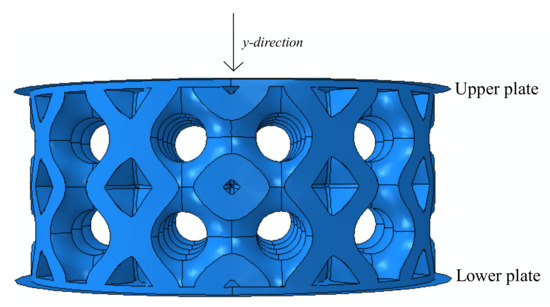
Figure 8.
Analytical rigid plates and preferential direction y.
After a variability analysis that did not show major effects in a range from 0.025 to 0.3, a friction coefficient equal to was defined between the contact surfaces. Finally, the lattice structure’s typologies were formed as meshed units with linear solid tetrahedral elements, using a hybrid formulation that governs incompressible behaviors. The average mesh size of lattice structure elements was chosen as 1.6 mm, to have a good compromise between computational times and accuracy of the mechanical response in the simulations. This was carried out after a mesh independency analysis on varying the average mesh size from 0.8 mm to 2.4 mm, which showed no noticeably major changes in the mechanical response of the structures (Figure 9). Table 5 shows the resulting numbers of nodes and elements for the three geometrical configurations of lattice structures.
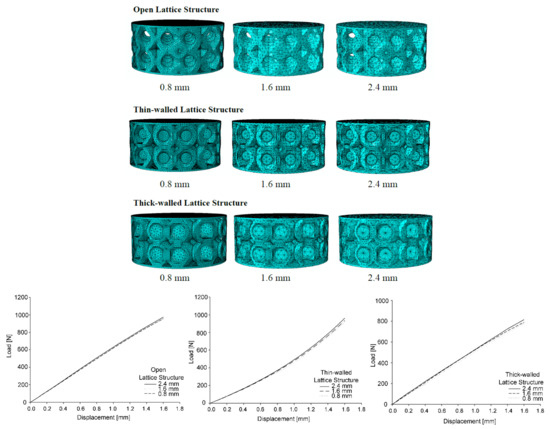
Figure 9.
Mesh independency analysis of lattice structures and convergence analysis.

Table 5.
Mesh of lattice structures: nodes and elements.
Load-displacement curves were obtained, as the reference point is affected by the sum of every single nodal response in the contact surface. From these curves, stiffness was calculated as the slope of the line that best fits the loading curve [33].
4. Results
All the obtained results, both experimental and numerical, are reported in Table 6. The nominal stress-strain curves in the range of interest, shown in Figure 10, were plotted through Equations (1) and (2), where the cross-sectional area of each typology of structures, , was calculated as follows:
where is the volume of lattice, and is the height of the specimen.

Table 6.
Specific stiffness of lattice structures.
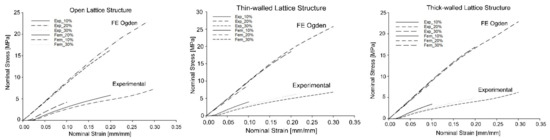
Figure 10.
Nominal stress-strain curves of lattice structures, experimental and numerical.
In accordance with the results shown in Table 6, the comparison between experimental and numerical nominal stress-strain curves highlighted a good reproduction of the real experimental trend by Ogden model simulations, even if a visible gap was apparent between them.
By plotting the stiffness results obtained for the hyperelastic model and experimental tests in a distinctive graph (Figure 11), it was revealed that the Ogden model is able to reproduce the exact trend of the experimental response of the lattice structures, but with a discrete gap. The same gap was also found between the isotropic and anisotropic linear elastic results (Figure 12). The linear elastic material model proved useful for identifying and studying the effects of 3D printing on the mechanical response of FDM printed parts.
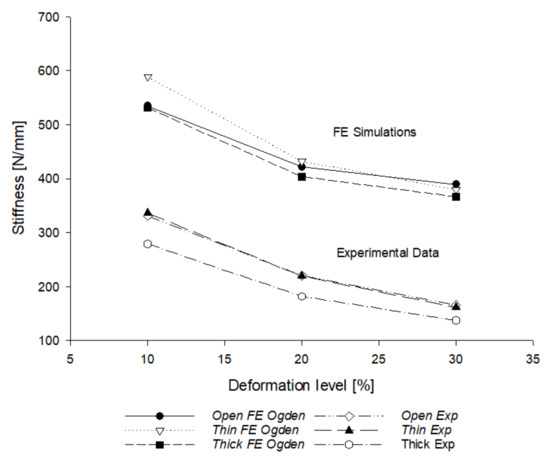
Figure 11.
FEM Ogden model vs. experimental results.
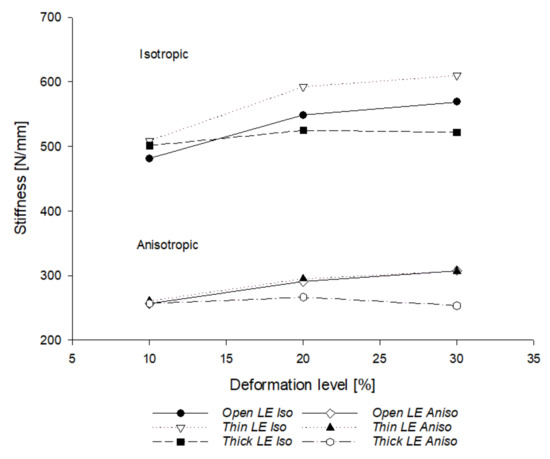
Figure 12.
FEM simulations with linear elastic material: isotropic vs. anisotropic.
The two graphs in Figure 11 and Figure 12 are similar; in fact, the simulation of the structures as isotropic cell solids showed a similar stiffness trend, but in the numerical results, it was double, compared to the anisotropic one. Therefore, the discrepancies between the experimental and numerical (by Ogden formulation) results are attributable to an anisotropic factor due to the printing process, i.e., to the various effects that occur in the printing phase. On the other hand, the simulations reflected the different mechanical responses of the three different geometrical configurations. For this reason, the aforementioned anisotropic layering factor is studied in depth in this discussion.
Geometrically, the graph in Figure 11 is able to highlight the lattice structure with the best mechanical response. In fact, in terms of stiffness, the thin-walled closed lattice structure showed the best performance, followed by the open typology, which showed a very similar mechanical response, especially in experimental tests. Finally, the thick-walled lattice structures showed a performance level always lower than the other two types, both numerically and experimentally.
Discrepancies in geometrical configurations response are certainly due to the effects of the FDM process [34]. In fact, as evident in Figure 2, the thick-walled structure had more deposited material in the walls, so it was more likely to have a high percentage of voids and layering effects inside. For this reason, it was desirable that these structures were weaker than the others, due to the greater and consistent presence of defects inside them.
5. Discussion
To understand the causes of discrepancies between experimental and numerical tests, all phenomena occurring in the printing process that influence the mechanical property of the FDM printed lattice structures were studied in depth. Several previous papers have found how FDM additive manufacturing technology widely affects the mechanical properties of printed parts [35,36]. FDM process is almost demanding due to the variability of its parameters and the uncontrollable printing effects such as porosity and layering.
Firstly, the porosity was studied both with SEM analysis and weight analysis. In their work, Abbot et al found that the simulated printed parts were at least 50% more solid than experimental printed samples [37]. This statement is in line with what was found in the present work, precisely shown in Figure 11, but it was found that this outcome is not due to the porosity of the FDM printed parts but to the layering effect that knocks down the mechanical properties of the additively manufacturing samples. In fact, SEM analysis on lattice structures conducted by Kumar et al. [38] revealed how the voids left by the FDM process have no major effects on the mechanical and functional properties of these structures. Moreover, through a weight analysis between real and virtual samples, no considerable differences in weight were found.
Finally, in the printing phase, there is another effect that is generated in the printed parts—the layering effect. It is extremely complex to simulate this phenomenon through a numerical model. For this reason, an anisotropic layering factor was identified, , which is able to describe how this effect acts on stiffness. Considering the similar precautions in the pre-printing phase (for example, care for the hygroscopicity of the TPU) and the same printing conditions for all the samples (i.e., the same process parameters on a unique batch and controllable boundary conditions), the focus was on the post-printing effects. In this way, all printed lattice structures were produced at the same time; hence, they had the same aging time, always showing comparable characteristics. Following a phenomenological approach, by defining as a function of geometry (i.e., number of wall’s contours, N) and imposed deformation , Equation (6) can be written as
where is a function of the number of contours N in a cell’s wall, equal to , is a constant equal to 0.02, and is the strain level in percentage (i.e., 10, 20 and 30%).
Firstly, the real trend of experimental curves was reproduced by means of a regression model with the R-squared coefficient of 0.98. Consequently, the parameters of Equation (6), α and β, were identified through an iterative process on varying the critical parameters that adversely affect stiffness, and ε. Finally, when the optimal match between curves was reached, was described as used in Equation (6).
The plot of Equation (6) reveals an increasing effect of the number of layers N on the deformation level (Figure 13). This is due to the fact that with the increase of deformation, the stresses acting on layers and printing defects increase, determining a drastic decrease in the stiffness.
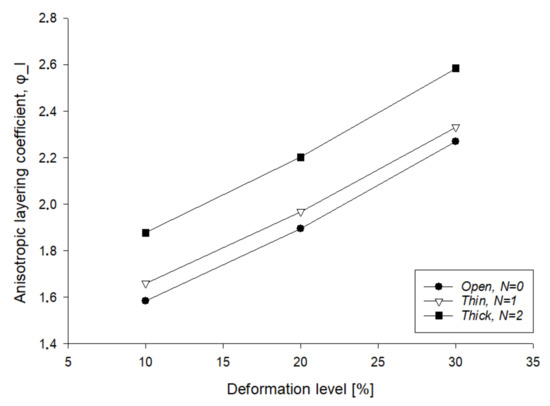
Figure 13.
Anisotropic layering factor trend for each configuration.
Now, after recalibration of the simulated curves obtained by the Ogden hyperelastic model by dividing the stiffness values by the factor, a very good agreement can be found with the experimental results, as presented in the plot of Figure 14 and more precisely in the bar plot of Figure 15.
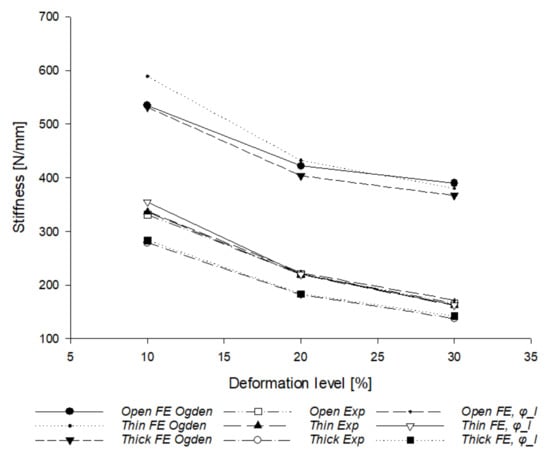
Figure 14.
Experimental results and FE simulation results with the Ogden model.
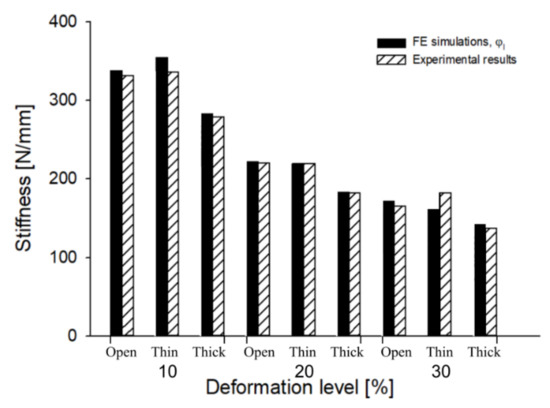
Figure 15.
Experimental results and FE simulations corrected with .
6. Conclusions
This study was conducted in order to analyze and understand the mechanical behavior of specimens of cellular structures obtained by additive deposition process fused in thermoplastic polyurethane. Particular attention was paid to the layer-by-layer deposition effect on the resulting stiffness, showing that the mechanical behavior of printed samples with this technology is not easily predictable. Major findings can be summarized as follows:
- By the traditional FE analysis, an anisotropic behavior of such structures was proven;
- Anisotropy was ascribed to the layering process of filament, not always quantifiable a priori;
- A phenomenological layering factor φl was defined that tries to correlate the number of FDM contours, the deformation level, with the anisotropy degree;
- On the basis of the layering factor, thin-walled cell structures were confirmed to be the less affected, whereas larger walled structures were negatively affected;
- The mechanical and functional behaviors of this kind of structure were confirmed to be influenced by many parameters, related to material and process, as well asa specific geometry.
Author Contributions
Conceptualization and methodology, writing—review and editing, L.C.; running of simulations, formal analysis, and data curation, writing—original draft preparation, C.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been possible thanks to the Overworld Mobility & Exchange Programme of the University of Parma.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available on request due to restrictions eg privacy or ethical.
Acknowledgments
Authors want to acknowledge Jeng and Kumar from the Department of Mechanical Engineering, National Taiwan University of Science and Technology, Taiwan, for providing experimental data and technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, P.; Zou, B.; Ding, S.; Li, L.; Huang, C. Effects of FDM-3D printing parameters on mechanical properties and microstructure of CF/PEEK and GF/PEEK. Chin. J. Aeronaut. 2021, 34, 236–246. [Google Scholar] [CrossRef]
- Ziemian, C.; Sharma, M.; Ziemian, S. Anisotropic mechanical properties of ABS parts fabricated by fused deposition modelling. In Mechanical Engineer; Gokcek, M., Ed.; InTech: London, UK, 2017; pp. 159–180. [Google Scholar]
- Durgun, I.; Ertan, R. Experimental investigation of FDM process for improvement of mechanical properties and production cost. Rapid Prot. J. 2014, 20, 228–235. [Google Scholar] [CrossRef]
- Pagac, M.; Schwarz, D.; Petru, J.; Polzer, S. 3D printed polyurethane exhibits isotropic elastic behavior despite its anisotropic surface. Rapid Prot. J. 2020, 26. [Google Scholar] [CrossRef]
- Garzon-Hernandez, S.; Garcia-Gonzalez, D.; Jérusalem, A.; Arias, A. Design of FDM 3D printed polymers: An experimental-modelling methodology for the prediction of mechanical properties. Mater. Des. 2020, 188, 108414. [Google Scholar] [CrossRef]
- Ahn, S.H.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic material properties of fused deposition modeling ABS. Rapid Prot. J. 2002, 8, 248–257. [Google Scholar] [CrossRef] [Green Version]
- Baich, L.; Manogharan, G.; Marie, H. Study of infill print parameters on mechanical strength and production cost-time of 3D printed ABS parts. Int. J. Rapid Manuf. 2015, 5, 308–319. [Google Scholar] [CrossRef]
- Bhate, D.; Penick, C.A.; Ferry, L.A.; Lee, C. Classification and selection of cellular materials in mechanical design: Engineering and biomimetic approaches. Designs 2019, 3, 19. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Verma, S.; Jeng, J.-Y. Supportless Lattice structures for energy absorption fabricated by fused deposition modeling. 3D Print. Add. Manuf. 2020, 7, 85–96. [Google Scholar] [CrossRef]
- Askari, M.; Hutchins, D.A.; Thomas, P.J.L.; Astolfi, R.L.; Watson, M.; Abdi, M.; Ricci, S.; Laureti, L.; Nie, S.; Freear, R.; et al. Additive manufacturing of metamaterials: A. review. Add. Manuf. 2020, 36, 101562. [Google Scholar] [CrossRef]
- Nazir, A.; Abate, K.M.; Kumar, A.; Jeng, J.-Y. A state-of-the-art review on types, design, optimization, and additive manufacturing of cellular structures. Int. J. Adv. Manuf. Technol. 2019, 104, 3489–3510. [Google Scholar] [CrossRef]
- Bartolomé, L.; Aginagalde, A.; Martínez, A.B.; Urchegui, M.A.; Tato, W. Experimental characterization and modelling of large-strain viscoelastic behavior of a thermoplastic polyurethane elastomer. Rubber Chem. Technol. 2013, 86, 146–164. [Google Scholar] [CrossRef]
- Solomon, I.J.; Sevvel, P.; Gunasekaran, J. A review on the various processing parameters in FDM. Mater. Today Proc. 2021, 37, 509–514. [Google Scholar] [CrossRef]
- Panda, B.; Leite, M.; Biswal, B.B.; Niu, X.; Garg, A. Experimental and numerical modelling of mechanical properties of 3D printed honeycomb structures. Measurement 2018, 116, 495–506. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Experimental investigation and empirical modeling of FDM process for compressive strength improvement. J. Adv. Res. 2012, 3, 81–90. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Geng, P.; Li, G.; Zhao, D.; Zhang, H.; Zhao, J. Influence of layer thickness and raster angle on the mechanical study between PEEK and ABS. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef]
- Hernandez, R.; Slaughter, D.; Whaley, D.; Tate, J.; Asiabanpuor, B. Analyzing the tensile, compressive, and flexural properties of 3D printed ABS parts. In Proceedings of the 27th Annual International Solid Freeform Fabrication Symposium, San Marcos, TX, USA, 8–10 August 2016; pp. 939–950. [Google Scholar]
- Motaparti, K.P. Effect of Build Parameters on Mechanical Properties of Ultem 9085 Parts by Fused Deposition Modeling. Masters’ Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2016. [Google Scholar]
- Vega, V.; Clements, J.; Lam, T.; Abad, A.; Fritz, B.; Ula, N.; Es-Said, O.S. The effect of layer orientation on the mechanical properties and microstructure of a polymer. J. Mater. Eng. Perform. 2011, 20, 978–988. [Google Scholar] [CrossRef]
- Mohaed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of FDM process parameters: A review of current research and future prospects. Adv. Manuf. 2015, 3, 42–52. [Google Scholar] [CrossRef]
- Torrado, A.R.; Shemelya, C.M.; English, J.D.; Lin, Y.; Wicker, R.B.; Roberson, D.A. Characterizing the effect of additives to ABS on the echanical property anisotropy of specimens fabricated by material extrusion 3D printing. Add. Manuf. 2015, 6, 16–29. [Google Scholar]
- Dawoud, M.; Taha, I.; Ebeid, S.J. Mechanical behaviour of ABS: An experimental study using FDM and injection moulding techniques. J. Manuf. Process. 2016, 21, 39–45. [Google Scholar] [CrossRef]
- Hmeidat, N.S.; Pack, R.C.; Talley, S.J.; Moore, R.B.; Compton, B.G. Mechanical anisotropy in polymer composites produced by material extrusion additive manufacturing. Add. Manuf. 2020, 34, 101385. [Google Scholar] [CrossRef]
- Rybachuk, M.; Mauger, C.A.; Fiedler, T.; Öchsner, A. Ochsner, Anisotropic mechanical properties of fused deposition modeled parts fabricated by using acrylonitrile butadiene styrene polymer. J. Polym. Eng. 2017, 37, 699–706. [Google Scholar] [CrossRef]
- Anitha, R.; Arunachalam, S.; Radhakrishnan, P. Critical parameters influencing the quality of prototypes in fused deposition modelling. J. Mater. Proc. Technol. 2001, 118, 385–388. [Google Scholar] [CrossRef]
- Rodríguez-Panes, A.; Claver, J.; Camacho, A.M. The influence of Manufacturing parameters on the mechanical behaviour of PLA and ABS pieces manufactured by FDM: A comparative analysis. Materials 2018, 11, 1333. [Google Scholar] [CrossRef] [Green Version]
- Lee, B.; Abdullah, J.; Khan, Z. Optimization of rapid prototyping parameters for production of flexible ABS object. J. Mater. Proc. Technol. 2005, 169, 54–61. [Google Scholar] [CrossRef]
- Popescu, D.; Zapciu, A.; Amza, C.; Baciu, F.; Marinescu, R. FDM process parameters influence over the mechanical properties of polymer specimens: A. review. Polym. Test. 2018, 69, 157–166. [Google Scholar] [CrossRef]
- Qi, H.; Boyce, M. Stress-strain behavior of thermoplastic polyurethanes. Mech. Mater. 2005, 37, 817–839. [Google Scholar] [CrossRef]
- Bergström, J.; Boyce, M. Constitutive modeling of the time-dependent and cyclic loading of elastomers and application to soft biological tissues. Mech. Mater. 2001, 33, 523–530. [Google Scholar] [CrossRef]
- Hohimer, C.; Christ, J.; Aliheidari, N.; Mo, C.; Ameli, A. 3D printed thermoplastic polyurethane with isotropic material properties. In Behavior and Mechanics of Multifunctional Materials and Composites; SPIE: Bellingham, WA, USA, 2017; Article Number 1016511. [Google Scholar]
- Elmrabet, N.; Siegkas, P. Dimensional consideration on the mechanical properties of 3D printed polymer parts. Polym. Test. 2020, 90, 106656. [Google Scholar] [CrossRef]
- Kumar, A.; Collini, L.; Daurel, A.; Jeng, J.-Y. Design and additive manufacturing of closed cells from supportless lattice structure. Add. Manuf. 2020, 33, 101168. [Google Scholar] [CrossRef]
- Collini, L.; Ursini, C.; Kumar, A. Design and optimization of 3D fast printed cellular structures. Mater. Des. Proc. Commun. 2021, e227. [Google Scholar] [CrossRef]
- Cantrell, J.T.; Rohde, S.; Damiani, D.; Gurmani, R.; DiSandro, L.; Anton, J.; Young, A.; Jerez, A.; Steinbach, D.; Kroese, C.; et al. Experimental characterization of the mechanical properties of 3D-printed ABS and polycarbonate parts. In Advancement of Optical Methods in Experimental Mechanics; Yoshida, S., Lamberti, L., Sciammarella, C., Eds.; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2016; Volume 3. [Google Scholar]
- Zou, R.; Xia, Y.; Liu, S.; Hu, P.; Hou, W.; Hu, Q.; Shan, C. Isotropic and anisotropic elasticity and yielding of 3D printed material. Comp. Part B Eng. 2016, 99, 506–513. [Google Scholar] [CrossRef]
- Abbot, D.; Kallon, D.; Anghel, C.; Dube, P. Finite Element analysis of 3D printed model via compression tests. Procedia Manuf. 2019, 35, 164–173. [Google Scholar] [CrossRef]
- Kumar, A.; Collini, L.; Ursini, C.; Jeng, J.-Y. Analyzing the functional properties of closed cell cellular lattice structure designed with thin and thick wall for additive manufacturing. Mater. Des. 2021, submitted. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).