A Novel Design Method for Energy Absorption Property of Chiral Mechanical Metamaterials
Abstract
:1. Introduction
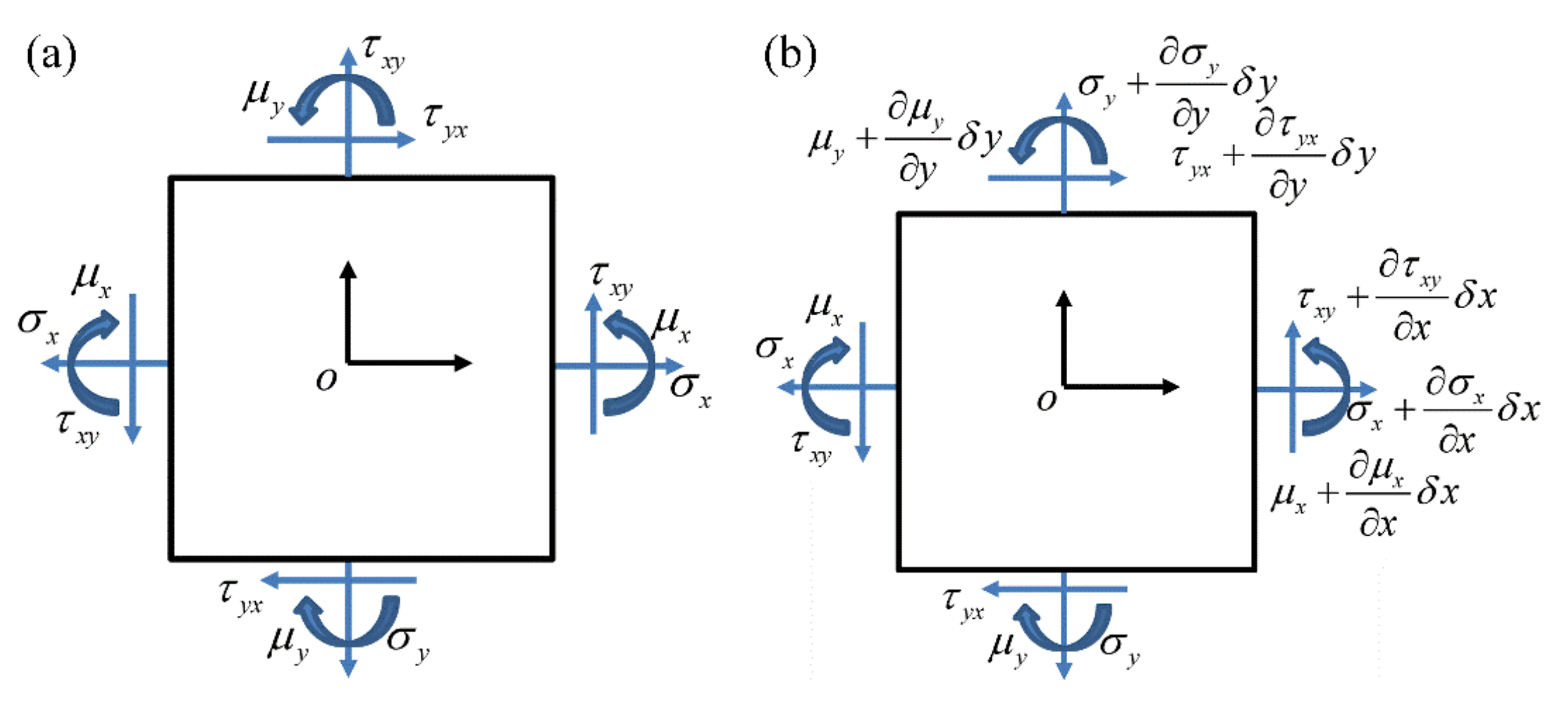
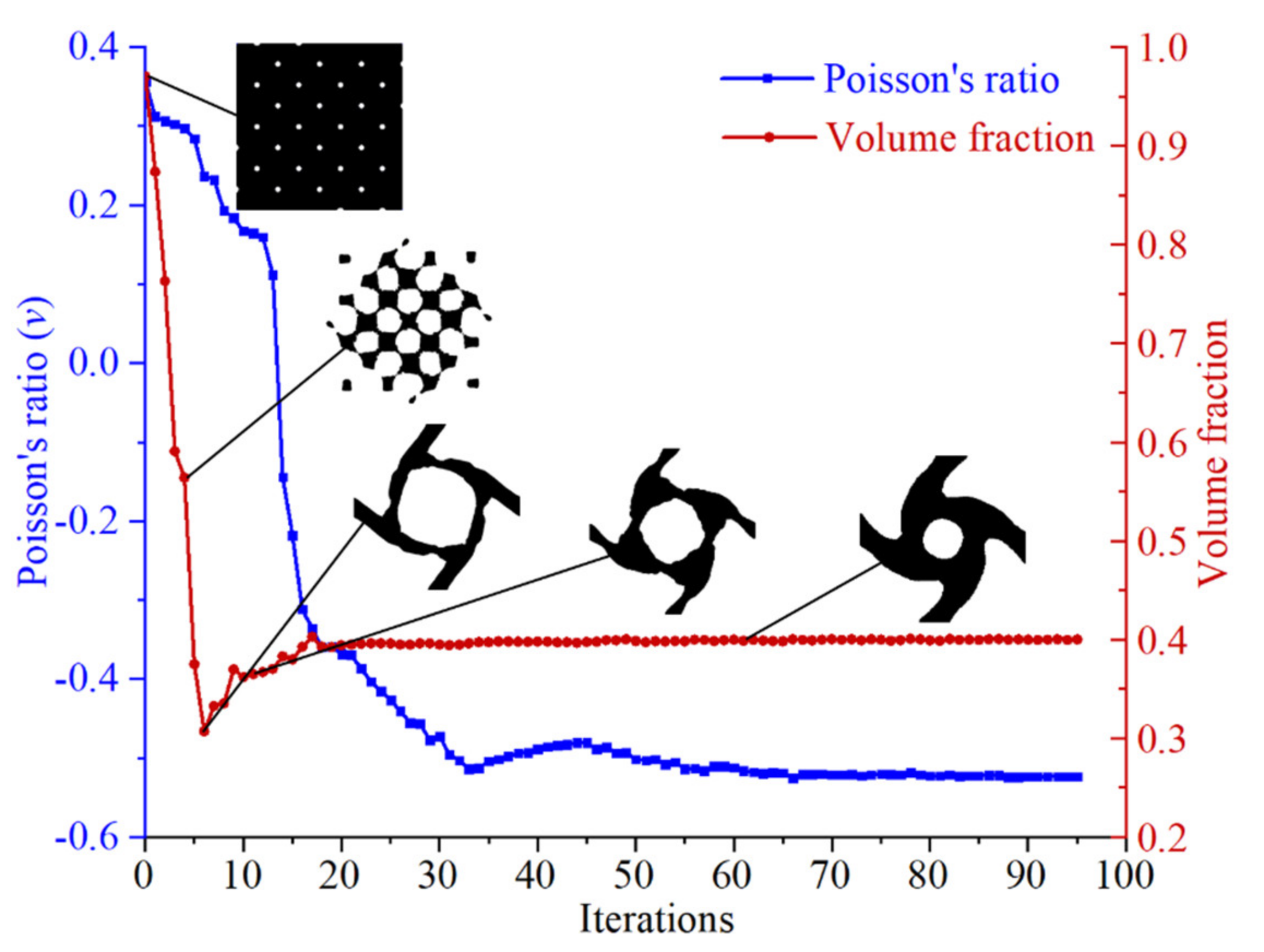
2. Topology Optimization of the Rotating Properties
3. Parametric Optimization of Chiral Metamaterials
3.1. Parametric Modeling
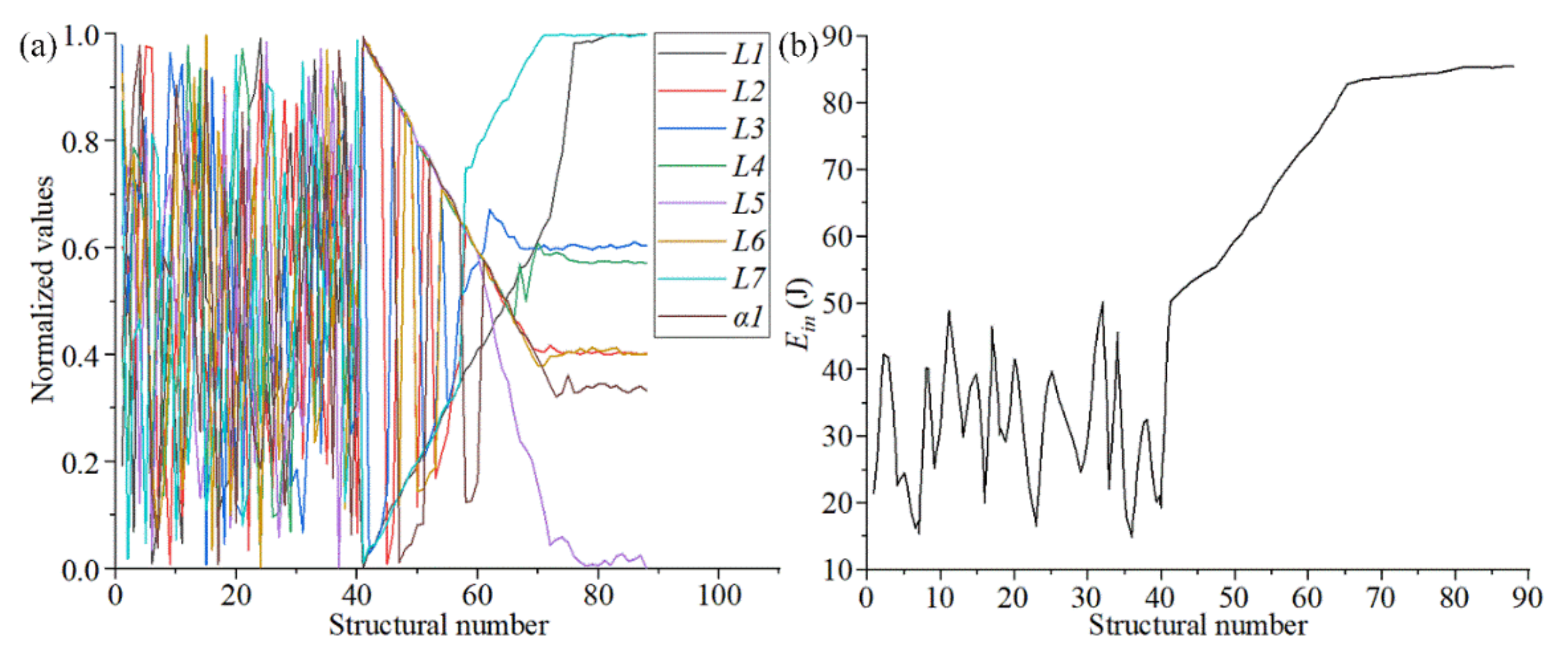
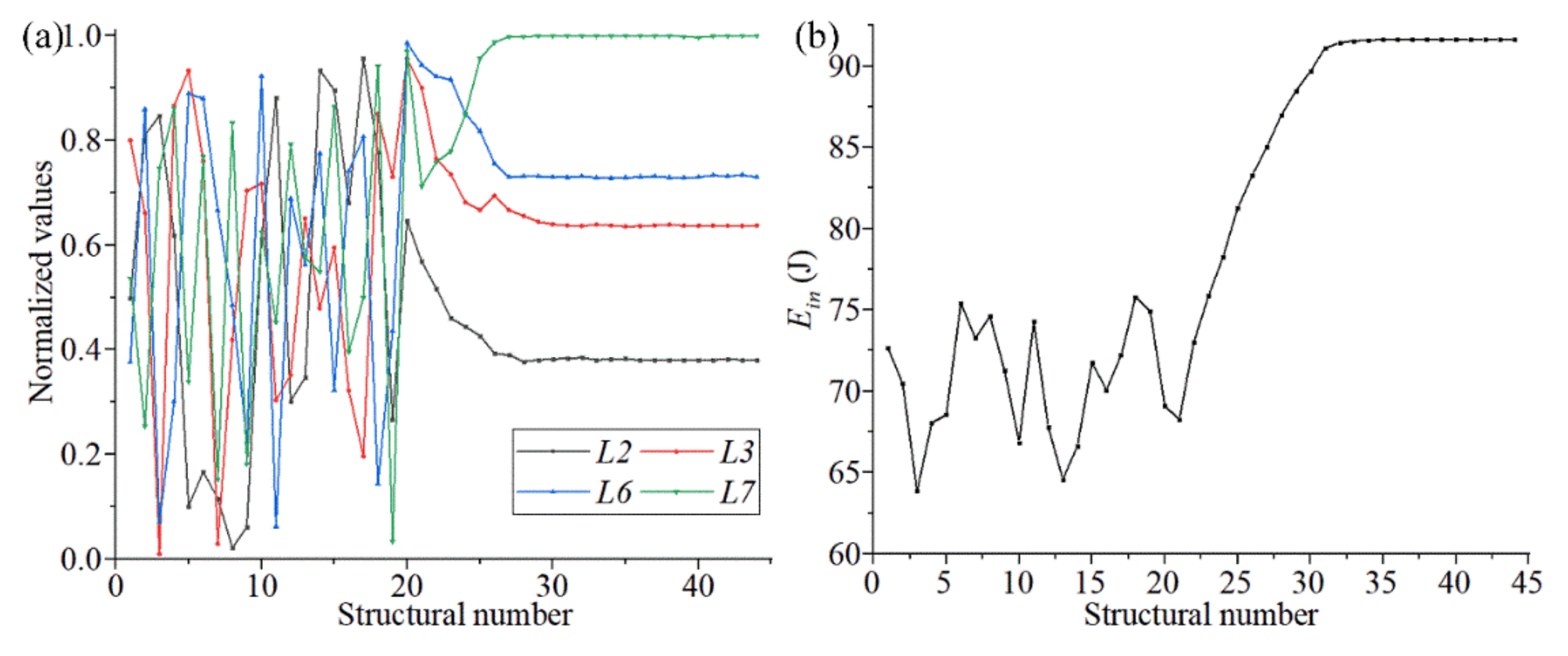
3.2. Parametric Optimization Based on a Surrogate Model
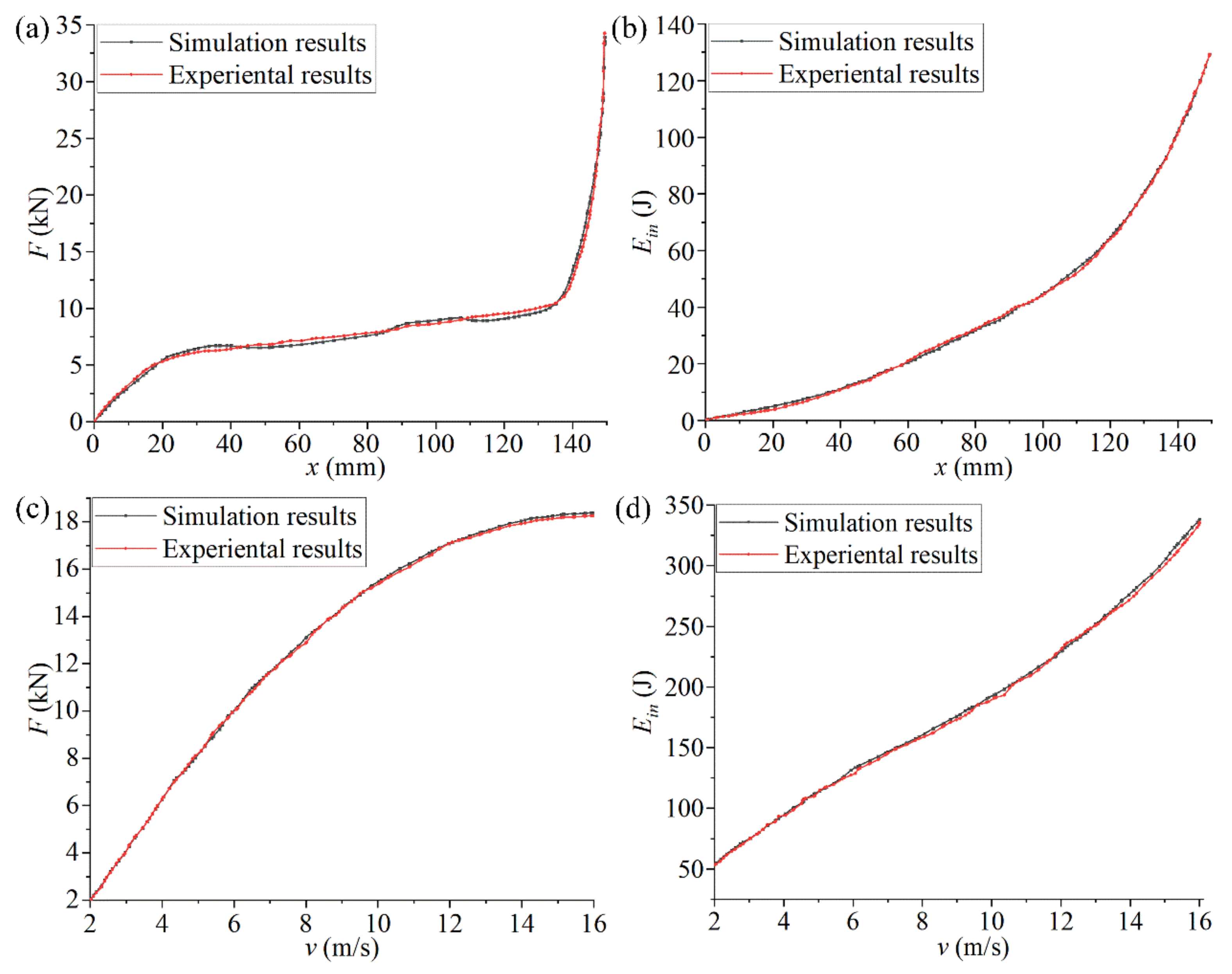
3.3. Analysis of the Parametric Optimization Results
- 1.
- The surge state of the initial compression reaction force is the change in stress caused by the impact load on the chiral structure. At this stage, the compression displacement produced by the structural deformation lags behind the compression reaction force, which leads to a sharp increase in the compression reaction force in the initial stage. The final surge state of the compression reaction force is the stage when the walls of solid holes in the chiral structure are in full contact. At this stage, the structural deformation is very small, the external force is close to lossless transmission, and the slight increase in compression displacement causes the compression load to rise sharply. The slow increase in the compression reaction force is the effective stage of the chiral structure. Due to the rotational deformation of the chiral structure, the stress generated by compression of the partial structures will be consumed and transferred. The macroscopic expression is the slow increase in the compression reaction force.
- 2.
- As the impact velocity increases, the compression reaction force corresponding to the same compression displacement increases, the compression reaction force leads to increased growth in the slow increase phase, and the compression displacement corresponding to the final surge state of the compression reaction force increases. This is because the greater the impact speed, the lower the efficiency of internal stress consumption and transfer through structural rotation deformation. The macroscopic manifestation is an increase in the compression reaction force and its related state.
- 1.
- As the compression displacement continues to increase, the energy absorbed by the chiral structure and its acceleration continues to increase. If we compare the energy absorption curves of chiral metamaterials at different impact speeds, it can be found that the energy absorbed by the chiral structure under the same compression displacement increases with an increase in the impact speed. The energy absorption efficiency of the chiral structure is highest in the middle of the compression displacement (80–140 mm).
- 2.
- Chiral metamaterials under high-speed impact will enter the nonlinear deformation stage more quickly, and the proportion of this stage is larger. These phenomena show that it is necessary to pre-select the appropriate impact velocity to make full use of the energy absorption properties of chiral structures. The safety interval of the chiral structure can be set, and its utilization efficiency can be improved according to this phenomenon.
- 1.
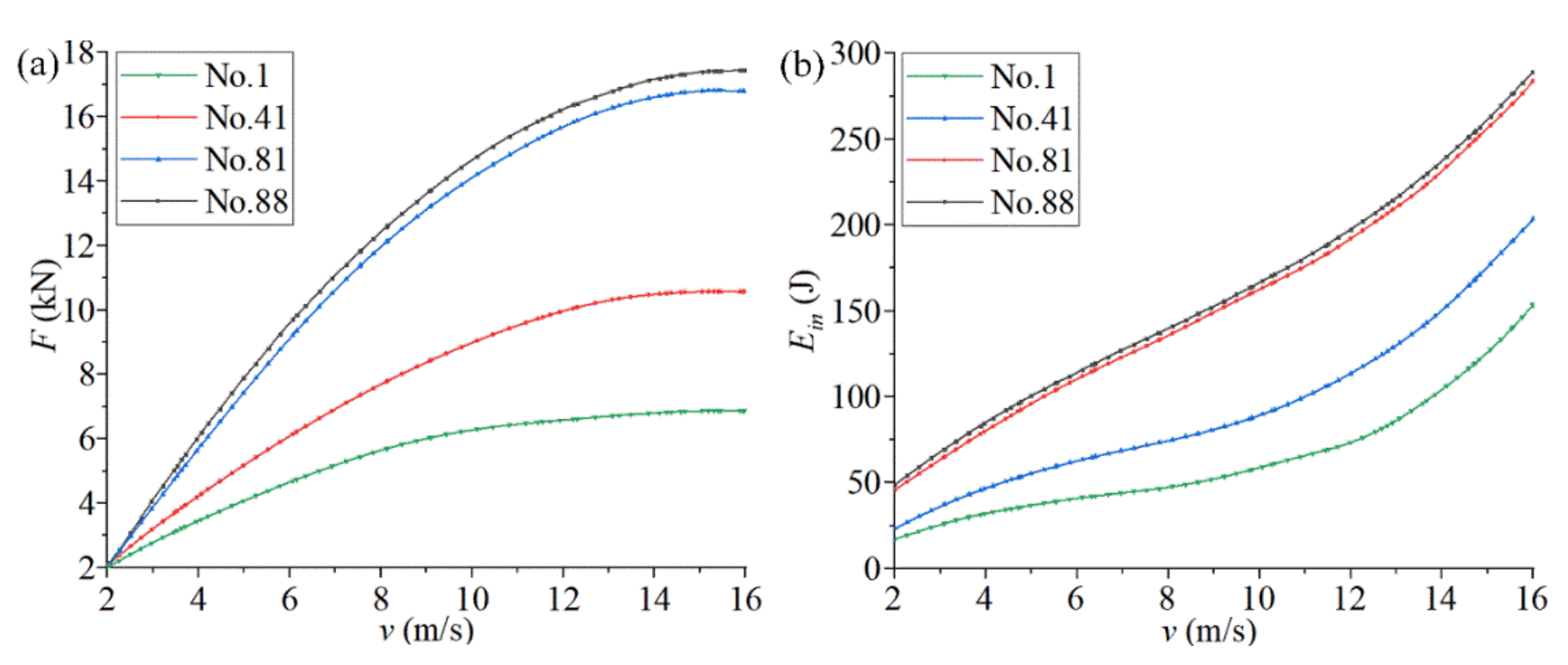
- For the optimized chiral metamaterials, the compression reaction force F and the absorbed energy Ein under the same impact velocity were greatly improved. This indicates the effectiveness of parametric optimization for improving the mechanical properties of chiral metamaterials.
- 2.
- For any chiral metamaterial structure in the parametric optimization, the compression reaction force F and the absorbed energy Ein increase continuously when the impact velocity increases. However, the growth rate of the compression reaction force F gradually decreases to zero, and the growth rate of the absorbed energy Ein continues to increase. These indicate that chiral metamaterials have a specific impact velocity range. The energy absorption properties of the chiral metamaterials can be maximized within a suitable range. If the application range is exceeded, the structure will fail, and thus, the energy absorption properties of the chiral metamaterials will be greatly reduced.
4. Experimental Analysis of Impact Compression
4.1. Specimen Manufacturing and Experimental Design
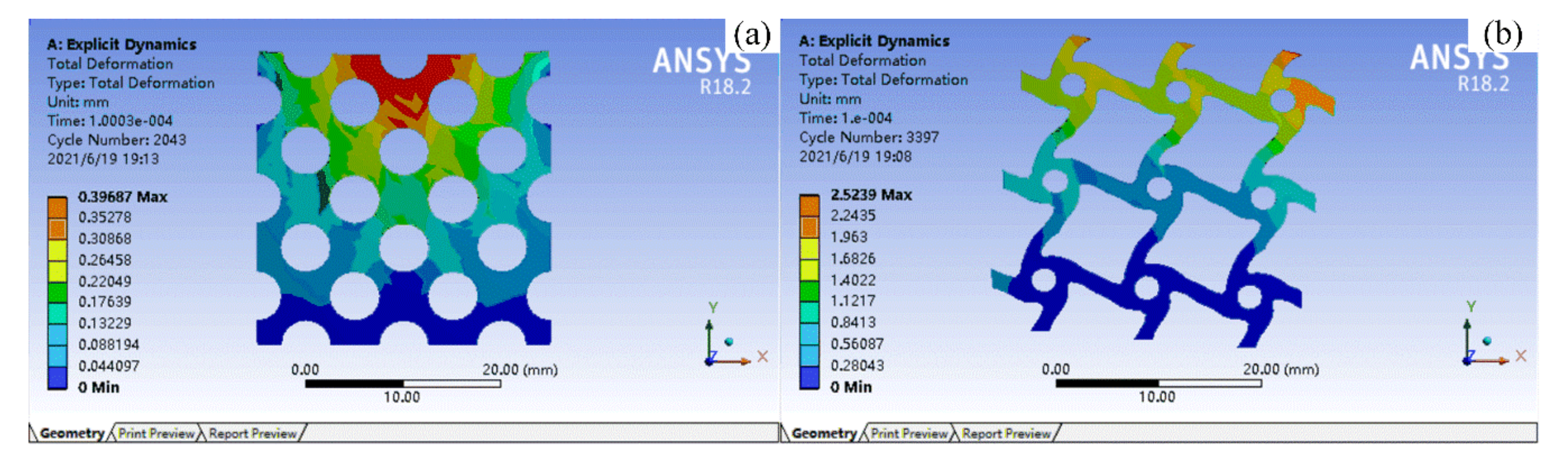
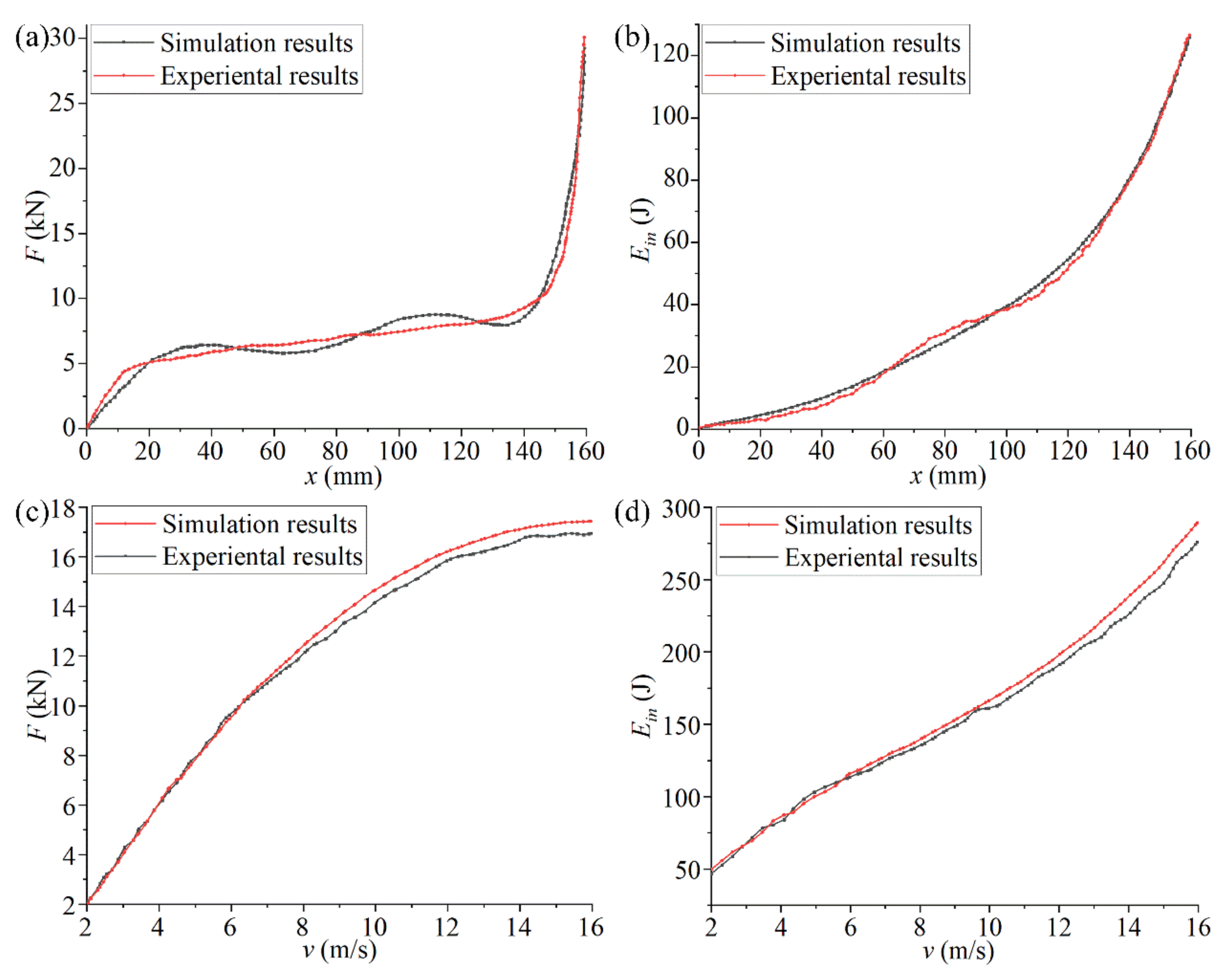
4.2. Impact Compression Experiment
4.3. Feedback Adjustment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, L.; Yang, J. Progresses in the Study on Vibration Damping Properties of Novel Lightweight Composite Sandwich Structures. Appl. Math. Mech. 2017, 38, 369–398. [Google Scholar]
- Koch, S.; Duvigneau, F.; Orszulik, R.; Gabbert, U.; Woschke, E. Partial filling of a honeycomb structure by granular materials for vibration and noise reduction. J. Sound Vib. 2017, 393, 30–40. [Google Scholar] [CrossRef]
- Haberman, M.R.; Seepersad, C.C.; Wilson, P.S. Vibration damping and isolation using negative stiffness structures. J. Acoust. Soc. Am. 2015, 138, 1920. [Google Scholar] [CrossRef]
- Wang, F. Systematic design of 3D auxetic lattice materials with programmable Poisson’s ratio for finite strains. J. Mech. Phys. Solids 2018, 114, 303–318. [Google Scholar] [CrossRef] [Green Version]
- Hou, X.; Yin, G. Dynamic Crushing Performance Analysis for Auxetic Honeycomb Structure. J. Mech. Strength 2016, 38, 905–910. [Google Scholar]
- Li, S.; Jiang, S.; Wang, Y.; Gu, J.; Xing, L. Study on “Metamaterial” Structural Absorbing Composite Technology. J. Mater. Eng. 2017, 45, 10–14. [Google Scholar]
- Mousanezhad, D.; Haghpanah, B.; Ghosh, R.; Hamouda, A.M.; Nayeb-Hashemi, H.; Vaziri, A. Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: A simple energy-based approach. Theor. Appl. Mech. Lett. 2016, 6, 81–96. [Google Scholar] [CrossRef] [Green Version]
- Tancogne-Dejean, T.; Karathanasopoulos, N.; Mohr, D. Stiffness and Strength of Hexachiral Honeycomb-Like Metamaterials. J. Appl. Mech. 2019, 86, 1–38. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Lepidi, M.; Gnecco, G.; Vadalà, F.; Gambarotta, L. Optimal Design of the Band Structure for Beam Lattice Metamaterials. Front. Mater. 2019, 6, 1–14. [Google Scholar] [CrossRef]
- Li, H.; Luo, Z.; Zhang, N.; Gao, L.; Brown, T. Integrated design of cellular composites using a level-set topology optimization method. Comput. Methods Appl. Mech. Eng. 2016, 309, 453–475. [Google Scholar] [CrossRef]
- Fu, J.; Li, H.; Xiao, M.; Gao, L.; Chu, S. Topology optimization of shell-infill structures using a distance regularized parametric level-set method. Struct. Multidiscip. Optim. 2019, 59, 249–262. [Google Scholar] [CrossRef]
- Kim, S.; Yun, G.J. Microstructure topology optimization by targeting prescribed nonlinear stress-strain relationships. Int. J. Plast. 2020, 128, 102684. [Google Scholar] [CrossRef]
- Behrou, R.; Ghanem, M.A.; Macnider, B.C.; Verma, V.; Alvey, R.; Hong, J.; Emery, A.F.; Kim, H.A.; Boechler, N. Topology optimization of nonlinear periodically microstructured materials for tailored homogenized constitutive properties. Compos. Struct. 2021, 266, 113729. [Google Scholar] [CrossRef]
- Hou, S. Optimization Design of the Thin-Walled Components with Crashworthiness Criterion; Hunan University: Changsha, China, 2007. [Google Scholar]
- Xu, Y. A Non-Dominated Sorting Differential Evolution Algorithm Assisted with Dynamic Surrogate Models; Huazhong University of Science and Technology: Wuhan, China, 2016. [Google Scholar]
- Cai, X.; Qiu, H.; Gao, L.; Wei, L.; Shao, X. Adaptive Radial-Basis-Function-Based Multifidelity Metamodeling for Expensive Black-Box Problems. AIAA J. 2017, 55, 2424–2436. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Y.; Wang, S. Kriging-Based Sequence Global Optimization Method for Multiple Sampling Points. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2015, 43, 12–16. [Google Scholar]
- Chyi-Yeu, L.; Shin-Hong, L. Artificial Neural Network Based Hole Image Interpretation Techniques for Integrated Topology and Shape Optimization. Comput. Methods Appl. Mech. Eng. 2005, 194, 3817–3837. [Google Scholar]
- Cho, C.-S.; Choi, E.-H.; Cho, J.-R.; Lim, O.-K. Topology and parameter optimization of a foaming jig reinforcement structure by the response surface method. Comput. Des. 2011, 43, 1707–1716. [Google Scholar] [CrossRef]
- Stansbury, J.W.; Idacavage, M.J. 3D printing with polymers: Challenges among expanding options and opportunities. Dent. Mater. 2016, 32, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Liu, R. Research Development of 3D Printing for Large Complex Metal Parts. Ordnance Ind. Autom. 2017, 36, 8–12. [Google Scholar]
- Gao, L.; Song, J.; Jiao, Z.B.; Liao, W.; Luan, J.; Surjadi, J.U.; Li, J.; Zhang, H.; Sun, D.; Liu, C.T.; et al. High-Entropy Alloy (HEA)-Coated Nanolattice Structures and Their Mechanical Properties. Adv. Eng. Mater. 2018, 20, 1700625. [Google Scholar] [CrossRef]
- Sun, P. Research on Structural Finite Element Method and Their Application Based on the Couple Stress Theory; Changsha University of Science and Technology: Changsha, China, 2013. [Google Scholar]
- Zhang, B. Finite Element Method Based on Couple Stress Theory; Shandong University: Jinan, China, 2006. [Google Scholar]
- Chen, W.; Huang, X. Topological design of 3D chiral metamaterials based on couple-stress homogenization. J. Mech. Phys. Solids 2019, 131, 372–386. [Google Scholar] [CrossRef]
- Duan, S.; Wen, W.; Fang, D. A predictive micropolar continuum model for a novel three-dimensional chiral lattice with size effect and tension-twist coupling behavior. J. Mech. Phys. Solids 2018, 121, 23–46. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, X.; Zhang, Q. ANSYS Nonlinear Finite Element Analysis Method and Example Application; China Water and Power Press: Beijing, China, 2013. [Google Scholar]
- Zhu, B.; Chen, Q.; Wang, R.; Zhang, X. Structural Topology Optimization Using a Moving Morphable Component-Based Method Considering Geometrical Nonlinearity. J. Mech. Des. 2018, 140, 081403. [Google Scholar] [CrossRef]
- Belytschko, T.; Liu, W.K.; Moran, B.; Elkhodary, K. Nonlinear Finite Elements for Continua and Structures; John Wiley & Sons Ltd.: Chichester, UK, 2014. [Google Scholar]
- Qiu, X.; Guo, T.; Huang, K.; Hwang, K. FEM solutions for plane stress mode-I and mode-II cracks in strain gradient plasticity. Sci. China Ser. A Math. 2000, 43, 969–979. [Google Scholar] [CrossRef]
- Li, H.; Gao, L.; Li, H.; Li, X.; Tong, H. Full-scale topology optimization for fiber-reinforced structures with continuous fiber paths. Comput. Methods Appl. Mech. Eng. 2021, 377, 113668. [Google Scholar] [CrossRef]
- Li, H.; Luo, Z.; Gao, L.; Walker, P. Topology optimization for functionally graded cellular composites with metamaterials by level sets. Comput. Methods Appl. Mech. Eng. 2018, 328, 340–364. [Google Scholar] [CrossRef] [Green Version]
- Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. Acoustic performance of periodic steel cylinders embedded in a viscoelastic medium. J. Sound Vib. 2018, 443, 652–665. [Google Scholar] [CrossRef]
- Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. Sound absorption by rubber coatings with periodic voids and hard inclusions. Appl. Acoust. 2019, 143, 200–210. [Google Scholar] [CrossRef]
- Sharma, G.S.; Faverjon, B.; Dureisseix, D.; Skvortsov, A.; MacGillivray, I.; Audoly, C.; Kessissoglou, N. Acoustic Performance of a Periodically Voided Viscoelastic Medium with Uncertainty in Design Parameters. J. Vib. Acoust. 2020, 142, 1–23. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Xiao, M.; Zhang, Y.; Fu, J.; Gao, L. Robust topology optimization of thermoelastic metamaterials considering hybrid uncertainties of material property. Compos. Struct. 2020, 248, 112477. [Google Scholar] [CrossRef]
- Berger, P.D.; Maurer, R.E.; Celli, G.B. Introduction to Response-Surface Methodology; Springer: Cham, Switzerland, 2018. [Google Scholar]
- White, H. Learning in Artificial Neural Networks: A Statistical Perspective. Neural Comput. 1989, 1, 425–464. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Mu, X.; Yao, W.; Yu, X.; Liu, K.; Xue, F. A Survey of Surrogate Models used in MDO. Chin. J. Comput. Mech. 2005, 22, 100–104. [Google Scholar]
- Yu, X.; Zhang, L.; Li, C.; Li, Z.; Liu, W. Applying Kriging Model for Global Design Optimization. Chin. J. Constr. Mach. 2006, 4, 259–261. [Google Scholar]
- Ye, M.; Li, H.; Cai, X.; Gao, L.; Zhang, A.; Zhao, Z. Progressive design of gradually stiffer metamaterial using surrogate model. Compos. Struct. 2021, 264, 113715. [Google Scholar] [CrossRef]
- Lai, C.; Yan, C.; Ren, B.; Lv, B.; Zhou, Y. Optimization of Vehicle Aerodynamic Drag Based on EGO. In Proceedings of the International Conference on Mechatronics and Intelligent Robotics, Kunming, China, 19–20 May 2018. [Google Scholar]
- Zhou, Y.; Zhang, J.; Cheng, G. Comparison of Two Global Optimization Algorithms based on Kriging Surrogate Model. Chin. J. Comput. Mech. 2015, 32, 451–456. [Google Scholar]
- Garcia, C.R.; Correa, J.; Espalin, D.; Barton, J.H.; Rumpf, R.C.; Wicker, R.; Gonzalez, V. 3D printing of anisotropic metamaterials. Prog. Electromagn. Res. Lett. 2012, 34, 75–82. [Google Scholar] [CrossRef] [Green Version]
- Bodaghi, M.; Damanpack, A.; Hu, G.; Liao, W. Large deformations of soft metamaterials fabricated by 3D printing. Mater. Des. 2017, 131, 81–91. [Google Scholar] [CrossRef]
- Su, J.; Wu, J.; Liu, Y. Progress in Elastic Property and Impact Resistance of Honeycomb Structure Mechanical Metamaterials. J. Mater. Eng. 2019, 47, 49–58. [Google Scholar]
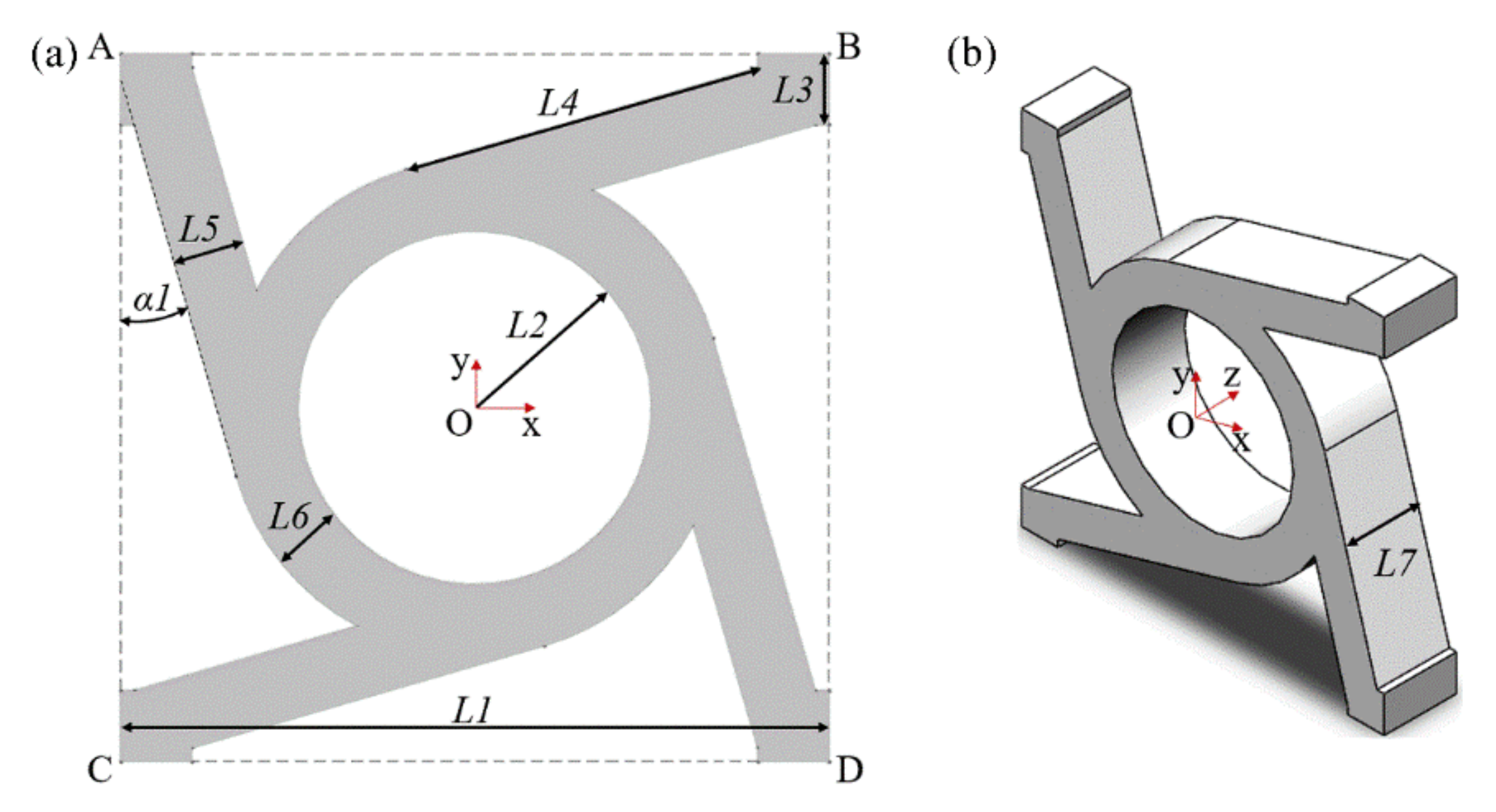








| Type | Structural Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | L5 | L6 | L7 | α1 | |
| Range (mm/°) | 80–100 | 20–35 | 5–15 | 45–60 | 10–20 | 10–20 | 20–40 | 15–20 |
| Type | Property Parameters | ||||
|---|---|---|---|---|---|
| Density | |||||
| Value | 0.3 | ||||
| Type | Structural Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | L5 | L6 | L7 | ||
| Value (mm/°) | 100 | 23 | 11 | 52 | 10 | 12 | 40 | 16 |
| Type | Structures | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial Structure | Optimized Structures | Optimal Structure | |||||||||
| 1 | 41 | 46 | 51 | 56 | 61 | 66 | 71 | 76 | 81 | 88 | |
| Number | A | B | C | D | E | F | G | H | I | J | K |
| Type | Structural Parameters | |||
|---|---|---|---|---|
| L2 | L3 | L6 | L7 | |
| Ranges (mm/°) | 18.4–27.6 | 8.8–13.2 | 9.6–14.4 | 32–40 |
| Results (mm/°) | 21.9 | 11.6 | 13.1 | 40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, M.; Gao, L.; Wang, F.; Li, H. A Novel Design Method for Energy Absorption Property of Chiral Mechanical Metamaterials. Materials 2021, 14, 5386. https://doi.org/10.3390/ma14185386
Ye M, Gao L, Wang F, Li H. A Novel Design Method for Energy Absorption Property of Chiral Mechanical Metamaterials. Materials. 2021; 14(18):5386. https://doi.org/10.3390/ma14185386
Chicago/Turabian StyleYe, Mengli, Liang Gao, Fuyu Wang, and Hao Li. 2021. "A Novel Design Method for Energy Absorption Property of Chiral Mechanical Metamaterials" Materials 14, no. 18: 5386. https://doi.org/10.3390/ma14185386
APA StyleYe, M., Gao, L., Wang, F., & Li, H. (2021). A Novel Design Method for Energy Absorption Property of Chiral Mechanical Metamaterials. Materials, 14(18), 5386. https://doi.org/10.3390/ma14185386







