Modeling Bioinspired Fish Scale Designs via a Geometric and Numerical Approach
Abstract
:1. Introduction
2. Methods
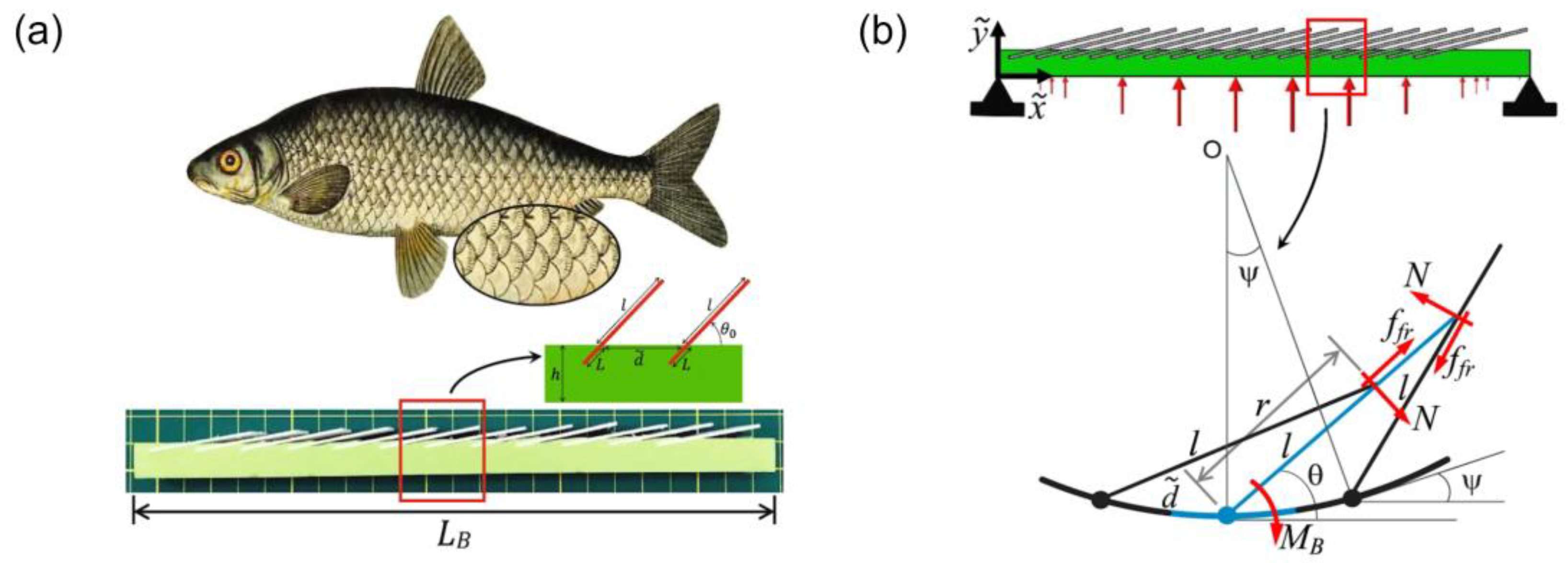
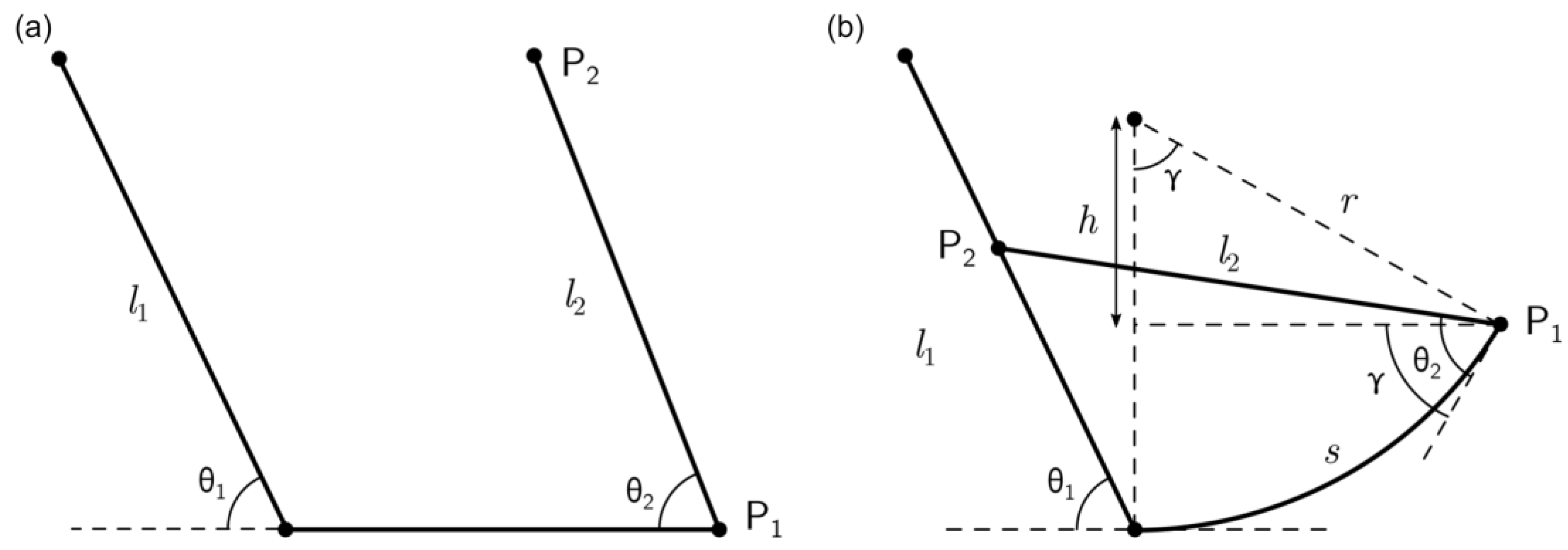
2.1. Geometric Model
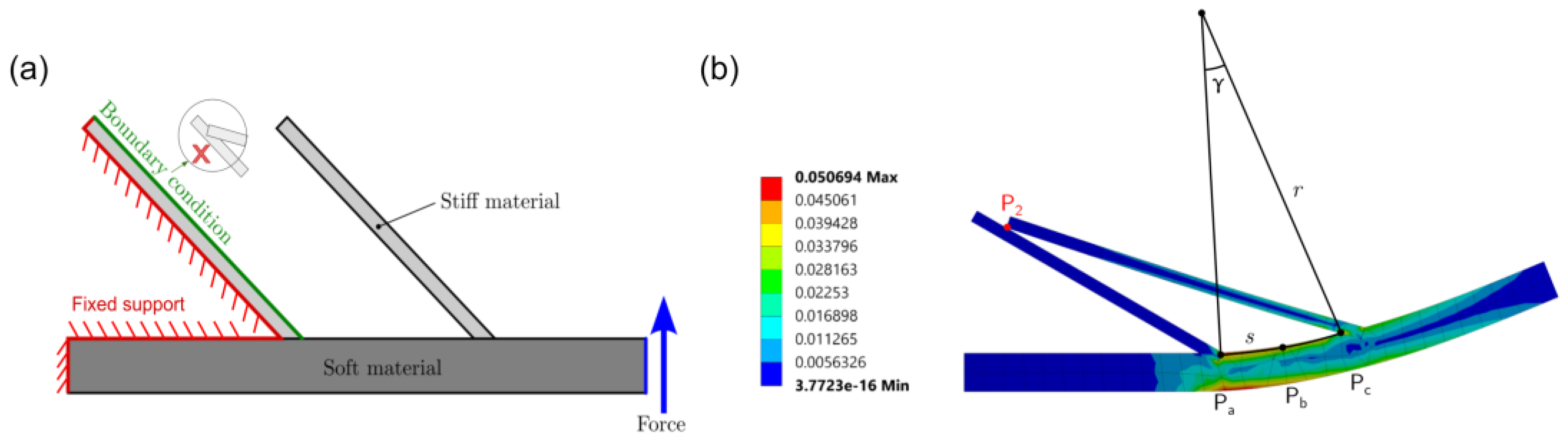
2.2. FEA Model
3. Results
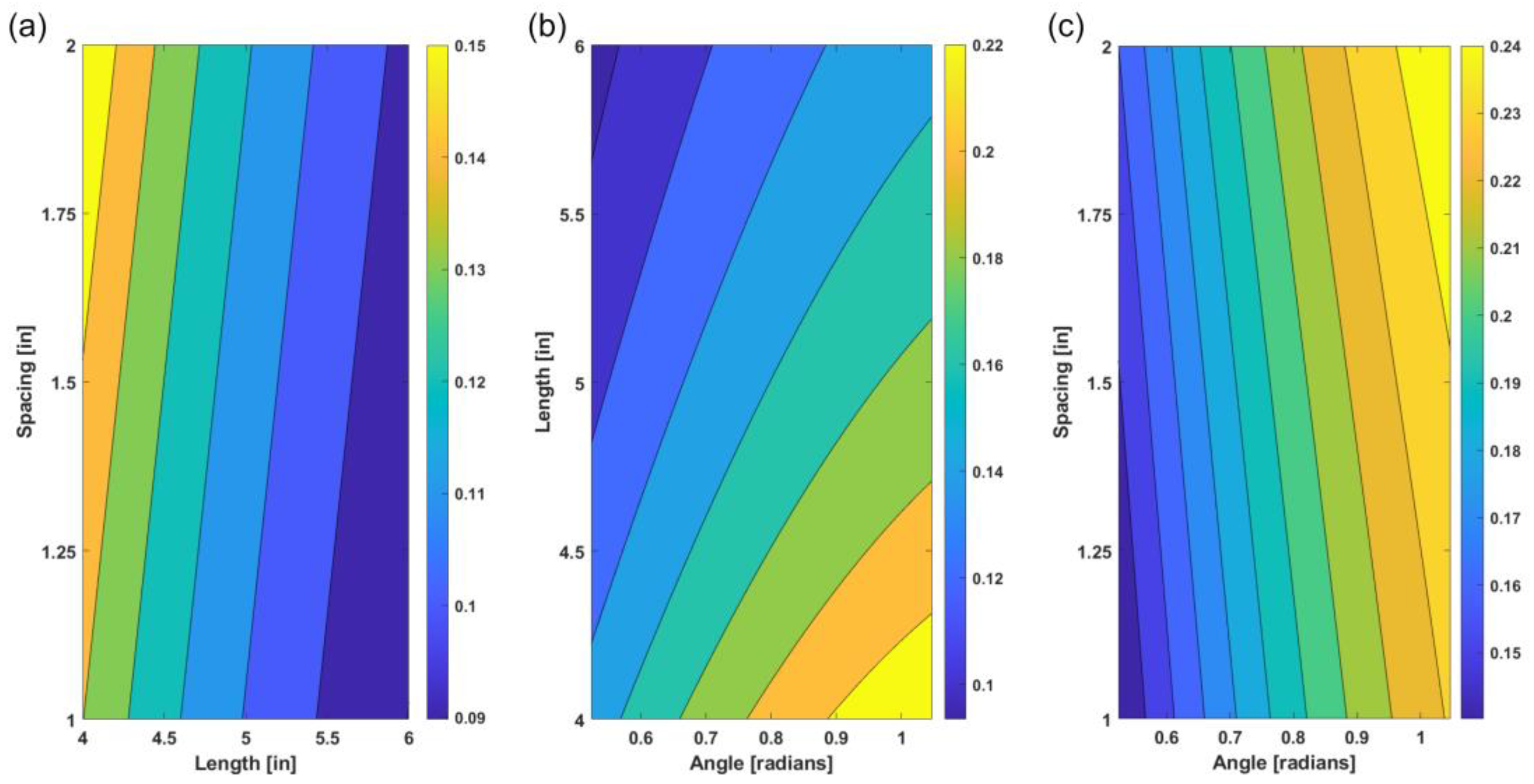
3.1. Geometric Model Result
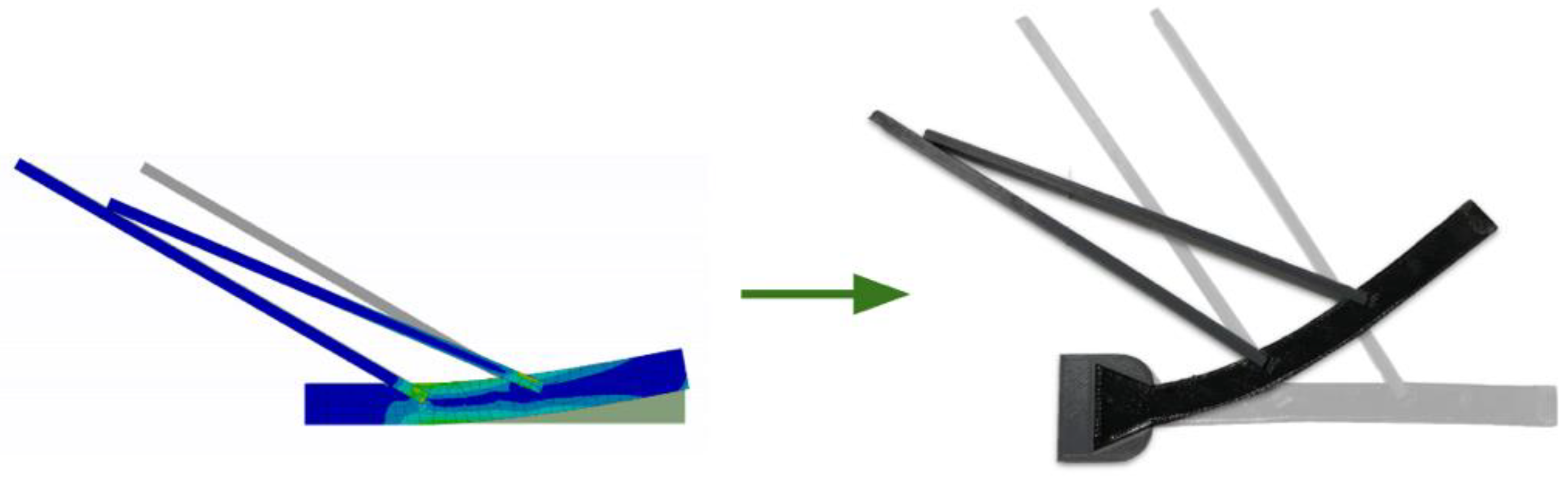
3.2. FEA Model Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Meyers, M.A.; Lin, Y.S.; Olevsky, E.A.; Chen, P.-Y. Battle in the Amazon: Arapaima versus piranha. Adv. Eng. Mater. 2012, 14, B279–B288. [Google Scholar] [CrossRef]
- Yang, Y.; Song, X.; Li, X.; Chen, Z.; Zhou, C.; Zhou, Q.; Chen, Y. Recent progress in biomimetic additive manufacturing technology: From materials to functional structures. Adv. Mater. 2018, 30, 1706539. [Google Scholar] [CrossRef]
- Gu, G.X.; Takaffoli, M.; Buehler, M.J. Hierarchically enhanced impact resistance of bioinspired composites. Adv. Mater. 2017, 29, 1700060. [Google Scholar] [CrossRef]
- Habibi, M.K.; Tam, L.H.; Lau, D.; Lu, Y. Viscoelastic damping behavior of structural bamboo material and its microstructural origins. Mech. Mater. 2016, 97, 184–198. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Ritchie, R.O. On the materials science of nature’s arms race. Adv. Mater. 2018, 30, 1705220. [Google Scholar] [CrossRef] [PubMed]
- Ott, J.; Lazalde, M.; Gu, G.X. Algorithmic-driven design of shark denticle bioinspired structures for superior aerodynamic properties. Bioinspir. Biomim. 2020, 15, 026001. [Google Scholar] [CrossRef]
- Tsai, Y.-Y.; Chiang, Y.; Buford, J.L.; Tsai, M.-L.; Chen, H.-C.; Chang, S.-W. Mechanical and crack propagating behavior of Sierpiński carpet composites. ACS Biomater. Sci. Eng. 2021. [Google Scholar] [CrossRef] [PubMed]
- Velasco-Hogan, A.; Xu, J.; Meyers, M.A. Additive manufacturing as a method to design and optimize bioinspired structures. Adv. Mater. 2018, 30, e1800940. [Google Scholar] [CrossRef] [PubMed]
- Gu, G.X.; Chen, C.-T.; Richmond, D.J.; Buehler, M.J. Bioinspired hierarchical composite design using machine learning: Simulation, additive manufacturing, and experiment. Mater. Horiz. 2018, 5, 939–945. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.-Y.; Li, Q.; Zhao, H.-P.; Zhou, K.; Feng, X.-Q. Functional map of biological and biomimetic materials with hierarchical surface structures. RSC Adv. 2015, 5, 66901–66926. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Dou, X.; Zuo, P.; Liu, J. Hard to be killed: Load-bearing capacity of the leech Hirudo nipponia. J. Mech. Behav. Biomed. Mater. 2018, 86, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Ortiz, C.; Boyce, M.C. Threat-protection mechanics of an armored fish. J. Mech. Behav. Biomed. Mater. 2011, 4, 699–712. [Google Scholar] [CrossRef]
- Yang, W.; Chen, I.H.; Gludovatz, B.; Zimmermann, E.; Ritchie, R.O.; Meyers, M.A. Natural Flexible Dermal Armor. Adv. Mater. 2012, 25, 31–48. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.-Y.; Schirer, J.; Simpson, A.; Nay, R.; Lin, Y.-S.; Yang, W.; Lopez, M.I.; Li, J.; Olevsky, E.A.; Meyers, M. Predation versus protection: Fish teeth and scales evaluated by nanoindentation. J. Mater. Res. 2011, 27, 100–112. [Google Scholar] [CrossRef] [Green Version]
- Chintapalli, R.K.; Mirkhalaf, M.; Dastjerdi, A.K.; Barthelat, F. Fabrication, testing and modeling of a new flexible armor inspired from natural fish scales and osteoderms. Bioinspir. Biomim. 2014, 9, 036005. [Google Scholar] [CrossRef] [Green Version]
- Vernerey, F.J.; Musiket, K.; Barthelat, F. Mechanics of fish skin: A computational approach for bio-inspired flexible composites. Int. J. Solids Struct. 2014, 51, 274–283. [Google Scholar] [CrossRef] [Green Version]
- Vernerey, F.J.; Barthelat, F. Skin and scales of teleost fish: Simple structure but high performance and multiple functions. J. Mech. Phys. Solids 2014, 68, 66–76. [Google Scholar] [CrossRef]
- Funk, N.; Vera, M.; Szewciw, L.J.; Barthelat, F.; Stoykovich, M.P.; Vernerey, F.J. Bioinspired fabrication and characterization of a synthetic fish skin for the protection of soft materials. ACS Appl. Mater. Interfaces 2015, 7, 5972–5983. [Google Scholar] [CrossRef]
- Porter, M.M.; Ravikumar, N.; Barthelat, F.; Martini, R. 3D-printing and mechanics of bio-inspired articulated and multi-material structures. J. Mech. Behav. Biomed. Mater. 2017, 73, 114–126. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Barthelat, F.; Vernereyb, F. Intricate Multiscale Mechanical Behaviors of Natural Fish-Scale Composites. Handbook of Micromechanics and Nanomechanics; Li, S., Gao, X., Eds.; Taylor & Francis Group, LLC: Milton Park, UK, 2013. [Google Scholar]
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Mackey, M.; Zimmermann, E.; Chang, E.H.; Schaible, E.; Qin, Z.; Buehler, M.; Ritchie, R.O.; et al. Protective role of Arapaima gigas fish scales: Structure and mechanical behavior. Acta Biomater. 2014, 10, 3599–3614. [Google Scholar] [CrossRef] [PubMed]
- Browning, A.; Ortiz, C.; Boyce, M.C. Mechanics of composite elasmoid fish scale assemblies and their bioinspired analogues. J. Mech. Behav. Biomed. Mater. 2013, 19, 75–86. [Google Scholar] [CrossRef]
- Zhu, D.; Fuentes Ortega, C.; Motamedi, R.; Szewciw, L.; Vernerey, F.; Barthelat, F. Structure and mechanical performance of a “modern” fish scale. Adv. Eng. Mater. 2012, 14, B185–B194. [Google Scholar] [CrossRef]
- Zhu, D.; Szewciw, L.; Vernerey, F.; Barthelat, F. Puncture resistance of the scaled skin from striped bass: Collective mechanisms and inspiration for new flexible armor designs. J. Mech. Behav. Biomed. Mater. 2013, 24, 30–40. [Google Scholar] [CrossRef]
- Ali, H.; Ebrahimi, H.; Ghosh, R. Frictional damping from biomimetic scales. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, R.; Ebrahimi, H.; Vaziri, A. Non-ideal effects in bending response of soft substrates covered with biomimetic scales. J. Mech. Behav. Biomed. Mater. 2017, 72, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Stephen, J. Contact Mechanics of Fish Scale Inspired Exoskeletal Components on a Nonlinear Elastic Substrate. Master’s Thesis, College of Engineering and Computer Science, University of Central Florida, Orlando, FL, USA, 2020. [Google Scholar]
- Ali, H.; Ebrahimi, H.; Ghosh, R. Bending of biomimetic scale covered beams under discrete non-periodic engagement. Int. J. Solids Struct. 2019, 166, 22–31. [Google Scholar] [CrossRef] [Green Version]
- Tymrak, B.; Kreiger, M.; Pearce, J.M. Mechanical properties of components fabricated with open-source 3-D printers under realistic environmental conditions. Mater. Des. 2014, 58, 242–246. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, R.; Ebrahimi, H.; Vaziri, A. Contact kinematics of biomimetic scales. Appl. Phys. Lett. 2014, 105, 233701. [Google Scholar] [CrossRef] [Green Version]
- Demir, K.G.; Zhang, Z.; Yang, J.; Gu, G.X. Computational and Experimental Design Exploration of 3D-Printed Soft Pneumatic Actuators. Adv. Intell. Syst. 2020, 2, 2000013. [Google Scholar] [CrossRef] [Green Version]
- Vangelatos, Z.; Gu, G.X.; Grigoropoulos, C.P. Architected metamaterials with tailored 3D buckling mechanisms at the microscale. Extrem. Mech. Lett. 2019, 33, 100580. [Google Scholar] [CrossRef]
- Guo, N.; Leu, M.C. Additive manufacturing: Technology, applications and research needs. Front. Mech. Eng. 2013, 8, 215–243. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, Z.; Ott, J.; Gu, G.X. Precise localization and semantic segmentation detection of printing conditions in fused filament fabrication technologies using machine learning. Addit. Manuf. 2020, 37, 101696. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer: New York, NY, USA, 2021; Volume 17. [Google Scholar]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.; Wang, C.C.; Shin, Y.C.; Zhang, S.; Zavattieri, P. The status, challenges, and future of additive manufacturing in engineering. Comput. Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, Z.; Demir, K.; Gu, G.X. Machine Learning for Advanced Additive Manufacturing. Matter 2020, 3, 1541–1556. [Google Scholar] [CrossRef]
- Ghimire, A.; Tsai, Y.-Y.; Chen, P.-Y.; Chang, S.-W. Tunable interface hardening: Designing tough bio-inspired composites through 3D printing, testing, and computational validation. Compos. Part B Eng. 2021, 215, 108754. [Google Scholar] [CrossRef]
- Yang, C.; Vora, H.D.; Chang, Y. Behavior of auxetic structures under compression and impact forces. Smart Mater. Struct. 2018, 27, 025012. [Google Scholar] [CrossRef]
- Reppel, T.; Weinberg, K. Experimental determination of elastic and rupture properties of printed Ninjaflex. Technische Mechanik 2018, 38, 104–112. [Google Scholar]
- Léger, J.-C. Menger curvature and rectifiability. Ann. Math. 1999, 149, 831–869. [Google Scholar] [CrossRef]
- Chen, C.-T.; Chrzan, D.C.; Gu, G.X. Nano-topology optimization for materials design with atom-by-atom control. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Gu, G.X. Machine learning-based detection of graphene defects with atomic precision. Nano Micro Lett. 2020, 12, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.; Chen, G.; Li, T.; Chen, Q.; Li, S. A deep learning-based computational algorithm for identifying damage load condition: An artificial intelligence inverse problem solution for failure analysis. Comput. Modeling Eng. Sci. 2018, 117, 287–307. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Yang, C.; Kim, Y.; Gu, G.X.; Ryu, S. Designing an adhesive pillar shape with deep learning-based optimization. ACS Appl. Mater. Interfaces 2020, 12, 24458–24465. [Google Scholar] [CrossRef] [PubMed]
- Theodoridis, S. Machine Learning: A Bayesian and Optimization Perspective; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
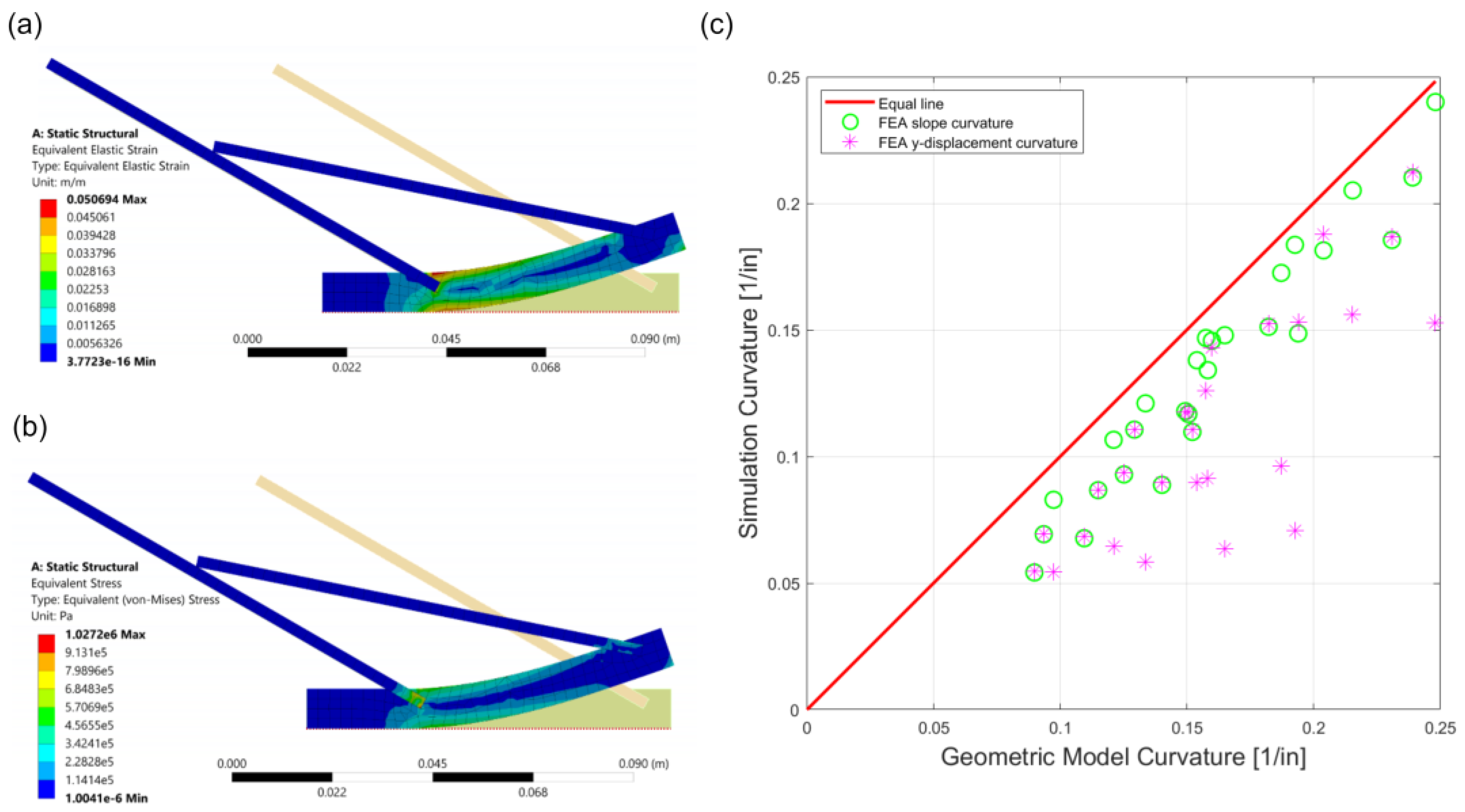
| Geometric Model | FEA by Slope | FEA by y-Displacement | |
|---|---|---|---|
| Curvature [1/in] | 0.1599 | 0.1457 | 0.1430 |
| Percent Error [%] | - | −8.880% | −10.57% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, A.; Thind, K.; Demir, K.G.; Gu, G.X. Modeling Bioinspired Fish Scale Designs via a Geometric and Numerical Approach. Materials 2021, 14, 5378. https://doi.org/10.3390/ma14185378
Chen A, Thind K, Demir KG, Gu GX. Modeling Bioinspired Fish Scale Designs via a Geometric and Numerical Approach. Materials. 2021; 14(18):5378. https://doi.org/10.3390/ma14185378
Chicago/Turabian StyleChen, Ailin, Komal Thind, Kahraman G. Demir, and Grace X. Gu. 2021. "Modeling Bioinspired Fish Scale Designs via a Geometric and Numerical Approach" Materials 14, no. 18: 5378. https://doi.org/10.3390/ma14185378
APA StyleChen, A., Thind, K., Demir, K. G., & Gu, G. X. (2021). Modeling Bioinspired Fish Scale Designs via a Geometric and Numerical Approach. Materials, 14(18), 5378. https://doi.org/10.3390/ma14185378








